1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2022

Известия РАН. Механика жидкости и газа, 2022, № 1, стр. 57-68

МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ ГИДРОФИЗИЧЕСКИХ ПРОЦЕССОВ НА ШЕЛЬФЕ ЯПОНСКОГО МОРЯ

В. Ю. Ляпидевский a, *, Ф. Ф. Храпченков b, **, А. А. Чесноков a, ***, И. О. Ярощук b, ****

a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

b Тихоокеанский океанологический институт им. В.И. Ильичева ДВО РАН
Владивосток, Россия

* E-mail: liapid@hydro.nsc.ru
** E-mail: fedi@poi.dvo.ru
*** E-mail: chesnokov@hydro.nsc.ru
**** E-mail: yaroshchuk@poi.dvo.ru

Поступила в редакцию 24.07.2021
После доработки 21.09.2021
Принята к публикации 21.09.2021

Полный текст (PDF)

Аннотация

Нелинейные уравнения многослойной мелкой воды в приближении Буссинеска применены для моделирования нестационарных гидрофизических процессов в шельфовой зоне приливного моря. Выполнен расчет вертикального распределения температуры и горизонтальной компоненты скорости вдоль прямолинейной трассы на основе данных о вариации температуры на заданных горизонтах, полученных на одной из донных станций. Результаты численного моделирования верифицированы с использованием данных других контрольных станций, расположенных вдоль рассматриваемой трассы. Показано, что многослойная модель качественно воспроизводит структуру наблюдаемого волнового пакета, а уравнения двухслойного течения описывают динамику центральной части термоклина даже в том случае, когда стратификация существенно отличается от двухслойной. Сравнение результатов расчета с натурными данными позволяет сделать вывод о том, что гипотеза о квазидвумерном характере течения на шельфе, лежащая в основе применяемого подхода, соответствует реальности.

Ключевые слова: многослойная мелкая вода, внутренние волны, волновой бор, натурный эксперимент

Гидрофизические процессы в шельфовой зоне моря характеризуются большой пространственной и временной изменчивостью. Неоднородное вертикальное распределение плотности связано как с распреснением прибрежных вод, так и неравномерным прогревом верхних слоев, особенно в осенне-летний период. Стратификация существенно влияет на структуру разномасштабных течений и формирование нелинейных внутренних волн, регистрируемых в шельфовой зоне моря [1, 2]. Особое внимание исследователей привлекают внутренние боры, регулярно наблюдаемые в стратифицированных прибрежных водах в виде резкого вертикального смещения пикноклина с генерацией на фронте возмущения цуга внутренних волн [3–6].

Для описания структуры внутренних волн большой амплитуды широко применяются различные модификации уравнений Кортвега–де Фриза [7–9] и многослойные модели теории мелкой воды [10–12], учитывающие совместное влияние нелинейных и дисперсионных эффектов. Распространение и трансформация уединенных волн в трехслойной мелкой воде, в том числе, несимметричных внутренних волн второй моды, исследованы в недавних работах [13, 14]. Дисперсионная модель трехслойного течения стратифицированной жидкости с гидростатическим промежуточным слоем и некоторые ее упрощения использованы в [15, 16] для описания волновых процессов в шельфовой зоне моря. Более общая модель второго приближения теории длинных волн с произвольным числом гидростатических слоев, а также ее аппроксимация квазилинейными уравнениями первого порядка, выведены и верифицированы в [17, 18]. Эта многослойная модель будет использована в данной работе для описания гидрофизических процессов в шельфовой зоне приливного моря.

Одним из эффективных способов регистрации параметров внутренних волн и определения структуры волновых фронтов является применение термогирлянд, позволяющих регистрировать изменение температуры на заданных горизонтах и восстанавливать заглубления рассматриваемых изотерм в окрестности измерительного комплекса как функцию времени [19, 20]. Применение нескольких измерительных станций, расположенных на некотором расстоянии друг от друга, дает возможность идентифицировать определенные волновые структуры, например, отдельные уединенные волны или фронты распространяющихся возмущений, и отследить их фазовые и амплитудные характеристики, а также найти среднюю скорость распространения возмущений [21]. Полученная информация является основой для верификации математических моделей распространения внутренних волн. Попытки восстановить фазовые и амплитудные характеристики внутри волнового пакета при прохождении внутреннего бора на некотором расстоянии от измерительного комплекса предприняты в [8, 15, 16]. Сравнения с натурными измерениями, выполненными на конкретных станциях, показали, что удовлетворительных результатов можно достичь только на относительно небольших пространственных масштабах (порядка одного километра для шельфа Японского моря) из-за интенсивного взаимодействия отдельных волн внутри волнового пакета.

В данной работе исследуется возможность восстановления поля температуры и скорости в некоторой области шельфовой зоны по модифицированным уравнениям многослойной мелкой воды [18] на основе данных одного или нескольких измерительных комплексов. Физическая постановка задачи близка к рассматриваемой в [15, 16], однако речь идет о распределении фоновых гидрофизических характеристик без выделения внутренней структуры отдельных волновых пакетов. Такой подход оправдан, если основное поле внутренних волн является квазидвумерным и преобладает однонаправленное распространение возмущений от свала глубин в сторону берега. Результаты работы подтверждают эту гипотезу, по крайней мере, для выбранного времени проведения натурного эксперимента (сентябрь–октябрь 2019).

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Система уравнений, описывающая распространение нелинейных волн в многослойной стратифицированной мелкой воде с учетом негидростатического распределения давления, выведена в [12]. Эти уравнения для двухслойных течений широко используются для моделирования уединенных внутренних волн [11]. В данной работе рассматривается упрощенная версия многослойной модели [12], в которой негидростатические эффекты учитываются только в верхнем (нижнем) слое. В приближении Буссинеска ($0 < ({{\rho }_{i}} - {{\rho }_{1}}){\text{/}}{{\rho }_{1}} \ll 1$, ${{\rho }_{i}}$ – плотность жидкости в i-м слое, ${{\rho }_{{i + 1}}}$ > ρi) для течений над плавно меняющимся рельефом дна многослойные уравнения [12] принимают вид [17, 18]

(1.1)
$\begin{array}{*{20}{c}} {{{h}_{{it}}} + {{{({{u}_{i}}{{h}_{i}})}}_{x}} = 0,\quad (i = 1, \ldots ,n)} \\ {{{u}_{{1t}}} + {{{\left( {\frac{{u_{1}^{2}}}{2} + \Pi + \frac{{{{\varepsilon }^{2}}{{h}_{1}}}}{3}\frac{{{{d}^{2}}{{h}_{1}}}}{{d{{t}^{2}}}} + \frac{{{{\varepsilon }^{2}}}}{6}{{{\left( {\frac{{d{{h}_{1}}}}{{dt}}} \right)}}^{2}}} \right)}}_{x}} = {{f}_{1}},} \\ {{{u}_{{it}}} + {{{(u_{i}^{2}{\text{/}}2 + {{p}_{i}})}}_{x}} = - {{b}_{i}}{{Z}_{x}} + {{f}_{i}},\quad (i = 2, \ldots ,n).} \end{array}$

Здесь ${{u}_{i}}$ и ${{h}_{i}}$ – скорость и толщина $i$-го слоя жидкости, уравнение $z = Z(x)$ задает рельеф дна, ${{b}_{i}} = g({{\rho }_{i}} - {{\rho }_{1}}){\text{/}}{{\rho }_{1}} \geqslant 0$ – коэффициенты плавучести, $g$ – ускорение силы тяжести, ${{\rho }_{1}}\Pi $ – модифицированное давление на верхней границе, $\varepsilon $ – длинноволновый параметр (отношение полной глубины канала к характерной длине волны). Нумерация слоев ведется сверху вниз. Переменные ${{p}_{i}}$ и оператор $d{\text{/}}dt$ имеют вид

(1.2)
${{p}_{i}} = \Pi + \sum\limits_{j = 2}^{i - 1} {{{b}_{j}}} {{h}_{j}} + {{b}_{i}}\sum\limits_{j = i}^n {{{h}_{j}}} ,\quad \frac{d}{{dt}} = \frac{\partial }{{\partial t}} + {{u}_{1}}\frac{\partial }{{\partial x}}.$

Функции fi задают трение на границах слоев и при учете диссипативных эффектов (постоянная ${{c}_{f}} > 0$) определяются следующим образом

(1.3)
$\begin{array}{*{20}{c}} {{{f}_{1}} = - \frac{{{{c}_{f}}}}{{{{h}_{1}}}}({{u}_{1}} - {{u}_{2}})\left| {{{u}_{1}} - {{u}_{2}}} \right|,\quad {{f}_{n}} = - \frac{{{{c}_{f}}}}{{{{h}_{n}}}}({{u}_{n}} - {{u}_{{n - 1}}})\left| {{{u}_{n}} - {{u}_{{n - 1}}}} \right|,} \\ {{{f}_{i}} = - \frac{{{{c}_{f}}}}{{{{h}_{i}}}}\left( {({{u}_{i}} - {{u}_{{i - 1}}})\left| {{{u}_{i}} - {{u}_{{i - 1}}}} \right| + ({{u}_{i}} - {{u}_{{i + 1}}})\left| {{{u}_{i}} - {{u}_{{i + 1}}}} \right|} \right),\quad (i = 2,\; \ldots ,\;n - 1).} \end{array}$

Диссипация энергии при распространении внутренних волн в многослойной среде в основном определяется перемешиванием и генерацией коротких волн на внутренних границах течения. Трение о дно также оказывает влияние на эволюцию придонных внутренних волн и может быть включено в модель соответствующим образом.

Необходимо отметить, что в приближении Буссинеска верхняя граница фиксирована и полный расход жидкости Q является функцией времени:

(1.4)
$H + Z(x) = {{H}_{0}} = {\text{const}},\quad H = \sum\limits_{i = 1}^n {{{h}_{i}}} ,\quad Q(t) = \sum\limits_{i = 1}^n {{{u}_{i}}{{h}_{i}}} .$

Систему (1.1) дополним соотношениями (1.4), которые позволяют выразить переменные ${{u}_{n}}$ и ${{h}_{n}}$ через остальные искомые функции ${{u}_{i}}$, ${{h}_{i}}$ ($i = 1,\; \ldots ,\;n - 1$).

Для численного моделирования распространения волновых возмущений в многослойной жидкости систему (1.1) удобно аппроксимировать квазилинейными уравнениями первого порядка. Следуя [10, 18], введем новые переменные $\eta $ и ${v}$ (“мгновенные” толщина и скорость жидкости верхнего слоя) по правилу

$\frac{{d\eta }}{{dt}} = {v},\quad \frac{{d{v}}}{{dt}} = \frac{{\alpha b}}{{{{h}_{1}}}}({{h}_{1}} - \eta ),$
где $\alpha > 0$ безразмерный параметр и $b = {{b}_{n}}$. Заменим дисперсионные члены в уравнении импульса верхнего слоя системы (1.1) следующим образом
$\frac{{d{{h}_{1}}}}{{dt}} \to {v},\quad \frac{{d_{{}}^{2}{{h}_{1}}}}{{d{{t}^{2}}}} \to \frac{{\alpha b}}{{{{h}_{1}}}}({{h}_{1}} - \eta )$
и переходом к переменным ${{s}_{i}} = {{u}_{{i + 1}}} - {{u}_{i}}$ исключим функцию $\Pi $ из уравнений движения. В результате получим замкнутую неоднородную систему законов сохранения [18] для определения $2n$ искомых функций $U = (\eta ,{v},{{s}_{1}},\; \ldots ,\;{{s}_{{n - 1}}},{{h}_{1}},\; \ldots ,\;{{h}_{{n - 1}}})$:

(1.5)
$\begin{array}{*{20}{c}} {{{{({{h}_{1}}\eta )}}_{t}} + {{{({{u}_{1}}{{h}_{1}}\eta )}}_{x}} = {v}{{h}_{1}},\quad {{{({v}{{h}_{1}})}}_{t}} + {{{({{u}_{1}}{v}{{h}_{1}})}}_{x}} = \alpha b({{h}_{1}} - \eta ),} \\ {{{s}_{{1t}}} + {{{\left( {\frac{{{{u}_{2}} + {{u}_{1}}}}{2}{{s}_{1}} - {{b}_{2}}{{h}_{1}} - \frac{{\alpha b{{\varepsilon }^{2}}}}{3}({{h}_{1}} - \eta ) - \frac{{{{\varepsilon }^{2}}{{{v}}^{2}}}}{6}} \right)}}_{x}} = {{\varphi }_{1}},} \\ {{{s}_{{it}}} + {{{\left( {\frac{{{{u}_{{i + 1}}} + {{u}_{i}}}}{2}{{s}_{i}} - ({{b}_{{i + 1}}} - {{b}_{i}})\sum\limits_{j = 1}^i {{{h}_{j}}} } \right)}}_{x}} = {{\varphi }_{i}},\quad (i = 2,\; \ldots ,\;n - 1)} \\ {{{h}_{{it}}} + {{{({{u}_{i}}{{h}_{i}})}}_{x}} = 0\quad (i = 1,\; \ldots ,\;n - 1).} \end{array}$

Здесь

$\begin{array}{*{20}{c}} {{{u}_{{i + 1}}} = {{s}_{i}} + {{u}_{i}},\quad {{u}_{1}} = \frac{1}{H}\left( {Q - \sum\limits_{i = 2}^n {{{h}_{i}}} \sum\limits_{j = 1}^{i - 1} {{{s}_{j}}} } \right),} \\ {{{h}_{n}} = {{H}_{0}} - Z - \sum\limits_{i = 1}^{n - 1} {{{h}_{i}}} ,\quad {{\varphi }_{i}} = {{f}_{{i + 1}}} - {{f}_{i}}.} \end{array}$

Неоднородные законы сохранения (1.5) будут использоваться далее для проведения численного моделирования распространения нестационарных внутренних волн.

При $n = 2$ (двухслойная жидкость) система (1.5) упрощается, что позволяет в явном виде определить скорости характеристик. При этом гиперболичность уравнений двухслойного течения обеспечивается условием

$\alpha > \frac{3}{{{{\varepsilon }^{2}}}}\left( {\frac{{{{{({{u}_{2}} - {{u}_{1}})}}^{2}}}}{{bH}} - 1} \right).$

В общем случае можно утверждать, что система (1.5) является гиперболической при небольшом сдвиге скорости в слоях [18]. Отметим, что при $\varepsilon = 0$, $\alpha = 0$ модели (1.1) и (1.5) редуцируются к системе уравнений многослойной мелкой воды для гидростатических течений в приближении Буссинеска.

Согласно [10] при $\alpha \to \infty $ решения системы (1.5) аппроксимируют решения исходной дисперсионной модели (1.1). Очевидно, что увеличение параметра $\alpha $ приводит к увеличению скоростей характеристик и замедлению численных расчетов в силу условия Куранта. Выполненные в [14, 18] сравнения решений дисперсионных уравнений и их аппроксимаций показывают, что уже при $\alpha \sim 10$ уравнения первого порядка достаточно точно воспроизводят форму, по крайней мере, головной волны. В последнее время предложенный в [10] метод аппроксимации дисперсионных уравнений теории волн квазилинейными системами первого порядка путем введения дополнительных ‘мгновенных’ переменных получил широкое распространение [14, 22, 23]. Это объясняется простотой численной реализации гиперболических систем законов сохранения, сравнительно невысокой трудоемкостью вычислений и понятной постановкой граничных условий, связанных с характеристиками уравнений движения.

Для течений над ровным дном ($Z = 0$) рассматриваемая модель инвариантна относительно преобразования Галилея, поэтому решения в классе бегущих волн (искомые функции зависят от переменной $\zeta = x - Dt$, $D = {\text{const}}$) эквивалентны стационарным решениям ($D = 0$), определяемым системой

(1.6)
$\begin{array}{*{20}{c}} {({{u}_{i}}{{h}_{i}}){\text{'}} = 0,\quad (u_{i}^{2}{\text{/}}2 + {{p}_{i}}){\text{'}} = {{f}_{i}},\quad (i = 2,\; \ldots ,\;n),} \\ {(u_{1}^{2}{\text{/}}2 + \Pi + \alpha {{\varepsilon }^{2}}b({{h}_{1}} - \eta ){\text{/}}3 + {{{v}}^{2}}{\text{/}}6){\text{'}} = {{f}_{1}},\quad {{u}_{1}}\eta {\text{'}} = {v},} \\ {{{u}_{1}}{v}{\kern 1pt} ' = \alpha b({{h}_{1}} - \eta ){\text{/}}{{h}_{1}},\quad \sum\limits_{i = 1}^n {{h}_{i}} = {{H}_{0}},\quad \sum\limits_{i = 1}^n {{u}_{i}}{{h}_{i}} = Q.} \end{array}$

Здесь штрих означает дифференцирование по переменной $x$, функции ${{p}_{i}}$ и ${{f}_{i}}$ определены формулами (1.2), (1.3). Для построения решений обыкновенных дифференциальных уравнений (1.6) применяется изложенный в [18] алгоритм приведения этой системы к разрешенному относительно производных виду. Условия при $x = {{x}_{0}}$, обеспечивающие примыкание нетривиального решения уравнений движения к постоянному потоку ${{h}_{i}} = h_{i}^{0}$, ${{u}_{i}} = u_{i}^{0}$, также сформулированы в [18].

2. НАТУРНЫЙ ЭКСПЕРИМЕНТ

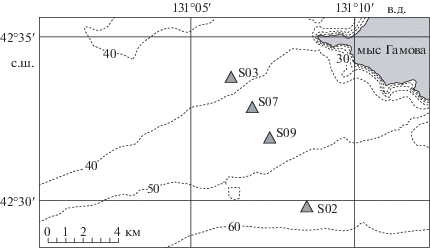
Исследования нестационарных волновых процессов на гидрофизическом полигоне Тихоокеанского океанологического института им. В.И. Ильичева ДВО РАН проводятся в течение ряда лет [19, 20]. Непрерывный мониторинг в различных точках шельфовой зоны на глубинах от 20 до 80 м осуществляется в летне-осенний период на протяжении 1–4 нед. В работе использованы данные измерений, полученные в октябре 2019 г. для последовательности донных станций S02, S09, S07 и S03, расположенных на линейной трассе (как показано на рис. 1). Из рисунка видно, что трасса пересекает изобаты практически по нормали. Расстояние между станциями: S02 и S09 – 4100 м, S09 и S07 – 1987 м, S07 и S03 – 1881 м. Глубина на соответствующих донных станциях: S02 – 55 м, S09 – 47.5 м, S07 – 42.5 м, S03 – 39 м. Достаточное количество датчиков на термогирляндах (36–37 датчиков через 1 м на S02, S09, S03 и 12 датчиков через 3 м на S07) позволяет получить детальную зависимость положения выбранных изотерм как функцию времени. Заметим, что в районе гидрофизического полигона соленость меняется незначительно. Поэтому в летне-осенний период основной вклад в стратификацию прибрежных вод вносит вертикальное распределение температуры.

Рис. 1.

Карта-схема района натурных наблюдений в северо-западной части залива Петра Великого с указанием места расположения донных станций S02, S03, S07 и S09. Пунктирные линии – изобаты, числа на них соответствуют глубине в метрах.

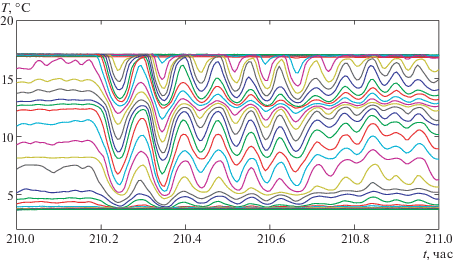
Данные, полученные со всех донных станций, синхронизованы по времени. Начало отсчета – 12:00, 6 октября 2019 г. На рис. 2 показан фрагмент записи распределения температуры в градусах Цельсия на заданном горизонте. График демонстрирует изменение температуры на различных горизонтах при прохождении волнового бора. Такое представление данных удобно для визуализации внутренних волн, но для сравнения с результатами численного моделирования необходимо рассчитать нестационарное распределение изотерм в окрестности измерительной станции на основе полученных данных. Естественно, рассматриваемые изотермы должны представлять эволюцию основного термоклина, связанную с распространением внутренних волн. Количество изотерм, необходимое для сравнения с численными результатами, зависит от используемой математической модели. В двухслойных моделях выбирается изотерма, соответствующая центральной части термоклина. При использовании уравнений многослойного течения появляется возможность учесть как толщину, так и реальное распределение температуры внутри термоклина.

Рис. 2.

Зависимость температуры на различных горизонтах от времени, полученная на станции S03 в октябре 2019 г.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Численное моделирование распространения внутренних волн проводится на основе уравнений (1.5) с использованием простой и надежной TVD схемы второго порядка аппроксимации [24]. Расчетная область совпадает с участком трассы, направленной в сторону береговой линии от выбранной станции и включает одну или несколько других станций в качестве контрольных. Число узлов $N$ по пространственной переменной $x$ варьируется от 500 до 1000, сетка равномерная. Шаг по времени определяется из условия Куранта. Число слоев $n$ в уравнениях (1.5) берется равным шести или двум. Все расчеты проведены при $\alpha = 10$ и $\varepsilon = 1$. Коэффициент трения между слоями ${{c}_{f}} = 0.006$ (либо равен нулю при игнорировании диссипативных эффектов). Рельеф дна аппроксимируется функцией

(3.1)
$Z(x) = a(1 - exp( - kx)),$
где параметры $a$ и $k$ варьируются в зависимости от выбора расчетной области так, чтобы глубины основной и контрольных станций соответствовали данным натурного эксперимента.

В качестве граничных условий на левой границе расчетной области $x = 0$ используются данные о структуре термоклина на одной из донных станций, что позволяет определить толщины стратифицированных слоев $h_{i}^{l}(t)$ и задать условия: ${{h}_{i}}(t,0) = h_{i}^{l}(t)$. При этом натурные данные осредняются на небольшом временном интервале (от 1 до 10 мин). Такое осреднение позволяет воспроизводить особенности волновых процессов в достаточно широком диапазоне параметров течения. Скорости жидкости в слоях на левой границе определяются на основе линеаризованных соотношений на разрыве по правилу:

$u_{i}^{l}(t) = ({{h}_{i}}(t,{{x}_{1}}){{u}_{i}}(t,{{x}_{1}}) + \lambda (h_{i}^{l} - {{h}_{i}}(t,{{x}_{1}}))){\text{/}}h_{i}^{l},$
где $\lambda $ – приближенно вычисленная максимальная скорость характеристик. Условия для ‘мгновенных’ переменных $\eta $ и $v$ имеют вид:

${{\eta }^{l}}(t) = h_{1}^{l}(t),\quad {{{v}}^{l}}(t) = \frac{{(\lambda - {{u}_{1}}(t,{{x}_{1}})){{h}_{1}}(t,{{x}_{1}}){v}(t,{{x}_{1}})}}{{(\lambda - u_{1}^{l})h_{1}^{l}}}.$

С использованием данных при $x = 0$ вычисляются потоки на границе первой ячейки с центром в точке $x = {{x}_{1}}$. На правой границе расчетной области задаются ‘мягкие’ граничные условия ${{U}_{N}} = {{U}_{{N - 1}}}$, обеспечивающие отсутствие отраженных волн (${{U}_{i}}$ – значения искомых функций в узловой точке ${{x}_{i}}$).

В начальный момент времени $t = 0$ в узловых точках расчетного интервала $[0,L]$ задаются постоянные толщины слоев ${{h}_{i}} = h_{i}^{l}(0)$ и нулевые скорости ${{u}_{i}} = 0$, а также $\eta = h_{1}^{l}(0)$ и ${v} = 0$. Заметим, что данные о вертикальном распределении температуры и скорости на трассе между станциями, как правило, отсутствуют. Поэтому как пространственное распределение температуры в слоях, так и горизонтальные компоненты скорости вдоль трассы в начальный момент могут задаваться произвольно. Но через некоторое время, достаточное для прохождения возмущений с левой границы через всю расчетную область, начальные данные “забываются” и построенное численное решение можно сравнивать с натурными данными, полученными на контрольных станциях.

Как отмечалось выше, при постановке граничных условий используется предположение о квазидвумерном характере распространения волновых фронтов в шельфовой зоне. Эта гипотеза может быть подтверждена сравнением натурных данных и численных расчетов. Для корректной постановки граничных условий в многослойных моделях требуется информация о скоростях распространения высших мод (о характеристиках в области гиперболичности). Упрощенный подход, используемый в этой работе, состоит в том, что как и в случае стратифицированных течений с небольшим сдвигом скорости в слоях, для многослойной модели (1.5) достаточно задать на границе толщины каждого из слоев как функцию времени. Для двухслойных течений такой подход является корректным и для конечного сдвига горизонтальной скорости в слоях, так как гиперболичность системы уравнений (1.5) при $n = 2$ и докритический режим течения во всей рассматриваемой области может быть обеспечен выбором параметра $\alpha $. Поэтому для расчетов, охватывающих достаточно большой временной интервал, двухслойная модель является более предпочтительной.

3.1. Верификация многослойной модели

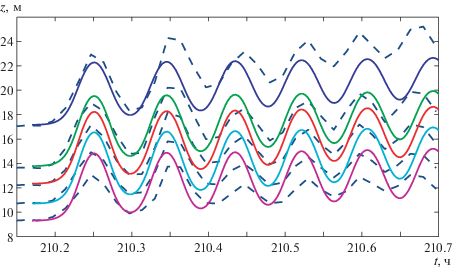
На рис. 3 показаны результаты численного моделирования волновых процессов на участке между станциями S07 и S03, полученные по многослойным уравнениям (1.5). В качестве граничных условий для уравнений движения задавались толщины слоев, соответствующие изотермам с интервалом $\Delta T = 2$°С для диапазона температур 6–14°С на станции S07. Аналогичные изотермы, полученные на станции S03, показаны тонкими сплошными линиями на рис. 3а. Толстыми сплошными кривыми изображены границы раздела между слоями, полученные по многослойной модели (1.5) при $n = 6$. Пунктиром показаны результаты расчета при двухслойном представлении течения (уравнения (1.5) при n = 2). Результаты расчета изменения скорости в слоях в зависимости от времени на станции S03 представлены на рис. 3б. В данном случае плавучести для 6-слойной модели задавались по правилу ${{b}_{i}} = 0.02(1 - 0.2(6 - i))$ м/с2 ($i = 2,\; \ldots ,\;6$), для двухслойной – $b = 0.02$ м/с2. Коэффициенты в формуле рельефа дна (3.1) – $a = 8.5$ м и $k = 2.8 \times {{10}^{{ - 4}}}$ м–1, что обеспечивает требуемый перепад глубины 3.5 м на расстоянии 1881 м между станциями.

Рис. 3.

Результаты расчета эволюции течения на промежутке 14 ч на станции S03 по данным станции S07: а – границы раздела слоев (толстые линии – расчет по 6-слойной модели (1.5), пунктир – по двухслойным уравнениям, тонкие кривые – данные натурных измерений станции S03); б – скорость жидкости в слоях 1–6.

На выбранном временном интервале 208–218 ч возмущения термоклина соответствуют прохождению двух придонных волновых боров. Более детальная структура первого бора представлена на рис. 2, показывающем изменение температуры на различных горизонтах. Из рис. 3 следует, что многослойная модель качественно воспроизводит осредненную структуру наблюдаемого волнового пакета, а двухслойные модели описывают динамику центральной части термоклина даже в том случае, когда стратификация существенно отличается от двухслойной.

Для того, чтобы численно воспроизвести структуру короткопериодных волн, генерируемых на фронте внутреннего бора (рис. 2), необходимо использовать второе приближение теории многослойной мелкой воды [15, 16]. Однако для моделирования процессов распространения более длинных нелинейных волн можно использовать и первое приближение, соответствующее гидростатическому распределению давления во всех слоях. При этом основная динамика развития гидродинамических процессов в шельфовой зоне все еще воспроизводится достаточно детально и результаты расчетов могут быть использованы для построения фоновой картины при изучении распространения короткопериодных внутренних волн и вихревых образований небольшого масштаба.

На рис. 3б показано, как меняются скорости на правой границе, соответствующей станции S03. Линии 1, 6 представляют скорости жидкости в приповерхностном и придонном слоях, кривые 2–5 – изменение скорости во внутренних слоях термоклина. Следует отметить, что перед внутренним бором, изображенном на рис. 3а ($t = 210$), толщина нижнего слоя уменьшается и скорость в этом слое становится отрицательной. Такое поведение изотерм соответствует механизму генерации придонного волнового бора при распаде внутреннего прилива над шельфом ([16], рис. 2). Таким образом, внутренний бор распространяется в стратифицированной среде со сдвигом скорости в слоях и скорость его распространения может зависеть от этого сдвига. Другой характерной особенностью прохождения придонного внутреннего бора является изменение направления течения в слоях.

Отметим, что учет трения при расчетах на непродолжительных промежутках времени несущественно влияет на результат, поэтому в данном тесте коэффициент ${{c}_{f}} = 0$. В проводимом ниже моделировании волновых процессов на промежутках времени в несколько суток диссипативные эффекты учитываются (${{c}_{f}} = 0.006$).

3.2. Расчеты по двухслойной модели на длительном интервале времени

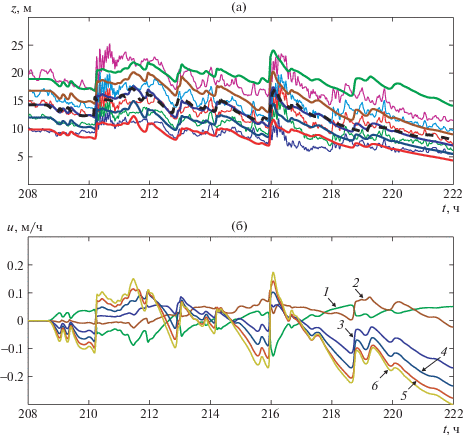
На рис. 4, 5 приведены результаты расчета положений термоклина на контрольных станциях в течение нескольких суток с использованием двухслойной модели (уравнения (1.5) при $n = 2$). На рис. 4 линия 1 показывает положение изотермы $T = 10$°С, измеренное на станции S02 и поднятое на 20 м над дном для удобства изображения. Эти данные использовались в качестве граничных условий на левой границе расчетной области по пространственной переменной. Линия 2 соответствует натурным данным о положении изотермы $T = 10$°С на контрольной станции S09 (правом конце расчетного интервала по $x$). Кривая 3 показывает результаты численного моделирования горизонта термоклина в зависимости от времени на правой границе расчетной области. Пунктирная линия, практически совпадающая с кривой 3, соответствует расчету по двухслойной гидростатической модели. Как видно из рисунка, негидростатическое распределение давления в верхнем слое не оказывает заметного влияния на структуру волн при расчете на протяжении нескольких суток. Коэффициент плавучести $b = 0.02$ м/с2; параметры в формуле (3.1) – $a = 19.1$ м и $k = 1.2 \times {{10}^{{ - 4}}}$ м–1.

Рис. 4.

Положение изотермы $T = 10$°С в зависимости от времени на станциях S02 (кривая 1, поднятая вверх на 20 м) и S09 (линия 2); кривая 3 – расчет по уравнениям (1.5) при $n = 2$; пунктир – по двухслойной гидростатической модели.

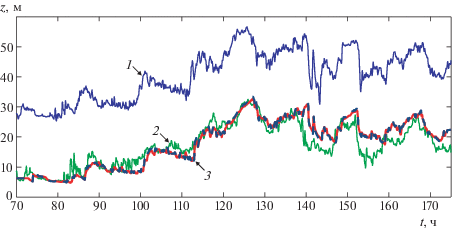
Рис. 5.

Положение изотермы $T = 10$°С в зависимости от времени на станциях S09 (кривая 1, поднята на 40 м), S07 (линия 2, поднята на 20 м) и S03 (кривая 3); линии 4 и 5 – расчет по двухслойным уравнениям (1.5).

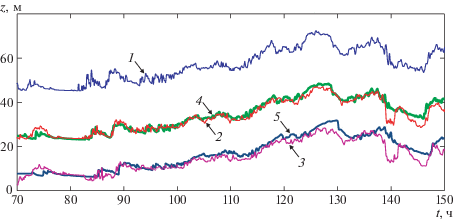
На рис. 5 показана аналогичная зависимость положения термоклина от времени. Линия 1 – изотерма $T = 10$°С на станции S09, поднятая над дном на 40 м. Эти данные используются при проведении расчета в качестве граничного условия на левой границе. Линии 2 и 3 представляют эту же изотерму на станциях S07 (поднята на 20 м) и S03, соответствующих промежуточному положению контрольной станции и правой границе расчетного интервала по пространству. Кривые 4 и 5 – результаты расчета положения термоклина на станциях S07 и S03 в зависимости от времени. Для обеспечения требуемого перепада глубин 5 м между станциями S09, S07 и 3.5 м между S07, S03 выбираются параметры $a = 16.5$ м и $k = 1.9 \times {{10}^{{ - 4}}}$ м–1. Из представленных рисунков можно сделать вывод, что двухслойные модели мелкой воды достаточно полно описывают эволюцию основного термоклина на протяжении длительного интервала времени и могут быть использованы для мониторинга нелинейных волновых процессов, связанных с плотностной стратификацией прибрежных вод.

Интересной особенностью представленных на рис. 4, 5 расчетов является локальное отклонение натурных данных и расчетных кривых на некоторых участках. Наиболее выражено это явление на рис. 5 в интервале 140–150 ч на станциях S07 и S03. Именно на этом участке гипотеза о квазидвумерной структуре внутренних волн перестает быть справедливой, что свидетельствует о наличии возмущения поля температуры источником другого типа. Поэтому информация о фоновом распределении гидродинамических полей в шельфовой зоне, полученная с использованием вертикальных термогирлянд, может оказаться полезной при интерпретации натурных данных о вихре-волновом взаимодействии возмущений различной природы на шельфе.

3.3. Бегущие волны

Как было показано выше, дисперсионные эффекты слабо влияют на структуру волн при проведении расчетов на значительных (несколько суток) временных интервалах. Однако для корректного моделирования мелкомасштабных процессов необходимо учитывать негидростатическое распределение давления. Продемонстрируем это сравнением решения уравнений (1.5) в классе бегущих волн с данными натурных наблюдений станции S03 на коротком интервале времени. Для построения решения системы обыкновенных дифференциальных уравнений (1.6) выполнено ее приведение к виду, разрешенному относительно производных, а также использованы условия примыкания нетривиального решения к заданному постоянному потоку [18].

Пунктирные линии на рис. 6 соответствуют границам раздела слоев с интервалом 2°С по данным натурных наблюдений на станции S03 (увеличение рис. 3а в окрестности $t = 210.5$ ч). Сплошные кривые – расчет по стационарным уравнениям (1.6) с шестью слоями в системе координат, движущейся со скоростью $D$. Значения толщин слоев на правой границе ${{h}_{1}} = 21.85$, ${{h}_{2}}$ = 3.38, ${{h}_{3}} = 1.44$, ${{h}_{4}} = 1.63$, ${{h}_{5}} = 1.4$, ${{h}_{6}} = 9.3$ (полная глубина $H = 39$ м), а также плавучести в слоях ${{b}_{k}} = (k - 1)b{\text{/}}5$, $b = 0.02$ м/с2 задаются согласно данным натурного эксперимента на станции S03. Число Фруда Fr = ${{D}_{0}}{\text{/}}\sqrt {bH} = 0.46$ подобрано из условия соответствия амплитуды головной волны данным натурных наблюдений. Сдвиг скорости в слоях не учитывался (${{u}_{k}} = {{D}_{0}} \approx 0.4063$ м/с), коэффициент трения ${{c}_{f}} = 0.006$. Переход от расчетного интервала по пространству $X = [0,L]$ (в метрах) к интервалу по времени $\tau = [{{t}_{0}},{{t}_{1}}]$ (часы) дается формулой $\tau = {{({{60}^{2}}D)}^{{ - 1}}}X$ + t0, где D = $1.4{{D}_{0}}$. Как видно из рисунка, модель достаточно точно описывает структуру волнового бора, если ввести поправку на абсолютную скорость распространения фронта волны $D$. По всей вероятности, для более точного описания структуры волн и определения скорости распространения волновых фронтов необходимо учитывать вертикальную и горизонтальную неоднородность скорости в слоях, что предполагается сделать в дальнейшем.

Рис. 6.

Мелкомасштабная структура волн: сплошные линии – границы раздела слоев, полученные по модели (1.5) в классе бегущих волн; пунктир – данные натурных наблюдений на станции S03.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Применение теории мелкой воды для моделирования течений стратифицированной жидкости в гидрофизических приложениях является оправданным в силу того, что горизонтальные масштабы движения намного превосходят вертикальные масштабы. Уравнения многослойной мелкой воды позволяют учесть не только вертикальное распределение плотности, но и сдвиг скорости в слоях. Эти уравнения хорошо зарекомендовали себя при восстановлении внутренней структуры характерных волновых объектов (уединенные волны, внутренние боры и др.). Однако при численной реализации этой модели применительно к существующим нестационарным волновым процессам возникает ряд трудностей, связанных с устойчивостью численных решений и постановкой граничных условий.

В работе исследуется возможность применения уравнений многослойной мелкой воды и, в частности, двухслойной модели к проблеме мониторинга нестационарных гидрофизических процессов в шельфовой зоне приливного моря. Постановка задачи включает расчет вертикального распределения температуры и горизонтальной компоненты скорости вдоль прямолинейной трассы на основе данных о вариации температуры на заданных горизонтах, полученных на одной из донных станций. Верификация расчетов осуществляется с использованием данных других контрольных станций, расположенных вдоль этой трассы. Сравнение результатов численного расчета с натурными данными позволяет определить, насколько гипотеза о квазидвумерном характере течения на шельфе, лежащая в основе данного подхода, соответствует реальности. На рис. 6 представлена структура придонного волнового бора, построенного в классе бегущих волн для многослойной модели (1.6) при n = 6. Учет негидростатичности распределения давления в верхнем слое при построении такого решения является определяющим. Заметим, что пакет волн, генерируемых на фронте внутреннего бора, является короткопериодным (с периодом 5–6 мин). При осреднении моделируемых процессов на интервале 5–10 мин, используемом для мониторинга более плавных возмущений, короткопериодные волны сглаживаются, но волновая картина остается достаточно многообразной. На рис. 3 показан фрагмент расчета волновой структуры, содержащей два придонных волновых бора, полученный с использованием многослойной (n = 6) и двухслойной (n = 2) модели (1.5). Основной вывод, который можно сделать из сравнения расчетов, состоит в том, что двухслойные уравнения движения адекватно передают процесс трансформации термоклина при прохождении внутренних волн даже в случае, когда стратификация существенно отличается от двухслойной.

При увеличении интервала осреднения расчетных и натурных данных до 10 мин дисперсионные эффекты, связанные с вертикальным ускорением частиц жидкости, проявляются незначительно. На рис. 4, 5 расчеты по двухслойным уравнениям (1.5) при $\alpha = 10$, $\varepsilon = 1$ и $\alpha = \varepsilon = 0$ (т.е. по классическим уравнениям двухслойной мелкой воды) визуально неотличимы. Поэтому возникает вопрос о целесообразности применения более сложной модели, учитывающей дисперсионные эффекты. В пользу выбора используемых уравнений со значением параметров $\alpha > 0$, $\varepsilon = 1$ можно привести два аргумента: эта модель пригодна для расчета как короткопериодных, так и более длинных внутренних волн, а также при численной реализации обладает большей устойчивостью по сравнению с классической моделью. Отметим, что приведенные на рис. 3–5 расчетные кривые с хорошей точностью соответствуют натурным данным. Это означает, что гипотеза о двумерном характере распространения возмущений поля температуры находит свое подтверждение. Тем более вызывает интерес наличие относительно небольших временных интервалов (рис. 4, 5), где различие между расчетными и экспериментальными данными становится существенным. Изучение природы этих локальных аномалий является предметом дальнейших исследований. Для определения источника таких вихре-волновых возмущений потребуется пространственное размещение измерительных комплексов на достаточно большой акватории гидрофизического полигона.

Список литературы

  1. Helfrich K.R., Melville W.K. Long nonlinear internal waves // Annu. Rev. Fluid Mech. 2006. V. 38. P. 395–425. https://doi.org/10.1146/annurev.fluid.38.050304.092129

  2. Jackson C.R., da Silva J.C.B. Jeans G. The generation of nonlinear internal waves // Oceanogr. 2012. V. 25. P. 108–123. https://doi.org/10.5670/oceanog.2012.46

  3. Small J., Hallock Z., Pavey G., Scott J. Observations of large amplitude internal waves at the Malin Shelf edge during SESAME 1995 // Cont. Shelf Res. 1999. V. 19. P. 1389–1436. https://doi.org/10.1016/S0278-4343(99)00023-0

  4. Scotti A., Pineda J. Observation of very large and steep internal waves of elevation near the Massachusetts coast // Geophys. Res. Lett. 2004. V. 31. L22307. P. 1–5. https://doi.org/10.1029/2004GL021052

  5. Rayson M.D., Jones N.L., Ivey G.N. Observations of large-amplitude mode-2 nonlinear internal waves on the Australian North West shelf // J. Phys. Oceanogr. 2019. V. 49. P. 309–328. https://doi.org/10.1175/JPO-D-18-0097.1

  6. Серебряный А.Н., Пао К.П. Прохождение нелинейной внутренней волны через точку переворота на шельфе // Докл. РАН. 2008. Т. 420. № 4. С. 543–547.

  7. Yuan C., Grimshaw R., Johnson E. The evolution of second mode internal solitary waves over variable topography // J. Fluid Mech. 2018. V. 836. P. 238–259. https://doi.org/10.1017/jfm.2017.812

  8. Талипова Т.Г., Пелиновский Е.Н., Куркин А.А., Куркина О.Е. Моделирование динамики интенсивных внутренних волн на шельфе // Известия РАН. Физика атмосферы и океана. 2014. Т. 50. № 6. С. 714–722. https://doi.org/10.7868/S0002351514060169

  9. Novotryasov V.V., Stepanov D.V., Yaroshchuk I.O. Observations of internal undular bores on the Japan/East Sea shelf-coastal region // Ocean Dyn. 2016. V. 66. P. 19–25. https://doi.org/10.1007/s10236-015-0905-z

  10. Ляпидевский В.Ю., Тешуков В.М. Математические модели распространения длинных волн в неоднородной жидкости. Новосибирск: Изд-во СО РАН, 2000. 420 с.

  11. Choi W., Camassa R. Fully nonlinear internal waves in a two-fluid system // J. Fluid Mech. 1999. V. 386. P. 1–36. https://doi.org/10.1017/S0022112099005820

  12. Choi W. Modeling of strongly nonlinear internal gravity waves // Proc. Fourth Inter. Conf. Hydrodynamics / Eds. Y. Goda, M. Ikehata, K. Suzuki. 2000. P. 453–458.

  13. Barros R., Choi W., Milewski P.A. Strongly nonlinear effects on internal solitary waves in three-layer flows // J. Fluid Mech. 2020. V. 883. A16. P. 1–36. https://doi.org/10.1017/jfm.2019.795

  14. Chesnokov A.A., Liapidevskii V.Yu. Hyperbolic model of internal solitary waves in a three-layer stratified fluid // Europ. Phys. J. Plus. 2020. V. 135. P. 1–19. https://doi.org/10.1140/epjp/s13360-020-00605-3

  15. Ляпидевский В.Ю., Новотрясов В.В., Храпченков Ф.Ф., Ярощук И.О. Внутренний волновой бор в шельфовой зоне моря // ПМТФ. 2017. Т. 58. № 5. С. 60–71. https://doi.org/10.15372/PMTF20170506

  16. Кукарин В.Ф., Ляпидевский В.Ю., Храпченков Ф.Ф., Ярощук И.О. Нелинейные внутренние волны в шельфовой зоне моря // Изв. РАН. Механика жидкости и газа. 2019. № 3. С. 38–47. https://doi.org/10.1134/S0568528119030083

  17. Ляпидевский В.Ю., Турбин М.В., Храпченков Ф.Ф., Кукарин В.Ф. Нелинейные внутренние волны в многослойной мелкой воде // ПМТФ. 2020. Т. 61. № 1. С. 53–61. https://doi.org/10.15372/PMTF20200105

  18. Ляпидевский В.Ю., Чесноков А.А., Ермишина В.Е. Квазилинейные уравнения динамики внутренних волн в многослойной мелкой воде // ПМТФ. 2021. Т. 62. № 4. С. 34–45. https://doi.org/10.15372/PMTF20210404

  19. Леонтьев А.П., Ярощук И.О., Смирнов С.В., Кошелева А.В., Пивоваров А.А., Самченко А.Н., Швырев А.Н. Пространственно-распределенный измерительный комплекс для мониторинга гидрофизических процессов на океаническом шельфе // Приборы и техника эксперимента. 2017. № 1. С. 128–135. https://doi.org/10.7868/S0032816216060227

  20. Пивоваров А.А., Ярощук И.О., Долгих Г.И., Швырев А.Н., Самченко А.Н. Автономный акустический регистратор и его применение в составе гидрофизического комплекса // Приборы и техника эксперимента. 2021. № 3. С. 123–128. https://doi.org/10.31857/S0032816221030253

  21. Lien R.-Ch., Henyey F., Ma B., Yang Y.J. Large-amplitude internal solitary waves observed in the northern South China sea: properties and energetic // J. Phys. Oceanogr. 2014. V. 44. № 4. P. 1095–1115. https://doi.org/10.1175/JPO-D-13-088.1

  22. Favrie N., Gavrilyuk S. A rapid numerical method for solving Serre–Green–Naghdi equations describing long free surface gravity waves // Nonlinearity. 2017. V. 30. P. 2718–2736. https://doi.org/10.1088/1361-6544/aa712d

  23. Busto S., Dumbser M., Escalante C., Favrie N., Gavrilyuk S. On high order ADER discontinuous Galerkin schemes for first order hyperbolic reformulations of nonlinear dispersive systems // J. Sci. Comput. 2021. V. 87. 48. P. 1–47. https://doi.org/10.1007/s10915-021-01429-8

  24. Nessyahu H., Tadmor E. Non-oscillatory central differencing schemes for hyperbolic conservation laws // J. Comput. Phys. 1990. V. 87. P. 408–463. https://doi.org/10.1016/0021-9991(90)90260-8

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал