1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2021

Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 84-97

ГИСТОГРАММЫ, КУМУЛЯНТЫ И СПЕКТРЫ МЕХАНИЧЕСКИХ И ВЕТРОВЫХ ВОЛН В ВЕТРО-ВОЛНОВОМ КАНАЛЕ

В. Г. Полников a, *

a Институт физики атмосферы им. А.М. Обухова РАН
Москва, Россия

* E-mail: polnikov@mail.ru

Поступила в редакцию 23.11.2020
После доработки 10.02.2021
Принята к публикации 10.03.2021

Полный текст (PDF)

Аннотация

С целью изучения взаимосвязи статистических характеристик волнения на поверхности воды и закономерностей их изменчивости построены гистограммы, а также рассчитаны кумулянты и спектры для механических и ветровых волн в ветро-волновом канале. Анализируется многообразие гистограмм волн различной природы и их изменчивость c изменением типа и параметров волн, а также с разгоном волн. Отмечается регулярность в отклонении от гауссова распределения амплитуд волн, в числовом виде представленная их кумулянтами. С учетом закономерностей эволюции частотного спектра установившихся волн вдоль канала утверждается, что изменчивость статистик волн однозначно определяется изменчивостью формы их спектра, а не отдельными характеристиками системы (разгон, крутизна или возраст волн). Дается теоретическое обоснование приведенному утверждению.

Ключевые слова: статистика волн, гистограммы, кумулянты, спектры, измерения в лотке

Изучению статистических характеристик волн на воде издавна уделяется большое внимание, начиная со знаменитых работ Лонге-Хиггинса [1, 2] и монографии Кинсмана [3] и заканчивая работами последних лет. Следует отметить экспериментальные работы [4–9] и теоретические исследования [10–15]. Подробный обзор полученных результатов представлен в [9]. Значимость исследования статистических характеристик волнения обусловлена как чисто научными интересами в области механики жидкости, так и практикой использования статистик в инженерных расчетах безопасности морской индустрии и судоходства [16–18]. Отдельного внимания заслуживает учет статистики волнения в интерпретации данных дистанционного зондирования поверхности моря [19, 20].

Основной итог многолетних исследований заключается в доказательстве отклонения статистики реальных ветровых волн от гауссовой (напр., [3, 9, 11, 21]) и возникновения так называемых волн-убийц экстремальных амплитуд [4, 5, 14], что обусловлено нелинейной природой как механических, так и ветровых волн на воде, сопровождаемой различного рода их неустойчивостью [4, 5]. Так, в [9] для лотка с рабочим размером около 5 м детально изучены формы спектров, законы роста волн, рассчитаны кумулянты 3-го и 4-го порядка и приведены графики их зависимости от разгона и возраста волн. Однако малые размеры лотка не позволили [9] провести завершенный анализ результатов, так как все данные были получены для ранних стадий развития волн, далеких от реальных ветровых волн в природе. Кроме того, в экспериментальных работах [4, 5, 9, 21] детальная связь статистик волн с их спектрами просто не рассматривалась. По этой причине начиная с работ [9, 21] исследователи пытаются установить зависимость отклонений статистики от гауссовой как функции отдельных параметров системы, например, разгонов волн [4, 5], их крутизны [5, 9, 14, 21] или возраста волн [8]. Для этой цели используются сложные теоретические построения и соотношения [2, 5, 13, 22].

В данной работе на основе собственных измерений механических и ветровых волн в большом ветро-волновом канале показывается, что статистика волн (гистограммы, статистические моменты) проявляет значительную изменчивость, которую легко оцифровать и проанализировать путем расчета кумулянтов временных рядов измеренных волнограмм. Для этого строятся гистограммы для различных типов волн и приводятся соответствующие им величины кумулянтов и спектров в ряде точек измерений вдоль канала. С использованием установленных ранее [23] закономерностей эволюции частотного спектра волн вдоль ветро-волнового канала показано, что изменчивость статистик волн однозначно определяется изменчивостью формы их спектра, а не такими отдельными характеристиками системы, как разгон, крутизна или возраст волнения, как это часто трактуется [5, 9, 21]. Дается теоретическое обоснование приведенному утверждению.

1. ДАННЫЕ ИЗМЕРЕНИЙ

Измерения выполнялись в ветро-волновом канале Первого института океанографии, расположенного в Циндао, Китай. Размеры лотка и расположение оборудования приведены на рис. 1.

Рис. 1.

Канал и расположение оборудования: 1 – ветер; 2 – волнопродуктор; 3 – волногаситель; 4 – вентилятор; WG – волновые датчики; PT – трубки Пито; ADV – набор акустических доплеровских велосиметров; IP – устройство введения поплавков или красителя.

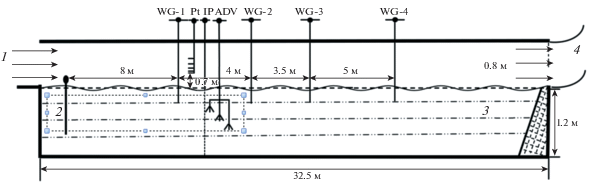
Для волновых измерений использовались емкостные волновые датчики (WG). Трубки Пито (PT) и три акустических доплеровских велосиметра (ADV) применялись для измерения профилей ветра и скорости течений. Места расположения датчиков WG1–WG4 далее обозначаются как точки измерений P1–P4.

Ветровые волны генерировались ветром W, создаваемым вентилятором. Задавалось пять значений скорости ветра W – 4, 6, 8, 10 и 12 м/с. Помимо ветровых волн, изучались два вида механических волн: регулярные (квазимонохроматические) волны, и стохастические волны с широкой спектральной полосой, типа спектров Пирсона–Московица (PM) или JONSWAP [25, 26] с тремя программными частотами волнопродуктора  f0 = 1.5, 1.0 и 0.7 Гц, и с пятью значениями значительной высоты волн HS для каждой частоты. Записи временн${\text{ы}}'$х рядов возвышений поверхности воды h(t) (волнограммы) имели длительность 10 мин с частотой дискретизации 50 Гц, что составляет 30 000 отсчетов в каждой записи. Результаты других измерений в данной работе не используются и не обсуждаются.

Всего выполнено 42 серии измерений эволюции волн в канале, полная информация о которых представлена в [23]. Ниже рассмотрены лишь некоторые из данных для механических волн, поскольку они имеют лишь академический интерес в силу специфичности природы их генерации, обусловленной механикой волнопродуктора. Для ветровых волн, представляющих практический интерес, будут проанализированы все данные измерений.

2. МЕТОДЫ ИССЛЕДОВАНИЯ И ОСНОВНЫЕ СООТНОШЕНИЯ

Обработка рядов волнограмм возвышений поверхности h(t) проводилась в оболочке MATLAB. Для визуализации функций плотности распределения вероятности P(h) (ПРВ) рассчитывались гистограммы $P(h{\text{/}}si)$ в полосе значений h/si от –3.5 до 3.5 (т.е. в нормировке h(t) на стандартное отклонение ряда si) с шагом ${{\Delta }_{{h/si}}}$ = 0.1 по оси h/si. На наш взгляд, анализ гистограмм, как аналога функции ПРВ амплитуд волн P(h), более предпочтителен в задачах изучения их статистики, чем распространенный анализ интегральных функций распределения высот волн, принятый в [6, 9, 14, 17], поскольку для амплитуд волн может быть построена теория на базе уравнений Эйлера, а функции ПРВ выражены через статистические моменты рядов h(t), что облегчает трактовку наблюдений.

Помимо реальных рядов измерений, для полноты картины и понимания характера изменчивости гистограмм использовались модельные ряды, описывающие синусоидальные, трохоидальные и стоксовы волны, задаваемые соответственно соотношениями

(2.1а)
${{h}_{{\text{S}}}}{\text{(}}t{\text{)}} = {\text{cos(}}{{\omega }_{p}}t{\text{)}}$
(2.1б)
${{h}_{{\text{T}}}}{\text{(}}t{\text{)}} = {\text{exp[}}\varepsilon \cdot {\text{cos(}}{{\omega }_{p}}t{\text{)]cos(}}{{\omega }_{p}}t{\text{)}}$
(2.1в)
${{h}_{{{\text{St}}}}}{\text{(}}t{\text{)}} = {\text{cos(}}{{\omega }_{p}}t{\text{)}} + {{\varepsilon }^{2}} \cdot {\text{cos(2}}{{\omega }_{p}}t{\text{)}}$
с дискретностью Δt = 0.01 на интервале времен [0 < t ≤ Т = 628] (размерность единиц не требуется). В формулах (2.1) параметры ${{\omega }_{p}}{\text{ = 2}}\pi {{f}_{p}}$ и $\varepsilon $ играют роль угловой частоты и крутизны волн соответственно. В расчетах принимается фиксированное значение ${{\omega }_{p}}$ = 6.28, что соответствует циклической частоте fp = 1.

Статистика волн в цифровом представлении описывается центральными статистическими моментами i-го порядка μi ряда η(t)

${{\mu }_{i}} = \int\limits_{ - \infty }^\infty {{{{\left( {\eta - \left\langle \eta \right\rangle } \right)}}^{i}}P(\eta )d\eta } \approx \frac{1}{N}\sum\limits_{k = 1}^{k = N} {{{{\left( {\eta {\text{(}}{{t}_{k}}{\text{)}} - \left\langle \eta \right\rangle } \right)}}^{i}}} $
где $\left\langle \eta \right\rangle = \int\limits_{ - \infty }^\infty {\eta P(\eta )d\eta } \approx \frac{1}{N}\sum\limits_{k = 1}^{k = N} {{{\eta (}}} {{t}_{k}}{\text{)}}$ – среднее значение ряда (вначале дано теоретическое определение, затем – практическая формула); N – длина ряда.

Известно (см., напр., [21]), что функция ПРВ P(η) может быть аналитически выражена через моменты μi, однако наиболее компактное выражение через моменты имеет характеристическая функция F, представляющая собой Фурье-образ от P(η)

$F{\text{(}}x{\text{)}} = \int\limits_{ - \infty }^\infty {P{\text{(}}\eta {\text{)exp(}}ix\eta {\text{)}}d\eta } = 1 + \sum\limits_{n = 1}^\infty {{{\mu }_{n}}\frac{{{{{{\text{(}}ix{\text{)}}}}^{n}}}}{{n{\text{!}}}}} $

Если записать $F{\text{(}}x{\text{)}}$ в форме

(2.2)
$F{\text{(}}x{\text{)}} = {\text{exp}}\left[ {\sum\limits_{n = 1}^\infty {{{\chi }_{n}}\frac{{{{{{\text{(}}ix{\text{)}}}}^{n}}}}{{n{\text{!}}}}} } \right]$
то в экспоненте появляется комбинация моментов χn, называемая кумулянтами, представляющими наибольший интерес в статистике моментов. Первые шесть кумулянтов в (2.2) таковы [21]

${{\chi }_{1}} = 0,\quad {{\chi }_{2}} = {{\mu }_{2}},\quad {{\chi }_{3}} = {{\mu }_{3}},\quad {{\chi }_{4}} = {{\mu }_{4}} - 3\mu _{2}^{2}$
(2.3)
${{\chi }_{5}} = {{\mu }_{5}} - 10{{\mu }_{3}}\mu _{2}^{{}},\quad {{\chi }_{6}} = {{\mu }_{6}} - 15{{\mu }_{4}}\mu _{2}^{{}} - 10\mu _{3}^{2} + 30\mu _{2}^{3}$

Сказанное выше обусловлено тем, что для исследований статистики волн наиболее часто привлекается ПРВ Гаусса вида [18]

(2.4)
$P(\eta ) = \frac{1}{{\sqrt {2\pi {{\mu }_{2}}} }}{\text{exp}}\left[ { - \frac{{{{\eta }^{2}}}}{{2{{\mu }_{2}}}}} \right]$
для которой нечетные моменты μi равны нулю, а четные выражаются через μ2 формулой ${{\mu }_{{2n}}} = \frac{{(2n)!}}{{{{2}^{n}}n!}}\mu _{2}^{n}$. Тогда все кумулянты с порядками выше второго обращаются в нуль, что служит удобным инструментом изучения отклонения статистик волн от гауссовой формы (2.4). С учетом изменчивости дисперсий (si)2 = μ2 исследуемых рядов далее будут использоваться кумулянты Kn, записанные в нормировке на μ2

(2.5)
${{K}_{n}} = {{\chi }_{n}}{\text{/}}{{(\sqrt {\mu _{2}^{{}}} )}^{n}}$.

Ввиду важности значений кумулянтов для оценки статистки волн часть из них имеет свои названия. Так, величина K3 носит название асимметрии, а K4 – эксцесс. Другие кумулянты менее востребованы, но здесь они приводятся для полноты картины, поскольку в кумулянтах высших порядков происходит смена знака, представляющая интерес при проверке применимости теоретических моделей статистики волнения.

Привлекаемые далее для трактовки статистики волн частотные спектры S(f) рассчитывались методом авторегрессии [27]. Как показано в [23], такой метод оценивания S(f) для имеющихся рядов η(t) обеспечивает стандартные отклонения ΔS спектральных интенсивностей S(f) в билогарифмических координатах (logS–logf) всего 3–5%, что позволяет с высокой точностью оценивать индекс n частотного спадания хвоста спектра вида

$S(f) = C{{f}^{{ - n}}}\quad {\text{при}}\quad f > 2{{f}_{p}}~$
и его интенсивность (т.е. величину C), а также следующие интегральные характеристики волнения: частота пика fp, волновое число kp = (2πfp)2/g (здесь использовано дисперсионное соотношение для гравитационных волн на глубокой воде, g – ускорение силы тяжести), средняя амплитуда $a = {{\left( {2\int {S(f)df} } \right)}^{{1/2}}}$ и средняя крутизна $\varepsilon = a{{k}_{p}}$ волн. Для анализа характеристик ветровых волн часто привлекается параметр возраста волн

(2.6)
$A = {{c}_{{ph}}}{\text{/}}W = g{\text{/(}}2\pi {{f}_{p}}{\text{)}}W$

Детальное исследование изменчивости всех указанных характеристик волнения с разгоном волн по каналу представлено в [23]. Связь моментов со спектрами описана ниже при интерпретации результатов.

Сначала рассматриваются гистограммы и кумулянты модельных рядов (2.1), затем те же характеристики для механических волн, которые практически не обсуждались в литературе. И, наконец, будут рассмотрены те же характеристики для ветровых волн, которые неоднократно изучались ранее, напр., в [9, 21, 24]. Сопоставление различий характеристик для всех рассмотренных типов волн, а также их отличие от установленных ранее в [9, 21], впервые интерпретируются с привлечением сведений об изменчивости спектров волн, полученных в [23]. В заключение будет дано теоретическое обоснование приведенной интерпретации.

3. ВЗАИМОСВЯЗЬ ГИСТОГРАММ, КУМУЛЯНТОВ И СПЕКТРОВ

3.1. Модельные волны

Гистограммы $P{\text{(}}h{\text{/}}si{\text{)}}$ для модельных рядов волн h(t) вида (2.1) в нормировке

(3.1)
$\sum\limits_{i = 1}^{i = M} {P{\text{(}}{{h}_{i}}{\text{/}}si{\text{)}}} {{\Delta }_{{h/si}}} = 1$
(М – число ячеек в гистограмме) приведены на рис. 2 и 3.

Рис. 2.

Гистограммы: а – волна (2.1а); б – волна (2.1б) при $\varepsilon $ = 0.1; в – волна (2.1в) при ${{\varepsilon }^{2}}$ = 0.01.

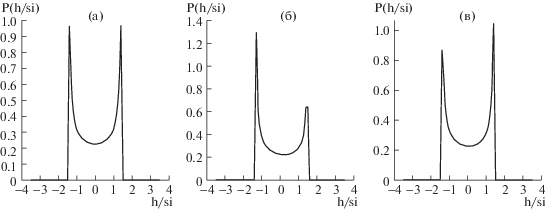
Рис. 3.

Гистограммы: а – (2.1б) при $\varepsilon $ = 0.2; б – волна (2.1в) при ${{\varepsilon }^{2}}$ = 0.1; в – волна (2.1в) при ${{\varepsilon }^{2}}$ = 0.16.

Как видно, в волнах синусоидального типа (2.1а), гистограмма симметрична и в ней существенно больше проявляются либо гребни, либо впадины, что вполне понятно из вида синусоид. Трохоидальность волны типа (2.1б) приводит к появлению асимметрии гистограммы и завышению вероятностей подошв (рис. 2б). Интересно, что с повышением $\varepsilon $ этот эффект сглаживается (рис. 3а). Для волны Стокса (2.1в), наоборот, малые ε2 сначала искажают гистограмму стоксовой волны в сторону гребней, но далее рост ε2 приводит к форме гистограммы, близкой к таковой для трохоидальной волны (рис. 3б, в).

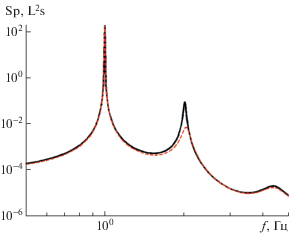
Все эти особенности регулярным образом проявляются в результатах оценок кумулянтов (табл. 1). Заметим, что близкий характер изменчивости величин кумулянтов для волн вида (2.1б) и (2.1в) обусловлен существенной близостью их спектров (рис. 4). Очевидно, что для волн (2.1б) и (2.1в) отличие всех кумулянтов от нуля есть прямое следствие их нелинейности по амплитуде волн.

Таблица 1.

Кумулянты модельных волн

Тип волны K3 K4 K5 K6
Формула (2.1а) 0.0 –1.5 0.0 10.
2.1б ε = 0.1 0.106 –1.48 –0.70 9.8
  ε = 0.2 0.21 –1.46 –1.39 9.19
2.1в ε2 = 0.01 0.02 –1.50 –0.14 9.99
  ε2 = 0.10 0.21 –1.47 –1.39 9.3
  ε2 = 0.16 0.33 –1.43 –2.16 8.29
Рис. 4.

Спектры волн (2.1б) $\varepsilon $ = 0.1 (штриховая кривая) и (2.1в) ${{\varepsilon }^{2}}$ = 0.1 (сплошная кривая).

Отметим, что для линейной волны синусоидального типа (2.1а) все нечетные моменты равны нулю, а эксцесс K4 отрицателен и не зависит от амплитуды волн. В нелинейных волнах (2.1б) и (2.1в) кумулянты K3 и K5 (по модулю) закономерно растут с увеличением уклона, в то время как K4 (по модулю) и K6 незначительно уменьшаются, при этом K4 и K5 – отрицательные, а K6 – положительный. Несмотря на формальность расчета кумулянтов для модельных (детерминированных) волн, приведенные результаты оказываются полезными при трактовке данных наблюдений.

3.2. Регулярные механические волны

Поскольку механические волны в канале имеют искусственное происхождение, их гистограммы (ГГ) проявляют широкое разнообразие форм, в значительной степени обусловленное самим волнопродуктором. Именно это разнообразие и интересно для понимания статистической природы волн.

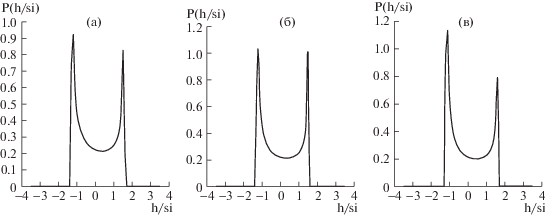
В качестве примера приведем ГГ для регулярных механических волн с программными параметрами частоты f0 = 1.5 Гц и высот Hs = 3 и 7 см в трех точках измерений по разгону (рис. 5).

Рис. 5.

Гистограммы для механических волн при f0 = 1.5 Гц в точках измерений Р1 (кривая 1), Р3 (2, сдвинута на 0.2) , Р4 (3, сдвинута на 0.4): а, б – Hs = 3, 7 см.

Видно, что по мере увеличения разгона волн их ГГ видоизменяются от двухмодовой (типичной для стоксовых волн) до ярко выраженной одномодовой, четко проявляющейся с ростом амплитуды волн (рис. 5б). С дальнейшим ростом Hs этот эффект проявляется еще сильнее (данные не приведены для краткости). Отметим, что для волн с меньшей программной частотой (f0 = = 1.0 Гц) указанный эффект изменения вида ГГ с разгоном уже не проявляется, что, по-видимому, связано с малостью крутизны волн и связанной с этим слабой изменчивостью их спектра в процессе эволюции по разгону (см. ниже). Соответственно изменяются и кумулянты, представленные в табл. 2.

Таблица 2.

Кумулянты регулярных механических волн

Hs, см Параметры волн Точки измерений
P1 P3 P4
f0 = 1.5 Гц
3 a0kp 0.126 0.10 0.10
  (μ2)1/2(м) 0.01 0.0081 0.0081
  K3 –0.0729 0.1945 0.0372
  K4 –1.4780 –1.5073 –1.4471
  K5 0.4185 –1.3761 –0.3053
  K6 9.7138 9.7267 9.3785
7 a0kp 0.26 0.23 0.2
  (μ2)1/2(м) 0.021 0.019 0.017
  K3 0.1497 0.2266 0.2745
  K4 –1.4174 –1.0608 –0.5028
  K5 –0.9748 –1.1157 –0.7604
  K6 8.9193 5.5835 1.1967
10 a0kp 0.31 0.24 0.18
  (μ2)1/2(м) 0.0245 0.021 0.017
  K3 0.2467 0.3037 0.3496
  K4 –1.3136 –0.8924 –0.0498
  K5 –1.5161 –1.3175 –0.3466
  K6 7.6013 3.9022 –0.8080
f0 = 1.0 Гц
3 a0kp 0.044   0.039
  (μ2)1/2(м) 0.0077   0.0069
  K3 –0.1174   –0.2239
  K4 –1.5155   –1.4523
  K5 0.7392   1.4523
  K6 10.081   9.0370
10 a0kp 0.15   0.14
  (μ2)1/2(м) 0.0256   0.0239
  K3 0.1010   0.0544
  K4 –1.4756   –1.5112
  K5 –0.6836   –0.3697
  K6 9.6252   10.091
15 a0kp 0.21   0.20
  (μ2)1/2(м) 0.0369   0.0349
  K3 0.2637   0.3308
  K4 –1.4263   –1.3622
  K5 –1.7439   –2.1501
  K6 8.6058   7.5592

Отметим, что в механических волнах при малых высотах (Hs = 3 см) правый максимум ГГ таков, что асимметрия волн K3 является отрицательной. При увеличении Hs левый максимум начинает превалировать (рис. 5б), и все кумулянты возвращаются к типовым значениями для стоксовых волн (ср. табл. 1 и 2). Значение крутизны a0kp, представленной в табл. 2 полужирным шрифтом, хотя и значимо, но не регулярно, влияет на величины K3, мало меняя значения высших кумулянтов.

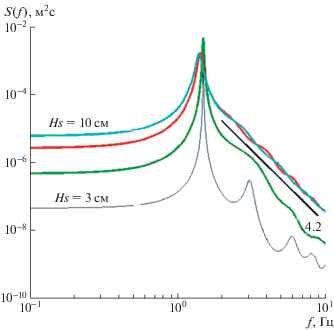
Все указанные особенности кумулянтов находят свое трактование при их сопоставлении с соответствующими спектрами волн, которые изображены на рис. 6 в точке Р4 для f0 = 1.5 Гц и различных значений Hs. Видно, что для волн с Hs = 3 см спектр сохраняет вид, типичный для стоксовой волны (см. рис. 4б), т.е. он мало меняется с разгоном; но для волн с Hs ≥ 7 см в точке Р4 спектры уже приобретают автомодельный вид (подробнее о спектрах см. в [23]). Поэтому и кумулянты волн в этой точке имеют одинаковые знаки и близкие значения, вне зависимости от значений крутизны волн. Эффект автомодельности спектра для волн с f0 =1.5 Гц и Hs ≤ 5 см, равно как и для всех волн с f0 ≤ 1.0 Гц, в канале не проявляется (в силу малости начальной крутизны волн), что и приводит к сохранению значений кумулянтов, типичных для стоксовой волны.

Рис. 6.

Спектры регулярных механических волн в точке Р4 при частоте f0 = 1.5 Гц и значениях Hs от 3 до 10 см. Число при отрезке черной линии указывает степенной закон спадания хвоста спектра.

3.3. Нерегулярные механические волны

Нерегулярные волны отличаются широкой полосой частот в спектре, что существенным образом меняет характер гистограмм, придавая им вид, похожий на гистограммы ветровых волн (рис. 7). Кумулянты этих волн проявляют широкий разброс значений (табл. 3), что обусловлено только спецификой формирования волнопродуктором спектров таких волн (видно даже несовпадение программной частоты f0 с частотой пика спектра волн fp) (рис. 8).

Рис. 7.

Гистограммы для нерегулярных механических волн в точках Р1 (кривая 1), Р4 (2, сдвинута на 0.2): а – Hs = 3 см,  f0 = 1.5 Гц; б – Hs = 10 см,  f0 = 1.0 Гц.

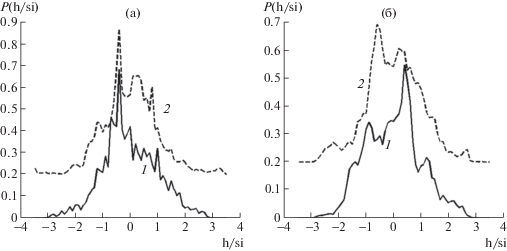
Таблица 3.

Кумулянты нерегулярных механических волн

Hs, см Параметры волн Точки измерений
P1 P4
f0 = 1.5 Гц
3 a0kp 0.047 0.041
  (μ2)1/2(м) 0.0063 0.0056
  K3 0.1334 0.1369
  K4 –0.0598 1.1403
  K5 –0.8822 –0.6048
  K6 –1.1695 –0.8662
10 a0kp 0.05 0.046
  (μ2)1/2(м) 0.0142 0.0131
  K3 0.0420 0.1085
  K4 –0.0824 –0.2725
  K5 –0.1772 0.0095
  K6 –0.5609 0.7868
f0 = 1.0 Гц
10 a0kp 0.04 0.04
  (μ2)1/2(м) 0.0141 0.013
  K3 0.1279 –0.0329
  K4 –0.3526 0.1222
  K5 –0.2324 0.0570
  K6 0.5002 –1.9996
15 a0kp 0.042 0.04
  (μ2)1/2(м) 0.0169 0.0158
  K3 0.2030 0.0
  K4 –0.4330 0.1140
  K5 –0.5432 0.7505
  K6 1.0643 –1.9371
Рис. 8.

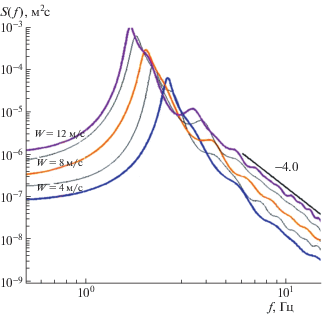
Спектры нерегулярных механических волн в точках Р1 (сплошная кривая) и Р4 (штриховая): а – Hs = 10 см,  f0 = 1.5 Гц; б – Hs = 10 см,  f0 = 1.0 Гц. Число при отрезке черной линии указывает степенной закон спадания хвоста спектра.

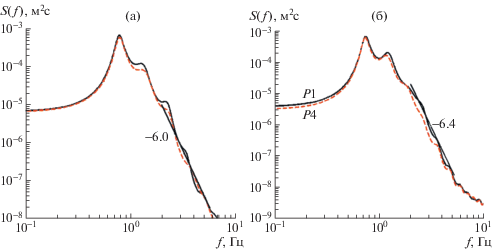
Как показано в [23], эти спектры не проявляют никакой автомодельности, что и обеспечивает хаотичность значений кумулянтов. Сказанное еще раз подтверждает наличие связи между формой спектра и кумулянтами и дает обоснование академической значимости приведенных выше результатов. В практическом плане изучение статистик более важно для ветровых волн.

3.4. Ветровые волны

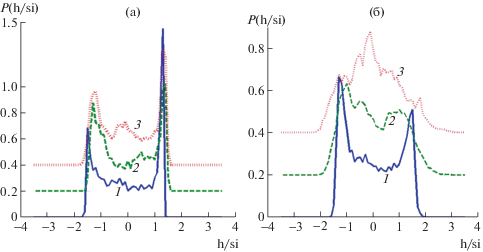
Гистограммы ветровых волн детально изучены в [21]. Для демонстрации их отличия от гистограмм, приведенных выше, приведем лишь наиболее представительные из них, полученные по данным настоящего эксперимента (рис. 9).

Рис. 9.

Гистограммы ветровых волн в точках Р1 (сплошная кривая) и Р4 (штриховая) и ПРВ Гаусса (пунктирная): а, б – ветер W = 8 и 12 м/с; в – то же, что и на панели б, но в полулогарифмическом масштабе.

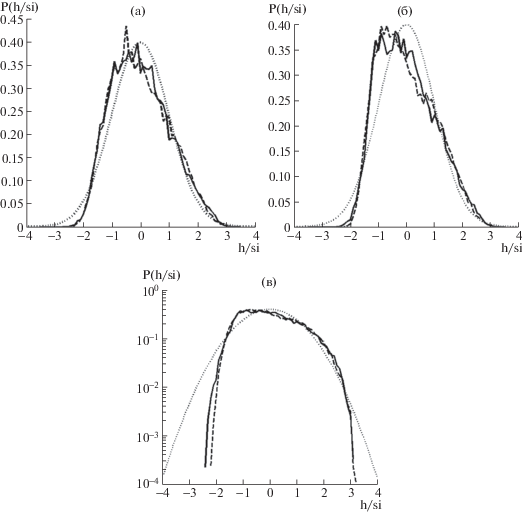
Отметим три особенности ГГ для ветровых волн, не указанные в более ранних исследованиях [16, 18, 21]: 1) постепенное смещение максимума гистограммы в область значений нормированной амплитуды h/si ∼ 0.1 по мере возрастания скорости ветра и разгона волн; 2) постепенное приобретение гистограммой формы косого треугольника в пространстве (h/si, P) с координатами основания в области точек (–2.3, 0) и (3.2, 0) и вершиной в области точки (–1.0, 0.4), т.е. в области отрицательных амплитуд (h/si ≈ –0.1); 3) существенное занижение экстремальных значений ложбин и гребней волн по сравнению с гауссовым распределением (рис. 9в). Последняя из особенностей находится в противоречии с принятыми в настоящее время теоретическими воззрениями относительно свойств нелинейных волн [6, 14, 15, 22], что естественно требует дополнительных пояснений и дальнейших исследований.

Указанные выше особенности гистограмм ветровых волн в цифровом виде выражаются через кумулянты, приведенные в табл. 4.

Таблица 4.

Кумулянты ветровых волн

Ветер, м/с Параметры волн Точки измерений
P1 P3 P4
4 a0kp 0.27 0.23 0.20
  (μ2)1/2(м) 0.002 0.0043 0.0052
  K3 0.1124 0.5221 0.3429
  K4 –0.7096 –0.1962 –0.4420
  K5 –0.7369 –1.5222 –1.1276
  K6 2.7051 –1.9718 0.2647
8 a0kp 0.34 0.27 0.25
  (μ2)1/2(м) 0.0052 0.092 0.0105
  K3 0.3390 0.4049 0.3306
  K4 –0.4471 –0.5282 –0.5433
  K5 –1.1261 –1.6117 –1.2047
  K6 0.3016 0.3640 1.1195
12 a0kp 0.37 0.31 0.28
  (μ2)1/2(м) 0.0086 0.0146 0.0179
  K3 0.4027 0.4298 0.4120
  K4 –0.5038 –0.5580 –0.6201
  K5 –1.4969 –1.6634 –1.6430
  K6 0.3447 0.7930 1.2018

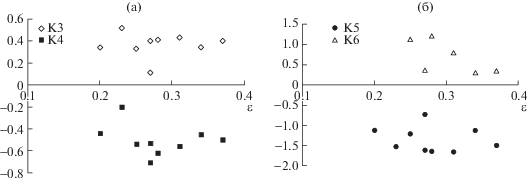
В отличие от выводов работ [9, 21], приведенные в табл. 4 величины свидетельствуют об отсутствии четкой статистической зависимости кумулянтов от крутизны волн и их возраста, (см. (2.6)). В качестве примера этот факт подтверждается на рис. 10. Вместе с тем обращает на себя внимание устойчивое соотношение знаков кумулянтов K3–K5, аналогичное [21]. Кроме того, настоящие результаты по величинам и знакам K3, K4 близки к таковым по натурным данным [24], а также они уточняют часть выводов для кумулянтов лотковых данных из работы [9], дополняя [9, 24] в части демонстрации кумулянтов K5, K6.

Рис. 10.

Соотношения кумулянтов и крутизны волн по табл. 4.

Как отмечено в [24], найденное поведение кумулянтов K3–K6 хорошо описывается в рамках модели по перенормировке теории возмущений для слабо нелинейных волн на воде [28]. Подчеркнем, что слабая изменчивость кумулянтов с разгоном и изменением крутизны ветровых волн прямо связана с устойчивой, почти автомодельной формой их спектров, наблюдаемой в данном эксперименте и детально описанной в [23], что демонстрируется на рис. 11.

Рис. 11.

Ансамбль спектров ветровых волн в точке P4 для пяти значений ветра W (кривые снизу вверх). Число при отрезке прямой линии указывает степенной закон спадания хвостов спектров.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Ниже основное внимание будет уделено вопросам новизны полученных результатов по затронутым аспектам статистики ветровых волн в сопоставлении с результатами других работ [4, 9, 14, 21].

Прежде всего отметим эффективность исследования функций распределения для волнения на воде именно в применении к амплитудам волн h, а не к их высотам H, как это широко принято [4, 5, 9, 18], и именно по гистограммам волн в нормировке (3.1). Здесь важно, что только амплитуды волн являются предметом теоретического анализа [2, 21, 25, 26], а функция ПРВ Гаусса для амплитуд (2.4) является базовой, в то время как ПРВ Релея для высот волн уже является конструктивной производной [2, 9, 16]. Более того, существенные отклонения статистики для амплитуд волн от гауссовой снимает и саму возможность использования распределения Рэлея, как следствие нарушения гауссовости распределения амплитуд волн [1].

В качестве нового результата отметим факт резкого спадания гистограмм для исследуемых лотковых ветровых волн в области значений h/si < –2 и h/si > 3 (рис. 8в), что не отмечалось ранее [4, 5, 9, 21]. Более того, в работах [4, 5, 14] используемая их теория предсказывает возможный рост экстремумов волн выше гауссовых. Полученный в настоящей работе результат говорит в пользу существенного отклонения статистики ветровых волн от гауссовой в сторону занижения экстремальных волн, что принципиальным образом должно сказаться на статистике предельных амплитуд (и высот) волн, играющей важнейшую роль в оценке рисков морской деятельности человека [16–18, 29].

Отметим, что в натурных условиях могут реализоваться несколько иные статистки ветровых волн по причине порывистости природного ветра. Теоретическое изучение статистик волн следует выполнять в рамках стационарной теории, а не в терминах кинетических уравнений, как это делалось в [4, 5, 14]. Дальнейшие исследования в этой области, построенные на выборках данных натурных и лотковых наблюдений в сотни тысяч отсчетов и покрывающих масштабы времени наблюдений в тысячи периодов основной волны, здесь весьма перспективны.

Дополнительно отметим, что использование гистограмм позволило установить наличие многих общих черт в этих характеристиках, как для модельных волн, так и механических, о чем свидетельствует сопоставление рис. 3 и 5. Однако отличие ГГ для механических волн с широким спектром (нерегулярных волн) от реальных ветровых волн не столь радикально, как для регулярных волн. Тем не менее использование нормированных кумулянтов, заданных формулами (2.3) и (2.5), позволяет установить такое отличие.

Кумулянты широко используются в исследованиях статистик как для эмпирических данных [9, 21, 24], так и в теории [1, 2, 6, 13–15, 28]. При этом часто предпринимаются попытки установления зависимости, в частности, кумулянтов K3 и K4 от крутизны ε волн [2, 9, 21] или от их возраста А [9]. Вместе с тем установлено [24, 28], что на самом деле все кумулянты фактически не зависят ни от ε, ни от А. Для натурных волн это показано в [24], а для лабораторных – представлено на рис. 10. Стационарная теория дана в [28]. Новизна нашего результата заключается в том, что наблюдаемая изменчивость кумулянтов (табл. 4) однозначно определяется изменчивостью формы спектров волн S(f). Этот факт лишний раз доказывают и наши расчеты кумулянтов для механических волн (табл. 2, 3), имеющих большое разнообразие форм S(f) (рис. 6, 8). Здесь впервые констатируется указанный факт как эмпирический, поскольку в большинстве работ по статистике волн [5, 6, 9, 21, 24], для интерпретации изменчивости кумулянтов спектры не привлекались.

ЗАКЛЮЧЕНИЕ

Проведена серия экспериментов по генерации механических и ветровых волн в большом ветро-волновом канале.

Показано, что изменчивость статистики волн (гистограммы, статистические моменты) может быть проанализирована путем расчета кумулянтов временных рядов измеренных волнограмм. Построены гистограммы для различных типов волн и приведены соответствующие им величины кумулянтов и спектров в ряде точек измерений вдоль канала.

С использованием закономерностей эволюции частотного спектра волн вдоль ветро-волнового канала показано, что изменчивость статистик волн однозначно определяется изменчивостью формы их спектра, а не отдельными характеристиками системы (разгон, крутизна или возраст волнения).

Работа выполнена при поддержке проекта РФФИ 18-05-00161. Автор благодарен китайским партнерам Ф. Цяо, Х. Ма и Ш. Чанг за участие в выполнении измерений.

Список литературы

  1. Longuet-Higgins M. On the statistical distribution of the heights of sea waves // J. Mar. Res., 1952. V. 11. P. 245–266.

  2. Longuet-Higgins M. The effect of nonlinearities on statistical distributions in the theory of sea waves // J. Fluid Mech. 1963. V. 17. P. 459–480.

  3. Kinsman B. Wind Waves. Prentice-Hall, Inc. 1965. 676 p.

  4. Onorato M., Osborne A.R., Serio M., Cavaleri L. Modulational instability and non-Gaussian statistics in experimental random water-wave trains // Phys. Fluids. 2005. V. 17. 078101. https://doi.org/10.1063/1.1946769

  5. Onorato M., Osborne A.R., Serio M., Cavaleri L., Brandini C., Stansberg C.T. Extreme waves, modulational instability and second order theory: Wave flume experiments on irregular waves // Eur. J. Mech. 2006. V. 25B. P. 586–601.

  6. Onorato M., Cavaleri L., Fouques S. et al. (13 coauthors) Statistical properties of mechanically generated surface gravity waves: A laboratory experiment in a three-dimensional wave basin // J. Fluid Mech. 2009. V. 627. P. 235–257. https://doi.org/10.1017/S002211200900603X

  7. Shemer L., Sergeeva A. An experimental study ofspatial evolution of statistical parameters in a unidirectional narrow-banded random wave field // J. Geophys. Res. 2009. V. 114. C01015.https://doi.org/10.1029/2008JC005077

  8. Shemer L., Sergeeva A., Liberzon D. Effect of the initial spectrum on the spatial evolution of statistics of unidirectional nonlinear random waves // J. Geophys. Res. 2010. V. 115, C12039. https://doi.org/10.1029/2010JC006326

  9. Zavadsky A., Liberson D., Shemer L. Statistical Analysis of the Spatial Evolution of the Stationary Wind Wave Field // J. Phys. Oceanogr. 2013. V. 43 (1). P. 65–79. https://doi.org/10.1175/JPO-D-12-0103.1

  10. Tayfun M.A. Narrow-band nonlinear sea waves // J. Geophys. Res. 1980. V. 85 (C3). P. 1548–1552.

  11. Tayfun M.A. Statistics of nonlinear wave crests and groups // Ocean Eng. 2006. V. 33. P. 1589–1622.

  12. Tayfun M.A., Fedele F. Wave height distributions and nonlinear effects // Ocean Eng. 2007. V. 34. P. 1631–1649.

  13. Socquet-Juglard H., Dysthe K., Trulsen K., Krogstad H.E., Liu J. Probability distributions of surface gravity waves during spectral changes // J. Fluid Mech. 2005, V. 542. P. 195–216. https://doi.org/10.1017/S0022112005006312

  14. Janssen P.A.E.M. Nonlinear Four-Wave Interactions and Freak Waves // J. Phys. Oceanogr. 2003. V. 33. P. 863–884.

  15. Janssen P.A.E.M., Janssen A.J.E.M. Asymptotics for the long-time evolution of kurtosis of narrow-band ocean waves // J. Fluid Mech. 2019. V. 859. P. 790–818. https://doi.org/10.1017/jfm.2018.844

  16. Давидан И.Н., Лопатухин Л.И., Рожков В.А. Ветровые волны в Мировом океане. Л.: Гидрометеоиздат. 1985. 256 с.

  17. Goda Y. Random Seas and Design of Marine Structures. World Scientific. 2000. 443 p.

  18. Лопатухин Л.И. Ветровое волнение: 2-е изд. СПб.: ВВМ. 2012. 165 с.

  19. Бондур В.Г. Проблемы аэрокосмического мониторинга океана. В сб. “Исследования в области океанологии, физики атмосферы, географии, экологии, водных проблем и геокриологии”. М.: ГЕОС, 2001. С. 87–94.

  20. Isaksen L., Janssen P.A.E.M. Impact of ERS scatterometer winds in ECMWF’s assimilation system // Q. J. R. Meteorol. Soc. 2004. V. 130. P. 1793–1814.

  21. Huang N.E., Long S.R. An experimental study of the surface elevation probability, distribution and statistics of wind-generated waves // J. Fluid Mech. 1980. V. 101. № 1. P. 179–200.

  22. Annenkov S.Y., Shrira V.I. Evolution of kurtosis for wind waves // Geophys. Res. Lett. 2009. V. 36. L13603. https://doi.org/10.1029/2009GL038613

  23. Полников В.Г., Цяо Ф., Ма Х., Чанг Ш. Новые эффекты эволюции спектра волн в лотке // Письма в ЖЭТФ. 2020. Т. 111. № 8. С. 501–508. https://doi.org/10.31857/S1234567820080042

  24. Бабанин А.В., Полников В.Г. О негауссовости ветровых волн // Морской гидрофизический журнал.1994. № 3. С. 79–82.

  25. Komen G.I., Cavaleri L., Donelan M. et al. Dynamics and Modelling of Ocean Waves. London: Cambridge University Press, 1994. 554 p.

  26. Филлипс О.М. Динамика верхнего слоя океана. Л.: Гидрометеоиздат, 1980. 320 с.

  27. Kay S.M. Modern Spectral Estimation, Theory and Application. Englewood Cliffs, NJ: Prentice Hall, New Jersey. 1988. 540 p.

  28. Полников В.Г. Метод перенормировки в теории возмущений для случайного поля нелинейных поверхностных волн // Мор. гидрофиз. журн. 1988. № 3. С. 34–41.

  29. Полников В.Г., Гоморев И.А. Об оценках режимных значений временных рядов скорости ветра и высот волнения // Метеорология и гидрология. 2015. № 12. С. 64–73.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал