1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2021

Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 98-108

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПСЕВДОСКАЧКА В ТРАНСЗВУКОВОМ ТЕЧЕНИИ ГАЗА В ДИФФУЗОРЕ

И. И. Липатов a, *, В. Ю. Ляпидевский b, c, **, А. А. Чесноков b, c, ***

a Центральный аэрогидродинамический институт им. Н.Е. Жуковского
Жуковский, Московская обл., Россия

b Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

c Новосибирский государственный университет
Новосибирск, Россия

* E-mail: igor_lipatov@mail.ru
** E-mail: liapid@hydro.nsc.ru
*** E-mail: chesnokov@hydro.nsc.ru

Поступила в редакцию 14.05.2021
После доработки 22.06.2021
Принята к публикации 22.06.2021

Полный текст (PDF)

Аннотация

Математическая модель движения баротропного газа, основанная на двухслойном представлении течения с областями сверхзвукового ядра и пристеночного пограничного слоя, применена для описания ударно-волновых структур в каналах и соплах переменного сечения. Нестационарная модель псевдоскачка записывается в виде системы пяти неоднородных законов сохранения. Определены скорости распространения возмущений и сформулированы достаточные условия гиперболичности уравнений движения. Проведено численное моделирование формирования квазистационарных ударных волн и осцилляций фронта псевдоскачка при периодическом вдуве или изменении выходного сечения канала. Модель верифицирована сравнением с известными экспериментальными данными вынужденных колебаний псевдоскачка в трансзвуковом канале.

Ключевые слова: псевдоскачок, трансзвуковое течение, уравнения длинных волн, баротропный газ

Формирование сложных газодинамических структур, таких как псевдоскачок и отрывное течение, является характерной особенностью процессов торможения сверхзвукового потока в каналах и соплах переменного сечения [1, 2]. Под псевдоскачком понимается область перехода от сверхзвукового к дозвуковому течению, связанная с отрывом и интенсивным развитием пограничного турбулентного слоя. Математическое описание структуры внутренних отрывных течений сопряжено со значительными трудностями, поскольку непосредственное применение теории пограничного слоя или решений для вязкого установившегося внешнего течения, как правило, не представляется возможным. Многочисленные экспериментальные исследования процессов торможения сверхзвуковых течений газа в каналах показывают, что изучаемые явления характеризуются разными режимами и масштабами [3–5]. При этом на структуру потока оказывают влияние нестационарные процессы, развивающиеся в стационарном сверхзвуковом течении газа при взаимодействии с турбулентным пограничным слоем. Современное состояние дел в области изучения взаимодействия ударной волны с пограничным слоем и управления им во внутренних и внешних потоках представлено в недавних обзорных работах [6, 7]. Эксперименты показывают, что введение различных возмущений в поток за псевдоскачком (сужение канала, приток массы или энергии, химические реакции) приводит к перемещению псевдоскачка вверх по потоку. Периодическое механическое или энергетическое воздействие на поток может вызвать вынужденные колебания псевдоскачка вокруг нового квазистационарного положения [8–10]. Попытки описать характерные особенности псевдоскачка в рамках простых одномерных моделей предприняты в [11, 12]. В недавних работах [13–16] экспериментально и численно исследованы возникновение и распространение нестационарных низкочастотных ударных колебаний в присоединенном и отрывном потоках, реализующихся в сверхзвуковой аэродинамической трубе с различными типами препятствий. Несмотря на многолетние исследования особенностей вынужденных колебаний псевдоскачка, остается ряд открытых вопросов, связанных с определением условий вниз по потоку, обеспечивающих контроль положения псевдоскачка, а также с выяснением механизма передачи возмущений вверх по потоку в течениях со сверхзвуковым ядром.

В работе используется предложенная в [10] одномерная модель нестационарного псевдоскачка в баротропном течении газа, основанная на двухслойном представлении течения (потенциальное сверхзвуковое ядро и турбулентный пограничный слой). Уравнения движения представляются в виде системы из пяти законов сохранения с правой частью, включающих эмпирические постоянные, отвечающие за интенсивность массообмена между слоями, диссипацию энергии и трение о стенки канала. Модель позволяет определить качественные и количественные характеристики вынужденных колебаний псевдоскачка при периодическом воздействии на поток в выходной части канала. В отличие от [10] рассматриваются течения в расширяющихся каналах и соплах. Известно, что при взаимодействии сверхзвукового ядра потока с турбулентным пограничным слоем в сверхзвуковой части течения формируется сложная структура из взаимодействующих ударных волн. Однако эксперименты показывают [8, 9], что при умеренных числах Маха в расширяющихся каналах формируется прямой скачок уплотнения, за которым начинается интенсивное развитие турбулентного пограничного слоя. Представляемая ниже модель описывает формирование и эволюцию псевдоскачка, фронт которого будет далее ассоциироваться с этим скачком уплотнения. Выполнено численное моделирование сверхзвуковых и трансзвуковых течений, представляющих эволюцию псевдоскачка при периодической подкачке газа или изменении выходного сечения канала. Результаты расчетов верифицированы экспериментальными данными вынужденных колебаний псевдоскачка в трансзвуковом канале.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассматривается течение баротропного газа в плоском канале переменного сечения, в котором реализуется псевдоскачок. Механизм перехода от сверхзвукового течения к дозвуковому в псевдоскачке связан с развитием пристеночного пограничного слоя. В предположении о том, что пограничный слой формируется в окрестности стенок канала и течение симметрично относительно его оси, в [10] предложена одномерная модель нестационарного псевдоскачка, основанная на двухслойном представлении течения. Уравнения движения имеют вид

(1.1)
$\begin{array}{*{20}{c}} {{{{(\rho h)}}_{t}} + {{{(u\rho h)}}_{x}} = - \sigma q\rho ,\quad {{{(\rho H)}}_{t}} + {{Q}_{x}} = f,\quad {{u}_{t}} + {{{({{u}^{2}}{\text{/}}2 + i)}}_{x}} = 0,} \\ {{{Q}_{t}} + {{{({{u}^{2}}\rho h + ({{{v}}^{2}} + {{q}^{2}})\rho \eta + Hp)}}_{x}} = - p{{z}_{x}} - {{c}_{f}}\rho {{{v}}^{2}} + {v}f} \end{array}$
и замыкаются дополнительным соотношением

(1.2)
$\begin{gathered} {{({{u}^{2}}\rho h + ({{{v}}^{2}} + {{q}^{2}})\rho \eta + 2H\varepsilon \rho )}_{t}} + {{({{u}^{3}}\rho h + ({{{v}}^{2}} + 3{{q}^{2}}){v}\rho \eta + 2Qi)}_{x}} = \\ = \;2p{{z}_{t}} - \sigma \kappa \rho {{q}^{3}} - 2{{c}_{f}}\rho {{{v}}^{3}} + 2\varepsilon {v}. \\ \end{gathered} $

Здесь $\rho $ – плотность газа; h и $\eta $ – толщины сверхзвукового ядра и пограничного слоя; $u$ и ${v}$ – скорость газа в этих слоях; $Q = (uh + {v}\eta )\rho $ – расход; величина q характеризует сдвиговой характер течения в пограничном слое. Заметим, что в рамках этой модели рассматривается средняя скорость ${v}$ пограничного слоя, поэтому даже в области отрыва величина ${v}$ остается положительной (${v} > 0$). Гладкая функция $z = z(t,x)$ задает профиль канала полуширины $H = h + \eta = {{H}_{0}} - z$. Предполагается, что во входном сечении канала z = 0. Функция $f(t,x)$ задает приток газа в пристеночный пограничный слой (равна нулю при отсутствии вдува). Постоянные $\sigma $, $\kappa $ и cf – эмпирические параметры, отвечающие за интенсивность массообмена (скорость вовлечения газа в турбулентный слой), диссипацию энергии и трение о стенки канала. Давление, внутренняя энергия, скорость звука и энтальпия политропного газа задаются формулами

$p = {{p}_{0}}{{\left( {\frac{\rho }{{{{\rho }_{0}}}}} \right)}^{\gamma }},\quad \varepsilon = \frac{p}{{(\gamma - 1)\rho }},\quad {{c}^{2}} = \frac{{\gamma p}}{\rho },\quad i = \frac{{{{c}^{2}}}}{{\gamma - 1}}.$

Переходя к безразмерным переменным, полагаем ${{H}_{0}} = 1$, ${{\rho }_{0}} = 1$, ${{p}_{0}} = 1{\text{/}}\gamma $ и $c_{0}^{2} = 1$.

Получение модели (1.1), (1.2) основано на процедуре осреднения двумерных уравнений движения газа в плоском канале переменного сечения в длинноволновом приближении [17]

(1.3)
$\begin{array}{*{20}{c}} {{{\rho }_{t}} + {{{(U\rho )}}_{x}} + {{{(V\rho )}}_{y}} = 0,\quad {{{(U\rho )}}_{t}} + {{{({{U}^{2}}\rho + p)}}_{x}} + {{{(UV\rho )}}_{y}} = - {{c}_{f}}\rho {{U}^{2}},} \\ {{{p}_{y}} = 0,\quad {{e}_{t}} + {{{((e + p)U)}}_{x}} + {{{((e + p)V)}}_{y}} = 0.} \end{array}$

Система (1.3) дополняется граничными условиями

${{\left. V \right|}_{{y = 0}}} = 0,\quad {{z}_{t}} + U{{z}_{x}} + {{\left. V \right|}_{{y = {{H}_{0}} - z}}} = 0.$

Здесь $U(t,x,y)$ и $V(t,x,y)$ – компоненты вектора скорости газа, $e = (\varepsilon + {{U}^{2}}{\text{/}}2)\rho $ – полная энергия. В случае баротропного газа последнее уравнение системы (3) является следствием предыдущих. Осреднение уравнений (1.3) по ширине канала с использованием предположения о структуре течения (потенциальное сверхзвуковое ядро, пристеночный пограничный слой) и введение обозначений

$u = \frac{1}{h}\int\limits_0^h U dy,\quad {v} = \frac{1}{\eta }\int\limits_h^{{{H}_{0}} - z} U dy,\quad {{q}^{2}} = \frac{1}{\eta }\int\limits_h^{{{H}_{0}} - z} {{{{(U - {v})}}^{2}}} dy$
приводит к модели (1.1), (1.2).

Первые два уравнения системы (1.1) выражают баланс массы в ядре потока и полный закон сохранения массы, третье – уравнение Бернулли для скорости в потенциальном сверхзвуковом ядре потока, четвертое – закон сохранения полного импульса. Замыкающее уравнение (1.2) соответствует полному закону сохранения энергии. Для проведения численных расчетов уравнение (1.2) удобно заменить дифференциальным следствием

(1.4)
${{q}_{t}} + {{({v}q)}_{x}} = \frac{\sigma }{{2\eta }}({{(u - {v})}^{2}} - (1 + \kappa ){{q}^{2}}).$

Непрерывные решения систем (1.1), (1.2) и (1.1), (1.4) совпадают. При рассмотрении разрывных течений требуются дополнительный анализ и сопоставление решений.

Отметим, что аналогичные двухслойные и трехслойные модели применяются для описания эволюции турбулентных боров и слоев смешения в сдвиговых течениях жидкости со свободной границей [17], в каналах с упругими стенками [18] и в ячейке Хеле–Шоу [19].

1.1. Характеристики уравнений движения

Покажем, что система (1.1), (1.4) всегда имеет три вещественные характеристики и сформулируем достаточные условия гиперболичности модели. Из уравнения полного импульса следует, что

${{{v}}_{t}} + {v}{{{v}}_{x}} + \frac{{{{c}^{2}}}}{\rho }{{\rho }_{x}} + \frac{1}{{\rho \eta }}{{(\rho \eta {{q}^{2}})}_{x}} = \frac{{\sigma q}}{\eta }(u - {v}) - \frac{{{{c}_{f}}{{{v}}^{2}}}}{\eta }.$

С использованием этого следствия рассматриваемую систему уравнений представим в виде ${{U}_{t}} + A{{U}_{x}} = F$, где $U = {{(\rho ,h,u,{v},q)}^{{\text{т}}}}$ – вектор искомых величин (верхний индекс означает транспонирование), A – матрица размерности 5 × 5, F – правая часть. Вычисление собственных значений матрицы A сводится к решению алгебраического уравнения ${\text{det}}(A - \lambda I) = ({v} - \lambda )\chi (\lambda ) = 0$, где полином $\chi (\lambda )$ имеет вид

(1.5)
$\chi (\lambda ) = \left( {{{{(u - \lambda )}}^{2}} - \frac{{h{{c}^{2}}}}{H}} \right)({{({v} - \lambda )}^{2}} - 3{{q}^{2}}) - \frac{{\eta {{c}^{2}}}}{H}{{(u - \lambda )}^{2}}.$

Корни уравнения $\chi (\lambda ) = 0$ определяют скорости звуковых характеристик $dx{\text{/}}dt = \lambda $ системы (1.1), (1.4). При этом всегда имеется одна контактная характеристика $dx{\text{/}}dt = {v}$. Для выяснения условий существования четырех вещественных корней полинома (1.5) удобно воспользоваться аналогом предложенного в [20] геометрического подхода.

Введем новые переменные

(1.6)
$\Phi = \frac{{u - \lambda }}{c}\sqrt {\frac{H}{h}} ,\quad \Psi = \frac{{{v} - \lambda }}{{q\sqrt 3 }}.$

Тогда уравнение $\chi (\lambda ) = 0$ записывается следующим образом

(1.7)
$({{\Phi }^{2}} - 1)({{\Psi }^{2}} - 1) = {{a}^{2}}{{\Phi }^{2}},\quad {{a}^{2}} = \frac{{\eta {{c}^{2}}}}{{3H{{q}^{2}}}},$
а исключение $\lambda $ из (1.6) дает соотношение

(1.8)
$\Psi = {{a}_{1}}\Phi + {{a}_{2}}\quad \left( {{{a}_{1}} = \frac{c}{q}\sqrt {\frac{h}{{3H}}} ,\quad {{a}_{2}} = - \frac{{u - {v}}}{{q\sqrt 3 }}} \right).$

На плоскости $(\Phi ,\Psi )$ уравнение (1.7) описывает кривую четверного порядка, имеющую четыре оси симметрии $\Phi = \pm 1$ и $\Psi = \pm \sqrt {{{a}^{2}} + 1} $. Характерный вид кривой (1.7), состоящей из четырех неограниченных ветвей и вписанного в квадрат “эллипса” с полуосями $1{\text{/}}\sqrt {{{a}^{2}} + 1} $ и 1, показан на рис. 1 сплошными линиями; пунктир – прямая (1.8). График получен при $u - {v} = 0.15$, $c = 1$, $q = 0.3$, $h = 0.7$, $\eta = 0.3$. Число вещественных корней полинома $\chi (\lambda )$ совпадает с числом точек пересечения кривой (1.7) и прямой (1.8). При ${{a}_{1}} \ne 0$ всегда имеется две точки пересечения вне квадрата со стороной длины 2 и центром в начале координат. Если ордината прямой (1.8) при Φ = 0 по модулю меньше единицы (т.е. $\left| {{{a}_{2}}} \right| < 1$), то имеется еще две точки пересечения. Таким образом, достаточное условие существования четырех вещественных корней полинома (1.5) имеет вид

(1.9)
$\left| {(u - {v}){\text{/}}q} \right| < \sqrt 3 .$
Рис. 1.

Геометрическая интерпретация условий гиперболичности уравнений (1.1), (1.4) на плоскости $(\Phi ,\Psi )$: кривая (1.7) – сплошные линии, прямая (1.8) – пунктир.

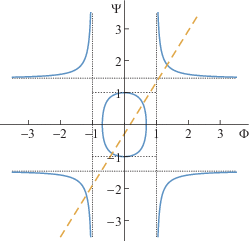
При выполнении условия (1.9) система (1.1), (1.4) является гиперболической.

Заметим, что наличие комплексных характеристик в рассматриваемой модели свидетельствует о развитии длинноволновой неустойчивости сдвигового течения. Но уравнения (1.1), (1.4), собственно говоря, и описывают нелинейную фазу развития этой неустойчивости. Поэтому модель применима во всей области допустимых параметров течения.

1.2. Соотношения на разрыве

В силу неоднородных законов сохранения (1.1), (1.4) на сильном разрыве выполняются соотношения

$\begin{array}{*{20}{c}} {[{{{(u - D)}}^{2}} + 2i] = 0,\quad \left[ {(u - D)\rho h} \right] = 0,\quad \left[ {({v} - D)\rho \eta } \right] = 0,} \\ {[{{{(u - D)}}^{2}}\rho h + ({{{({v} - D)}}^{2}} + {{q}^{2}})\rho \eta + Hp] = 0,\quad \left[ {({v} - D)q} \right] = 0} \end{array}$
(квадратные скобки означают разность предельных значений функций на фронте разрыва). Без ограничения общности полагаем скорость распространения разрыва D = 0, что соответствует системе координат, движущейся вместе с волной. Пусть по одну сторону от разрыва решение известно (соответствующие функции обозначены индексом “1”). Тогда искомые величины с другой стороны разрыва выражаются по формулам
(1.10)
$\begin{array}{*{20}{c}} {u(\rho ) = \sqrt {u_{1}^{2} + \frac{2}{{\gamma - 1}}(\rho _{1}^{{\gamma - 1}} - {{\rho }^{{\gamma - 1}}})} ,\quad h(\rho ) = \frac{{{{u}_{1}}{{\rho }_{1}}{{h}_{1}}}}{{\rho u(\rho )}},} \\ {\eta (\rho ) = {{H}_{1}} - h(\rho ),\quad {v}(\rho ) = \frac{{({{H}_{1}} - {{h}_{1}}){{\rho }_{1}}{{{v}}_{1}}}}{{({{H}_{1}} - h(\rho ))\rho }},\quad q(\rho ) = \frac{{{{{v}}_{1}}{{q}_{1}}}}{{{v}(\rho )}},} \end{array}$
где ρ – корень алгебраического уравнения

(1.11)
${{u}_{1}}{{\rho }_{1}}{{h}_{1}}u(\rho ) + {{{v}}_{1}}{{\rho }_{1}}{{\eta }_{1}}{v}(\rho ) + {{q}^{2}}(\rho )\rho \eta (\rho ) + \frac{{{{H}_{1}}}}{\gamma }{{\rho }^{\gamma }} = u_{1}^{2}{{\rho }_{1}}{{h}_{1}} + (u_{1}^{2} + q_{1}^{2}){{\rho }_{1}}{{\eta }_{1}} + \frac{{{{H}_{1}}}}{\gamma }\rho _{1}^{\gamma }.$

Решения уравнений (1.1) с замыкающим соотношением (1.2) или (1.4) совпадают в области гладкого течения, но могут различаться на скачке. В случае использования консервативной формы уравнений с законом сохранения энергии (1.2) последнее соотношение в (1.10) следует заменить выражением

${{q}^{2}}(\rho ) = \frac{1}{{3{{{v}}_{1}}{{\rho }_{1}}{{\eta }_{1}}}}({{\psi }_{1}} - 2{{Q}_{1}}i(\rho ) - {{u}_{1}}{{\rho }_{1}}{{h}_{1}}{{u}^{2}}(\rho ) - {{{v}}_{1}}{{\rho }_{1}}{{h}_{1}}{{{v}}^{2}}(\rho )),$
где ${{\psi }_{1}} = u_{1}^{3}{{\rho }_{1}}{{h}_{1}}(v_{1}^{2} + 3q_{1}^{2}){{{v}}_{1}}{{\rho }_{1}}{{\eta }_{1}} + 2{{Q}_{1}}{{i}_{1}}$.

В рассмотренных ниже примерах соотношения (1.10), (1.11) используются для определения состояния за скачком. При этом выбирается ближайший к ${{\rho }_{1}}$ корень уравнения (1.11) ($\rho \ne {{\rho }_{1}}$) и проверяются условия устойчивости разрыва. Далее будет показано, что несмотря на различия в определении разрывного решения с использованием замыкающих уравнений (1.4) и (1.2), в области за скачком решения почти не различаются всюду, кроме малой окрестности фронта разрыва.

Следует отметить, что скорости характеристик уравнений двухслойного течения (1.1), (1.4) (корни полинома (1.5)) отличаются от звуковых характеристик одномерных уравнений газовой динамики. Поэтому для описания режимов течения будут использованы термины сверхкритический (докритический) вместо сверхзвуковой (дозвуковой).

1.3. Стационарные решения

Для построения решений уравнений движения в случае стационарных течений соответствующую систему обыкновенных дифференциальных уравнений удобно привести к разрешенному относительно производных виду [10]:

(1.12)
$\begin{array}{*{20}{c}} {u{\text{'}} = - \frac{{{{c}^{2}}}}{{\rho u}}\rho {\text{'}},\quad \eta {\text{'}} = \frac{{\sigma q}}{u} + \left( {1 - \frac{{{{c}^{2}}}}{{{{u}^{2}}}}} \right)\frac{h}{\rho }\rho {\text{'}} - z{\text{'}},\quad {v}{\text{'}} = \frac{{\sigma q}}{\eta } - \frac{{v}}{\rho }\rho {\text{'}} - \frac{{v}}{\eta }\eta {\text{'}},} \\ {q{\text{'}} = \frac{\sigma }{{2\eta {v}}}({{{(u - {v})}}^{2}} - (1 + \kappa ){{q}^{2}}) - \frac{q}{{v}}{v}{\text{'}},\quad \rho {\text{'}} = \left( {\left( {z{\text{'}} - \frac{{\sigma q}}{u}} \right)({{{v}}^{2}} - 3{{q}^{2}}) + F} \right)\frac{\rho }{\Delta }.} \end{array}$

Здесь штрих означает дифференцирование по x и

(1.13)
$\Delta = \left( {H - \frac{{h{{c}^{2}}}}{{{{u}^{2}}}}} \right)({{{v}}^{2}} - 3{{q}^{2}}) - \eta {{c}^{2}},\quad F = {{c}_{f}}{{{v}}^{2}} + \frac{{\sigma q}}{{v}}({{u}^{2}} - 3u{v} + 3{{{v}}^{2}} - (3 + \kappa ){{q}^{2}}).$

Знак определителя Δ указывает на тип течения: в среднем дозвуковой (докритический) при $\Delta < 0$, в среднем сверхзвуковой (сверхкритический) при $\Delta > 0$. Поскольку $\Delta = \chi (0)H{\text{/}}{{u}^{2}}$, то обращение в нуль Δ соответствует тому, что λ = 0 корень характеристического полинома (1.5).

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ И СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ

Приведены тестовые расчеты формирования и эволюции псевдоскасчка в канале переменного сечения на основе уравнений двухслойного движения баротропного газа. Для проведения расчетов применяется TVD-схема второго порядка аппроксимации [21]. Тесты включают: 1) реализацию квазистационарного режима течения, в котором положение псевдоскачка и другие параметры потока с высокой точностью совпадают при расчетах по стационарным и нестационарным уравнениям движения; 2) колебания псевдоскачка и генерацию вторичных волн при периодической подкачке газа; 3) сравнение результатов расчета эволюции псевдоскачка при периодическом изменении выходного сечения канала с экспериментальными данными [9].

2.1. Квазистационарный псевдоскачок

Проведено численное моделирование формирования квазистационарного псевдоскачка в рамках двухслойных уравнений движения (1.1), (1.4) в расширяющемся канале полутолщины $H = {{H}_{0}} - z$, где

(2.1)
$z = Z(x) = - {{k}_{0}}(arctan(x - {{x}_{c}}) - arctan({{x}_{c}})).$

Расчеты проводятся в безразмерных переменных. При t = 0 задан постоянный поток, имеющий скорость $u = {v} = 1.025$ и плотность ρ = 1. Начальная толщина турбулентной прослойки $\eta = 0.02$, переменная $q = {{10}^{{ - 4}}}$. Эти же условия используются в качестве граничных условий во входном сечении канала x = 0. На правой границе расчетной области $x = {{x}_{b}} = 18$ задаются “мягкие” граничные условия (${{{\mathbf{u}}}_{{N + 1}}} = {{{\mathbf{u}}}_{N}}$). Обозначение ${{{\mathbf{u}}}_{i}}$ соответствует искомым функциям в узловой точке $x = {{x}_{i}}$. Для дискретизации по x выбрана равномерная сетка из $N = 900$ узлов. Шаг по времени определяется автоматически из условия Куранта. Компьютерный код реализован в среде Matlab. Постоянные определяющие профиль канала (2.1) следующие ${{k}_{0}} = 0.16$, ${{x}_{c}} = 9$, ${{H}_{0}} = 1$. Здесь и далее полагаем $\gamma = 1.4$, ${{c}_{f}} = 0.003$, $\sigma = 0.2$ и $\kappa = 4$.

Напомним, что псевдоскачок – это область перехода сверхзвукового течения к дозвуковому, связанная с отрывом и интенсивным развитием пограничного слоя. В рамках используемой двухслойной модели течения газа в диффузоре в области псевдоскачка имеются сильные разрывы, первый из которых является фронтом псевдоскачка. Это отличает течения в диффузоре от рассмотренных ранее течений в канале постоянного сечения [10], для которых характерен непрерывный переход от сверхзвукового течения к дозвуковому. Формирование псевдоскачка осуществляется за счет управления препятствием, уменьшающим сечение канала в окрестности правой границы. В модели за это отвечает функция $z(t,x)$. При $x < {{x}_{ * }} = 15.3$ форма канала определяется формулой (2.1). В области $x \in ({{x}_{ * }},{{x}_{b}})$ функция z непрерывно продолжается параболой $z = Z({{x}_{ * }}) + a(t)(x - {{x}_{ * }})({{x}_{b}} - x)$, где коэффициент $a(t)$ монотонно меняется от нуля до 0.15 и для $t > 8$ сохраняет это значение. Такой выбор параметров обеспечивает локальное сужение канала и формирование квазистационарного разрывного решения, показанного на рис. 2 сплошными линиями при t = 150.

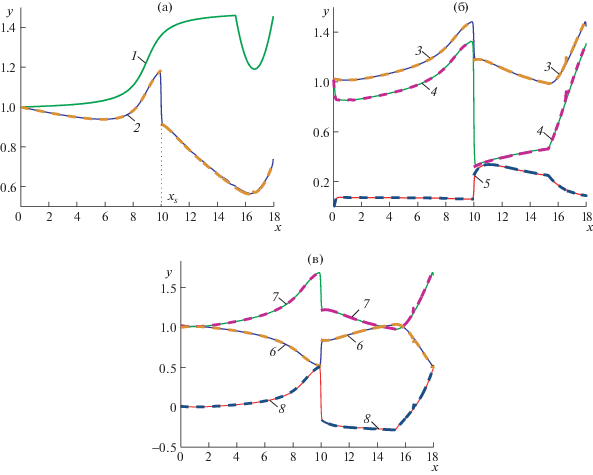
Рис. 2.

Выход на стационарный режим разрывного решения: а – форма канала $y = {{H}_{0}} - z$ и толщина сверхзвукового ядра течения $h$ (кривые 1 и 2); б – скорости в слоях $u$, ${v}$ и переменная q (кривые 3, 4 и 5); в – плотность $\rho $, число Маха $M = u{\text{/}}c$ и определитель $\Delta {\text{/}}3$ (кривые 6, 7 и 8). Сплошные линии – решение уравнений (1.1) при $t = 150$, пунктир – решение стационарных уравнений (1.12). Графики приведены в безразмерных переменных.

В результате эволюции течения развивается пристеночный пограничный слой. Расширение канала приводит к увеличению скорости в сверхзвуковом ядре потока. Число Маха ($M = u{\text{/}}c$) возрастает более чем в полтора раза и достигает максимального значения $M \approx 1.7$ перед скачком. Возмущения, формирующиеся в окрестности препятствия, распространяются как вверх, так и вниз по потоку. При $t \approx 70$ возмущения стабилизируются и течение переходит в квазистационарный режим, характеризующийся наличием сильного разрыва в окрестности сечения $x = {{x}_{s}} \approx 10$.

На рис. 2а кривая 1 задает форму канала $y = {{H}_{0}} - z$, линия 2 соответствует границе сверхзвукового ядра потока $y = h(t,x)$. Скорости газа в ядре течения и в пограничном слое, а также переменная q, определяющая сдвиговой характер течения в пристеночном слое, показаны на рис. 2б (кривые 3–5). Плотность $\rho $ и число Маха M представлены на рис. 2в (кривые 6, 7). На этом же графике показана переменная $\Delta $, заданная первой формулой (1.13). Как видно из графика, перед скачком в области $x < {{x}_{s}}$ течение является сверхкритическим ($\Delta > 0$), за скачком – докритическим ($\Delta < 0$). В области сверхкритического течения наблюдаются увеличение скорости ядра потока и уменьшение плотности. Докритическое течение характеризуется быстрым увеличением толщины пограничного слоя, торможением потока и ростом плотности. Заметим, что над обтекаемым препятствием при $x \approx 16.65$ течение непрерывно переходит в сверхкритический режим. Пунктирные кривые соответствуют решениям стационарных уравнений (1.12), построенным в областях $x < {{x}_{s}}$ и $x > {{x}_{s}}$. При x = 0 задаются условия, используемые в качестве начальных данных для нестационарной задачи. Значения функций за разрывом определяются по формулам (1.10), (1.11). Эти данные задаются при $x = {{x}_{s}}$ для построения стационарного решения за скачком. Как видно из графиков, стационарные и нестационарные решения практически полностью совпадают.

2.2. Колебания псевдоскачка при периодическом вдуве

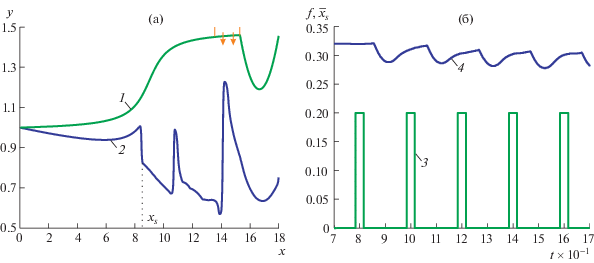
Одним из возможных способов воздействия на псевдоскачок является вдув (отсос) газа на заданной части стенки канала. В условиях предыдущего примера после формирования квазистационарного псевдоскачка (при $t > 70$) через стенку канала на интервале $x \in (13.5,\;15.3)$ проводится периодический вдув газа (в модели за это отвечает функция $f(t,x)$). Такое воздействие приводит к смещению псевдоскачка и формированию вторичных волн. Если левая граница псевдоскачка совершает колебания, близкие к периодическим, то за фронтом формируется достаточно сложное нестационарное течение. Как видно из рис. 3а, за фронтом псевдоскачка (первый разрыв слева $x = {{x}_{s}}(t)$) образуются еще два скачка, которые перемещаются вниз по потоку и, при достаточно большом периоде процесса инжектирования, покидают расчетную область. График для толщины потенциального слоя $y = h$ (кривая ) выведен при t = 170. Постоянные в модели (1.1), (1.4) и разрешение по пространству выбраны такими же, как и в разделе 2.1. На рис. 3б показаны интенсивность подачи газа как функция времени (кривая 3) и нормированное (для удобства представления на графике) положение псевдоскачка $x = {{x}_{s}}(t){\text{/}}30$. Как отмечалось выше, при t ≈ 70 течение выходит на квазистационарный режим, фронт псевдоскачка находится в сечении $x \approx 9.6$. Под воздействием притока массы псевдоскачок смещается вверх по потоку и затем (при прекращении закачки) возвращается в положение, близкое к начальному. Амплитуда колебаний псевдоскачка составляет примерно 0.9. Отметим, что смещение псевдоскачка в крайнее левое (правое) положение происходит с запаздыванием по отношению к режиму закачки. Кроме того, процесс смещения псевдоскачка влево занимает меньшее время, чем его движение в обратном направлении.

Рис. 3.

Структура псевдоскачка при периодической закачке газа: а – форма канала и толщина сверхзвукового ядра течения (кривые 1 и 2) при $t = 170$; б – режим закачки газа через часть канала (функция $f(t)$) и нормированное положение псевдоскачка ${{\bar {x}}_{s}}(t) = {{x}_{s}}(t){\text{/}}30$ (кривые 3, 4).

Описанные выше колебания скачка являются вынужденными, так как газ подается в канал по заданному закону. Для построения автоколебательного режима перемещения псевдоскачка можно использовать резонансные свойства канала. В частности, применить резонатор Гельмгольца для возбуждения автоколебаний в рассматриваемой системе. Этот подход предполагается развить в следующих работах.

2.3. Эволюция псевдоскачка при дроссилировании

Проводится моделирование вынужденных колебаний псевдоскачка в трансзвуковом канале. Результаты сопоставляются с приведенными в [9] экспериментальными данными и трудоемкими двумерными расчетами.

В работе [9] эксперименты проводились в трансзвуковом канале, рабочая часть которого начиналась в сечении $x = {{x}_{a}} = 60$ мм, где высота канала составляла $y = {{Y}_{0}} = 90$ мм и плавно увеличивалась до $y = 100$ мм на участке протяженностью примерно 200 мм. Воздействие на псевдоскачок осуществлялось вращающимся валом эллиптического сечения. Вал расположен на расстоянии $X = 469.5$ мм от входа в канал и генерировал возмущения давления с частотой ${{f}_{c}} = 40$ Гц. Скорость газа при $x = 60$ мм составляла ${{U}_{0}} = 384$ м/с, число Маха M = 1.1 и, соответственно, скорость звука ${{C}_{0}} = 349$ м/с. Отношение ${{T}_{0}} = {{Y}_{0}}{\text{/}}{{C}_{0}} \approx 2.58 \times {{10}^{{ - 4}}}$ с определяет масштаб времени. Таким образом, размерные величины можно связать с безразмерными следующими соотношениями

$x - {{x}_{a}} = {{Y}_{0}}x{\text{'}},\quad y = {{Y}_{0}}y{\text{'}},\quad u = {{U}_{0}}u{\text{'}},\quad t = {{T}_{0}}t{\text{'}}.$

В безразмерных переменных частота колебаний $f_{c}^{'} = {{f}_{c}}{{T}_{0}} \approx 0.0103$. Как отмечается в [9], положение псевдоскачка при осцилляциях меняется от ${{x}_{1}} \approx 145$ мм до ${{x}_{1}} \approx 185$ мм, что соответствует значениям $x_{1}^{'} = 0.944$ и $x_{2}^{'} = 1.389$ (далее штрихи отбрасываем). При этом число Маха меняется от 1.31 до 1.34.

Как и в предыдущем разделе, возьмем $\gamma = 1.4$, $\sigma = 0.2$, $\kappa = 4$, ${{c}_{f}} = 0.003$ и будем проводить расчеты в безразмерных переменных (${{H}_{0}} = 1$, ${{\rho }_{0}} = 1$, ${{c}_{0}} = 1$) в канале длины ${{x}_{b}} = 2$. Профиль канала определяется функцией z, имеющей в области $0 < x < {{x}_{ * }} = 1.8$ следующий вид

$z = - 0.1\frac{{1 - exp( - 0.9x)}}{{1 - exp( - 0.9{{x}_{ * }})}}.$

Такой выбор обеспечивает аппроксимацию рабочей части канала, в котором проводились эксперименты [9]. В области $x > {{x}_{ * }}$ функция z продолжается параболой, соединяющей точки ${{x}_{ * }}$ и xb, в которых $z = - 0.1$. Экстремум функции $z = {{z}_{ * }}(t)$ на интервале $({{x}_{ * }},{{x}_{b}})$, начиная с определенного момента времени, периодически меняется с указанной выше частотой. Это обеспечивает дроссилирование (периодическое изменение сечения), приводящее к перемещению псевдоскачка. В начальный момент времени $t = {{t}_{0}}$ в расчетнойобласти задаются $\rho = 1$, $u = {v} = 1.1$, $\eta = 0.02$, $q = {{10}^{{ - 4}}}$. Граничные условия соответствуют предыдущему тесту.

На первом этапе за счет управления препятствием строится квазистационарное разрывное решение рис. 4а. Как отмечалось выше, в области гладкого решения выбор замыкающего соотношения (уравнения (1.4) или (1.2)) не имеет значения, но определение решения за скачком по формулам (1.10), (1.11) зависит от выбора замыкающего соотношения. Сплошная кривая на рис. 4а получена в результате решения стационарных уравнений (1.12) до скачка, расположенного в точке $x = {{x}_{s}} = 0.945$, и за скачком. Для построения решения за фронтом разрыва использованы соотношения, ассоциированные с уравнением (1.4). Пунктиром показано решение этих же уравнений, но с условиями за скачком, вычисленным по условиям, соответствующими выбору уравнения энергии (1.2). Как видно из графика, использование различных консервативных форм записи уравнений движения приводит к заметным различиям в определении решения за фронтом разрыва. Однако эти различия проявляются в достаточно малой области, вне которой решения близки либо практически совпадают. Это относится не только к приведенному графику для функции h, но и ко всем остальным искомым переменным $\rho $, $u$, ${v}$ и $q$. Поэтому использование в качестве замыкающего соотношения дифференциального следствия (1.4) вместо громоздкого уравнения энергии (1.2) представляется оправданным.

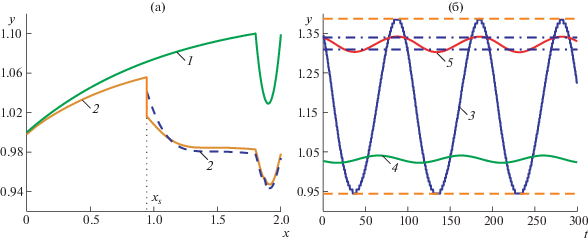
Рис. 4.

Осцилляции псевдоскачка: а – форма канала (кривая 1) и толщина сверхзвукового ядра течения h (кривая 2), вычисленная по модели (1.1) с замыканием (1.4) (сплошная линия) и (1.2) (пунктир); б – положение псевдоскачка в зависимости от времени (кривая 3), минимальное сечение канала в окрестности правой границы (кривая 4) и максимальное число Маха (кривая 5), пунктир и штрих-пунктир – предельные значения положения псевдоскачка и числа Маха согласно [9]. Графики приведены в безразмерных переменных.

После формирования квазистационарного разрывного решения будем периодически менять полутолщину канала ${{H}_{0}} - z$ в окрестности выходного сечения, что в свою очередь приводит к перемещению псевдоскачка. На рис. 4б показано перемещение псевдоскачка в зависимости от безразмерного времени (кривая 3) при изменении минимального сечения канала в окрестности правой границы по периодическому закону (кривая 4). Период изменения функции ${{z}_{ * }}(t)$ в безразмерных переменных равен $T = 1{\text{/}}(40{{T}_{0}}) \approx 97$ и соответствует периоду 0.025 с в исходных переменных. Положение псевдоскачка определяется по точке изменения знака переменной Δ, характеризующей переход течения от сверхкритического режима перед скачком ($\Delta > 0$) к докритическому ($\Delta < 0$) за фронтом разрыва.

Как видно из рис. 4б (кривая 3), амплитуда колебания псевдоскачка хорошо согласуется с экспериментальными данными [9], поскольку минимальная и максимальная координаты фронта псевдоскачка ${{x}_{s}}(t)$ соответствуют экспериментальным значениям 0.944 и 1.389 (в безразмерных переменных), показанным на графике пунктирными линиями. Кривой 5 на рис. 4б показано максимальное число Маха в области до локального сужения канала в зависимости от времени. Оно меняется от 1.303 до 1.342, что также хорошо согласуется с экспериментальными значениями (1.31 и 1.34 соответственно). Обратим внимание, что предельные значения положения препятствия (функции ${{z}_{ * }}(t)$) и предельные положения псевдоскачка имеют сдвиг по времени, примерно равный T/5. В эксперименте и расчетах [9] этот сдвиг составляет T/12. Указанные различия связаны с тем, что в использованной модели не представляется возможным точно описать применяемый в эксперименте процесс дросселирования. Кроме того, в приведенных расчетах длина канала (расстояние между препятствием и псевдоскачком) несколько меньше, чем в работе [9]. Тем не менее используемая одномерная модель позволила достаточно точно описать амплитудные характеристики колебаний пседвоскачка в трансзуковом канале.

3. ЗАКЛЮЧЕНИЕ

В рамках двухслойной схемы течения (сверхзвуковое потенциальное ядро, пристеночный понраничный слой) выполнено численное моделирование эволюции нестационарного псевдоскачка в каналах переменного сечения. Модель записывается в виде консервативной одномерной системы из пяти уравнений (1.1), (1.4), являющейся гиперболической при выполнении условий (1.9). Приведен пример формирования квазистационарного псевдоскачка в трансзвуковом расширяющемся канале с локальным сужением (рис. 2). Течение характеризуется переходом от сверхкритического режима течения к докритическому, в котором возмущения распространяются вверх по потоку. Периодическая подкачка газа в пограничный слой приводит к колебаниям псевдоскачка и формированию вторичных ударных волн, распространяющихся вниз по потоку (рис. 3). Проведено сопоставление результатов моделирования вынужденных осцилляций псевдоскачка в трансзвуковом канале при дросселировании с экспериментальными данными и двумерными расчетами [9]. Показано, что применяемая одномерная модель двухслойного течения позволяет корректно описать качественные и количественные характеристики колебаний псевдоскачка (рис. 4).

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта № 19-01-00498).

Список литературы

  1. Чжен П. Отрывные течения. М.: Мир, 1972. Т. 1. 1972. 299 с.; Т. 2. 1973. 280 с. Т. 3. 1973. 333 с.

  2. Пензин В.И. Экспериментальное исследование отрывных течений в каналах. М.: Изд. ЦАГИ, 2009. 280 с.

  3. Matsuo K., Miyazato Y., Kim H.-D. Shock train and pseudo-shock phenomena in internal gas flows // Prog. Aerosp. Sci. 1999. V. 35. P. 33–100.

  4. Гуськов О.В., Копченов В.И., Липатов И.И., Острась В.Н., Старухин В.П. Процессы торможения сверхзвуковых течений в каналах. М.: Физматлит, 2008. 168 с.

  5. Babinsky H., Harvey J.K. Shock Wave-Boundary-Layer Interactions, Cambridge Univ. Press, Cambridge, England, U.K., 2011. 461 p.

  6. Gaitonde D.V. Progress in shock wave/boundary layer interactions // Prog. Aerosp. Sci. 2015. V. 72. P. 80–99.

  7. Huang W., Wu H., Yang Y.-G., Yan L., Li Sh.-B. Recent advances in the shock wave/boundary layer interaction and its control in internal and external flows // Acta Astronaut. 2020. V. 174. P. 103–122.

  8. Bogar T.J., Sajben M., Kroutil J. Characteristics frequencies of transonic diffuser flow oscillations // AIAA J. 1983. V. 21. P. 1232–1240.

  9. Bur R., Benay R., Galli A., Berthouze P. Experimental and numerical study of forced shock-wave oscillations in a transonic channel // Aerosp. Sci. Technol. 2006. V. 10. P. 265–278.

  10. Липатов И.И., Ляпидевский В.Ю., Чесноков А.А. Модель нестационарного псевдоскачка в баротропном течении газа // Докл. РАН. 2016. Т. 466. № 5. С. 545–549.

  11. Ikui T., Matsuo K., Sasaguchi K. Modified diffusion model of pseudo-shock waves considering upstream boundary layers // Bull. Jpn. Soc. Mech. Eng. 1981. V. 24. № 197. P. 1920–1927.

  12. Kanda T., Tani K. Momentum balance model of flow field with pseudo-shock // JAXA Res. Develop. Rep. 2007. № JAXA-RR-06-037E. 17 p.

  13. Li N., Chang J.-T., Xu K.-J., Yu D.-R., Bao W., Song Y.-P. Oscillation of the shock train in an isolator with incident shocks // Phys. Fluids. 2018. V. 30. 116102. P. 1–20.

  14. Wang Z., Chang J., Hou W., Yu D. Propagation of shock-wave/boundary-layer interaction unsteadiness in attached and separated flows // AIP Adv. 2020. V. 10. 105011. P. 1–34.

  15. Wang Z., Chang J., Hou W., Yu D. Low-frequency unsteadiness of shock-wave/ boundary-layer interaction in an isolator with background waves // Phys. Fluids. 2020. V. 32. 056105. P. 1–33.

  16. Гунько Ю.П., Кавун И.Н. Нестационарный псевдоскачок в ударной трубе // Прикл. механика и техн. физика. 2020. Т. 61. № 2. С. 71–80.

  17. Ляпидевский В.Ю., Тешуков В.М. Математические модели распространения длинных волн в неоднородной жидкости. Новосибирск: Изд-во СО РАН, 2000. 420 с.

  18. Ляпидевский В.Ю., Хе А.К., Чесноков А.А. Режимы течения в плоском эластичном канале при наличии локального изменения жесткости стенок // Сиб. журн. индустр. матем. 2019. Т. 22. № 2. С. 37–48.

  19. Chesnokov A.A., Liapidevskii V.Yu. Mixing layer and turbulent jet flow in a Hele–Shaw cell // Int. J. Non-Linear. Mech. 2020. V. 125. 103534. P. 1–9.

  20. Овсянников Л.В. Модели двухслойной мелкой воды // Прикл. механика и техн. физика. 1979. № 2. С. 3–14.

  21. Nessyahu H., Tadmor E. Non-oscillatory central differencing schemes for hyperbolic conservation laws // J. Comput. Phys. 1990. V. 87. P. 408–463.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал