Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 74-83

2.1. Профили изгибно-гравитационных волн

Как показали эксперименты, форма профиля наблюдаемых изгибно-гравитационных волн существенным образом зависит от толщины и упругих свойств пластины, а также от высоты возбуждаемой волны.

Толщина h_p пластин из пенополиэтилена изменялась в широком диапазоне от 0.1 до 2 см, причем при h_p = 2 см возбуждение волн отсутствовало. Рассмотрим наиболее характерные значения h_p = 0.1, 0.5 и 1.8 см и их эффект на изгибно-гравитационные волны.

На рис. 2 представлены профили второй моды изгибно-гравитационной волны в случае пластины наименьшей толщины h_p = 0.1 см. При частоте колебаний сосуда $\Omega $ = 23.44 с^–1 высота наблюдаемой волны составляла $H$ = 6.2 см – рис. 2а. Волна указанной высоты близка к линейной – волна регулярная, профиль практически синусоидальный; колебания узлов стоячей волны малы; мелкомасштабные возмущения отсутствуют. Отметим, что под регулярными понимаются волны, профиль которых периодичен во времени и симметричен относительно вертикали, проходящей через пучность волны. Эффект пластины практически отсутствует, наблюдаемая изгибно-гравитационная волна тождественна стоячей гравитационной волне на свободной поверхности воды.

При частоте сосуда $\Omega $ = 22.20 с^–1 (рис. 2б) гребни волновых профилей сужаются, а подошвы уплощаются, причем высота волны возрастает до величины $H$ = 12 см. Изгибно-гравитационная волна остается регулярной, хотя становятся существенными колебания узлов, и можно выделить возмущения профиля масштабом порядка 10 см (в момент прохождения пластиной невозмущенного горизонтального уровня). Вследствие больших прогибов пластины и ее нерастяжимости в окрестности торцевых стенок сосуда появляются области свободной от пластины воды, длины которых максимальны для профилей наибольшего развития. Кроме того, наличие пластины проявляется в отсутствие заострения вершины гребня, наблюдаемого в случае чистой воды. Крутизна этой регулярной изгибно-гравитационной волны составляет величину $\Gamma = H{\text{/}}\lambda $ ∼ 0.24, являющуюся предельной для данной толщины пластины. Отметим, что для чистой воды [15] предельная крутизна регулярной волны составляла $\Gamma $ ∼ 0.22.

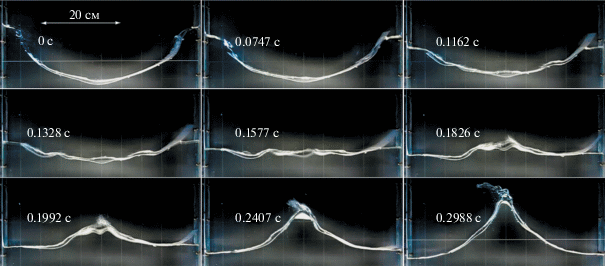
Дальнейшее уменьшение частоты сосуда приводит к переходу от регулярных изгибно-гравитационных волн к волнам разрушающимся. При $\Omega $ = 20.81 с^–1 наблюдалась разрушающаяся волна Фарадея, причем плавающая на поверхности воды тонкая пластина никакого регуляризующего эффекта не проявляла – рис. 3. Приведенная на рисунке последовательность кадров соответствует половине периода волны и отражает особенности профилей изгибно-гравитационной волны на временном интервале от момента максимальной глубины впадины в центре сосуда до сформировавшегося гребня. Волновые движения воды таковы, что плавающая на ее поверхности пластина не влияет на зарождение ($t$ = 0.1162–0.1577 с), развитие ($t$ = 0.1826–0.1577 с) и схлопывание каверны ($t$ = 0.1992 с) с последующим струйным выбросом ($t$ = 0.2407–0.2988 с). Отметим отрыв правого конца пластины на кадрах $t$ = 0.0747–0.1992 с, а также участки локального подтопления пластины ($t$ = 0.1162–0.2407 с). Не приводя количественных оценок, можно предположить, что это связано с инерционностью пластины. В заключение можно сделать вывод, что в рассматриваемом режиме колеблющаяся вода не замечает пластину, и разрушение стоячей изгибно-гравитационной волны происходит по сценарию разрушения гравитационных волн Фарадея на свободной поверхности воды [15].

Увеличение толщины ${{h}_{p}}$ пластины приводит к увеличению предельной крутизны $\Gamma $ регулярной волны. Максимальная крутизна стоячей изгибно-гравитационной волны $\Gamma $ ∼ 0.40 получена для пластины толщиной h_p = 0.51 см – рис. 4. Для приведенных волновых профилей характерно отсутствие заострения гребней (а) для гидроупругой системы (центральная часть сосуда) и их наличие на участках чистой воды (в) вблизи торцевых стенок (свойство чисто гравитационных волн). За исключением формы гребня колебания системы пластина–вода определяются волнами гравитационными.

При дальнейшем увеличении толщины пластины начинают преобладать ее упругие свойства, максимальная крутизна волн уменьшается. На рис. 5 показаны профили, соответствующие трем последовательным фазам регулярной гидроупругой волны при толщине пластины h_p = 1.79 см. Профили волн максимального развития (а, в) соответствуют изгибной стоячей волне, какие-либо признаки стоячей гравитационной волны (асимметрия профиля, заострение гребня и т.п.) отсутствуют. Толщина пластины такова, что мелкомасштабные возмущения при прохождении системы невозмущенного горизонтального уровня не наблюдаются (б). Наличие пластины сказывается и на значении максимальной крутизны регулярной гидроупругой волны, которая $\Gamma $ ∼ 0.20 оказывается меньше соответствующего значения для волн гравитационных.

При увеличении толщины пластины из пенополиэтилена до значения h_p = 2 см возбудить изгибно-гравитационные волны не удалось.

Таким образом, в случае пластин из пенополиэтилена толщиной 0.1 $ \leqslant {{h}_{p}} < $ 2 см экспериментально реализовано параметрическое возбуждение стоячих стационарных изгибно-гравитационных волн, форма профилей которых определялась параметром h_p. Так, при ${{h}_{p}} \leqslant $ 0.5 см свойства гидроупругой системы пластина–вода определяются в основном волнами гравитационными, тогда как при ${{h}_{p}} > $ 0.5 см превалируют волны изгибные.

Проведена серия экспериментов с плавающей на поверхности воды пластиной толщиной h_p = 0.3 см из пенополистирола, модуль упругости которого на два порядка больше по сравнению с пенополиэтиленом. Характерные профили наблюдаемых волн приведены на рис. 6.

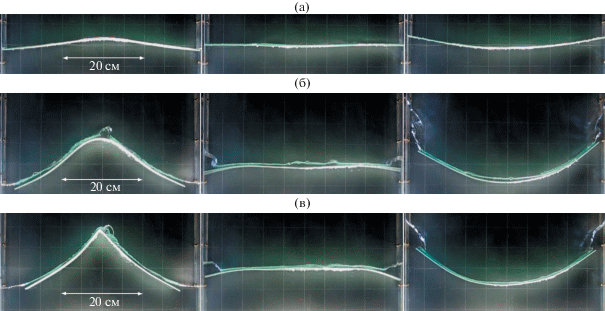
Профили на рис. 6а соответствуют линейной изгибно-гравитационной волне малой высоты ($\Gamma $ ∼ 0.05). Профили (б, в) показывают, что пластина, несмотря на избыточную плавучесть, в течение всего полупериода волны находится под тонким слоем воды. Из кадров (б) видно, что на поверхности этого слоя воды присутствуют мелкомасштабные возмущения и каплеподобные образования. Если на рисунках (а, б) пластина в центральной части сосуда изгибается равномерными дугами, то первый кадр (в) показывает наличие срединного локального перегиба пластины. В теории упругости такое образование определяется как пластический шарнир. Неспособный более воспринимать возрастающую гидродинамическую нагрузку материал пластины в центре сосуда интенсивно течет, и образуется локальная пластическая зона. Большие пластические деформации приводят к разрушению пластины на две части; происходит переход к гравитационным волнам на свободной поверхности воды (с плавающими обломками пластины).

Поскольку процесс образования пластического шарнира и последующее разрушение пластины из пенополистирола наблюдались в описываемых опытах неоднократно, то ниже обсуждаются только результаты опытов с пластинами из пенополиэтилена.

2.2. Резонансные зависимости и затухание изгибно-гравитационных волн

Рассмотрим влияние плавающей пластины на резонансные зависимости высоты H стационарной волны от частоты ${{\Omega }}$ вертикальных колебаний сосуда. В [12–14] эти зависимости $H({{\Omega }})$ использовались как интегральные характеристики регулярных гравитационных волн Фарадея.

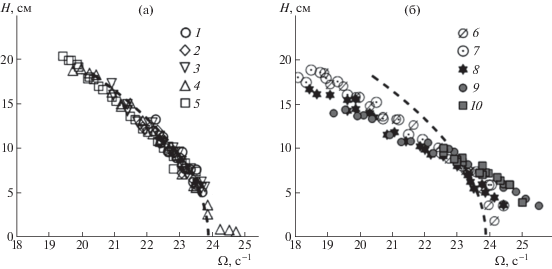
Из рис. 7 следует, что с ростом h_p зависимости $H({{\Omega }})$ становятся более пологими и смещаются в область высоких частот. Если сравнить резонансные зависимости изгибно-гравитационных и гравитационных волн, то в случае пластин с ${{h}_{p}} \leqslant $ 0.51 см частотный сдвиг между зависимостями отсутствует, хотя предельная высота изгибно-гравитационных волн существенно выше по сравнению с волной на свободной поверхности воды – рис. 7а, кривые 1–5. При ${{h}_{p}} \geqslant $ 0.77 см наличие пластин проявляется в высокочастотном сдвиге более пологих резонансных зависимостей – рис. 7б, кривые 6–10. Отметим, что при анализе профилей изгибно-гравитационных волн значение h_p ~ 0.5–0.6 см определяло переход от гравитационных к изгибным волнам.

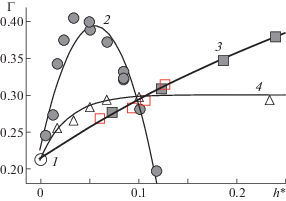
Использование плавающей пластины значительно увеличивает предельную крутизну $\Gamma = H{\text{/}}\lambda $ регулярной изгибно-гравитационной волны, как это показано на рис. 8. При увеличении толщины пластины сначала наблюдается рост крутизны, и при h_p = 0.51 см предельная крутизна равна $\Gamma = H{\text{/}}\lambda $ ∼ 0.4 – данные (2). Для сравнения на рис. 8 приведены полученные в [13, 14] зависимости крутизны регулярной волны от толщины слоя вязкой жидкости (двухслойная жидкость, баротропные волны) и толщины слоя плавающих частиц. В обоих случаях крутизна монотонно растет с увеличением толщины верхнего слоя. Дальнейшее увеличение h_p пластины приводит к снижению крутизны, которая при h_p = 1.79 см оценивается как $\Gamma \sim 0.2$ (предельная крутизна регулярных гравитационных волн на воде). Данные эксперимента (2) аппроксимируются перевернутой параболой $\Gamma = - 53.7h{{{\text{*}}}^{2}} + 5.9h{\text{*}} + 0.22$.

Дадим интерпретацию полученных экспериментальных результатов в рамках линейной теории гидроупругости [5–7].

В одномодовом приближении частота $\omega $ изгибно-гравитационных волн связана с волновым числом $k = n\pi {\text{/}}L$ следующим образом

где для настоящего эксперимента $n$ = 2; $L$ = 50 см; $k$ = 0.126 см^–1; коэффициент Пуассона $\nu $ = 0.3; ускорение силы тяжести $g$ = 981.7 см/с²; $E$ = 2.6 × 10⁶ дин/см².

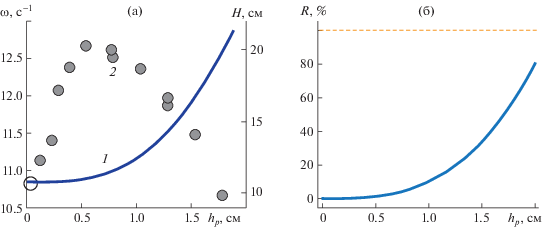
График зависимости частоты $\omega ({{h}_{p}})$ волн от толщины h_p пластины представлен на рис. 9а (кривая 1). При h_p = 0 имеем чисто гравитационные волны, частота которых равна ${{\omega }_{0}} = \sqrt {gk{\text{th}}kh} $ = = 10.85 с^–1. При увеличении толщины пластины до значения ${{h}_{p}} \leqslant $ 0.51 см собственная частота изгибно-гравитационных практически совпадает с ${{\omega }_{0}}$ и не превосходит $\omega \leqslant $ 10.88 с^–1. Поскольку при основном параметрическом резонансе частота вертикальных колебаний сосуда Ω ~ ${\text{2}}\omega \simeq {\text{2}}{{\omega }_{0}}$, то при ${{h}_{p}} \leqslant $ 0.51 см резонансные зависимости на рис. 7а совпадают с рассчитанными для гравитационных волн. При дальнейшем увеличении h_p наблюдается быстрый рост частоты $\omega $, которая при h_p = 1.75 см составляет $\omega $ = 12.46 с^–1. Увеличение собственной частоты изгибно-гравитационных волн приводит к смещению резонансных зависимостей на рис. 7б в область высоких частот.

Отметим, что поскольку частота чисто изгибной волны (колебания пластины в вакууме) определяется как

то совпадение частот $\omega * = {{\omega }_{0}}$ гравитационной и изгибной волн достигается при толщине плавающей пластины h_p = 0.23 см.

На рис. 9а приведены также данные (2), описывающие зависимость предельной высоты регулярной изгибно-гравитационной волны от толщины пластины. Видно, что максимальное значение H ∼ 20 см также соответствует h_p ∼ 0.5–0.7 см. Таким образом, при ${{h}_{p}} \leqslant $ 0.5–0.7 см колебания гидроупругой системы пластина–вода определяются стоячей гравитационной волной (не замечающей наличия пластины), а при увеличении h_p начинают сказываться свойства изгибных колебаний пластины.

Оценим энергозатраты, связанные с изгибом плавающей пластины. Поскольку гидроупругие колебания рассматриваемой системы пластина–вода являются двумерными, пластина в первом приближении может быть заменена упругой балкой. Кроме того, рассматривая профиль изгибно-гравитационной волны максимального развития

функция y(x) определяет также изгиб балки в пределах закона Гука. Тогда соответствующая потенциальная энергия деформации балки при изгибе определяется как [17]

Данное изменение потенциальной энергии деформации балки относительно равновесного (горизонтального) положения балки равно работе обобщенных гидродинамических сил, действующих на балку со стороны гравитационной волны того же профиля $y(x)$. Если полная энергия стоячей гравитационной волны высоты $H$ равна

то отношение определяет энергозатраты гравитационной волны на изгиб балки.

График $R({{h}_{p}})$ приведен на рис. 9б. Видно, что при ${{h}_{p}} \leqslant $ 0.5–0.7 см величина $R$ не превышает 4%, и колебания гидроупругой системы определяются волнами гравитационными. При толщине пластины ${{h}_{p}}\sim $ 1 см энергозатраты на возбуждение изгибных волн составляют $R\sim $ 9%; дальнейшее увеличение h_p приводит к быстрому возрастанию энергозатрат гравитационной волны – при ${{h}_{p}}\sim $ 1.75 см коэффициент R ~ 50%; колебания гидроупругой системы определяются изгибными волнами. При ${{h}_{p}}\sim $ 2 см энергозатраты $R\sim $ 80% настолько велики, что колебания отсутствуют.

Наличие плавающей пластины сказывается на диссипативных характеристиках рассматриваемой гидроупругой системы (рис. 10) – наблюдается неэкспоненциальный (и быстрый по сравнению с гравитационными волнами на воде) характер затухания волновых движений. Аналогичный характер затухания стоячей волны был выявлен в случае слоя плавающих частиц [13].

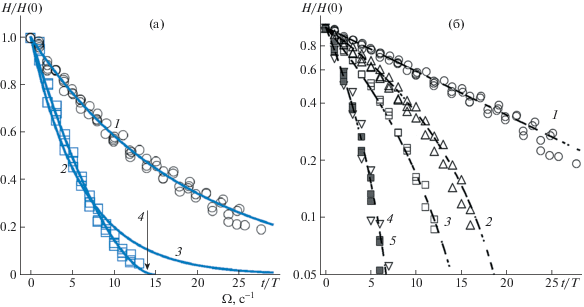
На рис. 10а экспоненциальная функция (3) не описывает весь процесс демпфирования волны при наличии пластины (2). Расхождение между экспериментальными данными (2) и аппроксимирующей функцией (3) начинается при $H{\text{/}}{{H}_{0}} \leqslant $ 0.25–0.3. Наилучшая аппроксимация (4) экспериментальных данных (2) обеспечивается степенной функцией вида

что совпадает с результатами исследования [13]. Таким образом, полное затухание волны в случае плавающей пластины достигается за конечное число колебаний ${{\tau }_{0}}$ = 15.

При неэкспоненциальном затухании дифференциальное уравнение для безразмерной высоты волны $y$ принимает вид [13]

где $\alpha = n{\text{/}}{{\tau }_{0}}$, $m = n - 1$, $z = t{\text{/}}T$; T – период волны. Отметим, что экспоненциальное затухание означает $y \to $ 0 при $z \to \infty $, причем этот тип затухания (временного или пространственного) положен в основу практически всех теоретических волновых моделей с диссипацией.

Обобщенные данные по затуханию изгибно-гравитационных волн в присутствии плавающей пластины приведены на рис. 10б. Видно, что экспериментальные данные для всех пластин хорошо аппроксимируются степенной функцией вида $H{\text{/}}{{H}_{0}} = {{(1 - z{\text{/}}{{\tau }_{0}})}^{n}}$ при ${{\tau }_{0}}$ = 6–19, $n$ = 2–2.7.