1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2021

Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 145-156

АНАЛИТИЧЕСКАЯ МОДЕЛЬ ТУРБУЛЕНТНОЙ ВЯЗКОСТИ ДЛЯ ПРОФИЛЕЙ СКОРОСТИ ВО ВНЕШНЕЙ ЧАСТИ ЗАКРЫТЫХ И ОТКРЫТЫХ ТЕЧЕНИЙ В КАНАЛЕ

R. Absi a, *, **

a ECAM-EPMI Graduate School of Engineering
95092 Cergy-Pontoise, France

* E-mail: r.absi@ecam-epmi.com
** E-mail: rafik.absi@yahoo.fr

Поступила в редакцию 14.06.2020
После доработки 08.11.2020
Принята к публикации 25.12.2020

Полный текст (PDF)

Аннотация

Основные уравнения, используемые для аналитического описания турбулентности в случае течений в открытых каналах, имеют параболический профиль турбулентной вязкости и экспоненциально убывающую зависимость турбулентной кинетической энергии. Однако, если использовать при определении турбулентной (вихревой) вязкости произведение масштабов скорости и длины и брать для масштаба скорости квадратный корень из турбулентной кинетической энергии, то, как можно показать, параболический профиль турбулентной вязкости несовместим с зависимостью для турбулентной кинетической энергии. Учитывая этот недостаток, рассмотрена такая зависимость для нахождения турбулентной вязкости, которая согласуется с профилем турбулентной кинетической энергии в равновесной области. Эта турбулентная вязкость записана в форме, допускающей калибровку по двум параметрам, зависящим от числа Рейнольдса по динамической скорости Reτ, которые линейно зависят от Reτ. Все результаты обоснованы как посредством прямого численного моделирования (ПЧМ), так и с помощью данных экспериментов в одном и том же диапазоне чисел Рейнольдса по динамической скорости, соответственно, $300 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 5200$ для течений в закрытых каналах и $923 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 6139$ для течений в открытых каналах. Сравнение с данными прямого численного моделирования (ПЧМ) турбулентной вязкости, проведенного для течений в закрытых каналах в случае восьми различных условий в потоке, продемонстрировало хорошее согласие. Средние скорости вдоль по потоку были получены из решения уравнения количества движения. Для течений в закрытых каналах профили средней скорости также показали очень хорошее согласие. Для течений в открытых каналах полученные результаты подтверждают, что использование турбулентной вязкости с параболическим профилем не может улучшить профили скорости, тогда как предлагаемый метод демонстрирует хорошее согласие. Эти результаты показывают возможность использования аналитической модели турбулентной вязкости для точного описания распределения скоростей во внешней области течений, как для закрытых, так и открытых потоков, без использования каких-либо специально подбираемых параметров или функций.

Ключевые слова: турбулентная (вихревая) вязкость, аналитическое выражение, профили скорости, внешняя часть, закрытые каналы, открытые каналы

Точный расчет скоростей течения в отрытых каналах является чрезвычайно важным из-за практической значимости исследований в связи с возможными приложениями в гидравлике [1–3]. В простом каноническом случае однородного потока в прямом открытом канале прямоугольного сечения исследование распределения скоростей является насущно необходимым, поскольку оно может быть использовано для других реальных экологических и городских течений (стоков), таких как водотоки, включая канализационные коллекторы. Течение в узких открытых каналах демонстрирует некоторые характерные особенности по сравнению с другими каноническими течениями (закрытые каналы, трубы и турбулентные пограничные слои). Углы, образованные стенками и свободной поверхностью (в качестве движущейся границы), приводят к анизотропии турбулентности, которая вызывает вторичные (индуцированные) потоки в трехмерных течениях [4–6]. Однако в широких открытых каналах и далеко от боковых стенок канала вторичные потоки очень слабые и практически исчезают в случае очень широкого открытого канала и вблизи его центральной линии.

В классическом двуслойном подходе к описанию двумерных течений в открытом канале (с “классическим” внутренним и внешним масштабированием) структура потока определяется двумя различными областями, а именно, некоторой внутренней (или пристеночной) областью, в которой определяющим является влияние вязкости и масштабы скорости и длины задаются динамической скоростью (скоростью трения) uτ и масштабом вязкой длины $\nu {\text{/}}{{u}_{\tau }}$ (или пристеночным масштабом), соответственно, и внешней областью [7], в которой важна инерция и масштаб длины задается значением h – глубиной потока для открытых каналов или полувысотой канала для закрытых каналов. Между внутренней и внешней областями вводится слой перекрытия или логарифмический слой [8]. Внутренняя или пристеночная область (при ${{\xi }} < 0.2$, где ${{\xi }} = y{\text{/}}h~$ есть отношение расстояния от дна канала к глубине потока) подразделяется на три слоя: вязкий подслой на расстоянии от стенки ${{y}^{ + }} < $ 5 (переменные с верхним индексом + нормализованы на пристеночный масштаб), буферный слой на интервале 5 $ < {{y}^{ + }} < 30$ и слой перекрытия или логарифмический слой при $30 < {{y}^{ + }} < 0.2~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$, в котором средние продольные скорости ${{U}^{ + }}({{y}^{ + }})$ точно описываются логарифмическим законом [9–11]. Для улучшения описания профилей скорости в вязком и буферном слоях были предложены соответствующие достаточно адекватные методы [12–14]. Во внешней области (${{\xi }} > 0.2)$ используются два основных аналитических метода, а именно, простой степенной закон [15, 16] и логарифмический закон для следа, который представляет собой расширение логарифмического закона за счет добавления функции следа Коулса [17, 18]. Однако функция следа не имеет реального физического смысла, по сути это эмпирический подбор измеренных распределений скорости [19] и вопросы неопределенности значения параметра Коулса ${{\Pi }}$, выражающего интенсивность функции турбулентного следа, остаются открытыми. Другой метод, используемый для улучшения описания профилей скорости во внешней области, требует решения уравнения количества движения (уравнения Навье–Стокса, осредненного по Рейнольдсу). Это решение требует адекватных моделей для используемых параметров турбулентности (т.е. турбулентной вязкости). Для течений в открытых каналах основными уравнениями при аналитическом моделировании турбулентности являются параболический профиль турбулентной вязкости и экспоненциально убывающая зависимость для турбулентной кинетической энергии [7]. Идея турбулентной вязкости очень важна, поскольку она используется не только для определения скоростей из уравнения количества движения, но также связана с предсказанием способности к диффузионному переносу осадка (определенной как произведение турбулентной (вихревой) вязкости и ${{\beta }}$-фактора, т.е. обратного турбулентного числа Шмидта) для описания профилей концентрации осадка (так же как хорошо известное уравнение Роуза)) [20].

Однако параболический профиль турбулентной вязкости и экспоненциально убывающий профиль турбулентной кинетической энергии несовместимы с использованием определения турбулентной вязкости как произведения масштабов скорости и длины. При взятии квадратного корня из турбулентной кинетической энергии в качестве масштаба скорости получающийся масштаб длины не согласуется с данными экспериментов. Как будет показано в дальнейшем, использование параболического профиля турбулентной вязкости в уравнении количества движения неспособно улучшить распределение скоростей во внешней области (которое остается близким к логарифмическому закону). Это и неудивительно, поскольку концепция турбулентной вязкости основывается на предположении о логарифмическом профиле скорости.

Учитывая этот недостаток при аналитическом моделировании турбулентности в течениях в открытых каналах, можно сформулировать цель настоящего исследования как улучшение описания профилей средней продольной скорости во внешней области за счет использования аналитической зависимости для турбулентной вязкости, которая согласуется с хорошо известным профилем турбулентной кинетической энергии. С этой целью рассмотрено стационарное однородное полностью развитое течение несжимаемой ньютоновской жидкости (вода), вначале в плоском закрытом канале, а затем в открытом канале, оба канала имеют гладкие стенки. В настоящем исследовании методология следует историческому подходу, в котором хорошо известные уравнения, используемые для описания течений в открытых каналах (такие как логарифмический закон), были впервые применены для закрытых каналов и труб. Пионерские исследования, выполненные Прандтлем, фон Карманом и другими исследователями [21, 22], были проведены с точки зрения экспериментов в турбулентных течениях в каналах (течение между двумя параллельными пластинами). Кроме того, в широких открытых каналах течение на центральной линии канала (далеко от боковых стенок) считается двумерным и подобным течению в широком закрытом канале (или течению между двумя параллельными пластинами). Взаимосвязанное предположение состоит в том, что влияние свободной поверхности ограничивается очень тонким слоем. В этом случае, по аналогии, глубина воды в открытых каналах подобна полувысоте канала в случае закрытых каналов. В следующих разделах вначале будут приведены основные уравнения для аналитического моделирования турбулентности в двумерных течениях в открытых каналах (разд. 1). В разд. 2 рассматривается аналитическая зависимость для турбулентной вязкости, которая анализируется и сравнивается с параболическим профилем турбулентной вязкости, а ее правильность обосновывается с помощью данных прямого численного моделирования полностью развитых турбулентных течений в закрытых каналах. В 3 разд. средние продольные скорости получены путем решения уравнения количества движения с предложенным уравнением для турбулентной вязкости. Эти скорости сравниваются с данными как прямого численного моделирования, так и экспериментальными данными, которые находятся в одном и том же диапазоне чисел Рейнольдса по динамической скорости Reτ, а именно, $300 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 5200$ для данных прямого численного моделирования течений в закрытых каналах [23–26] и $923 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 6139$ для экспериментальных данных для течений в открытых каналах [12].

1. ОСНОВНЫЕ УРАВНЕНИЯ ДЛЯ АНАЛИТИЧЕСКОГО МОДЕЛИРОВАНИЯ ТУРБУЛЕНТНОСТИ В ТЕЧЕНИЯХ В ОТКРЫТЫХ КАНАЛАХ

При анализе уравнений Навье–Стокса, усредненных по Рейнольсу, было получено следующее обыкновенное дифференциальное уравнение для распределения скорости U для течений в открытых каналах [27]

(1.1)
$\frac{{dU}}{{dy}} = \frac{{u_{\tau }^{2}}}{{{{\nu }} + {{{{\nu }}}_{t}}}}\left[ {\left( {1 - \frac{y}{h}} \right) - {{\alpha }}\frac{y}{h}} \right],$
где y – вертикальное расстояние от дна канала, h – максимальная глубина потока, ${{u}_{{{\tau }}}}$ – скорость касательного напряжения (динамическая скорость), ν – кинематическая вязкость, ${{{{\nu }}}_{t}}$ – турбулентная вязкость и параметр α связан с дип-эффектом (эффектом погружения, например, с расположением максимума скорости, который для узких каналов находится ниже свободной поверхности).

Для широких открытых каналов (отношение сторон $Ar > 5$, где $Ar = b{\text{/}}h$ – отношение ширины канала b к глубине потока h) максимум скорости находится на свободной поверхности и α = 0.

Для больших значений y+ (${{y}^{ + }} > 30)~$ влияние вязкости исчезающе мало ${{\nu }} \ll {{{{\nu }}}_{t}}$ и скорость задается логарифмическим законом $\frac{{dU}}{{dy}} = \frac{{{{u}_{{\tau ~}}}}}{{\kappa y}}$. Уравнение (1.1) обеспечивает турбулентную (вихревую) вязкость параболического вида

(1.2)
${{{{\nu }}}_{t}} = {{\kappa \;}}y~{{u}_{{{{\tau }}~}}}\left( {1 - \frac{y}{h}} \right).$

Параболический профиль для турбулентной вязкости (1.2) можно также найти из полного касательного напряжения, задаваемого формулой

(1.3)
${{{{\tau }}}_{T}} = ~{{{{\tau }}}_{0}}\left( {1 - \frac{y}{h}} \right),$
где ${{{{\tau }}}_{0}} = \rho u_{{{\tau }}}^{2}$ – касательное напряжение на стенке на дне канала ${{{{\tau }}}_{T}}\left( {y = 0} \right) = {{{{\tau }}}_{0}}$.

Турбулентное сдвиговое напряжение (или напряжение Рейнольдса) связано с турбулентной (вихревой) вязкостью через предположение Буссинеска

(1.4)
${{{{\tau }}}_{t}} = {{\rho }}~{{{{\nu }}}_{t}}~\frac{{dU}}{{dy}}.$

Далеко от дна (стенки) канала, где ${{{{\tau }}}_{T}} \approx {{{{\tau }}}_{t}}$ и в слое перекрытия или логарифмическом слое, логарифмический профиль скорости дает производную скорости $\frac{{dU}}{{dy}} = \frac{{{{u}_{{{\tau }}}}}}{{{{\kappa }}~y}}$. Из этих двух предположений и после приравнивания (1.3) и (1.4), можно получить (1.2).

С учетом этих предположений параболический профиль поэтому будет реализовываться только в слое перекрытия (или логарифмическом слое) и может быть продолжен на равновесную область. Он не должен быть использован всюду от дна канала до свободной поверхности.

Однако в равновесной области (где имеет место баланс между производством турбулентной кинетической энергии и ее диссипацией) турбулентная кинетическая энергия может быть задана полутеоретической экспоненциально убывающей функцией [7] в следующем виде:

(1.5)
$k = {{D}_{1}}~u_{{{\tau }}}^{2}~{\text{exp}}\left( { - {{C}_{1}}\frac{y}{h}} \right),$
где k есть турбулентная кинетическая энергия. Уравнения (1.2) и (1.5) представляют собой основные уравнения, которые используются, чтобы обеспечить аналитическое описание (количественное выражение) турбулентности в гидравлике (течения со свободной поверхностью, включая открытые каналы и водотоки).

Однако (1.2) и (1.5) несовместны при использовании определения турбулентной вязкости как произведения масштаба скорости и масштаба длины l, отнесенной к длине смешения length lm [28]. Выбирая масштаб скорости в виде квадратного корня из турбулентной кинетической энергии, для турбулентной вязкости получим следующее выражение

(1.6)
${{{{\nu }}}_{t}} = C_{\mu }^{{1/4}}~\sqrt k ~~{{l}_{m}},$
где Cμ – некоторый коэффициент, равный 0.09 [29]. Из (1.5) и (1.6) следует, что параболический профиль турбулентной вязкости (1.2) дает следующий масштаб длины (1.7), который не согласуется с логарифмическим законом и использованным предположением о локальном равновесии (которое влечет за собой $\frac{{dU}}{{dy}} = \frac{{C_{\mu }^{{1/4}}\sqrt k }}{{~{{l}_{m}}}}$) [14].

(1.7)
$~{{l}_{m}} = \frac{{{{{{\nu }}}_{t}}}}{{C_{\mu }^{{1/4}}~\sqrt k }} = \frac{{\kappa y{{u}_{{{{\tau }}~}}}\left( {1 - \frac{y}{h}} \right)}}{{C_{\mu }^{{1/4}}\sqrt {{{D}_{1}}} ~{{u}_{{{{\tau }}~}}}~{{e}^{{ - \frac{{{{C}_{1}}}}{2}\frac{y}{h}}}}}}.$

Чтобы разрешить это противоречие, введем новое аналитическое описание турбулентной вязкости.

2. ПРЕДЛАГАЕМАЯ МОДЕЛЬ ТУРБУЛЕНТНОЙ ВЯЗКОСТИ

При локальном равновесии (когда $\frac{{dU}}{{dy}} = \frac{{C_{\mu }^{{1/4}}\sqrt k }}{{~{{l}_{m}}}}$) и использовании квадратного корня из турбулентной кинетической энергии для масштаба скорости в виде $\sqrt k = C_{\mu }^{{ - 1/4}}~{{u}_{{{{\tau }}~}}}f\left( y \right)$ [30], выражение для длины смешения должно выглядеть как ${{l}_{m}} = {{\kappa }}~yf\left( y \right)$ в случае логарифмического слоя (в котором $\frac{{dU}}{{dy}} = \frac{{{{u}_{{{{\tau }}~}}}}}{{{{\kappa }}~y}}$), где $\kappa $ есть постоянная фон Кармана. В равновесной области (${{y}^{ + }} > 50$) турбулентная кинетическая энергия задается выражением (1.5) и в слое перекрытия ($30 < {{y}^{ + }} < 0.2~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$) распределение скорости задано логарифмическим законом. Эти два условия, которые заданы соотношениями $\frac{{dU}}{{dy}} \approx \frac{{\sqrt k }}{{~{{l}_{m}}}} = \frac{{{{u}_{{{{\tau }}~}}}}}{{{{\kappa }}~y}}$, показывают, что длину смешения можно представить в виде lm = = ${{\kappa }}~y~{{e}^{{ - 0.5~{{C}_{1}}(y/h)}}}$. Таким образом, турбулентная вязкость может быть задана выражением

(2.1)
${{\nu }_{t}} = {{{{\alpha }}}_{1}}{{\kappa }}~{{u}_{{{{\tau }}~}}}y~{\text{exp}}\left( { - {{C}_{1}}\frac{y}{h}} \right),$
где α1 – некоторый коэффициент, связанный с Cμ и D1. Турбулентная вязкость, заданная выражением (2.1), разрешает первое из двух вышеупомянутых противоречий, связанных с (1.2). Таким образом, в равновесной области ${{y}^{ + }} > 50$ профиль турбулентной кинетической энергии (1.5) находится в согласии с турбулентной вязкостью, заданной выражением (2.1), и логарифмическим профилем скорости.

Формула (2.1) близка к выражению для турбулентной вязкости, предложенному на основе экспериментальных наблюдений планетарного пограничного слоя [31] и успешно использованному для описания пограничных слоев для волн в разработках, нацеленных на решение инженерно-технических задач в океане и прибрежной зоне [32, 33].

Однако в настоящем виде выражение (2.1) неспособно точно описать турбулентную вязкость для разных условий течения. Чтобы получить более общее и точное уравнение, запишем (2.1) в следующем виде (в единицах пристеночного масштаба) [34]:

(2.2)
$\nu _{t}^{ + } = {{y}^{ + }}{\text{exp}}\left( { - \frac{{{{y}^{ + }} + {{a}^{ + }}}}{{{{A}^{ + }}}}} \right),~$
где параметры A+ и a+ задаются следующим образом [34]
(2.3)
${{A}^{ + }} = 0.46~{\text{R}}{{{\text{e}}}_{{{\tau }}}} - 5.98{\text{\;}}~$
и

(2.4)
${{a}^{ + }} = 0.34~{\text{R}}{{{\text{e}}}_{{{\tau }}}} - 11.5{\text{\;}}~.$

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

3.1. Анализ предложенной модели турбулентной вязкости. Предложенная зависимость для турбулентной вязкости (2.2)–(2.4) вначале анализируется посредством сравнения с (1.2) и затем проверяется с помощью прямого численного моделирования турбулентной вязкости, а также с помощью как прямого численного моделирования, так и экспериментальных данных для скоростей.

На рис. 1 изображены профили турбулентной вязкости, заданные формулой (1.2) и зависимостями (2.2)–(2.4), для различных условий течения (случаи с P2 по P5 в табл. 1 [12]).

Рис. 1.

Сравнение профилей турбулентной вязкости, полученных по предложенной модели (уравнения (2.2)–(2.4)) (сплошные линии), и параболический профиль (уравнение (1.2)) (пунктирные линии) для различных случаев (P2–P5, табл. 1).

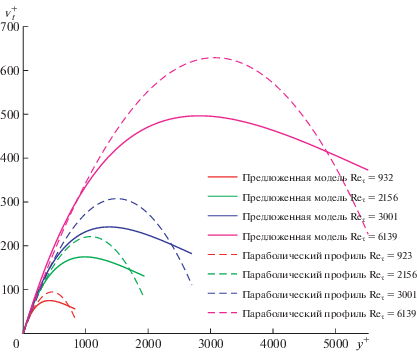
Таблица 1.

Условия течения [12]

Случай Глубина потока, h (см) Отношение ширины к глубине Число Рейнольдса, R = $\frac{{4R{{U}_{m}}}}{\nu }$ Число Фруда, Fr = $\frac{{{{U}_{m}}}}{{\nu \sqrt {(gh)} }}$ Число Рейнольдса по динамической скорости, Reτ = $\frac{{h{{u}_{\tau }}}}{\nu }$
P2 10.3 5.9 5.5 × 104 0.189 923
P3 10.0 6.0 14.3 × 104 0.488 2156
P4 10.0 6.0 21.0 × 104 0.704 3001
P5 10.5 5.7 44.0 × 104 1.170 6139

Um – среднемассовая скорость, R – гидравлический радиус

Рисунок показывает, что как уравнение (1.2), так и зависимости (2.2)–(2.4) дают близкие результаты во внутренней области ${{y}^{ + }} < 0.2~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$. Однако имеется расхождение, важное во внешней области, и в обеих упомянутых зависимостях максимальные значения турбулентной вязкости очевидно расположены в эквивалентных положениях (в каждом случае).

Для сравнения запишем как (1.2), так и (2.2) в единицах пристеночного масштаба в следующем виде: $\nu _{t}^{ + } = \kappa ~{{y}^{ + }}\left( {1 - \frac{{{{y}^{ + }}}}{{{\text{R}}{{{\text{e}}}_{\tau }}}}} \right)$ и $\nu _{t}^{ + } = {{e}^{{ - \left( {\frac{{{{a}^{ + }}}}{{{{A}^{ + }}}}} \right)}}}{{y}^{ + }}~{{e}^{{ - \left( {\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)}}}$. Разложение в ряд показательной функции $~{{e}^{{ - \left( {\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)}}}$ задается выражением

$~{{e}^{{ - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}}}} = \mathop \sum \limits_{n = 0}^\infty \frac{1}{{n!}}~{{\left( { - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)}^{n}} = 1 - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}} + \frac{1}{{2!}}~{{\left( {\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)}^{2}} + \ldots + \frac{1}{{n!}}~{{\left( { - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)}^{n}}{\text{\;}} + o\left( {{{{\left( { - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)}}^{n}}} \right)~.~~$

Заметим, что даже в первом приближении разложение в ряд показательной функции, заданное выражением $~{{e}^{{ - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}}}} = 1 - \frac{{{{y}^{ + }}}}{{{{A}^{ + }}}} + o\left( { - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)$ отличается от $\left( {1 - \frac{{{{y}^{ + }}}}{{{\text{R}}{{{\text{e}}}_{\tau }}}}} \right)$. Параболический профиль (1.2) включает в себя Reτ вместо A+ и в нем пренебрегается членом $o\left( { - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)$. Таким образом, различие между профилями (1.2) и (2.2) связано с членом $o\left( { - ~\frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)$ и значениями A+ и α1.

Чтобы лучше понять различие между зависимостями (1.2) и (2.2)–(2.4), можно определить промежуточные приближения, рассматривая члены разных порядков в разложении в ряд показательной функции в (2.2). Рисунок 2 изображает для случая P5 (табл. 1) различные профили, полученные с членами разных порядков в разложении в ряд по сравнению с предложенными выше зависимостями (2.2)–(2.4) и параболическим профилем турбулентной вязкости (1.2). В первом приближении форма зависимости, заданной формулой ${{\nu }}_{t}^{ + } = {{\kappa }}~{{{{\alpha }}}_{1}}~{{y}^{ + }}\left( {1 - \frac{{{{y}^{ + }}}}{{{{A}^{ + }}}}} \right)$, является параболической (самый маленький параболический профиль, изображенный голубой цепной линией на рис. 2) и близка к (1.2). Отличие от (1.2) связано с параметрами A+ и , которые для (1.2) не зависят от Reτ и равны Reτ и единице, соответственно, тогда как в предложенной аналитической модели оба параметра зависят от Reτ (задаются соотношениями (2.3) и (2.4)). Для промежуточных приближений с добавочными членами в разложениях в ряд показательной функции (цепные кривые, те, что имеют нечетные значения n), каждое дополнительное слагаемое в разложении в ряд делает возможным расширить достоверность на большие значения y+. В приближении 5-го порядка профиль может достичь наибольшей турбулентной вязкости, заданной выражением (2.2), и позволяет улучшить точность вычисления $\nu _{t}^{ + }$ вплоть до ${{y}^{ + }} \approx $ 0.5Reτ. Рисунок 2 показывает, что в (2.2) требуется значение ${{A}^{ + }} < {\text{R}}{{{\text{e}}}_{{{\tau }}}}$, чтобы достичь наибольшей турбулентной вязкости, расположенной приблизительно при ${{y}^{ + }} \approx 0.5~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$.

Рис. 2.

Сравнение профилей турбулентной вязкости, полученных по предложенной модели (уравнения (2.2)–(2.4)) (сплошные линии), и параболических профилей (уравнение (1.2)) и приближения различных порядков в разложении в ряд показательной функции для случая P5.

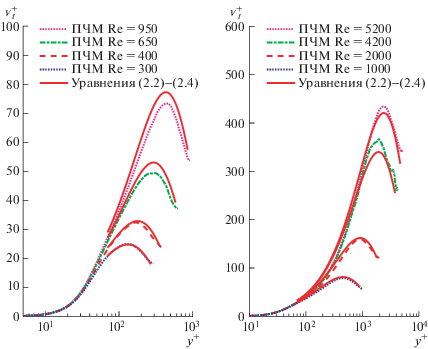
На рис. 3 изображены профили турбулентной вязкости, задаваемые предлагаемой моделью (уравнения (2.2)–(2.4)), в сравнении с данными прямого численного моделирования (Reτ = 300, 400 и 650 [23]; Reτ = 950 [24]; Reτ = 4200 [25] и Reτ = 1000, 2000 и 5200 [26]) для разных значений числа Рейнольдса, вычисленного по динамической скорости. Сравнение изображенных кривых говорит о хорошем согласии.

Рис. 3.

Профили турбулентной вязкости в течениях в закрытых каналах, задаваемые предложенной аналитической моделью (уравнения (2.2)–(2.4)), сравниваемые с данными прямого численного моделирования для различных чисел Рейнольдса; красные сплошные линии рассчитаны по предложенной модели.

3.2. Приложение к профилям средней продольной скорости. Чтобы улучшить предсказание профилей скорости во внешней области, уравнение количества движения (уравнение Навье–Стокса, осредненное по Рейнольдсу) было представлено в виде (в единицах пристеночного масштаба):

(3.1)
$\frac{{d{{U}^{ + }}}}{{d{{y}^{ + }}}} = \frac{1}{{{{\nu }}_{t}^{ + }}}\left( {1 - \frac{{{{y}^{ + }}}}{{{\text{R}}{{{\text{e}}}_{{{\tau }}}}}}} \right).$

Чтобы решить уравнение (3.1), требуется знать турбулентную вязкость $\nu _{t}^{ + }$. При аналитическом моделировании турбулентности используется турбулентная вязкость, заданная уравнениями (2.2)–(2.4) для течений в закрытых и открытых каналах. Произведем оценку применимости параболического профиля для течений в открытых каналах.

Профили средней продольной скорости, полученные при решении уравнения количества движения (3.1), сравниваются как с результатами прямого численного моделирования течений с полностью развитой турбулентностью в открытых каналах при $300 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 5200$, так и с экспериментальными данными для течений в открытых каналах при $923 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 6139$ [12]. Оба типа условий в потоке лежат в одном и том же диапазоне чисел Рейнольдса, вычисленных по динамической скорости (скорости трения). Поскольку цель настоящего исследования состоит в улучшении профиля скорости во внешней области, будем использовать граничное условие на нижнем пределе ${{y}^{ + }} = 0.2~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$ (или ξ = 0.2), где скорость задается логарифмическим законом.

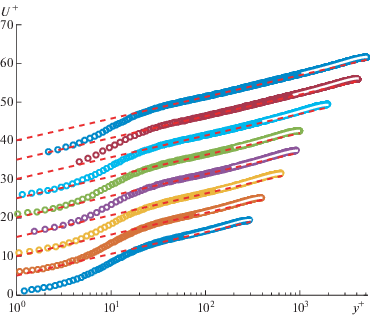
Для течений в закрытых каналах профили средней скорости находятся в очень хорошем согласии (рис. 4). Все вычисленные скорости, полученные при решении уравнения количества движения (3.1) с предложенной зависимостью для турбулентной вязкости (2.2)–(2.4), наложены на данные прямого численного моделирования. Графики показывают, что все вычисленные профили скорости (белые сплошные кривые) лежат внутри данных прямого численного моделирования (символы “кружок” представленные как полужирные сплошные линии).

Рис. 4.

Профили скорости для течений в закрытых каналах, полученные по (3.1) и предложенной модели (уравнения (2.2)–(2.4)) (белые сплошные линии), в сравнении с данными прямого численного моделирования при различных числах Рейнольдса по динамической скорости (возрастают снизу вверх); для большей ясности профили скорости смещены на пять единиц.

Для течений в открытых каналах средние скорости сравниваются с данными экспериментов [12]. Условия течений приведены в табл. 1.

Параболический профиль турбулентной вязкости (1.2) оценивается первым. Рисунок 5 показывает, что использование параболического профиля турбулентной вязкости в уравнении количества движения не может улучшить скорости во внешней области. Скорости (красные сплошные линии) очень близки к логарифмическому закону. Этот результат неудивителен, поскольку зависимость (1.2) основывается на предположении о логарифмическом профиле скорости.

Рис. 5.

Профили скорости для течений в открытых каналах, полученные по уравнению (3.1) и параболической турбулентной вязкости (уравнение 1.2) в сравнении с экспериментальными данными при различных числах Рейнольдса; для большей ясности профили скорости смещены на пять единиц.

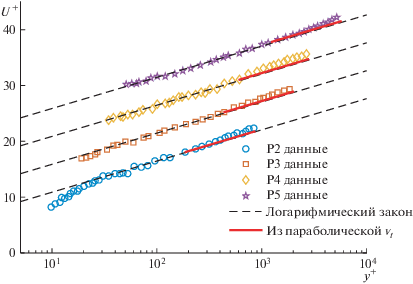
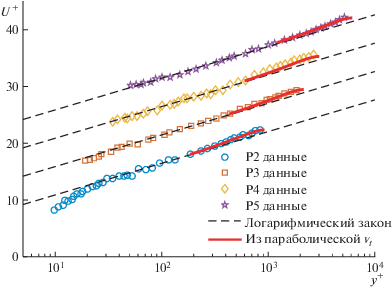
На рис. 6 приведены профили скорости во внешней области (красные сплошные линии), полученные из уравнения количества движения и предложенной зависимости для турбулентной вязкости (2.2)–(2.4). Эти профили показывают хорошее согласие. Этот результат демонстрирует способность аналитической модели турбулентной вязкости точно предсказать скорости во внешней области на основе уравнения количества движения без использования каких-либо специально подбираемых параметров или функций. Это важный результат, поскольку в нашем предыдущем исследовании [14] утверждалось, что профили скорости во внешней области могут быть точно описаны моделью турбулентной вязкости, основанной на экспоненциально убывающей зависимости для турбулентной кинетической энергии, но с коэффициентом затухания, связанным с затухающей функцией для турбулентной вязкости вблизи свободной поверхности.

Рис. 6.

Профили скорости для течений в открытых каналах, полученные по уравнению (3.1) и предложенной турбулентной вязкости (уравнения (2.2)–(2.4)) в сравнении с экспериментальными данными при различных числах Рейнольдса; для большей ясности профили скорости смещены на пять единиц.

ВЫВОДЫ

Параболический профиль турбулентной вязкости, используемый по большей части в течениях в отрытых каналах, основывается на том, что ${{{{\tau }}}_{T}} \approx {{{{\tau }}}_{t}}$ (${{\nu }} \ll {{{{\nu }}}_{t}}$) и логарифмическом законе для профиля скорости (при ${{y}^{ + }} > 30$). Следовательно, параболический профиль справедлив только в логарифмическом подслое (но мог быть расширен на равновесную область) и не должен использоваться от дна до свободной поверхности. В равновесной области (где имеется баланс между производством турбулентной кинетической энергии и ее диссипацией) турбулентная кинетическая энергия задается хорошо известной полутеоретической экспоненциально убывающей функцией. При использовании определения турбулентной вязкости как произведения масштаба скорости и масштаба длины l (связанного с длиной смешения lm) и выборе масштаба скорости, заданного квадратным корнем из турбулентной кинетической энергии, показано, что параболический профиль турбулентной вязкости несовместим с зависимостью для турбулентной кинетической энергии.

Учитывая этот недостаток, был рассмотрен метод, основанный на длине смешения, который позволяет записать выражение для турбулентной вязкости в согласии с профилем турбулентной кинетической энергии и логарифмическим законом для скорости в равновесной области ${{y}^{ + }} > 50$ (которые включают слой перекрытия). Полученное выражение для турбулентной вязкости представляет собой показательную функцию, модулированную линейной функцией. Чтобы дать более общую и более точную модель, выписано уравнение для турбулентной вязкости в виде, допускающем калибровку двух параметров, зависящих от Reτ, которые имеют вид линейных зависимостей. Сравнение предложенных и параболических зависимостей показывает, что обе зависимости близки во внутренней области ${{y}^{ + }} < 0.2~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$. Однако различие становится существенным во внешней области. Анализ, основывающийся на разложении в ряд показательной функции, показывает, что даже в приближении первого порядка эти две зависимости различаются.

Данные прямого численного моделирования турбулентной вязкости для течений в закрытых каналах, полученные при восьми разных условиях течения на интервале $300 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 5200$, были использованы для подтверждения правильности предложенного метода. Сравнения продемонстрировали хорошее согласие. Средние продольные скорости получены с помощью решения уравнения количества движения и сравнены как с результатами прямого численного моделирования, так и с данными экспериментов, которые находились в одном и том же диапазоне чисел Рейнольдса, вычисленных по динамической скорости, а именно в интервалах $300 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 5200$ для течений в закрытых каналах и $923 < {\text{R}}{{{\text{e}}}_{{{\tau }}}} < 6139~$ для течений в открытых каналах. Граничное условие налагалось на нижнем пределе внешней области ${{y}^{ + }} = 0.2~{\text{R}}{{{\text{e}}}_{{{\tau }}}}$ (или ξ = 0.2), где скорость задается логарифмическим законом. Для течений в закрытых каналах профили средней скорости показали хорошее согласие. Все вычисленные скорости, полученные с помощью решения уравнения количества движения по предлагаемой модели, были сопоставлены с данными прямого численного моделирования. Для течений в открытых каналах средние скорости сравниваются с данными экспериментов для четырех разных условий течения. Вначале проверен параболический профиль турбулентной вязкости. Результаты подтверждают, что использование параболического профиля турбулентной вязкости в уравнении количества движения не может улучшить скорости во внешней области. Скорости очень близки к логарифмическому закону. Во внешней области профили скорости, полученные из уравнения количества движения и предложенной турбулентной вязкости, показали хорошее согласие между собой. Эти результаты демонстрируют возможность использования аналитической модели турбулентной вязкости для точного предсказания скорости во внешней области для течений как в закрытых, так и в открытых каналах без использования каких-либо специально подбираемых параметров или функций. Это важный результат, поскольку большинство существующих методов используют дополнительные “искусственные” условия, такие как функция следа для профиля скорости или функция затухания для турбулентной вязкости вблизи свободной поверхности.

Список литературы

  1. Атанов Г.А., Воронин С.Т. Вариационная задача в гидродинамике открытых каналов // Изв. АН СССР. МЖГ. 1980. Т. 15. № 4. С. 159–162.

  2. Ляпидевский В.Ю., Чесноков А.А. Докритические и сверхкритические горизонтально-сдвиговые течения в открытом канале переменного сечения // Изв. РАН. МЖГ. 2009. Т. 44. № 6. С. 123–138.

  3. Peruzzi C., Poggi D., Ridol L., Manes C. On the scaling of large-scale structures in smooth-bed turbulent open-channel flows // J. Fluid Mech. 2020. V. 889. P. A1.

  4. Tominaga K., Nezu I., Ezaki K., Nakagawa H. Three-dimensional turbulent structure in straight open channel flows // J. Hydraulic Res. 1989. V. 27. № 1. P. 149–173.

  5. Guo J., Julien P.Y. Shear stress in smooth rectangular open-channel flows // J. Hydraulic Eng. ASCE; 2005. V. 131. № 1. P. 30–37.

  6. Cameron S.M., Nikora V.I., Stewart M.T. Very-large-scale motions in rough-bed open-channel flow // J. Fluid Mech. 2017. V. 814. P. 416–429.

  7. Nezu I., Nakagawa H. Turbulence in Open Channel Flows, Rotterdam: A.A. Balkema, 1993.

  8. Millikan C.B. A critical discussion of turbulent flows in channels and circular tubes // in: Proceedings of the Fifth International Congress on Applied Mechanics. Eds. J.P. Den Hartog and H. Peters. V. 218. New York. Wiley. 1938. P. 386.

  9. Cardoso A.H., Graf W.H., Gust G. Uniform flow in a smooth open channel // J. Hydraulic Res. 1989. V. 27. № 5. P. 603–616.

  10. Li X., Dong Z., Chen C. Turbulent flows in smooth-wall open channels with different slope // J. Hydraulic Res. 1995. V. 33. № 3. P. 333–347.

  11. Marusic I., Monty J.P., Hultmark M., Smits A.J. On the logarithmic region in wall turbulence // J. Fluid Mech. 2013. V. 716. P. R3.

  12. Nezu I., Rodi W. Open channel measurements with a laser Doppler anemometer // J. Hydraulic Eng. ASCE. 1986. V. 112. № 5. P. 335–355.

  13. Absi R. A simple eddy viscosity formulation for turbulent boundary layers near smooth walls // C.R. Mecanique. 2009. V. 337. № 3. P. 158–165.

  14. Welderufael M., Absi R., Mélinge Y. Assessment of velocity profile models for turbulent smooth wall open channel flows // ISH J. Hydraulic Eng. Available online. 2019.

  15. Afzal N. Power law and log law velocity profiles in turbulent boundary-layer flow: equivalent relations at large Reynolds numbers // Acta Mechanica. 2001. V. 151. № 3. P. 195–216.

  16. Cheng N.S. Power-law index for velocity profiles in open channel flows // Adv. Water Res. 2007. V. 30. № 8. P. 1775–1784.

  17. Coles D. The law of the wake in the turbulent boundary layer // J. Fluid Mech. 1956. V. 1. № 2. P. 191–226.

  18. Hinze J.O. Turbulence. New York: McGraw-Hill, 1975.

  19. Krug D., Philip J., Marusic I. Revisiting the law of the wake in wall turbulence // J. Fluid Mech. 2017. V. 811. P. 421–435.

  20. Absi R. Rebuttal on a mathematical model on depth-averaged β-factor in open-channel turbulent flow // Env. Earth Sci. 2020. V. 79. № 5. P. 113.

  21. Prandtl L. Uber die Ausgebildete turbulenz // Z. Angew. Math. Mech. 1925. V. 5. № 2. P. 136–139.

  22. von Karman Th. Mechanische Ahnlichkeit und turbulenz // Nachr. Ges. Wiss. Goettingen; Math.-Phys. Kl. 1930. V. 5. P. 58–76.

  23. Iwamoto K., Suzuki Y., Kasagi N. Reynolds number effect on wall turbulence: Toward effective feedback control // Int. J. Heat and Fluid Flow. 2002. V. 23. № 5. P. 678–689.

  24. del Alamo J.C., Jimenez J. Spectra of the very large anisotropic scales in turbulent channels // Phys. Fluids. 2003. V. 15. № 6. P. L41–L44.

  25. Lozano-Duran A., Jimenez J. Effect of the computational domain on direct simulations of turbulent channels up to ${\text{R}}{{{\text{e}}}_{{{\tau }}}} = 4200$ // Phys. Fluids. 2014. V. 26. № 1. P. 011702.

  26. Lee M., Moser R.D. Direct numerical simulation of turbulent channel flow up to ${\text{R}}{{{\text{e}}}_{{{\tau }}}} = 5200$ // J. Fluid Mech. 2015. V. 774. P. 395–415.

  27. Absi R. An ordinary differential equation for velocity distribution and dip phenomenon in open-channel flows // J. Hydraulic Res. 2011. V. 49. № 1. P. 82–89.

  28. Rodi W. Turbulence Models and Their Application in Hydraulics, a State of the Art. Review, Rotterdam, Balkema A.A., 1993.

  29. Pope S. Turbulent Flows. Cambridge: Cambridge University Press, 2000.

  30. Absi R. Comment on turbulent diffusion of momentum and suspended particles: A finite-mixing-length theory // Phys. Fluids. 2005. V. 17. № 7. P. 079101.

  31. Businger J.A., Arya S.P.S. Heights of the mixed layer in the stable stratified planetary boundary layer // Adv. Geophys. 1974. V. 18A. P. 73–92.

  32. Hsu T.W., Jan C.D. Calibration of Businger-Arya type of eddy viscosity model’s parameters // J. Waterw. Port Coastal. Ocean. Eng. ASCE. 1998. V. 124. № 5. P. 281–284.

  33. Absi R. Concentration profiles for fine and coarse sediments suspended by waves over ripples: An analytical study with the 1-DV gradient diffusion model // Adv. Water Res. 2010. V. 33. № 4. P. 411–418.

  34. Абси Р. Турбулентная вязкость и профили скорости в развитых турбулентных течениях в каналах // Изв. РАН. МЖГ. 2019. № 1. С. 138–150.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал