1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2021

Известия РАН. Механика жидкости и газа, 2021, № 4, стр. 9-18

ИССЛЕДОВАНИЕ ГИДРОДИНАМИЧЕСКИХ ПОТОКОВ В МИКРОМОДЕЛЯХ СРЕД С ДВОЙНОЙ ПОРИСТОСТЬЮ

О. А. Солнышкина a, *, Э. С. Батыршин a, b, **, Ю. А. Питюк a, b, ***

a Центр микро- и наномасштабной динамики дисперсных систем, Башкирский государственный университет
Уфа, Россия

b ООО “РН-БашНИПИнефть”
Уфа, Россия

* E-mail: olgasolnyshkina@gmail.com
** E-mail: batyrshine@mail.ru
*** E-mail: pityukyulia@gmail.com

Поступила в редакцию 30.09.2020
После доработки 24.12.2020
Принята к публикации 24.12.2020

Полный текст (PDF)

Аннотация

Предложены подходы для экспериментального и численного изучения особенностей течения жидкости в средах с двойной пористостью, основанные на использовании микромоделей пористых сред и технологий микрогидродинамики. Для экспериментального изучения течения жидкости в модельных средах использованы методы оптической микроскопии и трассерной визуализации потоков. Численный подход основан на трехмерном методе граничных элементов, ускоренном быстрым методом мультиполей на гетерогенных вычислительных архитектурах. Изучено влияние структурных параметров микромоделей на распределение потока между областями с различной пористостью. Рассмотрено изменение продольной и поперечной компонент скорости в малых и больших поровых каналах при варьировании их геометрических параметров и объемного расхода.

Ключевые слова: микрогидродинамика, экспериментальная гидродинамика, микромодель, двойная пористость, вычислительная гидродинамика, метод граничных элементов, визуализация потоков

Течение флюидов в пористых средах, в которых распределение пор по размерам имеет два (или несколько) характерных масштаба, является объектом активных научных исследований в течение длительного времени. Результаты этих исследований имеют важное прикладное значение для различных отраслей промышленности. Концепция модели среды с двойной пористостью и математическая модель фильтрации однофазного флюида предложены в работе [1] и до сих пор используются в сфере добычи нефти для описания на макроуровне фильтрации в трещиновато-пористых коллекторах, в которых присутствуют две поровые системы с различными геометрическими параметрами и значениями фильтрационно-емкостных свойств. Представление о среде с двойной пористостью также используется при решении задач индустрии композитных материалов. Наиболее распространенный способ изготовления полимерных композитов предполагает пропитку волокнистого армирующего материала жидким связующим полимером. Армирование, как правило, представляет собой текстиль, структура которого имеет два характерных масштаба. Один из них (микромасштаб) связан с диаметром и упаковкой отдельных волокон в нити, а второй (мезомасштаб) – с расположением нитей в структуре при формировании текстильного полотна и расстоянием между слоями в многослойных структурах. Вследствие сильной неоднородности пустотного пространства такого армирования при его пропитке вязким полимером могут образовываться пузырьки воздуха, которые, оставаясь в структуре композита как пустоты, значительно ухудшают его механические свойства. Исследования в этой области направлены на понимание механизмов образования пустот и разработку практических методов минимизации их количества при производстве композитов [2]. В биомедицинских приложениях среды с двойной пористостью применяются для более корректной оценки проницаемости биологических тканей [3].

Микромасштабные охлаждающие системы имеют широкий спектр применений, таких как охлаждение для интегральных схем, радиочастотной электроники и биомедицинских устройств. Эффективность микротеплообменников зависит от характеристик жидкости, материала, из которого изготавливается чип, и от параметров геометрии. В настоящее время изучение течений в микроканалах со сложной внутренней структурой, состоящей из упорядоченных массивов столбиков, имеет большое значение в сфере интенсификации теплообменных процессов в микротеплообменниках. Влияние геометрии таких структур активно изучается исследовательскими группами, как с экспериментальной, так и с теоретической точки зрения. Основное направление исследований связано с поиском наиболее эффективной для теплообмена формы столбиков и их пространственного упорядочения. В [4] описаны различные механизмы работы охлаждающих устройств с микроструктурами в виде распределенных столбиков различной формы. В [5] рассматривалось влияние плотности распределения цилиндрических элементов в микроканале на теплопередачу при течении охлаждающей жидкости. Подход с двойной пористостью в данном случае тоже может быть полезен для поиска оптимальной конфигурации микротеплообменников. В статье [6] с использованием винтовой системы координат численно исследовались особенности гидродинамических полей при течении вязкой жидкости в каналах с трехзаходной шнековой вставкой. Показано, что даже в случае стоксовых течений (числа Рейнольдса меньше 1) в рассматриваемом канале существуют поперечные потоки. При конструировании теплообменников на микроуровне особенно важным становится подбор геометрии для генерации поперечных потоков, поскольку это увеличивает интенсивность переноса тепла в поперечных направлениях, в то время как в каналах без особенностей внутренней структуры перенос тепла в этих направлениях обусловлен, прежде всего, теплопроводностью [6]. Таким образом, интересной является детализация закономерностей изменения соотношения продольной и поперечной компонент скорости потока в зависимости от структуры пространства внутри микроканала.

Для детального изучения особенностей течения флюида через проницаемую пористую среду и эффективного прогнозирования на макроуровне необходимо учитывать процессы, происходящие на микроуровне в масштабах отдельных пор. Численные методы моделирования течения в пористых средах в большинстве своем основаны на решении уравнения Дарси и заданной локальной проницаемости среды. Такие подходы хорошо известны и формализованы в пакетах прикладных программ, но они не позволяют в полной мере описать особенности течений в элементах пористой среды на микроуровне. Для этих целей применяются различные типы микромасштабных моделей пористой среды, представляющих собой или связанные сети каналов различных форм [7], или модели на основе представления как массива из упакованных недеформируемых элементов, между которыми происходит течение флюида [8]. Также численные модели среды с двойной пористостью стали предметом исследований большого числа работ, которые продолжаются и в настоящее время [9].

Для микрогидродинамики типичными являются течения при малых числах Рейнольдса, для которых уравнения Навье–Стокса могут быть упрощены до уравнений Стокса. Специфика уравнений Стокса заключается в том, что они линейны и могут быть решены методом граничных элементов (МГЭ) [10]. В данной работе в качестве основы численного подхода выбран МГЭ, который заключается в переходе от исходных дифференциальных уравнений в частных производных, описывающих поведение неизвестной функции внутри и на границе области, к интегральным уравнениям, связывающим значения неизвестных функций только на границах рассматриваемых объектов. Таким образом, нет необходимости покрывать сеткой всю расчетную область, как в случае конечно-разностных и конечно-элементных методов, а только границу моделируемых объектов, что для исследования трехмерных задач имеет большое значение в плане снижения вычислительной сложности, поскольку эффективная размерность задачи уменьшается на единицу. Кроме того, подобный подход к дискретизации рассматриваемой области позволяет точнее описывать границы сложных объектов, а также изменение их формы, и решать задачи для бесконечных областей с минимальными затратами оперативной памяти вычислительной системы и времени вычислений. Существует целый ряд публикаций, в которых МГЭ применялся для моделирования медленного течения вязкой жидкости в канале в трехмерной постановке для периодических и непериодических граничных условий [11] и в двумерной постановке для периодического потока [12]. Важно отметить, что большинство аналитических и численных исследований течения однофазных жидкостей и эмульсий проведены для плоских и осесимметричных каналов или в двумерном случае. Таким образом, вопрос об особенностях медленных течений в трехмерных областях со сложной структурой требует более детального изучения. В то же время численное моделирование трехмерных течений Стокса в каналах произвольной геометрии достаточно сложно. Одна из причин этого связана с тем, что для решения трехмерной задачи, даже для относительно простых форм, расчетная сетка на поверхности канала содержит десятки тысяч граничных элементов. В настоящее время новые методы, основанные на алгоритмических и аппаратных ускорениях вычислений, способны решать такие вычислительно сложные задачи. В настоящей работе при решении краевых задач метод граничных элементов ускорен с применением быстрого метода мультиполей (БММ). БММ является высоко параллелизуемым алгоритмом, допускающим возможность дополнительного ускорения за счет использования гетерогенных вычислительных архитектур.

Экспериментальное исследование течения жидкостей в естественных пористых средах, таких как горные породы или биологические ткани, зачастую сопряжено с рядом сложностей: плохой воспроизводимостью свойств образцов, быстрой деградацией образца в течение эксперимента, сложностью пробоподготовки, ограниченными возможностями визуализации процессов. В таких случаях задача существенно упрощается путем использования физических микромоделей пористых сред, которые воспроизводят заданные свойства реальных объектов, например, геометрические параметры структуры порового пространства, свойства поверхности пор, механические свойства матрицы пористой среды. Значительный прогресс в использовании микромоделей связан с развитием технологий микрогидродинамики, позволяющих создавать микрочипы, содержащие сложные сети микроканалов [13]. Микрочипы изготавливаются, главным образом, из оптически прозрачных материалов и основные методы исследования свойств течений в них основаны на применении методов оптической микроскопии, в том числе специальных методов, таких как флуоресцентная и конфокальная микроскопия, полного внутреннего отражения, трассерная визуализация потоков. Технологии производства таких чипов обеспечивают высокий уровень воспроизводимости геометрических и физических свойств, что положительно влияет на достоверность экспериментальных результатов. Исследования, проведенные в рамках настоящей работы, направлены на разработку и применение экспериментальной методики с использованием микромоделей пористых сред для изучения особенностей одно- и многофазных течений в средах с несколькими масштабами пористости.

Сложность и многопараметричность задач течений на микроуровне в областях с нетривиальной геометрией приводят к необходимости математического моделирования, основанного на решении классических уравнений механики и физики, разработке эффективных вычислительных подходов и проведении экспериментов, обеспечивающих связь моделей с реальностью. Целью данной работы является детальное изучение течения несжимаемой вязкой жидкости в модели двойной пористости на микроуровне. Новизна исследования заключается в комплексном экспериментально-численном исследовании особенностей гидродинамических потоков при течении вязкой жидкости в микромоделях сред с двумя масштабами пористости в зависимости от их геометрических параметров.

1. ЭКСПЕРИМЕНТ

Для целей настоящей работы при помощи методов мягкой литографии [14] с использованием сшитого полимера – полидиметилсилоксана изготовлены микрочипы с пористой структурой, образованной системой цилиндрических столбиков (рис. 1).

Рис. 1.

Схематичное изображение структуры порового пространства чипа: ch1–ch3 – (a, b) = (210, 210), (180, 270), (160, 310) мкм.

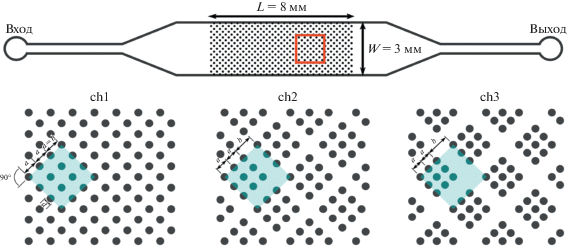
На схематичном изображении чипа (рис. 1) показаны пористая структура, места входа и выхода жидкости и прямоугольная область (выделена красным) пористой структуры, в которой производилась видеорегистрация потока. Диаметр и высота цилиндров составляют d = 120 мкм и h = 30 мкм. Особенности структуры порового пространства чипа определялись характером пространственного упорядочения цилиндров. Изготовлено три микрочипа (ch1, ch2, ch3) с различными параметрами порового пространства, их фрагменты показаны на рис. 1. Цилиндры находятся в узлах прямоугольной решетки.

Для чипа ch1 выбрана квадратная решетка с одним характерным пространственным периодом a = 210 мкм, a – расстояние между центрами цилиндров в одной группе элементов. В чипах ch2, ch3 сохранено прямоугольное упорядочение, но структуры имеют два пространственных масштаба. Для всех вариантов величина $2a + b = 630$ мкм остается постоянной, b – расстояние между центрами ближайших цилиндров из соседних групп. Соотношение масштабов пористости в микромоделях определяется соотношением величин a и b, при этом высота микроканалов и диаметр цилиндров остаются неизменными. Для оценки гидравлического радиуса образованных поровых каналов используется соотношение для канала с прямоугольным поперечным сечением ${{r}_{h}} = \frac{{h \times w}}{{2(h + w)}}$, где w – ширина канала. Тогда для рассматриваемых вариантов структур отношение гидравлического радиуса широких поровых каналов к узким равно kr = 1, 1.25 и 1.51 для ch1, ch2 и ch3 соответственно.

При изменении параметров пространственного расположения цилиндров общее количество цилиндров и размер пористой области чипа сохраняются неизменными, таким образом, общая пористость всех структур одинакова и составляет величину ϕ ≈ 0.67. На рис. 1 затенением выделены представительные области, трансляцией которых можно воспроизвести всю пористую структуру. Отметим, что размеры этих областей одинаковы для всех сконструированных вариантов.

В микрочипах с помощью шприцевого насоса создавался поток жидкости при постоянном объемном расходе. Использовался 25% (по объему) раствор глицерина в воде. Для визуализации потока в раствор добавлены полимерные частицы диаметром 3 мкм. Плотность материала частиц близка к плотности раствора, что обеспечивало нейтральную плавучесть частиц и их однородное распределение по высоте микроканала. Микрочип размещался на столике инвертированного оптического микроскопа Olympus IX-71, сопряженного с высокоскоростной камерой Photron Fastcam SA5. Видеорегистрация потоков производилась со скоростью от 500 до 2000 кадров в секунду в зависимости от скорости фильтрации. Для построения поля скорости течения использованы методы определения скорости по анализу динамики трассерных частиц с помощью программного пакета PIVlab [15].

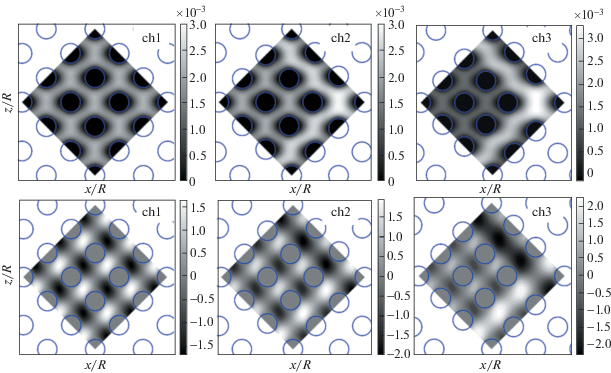
На рис. 2 представлено распределение скорости потока при одинаковом расходе жидкости Q = 10 мкл/мин, $\operatorname{Re} \approx 0.3$. Число Рейнольдса для равномерно распределенных по ширине канала столбиков рассчитывалось следующим образом [4]: $\operatorname{Re} = \rho {{u}_{{\max }}}d{\text{/}}\mu $, где ρ – плотность жидкости, umax = $Q{\text{/}}{{A}_{{\min }}}$, ${{A}_{{\min }}} = Wh(a - d){\text{/}}a$, $\mu = 1.805 \times {{10}^{{ - 3}}}$ Па · с – динамическая вязкость раствора. Необходимо отметить, что полученные распределения скорости потока основаны на допущении, что скорость жидкости совпадает со скоростью частиц. При трассерных исследованиях потоков в микрогидродинамике выделяют следующие причины, которые могут препятствовать микрочастицам полностью следовать потоку: броуновское движение, внешние силы и сила Саффмана [16]. При скоростях течения порядка 1 мм/с броуновское движение важно учитывать для частиц размером 0.5 мкм и менее [16], в нашем случае для частиц размеров 3 мкм влияние броуновского движения несущественно. Внешние силы в экспериментах не прикладывались, гравитация не оказывала влияние на движение частиц, поскольку плотность частиц близка к плотности жидкости. Сила Саффмана возникает при движении частиц в сдвиговом потоке и направлена перпендикулярно направлению потока жидкости, что приводит к миграции частиц и их неоднородному распределению в поперечном сечении потока. Согласно [16], если отношение Vm/Vs = = $0.343r\sqrt {G\rho {\text{/}}\mu } \ll 1$, (Vm – скорость миграции частиц, Vs – скорость частиц относительно жидкости, r – радиус частицы, G – скорость сдвига), то влияние миграции частиц на оценку скорости течения жидкости пренебрежимо мало. В нашем случае эта величина имеет порядок 10–3, таким образом мы можем считать, что частицы однородно распределены по высоте микроканалов, и полученные распределения скорости течения жидкости адекватны реальным.

Рис. 2.

Визуализация экспериментальных результатов: поле скорости течения жидкости и распределение его модуля $\left| {v} \right|$, м/с (верхняя строка) и гистограммы распределения $\left| {v} \right|$ (нижняя строка) для чипов со значениями kr = 1, 1.25 и 1.51 (слева направо).

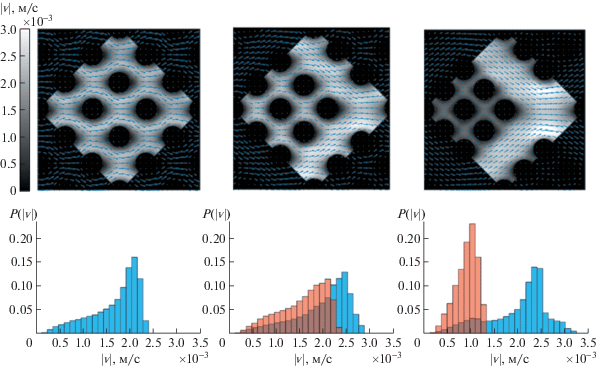
Наличие второго характерного размера пор значительно изменяет картину течения. При увеличении значения kr скорость течения потока в малых порах уменьшается, и основной поток жидкости происходит в крупных порах. Количественные изменения скорости потока также отражены на гистограммах распределения модуля скорости в малых (оранжевый цвет) и больших (голубой цвет) порах (рис. 2). Показано, что при увеличении kr распределение скоростей меняется, и выделяются два характерных максимума скорости, причем максимальное значение для широких пор практически не меняется, а максимум модуля скорости в узких порах снижается существенно.

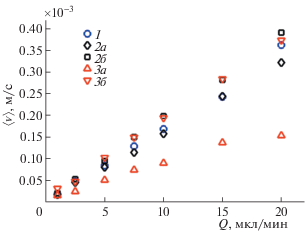
Зависимость средней скорости потока от объемного расхода жидкости показана на рис. 3. Из рисунка видно, что средняя скорость потока в крупных порах структур ch2, ch3 несколько выше средней скорости потока в ch1, при этом скорости в больших порах ch2 и ch3 почти не отличаются. С другой стороны, средняя скорость потока в малых порах быстро снижается при уменьшении их размера и различие в скоростях для ch2 и ch3 значительно. То есть в областях с малыми порами происходит стагнация потока, и общий вклад этих областей в перенос жидкости через пористую структуру уменьшается.

Рис. 3.

Зависимость средней скорости жидкости от объемного расхода: 1 – в структуре ch1; 2a, 3a – в малых порах для ch2, ch3; 2б, 3б – в больших порах для ch2, ch3.

2. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

В данной работе рассматривается течение вязкой несжимаемой жидкости вокруг фиксированных структур внутри плоского канала прямоугольного сечения при малых числах Рейнольдса $\operatorname{Re} \ll 1$ и изотермических условиях. Таким образом, силы вязкости гораздо значительнее сил инерции и установившееся течение жидкости будет описываться уравнением Стокса и уравнением неразрывности

(1)
$ - \nabla p + \mu {{\nabla }^{2}}{\mathbf{u}} = 0,\quad \nabla \times {\mathbf{u}} = 0,$
где u – скорость; μ – динамическая вязкость; p – давление, которое включает в себя гидростатический компонент.

Геометрия рассматриваемой области представляет собой структуру из цилиндрических элементов, расположенных поперек потока, ограниченную с четырех сторон плоскими стенками, которые образуют канал прямоугольного поперечного сечения. Схематическое изображение геометрии в декартовой системе координат в плоскостях xOz и yOz представлено на рис. 4. Рассматриваемая структура зафиксирована в неограниченном объеме вязкой несжимаемой жидкости, для которой задана постоянная скорость на бесконечности ${{{\mathbf{u}}}_{\infty }} = (u,0,0)$. Таким образом, на входе в канал задается объемный расход Q, соответствующий скорости внешней жидкости, и рассчитывается число Рейнольдса. Цилиндрические элементы расположены внутри канала на достаточном расстоянии от входа, чтобы течение установилось и приняло характерный для прямоугольного сечения профиль. На боковых поверхностях образованного канала и на поверхностях цилиндрических элементов внутренней структуры задается условие прилипания.

Рис. 4.

Схематическое изображение рассматриваемой геометрии в плоскостях xOz (слева) и yOz (справа).

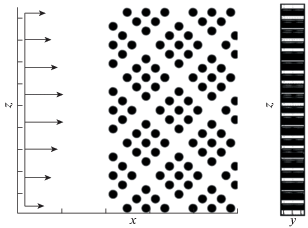
Разработана качественная триангуляция нескольких вариантов конфигураций структуры с двумя масштабами пористости. Соотношение гидравлических радиусов широких и узких поровых каналов соответствует параметрам микрочипов, используемых в экспериментальной части работы, kr = 1, 1.25 и 1.51. Геометрия расчетной области подобрана так, что общая пористость всех вариантов структур одинакова и соответствует пористости экспериментального чипа ϕ ≈ 0.67. Поверхность каждого рассматриваемого объекта покрывалась треугольной сеткой, суммарное количество треугольных элементов в задаче составило ${{N}_{\Delta }} = 533\,836$. Особое внимание при разработке триангуляции уделялось качеству расчетной сетки, в частности таким параметрам, как соотношение максимальной и минимальной сторон треугольников, площади треугольника к длинам его сторон, отношение углов в треугольнике.

Численное исследование гидродинамических потоков в микроструктурах с несколькими масштабами пористости проводилось с использованием эффективного подхода на основе метода граничных элементов. Для вычисления поверхностных интегралов использовались квадратурные формулы. Сингулярные интегралы определялись на основе известных интегральных тождеств для течений Стокса и метода линейных тестовых решений [11]. С использованием метода коллокаций в центрах треугольных элементов уравнения в граничных интегралах сводятся к СЛАУ. Далее, решив полученную систему и используя найденные граничные значения, можно вычислить поле скорости в любой точке области. Более подробно постановка данной задачи и гранично-интегральная формулировка описаны в работе [17].

В случае расчетных сеток небольшого размера при решении СЛАУ применялись стандартные прямые методы, но при увеличении масштаба задачи их использование затрудняется из-за ограничений, связанных с памятью вычислительной системы. Эту проблему можно решить, используя итерационные методы решения СЛАУ, реализуемые в виде последовательных приближений, которые в пределе сходятся к решению с некоторой заданной погрешностью (используется GMRES – метод обобщенных минимальных невязок). Для эффективной программной реализации матрично-векторное произведение, используемое в GMRES, ускорено с применением высокоэффективного масштабируемого алгоритма – быстрого метода мультиполей, распараллеленного на гетерогенных вычислительных системах, состоящих из нескольких многоядерных центральных процессоров (CPU) и графических процессоров (GPU). Несмотря на то что гетерогенный БММ позволяет решать системы большого размера, при моделировании течения в присутствии твердых стенок существует проблема, связанная с плохой обусловленностью матрицы системы линейных уравнений. Для решения этой проблемы применена гибкая версия GMRES, которая отличается от стандартной использованием правого предобуславливателя. Особенностью реализованного fGMRES является то, что в глобальных итерациях используется БММ повышенной точности, а в итерациях предобуславливателя – БММ пониженной точности. В предыдущих работах авторов подробно описан используемый численный подход, реализованные алгоритмы и их применение к различным типам задач [11, 17–19].

Проведены расчеты высокой вычислительной сложности для скорости жидкости в модели микроструктур с различным взаимным расположением цилиндрических элементов. Получены картины течения для трех конфигураций расположения цилиндрических элементов при $\operatorname{Re} \approx 0.3$ в плоскости канала y = h/2. Визуализация продольной и поперечной компонент скорости представлена на рис. 5. При изменении геометрии структуры от ch2 к ch3 максимум значения продольной компоненты скорости в широких каналах увеличился на 22.2%, а максимум поперечной – на 15%. В то время как в узких каналах максимум продольной компоненты скорости уменьшился значительнее – на 31.5%, а максимум поперечной компоненты – на 26.6%. В итоге максимальное значение модуля скорости в широких каналах увеличилось на 16%, в области с более узкими каналами – уменьшилось на 24%. Таким образом, показано, что при увеличении значения kr основной поток жидкости происходит в широких каналах, а в области модели с узкими каналами скорость течения существенно уменьшается, что согласуется с экспериментальными наблюдениями.

Рис. 5.

Визуализация численных результатов распределения продольной (верхняя строка) и поперечной (нижняя строка) компонент скорости для чипов со значениями kr = 1, 1.25 и 1.51 (слева направо) при $\operatorname{Re} \approx 0.3$.

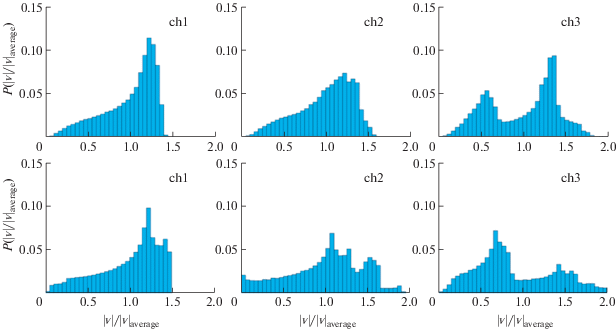
На рис. 6 представлены гистограммы распределения скорости во всей области, выделенной на рис. 1 цветом. Значения скорости отнесены к среднему значению скорости в рассматриваемой области. Видно, что полученные численно и экспериментально распределения имеют схожий характер. Некоторые расхождения и сдвиг пиковых значений вправо, возможно, связаны с неравномерным распределением трассерных частиц по высоте и ширине канала при визуализации течения, в то время как расчетные узлы расположены достаточно плотно (M = 90 000) и равномерно по всей области в центральной плоскости канала y = h/2. Таким образом, получено достаточно хорошее качественное согласование экспериментальных и численных результатов.

Рис. 6.

Экспериментальные (верхний ряд) и рассчитанные (нижний ряд) гистограммы распределения осредненной скорости для чипов со значениями kr = 1, 1.25 и 1.51 (слева направо).

Все расчеты проводились на персональной рабочей станции следующей конфигурации: CPU IntelXeon 5660, 2.8GHz, 12 GB RAM и GPU NVIDIA Tesla К20, 5 GB глобальной памяти (архитектура Kepler).

ЗАКЛЮЧЕНИЕ

Предложен подход с применением технологий микрогидродинамики для изучения особенностей течения жидкостей в структурах с двойной пористостью. Изготовлены микромодели пористых сред с одним и двумя характерными масштабами пор, образованные системой пространственно упорядоченных полимерных столбиков. В рамках численного исследования гидродинамических потоков в указанных моделях применены современные подходы, некоторые из которых впервые используются в России, основанные на трехмерном методе граничных элементов в совокупности с масштабируемым алгоритмом (быстрый метод мультиполей) и высокопроизводительными вычислениями на гетерогенных вычислительных архитектурах (CPU+GPU). Для сопоставления с экспериментальными данными реализована триангуляция структуры, соответствующая геометрии микрочипа в эксперименте. Показано, что при увеличении соотношения гидравлического диаметра широких поровых каналов к узким распределение скоростей меняется, и выделяются два характерных максимума скорости, причем максимальное значение для более широких каналов практически не меняется, а максимум модуля скорости в узких каналах снижается существенно.

Полученные результаты могут быть использованы для верификации моделей, описывающих течения в средах с двойной пористостью. Подобные модели используются для описания фильтрации в горных породах, технологических процессов изготовления волокнистых композитов и других прикладных задач. Результаты исследования могут быть использованы для решения задач, связанных с конструкцией микрогидродинамических устройств, и представляют интерес для вычислительной гидродинамики в целом. Предложенный подход и полученные результаты также могут быть использованы для исследования практически значимых проблем, связанных с изучением и разработкой методов воздействия на одно- и многофазные потоки в средах с различными масштабами пористости.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 18-38-20102. Библиотека БММ предоставлена Fantalgo, LLC (Maryland, USA).

Список литературы

  1. Баренблатт Г.И., Желтов Ю.П., Кочина И.Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах // ПММ. 1960. Т. 24. № 5. С. 852–864.

  2. Park C.H., Lee W. II. Modeling void formation and unsaturated flow in liquid composite molding processes: a survey and review // J. Reinf. Plast. Compos. 2011. V. 30. № 11. P. 957–977. https://doi.org/10.1177/0731684411411338

  3. Ooi E.H., J.Y. Chia N., Ooi E.T., Foo J.J., Liao I.Y., R. Nair S., Mohd Ali A.F. Comparison between single- and dual-porosity models for fluid transport in predicting lesion volume following saline-infused radiofrequency ablation // Int. J. Hyperth. Informa UK Ltd., 2018. V. 34. № 8. P. 1142–1156. https://doi.org/10.1080/02656736.2018.1437282

  4. Guo D. Design, Analysis, Modeling and Testing of a Micro-scale Refrigeration System // Carnegie Mellon University, 2014. 150 p.

  5. Peles Y., Kosar A., Mishra C., Kuo C.-J., Schneider B. Forced convective heat transfer across a pin fin micro heat sink // Int. J. Heat Mass Transf. 2005. V. 48. № 17. P. 3615–3627. https://doi.org/10.1016/j.ijheatmasstransfer.2005.03.017

  6. Вачагина Е.К., Кадыйров А.И., Конахина И.А., Хуснутдинова Э.М. Особенности гидродинамических полей в каналах с трехзаходной шнековой вставкой // Известия РАН. МЖГ. 2019. №3. С. 28–37.https://doi.org/10.1134/S0568528119020129

  7. Weishaupt K., Joekar-Niasar V., Helmig R. An efficient coupling of free flow and porous media flow using the pore-network modeling approach // J. of Computational Physics: X. 2019. V. 1. 100011.https://doi.org/10.1016/j.jcpx.2019.100011

  8. Zinchenko A.Z., Davis R.H. Motion of deformable drops through porous media // Annu. Rev. Fluid Mech. 2017. V. 49 (1) P. 71–90. https://doi.org/10.1146/annurev-fluid-010816-060331

  9. Berre I., Doster F., Keilegavlen E. Flow in Fractured Porous Media: A Review of Conceptual Models and Discretization Approaches // Transp. Porous Media. 2019. V. 130. P. 215–236. https://doi.org/10.1007/s11242-018-1171-6

  10. Pozrikidis C. Boundary Integral and Singularity Methods for Linearized Viscous Flow // Cambridge University Press, Cambridge, MA, 1992. 272 p.

  11. Абрамова О.А., Иткулова Ю.А., Гумеров Н.А. Моделирование трехмерного движения деформируемых капель в стоксовом режиме методом граничных элементов // Выч. мех. сплошных сред. 2013. Т. 6. № 2. С. 214–223. https://doi.org/10.7242/1999-6691/2013.6.2.25

  12. Pozrikidis C. Creeping flow in two dimensional channels // J. Fluid Mech. 1987. V. 180. P. 495–514. https://doi.org/10.1017/S0022112087001927

  13. Temiz Y., Lovchik R.D., Kaigala G.V., Delamarche E. Lab-on-a-chip devices: How to close and plug the lab? // Microelectron. Eng. 2015. V. 132. P. 156–175. https://doi.org/10.1016/j.mee.2014.10.013

  14. Xia Y., Whitesides G.M. Soft Lithography // Annu. Rev. Mater. Sci. 1998. V. 28. № 1. P. 153–184. https://doi.org/10.1146/annurev.matsci.28.1.153

  15. Thielicke W., Stamhuis E.J. PIVlab – Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB // J. Open Res. Softw. 2014. V. 2. https://doi.org/10.5334/jors.bl

  16. Wereley S., Meinhart C. Micron-Resolution Particle Image Velocimetry // In: Breuer K.S. (eds) Microscale Diagnostic Techniques. Springer, Berlin, Heidelberg. 2005. P. 51–112. https://doi.org/10.1007/3-540-26449-3_2

  17. Abramova O.A., Pityuk Y.A., Gumerov N.A., Akhatov I.S. Three-dimensional simulation of stokes flow around a rigid structure using FMM/GPU accelerated BEM // Commun. Comput. Inf. Sci. 2019. V. 965. P. 427–438. https://doi.org/10.1007/978-3-030-05807-4/_36

  18. Абрамова О.А., Ахатов И.Ш., Гумеров Н.А., Питюк Ю.А., Саметов С.П. Численно-экспериментальное изучение динамики пузырька, контактирующего с твердой поверхностью // Известия РАН. МЖГ. 2018. № 3. С. 3–13. https://doi.org/10.7868/S0568528118030015

  19. Абрамова О.А., Иткулова Ю.А., Гумеров Н.А., Ахатов И.Ш. Эффективный метод расчета динамики большого количества деформируемых капель в стоксовом режиме // ДАН. 2014. Т. 456. № 2. С. 1–5. https://doi.org/10.7868/S0869565214140084

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал