1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2021

Известия РАН. Механика жидкости и газа, 2021, № 3, стр. 48-55

ЭЛЕКТРОСТАТИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ ВЫСОКИХ АЗИМУТАЛЬНЫХ МОД ЗАРЯЖЕННОЙ СТРУИ

А. И. Григорьев a, *, С. О. Ширяева a, **

a Ярославский государственный университет им. П.Г. Демидова
Ярославль, Россия

* E-mail: grig@uniyar.ac.ru
** E-mail: shir@uniyar.ac.ru

Поступила в редакцию 28.08.2020
После доработки 12.10.2020
Принята к публикации 25.12.2020

Полный текст (PDF)

Аннотация

Впервые исследованы высокие азимутальные моды заряженной струи несжимаемой идеальной электропроводной жидкости, движущейся относительно окружающей диэлектрической среды. Показано, что имеются пороги по величине поверхностной плотности электрического заряда, при превышении которых реализуется электростатическая неустойчивость поверхности родительской струи, проявляющаяся в выбрасывании на два порядка более тонких дочерних струек, распадающихся на капельки. Высота этих порогов увеличивается с увеличением номера моды и уменьшением скорости движения относительно среды. Сходное явление фиксируется и по отношению к скорости относительного движения струи и среды, в этом случае неустойчивость называется аэродинамической, но реализуется при весьма больших скоростях.

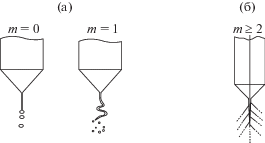
Ключевые слова: струя, электрическое поле, материальная среда, неустойчивость, азимутальное число

В экспериментальных работах [1–4], посвященных исследованию закономерностей реализации и классификации возможных режимов электродиспергирования заряженных струй, которых к концу двадцатого века насчитывалось в зависимости от физико-химических свойств жидкостей несколько десятков был обнаружен (но не истолкован) и режим электростатической неустойчивости, в котором неустойчивой становится поверхность струи. Кроме распада струи в осесимметричной азимутальной моде (азимутальный параметр m = 0) и в изгибной азимутальной моде (m = 1), см., например, рис. 1а, при высоком потенциале, подающемся на струю в [1–4], был зафиксирован так называемый режим “ветвящихся струй” ($m \geqslant 2$) (б), в котором неустойчивость претерпевает заряженная поверхность струи, выбрасывая на два порядка более тонкие дочерние струйки, распадающиеся на маленькие капельки. Отметим, что реальные фотографии этих режимов диспергирования приведены в [1–3, 5].

Рис. 1.

Схемы распада струи при возбуждении азимутальной моды с $m = 0,\;1$ (а) и $m \geqslant 2$ (б).

В экспериментах [1–3] использовались дистиллированная вода с добавкой небольшого количества ПВА, чистая вода и различные органические вещества (диэтил себакат, циклогексанол, этиловый спирт, дибутил фтолат, триэтилен гликоль) в чистом виде, и в виде смесей. Электропроводность чистых жидкостей изменялась в пределах от 9 до 9 × 108 СГСЕ. Объемный расход жидкости через капилляр изменялся в пределах – 10–3–10 мм3/сек. Использовались капилляры двух диаметров: внешний диаметр капилляра 0.12 мм, 0.3–1.5 мм. Коэффициент поверхностного натяжения рабочих жидкостей менялся в диапазоне 22–73 дин/см; коэффициент динамической вязкости рабочей жидкости – 0.004–15 г/см сек.

Для получения желательных физико-химических характеристик: электропроводности, вязкости, объемного расхода использовались смеси различных жидкостей.

В работе [4] рабочие жидкости имели физико-химические характеристики, приведенные в табл. 1.

Таблица 1.

Физико-химические характеристики рабочих жидкостей [4]

  Плотность, г/см3 Коэффициент вязкости, П Коэффициент поверхностного натяжения, дин/см Электропро-водность, СГСЕ Диэлектрическая проницаемость
дистиллированная вода 1 0.01 72.5 105 80.4
этилен гликоль 1.11 0.199 46.4 103 38.8
этанол 0.789 0.0116 22 2.7 × 105 25

Режим “ветвящихся струй” реализуется при весьма значительных напряженностях электрического поля (околопробойных в смысле возможности зажигания коронного разряда у поверхности струи [6]) и трудно реализуем на практике; в экспериментах достигается лишь для жидкостей с низким значением коэффициента поверхностного натяжения и при высоких давлениях в среде. Для критического значения напряженности радиального электрического поля зажигания короны у поверхности цилиндрической струи радиусом $r$ установлена следующая эмпирическая закономерность [6]

${{E}_{{{\text{кр}}}}} \approx 31\delta (1 + {{0.308} \mathord{\left/ {\vphantom {{0.308} {\sqrt {\delta \cdot r} }}} \right. \kern-0em} {\sqrt {\delta \cdot r} }})\;{{{\text{кВ}}} \mathord{\left/ {\vphantom {{{\text{кВ}}} {{\text{см}}}}} \right. \kern-0em} {{\text{см}}}}$
где $\delta $ – отношение плотности воздуха к нормальной, соответствующей 760 тор и температуре 25°С. Из этой формулы следует, что при уменьшении радиуса струи критическое значение напряженности электрического поля зажигания короны увеличивается, а при уменьшении давления в среде – уменьшается.

В связи со сказанным этот режим практически экспериментально не исследован. При его реализации с поверхности основной струи выбрасываются во все стороны значительно более тонкие дочерние струйки, распадающиеся на капельки, распадается и основная струя. В итоге функция распределения капель по размерам оказывается весьма широкой.

В [5] такой режим сфотографирован при распаде заряженной капли, пролетающей в свободном падении сквозь область резко неоднородного электростатического поля (между торцом проволоки и плоским противоэлектродом). Капля, испытывая электростатическую неустойчивость, выбрасывает струю, распадающуюся на мелкие капли, при этом реализуется распад в различных азимутальных модах, в том числе и $m \geqslant 2$.

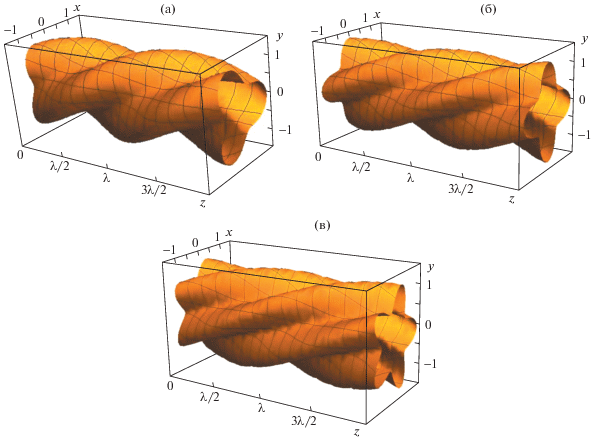
Теоретическое осмысление указанного режима электродиспергирования струй жидкости началось еще десять лет назад (см., например, [7] и указанные там публикации). Согласно существующим представлениям режим “ветвящихся струй” связан с электростатической неустойчивостью заряженной поверхности жидкости [8–12], а конкретно для струй: с неустойчивостью асимметричных азимутальных мод с азимутальным числом $m \geqslant 2$ [7]. На рис. 2а–в приведен внешний вид струй с возбужденными третьей, четвертой и пятой азимутальными модами. Расчеты поверхностей на рис. 2а–в проведены по простейшей формуле, обезразмеренной на радиус невозмущенной струи

$r = 1 + a \cdot \cos (kz + m\varphi )$
где a – амплитудный множитель; k – волновое число; r = 1 – безразмерное уравнение невозмущенной поверхности струи. При расчетах рис. 2а–в принималось $a = 0.3$; k = 2. Расчеты выполнены впервые.

Рис. 2.

Качественный вид формы поверхности струи при возбуждении азимутальной моды: а–в $m = $ 3, 4 и 5.

Целесообразно также указать, в какой связи используется неопределенность типа $m \geqslant 2$, а не указание конкретного значения номера азимутальной моды. Поскольку в экспериментальных работах [1–4] не указываются конкретные величины напряженностей реализации режимов электродиспергирования, то теоретические расчеты невозможно сравнить с экспериментом. На данный момент невозможно точно сказать, сколь высоких азимутальных мод струи задействовано в реализации электростатической неустойчивости заряженной струи.

Данная работа предполагает теоретический анализ закономерностей возбуждения электростатической неустойчивости высоких азимутальных мод заряженной струи.

1. ФИЗИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

Будем решать задачу о капиллярных осцилляциях заряженной цилиндрической поверхности струи радиуса R идеальной электропроводной несжимаемой жидкости с коэффициентом поверхностного натяжения $\sigma $ и массовой плотностью ${{\rho }_{{in}}}$, движущейся вдоль оси симметрии со скоростью ${{{\mathbf{U}}}_{0}}$. Среду будем моделировать идеальной несжимаемой диэлектрической жидкостью с массовой плотностью ${{\rho }_{{ex}}}$ и диэлектрической проницаемостью, близкой к единице: ${{\varepsilon }_{{ex}}} \approx 1$. Задача рассматривается в инерциальной системе отсчета, связанной с осью симметрии невозмущенной струи в цилиндрической системе координат, орт ez которой совпадает по направлению с ${{{\mathbf{U}}}_{0}}$ и осью симметрии невозмущенной капиллярным волновым движением цилиндрической поверхности струи. Электрическое поле в окрестности струи будем считать стремящимся к нулю на бесконечности при удалении в радиальном направлении. Рассмотрение проведем в безразмерных переменных, в которых $R = {{\rho }_{{in}}} = \sigma = 1$.

Примем, что поверхность струи, возмущенная тепловым капиллярным волновым движением, описывается соотношением $F = r - 1 - {{\xi }}(\varphi ,z,t) = 0$, $\left| {{{\xi }}(\varphi ,z,t)} \right| \ll 1$, где ${{\xi }}(\varphi ,z,t)$ – капиллярное волновое возмущение цилиндрической поверхности струи. Это возмущение имеет малую амплитуду порядка $\sqrt {\kappa T{\text{/}}\sigma } $, где $\kappa $ – постоянная Больцмана; $T$ – абсолютная температура [9].

В качестве малого параметра задачи $\varepsilon $ примем безразмерную максимальную амплитуду волнового возмущения: $\varepsilon \equiv \frac{{\max \left| {{{\xi }}(\varphi ,z,t)} \right|}}{R}$.

2. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

Полная математическая формулировка задачи состоит из: уравнений Эйлера

(2.1)
$\frac{{\partial {{{\mathbf{u}}}_{j}}({\mathbf{r}},t)}}{{\partial t}} + \left( {{{{\mathbf{u}}}_{j}}({\mathbf{r}},t),\nabla } \right){{{\mathbf{u}}}_{j}}({\mathbf{r}},t) = - \nabla {\text{p}}({\mathbf{r}},t),\quad j = \left( {in,ex} \right)$
уравнения непрерывности
${\text{div}}\,{{{\mathbf{u}}}_{j}}({\mathbf{r}},t) = 0$
уравнений для расчета напряженности электрического поля
$\left( {1 + {{\xi }}\left( {\varphi ,z,t} \right) < {\text{r}}\left( t \right) < \infty } \right){\kern 1pt} :\quad {\text{rot}}\,{\mathbf{E}}{\kern 1pt} ({\mathbf{r}},t) = 0;\quad {\text{div}}\,{\mathbf{E}}{\kern 1pt} ({\mathbf{r}},t) = 0;\quad \Delta \Phi ({\mathbf{r}},t) = 0$
естественных граничных условий
$\begin{gathered} r \to 0{\kern 1pt} :\quad \left| {{{{\mathbf{u}}}_{{in}}}({\mathbf{r}},t)} \right| < \infty \\ r \to \infty ;\quad \left| {{{{\mathbf{u}}}_{{ex}}}({\mathbf{r}},t)} \right| \to - {{U}_{0}};\quad \left| {{\mathbf{E}}({\mathbf{r}},t)} \right| \to 0 \\ \end{gathered} $
кинематического и динамического гидродинамических граничных условий на возмущенной границе раздела сред
${{\left. {\frac{{dF}}{{dt}}} \right|}_{{F = 0}}} = 0,\quad {{p}_{{in}}}({\mathbf{r}},t) - {{p}_{{ex}}}({\mathbf{r}},t) + {{p}_{E}}({\mathbf{r}},t) - {{p}_{\sigma }}({\mathbf{r}},t) = 0$
и условия для электрического потенциала $\Phi ({\mathbf{r}},t)$
(2.2)
$\Phi ({\mathbf{r}},t) = {{\Phi }_{s}}(t)$
${{{\mathbf{u}}}_{j}}({\mathbf{r}})$ – поле скоростей течения жидкости в струе и в среде ${{p}_{{in}}}({\mathbf{r}},t)$ – гидродинамическое давление в струе; ${{p}_{{ex}}}({\mathbf{r}},t)$ – гидродинамическое давление во внешней среде; ${{p}_{E}}({\mathbf{r}},t)$ = $\frac{{{{\varepsilon }_{{ex}}}{{E}^{2}}({\mathbf{r}},t)}}{{8\pi }}$ – давление электрического поля [13]; ${\mathbf{E}}{\kern 1pt} ({\mathbf{r}},t) \equiv - \nabla \Phi ({\mathbf{r}},t)$; ${{\Phi }_{s}}(t)$ – потенциал поверхности струи; ${{p}_{\sigma }}({\mathbf{r}},t)$ – капиллярное давление

${{p}_{\sigma }}({\mathbf{r}},t) = 1 - {{\xi }}\left( {\varphi ,z,t} \right) - \frac{{{{\partial }^{2}}{{\xi }}\left( {\varphi ,z,t} \right)}}{{\partial {{\varphi }^{2}}}} - \frac{{{{\partial }^{2}}{{\xi }}\left( {\varphi ,z,t} \right)}}{{\partial {{z}^{2}}}}$

Введем также гидродинамические потенциалы ${{{{\psi }}}_{j}}({\mathbf{r}},t)$ [15] такие, что

${{{\mathbf{u}}}_{j}}({\mathbf{r}},t) \equiv \nabla {{{{\psi }}}_{j}}({\mathbf{r}},t)$

3. ДИСПЕРСИОННОЕ УРАВНЕНИЕ

Раскладывая сформулированную задачу по малому параметру ε, легко выделить задачи нулевого и первого порядков малости [7].

Решение задачи нулевого порядка тривиально, и определяет невозмущенную цилиндрическую струю, движущуюся вдоль оси симметрии со скоростью U0, с равномерно распределенным по ее поверхности электрическим зарядом, создающим электростатическое поле в окрестности струи, стремящееся к нулю на бесконечности.

В первом порядке малости по $\varepsilon $ будем искать решение стандартными методами [7].

В указанном приближении решения задачи (2.1), удовлетворяющие граничным условиям (2.2), для возмущения границы раздела сред ${{\xi }}\left( {\varphi ,z,t} \right)$, гидродинамических потенциалов в среде ${{{{\psi }}}_{{ex}}}({\mathbf{r}},t)$ и струе ${{{{\psi }}}_{{in}}}({\mathbf{r}},t)$, а также для электростатического потенциала $\Phi ({\mathbf{r}},t)$ будем искать в виде

${{\xi }}\left( {\varphi ,z,t} \right) = a \cdot \exp (is\,t) \cdot \exp (ikz + im\varphi )$
${{{{\psi }}}_{{ex}}}({\mathbf{r}},t) = b \cdot \exp (is\,t) \cdot \exp (ikz + im\varphi ) \cdot {{{\text{K}}}_{m}}\left( {kr} \right)$
${{{{\psi }}}_{{in}}}({\mathbf{r}},t) = c \cdot \exp (is\,t) \cdot \exp (ikz + im\varphi ) \cdot {{{\text{I}}}_{m}}\left( {kr} \right)$
$\Phi ({\mathbf{r}},t) = d \cdot \exp (is\,t) \cdot \exp (ikz + im\varphi ) \cdot {{{\text{K}}}_{m}}\left( {kr} \right)$
где ${{{\text{I}}}_{m}}\left( {kr} \right)$ и ${{{\text{K}}}_{m}}\left( {kr} \right)$ – модифицированные функции Бесселя первого и второго рода, порядка m [14]; m – азимутальный параметр; $s$ – комплексная частота капиллярных волн; $a,b,c,d$ – неизвестные коэффициенты.

Подставляя выписанные решения в систему граничных условий задачи, можно получить дисперсионное уравнение с произвольным азимутальным числом $m$

${{\omega }^{2}} + 2\omega \cdot k \cdot \sqrt {{{\rho }_{{ex}}}} \cdot \sqrt {{\text{We}}} \cdot {{\beta }}(m,k) - \omega _{0}^{2} = 0$
(3.1)
$\begin{gathered} \omega _{0}^{2} \equiv {{h}_{m}}\left( k \right){{{{\beta }}}_{m}}\left( k \right)\left( {{{k}^{2}} + {{m}^{2}} - 1 + w\left( {1 + {{h}_{m}}\left( k \right)} \right) + \frac{{{{k}^{2}}{\text{We}}}}{{{{h}_{m}}\left( k \right)}}} \right) \\ {\text{We}} \equiv U_{0}^{2}{{\rho }_{{ex}}};\quad w \equiv 4\pi \chi _{{}}^{2} \equiv \frac{{{{E}^{2}}}}{{4\pi }};\quad {{{\text{g}}}_{m}}(k) = \frac{{kI_{m}^{'}(k)}}{{{{I}_{m}}(k)}} \\ \end{gathered} $
${{h}_{m}}(k) = \frac{{kK_{m}^{'}(k)}}{{{{K}_{m}}(k)}};\quad {{{{\beta }}}_{m}}\left( k \right) = \frac{{{{{\text{g}}}_{m}}\left( k \right)}}{{{{h}_{m}}\left( k \right) - {{\rho }_{{ex}}}{{g}_{m}}\left( k \right)}}$
где k – волновое число; m – азимутальное число; ${{{{\omega }}}_{m}}(k)$ – частота капиллярных волн (в общем случае комплексная), так что ${{\xi }} = {{\xi }_{0}} \cdot {\text{exp}}[i \cdot \,{{{{\omega }}}_{m}}\left( k \right)\, \cdot t]$, ${{\xi }_{0}}$ – начальная амплитуда; штрих у функций Бесселя обозначает производную по аргументу.

Корни (3.1) легко находятся в виде

(3.2)
${{\omega }_{{1;2}}} \equiv - k\sqrt {{{\rho }_{{ex}}}} \cdot \sqrt {{\text{We}}} \cdot \beta (m,k) \mp \sqrt {{{k}^{2}}{{\rho }_{{ex}}}{\text{We}} \cdot {{\beta }}{{{(m,k)}}^{2}} + \omega _{0}^{2}} $

Корни дисперсионного уравнения имеют комплексный вид из-за реализации на границе раздела сред неустойчивости Кельвина–Гельмгольца [15–17].

Видно, что при We = 0 (при равенстве нулю скорости относительного движения или когда окружающая среда – вакуум) дисперсионное уравнение (3.1) переходит в дисперсионное уравнение для волнового движения на поверхности заряженной струи идеальной жидкости [18, 19]. При w = 0 получим дисперсионное уравнение для аэродинамической неустойчивости [16, 20, 21]. Отметим, что расчеты по (3.2) критического для реализации аэродинамической неустойчивости значения параметра Вебера (табл. 2) согласуются по величине с экспериментальными результатами [22].

Таблица 2.

Значения физических величин, характеризующих графики ${\text{W}}{{{\text{e}}}_{{cr}}} = {\text{W}}{{{\text{e}}}_{{cr}}}(k)$, построенные при $m = 3;4;5$ и различных значениях зарядового параметра $w = 0,1,2,3$

w U, см/с Weкр, мин E, СГСЕ kмин kразм, 1/см λразм, см
m = 3
0 6757 8 0 4.092 409 0.015
1 6108 6.54 30.2 3.74 374 0.017
2 5327 5 42.8 3.29 329 0.019
3 4275 3.2 54.2 2.65 265 0.024
m = 4
0 7808 10.7 0 5.5 555 0.011
1 7251 9.2 30.2 5.2 518 0.012
2 6615 7.7 42.8 4.8 475 0.013
3 5854 6 54.2 4.2 420 0.015
m = 5
0 8723 13.3 0 7 699 0.009
1 8226 11.9 30.2 6.6 661 0.01
2 7675 10.2 42.8 6.2 618 0.01
3 7047 8.7 54.2 5.7 567 0.011

4. АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Проанализируем критические условия реализации неустойчивости трех азимутальных мод, начиная с m = 3. Обозначим подкоренное выражение в (3.2) как $H(k)$

$H(k) \equiv {{k}^{2}}{{U}^{2}}\beta {{(k)}^{2}} + \omega _{0}^{2}$

При $F(k) < 0$ частота $\omega $ в (3.2) комплексная, ее вещественная часть

$k \cdot {{\rho }_{{ex}}} \cdot {{U}_{0}} \cdot {{\beta }}(m,k)$
определяет частоту, а мнимая часть: $ \mp \sqrt {{\text{H}}(k)} $, отвечает за неустойчивость волн, она определяет их инкремент, при $\sqrt {{\text{H}}(k)} < 0$, или декремент $\sqrt {{\text{H}}(k)} > 0$. При We = 0 и $w \ne 0$ область отрицательности H(k) соответствует электрической неустойчивости, а при w = 0 и ${\text{We}} \ne 0$ – аэродинамической.

Требование отрицательности H(k) при проявлении неустойчивости позволяет получить критическое условие возникновения неустойчивости в аналитическом виде

(4.1)
$w \geqslant \frac{{(1 - {{k}^{2}} - {{m}^{2}})h(m,k) - {{k}^{2}}{\text{We}}}}{{\left( {1 + h(m,k)} \right)h(m,k)}}$
при фиксированном параметре ${\text{We}}$, или в виде
(4.2)
${\text{W}}{{{\text{e}}}_{{cr}}} \geqslant {\text{ (}}1 - k_{{}}^{2} - {{m}^{2}} - w(1 + h(m,k)){\text{)}} \cdot \frac{{h(m,k)}}{{{{k}^{2}}}}$
при задании зарядового параметра $w$.

На рис. 3 приведены зависимости критического значения полевого параметра ${{w}_{{cr}}}$ от волнового числа k для третьей азимутальной моды m = 3 при различных фиксированных значениях параметра Вебера ${\text{We}}$, рассчитанные по (4.1). Аналогичные зависимости для четвертой и пятой азимутальных мод имеют качественно схожий вид, отличаясь лишь количественно, а потому не приводятся. В табл. 3 для оценки отличий приведены значения физических величин, характеризующих графики ${{w}_{{cr}}} = {{w}_{{cr}}}(k)$ при $m = 3;4;5$. Из табл. 3 видно, что критические зависимости ${{{\text{w}}}_{{cr}}}(k)$ для азимутальных мод с $m = 3;4;5$ имеют пороговый характер, как и азимутальная мода с m = 2 [23], в отличие от осесимметричной и изгибной мод [23]. Порог реализации неустойчивости увеличивается с ростом номера моды, но снижается с ростом скорости обдувающего потока (с увеличением параметра Вебера ${\text{We}}$). Величина волнового числа, при котором реализуется неустойчивость, растет с увеличением параметра Вебера и номера азимутальной моды.

Рис. 3.

Зависимости ${{w}_{{cr}}} = {{{\text{w}}}_{{cr}}}(k)$, рассчитанные при $m = 3$ и различных фиксированных значениях параметра Вебера: 1–4 – ${\text{We = }}$ 0, 1, 2 и 3.

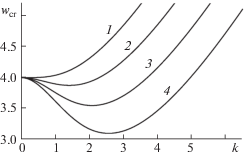
Таблица 3.

Значения физических величин, характеризующих графики ${{w}_{{cr}}} = {{{\text{w}}}_{{cr}}}(k)$, построенные при $m = 3;4;5$ и различных значениях параметра Вебера ${\text{We}} = 0,1,2,3$

We U, см/с wкр, мин E, СГСЕ kмин kразм, 1/см λразм, см
m = 3
0 0 4 60.5 0 0 ∞
1 2389 3.85 59.6 1.4 141.6 0.044
2 3379 3.55 57 2.1 207.8 0.03
3 4138 3.1 53 2.6 256.7 0.024
m = 4
0 0 5 67.7 0 0 0.011
1 2389 4.99 67.5 1 103.3 0.012
2 3379 4.81 66.3 2.1 213.1 0.013
3 4138 4.48 64 2.8 282.8 0.015
m = 5
0 0 6 74.1 0 0 0.009
1 2389 6 74.07 0 0 0.01
2 2379 5.94 73.7 1.88 187.9 0.01
3 4138 5.72 72.3 2.88 287.5 0.011

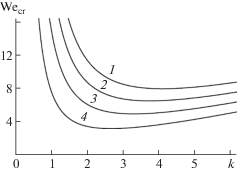
На рис. 4 приведены зависимости критического значения параметра Вебера от волнового числа $k$ для третьей m = 3 азимутальной моды ${\text{W}}{{{\text{e}}}_{{cr}}}(k)$ при различных фиксированных значениях параметра $w$, рассчитанные по (4.2). Аналогичные зависимости для четвертой и пятой азимутальных мод имеют качественно схожий вид, отличаясь лишь количественно, а потому не приводятся. В табл. 2 для оценки отличий приведены значения физических величин, характеризующих графики ${\text{W}}{{{\text{e}}}_{{cr}}} = {\text{W}}{{{\text{e}}}_{{cr}}}(k)$ при $m = 3;4;5$.

Рис. 4.

Зависимости ${\text{W}}{{{\text{e}}}_{{cr}}} = {\text{W}}{{{\text{e}}}_{{cr}}}(k)$, рассчитанные при $m = 3$ и различных фиксированных значениях полевого параметра 1–4 – $w = $ 0, 1, 2 и 3.

Из рис. 3, 4 и табл. 2, 3 видно, что зависимости ${{w}_{{cr}}} = {{w}_{{cr}}}(k)$ при ${\text{We}} = {\text{const}}$ и ${\text{W}}{{{\text{e}}}_{{cr}}} = {\text{W}}{{{\text{e}}}_{{cr}}}(k)$ при $w = {\text{const}}$ имеют качественно схожий характер, различаясь лишь численными значениями.

Рассматриваемую неустойчивость следует именовать электростатически-аэродинамической, поскольку имеются два фактора, способствующих отрыву капель: электростатическое и аэродинамическое поля в окрестности струи [16–20], поскольку скорости относительного движения струи и среды, приводящие к аэродинамической неустойчивости, весьма велики, а в экспериментах [1–4] использовались много меньшие (примерно на два порядка), в то время как напряженность электростатического поля достигала критических величин, то уместно говорить об электростатической неустойчивости при наличии усложняющего наблюдаемую картину аэродинамического воздействия.

ЗАКЛЮЧЕНИЕ

Теоретически исследованы закономерности реализации смешанной электростатически-аэродинамической неустойчивости трех высоких азимутальных мод жидких струй, начиная с третьей. Качественно ход критических зависимостей от волнового числа в рассмотренных ситуациях схож и различается лишь количественно. Во всех случаях неустойчивость высоких азимутальных мод имеет пороговый характер как по величине напряженности внешнего электростатического поля, так и по скорости относительного движения струи и материальной среды.

Список литературы

  1. Cloupeau M., Prunet Foch B. Electrostatic spraying of liquids in cone-jet mode // J. Electrostatics. 1989. V. 22. P. 135–159.

  2. Cloupeau M., Prunet Foch B. Electrostatic spraying of liquids: main functioning modes // J. Electrostatics. 1990. V. 25. P. 165–184.

  3. Cloupeau M., Prunet Foch B. Electrohydrodynamic spraying functioning modes: a critical review // J. Aerosol Sci. 1994. V. 25. № 6. P. 1021–1035.

  4. Jaworek A., Krupa A. Classification of the Modes of EHD Spraying // J. Aerosol Sci. 1999. V. 30. № 7. P. 873–893.

  5. Kim O.V., Dunn P.F. Control Production by in-flight Electrospraying // Langmuir. 2010. V. 26. P. 15807–15813.

  6. Райзер Ю.П. Физика газового разряда. М.: Наука, 1987. 592 с.

  7. Григорьев А.И., Михеев Г.Е., Ширяева С.О. Электростатическая неустойчивость поверхности объемно заряженной струи диэлектрической жидкости, движущейся относительно материальной среды // Известия РАН. МЖГ. 2017. № 5. С. 3–14.

  8. Tonks L. A theory of liquid surface rupture by uniform electric field // Phys. Rev. 1935. V. 48. P. 562–568.

  9. Френкель Я.И. К теории Тонкса о разрыве поверхности жидкости постоянным электрическим полем в вакууме // ЖЭТФ. 1936. Т. 6. № 4. С. 348–350.

  10. Остроумов Г.А. Взаимодействие электрических и гидродинамических полей. М.: Наука, 1979. 320 с.

  11. Duft D., Achtzehn T., Muller R. et al. Rayleigh jets from levitated microdroplets // Nature. 2003. V. 421. № 6919. P. 128.

  12. Taylor G.I. Disintegration of water drops in an electric field // Proc. Roy. Soc., London. 1964. V. A280. P. 383–397.

  13. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1975. 532 с.

  14. Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979. 830 с.

  15. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 733 с.

  16. Дразин Ф. Введение в теорию гидродинамической неустойчивости. М.: Физматлит, 2005. 288 с.

  17. Григорьев А.И., Суханов С.А., Ширяева С.О. Об устойчивости волнового движения на заряженной границе раздела несмешивающихся жидкостей при наличии тангенциального скачка поля скоростей // Изв. РАН. МЖГ. 2012. № 4. С. 99–109.

  18. Taylor G. Electrically driven jet // Proc. Roy. Soc., London. 1969. V. A313. P. 453–470.

  19. Saville D.A. Stability of an Electrically Charged Viscous Cylinders // Phys. Fluids. 1971. V. 14. № 6. P. 1095–1099.

  20. Eggers J., Willermaux E. Physics of liquid jets // Rep. Prog. Phys. 2008. V. 71. № 036601. P. 1–79.

  21. Ентов В.М., Ярин А.Л. Динамика свободных струй и пленок вязких и реологически сложных жидкостей // ВИНИТИ. Итоги науки и техники. Сер. “Механика жидкости и газа”. 1984. Т. 17. С. 112–197.

  22. Hoyt J.W., Taylor G.I. Waves on water jets // J. Fluid Mech. 1977. V. 83. P. 119–127.

  23. Григорьев А.И. Электростатическая неустойчивость сильно заряженной струи электропроводной жидкости // ЖТФ. 2009. Т. 79. № 4. С. 36–45.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал