1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2021

Известия РАН. Механика жидкости и газа, 2021, № 3, стр. 90-99

БИГАРМОНИЧЕСКИЕ АТТРАКТОРЫ ВНУТРЕННИХ ГРАВИТАЦИОННЫХ ВОЛН

Д. А. Рязанов b, c, М. И. Провидухина d, И. Н. Сибгатуллин d, c, b, *, **, Е. В. Ерманюк a

a Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

b Институт системного программирования им. В.П. Иванникова РАН
Москва, Россия

c Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

d Институт океанологии им. П.П. Ширшова РАН
Москва, Россия

* E-mail: ilias.sibgat@gmail.com
** E-mail: sibgat@imec.msu.ru

Поступила в редакцию 27.02.2020
После доработки 21.10.2020
Принята к публикации 01.12.2020

Полный текст (PDF)

Аннотация

Исследуется гидродинамическая система, допускающая возникновение аттракторов внутренних волн, при бигармонических воздействиях. Показано, что при малой максимальной амплитуде колебаний волновая картина состоит из двух аттракторов, которые практически не взаимодействуют друг с другом: суммарная энергия системы с высокой точностью равна сумме энергий составляющих. В нелинейном случае имеет место сложное взаимодействие аттракторов, приводящее к развитию каскада триадных взаимодействий, порождающего богатый набор временных масштабов. В случае близких частот составляющих бигармонического возмущения возникает нелинейный режим “биений”: средняя энергия системы связанных аттракторов совершает колебания на большом временном масштабе, соответствующем периоду биений. Обнаружено, что высокочастотные пульсации энергии, соответствующие одному и тому же значению средней энергии, могут на порядок отличаться в зависимости от того, происходит ли рост или убывание огибающей среднего значения.

Ключевые слова: волновые аттракторы, инерционные волны, внутренние волны, волновая турбулентность

Внутренние волны в однородно стратифицированной по плотности жидкости подчиняются специфическому дисперсионному соотношению [1], которое связывает частоту волн и угол наклона волнового пучка по отношению к вектору силы тяжести, но не содержит масштаба длины. Следствием дисперсионного соотношения является специфический закон отражения от границ, при котором сохраняется угол с вертикалью, а не нормалью к поверхности. В свою очередь, такой закон отражения приводит к фокусировке пучков волн при отражении от наклонной стенки [2, 3]. В замкнутом объеме стратифицированной жидкости при наличии наклонных стенок фокусировка волн может приводить к концентрации энергии на замкнутых траекториях – волновых аттракторах [4, 5]. Волновым аттракторам посвящено большое число работ, обзор которых имеется в [3, 6]. В геофизических приложениях в качестве источника энергии, вызывающего внутренние волновые движения, рассматриваются приливные течения [7, 8]. Взаимодействие поверхностных приливов с топографией дна стратифицированного водоема приводит к генерации внутренних приливов, причем при определенных условиях внутреннее приливное движение может существовать в форме аттракторов [9–12]. Известно, что поверхностные приливы имеют достаточно сложный спектр и хорошо изученный детерминистский характер. Натурные измерения показывают, что внутренние приливы отличаются гораздо меньшей предсказуемостью, что связано с высокой чувствительностью внутренних волн к тонкой структуре стратификации [13], а также с развитием неустойчивости [14, 15].

Для исследования особенностей динамики режимов с волновыми аттракторами применялись специальные методы обработки и визуализации данных, как экспериментальных, так и численных, которые включают частотно-временные диаграммы, биспектры, бикорреляции, преобразования Гильберта с фильтрацией диапазонов частот и волновых векторов [16, 17]. Первые попытки двумерного численного моделирования показали качественное соответствие малоамплитудных режимов волновых аттракторов [18, 19]. Проведенное в [20, 21] исследование трехмерных эффектов волновых аттракторов показало хорошее качественное и количественное соответствие результатов прямого численного моделирования и экспериментов, было дано объяснение отличия результатов предшествующих двумерных и трехмерных численных расчетов. Следует отметить, что практически вся литература в области моделирования внутренних приливов и волновых аттракторов посвящена исследованию монохроматического внешнего воздействия [3, 6]. В настоящей работе выполнено численное исследование линейной и нелинейной динамики стратифицированной жидкости в модельной системе, допускающей существование аттракторов внутренних волн, при воздействии бигармонического возмущения.

1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

Рассматривается резервуар в форме трапеции с большим основанием сверху, заполненный однородно стратифицированной жидкостью в поле силы тяжести, рис. 1. Данная геометрическая конфигурация хорошо изучена в литературе – имеется подробная классификация геометрических конфигураций аттракторов в рамках лучевой теории [5], построены функции тока в рамках модели невязкой жидкости [22], исследован линейный [18] и нелинейный [23] скейлинг для ширины волновых пучков аттрактора, описан каскад энергии в нелинейном режиме [24]. Стратификация характеризуется градиентом солености, сонаправленным с вектором ускорения свободного падения. В начальном состоянии частота плавучести

$N(y) = \sqrt { - \frac{g}{{\rho (y)}}\frac{{d\rho (y)}}{{dy}}} $
постоянна во всем резервуаре. На всех границах (кроме верхней) выполняется условие прилипания для скорости ${{v}_{n}} = 0$, ${{v}_{\tau }} = 0$. Для солености на всех границах выполняется условие изоляции $\partial {{\rho }_{s}}{\text{/}}\partial n = 0$. На верхней границе резервуара задается вертикальная компонента скорости, моделирующая волнопродуктор, совершающий гармонические колебания в соответствии со следующими выражениями:

Рис. 1.

(а) схема расчетной области, (б) поле вертикальной компоненты скорости при монохроматическом воздействии с амплитудой a = 0.02, (в) соответствующий график зависимости вертикальной скорости в середине первого луча аттрактора от времени, (г) зависимость кинетической энергии от времени.

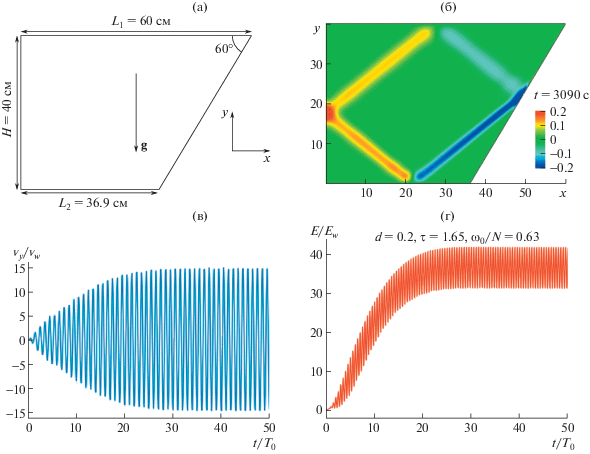
для монохроматических колебаний $y(0,x,t) = asin(2\pi x{\text{/}}{{L}_{1}})cos({{\omega }_{0}}t)$;

для бигармонических колебаний $y(0,x,t) = {{a}_{1}}sin(2\pi x{\text{/}}{{L}_{1}})cos({{\omega }_{1}}t)$ + ${{a}_{2}}sin(2\pi x{\text{/}}{{L}_{1}})cos({{\omega }_{2}}t)$.

В дальнейшем, в качестве модельного примера рассмотрен случай ${{a}_{1}} = {{a}_{2}} = a$. Малая величина перепада плотности по глубине резервуара $H$ позволяет использовать уравнение Навье– Стокса в приближении Буссинеска

(1.1)
$\frac{{\partial{ \vec {V}}}}{{\partial t}} + (\vec {V} \cdot \nabla )\vec {V} = - \frac{1}{{{{\rho }_{m}}}}\nabla \hat {p} + \nu \Delta \vec {V} + \vec {f}$
(1.2)
$\frac{{\partial {{\rho }_{s}}}}{{\partial t}} + \vec {V} \cdot \nabla {{\rho }_{s}} = \nabla \cdot \frac{\nu }{{Sc}}\left( {\nabla {{\rho }_{s}}} \right)$
(1.3)
$\nabla \cdot \vec {V} = 0$

Здесь $\vec {V}$ – вектор скорости с компонентами $\{ {{v}_{x}},{{v}_{y}}\} $; $\nu $ – кинематическая вязкость жидкости; ${{\rho }_{m}}$ – значение плотности на верхней границе; ${{\rho }_{s}}$ – добавка плотности, обусловленная наличием солености; приведенное давление $\hat {p}$ – разница между полным давлением и гидростатическим для пресной воды (при плотности ${{\rho }_{m}}$); $\vec {f} = {{\rho }_{s}}{\text{/}}{{\rho }_{m}}\vec {g}$, $Sc = \nu {\text{/}}\varkappa $ – число Шмидта, где $\varkappa $ – коэффициент диффузии.

В линейном режиме характерное значение ширины волнового пучка вырабатывается системой как результат баланса между эффектами геометрической фокусировки при отражении волнового пучка от наклонной стенки и вязкости [18, 23]. В качестве параметров, характеризующих возмущающее воздействие, могут быть введены безразмерная частота $\omega {\text{/}}N$ и безразмерная амплитуда $a{\text{/}}H$. В численных экспериментах характерная величина безразмерной амплитуды имеет порядок O(10–3), а значение частоты $\omega {\text{/}}N$ задается в диапазоне существования аттрактора, лучевой “скелет” которого имеет форму параллелограмма с одной точкой отражения на горизонтальной и вертикальной границах. Аттрактор такой формы будем называть аттрактором типа (1, 1), следуя [5]. Вырожденными формами аттрактора (1, 1), соответствующими границам его диапазона существования, являются диагонали трапеции. В качестве безразмерного параметра, характеризующего возмущение, может быть введено число Рейнольдса, определенное по максимальной скорости движения волнопродуктора и глубине: $Re = a{{\omega }_{0}}H{\text{/}}\nu $. Данная работа является продолжением серии работ [20, 23–25] по экспериментальному и численному исследованию волновых аттракторов в установках лабораторного масштаба. Для удобства проведения сопоставлений численные значения параметров приводятся в безразмерных и размерных величинах.

В двумерной постановке численное моделирование системы (1.1)–(1.3) с применением метода контрольного объема осуществлено в [18, 26], получено качественное соответствие формы аттрактора в расчете и в линейной теории. При количественном сопоставлении с экспериментом наблюдалась разница в амплитудах волновых движений примерно в два раза. Первое трехмерное моделирование было проведено в [20, 24] с помощью метода спектральных элементов [27], и получено как качественное, так и количественное соответствие с экспериментом.

Все дальнейшие результаты численного моделирования нелинейной системы уравнений Навье–Стокса в приближении Буссиненска.

2. МОНОХРОМАТИЧЕСКОЕ ВОЗМУЩЕНИЕ

На первом этапе исследования проведено моделирование монохроматических режимов с целью оценки эффективности генерации аттракторов при фиксированной амплитуде волнопродуктора и вариации частоты возмущения в диапазоне существования аттрактора вида (1, 1) [5]. Для геометрии, показанной на рис. 1, нижняя и верхняя границы диапазона существования аттрактора вида (1, 1) соответствуют ${{\omega }_{{cr1}}}{\text{/}}N = 0.55$ и ${{\omega }_{{cr2}}}{\text{/}}N = 0.74$. При достижении этих критических значений частот происходит вырождение параллелограмма в диагональ трапеции. В качестве интегральной размерной меры эффективности генерации аттрактора при постоянной амплитуде волнопродуктора и неизменной форме резервуара принята кинетическая энергия жидкости, проинтегрированная по площади трапеции $S$

${{E}_{k}}(t) = \int\limits_S {\frac{{{{\rho }_{m}}}}{2}} [v_{y}^{2}(t) + v_{x}^{2}(t)]dS$

Для этой меры можно ввести значение, усредненное в скользящем временном окне по достаточно большому числу периодов колебаний $\left\langle {{{E}_{k}}(t)} \right\rangle $, и вариацию относительно среднего, рассчитываемую как $r = D\left( {{{E}_{k}}(t) - \langle {{E}_{k}}(t)\rangle } \right){\text{/}}\langle {{E}_{k}}(t)\rangle $, где $D\left( {{{E}_{k}}(t) - \left\langle {{{E}_{k}}(t)} \right\rangle } \right)$ – дисперсия относительно среднего. Безразмерные величины ${{\bar {E}}_{k}}(t)$ и $\left\langle {{{{\bar {E}}}_{k}}(t)} \right\rangle $ определены путем нормировки на величину ${{\rho }_{m}}S{{(a\omega )}^{2}}{\text{/}}2$. Известно, что режимы движения в аттракторах могут быть близки как к прогрессивным, так и к стоячим волнам [25]. Величина $r$ позволяет дать количественную оценку близости наблюдаемого режима к одному из этих предельных случаев [25].

2.1. Линейный режим

Характерный вид зависимостей, наблюдаемых в монохроматическом режиме при малой амплитуде колебаний, показан на рис. 1 для a = 0.02 cм ($a{\text{/}}H = 5 \times {{10}^{{ - 4}}}$), $\omega {\text{/}}N = 0.63$. Характерное время выхода системы на установившийся режим составляет порядка 30 периодов колебаний, спектр сигнала является с высокой точностью монохроматическим, колебания кинетической энергии относительно среднего имеют небольшую амплитуду ($r = 0.103$). За первую ветвь аттрактора принят пучок с наибольшим значением плотности энергии, возникающий после фокусирующего отражения от наклонной стенки. Величины интегральных параметров, характеризующих линейные монохроматические режимы при фиксированном значении $a{\text{/}}H = 5 \times {{10}^{{ - 4}}}$ в частотном диапазоне от ${{\omega }_{{cr1}}}{\text{/}}N = 0.55$ до ${{\omega }_{{cr2}}}{\text{/}}N = 0.74$ приведены в табл. 1. Видно, что при фиксированной амплитуде колебаний величина кинетической энергии аттрактора максимальна при $\omega {\text{/}}N = 0.63$. Очевидно, что при этом значении частоты возмущающего воздействия следует ожидать сильных нелинейных эффектов при увеличении амплитуды колебаний волнопродуктора. Величина $r$ при $\omega {\text{/}}N = 0.63$ достигает минимума: движение в аттракторе представлено прогрессивной волной.

Таблица 1.

Кинетическая энергия при монохроматических воздействиях с амплитудой a = 0.02

ω0/N Ek 〈${{\bar {E}}_{k}}$〉 r
0.55 (ωcr, 1) 1.32 × 10–4 2.151 0.618
0.58 8.45 × 10–4 12.56 0.281
0.59 12 × 10–4 17.33 0.3
0.63 29 × 10–4 36.68 0.103
0.641 23 × 10–4 28.55 0.1129
0.66 13.2 × 10–4 15.14 0.152
0.70 2.84 × 10–4 2.896 0.295
0.74 (ωcr, 2) 1.50 × 10–4 1.356 0.215

2.2. Нелинейный режим

Характерные картины течения и зависимости, наблюдаемые в случае слабонелинейного режима при $\omega {\text{/}}N = 0.63$, приведены на рис. 2 для a = 0.05 см ($a{\text{/}}H = 1.25 \times {{10}^{{ - 3}}}$). В слабонелинейном режиме имеет место триадный резонанс [15], при котором генерируются две дочерние субгармонические волны малой амплитуды. Частотно-временная диаграмма, показанная на рис. 2, представляет собой спектр сигнала, вычисленный в скользящем окне и осредненный по окрестности точки, лежащей в середине первой ветви аттрактора. Частотный спектр внутренних волн при данном режиме является дискретным, с доминирующим вкладом, соответствующим частоте возмущения ${{\omega }_{0}}$, двумя дочерними субгармоническими частотами $\omega _{1}^{*} + \omega _{2}^{*} = {{\omega }_{0}}$, двумя супергармоническими частотами $\omega _{1}^{{**}} = \omega _{1}^{*} + {{\omega }_{0}}$, $\omega _{2}^{{**}} = \omega _{2}^{*} + {{\omega }_{0}}$ и удвоенной частотой $2{{\omega }_{0}}$.

Рис. 2.

(а) Поле вертикальной компоненты скорости при монохроматическом внешнем воздействии с амплитудой ($a{\text{/}}H = 5 \times {{10}^{{ - 4}}}$) и соответствующие: (б) поле давления, (в) безразмерная скорость в середине первого луча аттрактора, (г) безразмерная кинетическая энергия, (д) спектр, (е) частотно-временная диаграмма.

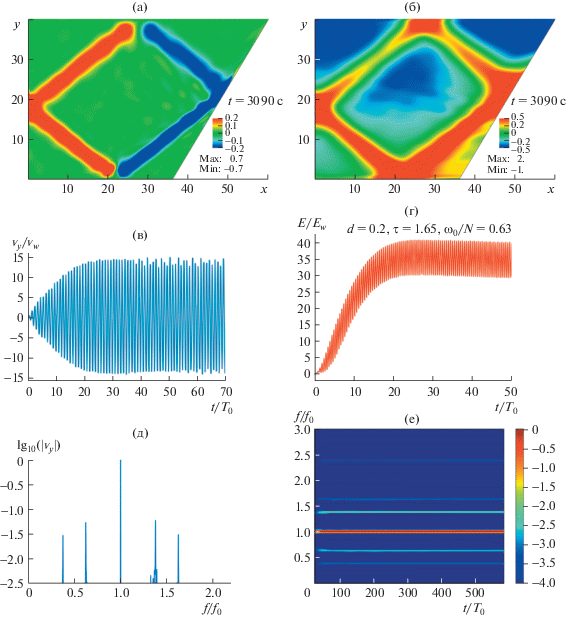
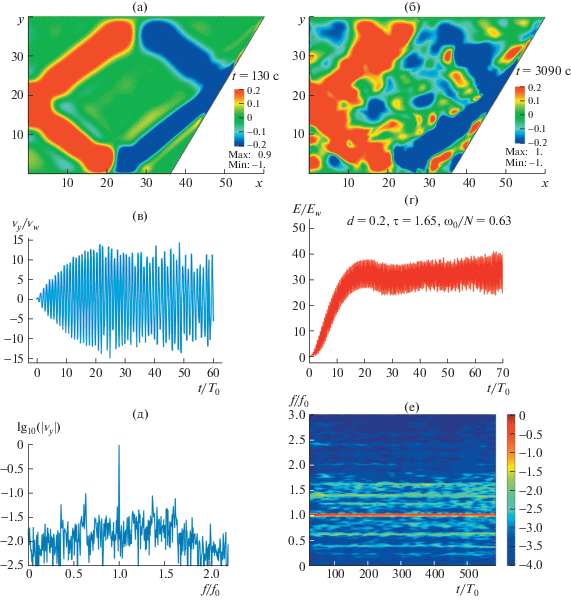
При дальнейшем увеличении амплитуды возмущения до a = 0.1 см ($a{\text{/}}H = 2.5 \times {{10}^{{ - 3}}}$) происходит развитие каскада триадных взаимодействий. Характерные картины волновых полей, спектров и развития во времени процесса колебаний и кинетической энергии системы приведены на рис. 3. В частотном спектре сигнала доминируют дискретные компоненты, соответствующие частотам дочерних волн, возникающих при триадном резонансе, аналогичные компонентам спектра, возникающим в слабонелинейном случае ($a{\text{/}}H = 1.25 \times {{10}^{{ - 3}}}$). При этом полный спектр сигнала представляет собой суперпозицию дискретного и непрерывного спектра. Наличие непрерывного спектра свидетельствует о возникновении режима развитой волновой турбулентности [24, 25]. Соответствующие характеристики для кинетической энергии системы в сильно нелинейном режиме приведены в табл. 2. Из сопоставления табл. 1 и 2 видно, что величины глобальных безразмерных энергетических характеристик системы (средней энергии $\left\langle {{{{\bar {E}}}_{k}}} \right\rangle $ и вариации относительно среднего r) в случае режима развитой волновой турбулентности слабо отличаются от безразмерных величин, характерных для линейного режима. Сопоставление волновых картин в линейном и нелинейном случаях показывает, что во втором случае энергия более равномерно распределена по изучаемой области: ветви аттрактора имеют большую ширину, а дочерние волны заполняют все пространство.

Рис. 3.

Поле вертикальной компоненты скорости в монохроматическом режиме с амплитудой a = 0.1 см/с при образовании аттрактора (а) и после каскада неустойчивостей (б), (в) зависимость скорости в середине первого луча аттрактора от времени, (г) зависимость кинетической энергии от времени, (д) частотный спектр скорости в режиме волновой турбулентности, (е) частотно-временная диаграмма.

Таблица 2.

Кинетическая энергия при монохроматических воздействиях с амплитудной a = 0.1

ω0/N Ek(эрг) 〈${{\bar {E}}_{k}}$〉 r
0.55 (ωcr, 1) 33.0 × 10–4 2.14 0.6193
0.63 725× 10–4 36.7 0.1346
0.74 (ωcr, 2) 37.0 × 10–4 1.35 0.2192

3. РЕЖИМЫ С БИГАРМОНИЧЕСКИМ ВОЗМУЩЕНИЕМ

3.1. Линейный режим

Характерный пример волновой картины и основных качественных и количественных характеристик системы в линейном случае при бигармоническом внешнем воздействии приведен на рис. 4 для следующих значений параметров: ${{\omega }_{1}}{\text{/}}N = 0.58$, ${{\omega }_{2}}{\text{/}}N = 0.66$, $a = 0.02$ см. Видно, что система выходит на режим квазистационарных биений за время порядка 40 периодов колебаний, что близко к характерному времени выхода на процесс стационарных колебаний в монохроматическом случае. На частотном спектре доминируют пики, соответствующие частотам внешнего возмущения, имеются также пики, соответствующие частоте $2{{\omega }_{1}}{\text{/}}N$ и разностной частоте $({{\omega }_{2}} - {{\omega }_{1}}){\text{/}}N$, но их величина более чем на два порядка меньше основного пика. Моменты времени, соответствующие максимальным значениям кинетической энергии, существенно отстают от моментов времени, соответствующих максимальным значениям амплитуды колебаний волнопродуктора. Важно отметить, что после выхода системы на режим установившихся биений средняя кинетическая энергия системы, возбуждаемой бигармоническим возмущением, с высокой точностью равна сумме энергий аттракторов, возбуждаемых монохроматическими возмущениями по отдельности ${{\bar {E}}_{k}} = 21.7 \times {{10}^{{ - 4}}} \approx {{\bar {E}}_{{k1}}} + {{\bar {E}}_{{k2}}} = $ $(8.45 + 13.2) \times {{10}^{{ - 4}}}$ = 21.65 × 10–4 (эрг/см2). Таким образом, в линейном режиме с высокой точностью соблюдается принцип линейной суперпозиции, что выполняется также при малой разности частот $({{\omega }_{1}} - {{\omega }_{2}}){\text{/}}N$.

Рис. 4.

Вертикальная компонента скорости ${{v}_{y}}$ (а) и давление (б) в бигармоническом режиме с амплитудами a = 0.02 см/с, соответствующие: (в) вертикальная компонента скорости в середине первого луча аттрактора, (г) кинетическая энергия, (д) спектр, (е) частотно-временная диаграмма. Черной линией на (в) и (г) показана огибающая амплитуды колебаний волнопродуктора.

3.2. Нелинейный режим

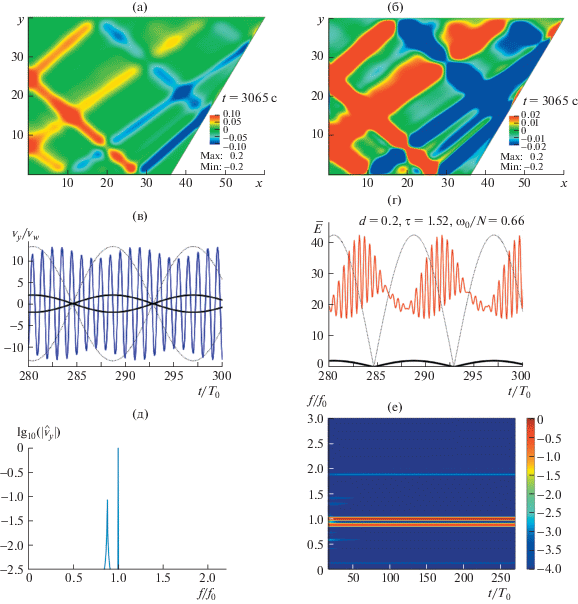
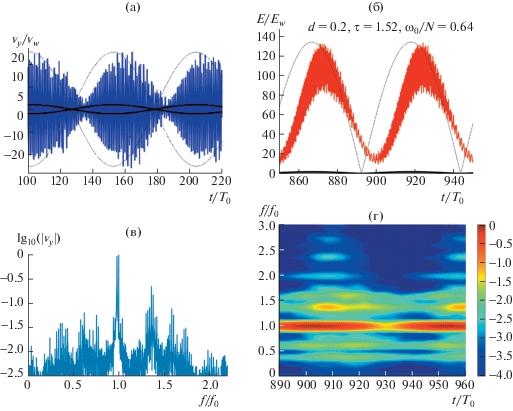
Примеры нелинейной динамики волновых аттракторов, генерируемых бигармоническими колебаниями волнопродуктора, приведены на рис. 5 (${{\omega }_{1}}{\text{/}}N = 0.66$, ${{\omega }_{2}}{\text{/}}N = 0.628$, $\delta \omega {\text{/}}N = 0.031$) и 6, (${{\omega }_{1}}{\text{/}}N = 0.628$, ${{\omega }_{2}}{\text{/}}N = 0.641$, $\delta \omega {\text{/}}N = 0.013$). Во всех случаях амплитуды колебаний волнопродуктора составили ${{a}_{1}} = {{a}_{2}} = 0.05$ см. Можно видеть, что в обоих случаях формируется движение, для которого характерен сложный частотный спектр, причем при уменьшении расстройки частот $\delta \omega $ наблюдается тенденция к более густому “заселению” спектра. На графиках зависимости вертикальной скорости от времени виден характерный процесс биений, но помимо колебаний среднего значения энергии имеет место нетривиальная динамика высокочастотных пульсаций энергии: на фазах роста и убывания огибающей амплитуды колебаний волнопродуктора амплитуды пульсаций могут отличаться на порядок. Таким образом, для нелинейного бигармонического режима характерны периодические “вспышки” волновой турбулентности. Такие “вспышки” хорошо видны на частотно-временных диаграммах, приведенных на рис. 5 и 6. В частности, на частотно-временной диаграмме, приведенной на рис. 5, можно видеть, что “биения” амплитуды сигнала на частоте, близкой к частоте возмущающего воздействия, сдвинуты по времени относительно “биений” дочерних волн. Таким образом, “биения” огибающей колебаний волнопродуктора, “биения” средней кинетической энергии и “вспышки” волновой турбулентности рассогласованны между собой по времени. Можно предположить, что и в природных системах имеется рассогласование по времени между огибающей амплитуды внутреннего прилива и интенсификацией внутренней волновой турбулентности и перемешивания. Предварительное исследование энергии аттракторов, генерируемых бигармоническим возмущением, показывает, что в нелинейном случае средняя энергия системы существенным образом отличается от суммы энергий составляющих.

Рис. 5.

Вертикальная компонента скорости при формировании (а) и установлении (б) бигармонического аттрактора амплитудами a = 0.05 см/с и относительной разностью между частотами 0.05, соответствующие: в) вертикальная скорость, г) кинетическая энергия, д) спектр, е) частотно-временная диаграмма. Черной линией на (в) и (г) показана огибающая амплитуды колебаний волнопродуктора.

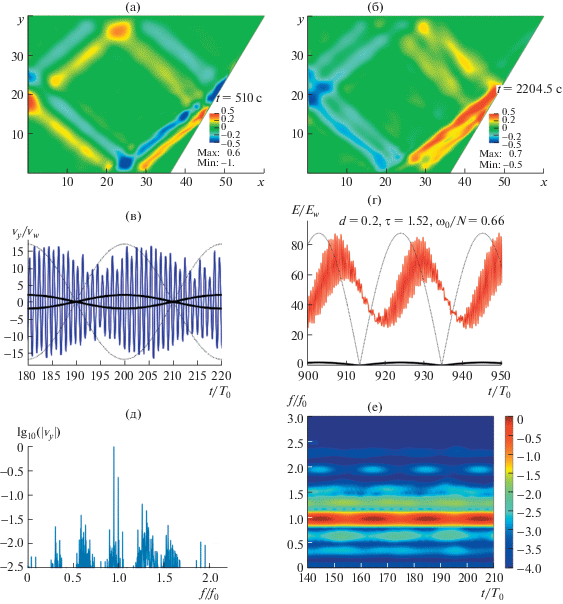
Рис. 6.

Вертикальная компонента скорости (а), кинетическая энергия (б), спектр (в) и частотно-временная диаграмма (г) в бигармоническом режиме с амплитудами a = 0.05 см/с и относительной разностью между частотами 0.02. Черной линией на (а) и (б) показана огибающая амплитуды колебаний волнопродуктора.

ЗАКЛЮЧЕНИЕ

Впервые проведено исследование динамики аттракторов внутренних волн при бигармоническом внешнем воздействии. Для определения наиболее интересного диапазона параметров выполнено подробное исследование генерации аттракторов при монохроматическом возмущении, в результате чего определен частотный диапазон, в котором генерация аттракторов наиболее эффективна. Исследование поведения аттракторов при бигармоническом внешнем воздействии показало, что в линейном случае справедлив принцип суперпозиции: аттракторы, генерируемые каждой из компонент бигармонического возмущения, практически не взаимодействуют друг с другом. В нелинейном случае при бигармоническом внешнем воздействии наблюдается режим биений, сопровождающийся вспышками волновой турбулентности, возникающей вследствие каскада триадных взаимодействий. При этом уровень пульсаций кинетической энергии на фазе роста огибающей амплитуды волнопродуктора может на порядок превышать уровень, соответствующий спаду амплитуды колебаний волнопродуктора.

Работа выполнена при финансовой поддержке Российского научного фонда (РНФ), грант 19-11-00169 с использованием оборудования Центра коллективного пользования высокопроизводительными вычислительными ресурсами МГУ им. М.В. Ломоносова и вычислительного комплекса Центра коллективного пользования НИЦ Курчатовский институт.

Список литературы

  1. Mowbray D.E., Rarity B.S.H. A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid // J. Fluid Mech. 1967. P. 1–16.

  2. Dauxois T., Young W. Near-critical refection of internal waves // J. Fluid Mech. 1999. P. 271–295.

  3. Maas L. Wave attractors: linear yet non linear // Intl J. Bifurcation Chaos. 2005. P. 2757–2782.

  4. Lam F., Maas L. Geometric focusing of internal waves // J. Fluid Mech. 1995. P. 1–41.

  5. Observations of an internal wave attractor in a confined stably stratified fluid / F.P.A. Lam, D. Benielli, J. Sommeria, L.R.M. Maas // Nature. 1997. P. 557–561.

  6. Sibgatullin I., Ermanyuk E. Internal and inertial wave attractors: a review // Journal of Applied Mechanics Technical Physics. 2019. P. 284–302.

  7. Morozov E. Semidiurnial internal wave global field // Deep-Sea Res. 1995. P. 135–148.

  8. Garrett K., Kunze E. Internal tide generation in deep ocean // Annu. Rev. Fluid Mech. 2007. P. 57–87.

  9. Tang W., Peacock T. Lagrangian coherent structures and internal wave attractors // Chaos. 2010.

  10. Echeverri P., Yokossi T., Balmforth N.J., Peacock T. Tidally generated internal-wave attractors between double ridges // J. Fluid Mech. 2011. P. 354–374.

  11. Wang G., Zheng Q., Lin M., Qiao F. Three dimensional simulation of internal wave attractors in the luzon strait // Acta. Oceanol. Sin. 2015. P. 14–21.

  12. Guo Y., Holmes-Cerfon M. Internal wave attractors over random, small-amplitude topography // J. Fluid Mech. 2016. P. 148–174.

  13. van H. Haren, Maas L., Gerkema T. Patchiness in internal tidal beams // Journal of Marine Research. 2010. P. 237–257.

  14. Sutherland B.R. Internal wave instability: Wave-wave vs wave-induced mean flow interactions // Phys. Fluids. 2006.

  15. Dauxois T., Joubaud S., Odier P., Venaille A. Instabilities of internal gravity wave beams // Annu. Rev. Fluid Mech. 2018. P. 131–156.

  16. Mercier J.M., Garnier N.B., Dauxois T. Reflection and diffraction of internal waves analyzed with the hilbert transform // Physics of Fluids. 2008.

  17. Провидухина М., Сибгатуллин И. Применение спектральных методов обработки данных к результатам численного моделирования аттракторов внутренних волн // Труды Института системного программирования РАН (электронный журнал). 2016. С. 275–282.

  18. Grisouard N., Staquet C., Pairaud I. Numerical simulation of a two-dimensional internal wave attractor // J. Fluid Mech. 2008. P. 1–14.

  19. Брузе К., Доксуа Т., Ерманюк Е., Жубо С., Крапошин M., Сибгатуллин И. Прямое численное моделирование аттракторов внутренних волн стратифицированной жидкости в трапециедальной области с колеблющейся вертикальной стенкой // Труды Института системного программирования РАН. 2014. С. 117–142.

  20. Brouzet C., Sibgatullin I.N., Scolan H. et al. Internal wave attractors examined using laboratory experiments and 3d numerical simulations // Journal of Fluid Mechanics. 2016. P. 429–432.

  21. Sibgatullin I.N., Ermanyuk E.V., Maas L. et al. Direct numerical simulation of three-dimensional inertial wave attractors // 2017 Ivannikov ISPRAS Open Conference (ISPRAS). 2017. P. 137–143.

  22. Lam F., Maas L. Internal wave focusing revisited; a reanalysis and new theoretical links // Fluid Dyn. Res. 2008. P. 95–122.

  23. Brouzet C., Sibgatullin I.N., Ermanyuk E.V. et al. Scale effects in internal wave attractors // Physical Review Letters. 2017.

  24. Brouzet C., Ermanyuk E.V., Joubaud S. et al. Energy cascade in internal wave attractors // Europhysics Letters. 2016.

  25. Brouzet C., Ermanyuk E.V., Joubaud S. et al. Internal wave attractors: different scenarios of instability // Journal of Fluid Mechanics. 2017. P. 544–568.

  26. Hazewinkel J., Grisouard N., Dalziel S. Comparison of laboratory and numerically observed scalar fields of an internal wave attractor // Eur. J. Mech. B Fluids. 2011. P. 51–56.

  27. Fischerand P., Ronquist E. Spectral element methods for large scale parallel navier–stokes calculations // Comput. Meth. Appl. Mech. Engng. 1994. P. 69–76.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал