Известия РАН. Механика жидкости и газа, 2021, № 3, стр. 39-47

ВЕРТИКАЛЬНЫЙ ПЕРЕНОС ИМПУЛЬСА ВНУТРЕННИМИ ВОЛНАМИ В ДВУМЕРНОМ ПОТОКЕ

Н. О. Анкудинов^b, А. А. Слепышев^a, b, *

^a Морской гидрофизический институт РАН
Севастополь, Россия

^b Филиал МГУ им. М.В. Ломоносова
Севастополь, Россия

^* E-mail: slep55@mail.ru

Поступила в редакцию 10.07.2020
После доработки 21.10.2020
Принята к публикации 23.12.2020

DOI: 10.31857/S0568528121030026

Полный текст (PDF)

Аннотация

В приближении Буссинеска рассматриваются свободные внутренние волны при учете вращения Земли на двумерном вертикально-неоднородном стратифицированном течении. Уравнение для амплитуды вертикальной скорости фиксированной моды внутренних волн имеет комплексные коэффициенты, поэтому собственная функция и частота волны – комплексные. Мнимая часть частоты мала и может быть как отрицательной, так и положительной. Поэтому возможно как слабое затухание, так и слабое усиление волны в зависимости от волнового числа и номера моды. Вертикальные волновые потоки импульса отличны от нуля и могут превосходить соответствующие турбулентные потоки.

Ключевые слова: внутренние волны, мнимая поправка к частоте, волновой поток импульса

Вертикальный перенос в морской среде обычно связывается с процессами обмена, ключевую роль в этом играет мелкомасштабная турбулентность. Механизмы генерации турбулентности самые разнообразные – ветровое перемешивание в приповерхностном слое, гидродинамическая неустойчивость течений и внутренних волн, обрушение внутренних волн, донное трение, продуцирующее генерацию турбулентности в придонном пограничном слое, захват и фокусировка внутренних волн горизонтально-неоднородным пикноклином [1] и наклонным дном на шельфе [2]. При определенной геометрии дна и бассейна в целом возможен геометрический аттрактор внутренних волн – область волновой турбулентности, связанная с фокусировкой внутренних волн за счет геометрии границ [2, 3]. Здесь реализуется каскадный механизм передачи энергии от крупномасштабных волновых возмущений к мелкомасштабным, за счет трехволновых взаимодействий [2, 3]. Внутренние волны повсеместно присутствуют в океане, благодаря действию источников, их порождающих. Это воздействие атмосферных возмущений, взаимодействие течений и приливов с неоднородностями рельефа дна, генерация внутренних волн вихрями. Мелкомасштабная турбулентность сильно подавлена в пикноклине и поэтому представляется актуальным исследование вклада внутренних волн в вертикальный обмен. Внутренние волны в океане распространяются преимущественно локализованными в пространстве волновыми пакетами [4]. Нелинейные эффекты при распространении пакетов внутренних волн проявляются в генерации средних на временном масштабе волны течений [5, 6]. Вертикальная скорость этих течений не переднем и заднем фронте пакета имеет разные знаки и интегрального переноса по вертикали не происходит.

Внутренние волны при учете турбулентной вязкости и диффузии затухают [7–9]. Вертикальные волновые потоки тепла, соли и импульса при этом отличны от нуля [10, 11]. Ниже будет показано, что в двумерном течении с вертикальным сдвигом скорости вертикальный волновой поток импульса отличен от нуля и без учета турбулентной вязкости и диффузии. Дело в том, что в этом случае уравнение для амплитуды вертикальной скорости имеет комплексные коэффициенты, собственная функция краевой задачи для внутренних волн – комплексная и частота волны также комплексная. Сдвиг фаз между колебаниями вертикальной и горизонтальной скорости отличен от π/2 и вертикальный волновой поток импульса отличен от нуля.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматриваются свободные инерционно-гравитационные внутренние волны на двумерном стратифицированном течении с вертикальным сдвигом скорости в безграничном бассейне постоянной глубины. Две компоненты скорости течения ${{U}_{0}}(z),\,\,{{V}_{0}}(z)$ зависят от вертикальной координаты. В линейном приближении решается краевая задача для амплитуды вертикальной скорости и находится дисперсионное соотношение. Во втором порядке по амплитуде волны определяются вертикальные потоки импульса.

Уравнения гидродинамики в приближении Буссинеска для волновых возмущений имеют вид

(1.1)

$\frac{{Du}}{{Dt}} - fv + w\frac{{d{{U}_{0}}}}{{dz}} = - \frac{1}{{{{{{\rho }}}_{0}}(0)}}\frac{{\partial P}}{{\partial x}}$

(1.2)

$\frac{{Dv}}{{Dt}} + fu + w\frac{{d{{V}_{0}}}}{{dz}} = - \frac{1}{{{{{{\rho }}}_{0}}(0)}}\frac{{\partial P}}{{\partial y}}$

(1. 3)

$\frac{{Dw}}{{Dt}} = - \frac{1}{{{{{{\rho }}}_{0}}(0)}}\frac{{\partial P}}{{\partial z}} - \frac{{g{{\rho }}}}{{{{{{\rho }}}_{0}}(0)}}$

(1.4)

$\frac{{D{{\rho }}}}{{Dt}} = - w\frac{{d{{{{\rho }}}_{0}}}}{{dz}}$

(1.5)

$\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$

где $u,v,w$ – соответственно две горизонтальные и вертикальная компоненты волновой скорости течения; ${{\rho }}$, $P$ – волновые возмущения плотности и давления, ${{{{\rho }}}_{0}}(z)$ – профиль средней плотности; $x,y,z$ – две горизонтальные и вертикальная координаты, ось $z$ направлена вертикально вверх; f – параметр Кориолиса, ${{U}_{0}}(z),{{V}_{0}}(z)$ – две компоненты скорости среднего течения, действие оператора $D{\text{/}}Dt$ раскрывается по формуле

$\frac{D}{{Dt}} = \frac{\partial }{{\partial t}} + (u + {{U}_{0}})\frac{\partial }{{\partial x}} + (v + {{V}_{0}})\frac{\partial }{{\partial y}} + w\frac{\partial }{{\partial z}}$

Граничное условие на поверхности моря – условие “твердой крышки”, которое отфильтровывает внутренние волны от поверхностных [12]

(1.6)

$z = 0{\kern 1pt} :\quad w = 0$

Граничное условие на дне – условие непротекания

(1.7)

$z = - H{\kern 1pt} :\quad w = 0$

2. ЛИНЕЙНОЕ ПРИБЛИЖЕНИЕ

Решения линейного приближения ищутся в виде

(2.1)

$\begin{gathered} u_{1}^{{}} = {{u}_{{10}}}(z)A{{e}^{{i\,{{\theta }}}}} + c.c.,\quad v_{1}^{{}} = {{v}_{{10}}}(z)A{{e}^{{i\,{{\theta }}}}} + c.c.,\quad {{w}_{1}} = {{w}_{{10}}}(z)A{{e}^{{i\,{{\theta }}}}} + c.c. \\ {{P}_{1}} = {{P}_{{10}}}(z)A{{e}^{{i\,{{\theta }}}}} + c.c.,\quad {{{{\rho }}}_{1}} = {{{{\rho }}}_{{10}}}(z)A{{e}^{{i\,{{\theta }}}}} + c.c. \\ \end{gathered} $

где $c.c.$ – комплексно сопряженные слагаемые, A – амплитудный множитель, ${{\theta }}$ – фаза волны; $\partial {{\theta /}}\partial x = k$, $\partial {{\theta /}}\partial t = - {{\omega }}$, $k$– горизонтальное волновое число, ${{\omega }}$ – частота волны. Предполагается, что волна распространяется вдоль оси $x$.

После подстановки (2.1) в систему (1.1)–(1.5) следует связь амплитудных функций u₁₀, ${{v}_{{10}}},{{{{\rho }}}_{{10}}},{{P}_{{10}}}$ с ${{w}_{{10}}}$

(2.2)

${{u}_{{10}}} = \frac{i}{k}\frac{{d{{w}_{{10}}}}}{{dz}},\quad \Omega = {{\omega }} - k \cdot {{U}_{0}}$

(2.3)

$\begin{gathered} \frac{{{{P}_{{10}}}}}{{{{{{\rho }}}_{0}}(0)}} = \frac{i}{k}\left[ {\frac{\Omega }{k}\frac{{d{{w}_{{10}}}}}{{dz}} + \frac{{d{{U}_{0}}}}{{dz}}{{w}_{{10}}} + \frac{f}{\Omega }\left( {i\frac{{d{{V}_{0}}}}{{dz}}{{w}_{{10}}} - \frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}}} \right)} \right] \\ {{{{\rho }}}_{{10}}} = - \frac{i}{\Omega }{{w}_{{10}}}\frac{{d{{\rho }_{0}}}}{{dz}},\quad {{v}_{{10}}} = \frac{1}{\Omega }\left( {\frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}} - i{{w}_{{10}}}\frac{{d{{V}_{0}}}}{{dz}}} \right) \\ \end{gathered} $

Функция ${{w}_{{10}}}$ удовлетворяет уравнению

(2.4)

$\begin{gathered} \frac{{{{d}^{2}}{{w}_{{10}}}}}{{d{{z}^{2}}}} + k\left[ {\frac{{if\frac{{d{{V}_{0}}}}{{dz}}}}{{{{\Omega }^{2}} - {{f}^{2}}}} - \frac{{{{f}^{2}}\frac{{d{{U}_{0}}}}{{dz}}}}{{\Omega ({{\Omega }^{2}} - {{f}^{2}})}}} \right]\frac{{d{{w}_{{10}}}}}{{dz}} + \\ \, + k{{w}_{{10}}}\left[ {\frac{{k({{N}^{2}} - {{\Omega }^{2}}) + \Omega \frac{{{{d}^{2}}{{U}_{0}}}}{{d{{z}^{2}}}} + if\frac{{{{d}^{2}}{{V}_{0}}}}{{d{{z}^{2}}}}}}{{{{\Omega }^{2}} - {{f}^{2}}}} + \frac{{ifk\frac{{d{{U}_{0}}}}{{dz}}\frac{{d{{V}_{0}}}}{{dz}}}}{{\Omega ({{\Omega }^{2}} - {{f}^{2}})}}} \right] = 0 \\ \end{gathered} $

где ${{N}^{2}} = - g{\text{/}}{{{{\rho }}}_{0}}(0) \cdot d{{{{\rho }}}_{0}}{\text{/}}dz$– квадрат частоты Брента–Вяйсяля.

Граничные условия для w₁₀

(2.5)

${{w}_{{10}}}(0) = 0$

(2.6)

${{w}_{{10}}}( - H) = 0$

Краевая задача (2.4)–(2.6) решалась аналитически в статье [13] при постоянной частоте Брента–Вяйсяля и линейном профиле скорости плоскопараллельного среднего течения. Волна распространялась перпендикулярно потоку. Было получено, что собственная функция – решение этой краевой задачи для фиксированной моды внутренних волн – комплексная, а частота волны – действительная. Ниже в ходе численных расчетов будет показано, что в двумерном течении частота волны комплексная.

Уравнение (2.4) решалось методом возмущений в [14] путем разложения в ряд по малому параметру ${{\varepsilon }} = V_{0}^{*}{\text{/}}(H{{{{\omega }}}_{*}})$, где $V_{0}^{*}$ – характерное значение скорости течения, ${{{{\omega }}}_{*}}$ – характерная частота волны. Однако этот параметр не всегда мал и применимость метода ограничена. Поэтому применена неявная схема Адамса третьего порядка точности для численного решения уравнения (2.4) для реальных профилей частоты Брента–Вяйсяля и течения.

3. ВОЛНОВЫЕ ПОТОКИ ИМПУЛЬСА

Вертикальные волновые потоки импульса $\overline {uw} $, $\overline {{v}w} $ находятся с учетом соотношений (2.1)–(2.3)

(3.1)

$\overline {uw} = \frac{i}{k}\left| {A_{1}^{2}} \right|\left( {w_{{10}}^{*}\frac{{dw_{{10}}^{{}}}}{{dz}} - w_{{10}}^{{}}\frac{{dw_{{10}}^{*}}}{{dz}}} \right)$

(3.2)

$\overline {vw} = \frac{{iw_{{10}}^{{}}w_{{10}}^{*}}}{{\Omega \Omega {\text{*}}}}\left| {A_{1}^{2}} \right|\left( {\Omega - \Omega {\text{*}}} \right)\frac{{dV_{0}^{{}}}}{{dz}} + \frac{f}{{\Omega \Omega {\text{*}}k}}\left| {A_{1}^{2}} \right|\left( {\Omega {\text{*}}w_{{10}}^{*}\frac{{dw_{{10}}^{{}}}}{{dz}} + {{\Omega }^{{}}}w_{{10}}^{{}}\frac{{dw_{{10}}^{*}}}{{dz}}} \right)$

где ${{A}_{1}} = A\exp ({{\delta \omega }} \cdot t)$, ${{\delta \omega }} = \operatorname{Im} ({{\omega }})$ – мнимая часть частоты. Черта сверху означает осреднение по периоду волны.

При $d{{V}_{0}}{\text{/}}dz = 0$ уравнение (2.4) имеет действительные коэффициенты, решение краевой задачи (2.4)–(2.6) – действительная функция и вертикальный волновой поток импульса $\overline {uw} $ (3.1) для фиксированной моды внутренних волн равен нулю. Мнимая часть частоты при этом тоже равна нулю. Вертикальный волновой поток импульса $\overline {{v}w} $ при $d{{V}_{0}}{\text{/}}dz = 0$ согласно (3.2) не равен нулю. Он равен нулю только при неучете вращения Земли, т.е. при f = 0. При $d{{V}_{0}}{\text{/}}dz \ne 0$, и $f \ne 0$, уравнение (2.4) имеет комплексные коэффициенты, и, как показали численные расчеты на двумерном течении, собственная функция внутренних волн – комплексная функция и вертикальный волной поток импульса $\overline {uw} $ (3.1) отличен от нуля. Волновой поток импульса $\overline {{v}w} $ (3.2) при этом также отличен от нуля. Таким образом, при наличии течения, у которого компонента скорости, поперечная к направлению распространения волны, зависит от вертикальной координаты, волновые потоки импульса $\overline {uw} $, $\overline {{v}w} $ отличны от нуля. При f = 0 уравнение (2.4) имеет действительные коэффициенты, собственная функция фиксированной моды внутренних волн – действительная, мнимая часть частоты равна нулю и волновые потоки импульса $\overline {uw} $ (3.1) и $\overline {{v}w} $ (3.2) – нулевые.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

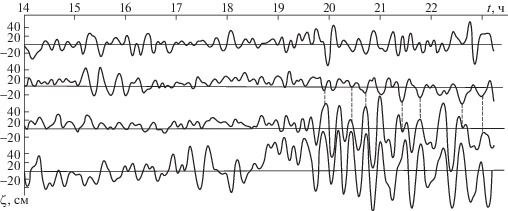
Для определения вертикальных волновых потоков импульса используются результаты третьего этапа 44-го рейса НИС “Михаил Ломоносов” на северо-западном шельфе Черного моря. По данным градиентно-распределенных датчиков температуры (приборов ГРАД) построен временной ход изолиний температуры (рис. 1, [15]).

Рис. 1.

Временной ход вертикальных смещений изолиний температуры.

Приборы располагались один над другим и пересекали слои 5–15 (первый прибор), 15–25 (второй), 25–35 (третий) и 35–60 м (четвертый прибор). Легко видеть, что мощные 15-минутные колебания в слое 25–60 находятся в противофазе с колебаниями в слое 15–25 м, что свидетельствует о присутствии внутренних волн второй моды.

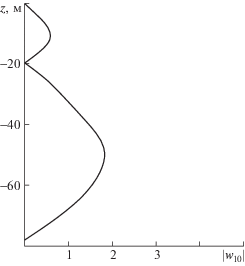
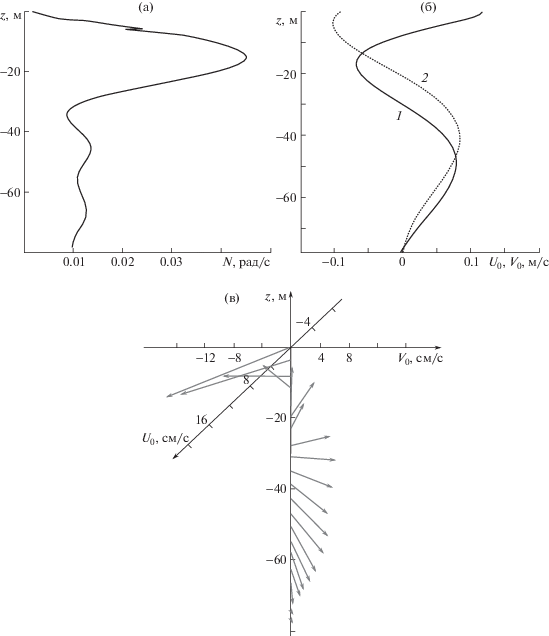
Краевая задача (2.4)–(2.6) по определению ${{w}_{{10}}}$ решается численно по неявной схеме Адамса третьего порядка точности. Вертикальные профили частоты Брента–Вяйсяля и двух компонент скорости течения показаны на рис. 2. Пространственная структура течения представлена на рис. 2в. Вектора скорости течения лежат в плоскостях, перпендикулярных оси Z. Частота волны при фиксированном волновом числе находится методом пристрелки, из необходимости выполнения граничных условий (2.5), (2.6). Профиль модуля собственной функции 15-минутных внутренних волн второй моды изображен на рис. 3.

Рис. 2.

Вертикальные профили: а – частоты Брента–Вяйсяля; б – компонент скорости течения ${{U}_{0}}$ (1), ${{V}_{0}}$ (2); в – пространственная структура течения.

Рис. 3.

Модуль собственной функции 15-минутных внутренних волн второй моды.

Зависимость действительной части частоты 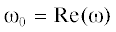от волнового числа для первых двух мод представлена на рис. 4.

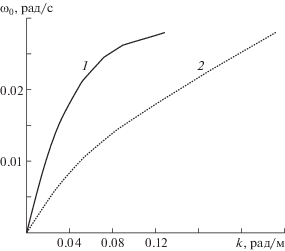
Рис. 4.

Зависимость действительной части частоты от волнового числа для первой (1) и второй (2) мод.

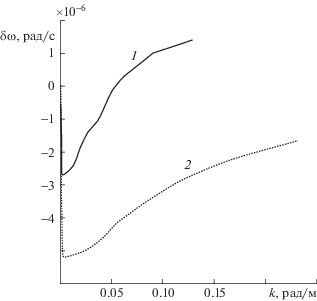
Зависимость мнимой части частоты 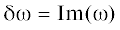от волнового числа представлена на рис. 5.

Рис. 5.

Зависимость мнимой части частоты от волнового числа для первой (1) и второй (2) мод.

Из рис. 5 следует, что у второй моды мнимая часть всегда отрицательная и волна слабо затухает, у первой моды затухание имеет место только в низкочастотной области, при $k < 0.06$ рад/м. При $k > 0.06$ рад/м мнимая часть частоты положительная, имеет место слабое усиление волны. В области затухания волны декремент ${{\delta \omega }}$ у второй моды по модулю больше, чем у первой моды.

Максимальная амплитуда 15-минутных внутренних волн второй моды составляет 0.5 м и это позволяет найти нормирующий множитель ${{A}_{1}}$. Действительно, вертикальная скорость связана с вертикальным смещением ${{\zeta }}$ соотношением $d{{\zeta /}}dt = w$. Отсюда находятся ${{\zeta }}$ и выражение для ${{A}_{1}}$

(4.1)

$\begin{gathered} {{\zeta }} = \frac{{i{{w}_{{10}}}}}{\Omega }{{A}_{1}}\exp (ikx - i{{{{\omega }}}_{0}}t) + c.c. \\ {{A}_{1}} = \frac{{\max {{\zeta }}}}{{2\max \left| {{{w}_{{10}}}{\text{/}}\Omega } \right|}} \\ \end{gathered} $

Из (4.1) следует, что максимум ${{\zeta }}$ соответствует максимуму функции $\left| {{{w}_{{10}}}{\text{/}}\Omega } \right|$, максимальное по модулю значение этого отношения по данным расчетов достигается на глубине 49.5 м, т.е. соответствует глубине максимальных возвышений по данным эксперимента (рис. 1).

Сравнение волнового потока импульса $\overline {uw} $ и турбулентного потока $\overline {u_{{}}^{/}w_{{}}^{/}} $ представлено на рис. 6. Турбулентный поток импульса определялся по формуле $\overline {u_{{}}^{/}w_{{}}^{/}} = - {{K}_{z}}d{{U}_{0}}{\text{/}}dz$, коэффициент вертикального турбулентного обмена оценивался по формуле ${{K}_{z}} \cong 0.93 \times {{10}^{{ - 4}}}N_{c}^{{ - 1}}$ м²/с, N_c соответствует частоте Брента–Вяйсяля в цикл/ч [16]. Волновой поток импульса $\overline {uw} $ определялся для 15-минутных внутренних волн первой (1) и второй (2) мод с максимальной амплитудой 0.5 м. Волновой поток импульса второй моды заметно уступает потоку первой моды и турбулентному потоку. У первой моды нет подавляющего преимущества волнового потока над турбулентным, в интервале глубин 10–30 м волновой поток импульса у первой моды по модулю сравним с турбулентным.

Рис. 6.

Профили волновых $\overline {uw} $ (1), (2) и турбулентного $\overline {u_{{}}^{/}w_{{}}^{/}} $ (3) вертикальных потоков импульса.

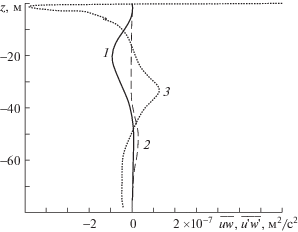
Вертикальные профили волнового $\overline {vw} $ и турбулентного $\overline {v_{{}}^{/}w_{{}}^{/}} $потоков импульса показаны на рис. 7. Турбулентный поток импульса определялся по формуле $\overline {v_{{}}^{/}w_{{}}^{/}} = - {{K}_{z}}d{{V}_{0}}{\text{/}}dz$. Волновой поток импульса $\overline {vw} $ определялся для 15-минутных внутренних волн первой (1) и второй (2) моды с максимальной амплитудой 0.5 м. Нельзя сказать, что волновой поток импульса второй моды всюду уступает турбулентному, скорее всего глубже 30 м они сопоставимы по модулю. Вертикальный поток импульса у первой моды по абсолютной величине доминирует над турбулентным и над потоком второй моды.

Рис. 7.

Профили волновых $\overline {vw} $ (1), (2) и турбулентного $\overline {v_{{}}^{/}w_{{}}^{/}} $ (3) вертикальных потоков импульса.

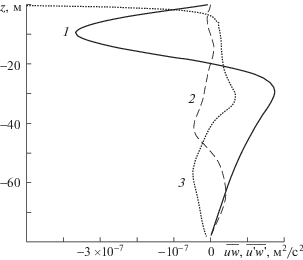
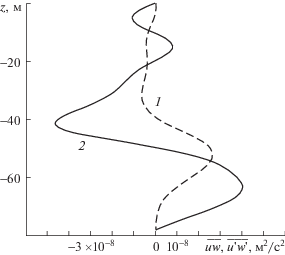
Представляет интерес сопоставить волновые потоки импульса $\overline {uw} $, $\overline {vw} $ для первой и второй мод. На рис. 8 представлены вертикальные профили потоков импульса $\overline {uw} $, $\overline {vw} $ для первой моды 15-минутных внутренних волн.

Рис. 8.

Вертикальное распределение потоков импульса $\overline {uw} $ (1), $\overline {vw} $ (2) для первой моды внутренних волн.

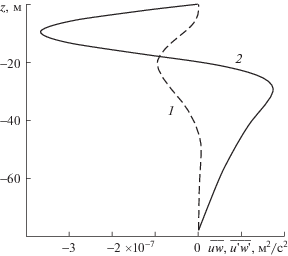
Из рис. 8 следует, что поток импульса $\overline {vw} $ доминирует по модулю над $\overline {uw} $. Аналогичные зависимости представлены для второй моды 15-минутных внутренних волн на рис. 9. Здесь также волновой поток импульса $\overline {vw} $ преобладает над $\overline {uw} $.

Рис. 9.

Вертикальное распределение потоков импульса $\overline {uw} $ (1), $\overline {vw} $ (2) для второй моды внутренних волн.

ЗАКЛЮЧЕНИЕ

Инерционно-гравитационные внутренние волны в двумерном стратифицированном течении имеют комплексную собственную функцию и частоту. Мнимая поправка к частоте по модулю на два-три порядка меньше действительной части частоты. Знак мнимой поправки к частоте у второй моды отрицательный, т.е. имеет место слабое затухание волны. У первой моды при волновом числе k = 0.06 рад/м знак мнимой части частоты меняется с отрицательной величины в низкочастотной области на положительную величину в высокочастотной области, т.е. там имеет место слабое усиление волны. Волновой поток импульса $\overline {vw} $ доминирует по модулю над потоком $\overline {uw} $ как для первой, так и для второй мод 15-минутных внутренних волн. Сравнение волнового $\overline {vw} $ и турбулентного $\overline {v_{{}}^{/}w_{{}}^{/}} $потоков импульса показывает, что для первой моды 15-минутных внутренних волн волновой поток по модулю доминирует над турбулентным. У второй моды эти потоки сравнимы по абсолютной величине. Волновой поток импульса $\overline {uw} $ у первой моды не превосходит по модулю турбулентный поток $\overline {u_{{}}^{/}w_{{}}^{/}} $, а у второй моды турбулентный поток импульса заметно больше по абсолютной величине волнового.

Работа выполнена в рамках государственного задания по теме: № 0827-2019-0003 “Фундаментальные исследования океанологических процессов, определяющих состояние и эволюцию морской среды под влиянием естественных и антропогенных факторов, на основе методов наблюдения и моделирования” (шифр “ОКЕАНОЛОГИЧЕСКИЕ ПРОЦЕССЫ”).

Список литературы

Бадулин С.И., Цимринг Л.Ш., Шрира В.И. Захват и вертикальная фокусировка внутренних волн в пикноклине горизонтальными неоднородностями стратификации и течений // Доклады АН СССР. 1983. Т. 273. № 2. С. 459–463.
Sibgatullin I.N., Ermanyuk E.V. Internal and Inertial Wave Attractors: a Review // Journal of Applied Mechanics and Technical Physics. 2019. V. 60. № 2. P. 284–302. https://doi.org/10.1134/S002189441902010X
Brouzet C., Ermanyuk E.V., Joubaud S., Sibgatullin I., Dauxois T. Energy cascade in internal-wave attractors // EPL (Europhysics Letters), V. 113. № 4. https://doi.org/10.1209/0295-5075/113/44001
Булатов В.В., Владимиров Ю.В. Динамика негармонических волновых пакетов в стратифицированных средах. М.: Наука, 2010. 470 с.
Борисенко Ю.Д., Воронович А.Г., Леонов А.И., Миропольский Ю.З. К теории нестационарных слабонелинейных внутренних волн в стратифицированной жидкости // Изв. АН СССР. Физика атмосферы и океана. I976. Т. 12. № 3. С. 293–301.
Grimshaw R. The modulation of an internal gravity wave packet and the resonance with the mean motion // Stud. In Appl. Math. 1977. V. 56. P. 241–266.
Ле Блон П., Майсек Л. Волны в океане. М.: Мир, 1981. Ч. 2. 363 с.
LeBlond P.H. On damping of internal gravity waves in a continuously stratified ocean // J. Fluid Mech. 1966. V. 25. Iss. 1. P. 121–142. https://doi.org/10.1017/S0022112066000089
Островский Л.А., Соустова И.А. Верхний перемешанный слой как сток энергии внутренних волн // Океанология. 1979. Т. 19. Вып. 6. С. 973–981.
Слепышев А.А. Вертикальный перенос импульса внутренними волнами при учете турбулентной вязкости и диффузии // Изв. РАН. Физика атмосферы и океана. 2016. Т. 52. № 3. С. 342–350. https://doi.org/10.7868/S0002351516030111
Слепышев А.А. Вертикальные потоки, обусловленные внутренними волнами в бароклинном течении // Морской гидрофизический журнал. 2015. № 1. С. 64–78.
Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. Л.: Гидрометеоиздат, 1981. 302 с.
Слепышев А.А., Лактионова Н.В. Вертикальный перенос импульса внутренними волнами в сдвиговом потоке // Изв. РАН Физика атмосферы и океана. 2019. Т. 55. № 6. С. 194–200.
Воротников Д.И., Слепышев А.А. Вертикальные потоки импульса, обусловленные слабонелинейными внутренними волнами на шельфе // Изв. РАН. МЖГ. 2018. № 1. С. 23–35.
Отчет о работах в 44-м рейсе (3-й этап) НИС “Михаил Ломоносов” 7 августа–15 сентября 1985 г. Севастополь: МГИ АН УССР, 1985. Т. 1. 135 с.
Иванов В.А., Самодуров А.С., Чухарев А.М., Носова А.В. Интенсификация вертикального турбулентного обмена в районах сопряжения шельфа и континентального склона в Черном море // Доп. НАН України. 2008. № 6. С. 108–112.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал