1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2021

Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 19-31

РАСТЕКАНИЕ ЛАВЫ КАК НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ ПРИ УСЛОВИИ ЧАСТИЧНОГО ПРОСКАЛЬЗЫВАНИЯ НА ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ

Е. А. Веденеева a, b, *

a МГУ им. М.В. Ломоносова, НИИ механики
Москва, Россия

b Институт теории прогноза землетрясений и математической геофизики РАН
Москва, Россия

* E-mail: el_vedeneeva@imec.msu.ru

Поступила в редакцию 27.03.2020
После доработки 18.06.2020
Принята к публикации 20.06.2020

Полный текст (PDF)

Аннотация

Исследуется влияние граничного условия на подстилающей поверхности на распространение лавовых потоков в случае, когда требуется учитывать их неньютоновские свойства. Решается задача о растекании лавы по плоской горизонтальной поверхности. На подстилающей поверхности вместо условия прилипания ставится условие частичного проскальзывания. Лава моделируется степенной жидкостью. Течение считается осесимметричным. В приближении тонкого слоя задача сводится к решению одного нелинейного уравнения в частных производных второго порядка с дополнительным интегральным условием. Для степенной зависимости расхода лавы от времени получено автомодельное решение, которое, однако, существует только при ограничении на параметры задачи. Неавтомодельное решение рассматривается численно. Показано, что при учете проскальзывания скорость распространения лавы может быть существенно выше.

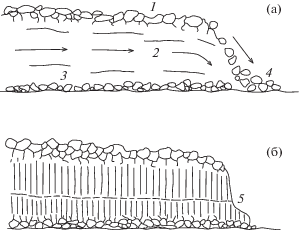
Ключевые слова: неньютоновская жидкость, проскальзывание, приближение тонкого слоя, автомодельное решение, лавовые потоки

Моделированию растекания лавовых потоков посвящено немало работ, учитывающих различные аспекты течения (см., например, [1–7]). Однако только в работах [6, 7] учитывается тот факт, что условие прилипания к подстилающей поверхности для лавы не всегда выполнимо. На подстилающей поверхности [1, 7–10] зачастую формируется подслой, содержащий значительную долю обломков остывшей породы, не сцепленных с подстилающей поверхностью (рис. 1 по [9]). Его образование связано с тем, что, во-первых, лавовые потоки часто движутся по уже извергнутому ранее материалу, во-вторых, на их поверхности за счет остывания может образовываться “корка”, которая растрескивается и обрушивается перед потоком. Этот подслой наблюдается в основании застывших лавовых потоков в виде породы, представляющей собой обломки лавы, ей же сцементированные – лавобрекчии [8–10].

Рис. 1.

Строение лавового потока [9]: (а, б) – во время движения и после остывания; 1 – глыбовая корка, 2 – расплав внутренней части потока, 3 – лавобрекчия в подошве потока, 4 – скатывание глыб с фронтальной части потока, 5 – столбчатая отдельность.

Лава (жидкий продукт вулканических извержений) представляет собой сильно вязкую жидкость со сложными свойствами, которые зависят от ее химического состава, температуры, содержания в ней пузырьков газов и кристаллов [1, 8–10] и может проявлять неньютоновские свойства [1, 5, 7, 11–14]. Для учета последних в литературе (см., например, [5, 7, 11–14]) используется либо степенной закон (закон Освальда–де Виля), либо его модификация с пределом текучести – закон Гершеля–Балкли [15].

В [6] оценивается влияние условия частичного проскальзывания на подстилающей поверхности на скорость распространения и толщину лавовых потоков в максимально упрощенной постановке. Лава моделируется несжимаемой жидкостью с постоянной вязкостью, подстилающая поверхность считается плоской и горизонтальной, течение – осесимметричным. Предполагается, что скорость на подстилающей поверхности является степенной функцией трения – используется обобщенное условие Навье [16–21] (если степень в этом законе первая, то условие на поверхности – условие Навье). В первой части работы считается, что лава растекается из точечного источника, а общий объем извергнутой магмы является степенной функцией времени; задача решается в приближении тонкого слоя и представляет собой обобщение классической работы [22] о растекании ньютоновской жидкости по плоской горизонтальной поверхности под действием силы тяжести в приближении тонкого слоя на случай проскальзывания жидкости по поверхности. Во-второй – обосновывается применимость модели для лавовых потоков.

Отметим аналогичные [22] работы [23–29] о растекании степенной жидкости в приближении тонкого слоя. Во всех этих работах на подстилающей поверхности ставится обычное условие прилипания. В [23–27] задачи решаются в осесимметричной постановке, в [28] – в плоской, в [29] – в осесимметричной и плоской. В [26] решение строится методом разделения переменных; в [26, 27] используется метод теории групп. Задачи, рассматриваемые в [23–25, 27–29], имеют автомодельные решения.

В [7] так же рассматривается осесимметричное растекание лавы по плоской горизонтальной подстилающей поверхности в приближении тонкого слоя, но лава считается подчиняющейся закону Гершеля–Балкли. Предполагается, что лава растекается из круглого канала. Проскальзывание по подстилающей поверхности допускается только в одном из разделов работы по закону несколько другого вида, чем в [6]. В [7] показано, что такая задача сводится к решению одного уравнения в частных производных, решение которого строится численно. Расчеты приведены для скорости на поверхности, прямо пропорциональной трению, коэффициентом пропорциональности является давление на поверхности с постоянным множителем. В частном случае – для степенной жидкости при условии прилипания на подстилающей поверхности найдено автомодельное решение, аналогичное [22].

При изучении вулканических извержений условие проскальзывания, аналогичное используемому в [6], применено в [30] при моделировании течения магмы в канале вулкана. Использование условия проскальзывания жидкости по поверхности встречается и в других геофизических задачах, прежде всего в гляциологии [7, 16].

Условие прилипания для вязкой жидкости является классическим, тем не менее в ряде задач использование условия частичного проскальзывания является более оправданным. Проскальзывание может быть обусловлено свойствами самой жидкости, свойствами поверхности или же самой постановкой задачи (см., например, обзоры [31, 32]).

Для неньютоновских жидкостей условие проскальзывания встречается не так редко – см. обзоры в [16, 31–36]. Для многокомпонентных систем, таких как концентрированные суспензии (жидкости с твердыми частицами), эмульсии (жидкости с каплями другой жидкости), гели (вещества, состоящие из высокомолекулярных и низкомолекулярных компонент, первые из которых выступают в роли каркаса, пустоты которого заполняют вторые), расплавы полимеров, проскальзывание может быть вызвано расслоением этих веществ вблизи стенки, в результате которого около нее формируется подслой с существенно меньшей вязкостью. Усилить этот эффект на микроскопическом уровне может шероховатость стенки.

С другой стороны, шероховатость поверхности может приводить к скоплению на ней в углублениях между микроскопическими выступами газовых пузырьков и, таким образом, с макроскопической точки зрения приводить к скольжению вязкой жидкости вдоль такой поверхности. Поверхности, обладающие этим свойством – супергидрофобные, вызывают широкий интерес в последнее время [31, 32, 37, 38].

Отметим работу [37], в которой исследуется растекание ньютоновской жидкости по супергидрофобной поверхности. Считается, что скорость на подстилающей поверхности пропорциональна касательному напряжению в первой степени, коэффициент пропорциональности между скоростью и трением на поверхности в общем случае непостоянен и является заданной функцией координат. Для такого вида закона проскальзывания построены различные асимптотические автомодельные решения, аналогичные [2, 22].

В задачах о растекании капли ньютоновской жидкости c учетом капиллярных сил в приближении тонкого слоя [39–43] считается, что скорость на подстилающей поверхности пропорциональна касательному напряжению в первой степени в окрестности контакта переднего фронта капли с поверхностью, чтобы избежать появления неинтегрируемой особенности в этой области.

Условие проскальзывания на стенке использовано в работах [17–21] для обобщенных течений Куэтта и Пуазейля, причем решения задач [17–20] получены аналитически или полуаналитически. В [17] рассматриваются течения Куэтта и Пуазейля в плоском случае для ньютоновской и неньютоновских жидкостей, в том числе для степенной жидкости и жидкости, подчиняющейся закону Гершеля–Балкли, при линейном и нелинейном условиях проскальзывания Навье, а также при других законах проскальзывания. В [18] изучается течение Пуазейля в плоской и осесимметричной постановках для вязкоупроугой жидкости (модель Олдройда-Б) с нелинейным условием проскальзывания Навье, причем с коэффициентом, экспоненциально зависящим от нормальной составляющей полного напряжения на стенке. В [19] изучается течение ньютоновской жидкости в трубе постоянного сечения в виде равностороннего треугольника, на одной из стенок которой ставится линейное условие проскальзывания при достижении критического напряжения. В [20] рассматриваются плоское и осесимметричное течения Пуазейля слабосжимаемой жидкости Гершеля–Балкли с линейным условием проскальзывания Навье на стенке, причем коэффициент в нем может зависеть от давления.

В [21] исследуется осесимметричное течение Пузейля жидкости Гершеля–Балкли с нелинейным законом проскальзывания Навье на стенке при достижении критического напряжения. Показано, что при определенных условиях течение останавливается. Для стационарного течения для некоторых значений параметров найдены аналитические решения, в нестационарном случае решение ищется численно методом конечных элементов.

В литературе при моделировании течений вязкой жидкости с условием проскальзывания условие Навье, когда скорость на стенке прямо пропорциональна с постоянным коэффициентом трению, и его различные усложнения используются в подавляющем числе работ [16–21, 30, 32–34, 36–38]. Условие Навье является самым простым, под его обобщением понимают использование степенной зависимости. При дальнейшем усложнении вводится предельное напряжение на стенке, при достижении которого прилипание на стенке сменяется проскальзыванием [16, 17, 19–21, 30]; коэффициент в степенном законе считается зависящим от давления на стенке [7, 20], в более общем случае – от суммарного нормального напряжения на ней [18], а также учитываются зависимости от доли примеси в жидкости, свойств подстилающей поверхности, температуры и т.п.

В настоящей работе решается задача, аналогичная [6], о растекании лавы как неньютоновской жидкости с условием частичного проскальзывания на подстилающей поверхности. Для вязкости лавы выбран степенной закон как имеющий наиболее простую форму. Насколько известно автору, для лавовых потоков нет данных, позволяющих сделать выводы о виде закона проскальзывания лавы, поэтому используется обобщенное условие Навье как простое, но имеющее более общий вид, чем условие Навье. Целью работы является изучение влияния указанного граничного условия на подстилающей поверхности на скорость распространения и толщину лавовых потоков тогда, когда необходимо учитывать их неньютоновские свойства.

Так же как и в случае растекания ньютоновской жидкости при условии прилипания [2, 22], и в случае проскальзывания по поверхности [6, 37], и в случае степенной жидкости при условии прилипания [23–27, 29], и в случае жидкости Гершеля–Балкли при условиях прилипания и проскальзывания [7], в приближении тонкого слоя задача сводится к решению одного нелинейного уравнения в частных производных второго порядка с интегральным условием на решение. За счет проскальзывания в этом уравнении появляется дополнительное слагаемое по сравнению со случаем прилипания к поверхности.

В предположении, что общий объем вытекающей лавы является степенной функцией времени, это уравнение имеет автомодельное решение, аналогичное [2, 6, 7, 22–25, 27, 29, 37], однако, как и для ньютоновской жидкости [6], оно существует только при ограничении на степени в законах, входящих в постановку задачи, и находится из решения обыкновенного нелинейного дифференциального уравнения второго порядка. Как и в [6, 37], оно содержит параметр, значение которого должно быть найдено из решения самого уравнения. Так как автомодельное решение существует не всегда, исходное нелинейное уравнение в частных производных второго порядка решается численно.

Учитывая возросший интерес к течениям вязкой жидкости с проскальзыванием [16–21, 30–38], полученное автомодельное решение задачи о растекании неньютоновской жидкости с проскальзыванием полезно для решения подобных задач.

1. ПОСТАНОВКА ЗАДАЧИ

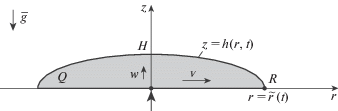
Рассматривается растекание лавы, моделируемой степенной несжимаемой жидкостью с плотностью ρ, от источника в начале координат, который считается точечным. Подстилающая поверхность считается плоской и горизонтальной, течение – осесимметричным. Ось $z$ направлена вертикально против действия силы тяжести $\vec {g}$, ось $r$ – по радиусу; ${v}$ и w – радиальная и вертикальные компоненты скорости соответственно (рис. 2).

Рис. 2.

Схема течения и обозначения.

Эффективная вязкость лавы равна [15]

(1.1)
$\mu = {{\mu }_{0}}\mathop {\dot {\gamma }}\nolimits^{N - 1} ,\quad \dot {\gamma } = \sqrt {2{{e}^{{ij}}}{{e}_{{ij}}}} $
где ${{\mu }_{0}}$ и $N$ – константы, $\dot {\gamma }$ – скорость сдвига, ${{e}_{{ij}}}$ – тензор скоростей деформаций. Лава чаще ведет себя как псевдопластичная жидкость (N < 1), но может вести себя и как дилатантная (N > 1). При N = 1 в (1.1) жидкость ньютоновская. Для лавовых потоков характерные значения $N \in [0.5;\;1.5]$, чаще N < 1 [5, 7, 11–14].

Система уравнений, описывающая такое течение, состоит из уравнения неразрывности и уравнений движения. Рассматривается приближение тонкого слоя: характерная толщина слоя $H$ мала по сравнению с характерным радиусом растекания жидкости $R$: $\varepsilon = H{\text{/}}R \ll 1$. Далее делаются преобразования, аналогичные [6], для случая степенной жидкости.

Из уравнения неразрывности, чтобы удержать в нем оба слагаемых, следует, что характерные скорости течения вдоль радиуса ${{{v}}_{0}}$ и вертикальной оси w0 должны быть связаны соотношением: ${{{v}}_{0}}{\text{/}}{{w}_{0}} \sim R{\text{/}}H = 1{\text{/}}\varepsilon $, т.е. должны иметь разный порядок.

Оставляя только старшие члены, $\dot {\gamma } = \left| {\partial {v}{\text{/}}\partial z} \right|$. Лавовые потоки обладают большой вязкостью при малой скорости течения: для рассматриваемых потоков вязкость $(\mu )$ составляет ~105–1012 Па⋅с, характерные скорости течения (${{{v}}_{0}}$) – сантиметры или миллиметры в секунду; толщина $(H)$ – метры и десятки метров [1, 2, 5, 7–14]. В силу этого для порядка обобщенного числа Рейнольдса [15], при характерных для лавы значениях N (1.1), справедлива оценка: Re = $\rho {{H}^{N}}{v}_{0}^{{2 - N}}{\text{/}}{{\mu }_{0}} \lesssim 1{\text{/}}\varepsilon $. Это позволяет пренебречь в уравнении движения нестационарными и конвективными членами по сравнению с вязкими. Тогда из уравнений движения следует оценка для изменения давления $p$ по осям $r$ и $z$

${{\frac{{\partial (p - \rho gz)}}{{\partial z}}} \mathord{\left/ {\vphantom {{\frac{{\partial (p - \rho gz)}}{{\partial z}}} {\frac{{\partial (p - \rho gz)}}{{\partial r}}}}} \right. \kern-0em} {\frac{{\partial (p - \rho gz)}}{{\partial r}}}} = {{\left( {\frac{{\partial p}}{{\partial z}} - \rho g} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{\partial p}}{{\partial z}} - \rho g} \right)} {\frac{{\partial p}}{{\partial r}}}}} \right. \kern-0em} {\frac{{\partial p}}{{\partial r}}}} \sim {{\varepsilon }^{2}}$
что позволяет пренебречь изменением давления вдоль оси $z$ за счет вязких членов.

Пренебрегая малыми слагаемыми по сравнению с оставленными ниже членами уравнений, отношения которых имеют порядок ε2 и ε ⋅ Re, полная система уравнений, описывающая течение, сводится к следующей

(1.2)
$\begin{array}{*{20}{c}} {\frac{1}{r}\frac{\partial }{{\partial r}}(r{v}) + \frac{{\partial w}}{{\partial z}} = 0} \\ {\frac{{\partial p}}{{\partial r}} = \frac{\partial }{{\partial z}}\left( {\mu \frac{{\partial {v}}}{{\partial z}}} \right),\quad \frac{{\partial p}}{{\partial z}} = - \rho g} \end{array}$
где $\mu = {{\mu }_{0}}\mathop {\left| {\partial {v}{\text{/}}\partial z} \right|}\nolimits^{N - 1} $ согласно (1.1).

Для задачи ставятся следующие начальное и граничные условия. Считается, что общий объем извергнутой магмы Q задан как функция времени $t$. Для построения автомодельного решения используется степенная зависимость

(1.3)
$Q(t) = q{{t}^{\beta }}$
где q и $\beta $ – некоторые константы. C точки зрения приложения к вулканическим извержениям имеют смысл только неотрицательные значения показателя $\beta $, далее $\beta > 0$. Во второй части работы решение строится численно и, вообще говоря, вид функции $Q(t)$ может быть любым.

На свободной поверхности выполнены кинематическое и динамическое (считается, что давление постоянно и отсутствуют касательные напряжения) условия

(1.4)
$z = h(r,t){\text{:}}\quad w = \frac{{\partial h}}{{\partial t}} + {v}\frac{{\partial h}}{{\partial r}},\quad p = {{p}_{0}},\quad \frac{{\partial {v}}}{{\partial z}} = 0$

В последнем условии оставлены только члены старшего порядка.

На подстилающей поверхности ставится обобщенное условие проскальзывания Навье [16–21], предполагая, что у скорости есть только радиальная составляющая, которое, оставляя только старшие слагаемые, записывается как

(1.5)
$z = 0{\text{:}}\quad {v} = {{B}_{d}}\mathop {\left( {\frac{{\partial {v}}}{{\partial z}}} \right)}\nolimits^n ,\quad w = 0$
где ${{B}_{d}}$ и $n$ – некоторые положительные константы.

Связь между формой свободной поверхности $h(r,t)$ и компонентой скорости ${v}$ по оси $r$ находится при интегрировании по z от 0 до $h(r,t)$ уравнения неразрывности в (1.2) с использованием условия для $w$ при $z = 0,h(r,t)$ из (1.5), (1.4)

(1.6)
$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\int\limits_0^{h(r,t)} {v} dz} \right) + \frac{{\partial h}}{{\partial t}} = 0$

Интегрирование уравнений движения в (1.2) с использованием граничных условий (1.4), (1.5) приводит к выражениям

(1.7)
$\begin{gathered} p = \rho g(h - z) + {{p}_{0}} \\ {v} = \frac{N}{{N + 1}}\mathop {\left( {a\left( { - \frac{{\partial h}}{{\partial r}}} \right)} \right)}\nolimits^{\tfrac{1}{N}} \left( {{{h}^{{1 + \tfrac{1}{N}}}} - \mathop {\left( {h - z} \right)}\nolimits^{1 + \tfrac{1}{N}} } \right) + {{B}_{d}}\mathop {\left( {a\left( { - \frac{{\partial h}}{{\partial r}}} \right)h} \right)}\nolimits^{\tfrac{n}{N}} ,\quad a = \frac{{\rho g}}{{{{\mu }_{0}}}} \\ \end{gathered} $

При подстановке выражения для радиальной компоненты скорости ${v}$ через форму свободной поверхности $h(r,t)$ из (1.7) в (1.6), задача сводится к отысканию формы свободной поверхности $h(r,t)$ из решения одного нелинейного уравнения в частных производных второго порядка

(1.8)
$\frac{{\partial h}}{{\partial t}} + \frac{N}{{2N + 1}}{{a}^{{\tfrac{1}{N}}}}\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\mathop {\left( { - \frac{{\partial h}}{{\partial r}}} \right)}\nolimits^{\tfrac{1}{N}} {{h}^{{2 + \tfrac{1}{N}}}}} \right) + {{B}_{d}}{{a}^{{\tfrac{n}{N}}}}\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\mathop {\left( { - \frac{{\partial h}}{{\partial r}}} \right)}\nolimits^{\tfrac{n}{N}} {{h}^{{1 + \tfrac{n}{N}}}}} \right) = 0$
с условием (1.3), определяющим общий объем вытекшей магмы, которое, в терминах функции $h(r,t)$ и радиуса растекания лавы на текущий момент $\tilde {r}(t)$, имеет вид

(1.9)
$2\pi \int\limits_0^{\tilde {r}} h (r,t)rdr = q{{t}^{\beta }},\quad h(\tilde {r}(t),t) = 0$

После этого распределения радиальной компоненты скорости ${v}$ и давления p находятся из (1.7).

Таким образом, задача сводится к отысканию формы свободной поверхности $h(r,t)$ из уравнения (1.8) с условием (1.9). В (1.8), (1.9) входит 6 параметров: три размерных – a, Bd и q и три безразмерных – $N$, $n$ и $\beta $. Чтобы уменьшить их число, эти уравнения обезразмериваются следующим образом

(1.10)
$\begin{array}{*{20}{c}} {h{\text{'}} = h{\text{/}}H,\quad r{\text{'}} = r{\text{/}}H,\quad H = \mathop {\left( {\frac{q}{{{{a}^{{\tfrac{\beta }{N}}}}}}} \right)}\nolimits^{\tfrac{1}{{\tfrac{\beta }{N} + 3}}} } \\ {t{\text{'}} = \frac{t}{T},\quad T = \frac{1}{{\mathop {\left( {aH} \right)}\nolimits^{\tfrac{1}{N}} }}} \end{array}$
где $H$ и $T$ – масштабы длины и времени, а штрихами отмечены соответствующие безразмерные величины. Далее штрихи в обозначении безразмерных переменных опускаются.

В безразмерном виде уравнения (1.8), (1.9) записываются как

(1.11)
$\begin{array}{*{20}{c}} {\frac{{\partial h}}{{\partial t}} + \frac{N}{{2N + 1}}\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\mathop {\left( { - \frac{{\partial h}}{{\partial r}}} \right)}\nolimits^{\tfrac{1}{N}} {{h}^{{2 + \tfrac{1}{N}}}}} \right) + B\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\mathop {\left( { - \frac{{\partial h}}{{\partial r}}} \right)}\nolimits^{\tfrac{n}{N}} {{h}^{{1 + \tfrac{n}{N}}}}} \right) = 0} \\ {2\pi \int\limits_0^{\tilde {r}} h (r,t)rdr = {{t}^{\beta }},\quad h(\tilde {r}(t),t) = 0,\quad B = {{B}_{d}}{{q}^{{\tfrac{{n - N - 1}}{{\beta + 3N}}}}}{{a}^{{\tfrac{{3(n - 1) + \beta }}{{\beta + 3N}}}}},\quad a = \frac{{\rho g}}{{{{\mu }_{0}}}}} \end{array}$
$r = \tilde {r}(t)$ – радиус растекания лавы на текущий момент времени. В (1.11) всего 4 параметра: B, $N$, $n$ и $\beta $.

Отметим, что уравнение для $h(r,t)$ в (1.11) совпадает с частным случаем соответствующего уравнения в [7], если в последнем рассмотреть жидкость Гершеля–Балкли с нулевым пределом текучести – т.е. степенную жидкость и использовать на твердой стенке обобщенное условие Навье.

В уравнении (1.11) за проскальзывание на подстилающей поверхности отвечает слагаемое с коэффициентом $B$. При B = 0 это уравнение описывает растекание степенной жидкости с условием прилипания на подстилающей поверхности, рассматриваемое в [23–27, 29].

2. АВТОМОДЕЛЬНОЕ РЕШЕНИЕ

Уравнение (1.11) может быть решено непосредственно численно, что и делается в разд. 3. Однако известно, что аналогичные задачи [2, 6, 7, 22–25, 27, 29, 37] имеют автомодельные решения; в [26] задача решается методом разделения переменных. Поскольку автомодельные решения более наглядные и простые, сначала ищется автомодельное решение рассматриваемой задачи.

В (1.11) делается замена переменных: от $(r,t)$ осуществляется переход к переменным $(\xi ,t)$, где $\xi = r{\text{/}}\tilde {r}(t)$ – положение точки по радиусу относительно радиуса растекания лавы на текущий момент $\tilde {r}(t)$. Искомая функция ищется методом разделения переменных: $h(r,t) = \tilde {h}(\xi ,t) = c(t)G(\xi )$. Из (1.11) следует, что для существования такого решения, во-первых, функция $c(t)$ должна быть степенной функцией времени $c(t) = {{c}_{0}}{{t}^{k}}$ с определенным значением показателя степени:

(2.1)
$h(r,t) = \tilde {h}(\xi ,t) = {{c}_{0}}{{t}^{k}}G(\xi ),\quad k = \frac{{(1 + N)\beta - 2N}}{{5 + 3N}}$
c0 – некоторая произвольная константа. Во-вторых, показатели степеней, входящих в постановку задачи, должны быть не независимыми: показатель степени N в законе, определяющем реологию магмы (1.1), показатель степени $n$ в законе проскальзывания (1.5) и $\beta $ в функции, задающей общий объем вытекшей магмы, (1.3) должны быть связаны следующим образом

(2.2)
$\beta = \frac{{5 + 2N - 5n}}{{2 + N - n}}$

Условие (2.2) накладывает ограничения на значения $n$ при фиксированном значении N. Так как рассматривается случай $\beta > 0$ (1.3), учитывая, что N > 0 (1.1), значения $n$ должны лежать в следующем диапазоне

(2.3)
$n \in \left( { - \infty ;\frac{2}{5}N + 1} \right) \cup (N + 2; + \infty )$

Тогда, согласно (2.1), из интегрального условия в (1.11) радиус растекания лавы в текущий момент времени определяется как

(2.4)
$\tilde {r}(t) = {{(2\pi {{G}_{0}}{{c}_{0}})}^{{ - 1/2}}}{{t}^{l}},\quad l = \frac{1}{2}(\beta - k) = \frac{{(2 + N)\beta + N}}{{5 + 3N}},\quad {{G}_{0}} = \int\limits_0^1 G (\xi )\xi d\xi $

При выполнении условия (2.3) выполнено неравенство l > 0, т.е. радиус растекания лавы увеличивается со временем, как и ожидается при увеличивающемся объеме вытекающей лавы $\beta > 0$ (1.3).

Далее значение c0 выбрано как ${{c}_{0}} = {{(2 + 1{\text{/}}N)}^{{\tfrac{2}{3}\left( {1 - \tfrac{5}{{3N + 5}}} \right)}}}{{(2\pi {{G}_{0}})}^{{ - \tfrac{1}{3}\left( {1 - \tfrac{2}{{3N + 5}}} \right)}}}$. Тогда, согласно (1.11), функция $G(\xi )$ (2.1) удовлетворяет следующему обыкновенному нелинейному дифференциальному уравнению второго порядка с граничным условием на полуинтервале

(2.5)
$\begin{array}{*{20}{c}} {\frac{d}{{d\xi }}\left( {\xi \mathop {\left( { - \frac{{dG}}{{d\xi }}} \right)}\nolimits^{\tfrac{1}{N}} {{G}^{{2 + \tfrac{1}{N}}}}} \right) + \tilde {B}\frac{d}{{d\xi }}\left( {\xi \mathop {\left( { - \frac{{dG}}{{d\xi }}} \right)}\nolimits^{\tfrac{n}{N}} {{G}^{{1 + \tfrac{n}{N}}}}} \right) - l{{\xi }^{2}}\frac{{dG}}{{d\xi }} + k\xi G = 0} \\ {\tilde {B} = \mathop {\left( {2 + \frac{1}{N}} \right)}\nolimits^{\tfrac{1}{3}\left( {1 + 5\tfrac{{3n - 1}}{{3N + 5}}} \right)} {{{(2\pi {{G}_{0}})}}^{{\tfrac{1}{3}\left( {1 - \tfrac{{3n - 1}}{{3N + 5}}} \right)}}}B} \\ {G(1) = 0,\quad \xi \in (0;1]} \end{array}$

Решение (2.1), (2.4), (2.5) представляет собой автомодельное решение исходной задачи (1.11) о растекании степенной жидкости при условии проскальзывания на подстилающей поверхности. В (2.5) за проскальзывание отвечает слагаемое с коэффициентом $\tilde {B}$. При N = 1 эти уравнения описывают растекание ньютоновской жидкости.

При $\tilde {B} = 0$ (2.1), (2.4), (2.5) соответствуют автомодельному решению задачи о растекании степенной жидкости (1.1) с условием прилипания на подстилающей поверхности и полностью совпадают с рассматриваемыми в работах [7, 23–25, 27, 29], при N = 1 – решению задачи о растекании ньютоновской жидкости с условием проскальзывания и совпадают с уравнениями в [6, 37], при N = 1 и $\tilde {B} = 0$ – решению задачи о растекании ньютоновской жидкости с условием прилипания [2, 22].

Аналогично ньютоновской жидкости с условием проскальзывания [6, 37], автомодельное решение существует только при ограничении на параметры задачи. Для рассматриваемой степенной жидкости (1.1) это ограничения (2.2) на степени $N$, $n$, $\beta $. Если на подстилающей поверхности ставится условие прилипания, автомодельное решение существует без каких-либо ограничений на параметры. Кроме того, коэффициент $\tilde {B}$ зависит от интеграла от самой искомой функции $G(\xi )$ через ${{G}_{0}}$ в соответствии с (2.4). То есть как и в [6, 37], уравнение в (2.5) содержит параметр, значение которого должно быть найдено при решении самого этого уравнения.

Как и для ньютоновской жидкости [6], уравнение (2.5) в точке $\xi = 1$ оказывается вырожденным в силу условия $G(1) = 0$: коэффициент при старшей производной обращается в ноль и из уравнения следует, что и $dG{\text{/}}d\xi (1) = 0$, если эта величина имеет конечное значение. Тривиальное решение задачи Коши: $G(\xi ) \equiv 0$ удовлетворяет этим условиям. Чтобы найти решение, отличное от нулевого, условия задачи Коши в точке ξ = 1 интерпретируются как

(2.6)
$\mathop {lim}\limits_{\xi \to 1} G(\xi ) = 0,\quad \mathop {lim}\limits_{\xi \to 1} \frac{{dG}}{{d\xi }} = \infty $

Решение (2.5) с условиями (2.6) в окрестности точки ξ = 1 можно найти в виде разложения в ряд по нецелым степеням: $G(\xi ) = \sum\limits_{m = - \infty }^{ + \infty } {{{a}_{m}}} {{(1 - \xi )}^{{m/M}}}$, где M – целое число. Откуда в окрестности точки $\xi = 1$

(2.7)
$\begin{gathered} \begin{array}{*{20}{c}} {G(\xi ) = {{a}_{1}}\sqrt {1 - \xi } + {{a}_{2}}(1 - \xi ) + O({{{\sqrt {1 - \xi } }}^{3}})} \end{array} \\ {{a}_{1}} = \sqrt 2 \mathop {\left( {\frac{l}{{\tilde {B}}}} \right)}\nolimits^{\tfrac{N}{{2n}}} ,\quad {{a}_{2}} = - \frac{2}{3}\frac{N}{{nl}}\mathop {\left( {\frac{{a_{1}^{2}}}{2}} \right)}\nolimits^{1 + \tfrac{1}{N}} \\ \end{gathered} $

Тогда автомодельное решение (2.1), (2.4), (2.5) можно искать как решение задачи Коши в точке $\xi = 1 - \delta $, где δ – малое число, с условиями для значения функции $G(\xi )$ и ее производной из (2.7). Далее решение строится численно.

Такой подход к интерпретации граничного условия в окрестности ξ = 1 полностью соответствует [6]. При решении аналогичных задач о растекании ньютоновской жидкости [22] и степенной жидкости [23, 25] с условием прилипания на подстилающей поверхности автомодельные решения также ищутся численно с использованием разложений в окрестности ξ = 1, подобных (2.7).

Уравнение (2.5) с условиями для $G(\xi )$, согласованными с (2.7), решалось методом Рунге–Кутты–Фельберга для $\xi \in (0;1 - \delta ]$, значение параметра ${{G}_{0}}$ определялось методом пристрелки. В расчетах значения $\delta $ варьировались в пределах $\delta \sim 0.01{\kern 1pt} - {\kern 1pt} 0.001$. Расчеты показали, что решение (для используемых ниже значений параметров) мало зависит от конкретных значений функции и ее производной в точке $\xi = 1 - \delta $ – достаточно, чтобы значение функции было малым положительным числом, а значение производной – большим отрицательным (в расчетах $G(\xi ) \sim 0.01{\kern 1pt} - {\kern 1pt} 0.001$ и $ - dG{\text{/}}d\xi \sim 10{\kern 1pt} - {\kern 1pt} 1000$).

Ниже приводятся результаты расчетов для следующих характерных физических свойств лавовых потоков [1, 2, 5, 7–14]

(2.8)
$\rho = 2500\;{\text{кг/}}{{{\text{м}}}^{3}},\quad q = 10.6\;{{{\text{м}}}^{3}}{\text{/}}{{{\text{c}}}^{\beta }},\quad {{\mu }_{0}} = 5 \times {{10}^{7}}{\text{Па}} \cdot {{{\text{с}}}^{N}}$

Согласно (1.3) объемный расход магмы определяется как $dQ{\text{/}}dt = q\beta {{t}^{{\beta - 1}}}$. Соответственно, при $\beta = 1$ расход магмы постоянен и равен $q$. С точки зрения приложения задачи к растеканию лавовых потоков случай постоянного расхода кажется наиболее естественным и интересным. Поэтому все расчеты далее приводятся для β = 1. При этом ограничение (2.2) на существование автомодельного решения принимает вид ограничения на значения степени в законе проскальзывания (1.5)

(2.9)
$n = (N + 3){\text{/}}4$
параметр $\tilde {B}$ в (2.5) согласно (1.11) сводится к
(2.10)
$\tilde {B} = \mathop {\left( {\mathop {\left( {2 + \frac{1}{N}} \right)}\nolimits^3 2\pi {{G}_{0}}} \right)}\nolimits^{\tfrac{1}{4}} B,\quad B = {{B}_{d}}\mathop {\left( {\frac{a}{q}} \right)}\nolimits^{\tfrac{1}{4}} ,\quad a = \frac{{\rho g}}{{{{\mu }_{0}}}}$
степени $k$ (2.1) и $l$ (2.4) приводятся к

(2.11)
$k = \frac{{1 - N}}{{5 + 3N}},\quad l = 2\frac{{N + 1}}{{5 + 3N}}$

Характерное поведение функции $G(\xi )$ и ее асимптотики по формуле (2.7) приведены на рис. 3а для $N = 1{\text{/}}2$ (лава моделируется псевдопластичной жидкостью) и на рис. 3б для N = 3/2 (лава – дилатантная жидкость) при различных B: $B = 0$, что соответствует условию прилипания на подстилающей поверхности, $0.825$, $1.650$. При $N = 1{\text{/}}2$ и 3/2, согласно (2.9), (2.11), $n = 7{\text{/}}8$, $k = 1{\text{/}}13$, $l = 6{\text{/}}13$ и $n = 9{\text{/}}8$, $k = - 1{\text{/}}19$, $l = 10{\text{/}}19$ соответственно; растеканию ньютоновской жидкости с проскальзыванием отвечает набор параметров $N = n = 1$, $k = 0$, $l = 1{\text{/}}2$; ньютоновской жидкости с условием прилипания – $N = 1$, B = 0. Кривые для последнего случая приведены на рис. 3 для сравнения. Значения $B = 0.825$ и 1.650 при значениях параметров из (2.8) соответствуют следующим величинам Bd = 10 м ⋅ сn– 1 и 20 м ⋅ сn– 1.

Рис. 3.

Графики функции $G(\xi )$: (а, б) – $N = 0.5$ и $1.5$, 1–3 – $B = 0$, $0.825$, $1.650$; пунктирные кривые – N = 1 при $B = 0$, штриховые – асимптотики (2.7).

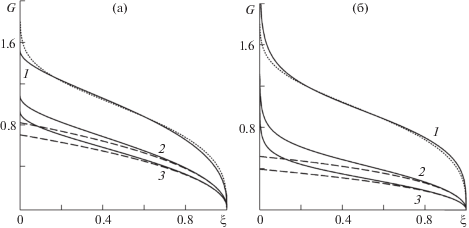
Как видно из рис. 3, различия в поведении функции $G(\xi )$ для ньютоновской и неньютоновской жидкости при условии прилипания на подстилающей поверхности несущественны. С увеличением значения параметра $B$ (2.10) различия между формой функции $G(\xi )$ для рассматриваемых значений N становятся более заметными: для $N = 1{\text{/}}2$ (а) профили функции $G(\xi )$ более выпуклые, чем для $N = 3{\text{/}}2$ (б). Отметим, что соответствующие асимптотики (2.7) хорошо описывают поведение функции $G(\xi )$ не только в окрестности точки $\xi = 1$ – фактически они непригодны только около точки $\xi = 0$.

На рис. 4 приведено поведение функции $h(r,t)$, соответствующее функциям $G(\xi )$ на рис. 3. Следует отметить, что переход к безразмерным параметрам выполнен таким образом, что для разных $N$ используются разные характерные значения размерных параметров (1.10). Так, при значениях (2.8) для

(2.12)
$\begin{array}{*{20}{c}} {N = 1{\text{/}}2{\text{:}}\quad H = 3.804\;{\text{м}},\quad T = 3644.881\;{\text{с}}} \\ {N = 3{\text{/}}2{\text{:}}\quad H = 7.610\;{\text{м}},\quad T = 41.586\;{\text{с}}} \end{array}$
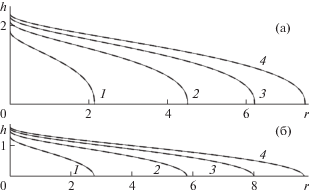
т.е. характерное время $T$ отличается для этих значений $N$ на два порядка.

Рис. 4.

Графики функции $h(r,t)$: (а, б) – $N = 0.5$ и $1.5$; пунктирные, штриховые, сплошные кривые – $B = 0$, $0.825$, $1.650$. Группы кривых 1–3 соответствуют моментам времени $t = {{t}_{0}}$, $5{{t}_{0}}$, $10{{t}_{0}}$; ${{t}_{0}} = 13.72$ для а, $120.22$ – б.

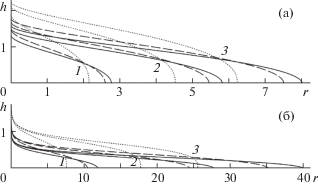
Как видно из рис. 4, значение размерного параметра ${{B}_{d}}$ может быть подобрано таким образом, что скорость распространения лавового потока окажется в полтора раза быстрее при использовании условия проскальзывания на подстилающей поверхности по сравнению с условием прилипания – см. сплошные и пунктирные кривые на 4б.

Как особенность поведения функции $G(\xi )$, отметим вертикальную касательную в окрестности точки $\xi = 0$ (рис. 3), что приводит к аналогичному нефизичному поведению $h(r,t)$ в окрестности r = 0 (рис. 4). В [6] показано, что в случае ньютоновской жидкости функция $G(\xi )$ ведет себя так же, однако решения задачи в приближении тонкого слоя и в полной постановке при решении полных уравнений Навье–Стокса и вытекании жидкости из круглого отверстия конечного радиуса хорошо соответствуют друг другу: существенная разница в их поведении наблюдается лишь на начальной стадии растекания и в окрестности источника.

3. ЧИСЛЕННОЕ РЕШЕНИЕ ИСХОДНОЙ ЗАДАЧИ

Так как автомодельное решение может быть построено только при ограничении на $N$, $n$ и $\beta $ (2.2), которое при $\beta = 1$ может рассматриваться как ограничение на степень $n$ (2.9) в законе проскальзывания (1.5), ниже рассматривается численное решение исходной задачи (1.11).

Задача (1.11) решалась разностным методом. Использовалась полностью неявная схема с динамическим шагом по времени. Аппроксимация по времени и пространству выполнялась с первым порядком точности, считая, что поведение искомой функции линейно между узлами по пространству. Решение строилось относительно поправок к значениям функции в узловых точках, которые находились методом прогонки из линеаризованной системы уравнений. В окрестности нуля течение моделировалось как растекание из боковой стенки кругового цилиндра.

На рис. 5 для иллюстрации точности численного решения приведено сравнение решения исходной задачи (1.11) и автомодельного решения (2.1), (2.5) для $N = 0.5$ в случаях, когда последнее существует. Автомодельное решение существует при условии прилипания на подстилающей поверхности – B = 0 и в случае проскальзывания (1.5) при $n = 7{\text{/}}8$ (2.9). Значение Bd = 20 м ⋅ сn– 1, значения остальных параметров – из (2.8), что соответствует $B = 1.650$ (1.11). Как видно из приведенных графиков, в обоих случаях решения совпадают так, что неразличимы на них.

Рис. 5.

Графики функции $h(r,t)$ для $N = 0.5$: (а, б) – $B = 0$ и $1.650$; решения исходного уравнения и автомодельные – сплошные и штриховые кривые 1–4 в последовательные моменты времени $t = {{t}_{0}} = 13.72$, $5{{t}_{0}}$, $10{{t}_{0}}$, $15{{t}_{0}}$.

В безразмерных переменных в постановку задачи (1.11) входит 4 параметра $B$, $N$, $n$ и β = 1. При фиксированных свойствах лавы и ее расходе ($\rho $, ${{\mu }_{0}}$, $N$, $q$, $\beta $) изменение размерного коэффициента ${{B}_{d}}$ в законе проскальзывания (1.5) соответствует изменению параметра $B$ в (1.11), и наоборот. Автомодельное решение может быть построено только при ограничении (2.2) на $N$, $n$ и $\beta $ – (2.9) для $\beta = 1$. Поэтому в рамках него для фиксированных свойств лавы и ее расхода можно только исследовать влияние коэффициента ${{B}_{d}}$ в законе проскальзывания (1.5), что и было проиллюстрировано на рис. 4, но не степени $n$.

Влияние степени $n$ в (1.5) на решение (1.11) исследуется в рамках его численного решения. На рис. 6 продемонстрировано поведение решения $h(r,t)$ при фиксированных $N$ и $B$ ($\beta = 1$) для различных $n$ – при $N = 0.5$, $B = 1.650$ для $n = 0.5$, 7/8, 1, 1.5. При $n = 7{\text{/}}8$ выполнено условие (2.9) существования автомодельного решения (2.1), (2.5). Для фиксированных свойств лавы, ее расхода (2.8) и $B = 1.650$, разным значениям $n$ отвечают разные значения размерного параметра ${{B}_{d}}$ (1.5): $n = 0.5$ – ${{B}_{d}} = 0.923$ м · с–0.5, $n = 7{\text{/}}8$ – Bd = 20 м ⋅ с—1/8, $n = 1$ – ${{B}_{d}} = 55.750$ м, $n = 1.5$ – ${{B}_{d}} = 3365.752$ м · с0.5 (1.11).

Рис. 6.

Графики функции $h(r,t)$ при $N = 0.5$, $B = 1.650$: (а и г, б, в) – $n = 1.5$, $1$, $0.5$; пунктир – $B = 0$; а–в, штриховые кривые – $n = 7{\text{/}}8$; г, штриховые и штрихпунктирные кривые – при N = 1 для $n = 1.5$ и $B = 0$. Группы кривых 1–3 соответствуют моментам времени $t = {{t}_{0}} = 13.72$, $5{{t}_{0}}$ и $15{{t}_{0}}$.

Для сравнения на рис. 6 для $N = 0.5$ приведено решение с условием прилипания на стенке (при $B = 0$). Так же для сравнения на рис. 6г приведены графики функции $h(r,t)$ для случая, когда лава моделируется ньютоновской жидкостью ($N = 1$) при условии проскальзывания на подстилающей поверхности при том же $B = 1.650$ для $n = 1.5$ – как для рис. 6а (что в этом случае соответствует ${{B}_{d}}{\text{ = 259}}{\text{.451}}$ м · с0.5) и при условии прилипания (B = 0). Соответствующие радиусы растекания лавы $\tilde {r}(t)$ (1.11) приведены на рис. 7.

Рис. 7.

Положение фронта лавового потока с течением времени $\tilde {r}(t)$ при $N = 0.5$, $B = 1.650$: (а, б) – безразмерный и размерный виды, 1–4 – $n = 1.5$, $1$, 7/8, $0.5$; 5 – $B = 0$; 6–7 – при N = 1 для $n = 1.5$ и $B = 0$.

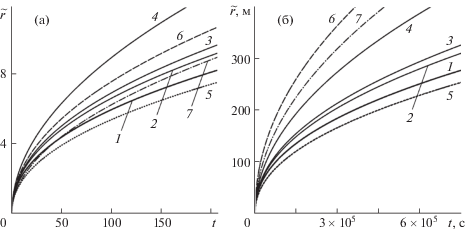
При обезразмеривании (1.10) масштабы длины и времени зависят от значения степени $N$ в законе, определяющем реологию лавы (1.1). При $N = 0.5$ – см. (2.12), для ньютоновской жидкости ($N = 1$) – $H = 12.127$ м и $T = 168.288$ с. Вследствие чего на рис. 7 при сравнении положений фронта лавового потка $\tilde {r}(t)$ в случаях, когда лава моделируется степенной жидкостью и ньютоновской (см. кривые 1–5 и 6–7), взаимные расположения соответствующих кривых в размерном (а) и безразмерном (б) видах различаются.

Как видно из рис. 6 и 7, при уменьшении параметра $n$ при фиксированном $B$ скорость лавового потока увеличивается: так, для $n = 0.5$ радиус растекания лавы за счет проскальзывания при $B = 1.650$ увеличивается в полтора раза по сравнению со случаем, когда на подстилающей поверхности выполнено условие прилипания $B = 0$ (1.5) (рис. 6в, рис. 7, кривые 4 и 5), тогда как для $n = 1.5$ эта разница не превосходит 10% (рис. 6а, рис. 7, кривые 1 и 5). Таким образом, существенного увеличения скорости течения можно достичь подбором степени $n$ при фиксированном $B$.

При дальнейшем увеличении $n$ различия между случаями условия проскальзывания по подстилающей поверхности и прилипания исчезают. Отметим, что такой же характер поведения наблюдается и для лавы, рассматриваемой как ньютоновская жидкость (рис. 6г, рис. 7, кривые 6, 7).

Лава, рассматриваемая как псевдопластичная жидкость ($N = 0.5$ на рис. 6 и 7), распространяется существенно медленнее, чем лава – ньютоновская жидкость при фиксированных $B$ и $n$.

ЗАКЛЮЧЕНИЕ

В приближении тонкого слоя рассмотрена задача о растекании лавы, моделируемой неньютоновской жидкостью, подчиняющейся степенному закону с условием проскальзывания на подстилающей поверхности. При ограничении на параметры задачи найдено ее автомодельное решение, которое может непосредственно использоваться для оценки скоростей распространения лавовых потоков и их толщин. Это решение также полезно для тестирования численных схем, предназначенных для решения задач о растекании неньютоновских жидкостей с условием частичного проскальзывания на подстилающей поверхности.

Рассмотрено неавтомодельное решение этой задачи. Исследовано влияние параметров в законе проскальзывания на решение. Показано, что для характерных для течения лавы значений параметров при учете проскальзывания за счет выбора коэффициентов в обобщенном законе Навье скорость распространения лавовых потоков может быть в полтора раза больше, чем при условии прилипания на подстилающей поверхности.

Автор выражает благодарность О.Э. Мельнику за внимание к работе и ее обсуждение.

Работа выполнена при финансовой поддержке Российского научного фонда (РНФ 19-17-00027).

Список литературы

  1. Griffiths R.W. The dynamics of lava flows // Annu. Rev. Fluid Mech. 2000. V. 32. P. 477–518.

  2. Huppert H.E., Shepherd J.B., Sigurdsson H., Sparks R.S.J. On lava dome growth, with application to the 1979 lava extrusion of the Soufriere of St. Vincent // J. Volc. Geotherm. Res. 1982. V. 14. P. 199–222.

  3. Dragoni M., Borsari I., Tallarico A. A model for the shape of lava flow fronts // J. Geophys. Res. 2005. V. 110. B09203.

  4. Осипцов А.А. Трехмерные изотермические течения лавы на неосесимметричной конической поверхности // Изв. РАН. МЖГ. 2006. 2. С. 31–45.

  5. Tallarico A., Dragoni M., Filippucci M., Piombo A., Santini S., Valerio A. Cooling of a channeled lava flow with non-newtonian rheology: Crust formation and surface radiance // Annals of Geophysics. 2011. V. 54. 5. P. 510–520.

  6. Веденеева Е.А. Растекание лавы во время вулканических извержений при условии частичного проскальзывания на подстилающей поверхности // Изв. РАН. МЖГ. 2015. Т. 2. С. 27–40.

  7. Balmforth N.J., Burbidge A.S., Craster R.V., Salzig J., Shen A. Viscoplastic models of isothermal lava domes // J. Fluid Mech. 2000. V. 403. P. 37–65.

  8. Короновский Н.В. Общая геология: учебник. М.: КДУ, 2006. 528 с.

  9. Короновский Н.В., Якушова А.Ф. Основы геологии: учеб. для географ. спец. вузов. М.: Высш. шк., 1991. 416 с.

  10. Sigurdsson H., Houghton B., McNutt S., Rymer H., Stix J. The Encyclopedia of Volcanoes. 2nd Ed. Elsevier, 2015. 1456 p.

  11. Chevrel M., Cimarelli C., deBiasi L., Hanson J.B., Lavallee Y., Arzilli F., Dingwell D.B. Viscosity measurements of crystallizing andesite from Tungurahua volcano (Ecuador) // Geochem. Geophys. Geosyst. 2015. V. 16. 3. P. 870–889.

  12. Pistone M., Cordonnier B., Ulmer P., Caricchi L. Rheological flow laws for multiphase magmas: An empirical approach // J. Volc. Geoth. Res. 2016. V. 321. P. 158–170.

  13. Castruccio A., Rust A.C., Sparks R.S.J. Rheology and flow of crystal-bearing lavas: Insights from analogue gravity currents // Earth Planet. Sci. Lett. 2010. V. 297. № 3–4. P. 471–480.

  14. Tran A., Rudolph M.L., Manga M. Bubble mobility in mud and magmatic volcanoes // J. Volcanol. Geotherm. Res. 2015. V. 294. P. 11–24.

  15. Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. М.: Бюро Квантум, 1996. 336 с.

  16. Ovarlez G., Hormozi S. Lectures on Visco-Plastic Fluid Mechanics. Springer International Publishing, 2019. 259 p.

  17. Ferras L.L., Nobrega J.M., Pinho F.T. Analytical solutions for Newtonian and inelastic non-Newtonian flows with wall slip // J. Non-Newtonian Fluid Mech. 2012. V. 175–176. P. 76–88.

  18. Housiadas K.D. Viscoelastic Poiseuille flows with total normal stress dependent, nonlinear Navier slip at the wall // Phys. Fluids. 2013. V. 25. 4. 043105.

  19. Georgiou C.G., Kaoullas G. Newtonian flow in a triangular duct with slip at the wall // Meccanica. 2013. V. 48. P. 2577–2583.

  20. Damianou Y., Georgiou C.G., Moulitsas I. Combined effects of compressibility and slip in flows of a Herschel-Bulkley fluid // J. Non-Newtonian Fluid Mech. 2013. V. 193. P. 89–102.

  21. Damianou Y., Philippou M., Kaoullas G., Georgiou C.G. Cessation of viscoplastic Poiseuille flow with wall slip // J. Non-Newtonian Fluid Mech. 2014. V. 203. P. 24–37.

  22. Huppert H.E. The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface // J. Fluid Mech. 1982. V. 21. P. 43–58.

  23. Sayag R., Grae Worster M. Axisymmetric gravity currents of power-law fluids over a rigid horizontal surface // J. Fluid Mech. 2013. V. 716(R5).

  24. Di Federico V., Cintoli S., Bizzarri G. Viscous spreading of non-Newtonian gravity currents in radial geometry // WIT Transactions on Engineering Sciences. 2006. V. 52 (Advances in Fluid Mechanics VI). P. 399–409.

  25. Longo S., Di Federico V., Archetti R., Chiapponi L., Ciriello V., Ungarish M. On the axisymmetric spreading of non-Newtonian power-law gravity currents of time-dependent volume: An experimental and theoretical investigation focused on the inference of rheological parameters // J. Non-Newtonian Fluid Mech. 2013. V. 201. P. 69–79.

  26. Neossi Nguetchue S.N., Momoniat E. Axisymmetric spreading of a thin power-law fluid under gravity on a horizontal plane // Nonlinear Dyn. 2008. V. 52. Issue 4. P. 361–366.

  27. Neossi Nguetchue S.N., Abelman S., Momoniat E. Symmetries and similarity solutions for the axisymmetric spreading under gravity of a thin power-law liquid drop on a horizontal plane // Appl. Math. Model. 2009. V. 33. P. 4364–4377.

  28. Di Federico V., Malavasi S., Cintoli S. Viscous spreading of non-Newtonian gravity currents on a plane // Meccanica. 2006. V. 41. P. 207–217.

  29. Gratton J., Minotti F., Mahajan S.M. Theory of creeping gravity currents of a non-Newtonian liquid // Phys. Rev. E. 1999. V. 60. 6. P. 6960–6967.

  30. Costa A., Wadge G., Melnik O. Cyclic extrusion of a lava dome based on a stick-slip mechanism // Earth Planet. Sci. Lett. 2012. V. 337–338. P. 39–46.

  31. Sochi T. Slip at Fluid-Solid Interface // Polym. Rev. 2011. V. 51. 4. P. 309–340.

  32. Малкин А.Я., Патлажан С.А., Куличихин В.Г. Физико-химические явления, приводящие к скольжению жидкости по твердой поверхности // Успехи химии. 2019. Т. 88. 3. С. 319–349. = Malkin A.Ya., Patlazhan S.A., Kulichikhin V.G. // Russ. Chem. Rev. 2019. V. 88. 3. P. 319–349.

  33. Malkin A.Ya., Patlazhan S.A. Wall slip for complex liquids – Phenomenon and its causes // Adv. Colloid Interface Sci. 2018. V. 257. P. 42–57.

  34. Hatzikiriakos S.G. Wall slip of molten polymers // Prog. Polym. Sci. 2012. V. 37. 4. P. 624–643.

  35. Hatzikiriakos S.G. Slip mechanisms in complex fluid flows // Soft Matter. 2015. V. 11. 40. P. 7851–7856.

  36. Cloitre M., Bonnecaze R.T. A review on wall slip in high solid dispersions // Rheol. Acta. 2017. V. 56. 3. P. 283–305.

  37. Агеев А.И., Осипцов А.Н. Автомодельные режимы растекания тонкого слоя жидкости вдоль супергидрофобной поверхности // Изв. РАН. МЖГ. 2014. 3. С. 37–51.

  38. Агеев А.И., Осипцов А.Н. Стоксово течение в микроканале с супергидрофобными стенками // Изв. РАН. МЖГ. 2019. Т. 2. С. 59–71.

  39. Hocking L.M., Rivers A.D. The spreading of a drop by capillary action // J. Fluid Mech. 1982. V. 121. P. 425–442.

  40. Hocking L.M. Rival contact-angle models and the spreading of drops // J. Fluid Mech. 1992. V. 239. P. 671–681.

  41. Oron A., Davis S.H., Bankoff S.G. Long-scale evolution of thin liquid films // Rev. Mod. Phys. 1997. V. 69. № 3. P. 931–980.

  42. Hocking L.M., Davis S.H. Inertial effects in time-dependent motion of thin films and drops // J. Fluid Mech. 2002. V. 467. P. 1–17.

  43. Reznik S.N., Yarin A.L. Spreading of an axisymmetric viscous drop due to gravity and capillarity on a dry horizontal wall // Int. J. Multiph. Flow. 2002. V. 28. P. 1437–1457.

  44. Калиткин Н.Н., Корякин П.В. Численные методы: в 2 кн. Кн. 2. Методы математической физики: учебник для студ. учреждений высш. проф. образования. М.: Академия, 2013. 304 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал