Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 52-66

КОЛЕБАНИЯ ПОГРУЖЕННОГО ТЕЛА В ЖИДКОСТИ ПОД ЛЕДЯНЫМ ПОКРОВОМ ВБЛИЗИ ВЕРТИКАЛЬНОЙ СТЕНКИ

Л. А. Ткачева^*

Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 05.06.2020
После доработки 21.06.2020
Принята к публикации 21.06.2020

DOI: 10.31857/S056852812101014X

Аннотация

Получено решение задачи о колебаниях погруженного тела, моделируемого диполем, в жидкости конечной глубины под ледяным покровом вблизи вертикальной стенки. Ледяной покров моделируется тонкой упругой полубесконечной пластиной постоянной толщины. Исследованы амплитуды колебаний прогиба ледяного покрова, амплитуды сил, действующих на стенку, в зависимости от частоты колебаний и расстояния до стенки.

Ключевые слова: тонкая упругая плавающая пластина, изгибно-гравитационные волны, диполь, преобразование Фурье, метод отражения

В последнее время в связи с освоением полярных районов, а также с решением важнейших хозяйственных и природоохранных проблем интерес вызывают задачи о взаимодействии волн с погруженными телами при наличии ледяного покрова. Достаточно хорошо изучены задачи о колебаниях тел цилиндрической или сферической формы под бесконечным ледяным покровом. Обзор полученных результатов можно найти в работе [1]. Отметим работы [2–12], где получены решения трехмерных задач. В [2–8] для построения решения использован метод разложения потенциала по мультиполям – потенциалам, удовлетворяющим уравнению Лапласа и всем граничным условиям, кроме условий на теле. Ранее аналогичные мультиполи были введены для случая жидкости со свободной поверхностью [13]. В работах [9, 10] изучено движение диполя в жидкости под ледяным покровом, моделирующего движение тела. Проведено экспериментальное и теоретическое исследование движения тонкого тела [11] и подводной лодки [12] в жидкости под ледяным покровом, тело моделировалось с помощью системы источников и стоков.

Однако в действительности ледяной покров может быть неоднородным. Он может покрывать не всю поверхность жидкости, могут быть трещины, полыньи. Обзор результатов, полученных при решении двумерной задачи о движении цилиндрического тела в жидкости под неоднородным ледяным покровом можно найти в [14]. В [15] исследовано поведение ледяного покрова при движении подводного тела в замерзшем канале.

В настоящей работе приведено решение задачи о колебаниях тела, моделируемого диполем, в жидкости под ледяным покровом при наличии неподвижной вертикальной стенки.

1. ПОСТАНОВКА ЗАДАЧИ

Ледяной покров моделируется упругой полубесконечной пластиной постоянной толщины $h$. Край пластины приморожен к стенке. Жидкость полагается идеальной несжимаемой, постоянной глубины H, течение ее потенциально. Рассматривается движение жидкости и пластины при колебаниях погруженного тела с заданной частотой $\omega $. Тело типа сферы с радиусом $a$ моделируется диполем. Задача решается в линейном приближении.

Введем декартову систему координат $Oxyz$ с центром O на верхней границе жидкости, осью Ox, перпендикулярной стенке, осью Oy, направленной горизонтально вдоль стенки, и осью Oz, направленной вдоль стенки вертикально вниз. Пластина занимает область x > 0. Диполь с центром в точке $({{x}_{0}},0,{{z}_{0}})$, $a < {{x}_{0}}$, $a < {{z}_{0}}$ совершает поступательные колебания с частотой ω и амплитудами A_j, $j = 1,2,3$ вдоль декартовых осей. Интенсивность диполя $q(t)$ равна [16]

$q(t) = 2\pi {{a}^{3}}U(t)$

где $U(t)$ – скорость его движения. Если $A$ – амплитуда колебаний диполя, то

$U(t) = - i\omega A{{{\text{e}}}^{{ - i\omega t}}}$

При колебаниях диполя по осям Ox, Oy, Oz в безграничной жидкости потенциал скорости течения ${{\varphi }_{i}}$ равен соответственно

${{\varphi }_{1}} = q(t)\frac{{x - {{x}_{0}}}}{{4\pi {{r}^{3}}}},\quad {{\varphi }_{2}} = q(t)\frac{y}{{4\pi {{r}^{3}}}},\quad {{\varphi }_{3}} = q(t)\frac{{z - {{z}_{0}}}}{{4\pi {{r}^{3}}}}$

$r = \sqrt {{{{(x - {{x}_{0}})}}^{2}} + {{y}^{2}} + {{{(z - {{z}_{0}})}}^{2}}} $

Введем цилиндрические координаты на пластине (R, θ), связанные с диполем

$x = {{x}_{0}} + Rcos\theta ,\quad y = Rsin\theta ,\quad R = \sqrt {{{{(x - {{x}_{0}})}}^{2}} + {{y}^{2}}} $

Используем безразмерные переменные и функции

$(x{\text{'}},y{\text{'}},z{\text{'}},x_{0}^{'},z_{0}^{'},r{\text{'}},R{\text{'}},H{\text{'}}) = (x,y,z,{{x}_{0}},{{z}_{0}},r,R,H){\text{/}}a$

$\varphi = - i\omega A\varphi {\text{'}}{{{\text{e}}}^{{ - i\omega t}}},\quad w = Aw{\text{'}}{{{\text{e}}}^{{ - i\omega t}}}$

где $w(x,y,t)$ – прогиб пластины. Штрихи далее опускаются. Осадка пластины в воду не учитывается. Граничные условия на верхней границе жидкости сносятся на плоскость z = 0. Предполагается, что вся нижняя поверхность пластины находится в контакте с жидкостью, отрыва не происходит.

В безразмерных переменных получаем следующую краевую задачу.

(1.1)

$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 0\quad (x > 0,0 < z < H)$

(1.2)

$(\beta \Delta _{2}^{2} + 1 - \delta )\frac{{\partial \varphi }}{{\partial z}} + {{\lambda }^{2}}\varphi = 0,\quad {{\Delta }_{2}} = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}}\quad (z = 0)$

$\beta = \frac{D}{{\rho g{{a}^{4}}}},\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}},\quad \lambda = \omega \sqrt {a{\text{/}}g} ,\quad \delta = \frac{{{{\rho }_{0}}h{{\omega }^{2}}}}{{\rho g}}$

(1.3)

$\partial \varphi {\text{/}}\partial z = 0\quad (z = H),\quad \partial \varphi {\text{/}}\partial x = 0\quad (x = 0),\quad w = \partial \varphi {\text{/}}\partial z\quad (z = 0)$

(1.4)

$w(0,y) = \partial w{\text{/}}\partial x(0,y) = 0$

Здесь ρ₀, ρ – плотности льда и жидкости, $g$ – ускорение свободного падения, $D$ – цилиндрическая жесткость пластины, $E$ – модуль Юнга, $\nu $ – коэффициент Пуассона. На бесконечности ставится условие излучения (условие отсутствия приходящих волн).

2. РЕШЕНИЕ ЗАДАЧИ ДЛЯ СЛУЧАЯ ВЕРТИКАЛЬНЫХ КОЛЕБАНИЙ ДИПОЛЯ

Для построения решения будем использовать метод отражения. Вводим еще один диполь с центром в точке ($ - {{x}_{0}}$, 0, ${{z}_{0}}$), который колеблется таким образом, что его центр находится на одинаковом расстоянии от стенки, что и исходный диполь. Таким образом, отраженный диполь колеблется с амплитудами $ - {{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ по осям $x$, $y$, $z$. Вводим цилиндрические координаты (${{R}_{1}}$, ${{\theta }_{1}}$), связанные с этим диполем,

$x = - {{x}_{0}} + {{R}_{1}}cos{{\theta }_{1}},\quad y = {{R}_{1}}sin{{\theta }_{1}},\quad {{r}_{1}} = \sqrt {{{{(x + {{x}_{0}})}}^{2}} + {{y}^{2}} + {{{(z - {{z}_{0}})}}^{2}}} $

Рассмотрим случай вертикальных колебаний тела. Используя результаты работ [2, 13], потенциал диполя в жидкости под бесконечным ледяным покровом без стенки с центром в точке (${{x}_{0}}$, 0, ${{z}_{0}}$) можно записать в виде

${{\phi }_{0}} = \frac{{z - {{z}_{0}}}}{{2{{r}^{3}}}} + \frac{1}{2}{\text{vp}}\int\limits_0^\infty {\frac{{k{{J}_{0}}(kR)}}{{L(k)}}[ - ((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})} {{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{ch}}(k(H - z)) + $

(2.1)

$ + \;((\beta {{k}^{4}} + 1 - \delta )k{\text{ch}}kz - {{\lambda }^{2}}{\text{sh}}kz){{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk + i\frac{{\pi {{k}_{0}}{{\lambda }^{2}}{{J}_{0}}({{k}_{0}}R){\text{ch}}{{k}_{0}}(H - z){\text{sh}}{{k}_{0}}({{z}_{0}} - H)}}{{L'({{k}_{0}}){\text{sh}}{{k}_{0}}H}}$

(2.2)

$L(k) = (\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}kH - {{\lambda }^{2}}{\text{ch}}kH.$

Здесь ${{k}_{0}}$ – действительный положительный корень дисперсионного соотношения $L(k) = 0$, J₀ – функция Бесселя первого рода, интеграл понимается в смысле главного значения. Тогда ищем решение задачи в виде

(2.3)

$\varphi (x,y,z) = {{\phi }_{0}}(x,y,z) + {{\phi }_{1}}(x,y,z) + \psi (x,y,z)$

где ${{\phi }_{1}}(x,y,z)$ – потенциал отраженного диполя под бесконечным ледяным покровом, $\psi (x,y,z)$ – дополнительный потенциал. Потенциал отраженного диполя получается из формулы (2.1) заменой $r$ и $R$ на ${{r}_{1}}$ и ${{R}_{1}}$. Дополнительный потенциал $\psi (x,y,z)$ нужно построить таким образом, чтобы он удовлетворял уравнениям (1.1)–(1.3) и совместно с остальными членами удовлетворял условиям (1.4).

Для построения дополнительного потенциала применяем преобразование Фурье по переменной $y$ для потенциала $\psi (x,y,z)$ и функции

(2.4)

$u(x,y) = \partial \psi {\text{/}}\partial z(x,y,0)$

$\Psi (x,s,z) = \int\limits_{ - \infty }^\infty {{{{\text{e}}}^{{ - isy}}}} \psi (x,y,z)dy,\quad U(x,s) = \int\limits_{ - \infty }^\infty {{{{\text{e}}}^{{ - isy}}}} u(x,y)dy$

Для функции $U(x,s)$ справедливо уравнение

(2.5)

$\left( {\beta {{{\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} - {{s}^{2}}} \right)}}^{2}} + 1 - \delta } \right)U = - {{\lambda }^{2}}\Psi (x,s,0)$

Общее решение этого уравнения имеет вид

(2.6)

$U(x,s) = {{C}_{1}}(s){{{\text{e}}}^{{i{{\kappa }_{1}}x}}} + {{C}_{2}}(s){{{\text{e}}}^{{i{{\kappa }_{2}}x}}} + {{U}_{0}}(x,s)$

Здесь первые два члена представляют решение однородного уравнения, ${{\kappa }_{1}}$ и ${{\kappa }_{2}}$ являются корнями уравнения

$\beta {{({{\kappa }^{2}} + {{s}^{2}})}^{2}} + 1 - \delta = 0$

лежащими в верхней полуплоскости, ${{\kappa }_{2}} = - {{\bar {\kappa }}_{1}}$, ${{U}_{0}}(x,s)$ – частное решение уравнения (2.5).

Теперь проведем преобразование Фурье по переменной $x$

$\Psi (\alpha ,s,z) = \int\limits_{ - \infty }^\infty {{{{\text{e}}}^{{ - i\alpha x}}}} \Psi (x,s,z)dx,\quad U(\alpha ,s) = \int\limits_{ - \infty }^\infty {{{{\text{e}}}^{{ - i\alpha x}}}} U(x,s)dx$

Из уравнения (1.1) и первого условия (1.3) следует

$\Psi (\alpha ,s,z) = C(\alpha ,s){\text{ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} (H - z))$

Для функции ${{U}_{0}}(\alpha ,s)$ из уравнения (2.5) получаем

$(\beta {{({{\alpha }^{2}} + {{s}^{2}})}^{2}} + 1 - \delta ){{U}_{0}}(\alpha ,s) = - {{\lambda }^{2}}C(\alpha ,s){\text{ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} H)$

(2.7)

${{U}_{0}}(\alpha ,s) = - \frac{{{{\lambda }^{2}}C(\alpha ,s){\text{ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} H)}}{{\beta {{{({{\alpha }^{2}} + {{s}^{2}})}}^{2}} + 1 - \delta }}$

Из уравнений (2.4), (2.6), (2.7) находим

${{C}_{1}}\frac{{2i{{\kappa }_{1}}}}{{\kappa _{1}^{2} - {{\alpha }^{2}}}} + {{C}_{2}}\frac{{2i{{\kappa }_{2}}}}{{\kappa _{2}^{2} - {{\alpha }^{2}}}} - \frac{{{{\lambda }^{2}}C(\alpha ,s){\text{ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} H)}}{{\beta {{{({{\alpha }^{2}} + {{s}^{2}})}}^{2}} + 1 - \delta }} = $

$ = - C(\alpha ,s)\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{sh}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} H)$

Отсюда

$C(\alpha ,s) = 2\frac{{\beta {{{({{\alpha }^{2}} + {{s}^{2}})}}^{2}} + 1 - \delta }}{{L(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )}}\left( {{{C}_{1}}\frac{{i{{\kappa }_{1}}}}{{{{\alpha }^{2}} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{i{{\kappa }_{2}}}}{{{{\alpha }^{2}} - \kappa _{2}^{2}}}} \right)$

${{U}_{0}}(\alpha ,s) = - \frac{{2{{\lambda }^{2}}}}{{{{L}_{1}}(\alpha ,s)}}\left( {{{C}_{1}}\frac{{i{{\kappa }_{1}}}}{{{{\alpha }^{2}} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{i{{\kappa }_{2}}}}{{{{\alpha }^{2}} - \kappa _{2}^{2}}}} \right)$

${{L}_{1}}(\alpha ,s) = \frac{{L(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )}}{{{\text{ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} H)}} = (\beta {{({{\alpha }^{2}} + {{s}^{2}})}^{2}} + 1 - \delta )\sqrt {{{\alpha }^{2}} + {{s}^{2}}} {\text{th}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} H) - {{F}^{2}}{{s}^{2}}$

Функция L(k) определена формулой (2.2). Известно, что она имеет два действительных корня $ \pm {{k}_{0}}$, четыре комплексных корня $ \pm {{k}_{{ - 1}}}$, $ \pm {{k}_{{ - 2}}}$, ${{k}_{{ - 2}}} = - {{\bar {k}}_{{ - 1}}}$ и счетное множество мнимых корней $ \pm {{k}_{j}}$, $j = 1,2$, .... Корни ${{\alpha }_{j}} = \sqrt {k_{j}^{2} - {{s}^{2}}} $ будем выбирать в верхней полуплоскости. Применяя обратное преобразование Фурье, находим с помощью метода вычетов

${{U}_{0}}(x,s) = 2{{\lambda }^{2}}\sum\limits_{j = - 2}^\infty {} \frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}}}{{L_{1}^{'}({{\alpha }_{j}},s)}}\left( {{{C}_{1}}\frac{{{{\kappa }_{1}}}}{{\alpha _{j}^{2} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{{{\kappa }_{2}}}}{{\alpha _{j}^{2} - \kappa _{2}^{2}}}} \right) - {{C}_{1}}{{{\text{e}}}^{{i{{\kappa }_{1}}x}}} - {{C}_{2}}{{{\text{e}}}^{{i{{\kappa }_{2}}x}}}$

Подставляем это выражение в (2.6)

(2.8)

$U(x,s) = 2{{\lambda }^{2}}\sum\limits_{j = - 2}^\infty {\frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}}}{{L_{1}^{'}({{\alpha }_{j}},s)}}} \left( {{{C}_{1}}\frac{{{{\kappa }_{1}}}}{{\alpha _{j}^{2} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{{{\kappa }_{2}}}}{{\alpha _{j}^{2} - \kappa _{2}^{2}}}} \right)$

Из уравнений (1.4), (2.8) получаем систему уравнений для определения коэффициентов C₁, C₂

(2.9)

$\sum\limits_{j = 1}^2 {{{A}_{{ij}}}} {{C}_{j}} = {{B}_{i}}$

Коэффициенты матрицы системы и правой части имеют вид

${{A}_{{11}}} = 2{{\lambda }^{2}}{{\kappa }_{1}}\sum\limits_{j = - 2}^\infty {\frac{1}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{1}^{2})}}} ,\quad {{A}_{{12}}} = 2{{\lambda }^{2}}{{\kappa }_{2}}\sum\limits_{j = - 2}^\infty {\frac{1}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{2}^{2})}}} $

${{A}_{{21}}} = 2{{\lambda }^{2}}{{\kappa }_{1}}\sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}}}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{1}^{2})}}} ,\quad {{A}_{{22}}} = 2{{\lambda }^{2}}{{\kappa }_{2}}\sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}}}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{2}^{2})}}} $

${{B}_{1}} = - \int\limits_{ - \infty }^\infty {{{{\text{e}}}^{{ - isy}}}} (\partial {{\varphi }_{0}}{\text{/}}\partial z(0,y,0) + \partial {{\varphi }_{1}}{\text{/}}\partial z(0,y,0))dy,\quad {{B}_{2}} = 0$

В силу симметрии на стенке при x = 0, z = 0 имеем

$R = {{R}_{1}} = \sqrt {x_{0}^{2} + {{y}^{2}}} ,\quad r = {{r}_{1}} = \sqrt {x_{0}^{2} + {{y}^{2}} + z_{0}^{2}} $

Используя табличные интегралы [17] 2.5.6.4 стр. 315, [18] 2.12.22.6 стр. 180, находим

$\int\limits_0^\infty {\frac{{cos(sy)dy}}{{{{{(R_{0}^{2} + {{y}^{2}})}}^{{3/2}}}}}} = \frac{{s{{K}_{1}}(s{{R}_{0}})}}{{{{R}_{0}}}},\quad \int\limits_0^\infty {\frac{{cos(sy)dy}}{{{{{(R_{0}^{2} + {{y}^{2}})}}^{{5/2}}}}}} = \frac{{{{s}^{2}}{{K}_{2}}(s{{R}_{0}})}}{{3R_{0}^{2}}},\quad {{R}_{0}} = \sqrt {x_{0}^{2} + z_{0}^{2}} $

$\int\limits_0^\infty {cos(sy)} {{J}_{0}}(k\sqrt {x_{0}^{2} + {{y}^{2}}} )dy = ({{k}^{2}} - {{s}^{2}})_{ + }^{{ - 1/2}}cos({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )$

$({{k}^{2}} - {{s}^{2}})_{ + }^{n} = \left\{ {\begin{array}{*{20}{l}} {{{{({{k}^{2}} - {{s}^{2}})}}^{n}},}&{s < {{k}_{0}}} \\ {0,}&{s > {{k}_{0}}} \end{array}} \right.$

${{B}_{1}}(s) = - 2\left[ {\frac{{\left| s \right|{{K}_{1}}\left( {\left| s \right|{{R}_{0}}} \right)}}{{{{R}_{0}}}} - \frac{{z_{0}^{2}{{s}^{2}}{{K}_{2}}\left( {\left| s \right|{{R}_{0}}} \right)}}{{R_{0}^{2}}}} \right. + \int\limits_{|s|}^\infty {\frac{{{{k}^{2}}cos({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )}}{{L(k)\sqrt {{{k}^{2}} - {{s}^{2}}} }}} [((\beta {{k}^{4}} + 1 - \delta )k + $

(2.10)

$\left. { + \;{{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH - {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk + i\frac{{2\pi k_{0}^{2}{{\lambda }^{2}}{\text{sh}}{{k}_{0}}(H - {{z}_{0}})cos({{x}_{0}}\sqrt {k_{0}^{2} - {{s}^{2}}} )(k_{0}^{2} - {{s}^{2}})_{ + }^{{ - 1/2}}}}{{L{\text{'}}({{k}_{0}})}}} \right]$

K_n – модифицированные функции Бесселя. Интеграл в формуле (2.10) является сингулярным с особенностью в точке k = k₀ при $\left| s \right| < {{k}_{0}}$ и понимается в смысле главного значения.

Коэффициенты A₂₁ и A₂₂ можно вычислить точно, применяя прием, который использовался ранее в работе [19]. Используя теорию вычетов, запишем ряд в виде интеграла. Затем, замыкая его сначала в верхней, затем в нижней полуплоскости, преобразуем ряд через вычеты в точках, соответствующих корням полинома, стоящего в знаменателе.

$\sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}}}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{1}^{2})}}} = \frac{1}{{2\pi i}}\int\limits_{ - \infty }^\infty {\frac{{\alpha d\alpha }}{{{{L}_{1}}(\alpha ,s)({{\alpha }^{2}} - \kappa _{1}^{2})}}} + \frac{1}{{2{{\lambda }^{2}}}} = $

$ = - \sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}}}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{1}^{2})}}} + \frac{1}{{{{\lambda }^{2}}}}$

Отсюда находим

$\sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}}}{{L_{1}^{'}({{\alpha }_{j}},s)(\alpha _{j}^{2} - \kappa _{1}^{2})}}} = \frac{1}{{2{{\lambda }^{2}}}},\quad {{A}_{{21}}} = {{\kappa }_{1}},\quad {{A}_{{22}}} = {{\kappa }_{2}},\quad {{C}_{1}}{{\kappa }_{1}} + {{C}_{2}}{{\kappa }_{2}} = 0$

Таким образом, система (2.9) решается явно. После преобразований находим

${{C}_{1}}{{\kappa }_{1}}4i{{\lambda }^{2}}\sqrt {\beta (1 - \delta )} Q(s) = {{B}_{1}}(s),\quad Q(s) = \sum\limits_{j = - 2}^\infty {\frac{1}{{L_{1}^{'}({{\alpha }_{j}},s)(\beta k_{j}^{4} + 1 - \delta )}}} $

$C(\alpha ,s) = \frac{{i{{B}_{1}}(s)}}{{{{\lambda }^{2}}Q(s)L(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} )}}$

$\psi (x,y,z) = \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\text{e}}}^{{i(\alpha x + sy)}}}} } C(\alpha ,s){\text{ch}}(\sqrt {{{\alpha }^{2}} + {{s}^{2}}} (H - z))d\alpha ds = $

$ = - \frac{1}{{\pi {{\lambda }^{2}}}}\int\limits_0^\infty {\frac{{cos(sy){{B}_{1}}(s)}}{{Q(s)}}} \sum\limits_{j = - 2}^\infty {\frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}{\text{ch}}{{k}_{j}}(H - z)}}{{\mathop {L'}\nolimits_1 ({{\alpha }_{j}},s){\text{ch}}{{k}_{j}}H}}} ds$

Прогиб пластины находим из уравнений (1.3), (2.1), (2.3)

$w(x,y) = \frac{1}{2}\left[ {\frac{1}{{{{r}^{3}}}} + \frac{1}{{r_{1}^{3}}}} \right. - 3z_{0}^{2}\left( {\frac{1}{{{{r}^{5}}}} + \frac{1}{{r_{1}^{5}}}} \right) + i\frac{{2\pi k_{0}^{2}{{\lambda }^{2}}{\text{sh}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}({{J}_{0}}({{k}_{0}}R) + {{J}_{0}}({{k}_{0}}{{R}_{1}})) + $

$ + \;{\text{vp}}\left. {\int\limits_0^\infty {\frac{{{{k}^{2}}({{J}_{0}}(kR) + {{J}_{0}}(k{{R}_{1}}))}}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH - {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk} \right] + $

(2.11)

$ + \frac{1}{\pi }\int\limits_0^\infty {\frac{{cos(sy){{B}_{1}}(s){{Q}_{1}}(x,s)}}{{Q(s)}}} ds,\quad {{Q}_{1}}(x,s) = \sum\limits_{j = - 2}^\infty {\frac{{{{{\text{e}}}^{{i{{\alpha }_{j}}x}}}}}{{L_{1}^{'}({{\alpha }_{j}},s)(\beta k_{j}^{4} + 1 - \delta )}}} $

Для вычисления последнего интеграла в формуле (2.11) подставляем выражение для функции ${{B}_{1}}(s)$ из (2.10) и в двойном интеграле меняем порядок интегрирования. Получаем

$\int\limits_0^\infty {\frac{{cos(sy){{B}_{1}}(s){{Q}_{1}}(x,s)}}{{Q(s)}}} ds = - 2\left[ {\int\limits_0^\infty {\frac{{cos(sy){{Q}_{1}}(x,s)}}{{Q(s)}}} } \right.\left( {\frac{s}{{{{R}_{0}}}}{{K}_{1}}(s{{R}_{0}}) - \frac{{z_{0}^{2}{{s}^{2}}}}{{R_{0}^{2}}}{{K}_{2}}(s{{R}_{0}})} \right)ds + $

$ + {\text{vp}}\int\limits_0^\infty {\frac{{{{k}^{2}}}}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH - {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{1}}(y,k,s)} {{Q}_{1}}(x,s)ds + $

$ + \;i\frac{{2\pi k_{0}^{2}{{\lambda }^{2}}{\text{sh}}({{k}_{0}}(H - z))}}{{L{\text{'}}({{k}_{0}})}}\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{1}}(y,{{k}_{0}},s){{Q}_{1}}(x,s)ds} } \right],$

${{f}_{1}}(y,k,s) = \frac{{cos(sy)cos({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )}}{{Q(s)\sqrt {{{k}^{2}} - {{s}^{2}}} }}$

На стенку действует горизонтальная сила со стороны жидкости

${{F}_{h}}(y) = \int\limits_0^H p (0,y,z)dz = - \rho \int\limits_0^H {( - gz + {{\varphi }_{t}})} dz = \rho g{{H}^{2}}{\text{/}}2 + \rho {{\omega }^{2}}{{a}^{2}}A\int\limits_0^H \varphi (0,y,z)dz$

Первый член в последней формуле представляет гидростатическую силу, а второй член – динамическую составляющую, которую обозначим ${{F}_{x}}(y)$

${{F}_{x}}(y) = \rho {{\omega }^{2}}{{a}^{2}}A\left[ {\frac{1}{{\sqrt {x_{0}^{2} + {{y}^{2}} + z_{0}^{2}} }}} \right. - \frac{1}{{\sqrt {x_{0}^{2} + {{y}^{2}} + {{{(H - {{z}_{0}})}}^{2}}} }} + {\text{vp}}\int\limits_0^\infty {\frac{{{{J}_{0}}(k\sqrt {x_{0}^{2} + {{y}^{2}}} )}}{{L(k)}}} \times $

$ \times \;[ - ((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + ((\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}kH - {{\lambda }^{2}}({\text{ch}}kH - 1)){{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk + $

$ + \;i\frac{{2\pi {{\lambda }^{2}}{{J}_{0}}({{k}_{0}}\sqrt {x_{0}^{2} + {{y}^{2}}} ){\text{sh}}{{k}_{0}}({{z}_{0}} - H)}}{{L{\text{'}}({{k}_{0}})}} + \frac{2}{\pi }\int\limits_0^\infty {\frac{{cos(sy)}}{{Q(s)}}} \left( {\frac{{s{{K}_{1}}(s{{R}_{0}})}}{{{{R}_{0}}}} - \frac{{z_{0}^{2}{{s}^{2}}{{K}_{2}}(s{{R}_{0}})}}{{R_{0}^{2}}}} \right){{Q}_{2}}ds + $

$ + \;\frac{2}{\pi }{\text{vp}}\int\limits_0^\infty {\frac{{{{k}^{2}}}}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH - {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{1}}(y,k,s)} {{Q}_{2}}(s)ds + $

(2.13)

$ + \;i\frac{{4k_{0}^{2}{{\lambda }^{2}}{\text{sh}}{{k}_{0}}(H - {{z}_{0}})}}{{L'({{k}_{0}})}}\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{1}}(y,{{k}_{0}},s)} {{Q}_{2}}(s)ds} \right],\quad {{Q}_{2}}(s) = \sum\limits_{j = - 2}^\infty {\frac{1}{{k_{j}^{2}L_{1}^{'}({{\alpha }_{j}},s)(\beta k_{j}^{4} + 1 - \delta )}}} $

На стенку действует также вертикальная сила, равная перерезывающей силе в кромке, которая определяется только дополнительным потенциалом в силу симметрии

${{F}_{z}}(y) = - \frac{{DA}}{{{{a}^{3}}}}\frac{\partial }{{\partial x}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + (2 - \nu )\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\frac{{\partial \psi }}{{\partial z}}(0,y,0) = $

$ = \;\frac{{iDA}}{{\pi {{a}^{3}}}}\int\limits_0^\infty {\frac{{cos(sy){{B}_{1}}(s)}}{{Q(s)}}\sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})}}{{L_{1}^{'}({{\alpha }_{j}},s)(\beta k_{j}^{4} + 1 - \delta )}}} } ds$

Ряд можно точно вычислить, используя тот же прием, что и при вычислении коэффициентов матрицы системы (2.9). Находим

$\sum\limits_{j = - 2}^\infty {\frac{{{{\alpha }_{j}}(\alpha _{j}^{2} + (2 - \nu ){{s}^{2}})}}{{L_{1}^{'}({{\alpha }_{j}},s)(\beta k_{j}^{4} + 1 - \delta )}}} = \frac{1}{{2\beta {{\lambda }^{2}}}}$

Тогда формула для вертикальной силы записывается в виде

${{F}_{z}} = - i\frac{{DA}}{{\pi \beta {{\lambda }^{2}}{{a}^{3}}}}\left[ {\int\limits_0^\infty {\frac{{cos(sy)}}{{Q(s)}}} } \right.\left( {\frac{{s{{K}_{1}}(s{{R}_{0}})}}{{{{R}_{0}}}} - \frac{{z_{0}^{2}{{s}^{2}}{{K}_{2}}(s{{R}_{0}})}}{{R_{0}^{2}}}} \right)ds + $

$ + \;{\text{vp}}\int\limits_0^\infty {\frac{{{{k}^{2}}}}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH - {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{1}}} (y,k,s)ds + $

$ + \;i\frac{{2\pi k_{0}^{2}{{\lambda }^{2}}{\text{sh}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{1}}} (y,{{k}_{0}},s)ds} \right]$

3. РЕШЕНИЕ ЗАДАЧИ ДЛЯ СЛУЧАЯ КОЛЕБАНИЙ ДИПОЛЯ ПО ОСИ $Ox$

В этом случае отраженный диполь колеблется в противофазе с исходным. Потенциал исходного диполя имеет вид

${{\phi }_{0}} = \frac{{x - {{x}_{0}}}}{2}\left[ {\frac{1}{{{{r}^{3}}}}} \right. + \frac{1}{R}{\text{vp}}\int\limits_0^\infty {\frac{{k{{J}_{1}}(kR)}}{{L(k)}}[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})} {{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{ch}}(k(H - z)) + $

$ + \;((\beta {{k}^{4}} + 1 - \delta )k{\text{ch}}kz - {{\lambda }^{2}}{\text{sh}}kz){{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk + $

$ + \;i\left. {\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{{J}_{1}}({{k}_{0}}R){\text{ch}}{{k}_{0}}(H - z){\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{RL{\text{'}}({{k}_{0}}){\text{sh}}{{k}_{0}}H}}} \right]$

Потенциал отраженного диполя ${{\phi }_{1}}$ имеет такой же вид, только множитель $(x - {{x}_{0}})$ нужно заменить на $(x + {{x}_{0}})$, R и $r$ заменить на R₁ и ${{r}_{1}}$.

$\varphi (x,y,z) = {{\phi }_{0}}(x,y,z) - {{\phi }_{1}}(x,y,z) + \psi (x,y,z)$

Дополнительный потенциал строится таким же образом, как и в случае вертикальных колебаний диполя, коэффициенты матрицы системы те же самые, но отличается коэффициент правой части ${{B}_{1}}$

${{B}_{1}}(s) = \frac{{2{{s}^{2}}{{x}_{0}}{{z}_{0}}}}{{R_{0}^{2}}}{{K}_{2}}\left( {\left| s \right|{{R}_{0}}} \right) - 2\int\limits_{|s|}^\infty {\frac{{ksin({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )}}{{L(k)}}[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})} {{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}(kH) + $

$ + \;{{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk - i\frac{{4\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left\{ {\begin{array}{*{20}{l}} {sin({{x}_{0}}\sqrt {k_{0}^{2} - {{s}^{2}}} ),}&{\left| s \right| < {{k}_{0}}} \\ {0,}&{\left| s \right| > {{k}_{0}}} \end{array}} \right.$

Интеграл является сингулярным при $\left| s \right| < {{k}_{0}}$ и понимается в смысле главного значения.

Прогиб пластины определяется выражением

$w(x,y) = \frac{1}{2}\left[ {3{{z}_{0}}\left( {\frac{{x - {{x}_{0}}}}{{{{r}^{5}}}} - \frac{{x + {{x}_{0}}}}{{r_{1}^{5}}}} \right)} \right. - {\text{vp}}\int\limits_0^\infty {\frac{{{{k}^{2}}}}{{L(k)}}} \left( {\frac{{x - {{x}_{0}}}}{R}{{J}_{1}}(kR) - \frac{{x + {{x}_{0}}}}{{{{R}_{1}}}}{{J}_{1}}(k{{R}_{1}})} \right) \times $

$ \times \;[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk - i\frac{{2\pi k_{0}^{2}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}} \times $

$ \times \;\left. {\left( {\frac{{x - {{x}_{0}}}}{R}{{J}_{1}}({{k}_{0}}R) - \frac{{x + {{x}_{0}}}}{{{{R}_{1}}}}{{J}_{1}}({{k}_{0}}{{R}_{1}})} \right)} \right] + \frac{2}{\pi }\left[ {\frac{{{{x}_{0}}{{z}_{0}}}}{{R_{0}^{2}}}} \right.\int\limits_0^\infty {\frac{{cos(sy){{Q}_{1}}(x,s)}}{{Q(s)}}} {{s}^{2}}{{K}_{2}}(s{{R}_{0}})ds - $

$ - \;{\text{vp}}\int\limits_0^\infty {\frac{k}{{L(k)}}[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}(kH) + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]} dk\int\limits_0^k {{{f}_{2}}} (y,k,s){{Q}_{1}}(x,s)ds - $

$ - \;i\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{2}}} (y,{{k}_{0}},s){{Q}_{1}}(x,s)ds} \right]$

${{f}_{2}}(y,k,s) = \frac{{cos(sy)sin({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )}}{{Q(s)}}$

Динамическая составляющая горизонтальной силы, действующей на стенку, определяется формулой

${{F}_{x}}(y) = \rho {{\omega }^{2}}{{a}^{2}}A\left[ { - \frac{{{{x}_{0}}}}{{x_{0}^{2} + {{y}^{2}}}}} \right.\left( {\frac{{H - {{z}_{0}}}}{{\sqrt {x_{0}^{2} + {{y}^{2}} + {{{(H - {{z}_{0}})}}^{2}}} }} + \frac{{{{z}_{0}}}}{{\sqrt {x_{0}^{2} + {{y}^{2}} + z_{0}^{2}} }}} \right) - $

$ - \;\frac{{{{x}_{0}}}}{{\sqrt {x_{0}^{2} + {{y}^{2}}} }}{\text{vp}}\int\limits_0^\infty {\frac{{{{J}_{1}}(k\sqrt {x_{0}^{2} + {{y}^{2}}} )}}{{L(k)}}[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})} {{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + ((\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}kH - $

$ - \;{{\lambda }^{2}}({\text{ch}}kH - 1){{{\text{e}}}^{{k({{z}_{0}} - H)}}}))]dk - i\frac{{2\pi {{\lambda }^{2}}{{x}_{0}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}}){{J}_{1}}({{k}_{0}}\sqrt {x_{0}^{2} + {{y}^{2}}} )}}{{\sqrt {x_{0}^{2} + {{y}^{2}}} L{\text{'}}({{k}_{0}})}} + $

$ + \;\frac{2}{\pi }{\text{vp}}\int\limits_0^\infty {\frac{k}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{2}}} (y,k,s){{Q}_{2}}(s)ds + $

$ + \;i\frac{{4{{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\int\limits_0^{{{k}_{0}}} {{{f}_{2}}} (y,{{k}_{0}},s){{Q}_{2}}(s)ds - \frac{{2{{x}_{0}}{{z}_{0}}}}{{\pi R_{0}^{2}}}\left. {\int\limits_0^\infty {\frac{{cos(sy){{Q}_{2}}(s)}}{{Q(s)}}} {{s}^{2}}{{K}_{2}}(s{{R}_{0}})ds} \right]$

Вертикальная сила, действующая на стенку, записывается выражением

${{F}_{z}} = i\frac{{DA}}{{\pi {{a}^{3}}\beta {{\lambda }^{2}}}}\left[ {\frac{{{{x}_{0}}{{z}_{0}}}}{{R_{0}^{2}}}} \right.\int\limits_0^\infty {\frac{{cos(sy)}}{{Q(s)}}} {{s}^{2}}{{K}_{2}}(s{{R}_{0}})ds - $

$ - \;{\text{vp}}\int\limits_0^\infty {\frac{k}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{2}}} (y,k,s)ds - $

$ - \;i\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{2}}} (y,{{k}_{0}},s)ds} \right]$

4. РЕШЕНИЕ ЗАДАЧИ ДЛЯ СЛУЧАЯ КОЛЕБАНИЙ ДИПОЛЯ ПО ОСИ $Oy$

Потенциал исходного диполя определяется выражением

${{\phi }_{0}}(x,y,z) = \frac{y}{{2R}}\left[ {\frac{R}{{{{r}^{3}}}}} \right. + {\text{vp}}\int\limits_0^\infty {\frac{{k{{J}_{1}}(kR)}}{{L(k)}}[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})]} {{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{ch}}(k(H - z)) + $

$ + \;((\beta {{k}^{4}} + 1 - \delta )k{\text{ch}}kz - {{\lambda }^{2}}{\text{sh}}kz){{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk + $

$ + \;i\left. {\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - z){\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}}){\text{sh}}{{k}_{0}}H}}{{J}_{1}}({{k}_{0}}R)} \right]$

Потенциал отраженного диполя имеет тот же вид, только $R$ и $r$ нужно заменить на ${{R}_{1}}$ и ${{r}_{1}}$. Ищем решение задачи в виде (2.3). Дополнительный потенциал строится так же, как в случае вертикальных колебаний, коэффициенты матрицы системы (2.9) имеют те же выражения, отличается только коэффициент ${{B}_{1}}(s)$

${{B}_{1}}(s) = 2is\left[ {\frac{{\left| s \right|{{z}_{0}}}}{{{{R}_{0}}}}{{K}_{1}}\left( {\left| s \right|{{R}_{0}}} \right) - \int\limits_{|s|}^\infty {\frac{{kcos({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )}}{{L(k)\sqrt {{{k}^{2}} - {{s}^{2}}} }}} } \right.[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + $

$ + \;{{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk - i\left. {\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})cos({{x}_{0}}\sqrt {k_{0}^{2} - {{s}^{2}}} )(k_{0}^{2} - {{s}^{2}})_{ + }^{{ - 1/2}}}}{{L{\text{'}}({{k}_{0}})}}} \right]$

Интеграл является сингулярным при $\left| s \right| < {{k}_{0}}$ и понимается в смысле главного значения. В отличие от предыдущих двух случаев функция ${{B}_{1}}(s)$ нечетна, ${{B}_{1}}( - s) = - {{B}_{1}}(s)$.

Прогиб пластины определяется выражением

$w(x,y) = \frac{y}{2}\left[ {\frac{{3{{z}_{0}}}}{{{{r}^{5}}}} + \frac{{3{{z}_{0}}}}{{r_{1}^{5}}} - {\text{vp}}\int\limits_0^\infty {\frac{{{{k}^{2}}}}{{L(k)}}} \left( {\frac{{{{J}_{1}}(kR)}}{R} + \frac{{{{J}_{1}}(k{{R}_{1}})}}{{{{R}_{1}}}}} \right)} \right.[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}} \times $

$ \times \;{\text{sh}}(kH) + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk - i\frac{{2\pi k_{0}^{2}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left. {\left( {\frac{{{{J}_{1}}({{k}_{0}}R)}}{R} + \frac{{{{J}_{1}}({{k}_{0}}{{R}_{1}})}}{{{{R}_{1}}}}} \right)} \right] + $

$ + \;\frac{2}{\pi }\left[ {{\text{vp}}\int\limits_0^\infty \,\frac{k}{{L(k)}}} \right.[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{3}}} (y,k,s){{Q}_{1}}(x,s)ds + $

$ + \;i\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\int\limits_0^{{{k}_{0}}} {{{f}_{3}}} (y,{{k}_{0}},s){{Q}_{1}}(x,s)ds - \frac{{{{z}_{0}}}}{{{{R}_{0}}}}\left. {\int\limits_0^\infty {} \frac{{{{s}^{2}}sin(sy){{Q}_{1}}(x,s)}}{{Q(s)}}{{K}_{1}}(s{{R}_{0}})ds} \right]$

${{f}_{3}}(y,k,s) = \frac{{ssin(sy)cos({{x}_{0}}\sqrt {{{k}^{2}} - {{s}^{2}}} )}}{{Q(s)\sqrt {{{k}^{2}} - {{s}^{2}}} }}$

Динамическая составляющая горизонтальной силы, действующей на стенку, имеет вид

${{F}_{x}}(y) = \rho {{\omega }^{2}}{{a}^{2}}A\left\{ {\frac{y}{{x_{0}^{2} + {{y}^{2}}}}\left( {\frac{{H - {{z}_{0}}}}{{\sqrt {x_{0}^{2} + {{y}^{2}} + {{{(H - {{z}_{0}})}}^{2}}} }} + \frac{{{{z}_{0}}}}{{\sqrt {x_{0}^{2} + {{y}^{2}} + z_{0}^{2}} }}} \right)} \right. + $

$ + \;\frac{y}{{\sqrt {x_{0}^{2} + {{y}^{2}}} }}\left[ {{\text{vp}}\int\limits_0^\infty {\frac{{{{J}_{1}}(k\sqrt {x_{0}^{2} + {{y}^{2}}} )}}{{L(k)}}} } \right.[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + ((\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}kH - $

$ - \;{{\lambda }^{2}}({\text{ch}}kH - 1)){{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk + i\left. {\frac{{2\pi {{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}}){{J}_{1}}({{k}_{0}}\sqrt {x_{0}^{2} + {{y}^{2}}} )}}{{L{\text{'}}({{k}_{0}})}}} \right] + $

$ + \;\frac{2}{\pi }\left[ {\frac{{{{z}_{0}}}}{{{{R}_{0}}}}\int\limits_0^\infty {\frac{{{{s}^{2}}sin(sy){{Q}_{2}}(s)}}{{Q(s)}}} {{K}_{1}}(s{{R}_{0}})ds} \right. - {\text{vp}}\int\limits_0^\infty {\frac{k}{{L(k)}}[((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})} {{{\text{e}}}^{{ - k{{z}_{0}}}}}{\text{sh}}kH + $

$ + \;{{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{3}}} (y,k,s){{Q}_{2}}(s)ds - i\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left. {\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{3}}} (y,{{k}_{0}},s){{Q}_{2}}(s)ds} \right]} \right\}$

Вертикальная сила, действующая на стенку, определяется формулой

${{F}_{z}}(y) = - \frac{{iDA}}{{\pi \beta {{\lambda }^{2}}{{a}^{3}}}}\left[ {\frac{{{{z}_{0}}}}{{{{R}_{0}}}}\int\limits_0^\infty {\frac{{{{s}^{2}}sin(sy)}}{{Q(s)}}} } \right.{{K}_{1}}(s{{R}_{0}})ds - {\text{vp}}\int\limits_0^\infty {\frac{k}{{L(k)}}} [((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}}){{{\text{e}}}^{{ - k{{z}_{0}}}}} \times $

$ \times \;{\text{sh}}kH + {{\lambda }^{2}}{{{\text{e}}}^{{k({{z}_{0}} - H)}}}]dk\int\limits_0^k {{{f}_{3}}} (y,k,s)ds - i\frac{{2\pi {{k}_{0}}{{\lambda }^{2}}{\text{ch}}{{k}_{0}}(H - {{z}_{0}})}}{{L{\text{'}}({{k}_{0}})}}\left. {\int\limits_0^{{{k}_{0}}} {{{f}_{3}}} (y,{{k}_{0}},s)ds} \right]$

5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Проводились численные расчеты для ледяного покрова и погруженного тела при следующих входных параметрах: $E = 5$ ГПа, $\rho = 1025$ кг/м³, ${{\rho }_{0}} = 922.5$ кг/м³, $\nu = 0.3$, a = 5 м, H = 100 м. Толщина пластины $h = 0.3$ м, глубина погружения тела ${{z}_{0}} = 10$ м, т.е. в безразмерных переменных ${{z}_{0}} = 2$. Менялись частота колебаний $\omega $ и расстояние ${{x}_{0}}$ от центра тела до стенки. Амплитуды прогиба ледяного покрова представлены ниже на рисунках в безразмерном виде $w{\text{/}}A$, а силы, действующие на стенку, в размерном виде, при этом амплитуда колебаний тела полагалась во всех расчетах равной $A = 0.1$ м. Координаты $x$, $y$, параметр ${{x}_{0}}$ на всех графиках безразмерные. Изолинии прогиба ледяного покрова на всех графиках показаны с шагом 0.01. Чтобы получить значение амплитуды прогиба льда на линии, нужно номер линии умножить на 0.01.

На рис. 1а представлены графики амплитуд прогиба ледяного покрова $\left| {w(x,0)} \right|{\text{/}}A$ при вертикальных колебаниях тела с частотой $\omega = 1$ с^–1 для различных расстояний от стенки: ${{x}_{0}} = 2$, 4, 10, 20 (кривые 1–4), а также для тела под бесконечным ледяным покровом (без стенки) с центром на расстоянии ${{x}_{0}} = 2$ от начала координат (кривая 5). Видно, что наличие стенки может приводить как к увеличению амплитуды колебаний, так и к уменьшению. При больших расстояниях от стенки наблюдается колебательный характер кривых.

Рис. 1.

Зависимости амплитуд прогиба ледяного покрова при вертикальных колебаниях диполя: (а) $\left| {w(x,0)} \right|{\text{/}}A$ при $\omega = 1$ c^–1; 1–4 – ${{x}_{0}} = 2$, 4, 10, 20; 5 – случай бесконечного ледяного покрова при x₀ = 2; (б) $\left| {w({{x}_{0}},0)} \right|{\text{/}}A$, 1–3 – $\omega = 0.75$, 1, 1.5 с^–1; штриховые прямые – значения амплитуд в случае бесконечного ледяного покрова.

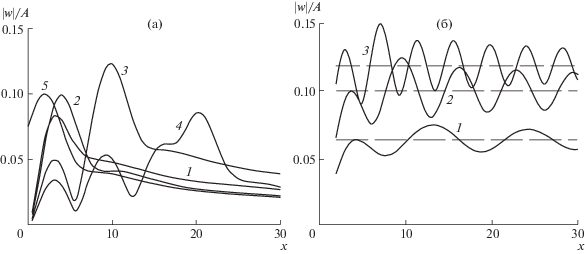
Расчеты показывают, что при ${{x}_{0}} \geqslant 4$ максимальные амплитуды прогиба льда при вертикальных колебаниях наблюдаются в точках, близких к центру тела. На рис. 1б показаны зависимости максимальных амплитуд колебаний прогиба льда $\left| {w({{x}_{0}},0)} \right|{\text{/}}A$ при вертикальных колебаниях тела и частотах $\omega = 0.75$, 1.0, 1.5 c^–1, а также соответствующие значения прогиба бесконечного ледяного покрова (штриховыми линиями). Видно, что при наличии стенки кривые осциллируют относительно штриховых прямых, которые соответствуют колебаниям тела под бесконечным ледяным покровом без стенки. С ростом частоты амплитуды колебаний ледяного покрова увеличиваются.

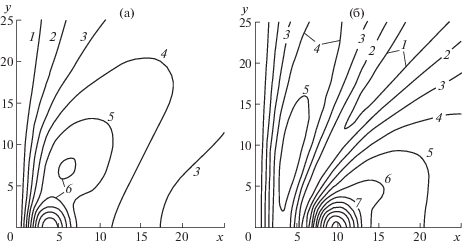
На рис. 2 представлены изолинии с шагом 0.01 прогиба ледяного покрова при вертикальных колебаниях тела с частотой $\omega = 1$ с^–1 и ${{x}_{0}} = 4$ и 10 . Значение амплитуды прогиба на линии получается умножением номера линии на 0.01. При увеличении расстояния тела от стенки изолинии прогиба льда напоминают лепестки.

Рис. 2.

Изолинии с шагом 0.01 амплитуд прогиба ледяного покрова при вертикальных колебаниях диполя: $\omega = 1$ c^–1, а, б – ${{x}_{0}} = 4$, 10.

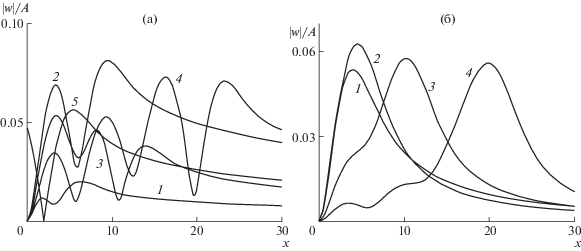
На рис. 3а показаны графики амплитуд прогиба льда $\left| {w(x,0)} \right|{\text{/}}A$ при горизонтальных колебаниях тела по оси $Ox$ с частотой $\omega = 1$ с^–1 и расстояниях от стенки ${{x}_{0}} = 2$, 6, 10, 20 (кривые 1–4), а также для случая бесконечного ледяного покрова (кривая 5) при ${{x}_{0}} = 2$. Отметим, что при горизонтальных колебаниях тела под бесконечным ледяным покровом в точке, соответствующей среднему положению тела, амплитуда колебаний ледяного покрова равна нулю. Максимальные амплитуды ледяного покрова наблюдаются на некотором расстоянии от среднего положения тела. Расчеты показали, что в отсутствие стенки при частотах $\omega = 0.75$, 1 с^–1 это расстояние примерно равно 3.5, а при $\omega = 1.5$ с^–1 – 3 в безразмерных переменных.

Рис. 3.

Зависимости амплитуд колебаний ледяного покрова (а) $\left| {w(x,0)} \right|{\text{/}}A$ при колебаниях диполя по оси $Ox$ при $\omega = 1$ c^–1: 1–4 – x₀ = 2, 6, 10, 20; 5 – случай бесконечного ледяного покрова при x₀ = 2; (б) $\left| {w(x,3.5)} \right|{\text{/}}A$ при колебаниях диполя по оси $Oy$ при $\omega = 1$ с^–1: 1–4 – x₀ = 2, 4, 10, 20.

Изолинии прогиба бесконечного ледяного покрова при горизонтальных колебаниях тела по оси Ox без стенки показаны на рис. 4а, где среднее положение тела расположено на расстоянии ${{x}_{0}} = 2$ от начала координат. На рис. 4б показаны изолинии прогиба ледяного покрова при колебаниях тела по оси Ox вблизи стенки с частотой $\omega = 1$ с^–1 и ${{x}_{0}} = 6$. Значение амплитуды прогиба на линии получается умножением номера линии на 0.01.

Рис. 4.

Изолинии с шагом 0.01 прогиба ледяного покрова при колебаниях диполя по оси $Ox$ (а, б) и оси $Oy$ (в, г): (а) для бесконечного ледяного покрова без стенки, $\omega = 1$ c^–1, x₀ = 2; (б) вблизи стенки $\omega = 1$ c^–1, ${{x}_{0}} = 6$; (в) $\omega = 1$ с^–1, ${{x}_{0}} = 4$; (г) $\omega = 1.5$ с^–1, ${{x}_{0}} = 10$.

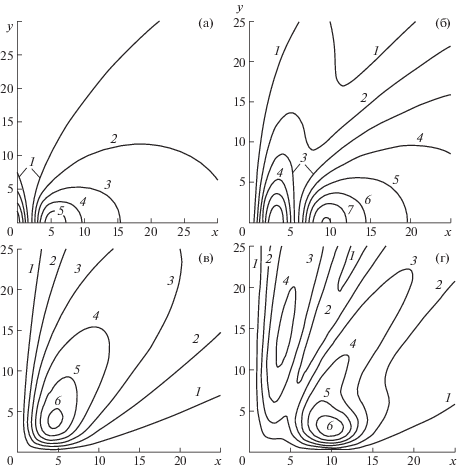
На рис. 3б представлены графики амплитуд прогиба льда $\left| {w(x,3.5)} \right|{\text{/}}A$ при колебаниях тела по оси Oy с частотой $\omega = 1$ с^–1 и расстояниях от стенки ${{x}_{0}} = 2$, 4, 10, 20 (кривые 1–4). На рис. 4в, г изображены изолинии прогиба ледяного покрова при колебаниях тела по оси Oy вблизи стенки с частотой $\omega = 1$ с^–1 и ${{x}_{0}} = 4$ (в), а также с частотой $\omega = 1.5$ с^–1, ${{x}_{0}} = 10$ (г). Видно, что в отличие от предыдущих двух случаев максимальные амплитуды колебаний наблюдаются не на оси Ox, а на некотором расстоянии от нее.

На рис. 5а показаны зависимости от координаты $y$ амплитуд динамической составляющей горизонтальной силы F_x, действующей на стенку со стороны жидкости, при вертикальных колебаниях тела с частотой $\omega = 1$ с^–1 и различных расстояниях тела от стенки. В данном случае максимальная амплитуда силы наблюдается при ${{x}_{0}} = 4$. При малых расстояниях от стенки закрепленный край ледяного покрова уменьшает амплитуды колебаний жидкости и соответственно амплитуду действующей силы. При больших расстояниях от стенки, поскольку максимальные амплитуды колебаний жидкости находятся вблизи центра тела, соответственно вблизи стенки уменьшаются амплитуды колебаний жидкости и действующей силы.

Рис. 5.

Зависимости от безразмерной координаты $y$ при вертикальных колебаниях диполя амплитуд: горизонтальной силы ${{F}_{x}}$ (а) при $\omega = 1$ c^–1, x₀ = 2, 4, 10, 20 (кривые 1–4) и вертикальной силы ${{F}_{z}}$ (б, в): (б) при $\omega = 1$ c^–1, x₀ = 2, 4, 10, 20 (кривые 1–4); (в) при x₀ = 2, $\omega = 0.75$, 1, 1.5 c^–1 (кривые 1–3).

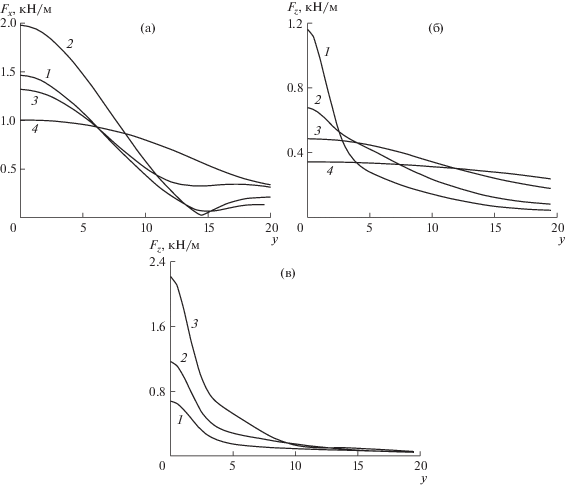
На рис. 5б изображены зависимости от координаты $y$ амплитуд вертикальной силы ${{F}_{z}}$, действующей на стенку, при вертикальных колебаниях тела при тех же значениях параметров, что на рис. 5а. Максимальная амплитуда вертикальной силы при вертикальных колебаниях наблюдается при малых расстояниях от стенки, ${{x}_{0}} = 2$. На рис. 5в представлены зависимости от координаты $y$ амплитуды силы ${{F}_{z}}$ при вертикальных колебаниях с различными частотами $\omega = 0.75$, 1, 1.5 c^–1 и расстоянием от стенки ${{x}_{0}} = 2$. С увеличением частоты колебаний амплитуда силы увеличивается.

На рис. 6а показаны зависимости ${{F}_{x}}(y)$ при колебаниях тела по оси $Ox$ с частотой $\omega = 1$ с^–1 и расстояниями тела от стенки ${{x}_{0}} = 2$, 6, 10, 20 (кривые 1–4). Такой же характер зависимости амплитуды силы ${{F}_{x}}(y)$ наблюдается и при других частотах. На рис. 6б представлены зависимости ${{F}_{x}}(y)$ при колебаниях тела по оси Ox с частотами $\omega = 0.75$, 1, 1.5 с^–1 и расстоянием от стенки ${{x}_{0}} = 2$. С увеличением частоты амплитуда силы растет. На рис. 6в изображены графики зависимости от координаты $y$ амплитуды вертикальной силы при колебаниях тела по оси Ox с частотой $\omega = 1$ с^–1 и расстоянием от стенки ${{x}_{0}} = 2$, 4, 10, 20 (кривые 1–4). Максимальная амплитуда силы достигается при ${{x}_{0}} = 4$.

Рис. 6.

Зависимости от безразмерной координаты $y$ при колебаниях диполя по оси $Ox$ амплитуд горизонтальной силы ${{F}_{x}}$ (а, б) и вертикальной силы ${{F}_{z}}$ (в): (а) при $\omega = 1$ c^–1, x₀ = 2, 6, 10, 20 (кривые 1–4); (б) при x₀ = 2, $\omega = 0.75$, 1, 1.5 c^–1 (кривые 1–3); (в) при $\omega = 1$ c^–1, x₀ = 2, 4, 10, 20 (кривые 1–4).

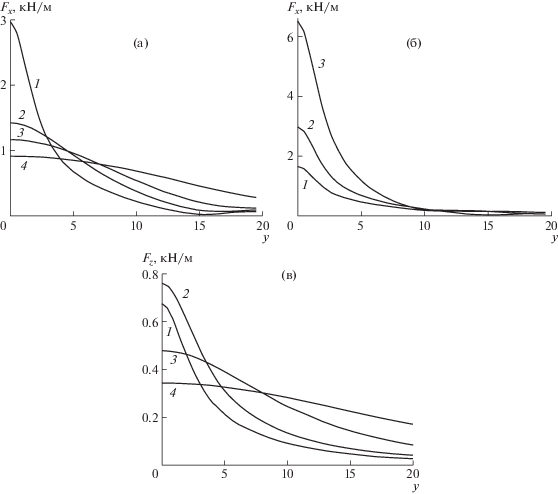
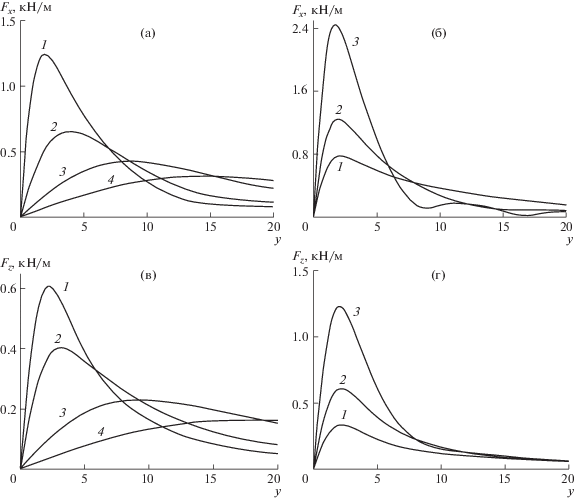
На рис. 7а, б показаны зависимости ${{F}_{x}}(y)$ и ${{F}_{z}}(y)$ амплитуд сил, действующих на стенку, при колебаниях тела по оси $Oy$ с частотой $\omega = 1$ с^–1 и расстоянием ${{x}_{0}} = 2$, 4, 10, 20 (кривые 1–4). Максимальные амплитуды сил достигаются при малых значениях параметра ${{x}_{0}}$ и не на оси Ox, а на некотором расстоянии от нее. На рис. 7в, г представлены зависимости от координаты $y$ амплитуд сил ${{F}_{x}}(y)$ и ${{F}_{z}}(y)$ при ${{x}_{0}} = 2$ и частотах $\omega = 0.75$, 1, 1.5 с^–1. Амплитуда сил растет с увеличением частоты.

Рис. 7.

Зависимости от безразмерной координаты $y$ при колебаниях диполя по оси $Oy$ амплитуд горизонтальной силы ${{F}_{x}}$ (а, б) и вертикальной силы ${{F}_{z}}$ (в, г): (а) при $\omega = 1$ c^–1, x₀ = 2, 4, 10, 20 (кривые 1–4); (б) при x₀ = 2, $\omega = 0.75$, 1, 1.5 c^–1 (кривые 1–3); (в) при $\omega = $1 c^–1, x₀ = 2, 4, 10, 20 (кривые 1–4); (г) при x₀ = 2, $\omega = 0.75$, 1, 1.5 c^–1 (кривые 1–3).

ЗАКЛЮЧЕНИЕ

Построено решение задачи о колебаниях тела, моделируемого диполем, в жидкости под ледяным покровом вблизи вертикальной стенки. Исследованы зависимости амплитуд прогиба ледяного покрова, вертикальных и горизонтальных сил, действующих на стенку, от частоты и расстояния тела от стенки. При вертикальных колебаниях тела максимальные амплитуды колебаний ледяного покрова наблюдаются вблизи точек, соответствующих среднему положению тела. При изменении расстояния тела от стенки амплитуда максимального прогиба ледяного покрова осциллирует относительно значения, соответствующего амплитуде колебаний под бесконечным ледяным покровом (без стенки). Амплитуды прогиба ледяного покрова и сил, действующих на стенку, растут с увеличением частоты колебаний. При больших расстояниях тела от стенки изолинии прогиба льда напоминают лепестки. Наибольшие амплитуды прогиба льда и вертикальной силы достигаются при вертикальных колебаниях тела. Наибольшие амплитуды горизонтальной силы, действующей на стенку, наблюдаются при колебаниях тела в перпендикулярном к стенке направлении и малых расстояниях от нее.

Автор выражает благодарность И.В. Стуровой за внимание к работе и полезное обсуждение результатов.

Список литературы

Sturova I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications // J. Fluid Mech. 2013. V. 730. P. 794–418. https://doi.org/10.1017/ jfm.2013.303
Das D., Mandal B.N. Water wave radiation by a sphere submerged in water with an ice-cover // Arch. Appl. Mech. 2008. V. 78. P. 649–661.
Das D., Mandal B.N. Wave radiation by a sphere submerged in a two-layer ocean with an ice-cover // Appl. Ocean Res. 2010. V. 32. P. 358–366.
Mohapatra S., Bora S.N. Radiation of water waves by a sphere in an ice-covered two-layer fluid of finite depth // J. Advanced Research in Appl. Mathem. 2010. V. 2. № 1. P. 46–63.
Стурова И.В. Движение погруженной сферы в жидкости под ледяным покровом // ПММ. 2012. Т. 76. Вып. 3. С. 406–417.
Das D., Thakur N. Water wave scattering by a sphere submerged in uniform finite depth water with an ice-cover // J. Mar. Struct. 2013. V. 30. P. 63–73.
Das D., Thakur N. Wave scattering by a sphere submerged in a two-layer fluid with an ice-cover // Int. J. Appl. Math. Eng. Sci. 2014. V. 8. P. 45–63.
Das L., Mohapatra S. Effects of flexible bottom on radiation of water waves by a sphere submerged beneath an ice-cover // Meccanica. 2019. V. 54. P. 985–999.
Савин А.А., Савин А.С. Пространственная задача о возмущении ледяного покрова движущимся в жидкости диполем // Изв. РАН. МЖГ. 2015. № 5. С. 16–23.
Ильичев А.Т., Савин А.С. Процесс установления системы плоских волн на ледовом покрове над диполем, равномерно движущимся в толще идеальной жидкости // Теор. и матем. физика. 2017. Т. 193. № 3. С. 455–465.
Погорелова А.В., Козин В.М., Земляк В.Л. Движение тонкого тела в жидкости под плавающей пластиной // ПМТФ. 2012. Т. 53. № 1. С. 32–43.
Pogorelova A.V., Zemlyak V.L., Kozin V.M. Moving of a submarine under an ice cover in fluid of finite depth // J. Hydrodynamics. 2018. https://doi.org/10.1007/s42241-018-0143-1
Thorne R.C. Multipole expansions in the theory of surface waves // Proc. Camb. Philos. Soc. 1953. V. 49. P. 707–716.
Ткачева Л.А. Колебания цилиндра в жидкости под ледяным покровом вблизи вертикальной стенки // Изв. РАН, МЖГ. 2020. № 3. С. 12–25.
Shishmarev K., Khabakhpasheva T., Korobkin A. Ice response to an underwater body moving in a frozen channel // Appl. Ocean Research. 2019. 91. 101877.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. М.: Гос. технико-теоретическое изд-во, 1955. 560 с.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Т. 1. Элементарные функции. М.: ФИЗМАТЛИТ, 2002. 632 с.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Т. 2. Специальные функции. М.: ФИЗМАТЛИТ, 2003. 664 с.
Ткачева Л.А. Пов едение полубесконечного ледяного покрова при периодическом динамическом воздействии // ПМТФ. 2017. Т. 58. № 4. С. 82–94.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал