Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 80-93

ЭВОЛЮЦИЯ ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ ПРИ ВЫТЕСНЕНИИ ВЯЗКИХ ЖИДКОСТЕЙ ИЗ ПОРИСТОЙ СРЕДЫ

Н. Н. Смирнов^a, b, В. Ф. Никитин^a, b, Е. И. Коленкина (Скрылева)^a, b, *, Д. Р. Газизова^a, b

^a Федеральный научный центр Научно-исследовательский институт системных исследований РАН
Москва, Россия

^b Московский государственный университет им. М.В. Ломоносова
Москва, Россия

^* E-mail: jennyne@yandex.ru

Поступила в редакцию 27.03.2020
После доработки 11.06.2020
Принята к публикации 21.06.2020

DOI: 10.31857/S0568528121010126

Полный текст (PDF)

Аннотация

Проведено численное моделирование процесса вытеснения вязкой жидкости из пористой среды с учетом капиллярных эффектов. В каждый момент времени рассчитывается площадь поверхности раздела фаз. Изучено влияние определяющих параметров на изменение площади поверхности раздела фаз. Описаны эксперименты по вытеснению нефти водой из неокомских песчаников. Экспериментальные данные сопоставлены с результатами численного моделирования.

Ключевые слова: вытеснение нефти, фильтрация, капиллярное давление, неустойчивость вытеснения вязкой жидкости, пористая среда

Процессы разработки и эксплуатации нефтяных, газовых и газоконденсатных месторождений тесно связаны с закономерностями просачивания углеводородов и воды в горных породах, которые образуют продуктивные пласты [1–3]. Поэтому свойства горных пород и пластовых флюидов предопределяют рациональную технологию разработки нефтяных и газовых месторождений и экономические показатели их извлечения из нефтяного пласта.

Результаты исследований, проведенных в данной работе, позволяют получить количественные параметры горных пород и характеристики процесса вытеснения, необходимые для описания коллекторов, их классификации, характеристики связей параметров для последующей интерпретации данных и построения моделей залежи [4, 5].

Основными параметрами, изучаемыми в керне нефтяных скважин, являются пористость, проницаемость горных пород, их минералогический и петрографический состав, а также начальное насыщение флюидами. Кроме того, важным фактором для планирования разработки нефтяного месторождения является оценка реакции модели пласта на различные воздействия с целью увеличения нефтеотдачи. Основным способом оценки конечного коэффициента извлечения нефти на месторождении является моделирование вытеснения нефти из нефтеносной породы, измерение коэффициента извлечения, абсолютной и относительной фазовой проницаемости. Для эффективной разработки нефтяных месторождений уже на стадии проектирования важно выбрать технологию, позволяющую извлекать максимальное количество нефти, содержащейся в пласте. В настоящее время в полевой практике для увеличения коэффициента извлечения нефти часто используется технология вытеснения нефти водой. Однако не всегда понятно, как оптимизировать эту технологию для получения максимального коэффициента извлечения нефти. Поэтому изучение процессов фильтрации на моделях пласта с целью выбора наиболее эффективных технологий и агентов вытеснения нефти для конкретных термобарических условий представляет несомненный научный и практический интерес.

Одна из технологий добычи жидких углеводородов заключается в вытеснении их из пористых пластов под воздействием градиента давления. Однако, когда более вязкая жидкость (нефть) вытесняется менее вязкой (вода), вытесняющая жидкость имеет тенденцию прорываться через слой вытесняемой жидкости, образуя в нем каналы, называемые “вязкими пальцами”. Результирующая нестабильность приводит к нарушению изначально плоской границы раздела и к прорыву отдельных пальцев вытесняющей жидкости.

В результате образования и роста водяных пальцев нефть может быть захвачена внутри пористого резервуара, что значительно снижает качество вытеснения и снижает добычу нефти – более половины углеводородов может оставаться в резервуаре. С развитием неустойчивости граница раздела жидкости искривляется, отдельные пальцы вытесняющей жидкости прорываются, и площадь границы раздела увеличивается.

Одним из наиболее эффективных методов изучения фильтрации является численный эксперимент; это намного дешевле и доступнее по сравнению с натурным экспериментом. Подготовка и проведение численного эксперимента требуют меньше времени, он легко воспроизводится и дает более полную информацию. С другой стороны, численное моделирование часто является единственной возможностью, поскольку уравнения, описывающие фильтрацию, в большинстве случаев не разрешимы аналитическими и приближенными методами. В результате возникает необходимость использования вычислительной техники.

Исследование неустойчивости рассматривалось во многих работах [3, 6–12]. Особенностью данной работы является количественная оценка развития неустойчивости. На каждом шаге по времени рассчитывается площадь поверхности раздела фаз и исследуется влияние различных параметров на изменение площади границы между вытесняемой и вытесняющей жидкостями.

Возможность расчета площади поверхности раздела фаз при трехмерном моделировании имеет большое прикладное значение. Во-первых, это позволит учесть мелкомасштабную неустойчивость, которая развивается на относительно небольших масштабах (несколько сантиметров): обычно процесс вытеснения моделируется на масштабе нефтяного месторождения (сотни метров), и когда используется крупная сетка, проблема оказывается подсеточной. В таких задачах расчет площади поверхности позволит охарактеризовать размер зоны смешения и учесть мелкомасштабную неустойчивость при перемасштабировании [9]. Во-вторых, площадь контакта важна в случае химических реакций во время добычи нефти, например, при использовании реагентов или термогазового метода [13]. Размер площади поверхности смешения является критическим параметром для точного моделирования такого вытеснения, так как влияет на интенсивность процесса.

1. МАТЕМАТИЧЕСКОЕ И ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Рассматривается вытеснение вязкой жидкости (нефти) из пористой среды менее вязкой жидкостью (водой). Область пористой среды, из которой вытесняется жидкость, имеет форму прямоугольного параллелепипеда (рис. 1). Первоначально почти вся область, за исключением небольшой части вблизи секции притока, заполнена вытесняемой жидкостью. Используется следующая система: ось Ox направлена вдоль области к секции оттока. Оси Oy и Oz размещены соответственно по вертикали и по горизонтали. Вытесняющая жидкость поступает через сечение x = 0, отток обеих жидкостей происходит через сечение x = L. В зависимости от режима работы программы на входе и выходе поддерживается постоянный перепад давления или расход. Боковые стенки считаются непроницаемыми. Капиллярные эффекты учитываются.

Рис. 1.

Расчетная область.

В любой момент времени рассчитывается насыщенность вытесняющей жидкости в каждой ячейке. Для визуализации динамики вытеснения и выделения границы двух сред выбирается некоторое значение для насыщенности s*. После чего считается, что граница проходит через те точки области, с одной стороны которых насыщенность больше чем заданное значение s*, а с другой стороны меньше чем s*. Эта поверхность – граница раздела.

Пористость и проницаемость неподвижного скелета зависят от пространственных координат. Вязкость каждой жидкости, поверхностное натяжение и угол смачивания считаются постоянными. Скорость жидкости достаточно мала. Обе жидкости несжимаемые и смешивающиеся. Температура постоянна. Межфазного массообмена нет.

В области решается следующая система уравнений.

Для каждой жидкости записывается закон сохранения массы

(1.1)

$\frac{{\partial \varphi {{s}_{k}}{{\varrho }_{k}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{j}}}}(\varphi {{s}_{k}}{{\varrho }_{k}}{{{v}}_{{k,j}}}) = 0$

Здесь φ – пористость, s – насыщенность, $\varrho $ – плотность (истинная), ${{{v}}_{{k,j}}}$ – j-я составляющая истинной скорости k-й фазы.

Скорость фильтрации ${{u}_{{k,j}}}$ выражается через истинную скорость ${{{v}}_{{k,j}}}$ фазы как

${{u}_{{k,j}}} = \varphi {{s}_{k}}{{{v}}_{{kj}}}$

Среднеобъемная скорость фильтрации жидкости определяется следующим образом

${{u}_{j}} = \mathop \sum \limits_k {{u}_{{kj}}}$

Суммирование уравнений (1.1) с учетом того, что жидкости несжимаемы и пористость не меняется со временем, приводит к

$\frac{{\partial {{u}_{j}}}}{{\partial {{x}_{j}}}} = 0$

Закон Дарси для каждой фазы

(1.2)

${{u}_{{k,j}}} = - \frac{{KK_{k}^{R}}}{{{{\mu }_{k}}}}\frac{{\partial {{p}_{k}}}}{{\partial {{x}_{j}}}}$

Здесь μ_k – вязкость фазы, ${{K}_{o}}$ – абсолютная проницаемость среды, $K_{k}^{R}$ – относительная проницаемость k-й фазы, p_k – внутрипоровое давление в фазе.

Моделирование относительных проницаемостей и капиллярного давления

Относительные проницаемости $K_{k}^{R}$ рассчитываются с использованием модели Брукса–Кори [14]

(1.3)

$K_{k}^{R} = \left\{ \begin{gathered} k_{k}^{0}S_{k}^{{n_{k}^{0}}},\quad {{s}_{k}} \geqslant s_{k}^{{res}} \hfill \\ 0,\quad {{s}_{k}} < s_{k}^{{res}} \hfill \\ \end{gathered} \right.,\quad {{S}_{k}} = \frac{{{{s}_{k}} - s_{k}^{{res}}}}{{1 - s_{1}^{{res}} - s_{2}^{{res}}}}$

Здесь $k_{k}^{0} > 0$ и $n_{k}^{0} > 0$ – параметры модели, приведенные же насыщенности S_k определяются остаточными насыщенностями $0 \leqslant s_{k}^{{res}} \leqslant 1$ ($s_{1}^{{res}} + s_{2}^{{res}} < 1$). Следует заметить, что при 0 ≤ S_k ≤ 1 моделируется пористая среда, пропитанная обоими флюидами; насыщение среды фазой при s_k ≤ $s_{k}^{{res}}$ этой моделью не описывается. Далее полагается, что пропитка обоими флюидами имела место, и в этих условиях можно не учитывать нулевую альтернативу (1.3). Отметим также, что ${{S}_{2}} = 1 - {{S}_{1}}$, и тем самым индекс “1” будем опускать далее и у приведенной насыщенности, выражая приведенную насыщенность второй фазы через первую. Для приведенной насыщенности и относительных мобильностей фаз ${{M}_{k}} = \frac{{K_{k}^{R}}}{{{{\mu }_{k}}}}$ мы имеем следующие выражения:

$\left\{ \begin{gathered} S = \frac{{s - s_{k}^{{res}}}}{{1 - s_{1}^{{res}} - s_{2}^{{res}}}} \hfill \\ {{M}_{1}} = \frac{{k_{1}^{0}}}{{{{\mu }_{1}}}}{{S}^{{n_{1}^{0}}}} \hfill \\ {{M}_{2}} = \frac{{k_{2}^{0}}}{{{{\mu }_{2}}}}{{\left( {1 - S} \right)}^{{n_{2}^{0}}}} \hfill \\ \end{gathered} \right.$

Локально разность давлений фаз выражается через капиллярное давление ${{p}^{c}}$:

(1.4)

${{p}_{2}} - {\text{\;}}{{p}_{1}} = {{p}^{c}}\left( s \right)~$

Определим среднее давление p по аналогии со средней плотностью и скоростью фильтрации. Для этого введем дополнительную поправку к давлению ξ(s) так, чтобы (1.4) было эквивалентно следующей факторизации

$\left\{ {\begin{array}{*{20}{c}} {{{p}_{1}} = p + \xi \left( s \right) - {{p}^{c}}\left( s \right){\text{/}}2,} \\ {{{p}_{2}} = p + \xi \left( s \right) + {{p}^{c}}\left( s \right){\text{/}}2} \end{array}} \right.$

Функцию ξ(s) определим так, чтобы закон Дарси для скорости фильтрации жидкости после суммирования уравнений (1.2) не зависел явно от ξ(s) и p^c(s) и имел вид:

${{u}_{j}} = - K\left( {{{M}_{1}} + {{M}_{2}}} \right)\frac{{\partial p}}{{\partial {{x}_{j}}}}$

Для этого необходимо выполнение следующего соотношения

$\frac{{d\xi }}{{ds}} = \frac{1}{2}\frac{{{{M}_{1}} - {{M}_{2}}}}{{{{M}_{1}} + {{M}_{2}}}}\frac{{d{{p}^{c}}}}{{ds}}$

Уравнение для динамики насыщенности получим из (1.1) с учетом введенных обозначений:

(1.5)

$\varphi \frac{{\partial s}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{{{M}_{1}}}}{{{{M}_{1}} + {{M}_{2}}}}} \right) = \frac{\partial }{{\partial {{x}_{j}}}}\left( {D\frac{{\partial s}}{{\partial {{x}_{j}}}}} \right)$

Коэффициент D выражается как

$D = - K\frac{{{{M}_{1}}{{M}_{2}}}}{{{{M}_{1}} + {{M}_{2}}}}\frac{{d{{p}^{c}}}}{{ds}}$

и играет роль коэффициента диффузии в уравнении (1.5), хотя физической диффузии в среде не происходит. Этот термин характеризует величину отклонения скорости фазы от среднеобъемной скорости фаз.

Капиллярное давление выражается через J-функцию Леверетта [1] и другие параметры следующим образом

${{p}^{c}} = {{C}_{J}}\frac{{\sigma \left| {{\text{cos}}\theta } \right|}}{{\sqrt {K/\phi } }} \cdot \left\{ \begin{gathered} {{S}^{{ - {{a}_{J}}}}},\quad \alpha \leqslant \pi {\text{/}}2 \hfill \\ {{\left( {1 - S} \right)}^{{ - {{a}_{J}}}}}{\text{,}}~\quad \alpha > \pi {\text{/}}2 \hfill \\ \end{gathered} \right.$

где ${\sigma }$ – поверхностное натяжение, а ${\theta }$ – угол смачивания.

Константы ${{C}_{J}}$ и ${{a}_{J}}$ в модели Леверетта могут быть определены с использованием экспериментальных данных [11].

Выражение для коэффициента диффузии D с учетом модели Леверетта имеет вид

$D = \frac{{{{a}_{J}}{{C}_{J}}\sigma \left| {\cos \alpha } \right|\sqrt {K\varphi } }}{{1 - s_{1}^{{res}} - s_{2}^{{res}}}} \cdot \frac{{{{M}_{1}}{{M}_{2}}}}{{{{M}_{1}} + {{M}_{2}}}} \cdot \left\{ \begin{gathered} {{S}^{{ - {{a}_{J}} - 1}}},\quad \alpha \leqslant \pi {\text{/}}2 \hfill \\ {{\left( {1 - S} \right)}^{{ - {{a}_{J}} - 1}}},\quad \alpha > \pi {\text{/}}2 \hfill \\ \end{gathered} \right.{\text{\;}}$

Граничные условия

На поверхности, через которую осуществляется приток жидкости (z = 0), задаются давление $p = {{p}_{{in}}}$ и максимальная насыщенность вытесняющей жидкости $s = 1 - s_{2}^{{res}}$. Под давлением здесь и далее понимается перепад между реальным давлением в порах и давлением на выходе.

На поверхности стока задается нулевое значение давления и нулевая нормальная производная насыщенности.

На непроницаемых стенках нормальные компоненты фазовых скоростей обнуляются, ${{u}_{{kn}}} = 0$, что соответствует нулевым нормальным производным давления и насыщенности.

Описание численного алгоритма

Для решения задачи, т.е. для вычисления набора переменных на новом временном слое, используется следующая последовательность процедур.

0. До каждого временного шага поле давления p и поле насыщенности s известны. Оба поля определяются на однородной кубической сетке в центрах ячеек. Поля ${{u}_{{kj}}}$ известны для обеих фаз, и они определяются на гранях ячеек. Каждая компонента вектора скорости определяется в центре грани с нормалью, соответствующей компоненте.

1. Рассчитываются массивы мобильности фаз M_k(s) и коэффициента диффузии D(s), доли мобильности и ее производная по s. Все эти массивы вычисляются с использованием алгебраических выражений в центрах ячеек; производная рассчитывается с использованием конечных разностей.

2. С использованием давления и мобильности в центрах ячеек вычисляется поле скоростей u_j на соответствующих гранях ячеек с применением подхода конечных разностей и арифметического усреднения; затем это поле проецируется на центры ячеек с использованием арифметического усреднения. На гранях, соответствующих стенкам, используется граничное условие непроницаемости.

3. Уравнение (1.5) представляется в следующей конечно-разностной форме при аппроксимации пространственных производных насыщенности схемой типа “крест”

$\frac{{\partial {{s}_{i}}}}{{\partial t}} = \mathop \sum \limits_k {{\lambda }_{{ik}}}\left( {{{s}_{k}} - {{s}_{i}}} \right) + {{\lambda }_{{i0}}}{{s}_{i}}$

После этого схема стабилизируется добавлением искусственной диффузии к ее коэффициентам, а второй порядок точности достигается вычитанием искусственной антидиффузии. Как диффузия, так и антидиффузия рассчитываются с использованием методов [15].

4. С использованием обновленных коэффициентов ${{{\lambda }}_{{ik}}}$, оценивается значение шага по времени

${\Delta }t = \frac{C}{{\max \sum\limits_k^{} {{\text{|}}{{\lambda }_{{ik}}}{\text{|}}} }}$

Это выражение обобщает критерий Куранта, который выполняется при C = 1. Значение множителя C вводится в качестве параметра расчета.

5. Вычисляется поле насыщенности на следующем шаге. Используются неявная численная схема и метод Bi-CGStab для решения системы линейных уравнений, относящихся к этой схеме.

6. Повторяется пункт 1 для следующего временного шага, т.е. рассчитываются обновленная мобильность, доли мобильности и ее производная.

7. Рассчитывается давление на новом временном шаге с использованием схемы “крест” для дискретизации; коэффициенты схемы взяты на новом временном шаге, а правая часть была вычислена ранее. На внешних стенках ставятся граничные условия непроницаемости, что приводит к условию нулевой нормальной производной. В случае использования размещения давления в центрах ячеек это условие очень простое: в схему не включаются члены с несуществующими ячейками. Для решения системы используется метод Bi-CGStab.

Этот алгоритм обрабатывается за один шаг времени; значение величины шага по времени вычисляется внутри тела метода. После выполнения шага значение времени обновляется.

2. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТОВ ПО ВЫТЕСНЕНИЮ ИЗ ОБРАЗЦА КЕРНА МОДЕЛИ НЕФТИ

На установке ПЛАСТ.АТМ-10 (рис. 2) было проведено 4 эксперимента. Для серии экспериментов был использован составной образец длиной 0.1 м из керна скважины 72 Туканской площади пласта БС-8. В качестве модели нефти поочередно выбирались 2 жидкости: керосин осветительный ТУ 38–401–58–10–01 и гидравлическое масло ВМГ 3 ТУ 0253–085–04001396–04. Вытесняющей жидкостью была выбрана дистиллированная вода.

Рис. 2.

Установка ПЛАСТ.АТМ-10 для проведения экспериментов по вытеснению вязкой жидкости из образца пористой среды.

В процессе подготовки жидкостей керосин был профильтрован через силикагель, дегазирован при комнатной температуре в вакуумизаторе при абсолютном давлении 60 мБар; масло дегазировано при комнатной температуре в вакуумизаторе при абсолютном давлении 15 мБар. Для всех жидкостей были измерены плотность и кинематическая вязкость. Результаты приведены в табл. 1.

Таблица 1.

Результаты исследования жидкостей

	Плотность, г/см³	Кинематическая вязкость, мм²/с	Динамическая вязкость, мПа ⋅ c
Вода	0.998	0.884	0.882
Модель нефти (керосин)	0.783	1.246	0.976
Модель нефти (масло)	0.855	28.181	24.095

Образец керна был составлен из трех цилиндрических образцов. Образцы были высушены до постоянной массы, измерена абсолютная проницаемость каждого образца по сжатому воздуху. Затем образцы керна были насыщены подготовленным керосином в вакууме. Измерены пористость и объем пор для каждого образца в отдельности (табл. 2).

Таблица 2.

Результаты исследования кернового материала

№ образца	Диаметр/длина, см	Абсолютная газопроницаемость, мД	Открытая пористость, %	Объем открытых пор, см³
1	3.00/3.61	652	23.0	5.82
2	3.00/3.61	510	22.1	5.62
3	3.00/3.61	463	21.3	5.39

Образцы керна находились в сосуде с жидкостью, моделирующей нефть, до помещения в кернодержатель.

Составной образец помещался в кернодержатель установки моделирования вытеснения жидкостей из керна ПЛАСТ.АТМ-10. Образцы керна устанавливались в порядке уменьшения их абсолютной проницаемости. Создано давление обжима в 4 МПа. Через керн прокачана модель нефти для удаления пузырьков воздуха до установления стабильных показаний перепада давления на входе и выходе кернодержателя.

Затем производилось вытеснение модели нефти из керна подачей воды во вход кернодержателя. В экспериментах 1 и 2 вода подавалась с поддержанием постоянного расхода; в экспериментах 3 и 4 – с поддержанием постоянного перепада давления порядка 0.5 атм.

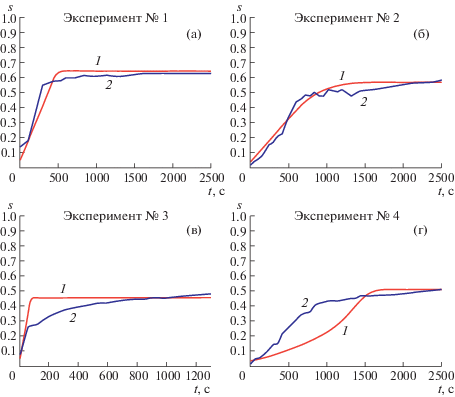
Жидкость на выходе из кернодержателя поступала в бюретку для сбора легкой фракции с отводом воды. Объем порового пространства, который изначально был заполнен моделью нефти, после вытеснения этой нефти оказался заполнен водой. Таким образом, считалось, что объем пор, занятых водой, равен объему вытесненной на данный момент нефти (${{V}_{{oil}}}$), собранной в бюретке. Насыщенность вытесняющей жидкости в образце рассчитывалась как $s = {{V}_{{oil}}}{\text{/}}{{V}_{{pore}}}$, где ${{V}_{{pore}}}{\text{\;}}$ – объем доступных пор. Погрешность определения объема по бюретке составляет 0.2 мл для керосина и 0.5 мл для масла (в связи с образованием водно-масляной эмульсии на месте мениска). Динамика вытеснения на основе расчета водонасыщенности в образце приведена на рис. 3.

Рис. 3.

Сравнение данных экспериментов (1–4, табл. 3) по вытеснению жидкости из образца керна с результатами численного моделирования: 1 – численный расчет; 2 – эксперимент.

После окончания процесса вытеснения для каждой из частей (ч1, ч2, ч3) составного образца раздельно измерена остаточная водонасыщенность.

Параметры всех экспериментов представлены в табл. 3.

Таблица 3.

Параметры экспериментов

Эксп. №	Модель нефти	Условие на входе	Объем воды измеренный (ч1/ч2/ч3), мл	Объем нефти рассчитанный (ч1/ч2/ч3), мл	Водонасы-щенность (ч1/ч2/ч3), %	Нефтенасы-щенность (ч1/ч2/ч3), %
1	Керосин	Постоянный расход	3.65/3.14/3.2	1.16/1.61/1.30	62.7/55.9/59.4	19.9/28.6/24.2
2	Масло	Постоянный расход	2.9/2.62/2.5	2.13/2.28/2.20	49.8/46.6/46.4	36.5/40.5/40.8
3	Керосин	Постоянный перепад давления	3.14/2.5/3.1	1.70/2.34/1.43	55.0/45.2/57.5	29.7/42.3/26.5
4	Масло	Постоянный перепад давления	2.5/1.8/1.94	2.88/3.50/3.30	43.1/32.1/34.8	49.6/62.4/59.3

На рис. 3 представлено сравнение динамики вытеснения в эксперименте и в численном расчете. Видно, что результаты численного моделирования хорошо согласуются с экспериментальными данными для экспериментов 1 и 2 (постоянный расход) и удовлетворительно согласуются с экспериментальными данными в случае экспериментов 3, 4 (постоянный перепад давления). Различие между расчетом и экспериментом можно объяснить тем, что образец керна является неоднородным: во-первых, в нем присутствует естественная неоднородность проницаемости, во-вторых, искусственная неоднородность – наличие стыков между составными частями. В расчете наличие таких неоднородностей не учитывалось. Эти эффекты проявляются только в случае постоянного перепада давления, так как неоднородности керна существенно влияют на расход жидкости. Когда задан постоянный расход, эти эффекты себя так сильно не проявляют.

Здесь эмпирические константы в модели Леверетта выбраны так, чтобы остаточная насыщенность и скорость вытеснения в расчете были как можно ближе к экспериментальному результату. Такой подбор коэффициентов подробно описан в работе [11]. Таким образом, показано, что определение некоторых реологических соотношений для учета влияния капиллярных сил в пористой среде возможно путем обработки результатов таких экспериментов.

На рис. 4а представлено изменение формы поверхности раздела жидкостей в численном расчете для случая вытеснения керосина из воды при постоянном расходе (эксперимент 1). Для эксперимента 3 картина аналогична: отношение вязкости жидкостей близко к 1, поэтому граница раздела в любой момент времени остается плоской (идеальный случай вытеснения возможный в теории, но никогда не реализующийся на практике). Рисунки 4б и 4в соответствуют экспериментам 2 и 4 соответственно. В этих случаях наблюдается неустойчивость, развивающаяся на фронте вытеснения.

Рис. 4.

Форма поверхности раздела жидкостей при численном моделировании.

3. РАСЧЕТ ПЛОЩАДИ ПОВЕРХНОСТИ РАЗДЕЛА ЖИДКОСТЕЙ

Граница раздела между двумя фазами не выделяется явно в процессе расчета. Значение насыщенности вытесняемой жидкости оценивается в каждом вычислительном узле (центре ячейки); поэтому за границу раздела принимается такая поверхность, с одной стороны от которой значение насыщенности больше некоторого заданного s*, а на другой стороне меньше. Ниже приведен способ расчета площади такой поверхности.

Требуется найти площадь поверхности, разделяющей область данных $s(\overrightarrow {x)} $ при помощи уравнения

${\Sigma } = \{ \vec {x}:~~s\left( {\vec {x}} \right) = s{\text{*}}\} ,\quad {{{\Sigma }}^{ + }} = \{ \vec {x}:~~s\left( {\vec {x}} \right) \geqslant s{\text{*}}\} .$

Здесь Σ – поверхность, площадь которой требуется определить, Σ⁺ – одна из областей, отделяемая этой поверхностью.

Исходим из того, что данные $s\left( {\vec {x}} \right)$ определены в центрах кубических ячеек так, что известны их целочисленные координаты

${{s}_{m}} = s\left( {\vec {x}} \right),\quad m = M\left( {\vec {n}} \right),$

где m – номер ячейки, $M(\vec {n})$ – взаимно-однозначный перевод целочисленных координат в целое число.

Каждая кубическая ячейка m имеет 8 вершин; в каждой из которых данные можно определить интерполяцией. В ином варианте распределения данных они изначально заданы в вершинах ячеек, ячейки же определенным образом группируют данные. Поскольку сетка кубическая, связь между координатами центров ячеек и целочисленными координатами данных в этих центрах такова

$\overrightarrow {{{x}_{m}}} = \left( {\overrightarrow {{{n}_{m}}} + \frac{1}{2}} \right)h - \overrightarrow {{{x}_{c}}.} $

Здесь h – размер ячейки, а $\overrightarrow {{{x}_{{\text{с}}}}} $ – смещение системы координат.

3.1. Предлагаемое решение

Инициализируем площадь поверхности |Σ| нулем. Обходим все ячейки домена, и для каждой ячейки m определяем число t_m выполнений условия

$\overrightarrow {{{x}_{{mj}}}} \in {{{\Sigma }}^{ + }},\quad j = 0,..,7$

где j – индекс вершины ячейки. Для расчета этого условия либо требуется интерполировать данные в вершину, либо напрямую использовать сами данные, если они заданы в вершинах. При расчете интерполяции удобно воспользоваться соотношением

${{x}_{{mji}}} = \left\{ {\begin{array}{*{20}{c}} {{{x}_{{mi}}} + \frac{h}{2},\quad {{j}_{i}} = 1,} \\ {{{x}_{{mi}}} - \frac{h}{2},\quad {{j}_{i}} = 0.} \end{array}} \right.$

Здесь ${{j}_{i}}{\text{\;}}$ – i-я двоичная цифра индекса j, i = 0, 1, 2.

Сама площадь определяется формулой

$\left| {\Sigma } \right| = \mathop \sum \limits_m W\left( {{{\delta }_{m}}} \right){{h}^{2}},$

где W(δ)-весовая функция, зависящая от целого числа δ = 0, 1, …, 7, 8. Физический смысл весовой функции – среднее значение площади поверхности, отсекающей t вершин кубической ячейки, деленная на площадь грани ячейки. Функция безразмерна.

Функцию W(δ) можно определить калибровкой на известных фигурах. Одно из ее свойств – симметрия, а также нулевые значения при δ = 0 и δ = 8. Симметрия проявляется в том, что

$W\left( {8 - \delta } \right) = W\left( \delta \right)$

Кроме того, логично, чтобы от ${\delta }$ = 1 до ${\delta }$ = 4 функция была положительной и возрастающей. Вследствие симметрии и нулевых значений $W\left( {\delta } \right)$ на краях диапазона, можно ограничиться набором независимых величин ${{w}_{k}},{\text{\;\;}}k = 0,{\text{\;}}1,{\text{\;}}2,{\text{\;}}3$ таких, что

$W\left( \delta \right) = \left\{ \begin{gathered} {{w}_{{\delta - 1}}},\quad 1 \leqslant \delta \leqslant 4, \hfill \\ {{w}_{{8 - \delta - 1{\text{\;}}}}},\quad 4 \leqslant \delta \leqslant 7, \hfill \\ 0,\quad \delta = 0,\quad \delta = 8. \hfill \\ \end{gathered} \right.$

3.2. Определение весовых коэффициентов

На основе случайных параметров строится N_t калибровочных тел, поверхность которых вложена в заданный домен, разбитый на кубы. По параметрам тел определяются истинные площади их поверхности A_n, $n = 0, \ldots ,{{N}_{t}} - 1.$ Далее для каждого теста n рассчитываются параметры

${{a}_{{nj}}} = \mathop \sum \limits_{m:{\text{\;}}{{\delta }_{m}} = j} {{\delta }_{m}}{{h}^{2}}.$

Пользуясь симметрией W(t) и игнорируя ее крайние значения, переходим к 4 независимым параметрам ${{b}_{{nj}}}$

${{b}_{{n,j - 1}}} = {{a}_{{n,j}}} + {{a}_{{n,8 - j}}},\quad j = 1, \ldots ,3;\quad {{b}_{{n,3}}} = {{a}_{{n,4}}}{\text{\;}}$

Требуется решить систему линейных уравнений

$\mathop \sum \limits_{j = 0}^3 {{b}_{{nj}}}{{w}_{j}} = {{A}_{n}}$

но при достаточно большом числе тестов это будет переопределенная система, решений не имеющая. Ее можно решить в смысле минимально возможного приближения по норме L2 (методом минимальных квадратов), для чего левую и правую части системы умножают на транспозицию матрицы ${{b}_{{nj}}}$

$\mathop \sum \limits_{j = 0}^3 {{B}_{{ij}}}{{w}_{j}} = {{C}_{i}},\quad i = 0, \ldots ,3;\quad {{B}_{{ij}}} = \mathop \sum \limits_{n = 0}^{{{N}_{{t{\text{\;}}}}} - 1} {{b}_{{ni}}}{{b}_{{nj}}},\quad {{C}_{i}} = \mathop \sum \limits_{n = 0}^{{{N}_{t}} - 1} {{b}_{{ni}}}{{A}_{n}}$

Линейная система имеет положительно определенную симметричную матрицу, если только число тестов не меньше 4, и не было набора одинаковых матричных коэффициентов ${{b}_{{nj}}}$ в двух или более различных тестах. Ее решение (например, методом Холецкого) дает систему весовых коэффициентов, минимизирующую отклонение расчетной площади поверхности от истинной для указанных тестов в смысле нормы L2.

3.3. Результаты для весовых коэффициентов

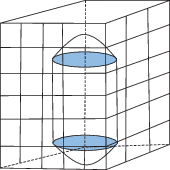
В качестве тестовых фигур брались модифицированные цилиндры высотой H и радиусом R, у которых плоские торцы заменены полушариями радиуса R (рис. 5).

Рис. 5.

Модифицированный цилиндр, помещенный в расчетную область.

Площадь поверхности такого модифицированного цилиндра равна

$A = 4\pi {{R}^{2}} + 2\pi RH.$

При $H = 0$ такой модифицированный цилиндр переходит в сферу.

Параметры R, H брались случайно с равномерным распределением

${{R}_{{min}}} \leqslant R \leqslant {{R}_{{max}}},{\text{\;\;}}{{H}_{{min}}} \leqslant H \leqslant {{H}_{{max}}}{\text{\;}}$

и смещением центра относительно начала координат в пределах куба:

$0 \leqslant \left| {{{x}_{{ci}}}} \right| \leqslant {{x}_{{max}}}$

Также цилиндрическое тело случайным образом располагалось в пространстве. Чтобы обеспечить равномерность распределения ориентации, использован подход случайного нормализованного кватерниона ориентации [16].

После расчетов весовых коэффициентов на основе площадей модифицированных цилиндров получены следующие результаты, с точностью до 10 десятичных знаков – табл. 4. Во второй колонке приведены данные без учета произвольной ориентации, в третьей – с учетом.

Таблица 4.

Результаты для весовых коэффициентов

t	W(δ)	W(δ) (поворот)
0	0	0
1	0.3260309507	0.4229994152
2	0.6234070489	0.6475331995
3	0.8802570752	0.7276973698
4	1.0140847622	0.9798320716
5	0.8802570752	0.7276973698
6	0.6234070489	0.6475331995
7	0.3260309507	0.4229994152
8	0	0

Результаты получены на сетке 200 × 200 × 200 с размером ячейки h = 0.01; число тестов ${{N}_{t}} = 50.$ Точность расчета площади поверхности по норме L2, проверенная на таких же фигурах (при ином их случайном расположении), оценена в 8.255 × 10^–6 без поворота, 1.96 × 10^–5 с поворотом.

4. ИССЛЕДОВАНИЕ ЭВОЛЮЦИИ ПЛОЩАДИ ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ

Описанный выше метод расчета площади поверхности позволяет количественно охарактеризовать развитие неустойчивости и изучить влияние на этот процесс различных параметров. Следует отметить, что точность такого алгоритма зависит от разрешения сетки: любая поверхность на уровне одной ячейки всегда может быть аппроксимирована цилиндром или полушарием. Чем мельче сетка, тем выше точность такого приближения.

Все представленные ниже графики показывают отношение площади поверхности раздела фаз к площади поперечного сечения керна, из которого происходит вытеснение. Далее это отношение называется безразмерной площадью поверхности раздела (Ω).

Граница раздела фаз была рассчитана для численного моделирования с параметрами, соответствующими экспериментам 1–4. Результаты представлены на рис. 6.

Рис. 6.

Эволюция безразмерной площади поверхности раздела фаз для численных расчетов, соответствующих экспериментам 1–4 (табл. 3): а–г – эксперименты 1–4.

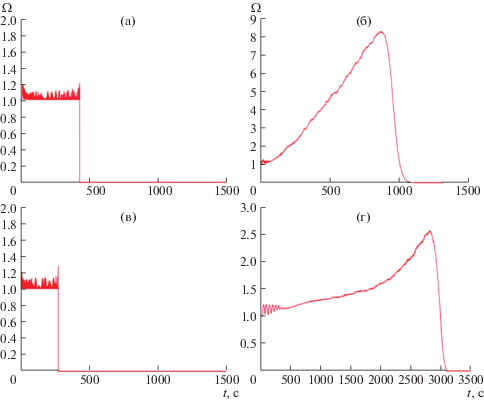
Теоретически, когда отношение вязкостей вытесняемой и вытесняющей жидкости меньше или равно 1, вытеснение имеет поршневой характер – фазовая граница раздела все время остается плоской, и неустойчивость не развивается, несмотря на возникающие флуктуации. На практике такой случай никогда не реализуется, поскольку условия эксперимента не идеальны, среды не однородны и т.д. Эволюция изменения площади раздела фаз для экспериментов 1 и 3 показана на рис. 6а и 6в соответственно. В случае, когда отношение вязкости около 1 (керосин–вода), вытеснение близко к поршневому (рис. 4а). Площадь поверхности колеблется вблизи значения 1. Неустойчивость не развивается, и случайные отклонения поверхности от плоской формы подавляются стабилизирующими факторами, такими как капиллярные эффекты. Когда поверхность достигает границы вычислительной области, значение площади резко падает до нуля.

Эволюция площади раздела фаз для экспериментов 2 и 4 показана на рис. 6б и 6г соответственно. В случае, когда коэффициент вязкости большой (масло–вода), имеет место развитие неустойчивости. Площадь поверхности в начале резко увеличивается, пока первый вязкий палец воды не пробьет поверхность выхода. Кроме того, жидкость движется в основном в образованном канале, и значение площади постепенно уменьшается и достигает постоянного значения после полного вытеснения.

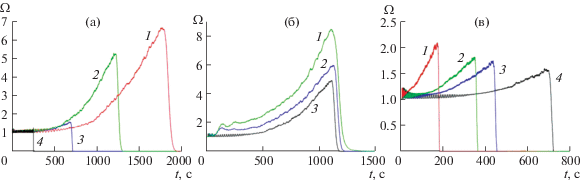
Также исследовалось влияние следующих параметров на эволюцию границы раздела фаз: отношение вязкостей вытесняемой и вытесняющей жидкостей; число Пекле; перепад давления на входе и выходе образца пористой среды, рис. 7.

Рис. 7.

Эволюция безразмерной площади поверхности раздела фаз для расчетов с различными значениями: а – отношения вязкостей вытесняемой и вытесняющей жидкостей $M = {{\mu }_{2}}{\text{/}}{{\mu }_{1}}$(1 – M = 15; 2 – M = 10; 3 – M = 5; 4 – M = 1); б – числа Пекле (1 – Pe = 600; 2 – Pe = 300; 3 – Pe = 30); в – перепада давления на входе и выходе образца пористой среды(1 – ΔP = 2 атм; 2 – ΔP = 1 атм; 3 – ΔP = 0.8 атм; 4 – ΔP = 0.5 атм).

Для вычисления числа Пекле использовалось выражение: ${\text{Pe}} = L{v}{\text{/}}{{D}_{0}}$, где L – характерный размер, ${v} = \frac{K}{{{{\mu }_{1}}}}\frac{{\Delta P}}{L}{\text{\;\;}}$ – скорость, ${{D}_{0}} = \frac{{{{a}_{J}}{{C}_{J}}\sigma \left| {{\text{cos}}\theta } \right|\sqrt {K\phi } {\text{\;}}}}{{{{s}_{{max}}} - {{s}_{{min}}}}} \cdot \frac{1}{{{{\mu }_{1}}}}$ – коэффициент диффузии, пропорциональный D.

Таким образом, ${\text{Pe}} = \frac{{\left( {{{s}_{{max}}} - {{s}_{{min}}}} \right)}}{{{{a}_{J}}{{C}_{J}}\sigma \left| {{\text{cos}}\theta } \right|}}\sqrt {\frac{K}{\phi }} \Delta P$.

Согласно результатам расчетов, с увеличением отношения вязкостей вытесняемой и вытесняющей жидкостей неустойчивость фронта вытеснения развивается сильнее, в то время как скорость фронта уменьшается, а время полного вытеснения увеличивается (рис. 7а).

Число Пекле характеризует связь между конвективными и молекулярными процессами. Как и ожидалось, результаты расчетов показали, что с увеличением числа Пекле неустойчивость фронта увеличивается, а время полного вытеснения существенно не изменяется (рис. 7б).

С увеличением перепада давления на на входе и выходе образца пористой среды развитие неустойчивости усиливается, а время полного вытеснения нефти из образца уменьшается (рис. 7в).

ЗАКЛЮЧЕНИЕ

Исследовано вытеснение вязкой жидкости из образца песчаника Неокомского нефтегазоносного комплекса, который является одним из основных источников углеводородов для Западносибирской нефтегазоносной провинции. Экспериментальные исследования показали, что заводнение керна с более вязкой жидкостью, моделирующей нефть, отличается меньшим извлечением углеводорода. Стационарный режим фильтрации (с постоянным расходом) приводит к более равномерному и более полному извлечению углеводородов. Также показано, что в случае, когда фильтрация происходит при постоянном перепаде давления, большое влияние на динамику вытеснения оказывают естественные и искусственные неоднородности в образце керна.

В результате сравнительного анализа экспериментальных данных получены уникальные возможности для определения неизвестных параметров модели, а именно капиллярных характеристик горных пород и насыщающих жидкостей. На основании экспериментальных данных определены коэффициенты в математических моделях и исследовано развитие фронта вытеснения для различных параметров.

Предложен новый метод подсчета площади изоповерхностей. Для корректной оценки площади необходимо использовать весовые коэффициенты, которые получены и приведены в данной работе. Данный метод можно применять для расчета площади нерегулярных межфазовых поверхностей при моделировании неустойчивого вытеснения из пористой среды. Проведен анализ эволюции поверхности раздела фаз для расчетов с различными определяющими параметрами, в том числе для расчетов соответствующим экспериментам.

Показано, что в случае, когда отношение вязкостей жидкостей около 1, вытеснение близко к поршневому. Неустойчивость в этом не развивается, случайные отклонения от плоской формы сглаживаются стабилизирующими факторами. В случае, когда отношение вязкостей больше 1, развивается неустойчивость и площадь поверхности раздела жидкостей увеличивается, затем, достигнув некоторого максимального значения (прорыв первого “вязкого пальца”), резко падает. Выявлено, что чем выше значение отношения вязкостей, тем большего значения достигает площадь раздела фаз. Также показано, что неустойчивость фронта возрастает с ростом числа Пекле и для фильтрации при постоянном перепаде давления, чем выше перепад давления, тем сильнее развивается неустойчивость, а фронт доходит до границы быстрее.

Работы, выполненные в МГУ им. М.В. Ломоносова, были поддержаны грантом РФФИ № 20-07-00378.

Список литературы

Баренблатт Г.И., Ентов В.М., Рыжик В.М. Теория нестационарной фильтрации жидкости и газа. М.: Недра, 1972. 288 с.
Kaviany M. Principles of heat transfer in porous media. NY: Dover Publications Inc., 1988. 626 p.
Nield D.A., Bejan A. Convection in Porous Media. NY: Springer-Verlag, 1992. 654 p.
Bear J., Bachmat Y. Introduction to Modelling of Transport Phenomena in Porous Media. M.: Kluwer Academic Publishers-Dordrecht, Boston, London, 1990. 554 p.
Andersen M.A., Duncan B., McLean R. Core Truth in Formation Evaluation // Oilfield Rewiew. 2013. V. 25. № 2. P. 16–25.
Smirnov N.N., Nikitin V.F., Dushin V.R., Phylippov Yu.G., Nerchenko V.A. Three-dimensional convection and unstable displacement of viscous fluids from strongly encumbered space // Acta Astronautica. 2010. V. 66. № 5. P. 844–863.
Logvinov O.A., Skryleva E.I. Displacement of a Viscous Fluid from a Hele-Shaw Cell with a Sink // Moscow University Mechanics Bulletin. 2016. = Логвинов О.А., Скрылева Е.И. Вытеснение вязкой жидкости из кольцеобразной ячейки Хеле-Шоу со стоком // Вестник Московского университета. Серия 1: Математика. Механика. 2016. № 4. С. 39–43.https://doi.org/10.3103/S0027133016040014
Никитин В.Ф., Смирнов Н.Н., Душин В.Р. Неустойчивое вытеснение жидкости из пористой среды с переменной проницаемостью // Вестник Московского университета. Серия 1: Математика. Механика. 2006. № 2. С. 33–40.
Smirnov N.N., Nikitin V.F., Maximenko A., Thiercelin M., Legros J.C. Instability and mixing flux in frontal displacement of viscous fluids from porous media // Physics of Fluids. 2005. V. 17. № 8. https://doi.org/10.1063/1.1990227
Smirnov N.N., Nikitin V.F., Skryleva E.I. Microgravity Investigation of Seepage Flows in Porous Media // Microgravity Science and Technology. 2019. V. 31. № 5. P. 629–639. https://doi.org/10.1007/s12217-019-09733-7
Козлов И.В., Скрылева Е.И. Математическое моделирование и обработка эксперимента по вытеснению нефти водой из неокомских песчаников // Вестник кибернетики. 2016. № 2. С. 138–145.
Dushin V.R., Nikitin V.F., Smirnov N.N., Skryleva E.I., Tyurenkova V.V. Microgravity Investigation of Capillary Driven Imbibition // Microgravity Science and Technology. 2018. V. 30. № 4. P. 393–398.
Вольпин С.Г., Саитгареев А.Р., Смирнов Н.Н., Кравченко М.Н., Корнаева Д.А., Диева Н.Н. Перспективы применения волновой технологии термогазохимического воздействия для повышения нефтеотдачи пластов // Нефтяное хозяйство. 2014. № 1. С. 62–66.
Lake L.W. Enhanced Oil Recovery. Englewood Cliffs. N.J.: Prentice-Hall, 1989. 550 p.
Kuzmin D., Möller M., Turek S. Multidimensional FEM-FCT schemes for arbitrary time-stepping // Int. J. Numer. Meth. Fluids. 2003. V. 42. № 3. P. 265–295.
Arribas M., Elipe A. Quaternions and the rotations of a rigid body // Palacios, M. Celest. Mech. Dyn. Astron. 2006. V. 96. № 3–4. P. 239–251.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал