Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 32-46
ПРОБЛЕМА ПЕРЕХОДА И ЛОКАЛИЗОВАННЫЕ ТУРБУЛЕНТНЫЕ СТРУКТУРЫ В ТРУБАХ
a МГУ им. М.В. Ломоносова, НИИ механики
Москва, Россия
* E-mail: nvnikitin@mail.ru
Поступила в редакцию 27.05.2020
После доработки 06.06.2020
Принята к публикации 21.06.2020
Аннотация
В классических опытах О. Рейнольдса 1883 г. определено критическое значение безразмерного параметра, называемого ныне числом Рейнольдса, ${\text{R}}{{{\text{e}}}_{c}} \approx 2000$, при превышении которого в трубе круглого сечения может устанавливаться турбулентный режим течения. Попытки уточнить это значение в течение XX века не увенчались успехом. В работе дается обзор выполненных в последние годы теоретических, экспериментальных и численных исследований течения в круглой трубе на стадии перехода к турбулентности, позволивших сформулировать новый взгляд на природу ламинарно-турбулентного перехода в этом течении.
Проблема возникновения турбулентности в круглой трубе является классической и одной из самых известных проблем теории гидродинамической устойчивости. Со времени первых экспериментов О. Рейнольдса проведено большое количество экспериментальных, теоретических и численных исследований, накоплен огромный объем численного и экспериментального материала, касающегося различных сторон ламинарно-турбулентного перехода в этом течении. Все это не привело, однако, к полному пониманию физических механизмов, определяющих смену режимов течения в круглой трубе, теоретическому обоснованию известных из экспериментов даже таких простейших законов, как зависимость коэффициента сопротивления от числа Рейнольдса.
Течение в круглой трубе является представителем класса течений, неустойчивость которых не описывается линеаризованными уравнениями. И экспериментальные, и численные исследования указывают на то, что ламинарное течение Пуазейля в трубе устойчиво к малым возмущениям при любых числах Рейнольдса. Это значит, что переход к турбулентности не может быть описан последовательностью усложняющихся состояний, возникающих в результате определенной цепочки бифуркаций, как это происходит во многих других течениях, таких, например, как течение Тейлора-Куэтта между вращающимися цилиндами, течение Рэлея–Бенара в слое, подогреваемом снизу, и даже в родственном течении Пуазейля в плоском канале, теряющем устойчивость при конечном значении числа Рейнольдса.
В экспериментах переход к турбулентности сопровождается интересным явлением. Турбулентные участки в трубе появляются первоначально в виде изолированных по длине трубы всплесков, уносящихся вниз по течению и не меняющих своей протяженности. С ростом числа Рейнольдса степень заполненности трубы турбулентностью повышается, и, наконец, возникает режим сплошного турбулентного течения. Течение в круглой трубе на этапе перехода является гидродинамическим примером возникновения пространственно-временной перемежаемости, наблюдающейся во многих проявлениях реального мира. В настоящей обзорной статье дается краткое описание выполненных в последние годы экспериментальных и численных исследований течения в круглой трубе на стадии перехода к турбулентности, позволивших сформулировать новый взгляд на природу ламинарно-турбулентного перехода в этом течении.
1. ВОЗНИКНОВЕНИЕ ТУРБУЛЕНТНОСТИ В КРУГЛОЙ ТРУБЕ
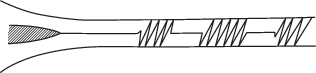
Мало кто не слышал об опытах Рейнольдса. Считается, что теория турбулентности приобрела статус самостоятельного раздела гидродинамики именно после опубликования О. Рейнольдсом (рис. 1) в 1883 г. результатов своих экспериментов [1]. Целью их было установление условий, определяющих характер движения воды в трубах круглого сечения. Экспериментальная установка Рейнольдса представляла собой широкий резервуар с водой, в который устанавливалась горизонтальная трубка (рис. 2). Один конец трубки служил входным отверстием для вытекающей воды и снабжался воронкой, обеспечивающей плавный вход. Другой конец выводился наружу, где соединялся с вертикальным водоводом с краном на конце. Перепад высот между уровнем воды в резервуаре и сливным отверстием в водоводе обеспечивался установкой резервуара на высокой платформе. Для визуализации течения устанавливалась прозрачная трубка из стекла, а во входную воронку подавалась струйка чернил, увлекаемая потоком. В экспериментах, кроме скорости истечения, варьировались диаметр и материал трубы, вязкость жидкости (путем ее нагревания), уровень возмущенности входящего в трубку потока. Установка О. Рейнольдса до наших дней сохраняется в работоспособном состоянии (рис. 3) и по праву считается образцом простоты и функциональности.
Рис. 3.
Экспериментальная установка О. Рейнольдса. Хранится в университете г. Манчестера, Великобритания.

Главный результат Рейнольдса – экспериментальное доказательство существования безразмерного параметра, ответственного за формирование того или иного режима течения в трубе
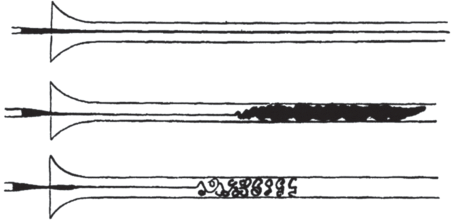
Здесь U – средняя скорость течения, $D$ – диаметр трубы, ρ, μ – плотность и вязкость жидкости. Сейчас этот параметр называется числом Рейнольдса. При малых ${\text{Re}}$ течение в трубе спокойное, слоистое – ламинарное, даже если на входе имеются значительные возмущения. При больших значениях числа Рейнольдса в жидкости возникают колебания, течение теряет прямолинейность, струйка чернил размывается и окрашивает все сечение трубы (рис. 4). Возникает турбулентное течение. При промежуточных значениях Re характер устанавливающегося течения зависит от степени успокоенности жидкости в резервуаре и от плавности входа в трубу. Рейнольдс дает следующие оценки для двух граничных значений ${\text{Re}}$. Нижнее критическое (или просто критическое) число Рейнольдса ${\text{R}}{{{\text{e}}}_{1}} \approx 2000$. Верхнее критическое число Рейнольдса Re2 ≈ 12 000. Итак, при ${\text{Re}} < {\text{R}}{{{\text{e}}}_{1}}$ течение ламинарное, а при ${\text{Re}} > {\text{R}}{{{\text{e}}}_{2}}$ – турбулентное, независимо от условий на входе. В диапазоне ${\text{R}}{{{\text{e}}}_{1}} < {\text{Re}} < {\text{R}}{{{\text{e}}}_{2}}$ спокойное течение во входном сечении остается ламинарным на всем протяжении трубы, а для перехода к турбулентности требуется некоторая возмущенность потока тем меньшая, чем больше Re.
Рис. 4.
Визуализация ламинарного, турбулентного и переходного течения, выполненная О. Рейнольдсом [1].
Выводы О. Рейнольдса подвергались многократной проверке в течение XX века. Что касается верхнего критического числа Рейнольдса, выяснилось, что уменьшая возмущенность потока на входе, переход к турбулентности удается затянуть до очень высоких чисел Рейнольдса, вплоть до ${\text{Re}} \sim {{10}^{5}}$ [2]. Таким образом, есть основания полагать, что верхнее критическое число Рейнольдса равно бесконечности, т.е. сколь бы велико ни было число Рейнольдса, все равно течение в трубе может оставаться ламинарным. Такая точка зрения согласуется с выводом об устойчивости течения Пуазейля к малым возмущениям при всех числах Рейнольдса [3, 4].
Попытки уточнить значение нижнего критического числа Рейнольдса не увенчались успехом — в разных экспериментах получены значения от ${\text{Re}} = {\text{17}}60$ до ${\text{Re}} = {\text{23}}00$ [5–10]. Стоит признать, что определение критического числа Рейнольдса, т.е. минимального Re, при котором возможно установление турбулентного режима в трубе, задача непростая. С одной стороны, если в данной экспериментальной установке при данном числе Рейнольдса не наблюдается перехода к турбулентности, это вообще говоря не означает, что число Рейнольдса меньше критического. Можно допустить, что какое-то специальное возмущение, не реализуемое в данном конкретном эксперименте, все-таки способно вызвать переход. С другой стороны, если течение под воздействием интенсивных входных возмущений выглядит турбулентным, то где гарантия, что эта турбулентность установившаяся, т.е. сохранится вниз по течению сколь бы ни увеличивалась длина трубы?
Начиная с конца 1980-х годов, прямое численное моделирование (DNS) турбулентных течений, основанное на прямом решении полных уравнений Навье–Стокса, приобрело статус конкурентного инструмента исследования турбулентности. Первые серьезные успехи DNS были связаны с расчетом течения в плоском канале [11, 12]. Течение же в круглой трубе до поры не поддавалось численному расчету. Причиной этому являлось отсутствие надежных методов решения 3-мерных уравнений Навье–Стокса в цилиндрической геометрии при наличии геометрической особенности на оси симметрии, а также недостаточность мощностей ЭВМ. К началу 80-х годов было лишь численно установлено, что ламинарное течение в круглой трубе (течение Гагена–Пуазейля) устойчиво к малым возмущениям [3]. Попытки учета конечности амплитуды возмущений в осесимметричной постановке [13, 14] также не выявили перехода к турбулентности. Впервые исходя из трехмерных уравнений Навье–Стокса незатухающие решения со свойствами, близкими к свойствам турбулентного течения, были численно получены в [15]. Более точные решения были построены в работах [16, 17]. Наконец, в [18, 19] были представлены численные решения с исчерпывающими сопоставлениями с экспериментальными данными.
Несмотря на успехи в численном моделировании развитых турбулентных течений, определение нижнего критического числа Рейнольдса численными методами также оказалось непростой задачей. Возвращение от турбулентного к ламинарному режиму (ламинаризация) при уменьшении числа Рейнольдса происходит при разных ${\text{Re}}$ в зависимости от используемого пространственного разрешения, размера расчетной области, величины временного шага и других факторов. Ламинаризация происходит спонтанно без каких-либо предшествующих признаков. Течение может длительное время оставаться турбулентным, а затем в какой-то момент вдруг превратиться в ламинарное. Таким образом, определение критического числа Рейнольдса в круглой трубе как минимального ${\text{Re}}$, при котором турбулентность имеет установившийся характер, т.е. может существовать бесконечно долго, оказалось не очень подходящим для практического использования. Полученная О. Рейнольдсом оценка ${\text{R}}{{{\text{e}}}_{1}} \approx 2000$ так и не была уточнена за прошедшие 130 лет.
2. СВЯЗЬ С ТЕОРИЕЙ ДИНАМИЧЕСКИХ СИСТЕМ
На определенном этапе возникло осознание того, что необходимо какое-то более четкое и более математически формальное определение понятия критического числа Рейнольдса. Интерес к проблеме получил новый импульс в начале 2000-х, когда были обнаружены и рассчитаны семейства 3-мерных решений уравнений Навье–Стокса в виде бегущей волны, т.е. стационарные решения в некоторой галилеевой системе координат [20, 21]. Рассчитаны течения с разной степенью периодичности в угловом направлении (с периодом $2\pi {\text{/}}n$ при n = 2, 3, 4, 5). Найденные решения существуют при уменьшении Re вплоть до Re = 1250. Позже были обнаружены новые семейства бегущих волн, существующие вплоть до 3 [22]. Оказалось однако, что все эти решения неустойчивы, т.е. не могут реализовываться в экспериментальных условиях в течение длительного времени. Тем не менее на определенных временных интервалах такие структуры могут существовать, что было показано в эксперименте [23].
С точки зрения теории динамических систем каждое решение из семейства трехмерных бегущих волн представляет собой седловую точку в фазовом пространстве. Эти решения неустойчивы, но размерность неустойчивого многообразия мала. Была выдвинута гипотеза, что такие решения могут представлять скелет турбулентного течения: траектория в фазовом пространстве случайно блуждает между бегущими волнами, попеременно притягиваясь к разным решениям семейства. В [24] была проверена эта гипотеза. Проанализировано численно рассчитанное турбулентное течение при Re = 2400. Вывод: представление турбулентного течения как блуждания между бегущими волнами маловероятно.
Традиционно турбулентные течения ассоциируются с поведением динамической системы на хаотическом (странном) аттракторе. Каждая траектория в фазовом пространстве неустойчива, что характеризуется наличием положительных показателей Ляпунова, однако любая траектория из некоторой окрестности аттрактора притягивается к нему и остается на нем неограниченно долгое время. Непредсказуемое поведение турбулентности в трубе при числах Рейнольдса Re ~ ~ 2000, когда турбулентность может неожиданно исчезнуть после продолжительного периода существования, требует более адекватного математического образа. Подходящим математическим объектом может быть хаотическое седло [25]. Простейший пример хаотического седла – движение частицы внутри замкнутого объема с криволинейными границами и небольшим отверстием [26]. Динамика движения частицы может быть хаотической, что характеризуется положительностью старшего показателя Ляпунова, но движение это временное и рано или поздно заканчивается вылетом частицы сквозь отверстие. Вероятность исхода частицы определяется размером отверстия и не зависит от меры хаотичности ее движения.
Аналогия с течением в трубе такова: турбулентность соответствует движению частицы внутри области, а спонтанная ламинаризация – исходу частицы сквозь отверстие. Характерными свойствами хаотического седла являются: а) чувствительная зависимость продолжительности (времени жизни) хаотической стадии от начальных условий, б) экспоненциальное распределение времени жизни, в) наличие положительного показателя Ляпунова для хаотической стадии, г) независимое изменение показателей Ляпунова и вероятности выхода из хаотической стадии при вариации параметров системы.
В [27] показано, что поведение турбулентности в круглой трубе при переходных числах Рейнольдса обнаруживает все свойства, характерные для хаотического седла. Эти выводы были сделаны на основании численного моделирования течения в трубе при ${\text{Re}} < 2300$. Уравнения Навье–Стокса решались с условием пространственной периодичности при относительно небольшом продольном периоде в 5 диаметров трубы. Обнаружено, что достаточно интенсивные начальные возмущения приводят к возникновению турбулентного движения, которое, однако, в какой-то момент затухает и происходит ламинаризация. Время существования турбулентной стадии чувствительно к малым изменениям начальных данных. Вариацией начальных данных в [27] установлено, что при фиксированном Re время жизни турбулентности как случайная величина распределена экспоненциально: вероятность $P(t)$ того, что турбулентность просуществует в течение времени $t$ выражается как
Поведение турбулентных решений с экспоненциальным распределением времени жизни свидетельствует о том, что наблюдаемая в численном эксперименте турбулентность соответствует марковскому случайному процессу: ее эволюция в будущем зависит только от текущего состояния и явно не зависит от прошлого. Параметр $\tau ({\text{Re}})$ в формуле (2.1) определяет характерную продолжительность существования процесса. Результаты, полученные в [27], показывают, что $\tau ({\text{Re}})$ растет при увеличении ${\text{Re}}$ по обратному к линейному закону
и обращается в бесконечность при ${\text{Re}} = {\text{R}}{{{\text{e}}}_{c}} \approx 2250$.Обращение среднего времени жизни турбулентности в бесконечность при ${\text{Re}} = {\text{R}}{{{\text{e}}}_{c}}$ можно интерпретировать как переход от временной к постоянно живущей турбулентности или превращения хаотического седла в фазовом пространстве в хаотический аттрактор. Полученное значение ${\text{R}}{{{\text{e}}}_{c}} \approx 2250$ приобретает при этом осмысленное значение критического числа Рейнольдса для течения в круглой трубе.
3. ТУРБУЛЕНТНЫЕ ПОРЫВЫ В ТРУБЕ
Хотя результаты [27] выглядят убедительно, а полученное значение критического числа Рейнольдса согласуется с результатами экспериментов, бросается в глаза неадекватность выбранных расчетных параметров. В частности, длина расчетной области в $5D$ недостаточна для воспроизводства наблюдаемых в экспериментах турбулентных структур при рассмотренных значениях Re. Течения при интенсивных возмущениях на входе в трубу в диапазоне переходных чисел Рейнольдса являются перемежающимися: участки турбулентного течения сносятся вниз по потоку и чередуются с участками спокойного, ламинарного течения. Это явление было замечено еще самим Рейнольдцем и было описано так: “Другим явлением, очень заметным в небольших трубках, был прерывистый характер возмущения. Возмущение внезапно возникало на определенной длине трубы и исчезало, а затем возникало снова, создавая видимость вспышек, и эти вспышки часто начинались последовательно в одной точке трубы. Внешний вид, когда вспышки быстро сменяли друг друга, был таким, как показано на рисунке” (рис. 5).
В эксперименте [28] локализованные в пространстве турбулентные структуры были разделены на два типа: турбулентные порывы и турбулентные пробки. Первые наблюдаются в диапазоне ${\text{Re}} = {\text{20}}00{\kern 1pt} - {\kern 1pt} 2700$ как результат интенсивных входных возмущений, а вторые – при больших значениях ${\text{Re}} > 3200$, только когда возмущения на входе недостаточно интенсивны, чтобы вызвать сплошную турбулентность. Турбулентные порывы имеют четко выраженную заднюю границу и размытую переднюю. Они имеют протяженность в $20{\kern 1pt} - {\kern 1pt} 25D$ и сносятся вниз по потоку со скоростью, близкой к средней скорости течения. Турбулентные пробки отличает в первую очередь то, что их протяженность увеличивается со временем – скорость передней границы больше скорости задней [29–31]. В результате на определенном расстоянии от входа последующие пробки нагоняют предыдущие, и течение из перемежающегося превращается в полностью турбулентное. Турбулентные порывы не обнаруживают тенденции к увеличению протяженности, однако они подвержены спонтанному исчезновению либо спонтанному делению. В [32] обнаружено, что при ${\text{Re}} = 2200{\kern 1pt} - {\kern 1pt} 2300$ количество порывов практически не меняется при их перемещении вдоль трубы, они находятся в равновесном состоянии. Экспериментально доказано, что турбулентные порывы, появляющиеся в ответ на возмущения на входе в трубу, не отличаются по своей структуре от порывов, инициируемых импульсным возмущением развитого течения Пуазейля на достаточном расстоянии от входа [29]. Показано также, что порывы одинаково возникают как в условиях контроля перепада давления, так и в условиях поддержания постоянного расхода в трубе [8].
В [33] турбулентные порывы и турбулентные пробки в круглой трубе впервые были получены численно. Расчеты проводились с условием периодичности вдоль трубы – стандартный подход при моделировании развитых турбулентных течений. Однако расчетная область выбиралась протяженной, длиной в $16\pi D$, достаточной, чтобы на этой длине могли разместиться моделируемые турбулентные структуры. Пространственно-локализованные решения получались в результате развития импульсных возмущений, вносимых в течение Пуазейля. При числах Рейнольдса ${\text{Re}} = 2200$ и $\operatorname{Re} = 5000$ эволюция возмущений приводит к образованию турбулентных порывов и турбулентных пробок, что согласуется с имеющимися экспериментальными данными. В [34], стартуя с развитого турбулентного течения при $\operatorname{Re} = 4000$, были рассчитаны течения при нескольких меньших ${\text{Re}}$. Обнаружено, что при Re = 2350 и ${\text{Re}} = 2200$ в трубе самопроизвольно возникает пространственная неоднородность, соответствующая образованию турбулентных порывов. Один из наиболее важных результатов этой работы состоит в доказательстве того, что пространственная локализация турбулентности в турбулентном порыве – это не следствие течения во входной части экспериментальной установки или пространственно-локализованного начального возмущения, а специфическое свойство решений уравнений Навье–Стокса в определенном диапазоне чисел Рейнольдса.
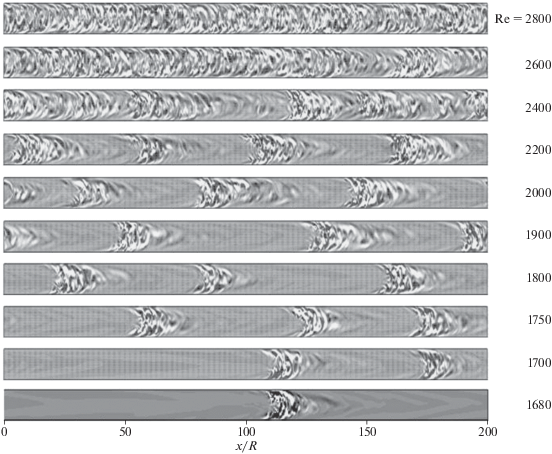
На рис. 6 приведена визуализация турбулентных структур, рассчитанных в [35] методом [36]. Уравнения Навье–Стокса записываются в универсальной векторной форме, в выражениях для векторных операций используются параметры Ламе. Пространственная дискретизация проводится конечно-разностным методом на разнесенных сетках со вторым порядком точности. Получающаяся дискретная система консервативна по энергии (нелинейные члены и градиент давления не производят кинетической энергии). Для интегрирования по времени используется полунеявный метод Рунге–Кутты 3-го порядка точности [37]. Расчеты проведены с условием пространственной периодичности с периодом длиной в 100D. На рис. 6 представлены результаты при последовательном уменьшении числа Рейнольдса от ${\text{Re}} = 2800$ до ${\text{Re}} = 1680$. Изображены распределения модуля завихренности за вычетом течения Пуазейля в диаметральном сечении трубы. Изображения сжаты по горизонтали примерно в 6 раз. При ${\text{Re}} = 2800$ турбулентность близка к однородной в направлении потока. Уже при ${\text{Re}} = {\text{26}}00$ появляются первые признаки пространственно-временной неоднородности [38], которые становятся очевидными при Re = = 2400. При ${\text{Re}} = {\text{2200}}$ в потоке отчетливо выделяются локализованные турбулентные структуры – турбулентные порывы протяженностью в 15–20D, двигающиеся цугом с постоянной скоростью (направление потока слева направо). При дальнейшем уменьшении Re часть структур погибает, а их протяженность несколько уменьшается. При наименьших из представленных Re турбулентные порывы живут какое-то время, но в конце концов погибают.
Рис. 6.
Изменение структуры турбулентности в круглой трубе при последовательном уменьшении числа Рейнольдса от ${\text{Re}} = 2800$ до ${\text{Re}} = 1680$ [35]. Направление потока слева направо. Расчет с условием периодичности при длине расчетной области (периоде) в 100 диаметров трубы.
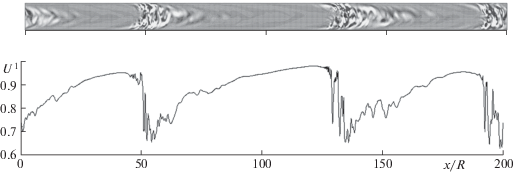
Передний фронт турбулентных порывов размыт, тогда как задняя граница – четко очерчена. Это наиболее отчетливо проявляется в мгновенном распределении продольной скорости вдоль оси симметрии трубы [39], представленном на рис. 7. При перемещении точки наблюдения навстречу потоку (справа налево) скорость на оси постепенно уменьшается от скорости в ламинарном течении Пуазейля (принимаемой за 1.0) до значения менее 0.7 вблизи задней границы порыва, после чего стремительно восстанавливается до ламинарного значения. Напомним, что движение турбулентных порывов происходит примерно со средней скоростью потока, что составляет 0.5 при выбранном масштабе скорости. Описанное поведение турбулентных порывов, полученных численно, совпадает с тем, что наблюдается экспериментально.
Рис. 7.
Изменение продольной скорости U вдоль оси симметрии трубы при наличии турбулентных порывов [39].
4. МЕХАНИЗМ ВОЗНИКНОВЕНИЯ И САМОПОДДЕРЖАНИЯ ТУРБУЛЕНТНЫХ ПОРЫВОВ
Интересен вопрос о причинах возникновения пространственной локализации пульсационного движения в турбулентных порывах. В [40] предложена следующая картина этого явления. Достаточно интенсивное локальное возмущение течения Пуазейля может вызвать перестройку профиля скорости с образованием точки перегиба в распределении U(r). Такие профили подвержены неустойчивости типа Кельвина–Гельмгольца с быстрым нарастанием пульсаций. Рождающаяся в результате неустойчивости завихренность приосевым потоком сносится вперед, деформируя профиль скорости в нижней части потока. Образующийся профиль скорости наполненного вида обладает меньшей энергией и не способен поддерживать колебания – турбулентность постепенно затухает, а профиль скорости возвращается к пуазейлевскому. В [40] экспериментально и численно показано, что осредненный по углу профиль скорости на задней границе турбулентного порыва имеет точку перегиба, на которой развиваются колебания. Приведенная точка зрения указывает на возможный способ управления турбулентными порывами. Если поток, настигающий порыв, будет обладать меньшей осевой скоростью, то его энергии не хватит для поддержания порыва, и порыв должен погибнуть. Проведенные численные эксперименты с искусственным понижением скорости потока на оси трубы в задней части порыва подтвердили сделанное предположение – порыв затухает. В пользу высказанной гипотезы также свидетельствуют эксперименты с генерацией двух порывов, следующих непосредственно друг за другом. Порыв, следующий вторым, искажает профиль скорости в нижней части потока перед собой. Так что если расстояние между импульсами недостаточно для восстановления пуазейлевского течения, то впереди следующий порыв оказывается в некомфортных условиях и погибает.
Механизм самоподдержания колебаний в турбулентном порыве был изучен в численном исследовании [41]. Как и в любом пристенном турбулентном движении турбулентность внутри порыва производит продольные полосы замедленного и ускоренного движения, вытянутые вдоль стенки трубы и чередующиеся в угловом направлении. Порыв перемещается вдоль трубы со скоростью, близкой к средней скорости потока. Это значит, что частицы жидкости вблизи оси симметрии трубы обгоняют порыв, а вблизи стенки, наоборот, отстают от него. Полосы замедления, расположеные в пристенной области, двигаются вверх по потоку относительно порыва, пересекают заднюю границу и образуют сильные тонкие сдвиговые слои в ламинарном потоке. Эти слои подвержены неустойчивости типа Кельвина–Гельмгольца. Возникающие в результате неустойчивости пульсации завихренности, удаляясь от стенки, попадают в область большой скорости и переносятся внутрь порыва, усиливая там турбулентность. Таким образом возникает цикл самопроизводства турбулентности. Близкие выводы были сделаны в экспериментальной работе [42].
Возбуждение пульсаций на фоне деформации профиля скорости продольными полосами – общий элемент возникновения турбулентности в пристенных течениях. Согласно общепринятой точке зрения полосчатые структуры возникают под действием так называемых продольных или квазипродольных вихрей – вытянутых вдоль потока областей концентрированной продольной завихренности, посредством так называемого “лифт-ап эффекта”. Связанное с продольными вихрями вращательное движение в перпендикулярной к потоку плоскости переносит быстрые частицы жидкости из внешнего потока к стенкам, так образуются полосы ускорения. В смежных областях, наоборот, медленные частицы от стенки переносятся во внешнюю область. Здесь образуются полосы замедления. Образующаяся локальная деформация профиля скорости характерна появлением точек перегиба в профиле U(r) над полосами замедления, а также возникновения профилей струйного типа $U(\theta )$ при изменении по углу. Подобные распределения скорости $U(r,\theta )$ неустойчивы. В [43] исследованы свойства устойчивости и описаны характерные черты собственных функций задачи устойчивости для подобных распределений скорости в плоском канале в параллельном приближении.
Таким образом, механизмы возникновения пульсаций в полосчатом течении и причины появления полос под действием продольных вихрей можно считать понятными. Для замыкания цикла самоподдержания турбулентности необходим какой-то механизм обратной связи, поддерживающий существование продольных вихрей за счет энергии возбуждающихся пульсаций. Предложено несколько механизмов образования продольных вихрей в пристенных турбулентных течениях, однако ни один из них не подтвержден в должной мере экспериментом или численным моделированием.
Течение в турбулентном порыве, несмотря на его пространственную локализацию, обладает сложной пространственной структурой (рис. 8a) [35] и хаотической динамикой, из которой также сложно вычленить искомые механизмы самоподдержания. Отдельные фазы процесса происходят в случайные моменты времени в разных точках пространства, что делает его изучение чрезвычайно трудоемким. В этих условиях определенная ясность может быть получена из анализа более простых структур, аппроксимирующих порыв, найденных численно в [44, 45]. Это предельные решения, возникающие на сепаратрисе, разделяющей в фазовом пространстве области притяжения решений, соответствующих ламинарному и турбулентному режимам течения. Решения на сепаратрисе неустойчивы, однако могут быть рассчитаны на значительном интервале времени, достаточном для выхода решения на предельное состояние. Такие решения, наследуя ряд качественных характеристик турбулентных течений, оказываются существенно более простыми как в пространственном, так и во временном поведении. В [45] обнаружено, что при наложении определенных дополнительных ограничений угловой симметрии ($\pi $ – периодичность, плюс симметрия относительно плоскости θ = 0) течение в турбулентном порыве упрощается пространственно (рис. 8б), хотя и сохраняет стохастическое поведение во времени. Соответствующее ему предельное решение на сепаратрисе (“модельный порыв”) оказывается периодическим по времени в системе отсчета, перемещающейся вдоль трубы с постоянной скоростью. В пространственном отношении модельный порыв в подвижной системе отсчета представляет собой четыре пары стационарных полос ускоренного и замедленного движения, на фоне которых зарождаются и бегут вниз по потоку периодические колебания (рис. 8в). Простота поведения модельного порыва позволяет провести исчерпывающее исследование его свойств [35, 46].
Рис. 8.
Визуализация течения в турбулентном порыве [35]. Изображены мгновенные поверхности +0.1 и –0.1 от скорости в течении Пуазейля (светлые и темные поверхности соответственно). (а) – турбулентный порыв при ${\text{Re}} = 2200$, (б) – решение при дополнительных условиях угловой симметрии, (в) – решение на сепаратрисе (модельный порыв).
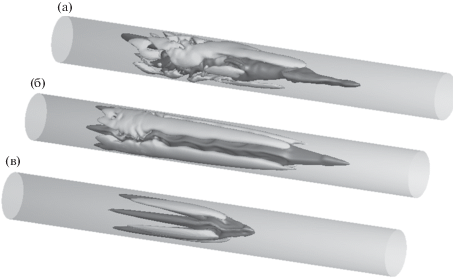
Полосы в распределении продольной компоненты скорости в модельном порыве образуются посредством лифт-ап эффекта под действием слабых продольных вихрей, интенсивность которых на порядок меньше амплитуды вызываемых деформаций продольной скорости. Протяженность продольных вихрей составляет примерно $10D$, тогда как протяженность образующихся полос превышает $35D$. Значительная вытянутость полос, особенно вблизи стенки вверх по потоку, возникает под растягивающим действием поперечного градиента скорости. Нестационарные пульсации возникают в результате линейной неустойчивости стационарной составляющей течения. При этом обнаружено, что основной причиной неустойчивости является не неустойчивость Кельвина–Гельмгольца, связанная с точками перегиба в радиальных распределениях скорости, а изменчивость скорости в угловом направлении.
Наиболее значительным результатом [46] является установление механизма обратной связи, обеспечивающей энергетическую подпитку продольных вихрей за счет нелинейного взаимодействия нестационарных пульсаций. Обнаружено, что основной вклад в источниковый член уравнения для стационарной составляющей продольной завихренности Ωx вносят слагаемые 〈$\omega _{x}^{{\text{'}}}\partial u{\text{'/}}\partial x$〉 – 〈$u{\text{'}}\partial \omega _{x}^{{\text{'}}}{\text{/}}\partial x$〉 ≈ 2〈$\omega _{x}^{{\text{'}}}\partial u{\text{'/}}\partial x$〉, отвечающие нелинейному взаимодействию продольных компонент пульсаций скорости и завихренности (угловые скобки обозначают осреднение по периоду колебаний). Распределение значений отмеченного слагаемого по сечению трубы имеет отчетливо выраженные максимумы и минимумы, совпадающие с максимумами и минимумами распределения Ωx. Таким образом, пульсации продольных компонент скорости и завихренности в областях концентрации Ωx происходят согласованным образом, так что корреляция $\omega _{x}^{'}$ и $\partial u{\text{'/}}\partial x$ положительна в областях ${{\Omega }_{x}} > 0$ и отрицательна в областях Ωx < 0. Другими словами, наличие продольных вихрей так деформирует пульсационное поле, что нелинейное взаимодействие пульсаций дает положительный обратный вклад в поддержание продольных вихрей. Математическим выражением найденного эффекта является доминирование слагаемых ${{\Omega }_{x}}\partial u{\text{'/}}\partial x$ в уравнении для пульсаций продольной компоненты завихренности
Из последнего равенства видно, что в области концентрации продольных вихрей пульсации $\omega _{x}^{'}$ стремятся к пропорциональности с $\partial u{\text{'/}}\partial x$, причем коэффициентом пропорциональности служит само значение Ωx. Таким образом, возникает корреляционная зависимость нужного знака и образуется обратная связь, подпитывающая продольные вихри.
5. ЭВОЛЮЦИЯ ТУРБУЛЕНТНЫХ ПОРЫВОВ
Выводы о продолжительности жизни турбулентности в диапазоне переходных Re, сделанные в [27], вызывают определенные сомнения из-за неадекватности использованных вычислительных параметров, в частности длины расчетной области, экспериментально наблюдаемым явлениям. Однако сама идея привлечения статистических соображений для определения характерного времени жизни турбулентных структур выглядит разумной. Она была использована в эксперименте [47], где исследовалась эволюция искусственно создаваемых турбулентных порывов. Эксперименты проводились в трубе длиной в 785 диаметров. Течение вызывалось движением поршня, что позволяло изменять число Рейнольдса в процессе эксперимента (путем изменения скорости движения поршня). Каждое испытание проводилось следующим образом. При Re = = 1800 на расстоянии в $185D$ от входа в развитый ламинарный поток вносилось импульсное возмущение, которое превращалось в турбулентный порыв по мере перемещения вниз по потоку. Через определенное время, за которое порыв проходил расстояние в 100D, движение поршня замедлялось, понижая тем самым число Рейнольдса. Наблюдая за дальнейшей эволюцией каждого порыва и отмечая продолжительность его жизни до исчезновения, авторам эксперимента удалось построить зависимости, аналогичные тем, что были получены в [27], а именно, распределения продолжительности жизни турбулентного порыва для нескольких чисел Рейнольдса. Оказалось, что и в этом случае продолжительность жизни распределена экспоненциально и описывается выражением (2.1). Более того, для характерной продолжительности жизни $\tau ({\text{Re}})$ также, как и в [27] справедлива формула (2), показывающая обращение $\tau ({\text{Re}})$ в бесконечность при конечном значении числа Рейнольдса. Однако для критического значения Rec, при котором характерная продолжительность жизни обращается в бесконечность, получено значение ${\text{R}}{{{\text{e}}}_{c}} = 1750 \pm 10$, что существенно отличается от ${\text{R}}{{{\text{e}}}_{c}} = 2250$, найденного в [27].
Заметное различие критических чисел, полученных в [27] и [47], может быть объяснено неадекватностью размера расчетной области в [27]. Для разрешения этого вопроса в [48] была проведена серия расчетов, аналогичных [27], но с длиной пространственного периода в $50D$, что достаточно для воспроизведения локализованных в пространстве турбулентных порывов. В качестве начальных данных в расчетах при различных ${\text{Re}}$ выбирались мгновенные распределения скорости, найденные в расчете турбулентного порыва при ${\text{Re}} = 1900$. Как и в предыдущих исследованиях, обнаружены экспоненциальное распределение вероятности для времени жизни турбулентных порывов и обратная к линейной зависимость характерного времени жизни (2.2) от числа Рейнольдса. Для критического значения получена оценка ${\text{R}}{{{\text{e}}}_{c}} = 1870$, что отличается от Rec = 1750, найденного в [47] на 7%.
Несмотря на некоторые количественные различия в результатах, в работах [27, 47, 48], как тогда казалось, получено главное – понятие критического числа Рейнольдса может быть поставлено на твердую математическую почву. Ему отвечает переход соответствующей динамической системы от хаотического седла к хаотическому аттрактору. Для уточнения конкретных значений критического числа Рейнольдса требуются более тщательные эксперименты. Такой эксперимент был задуман и осуществлен в [49]. Экспериментальная труба имела длину $7500D$, что позволило наблюдать эволюцию турбулентных порывов на больших временах и более точно определить характеристики распределения времени жизни. Результат более точных измерений оказался неожиданным – характерное время жизни порыва хоть и растет с увеличением числа Рейнольдса, однако не обращается в бесконечность при конечном Re. Для описания величины ${{\tau }^{{ - 1}}}({\text{Re}})$ (которую можно назвать характерной скоростью затухания турбулентности) больше подходит не линейный, а экспоненциальный закон.
Результат [49] опроверг сложившуюся точку зрения, подтвержденную работами [27, 47, 48], что критическое число Рейнольдса – это такое значение ${\text{Re}}$, при котором хаотическое седло, соответствующее поведению турбулентных структур, превращается в хаотический аттрактор. Более того, авторы статьи [49] пересмотрели результаты работы [27] и с учетом более точного определения параметра ${{t}_{0}}$ в формуле (1) пришли к убеждению, что $\tau (e)$ описывается экспоненциальным законом. Если принять точку зрения [49], то получается, что критическое число Рейнольдса в трубе вовсе отсутствует, а турбулентность при любых ${\text{Re}}$ есть преходящее явление, пусть и с очень большим, но конечным характерным временем жизни.
Экспериментальное изучение статистических свойств турбулентных порывов было продолжено в [50]. Измерения проводились на четырех установках в трех лабораториях. Были приняты дополнительные меры по обеспечению контролируемости всех экспериментальных параметров, таких, как температура (а следовательно и вязкость) рабочей жидкости, уровень входных возмущений, вариация числа Рейнольдса в процессе эксперимента, соосность секций, составляющих трубу и т.д. Получено, что характерное время жизни порыва $\tau ({\text{Re}})$ лучше всего аппроксимируется суперэкспоненциальным законом
(5.1)
$\tau ({\text{Re}}) = exp[exp({{C}_{1}}{\text{Re}} + {{C}_{2}})],\quad {{C}_{1}} = 0.0057,\quad {{C}_{2}} = - 8.7$Хотя характерное время жизни турбулентности согласно (5.1) растет быстрее, чем экспоненциально, однако оно остается конечным при всех Re. Следовательно, вывод об отсутствии перехода к хаотическому аттрактору, сделанный в [49], остается в силе. Вывод о суперэкспоненциальной зависимости $\tau ({\text{Re}})$ подтвержден экспериментом [51], где также высказано предположение о существовании другого механизма, ответственного за переход к установившейся турбулентности.
6. ДЕЛЕНИЕ ТУРБУЛЕНТНЫХ ПОРЫВОВ
Отсутствие перехода к аттрактору при развитии турбулентных порывов выглядит несколько неожиданно. Получается, что при любых, даже больших ${\text{Re}}$, остается ненулевая вероятность спонтанного затухания турбулентности. И хотя с практической точки зрения характерные времена жизни можно считать бесконечно большими, с математических позиций они остаются конечными, что меняет устоявшиеся взгляды на явление турбулентности и ее математическое описание.
Заметим, что в исследованиях эволюции турбулентных порывов в диапазоне малых чисел Рейнольдса ${\text{Re}} \sim 2000$ не принималось во внимание другое их свойство – способность к спонтанному делению [32]. А именно это свойство может быть ключевым для выживания турбулентности. Процесс деления индивидуального турбулентного порыва можно описать следующим образом. Завихренность, генерируемая внутри турбулентного порыва, выносится по приосевой части трубы вниз по потоку. Если интенсивность выносимого возмущения достаточно велика, то в какой-то момент там создаются условия для зарождения нового порыва, который удаляется от своего родителя на почтительное расстояние. После чего два порыва сосуществуют, практически не взаимодействуя друг с другом. Чем больше число Рейнольдса, тем более вероятно порождение нового турбулентного порыва.
Статистические закономерности процесса деления турбулентного порыва в диапазоне $2195\, \leqslant \,{\text{Re}}\, \leqslant \,2350$ изучены в [52] как экспериментально, так и численно. Обнаружено, что процесс деления порыва является марковским: вероятность его разделения в течение интервала времени $[t,t + \Delta t]$ зависит только от длины интервала $\Delta t$ и явно не зависит от значения времени t, т.е. процесс не имеет памяти. Пусть $P(t)$ – вероятность разделения порыва на интервале времени $[0,t]$, тогда $1 - P(t)$ – вероятность остаться неразделенным. Легко понять, что для марковского процесса эта величина распределена экспоненциально
Как экспериментальные, так и численные результаты [52] подтверждают справедливость формулы (6.1), а также хорошо согласуются между собой. Параметр $\tau ({\text{Re}})$ в (6.1) имеет смысл характерного периода деления турбулентного порыва. Другими словами, это среднее время, проходящее от образования порыва до его первого раздвоения. Чем меньше $\tau ({\text{Re}})$, тем быстрее уменьшается со временем вероятность $1 - P(t)$ найти порыв неразделенным. Скорость уменьшения $1 - P(t)$ увеличивается с ростом числа Рейнольдса, таким образом $\tau ({\text{Re}})$ – убывающая функция. В [52] найдено, что $\tau ({\text{Re}})$ подчиняется суперэкспоненциальному закону
(6.2)
$\tau ({\text{Re}}) = exp[exp({{C}_{3}}{\text{Re}} + {{C}_{4}})],\quad {{C}_{3}} = - 0.003115,\quad {{C}_{4}} = 9.161$Итак, эволюция турбулентного порыва происходит в условиях конкуренции двух тенденций: тенденции к исчезновению и тенденции к разделению. Характерные времена, определяющие среднюю продолжительность жизни порыва до его гибели или до его деления, изменяются с числом Рейнольдса противоположным образом: первое растет с ростом Re, а второе – падает. Обе величины, подчиняясь суперэкспоненциальным законам (5.1) и (6.2), остаются конечными при всех Re. Таким образом, неизбежно имеется значение (единственное) ${\text{Re}} = {\text{R}}{{{\text{e}}}_{c}}$, при котором характерные времена совпадают между собой. По оценке [52] пересечение линий (5.1) и (6.2) происходит при ${\text{R}}{{{\text{e}}}_{c}} = 2040 \pm 10$ рис. 9. Таким образом, при ${\text{Re}} < {\text{R}}{{{\text{e}}}_{c}}$ турбулентный порыв скорее затухнет, чем успеет разделиться, а при ${\text{Re}} > {\text{R}}{{{\text{e}}}_{c}}$, наоборот, порыв вероятнее успеет разделиться, т.е. дать потомство до своего исчезновения.
Рис. 9.
Сопоставление характерных времен жизни турбулентного порыва до его затухания (5.1) – левая кривая и до его разделения (6.2) – правая кривая.
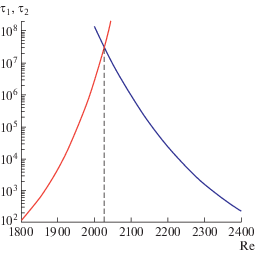
Одновременное сосуществование двух форм движения – турбулентной и ламинарной, можно сопоставить с сосуществованием различных фаз в термодинамических системах. В рамках такой аналогии точка ${\text{Re}} = {\text{R}}{{{\text{e}}}_{c}}$ может рассматриваться как точка статистического фазового перехода: в этой точке происходит изменение преимущественных тенденций в поведении системы. В рассматриваемом случае это переход локализованной турбулентности от стремления к затуханию к самоподдержанию. И хотя при ${\text{Re}} > {\text{R}}{{{\text{e}}}_{c}}$ не происходит выхода на аттрактор и поэтому чисто теоретически даже при очень больших Re возможно спонтанное затухание турбулентности, это событие невероятно с практической точки зрения.
В [53] проводится точка зрения, что появление перемежающегося течения с бесконечно живущими турбулентными структурами – это только начало пути к установлению развитого турбулентного режима в трубе. Перемежающиеся течения по статистическим характеристикам существенно отличаются от сплошной турбулентности, устанавливающейся при ${\text{Re}} > 2600$. Если рассмотреть каждую локализованную в пространстве структуру, то многие ее элементы напоминают элементы развитого турбулентного течения. В ней также можно рассмотреть полосчатые структуры, вызываемые квазипродольными вихрями, области зарождения мелкомасштабных пульсаций. Изменения, происходящие в переходном режиме, касаются пространственно-временной организации течения на больших пространственных масштабах: насколько отдельные локализованные структуры взаимодействуют друг с другом.
ЗАКЛЮЧЕНИЕ
В результате изучения поведения локализованных турбулентных структур в трубах предложена точка зрения, альтернативная к существовавшему до сих пор математическому образу турбулентности как движению на хаотическом аттракторе соответствующей динамической системы. Критическое число Рейнольдса в такой идеологии – это такое значение Re, при котором аттрактор появляется в фазовом пространстве. Новая концепция не предполагает наличия аттрактора, а критическое число Рейнольдса определяется как граница, на которой происходит изменение тенденций и возникают бесконечно живущие турбулентные структуры.
Отметим, что в цитированных работах по изучению свойств локализованных турбулентных структур в переходном диапазоне чисел Рейнольдса нет указаний на связь этих структур с однородной (нелокализованной) турбулентностью, наблюдающейся при больших Re. В частности, нельзя исключать появления там аттрактора, что вернуло бы ситуацию в рамки традиционных представлений. Таким образом, вопрос о переходе к турбулентности и критическом числе Рейнольдса в круглой трубе не получил еще окончательного разрешения.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-11-50023 с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова. Acknow-ledgments: The reported study was funded by RFBR, project number 19-11-50023.
Список литературы
Reynolds O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels // Philos. Trans. R. Soc. Lond. 1883. V. 174. P. 935–982.
Pfenniger W. Transition in the inlet length of tubes at high Reynolds numbers. In Boundary Layer and Flow Control Pergamon (Ed. G.V. Lachman). 1961. P. 970.
Salwen H., Cotton F.W., Grosch C.E. Linear stability of Poiseuille flow in a circular pipe // J. Fluid Mech. 1980. V. 98. P. 273–284.
Meseguer A., Trefethen L.N. Linearized pipe flow at Reynolds numbers 10,000,000 // J. Comp. Phys. 2003. V. 186. P. 178–197.
Binnie A.M., Fowler J.S. A study by a double refraction method of the development of turbulence in a long cylindrical tube // Proc. R. Soc. Lond. A. 1947. V. 192. P. 32.
Lindgren E.R. The transition process and other phenomena in viscous flow // Arkiv für Physik. 1958. V. 12. P. 1–169.
Leite R.J. An experimental investigation of the stability of Poiseuille flow // J. Fluid Mech. 1959. V. 5. P. 81–97.
Darbyshire A.G., Mullin T. Transition to turbulence in constant-mass-flux pipe flow // J. Fluid Mech. 1995. V. 289. P. 83–114.
Павельев А.А., Решмин А.И., Тепловодский С.X., Федосеев С.Г. О нижнем критическом числе Рейнольдса для течения в круглой трубе // Изв. РАН МЖГ. 2003. № 4. С. 47–55.
Павельев А.А., Решмин А.И., Трифонов В.В. Влияние структуры начальных возмущений на режим установившегося течения в трубе // Изв. РАН МЖГ. 2006. № 6. С. 68–76.
Rozhdestvensky B.L., Simakin I.N. Secondary flows in a plane channel: their relationship and comparison with turbulent flows // J. Fluid Mech. 1984. V. 147. P. 261–289.
Kim J., Moin P., Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number // J. Fluid Mech. 1987. V. 177. P. 133–166.
Itoh N. Nonlinear stability of parallel flows with subcritical Reynolds numbers. Part 2. Stability of Pipe Poiseuille flow to finite axisymmetric disturbances // J. Fluid Mech. 1977. V. 82. P. 469–479.
Patera A.T., Orszag S.A. Finite amplitude stability of axisymmetric pipe flow // J. Fluid. Mech. 1981. V. 112. P. 467–474.
Никитин Н.В. О жестком возбуждении автоколебаний в течении Гагена-Пуазейля // Изв. АН МЖГ. 1984. № 5. С. 181–183.
Приймак В.Г., Рождественский Б.Л. Вторичные течения вязкой несжимаемой жидкости в круглой трубе и их статистические свойства // ДАН СССР. Т. 297. 1987. № 6. С. 1326–1330.
Приймак В.Г. Результаты и возможности прямого численного моделирования турбулентных течений вязкой жидкости в круглой трубе // ДАН СССР. 1991. Т. 316. № 1. С. 71–76.
Никитин Н.В. Прямое численное моделирование трехмерных турбулентных течений в трубах кругового сечения // Изв. РАН МЖГ. 1994. № 6. С. 14–26.
Eggels J.G.M., Unger F., Weiss M.H., Westerweel J., Adrian R.J., Friedrich R., Nieuwstadt F.T.M. Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment // J. Fluid Mech. 1994. V. 268. P. 175–209.
Faisst H., Eckhardt B. Traveling waves in pipe flow // Phys. Rev. Let. 2003. V. 91. № 22. P. 224502(4).
Wedin H., Kerswell R.R. Exact coherent structures in pipe flow: travelling wave solutions // J. Fluid Mech. 2004. V 508. P. 333–371.
Pringle C.C.T., Kerswell R.R. Asymmetric, helical, and mirror-symmetric traveling waves in pipe flow // Phys. Rev. Lett. 2007. V. 99. № 7. P. 074502(4).
Hof B., van Doorne C.W.H., Westerweel J., Nieuwstadt F.T.M., Faisst H., Eckhardt B., Wedin H., Kerswell R.R., Waleffe F. Experimental observation of nonlinear traveling waves in turbulent pipe flow // Science 2004. V. 305. P. 1594–1598.
Kerswell R.R., Tutty O.R. Recurrence of travelling waves in transitional pipe flow // J. Fluid Mech. 2007. V 584. P. 69–102.
Eckhardt B., Schneider T.M., Hof B., Westerweel J. Turbulence transition in pipe flow // Annu. Rev. Fluid Mech. 2007. V. 39. P. 447–468.
Ott E. Chaos in Dynamical Systems. Cambridge, UK: Cambridge Univ. Press, 1993. 297 p.
Faisst H., Eckhardt B. Sensitive dependence on initial conditions in transition to turbulence in pipe flow // J. Fluid Mech. 2004. V 504. P. 343–352.
Wygnanski I.J., Champagne F.H. On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug // J. Fluid Mech. 1973. V. 59. P. 281–335.
Nishi M., Ünsal B., Durst F., Biswas G. Laminar-to-turbulent transition of pipe flows through puffs and slugs // J. Fluid Mech. 2008. V. 614, P. 425–446.
Duguet Y., Willis A.P., Kerswell R.R. Slug genesis in cylindrical pipe flow // J. Fluid Mech. 2010. V. 663. P. 180–208.
Barkley D., Song B., Mukund V., Lemoult G., Avila M., Hof B. The rise of fully turbulent flow // Nature 2015. V. 526. P. 550–553.
Wygnanski I., Sokolov M., Friedman D. On transition in a pipe. Part 2. The equilibrium puff // J. Fluid Mech. 1975. V 69. № 2. P. 283–304.
Shan H., Ma B., Zhang Z., Nieuwstadt F.T.M. Direct numerical simulation of a puff and a slug in transitional cylindrical pipe flow // J. Fluid Mech. 1999. V. 387. P. 39–60.
Priymak V.G., Miyazaki T. Direct numerical simulation of equilibrium spatially localized structures in pipe flow // Phys. Fluids 2004. V. 16. № 12. P. 4221–4234.
Никитин Н.В., Пиманов В.О. Численное исследование локализованных турбулентных структур в трубах // Изв. РАН МЖГ. 2015. № 5. С. 64–75.
Nikitin N. Finite-difference method for incompressible Navier-Stokes equations in arbitrary orthogonal curvilinear coordinates // J. Comput. Phys. 2006. V. 217. № 2. P. 759–781.
Nikitin N. Third-order-accurate semi-implicit Runge-Kutta scheme for incompressible Navier–Stokes equations // Int. J. Num. Meth. Fluids 2006. V. 51. № 2. P. 221–233.
Moxey D., Barkley D. Distinct large-scale turbulent-laminar states in transitional pipe flow // PNAS 2010. V. 107. № 18. P. 8091–8096.
Никитин Н.В., Пиманов В.О. Локализованные турбулентные структуры в круглой трубе // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки. 2015. Т. 157, кн. 3. С. 111–116.
Hof B., de Lozar A., Avila M., Tu X., Schneider T.M. Eliminating turbulence in spatially intermittent flows // Science 2010. V. 327. P. 1491–1494.
Shimizu M., Kida S. A driving mechanism of a turbulent puff in pipe flow // Fluid Dyn. Res. 2009. V. 41. P. 045501(27).
van Doorne C.W.H., Westerweel J. The flow structure of a puff // Phil. Trans. R. Soc. A 2009. V. 367. P. 489–507.
Schoppa W., Hussain F. Coherent structure generation in near-wall turbulence // J. Fluid Mech. 2002. V. 453. P. 57–108.
Skufca J.D., Yorke J.A., Eckhardt B. Edge of chaos in a parallel shear flow // Phys. Rev. Lett. 2006. V. 96. № 17. P. 174101.
Avila M., Mellibovsky F., Roland N., Hof B. Streamwise-localized solutions at the onset of turbulence in pipe flow // Phys. Rev. Lett. 2013. V. 110. № 22. P. 224502.
Никитин Н.В., Пиманов В.О. О поддержании колебаний в локализованных турбулентных структурах в трубах // Изв. РАН МЖГ. 2018. № 1. С. 68–76.
Peixinho J., Mullin T. Decay of turbulence in pipe flow // Phys. Rev. Let. 2006. V. 96. P. 094501(4).
Willis A.P., Kerswell R.R. Critical behavior in the relaminarization of localized turbulence in pipe flow // Phys. Rev. Let. 2007. V. 98. P. 014501(4).
Hof B., Westerweel J., Schneider T.M., Eckhardt B. Finite lifetime of turbulence in shear flows // Nature. 2006. V. 443. P. 59–62.
Hof B., de Lozar A., Kuik D.J., Westerweel J. Repeller or Attractor? Selecting the Dynamical Model for the Onset of Turbulence in Pipe Flow // Phys. Rev. Let. 2008. V. 101. P. 214501(4).
Kuik D.J., Poelma C., Westerweel J. Quantitative measurement of the lifetime of localized turbulence in pipe flow // J. Fluid Mech. 2010. V. 645. P. 529–539.
Avila K., Moxey D., de Lozar A., Avila M., Barkley D., Hof B. The onset of turbulence in pipe flow // Science. 2011. V. 333. P. 192–196.
Barkley D. Theoretical perspective on the route to turbulence in a pipe // J. Fluid Mech. 2016. V. 803. P. 1.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа