Известия РАН. Механика жидкости и газа, 2021, № 1, стр. 115-119

1. ПОСТАНОВКА ЗАДАЧИ, ОСНОВНЫЕ УРАВНЕНИЯ

В полярной системе координат (x, θ) уравнение теплопроводности имеет следующий вид [1]:

Здесь t, T – время и температура тела, ρ, c, λ – плотность, теплоемкость и коэффициент теплопроводности материала, принимаемые постоянными, x – расстояние, отсчитываемое от носка клина вдоль лучей, проходящих через него, а угол ${\theta }$ отсчитывается от оси клина, ${{{\theta }}_{0}}$ – угол раствора. Начальные и граничные условия:

Здесь q⁺ – тепловой поток к поверхности клина, T_in, T_w, T_e – начальная, при t = 0 его температура, температура его поверхности и так называемая равновесная температура внешнего потока (близкая к его температуре торможения). Формула (1.1) для теплового потока q⁺ взята той же, что и для плоской пластины (например, [2]), с неким коэффициентом ${{{\alpha }}_{n}}$, с n = 1/2 при ламинарном и n = 1/5 при турбулентном пограничных слоях. Такой закон теплообмена приводит к сингулярности управляющего уравнения ((1.4) ниже) в точке x = 0, что существенно осложняет задачу.

Проинтегрировав уравнение по θ, с учетом граничных условий (1.1) , вместо температуры T введем безразмерную среднюю (что допустимо для тонкого клина) температуру

В этом случае уравнение (с заменой ${{T}_{w}} = T$ в силу тонкости клина) примет вид

Введем безразмерные переменные ${\tau }$ и z, используя соответствующие масштабы времени t₀ и длины x₀, которые определим, поделив уравнение (1.2) на ${{\beta } \mathord{\left/ {\vphantom {{\beta } {x_{0}^{k}}}} \right. \kern-0em} {x_{0}^{k}}}$

После преобразований уравнение (1.2) примет следующий вид:

В новых переменных решение этого уравнения будет представлено в виде зависимостей лишь от переменных (τ, z), формулирующих, по сути, закон подобия таких задач, что позволяет проанализировать общие свойства их решений независимо от их определяющих параметров. Например, из формул (1.3) следует, что достигнутая при нагреве температура $T{\text{'}}({\tau },z)$ в какой-либо фиксированной точке (τ, z), с уменьшением угла θ₀ будет перемещаться вперед по координатам (t, x).

Уравнение (1.4) имеет особенность в точке z = 0, поэтому для анализа полезно “растянуть” ее заменой переменных $y = \ln (z)$, преобразовав это уравнение к виду

При этом $y \to - \infty $ при $z \to 0$.

2. ГРАНИЧНЫЕ УСЛОВИЯ И АНАЛИЗ АСИМПТОТИК

Рассмотрим начальные и краевые условия данной задачи. При t = 0 перед началом нагрева температура клина, согласно (1.1), равна начальной, которую, не теряя общности, примем за начало отсчета температур. Далее, на большом удалении от носка, при $z \gg 1$ приток тепла к клину убывает, т.е., согласно (1.1), ${{q}^{ + }} \to 0$ и его температура должна стремиться к начальной.

В качестве же граничного условия при $z \to 0$ примем естественное условие отсутствия сосредоточенного притока тепла в точку $x = z = 0$ для формализации которого используем уравнение баланса тепла в безразмерной форме для малой окрестности клина $\Delta z = z - 0 \ll 1$, которое в свою очередь получим, проинтегрировав по z уравнение (1.4), умноженное на z

Здесь $T_{a}^{'}$ – средняя по отрезку $\Delta z$ температура, в силу предполагаемой непрерывности решения стремящаяся к $T{\text{'}}$ при $z \to 0$. Очевидно, левая часть этого уравнения никак не может быть больше члена ${{q}_{0}}$ справа, исчезающего при $z \to 0$. Следовательно, при этом должно быть и ${{q}_{{\lambda }}} \to 0$. Однако это условие фактически является здесь следствием самого уравнения и, вообще говоря, не может еще считаться наложенным условием данной задачи. В принципе же, вблизи особой точки уравнение (1.4) может иметь множество интегральных кривых, в том числе и удовлетворяющих условию ${{q}_{{\lambda }}} \to 0$ при $z \to 0$, или $y \to - \infty $. И это при одновременном отсутствии условия $\partial T{\text{'/}}\partial y \to 0$, как и в данном случае, в котором из сопоставления двух членов в правой части уравнения (2.1) следует асимптотика $\partial T{\text{'/}}\partial z\sim {{z}^{{ - n}}}$ при $z \to 0$. Поэтому из физических соображений наложим на решение еще условие его ограниченности, т.е. примем уже для уравнения (1.5) условие $\partial T{\text{'/}}\partial y \to 0$ при $y \to - \infty $. Таким образом, искомое решение должно будет удовлетворять следующим условиям:

Установим далее асимптотический закон убывания температуры при $z \to \infty $. Для этого рассмотрим уравнение, получаемое из (1.4) отбрасыванием члена Z. Тогда это уравнение будет иметь решение, удовлетворяющее последнему условию (2.2)

Чтобы убедиться в достоверности этого асимптотического решения, вычислим на нем функцию Z

При этом отношение двух последних членов в уравнении (1.4) будет иметь порядок μ = = $ZT_{\infty }^{{' - 1}}{{z}^{k}} \approx \tau {{z}^{{ - 2}}}$. При $z \to \infty $ и фиксированном τ величина ${\mu } \to 0$, и членом Z в уравнении (1.4) действительно можно пренебречь по сравнению с последним членом. Уравнение (2.3) в этом случае будут справедливыми вместе с его предельным решением, которое таким образом и будет автоматическим “правым” асимптотическим граничным условием задачи. Но при фиксированном z и c ростом τ, при ${\tau /}{{z}^{2}}\sim 1$ и более, пренебречь членом Z в уравнении (1.4) будет уже нельзя, в том числе и в начале нагрева, при ${\tau } \approx 0$, $T{\text{'}} \approx 0$. Это обусловлено тем, что при любом сколь угодно малом ${\tau }$ в малой окрестности острия клина всегда будет присутствовать область с размером $z\sim {{{\tau }}^{{1/2}}}$, и даже с $z \ll {{{\tau }}^{{1/2}}}$ и, следовательно, с не малой величиной Z. Иными словами, продольный отток тепла в этом процессе начинается мгновенно и одновременно с началом внешнего нагрева.

Чтобы прояснить ситуацию в окрестности носка клина, при малыx аргументах ${\tau } \ll 1$, $z \ll 1$ заметим, что члены $\partial T{\text{'/}}\partial t$ и ${{q}_{{\lambda }}}$ в уравнении (2.1) не могут, очевидно, превосходить член ${{q}_{0}}$, т.е. приток тепла извне, и естественно предположить, что в этой окрестности все члены этого уравнения должны иметь одинаковый порядок. Иными словами, члены уравнения (2.1), обусловленные внешним притоком тепла и оттоком его за счет теплопроводности, должны быть сравнимы между собой и вместе определять порядок члена с производной $\partial T_{a}^{{\text{'}}}{\text{/}}\partial t$. Этим окрестность носка отличается от дальней периферии клина, в которой член с притоком тепла является преобладающим.

Тогда для оценок темпа роста температур можно воспользоваться решением (2.3), применив его уже для осредненной по малому отрезку с длиной $\Delta z = z - 0 \ll 1$ температуры в форме

Здесь γ ~ 1 – некоторый коэффициент, учитывающий в том числе и долю внешнего притока тепла, пошедшего на повышение температуры носка клина. Используя далее эту формулу для оценки члена ${{q}_{{\lambda }}}$ в уравнении (2.1), получим оценку отношения ${\mu '} = {{q}_{{\lambda }}}{\text{/}}{{q}_{0}}\sim {\tau /}{{z}^{2}}$. И, наконец, исключив переменную τ из постулированного выше условия (1.4) ${\mu '}\sim 1$, получим в таком приближении следующую оценку для начального мгновенного распределения температуры, осредненной по малой окрестности острия клина размером $\Delta z = z - 0 \ll 1$

А исключив из (2.4) $z\sim {{{\tau }}^{{1/2}}}$, получим зависимость температуры от ${\tau }$ при $z \to 0$

Таким образом, несмотря на неограниченность производной $\partial T{\text{'/}}\partial {\tau }\sim {{{\tau }}^{{m - 1}}} \to \infty $ в точке $z \to 0$ в начальный момент времени ${\tau } \to 0$, температура носка клина растет непрерывным образом. Заметим, что условие $z\sim {{{\tau }}^{{1/2}}}$ определяет порядок области прогрева окрестности носка клина за время τ, которое при малых $z$ и τ оказывается меньшим области $z\sim {{{\tau }}^{{1/k}}}$, чем это было бы при отсутствии оттока тепла из этой области (что следует из (1.2), так как $1 + n < 2$).

3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Производная $\partial T{\text{'/}}\partial z\sim {{z}^{{ - n}}} \to \infty $, при $z \to 0$, что затрудняет непосредственное применение стандартной процедуры метода конечных разностей к численному решению уравнения (1.4). Но этот недостаток устраняется переходом к эквивалентному уравнению (1.5), поскольку переменная $y = \ln z$ переводит сингулярную точку z = 0 в бесконечно удаленную $y \to - \infty $, в которой в силу граничного условия (2.2) обе первых производных по $y$ стремятся к нулю.

Численное решение уравнения (1.4) с условиями (2.2) было получено путем серии расчетов, с увеличивающейся расчетной областью и уменьшающимися шагами по обеим осям. Условиями завершения серии и получения решения являлись сходимость по расчетной сетке и неизменность сеточного решения при увеличении области (при крайне левой границе $y = - 50$ или $z = {{2}^{{ - 22}}}$).

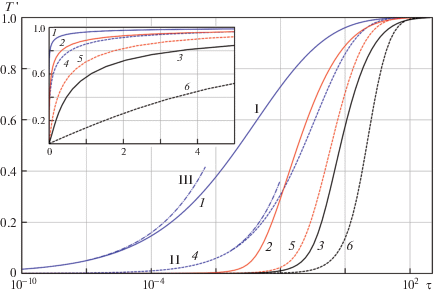
На рис. 1 приведены зависимости безразмерной температуры $T{\text{'}}$ от $\tau $ в логарифмическом и обычном масштабах координат в некоторых сечениях $z = 0{\kern 1pt} - {\kern 1pt} 5$. При этом расчетные кривые при данных z выходят на свои значения, близкие к равновесным, уже при ${\tau } \approx 3{\kern 1pt} - {\kern 1pt} 5$, а при z = 0 и небольших $T'(\tau ,0)$ хорошо согласуются со своими асимптотами $T{\text{'}} = A{{{\tau }}^{m}}$ с коэффициентами A = 5 при n = 1/2, A = 10 при n = 1/5, что подтверждает правильность асимптотики (2.5).

Рис. 1.

Зависимость безразмерной температуры $T{\text{'}}$ от безразмерного времени $\tau $ в логарифмическом масштабе: I – ламинарный режим; II – турбулентный; III – асимптотические решения z = 0, ${\tau } \to 0$; 1, 2 – $z = 0$; 3, 4 – $z = 0.2$; 5, 6 – z = 2.

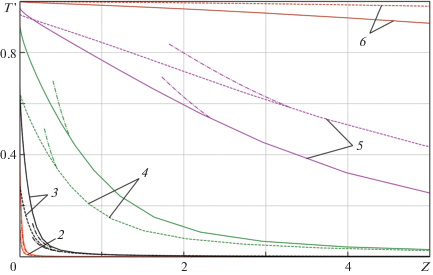
На рис. 2, 3 приведены аналогичные зависимости безразмерной температуры $T{\text{'}}$ от координаты $z$ (в логарифмическом и обыкновенном масштабе соответственно), а также асимптотические кривые (2.3) при фиксированных значениях ${\tau } \approx {{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} 60$. При больших ${\eta } = {\tau /}{{z}^{k}} \geqslant 0.5$ расчетные кривые хорошо соответствуют своим асимптотам, которые, как видно, при ${\tau } \geqslant 3$ вообще служат вполне приемлемой аппроксимацией точных кривых вплоть до предельных величин $T{\text{'}} \approx 1$. В глобальном масштабе задачи $({\tau },z\sim 1{\kern 1pt} - {\kern 1pt} 10)$ вся “переходная” область в окрестности острия клина на рис. 3 стягивается в точку.

Рис. 2.

Зависимость безразмерной температуры $T{\text{'}}$ от безразмерной координаты $z$ в логарифмическом масштабе: I, II как на рис. 1; III – асимптотические решения при $\tau < \infty $, $z \to + \infty $; 1–6 – ${\tau } = 2.5 \times {{10}^{{ - 5}}}$: $4.5 \times {{10}^{{ - 4}}}$, $8.5 \times {{10}^{{ - 3}}}$, $2.5 \times {{10}^{{ - 1}}}$, 2.8, 60.

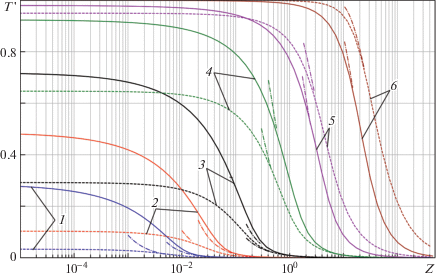
Рис. 3.

Зависимость безразмерной температуры $T'$ от безразмерной координаты $z$; I, II как на рис. 1; III – асимптотические решения при $\tau < \infty $, $z \to + \infty $; 2–5 ${\tau } = 4.5 \times {{10}^{{ - 4}}}$, $8.5 \times {{10}^{{ - 3}}}$, $2.5 \times {{10}^{{ - 1}}}$, 2.8, 60.

ЗАКЛЮЧЕНИЕ

Рассмотрена задача о нагреве острого клина, внезапно погруженного в высокотемпературный сверхзвуковой поток, при ламинарном и турбулентном законах теплообмена. Исследована асимптотика решения в окрестности особой точки на острие клина, температура в которой, однако, растет непрерывным по времени образом. Интенсивность оттока тепла за счет теплопроводности от носка клина сравнима с внешним притоком тепла, который в то же время является основным фактором роста температуры в дальней периферии клина. Исходное сингулярное уравнение теплопроводности преобразовано к виду, пригодному для численного его решения, результаты которого согласуются с полученной асимптотикой.