Известия РАН. Механика жидкости и газа, 2020, № 5, стр. 110-117
Численное моделирование взаимодействия скачка уплотнения с пограничным слоем над движущейся поверхностью
И. В. Егоров a, b, И. М. Илюхин a, b, *, В. Я. Нейланд a
a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Московская обл., Жуковский, Россия
b Московский физико-технический институт (НИУ)
Московская обл., Долгопрудный, Россия
* E-mail: ivan.ilyukhin@phystech.edu
Поступила в редакцию 29.02.2020
После доработки 12.03.2020
Принята к публикации 12.03.2020
Аннотация
Рассматриваются результаты численного моделирования взаимодействия скачка уплотнения с ламинарным пограничным слоем на движущейся плоской пластине, обтекаемой сверхзвуковым потоком совершенного газа при числе Маха М∞ = 3. Скачок уплотнения задается с помощью граничных условий Ренкина–Гюгонио, что соответствует в идеальном газе ударной волне от клина с заданным углом полураствора. Моделирование основано на численном решении двумерных нестационарных уравнений Навье–Стокса методом установления. Для верификации расчетных результатов проводится сравнение отрывного обтекания неподвижной плоской пластины с экспериментальными данными. На основе численных данных исследуется влияние скорости движения пластины на структуру отрывного течения и основные закономерности данной задачи. Показано, что движение стенки вниз по потоку уменьшает протяженность отрывной области, а обратное движение увеличивает.
Взаимодействие скачка уплотнения с пограничным слоем – распространенное явление в сверхзвуковых течениях. Локальный отрыв пограничного слоя, вызванный данным взаимодействием, может существенным образом повлиять на аэродинамическое нагревание и устойчивость течения [1]. Асимптотическая теория свободного взаимодействия для сверхзвукового ламинарного пограничного слоя в двумерной постановке [2–4] описывает отрыв, индуцируемый над неподвижной стенкой неблагоприятным градиентом давления. В частности, градиент давления может быть вызван падением на пограничный слой скачка уплотнения. Возникающее из-за этого возмущение передается вверх по потоку по дозвуковой части пограничного слоя, отклоняя струйки тока. Это, в свою очередь, изменяет внешнее невязкое течение через образование волн сжатия. В точке на стенке, в которой трение равно нулю, начинается отрыв пограничного слоя. Масштаб окрестности отрыва, согласно асимптотической теории, пропорционален Re$_{s}^{{ - 3{\text{/}}8}}$, где Res – число Рейнольдса, посчитанное по расстоянию от передней кромки пластины до точки отрыва. Скачок уплотнения отражается от оторвавшегося пограничного слоя в виде веера волн разряжения. За точкой отрыва внутри пограничного слоя находится рециркуляционная область, в которой давление примерно постоянно. В окрестности точки присоединения наблюдаются веер волн сжатия и скачок уплотнения.
На практике часто приходится иметь дело с ситуациями, в которых ударная волна может двигаться вниз и вверх по потоку. Такие течения встречаются в воздухозаборниках, каналах и других газодинамических устройствах. При построении асимптотической теории и численном исследовании можно перейти в систему координат, движущуюся со скоростью скачка уплотнения Vsh. В данной системе скачок уплотнения покоится, а стенка движется со скоростью –Vsh. В [5–7] получены асимптотические решения данной задачи, в [6] представлены также результаты численных расчетов.
В настоящей работе исследуется взаимодействие сверхзвукового ламинарного пограничного слоя на плоской пластине, движущейся вверх или вниз по потоку, с неподвижным скачком уплотнения. Моделирование основано на решении нестационарных двумерных уравнений Навье–Стокса с помощью оригинальных численных программ [8, 9].
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается обтекание плоской пластинки с различными значениями скорости ее поверхности. Выбрано два расчетных варианта. Первый из них использован для верификации численного решения задачи о взаимодействии скачка уплотнения с пограничным слоем. В этом случае параметры потока выбраны в соответствии с экспериментом [10], в котором проводились исследования отрывных течений ламинарного, переходного и турбулентного пограничного слоя. В этих экспериментах рассматривалась покоящаяся стенка. Другой вариант расчета соответствует режиму обтекания плоской пластины в сверхзвуковой аэродинамической трубе ЦАГИ. Основные определяющие параметры задачи обтекания плоской пластины для каждого из вариантов представлены в табл. 1 (индексом “∞” отмечены параметры набегающего потока, “w” – на стенке, “0” – параметры адиабатически заторможенного газа). Для второго расчетного случая скорость стенки, отнесенная к скорости набегающего потока, α изменялась в пределах от –0.02 до 0.02. Температура пластинки в обоих вариантах фиксирована и выбрана равной температуре восстановления. Это граничное условие соответствует нагреву теплоизолированной модели в сверхзвуковой аэродинамической трубе непрерывного действия. Общая схема течения представлена на рис. 1. В обоих расчетных случаях T∞ = 293 K, число Прандтля Pr = 0.72, показатель адиабаты γ = 1.4. Вязкость определяется по формуле Сазерленда. Скачок уплотнения, взаимодействующий с ламинарным пограничным слоем, был смоделирован с помощью внешних граничных условий, в которых использовано точное решение невязкой задачи обтекания клина с углом полураствора φ. Параметры за скачком уплотнения определяются с помощью соотношений Ренкина–Гюгонио.
Таблица 1.
Параметры газа для двух расчетных вариантов
| M∞ | Tw/T0 | ReL ⋅ 10–6 | φ | |
|---|---|---|---|---|
| 1 | 2.3 | 0.92 | 0.617 | 4° |
| 2 | 3 | 0.9 | 2 | 1.92° |
При решении уравнений Навье–Стокса на входной сверхзвуковой границе задаются значения зависимых переменных задачи, соответствующих невозмущенному потоку. На нижней поверхности расчетной области, совпадающей с плоской пластиной, использованы условия изотермической поверхности со значением температуры, равной температуре восстановления, нулевого значения нормальной компоненты вектора скорости, постоянного значения продольной компоненты вектора скорости ${{u}_{w}} = \alpha {{u}_{\infty }}$, соответствующей скорости движения плоской пластины. На верхней поверхности расчетной области значения зависимых переменных задачи равны их значениям, полученным при решении невязкой задачи обтекания клина с углом полураствора φ. Угол полураствора клина φ связан с компонентами скорости за скачком уплотнения: tg(φ) = ${\text{|}}{{{v}}_{{sh}}}{\text{/}}{{u}_{{sh}}}{\text{|}}$, а также с углом наклона ударной волны θ, определяемым из условий Ренкина–Гюгонио [11]
На выходной границе расчетной области, соответствующей сверхзвуковому течению, использованы мягкие условия экстраполяции зависимых переменных.
Значение угла полураствора клина, являющегося генератором скачка уплотнения, было выбрано достаточно малым, так как большие углы, соответствующие большим перепадам давления, могут привести к неустойчивости двумерного стационарного ламинарного отрывного течения [12]. В настоящей работе использовались два значения угла φ: 4° для сравнения с экспериментом и 1.92° для исследования влияния скорости стенки на течение в пограничном слое.
В свою очередь, наклон ударной волны θ связан с перепадом давления
2. ЧИСЛЕННЫЙ МЕТОД
Для численного решения задачи используются двумерные нестационарные уравнения Навье–Стокса и краевые условия, описанные выше. Расчеты выполнены с помощью оригинальных программ [8, 9], в которых решается система уравнений Навье–Стокса для совершенного газа с постоянными значениями показателя адиабаты и числа Прандтля. Используется неявная консервативная схема (метод конечных объемов) второго порядка точности по пространству. Конвективные члены уравнений аппроксимируются с помощью разностной схемы WENO третьего порядка [13]. Значение энтропийной коррекции ε [8] в приближенном методе Роу решения задачи Римана о распаде произвольного разрыва выбрано ε = 0.01.
Численную диссипацию данной схемы удается уменьшить, используя достаточно мелкую сетку.
Это позволяет надежно моделировать такие нестационарные процессы, как восприимчивость
и неустойчивость сверхзвуковых пограничных слоев [9], нелинейное развитие возмущений в пограничном слое на пластине [14] и в зоне ламинарного отрыва на угле сжатия [15]. Уравнения Навье–Стокса интегрируются в безразмерных переменных: $x = x{\text{*/}}L{\text{*}}$, $y = y{\text{*/}}L{\text{*}}$, u = = $u{\text{*/}}u_{\infty }^{*}$, ${v} = {v}{\text{*/}}u_{\infty }^{*}$, $t = t{\text{*}}u_{\infty }^{*}{\text{/}}L{\text{*}}$, $\rho = \rho {\text{*/}}\rho _{\infty }^{*}$, 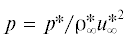 , $T = T{\text{*/}}T_{\infty }^{*}$, $\mu = \mu {\text{*/}}\mu _{\infty }^{*}$. Верхним индексом “*” отмечены размерные величины, L* – длина рассматриваемой пластины.
, $T = T{\text{*/}}T_{\infty }^{*}$, $\mu = \mu {\text{*/}}\mu _{\infty }^{*}$. Верхним индексом “*” отмечены размерные величины, L* – длина рассматриваемой пластины.
Стационарное решение получается методом установления по времени. При аппроксимации производных по времени в уравнениях Навье–Стокса использовалась неявная схема Эйлера первого порядка точности. В начальный момент времени значения зависимых переменных задаются равными их значениям в невозмущенном набегающем потоке.
На рис. 2 представлена топология расчетной сетки для случая M∞ = 3. Для эффективности распараллеливания вычислительного алгоритма [9] она была разбита на блоки, примерно одинаковые по числу узлов. Использование неструктурированной расчетной сетки обусловлено сокращением вычислительных затрат. Высота левой границы определяется углом наклона косой ударной волны таким образом, чтобы область взаимодействия скачка уплотнения с пограничным слоем находилась примерно в центре пластины.
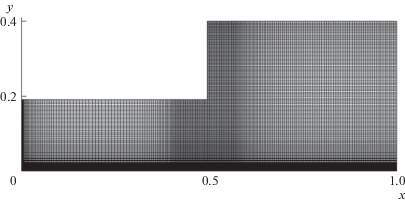
Рис. 2.
Топология расчетной сетки; для корректного представления на рисунке изображен каждый четвертый узел расчетной сетки.
Для разрешения ламинарного пограничного слоя [16] узлы расчетной сетки сгущены у пластины таким образом, чтобы на толщину пограничного слоя приходилось около 500 узлов в области его взаимодействия со скачком уплотнения. При этом распределение узлов в пограничном слое равномерно по нормальной координате, что обеспечивает второй порядок точности аппроксимации диссипативных членов в уравнениях Навье–Стокса с применением схемы центральных разностей. Следует отметить, что в вязкой подобласти толщиной Re$_{s}^{{ - 5.8}}$ содержится достаточно много расчетных точек.
Вдоль оси x сетка также имеет сгущения. У передней кромки это необходимо, чтобы точнее разрешить слабый скачок уплотнения от пограничного слоя. Для более детального разрешения отрывного течения в окрестности взаимодействия скачка уплотнения и пограничного слоя выбиралось сгущение узлов по координате x. При этом вся отрывная область покрыта равномерной расчетной сеткой по координатам x и y.
3. ВЕРИФИКАЦИЯ ЧИСЛЕННОГО МЕТОДА
На первом этапе численного решения задачи проведена верификация численного метода на основе сравнения расчетных данных и данных, полученных с помощью автомодельного решения уравнений пограничного слоя Блазиуса [16] для обтекания неподвижной плоской пластины сверхзвуковым потоком газа M∞ = 3. На рис. 3а представлены результаты сравнения профилей продольной компоненты вектора скорости в трех различных сечениях по x с автомодельным решением для вязкого сжимаемого пограничного слоя над плоской пластинкой. Согласно этим данным, максимальное различие в значениях скорости и температуры в области взаимодействия составляет менее 0.3% и обусловлено, в основном, изменениями параметров потока за слабым скачком уплотнения от передней кромки пластинки.
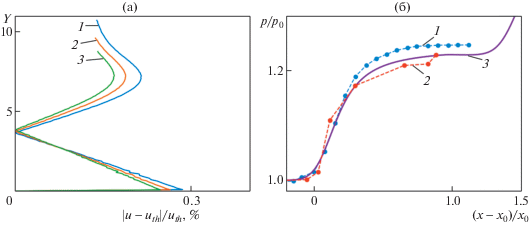
Рис. 3.
Верификация численного метода. Модуль разности продольной компоненты скорости в сечениях x = 0.4 (1), x = 0.5 (2), x = 0.6 (3) с автомодельным решением уравнений вязкого сжимаемого пограничного слоя над пластинкой (а); расчетное и экспериментальное [10] распределение нормированного давления в окрестности смещенной точки начала взаимодействия x0 для M∞ = 2.3; в расчете (3) Re0 = Rex(x0) = 0.172 ⋅ 106, 1, 2 – Re0 = 0.148 ⋅ 106, 0.2 ⋅ 106 (б).
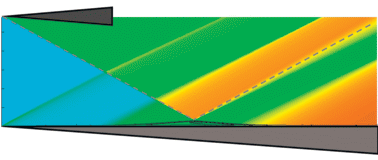
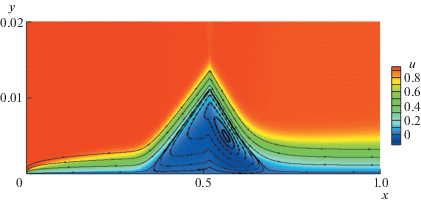
Для верификации результатов численного моделирования взаимодействия скачка уплотнения с пограничным слоем параметры набегающего потока (M∞ = 2.3) и скачок уплотнения были выбраны в соответствии с экспериментальными данными [10]. Поле продольной компоненты вектора скорости вблизи поверхности для данного режима показано на рис. 4. Для более наглядной визуализации течения данная картина растянута по нормальной координате. Линии I на рис. 4 соответствуют линиям тока, иллюстрирующим зону отрыва пограничного слоя и ее масштаб по сравнению с масштабом пограничного слоя. Следует отметить, что для данного расчетного случая область отрыва получается достаточно протяженной. В средней части отрывной зоны имеет место торможение линий тока возвратного течения. Это свидетельствует о возможности появления вторичного отрыва и, как следствие, неустойчивости двумерного стационарного отрывного течения [12].
Рис. 4.
Поле продольной компоненты вектора скорости и линии тока возвратного течения для расчетного варианта 1 (M∞ = 2.3).
Полученное в расчете распределение давления по поверхности пластины в окрестности точки отрыва показано на графике рис. 3б. Там же представлены экспериментальные данные из [10]. Символами 1, 2 обозначены экспериментальные данные при разных значениях числа Рейнольдса, посчитанного длине x0, соответствующей точке распространения возмущений вверх по потоку. Значение x0 можно определить как разность ${{x}_{{sh}}} - \lambda $, где xsh – координата падения скачка уплотнения на пограничный слой, а λ – глубина распространения возмущений давления вверх по потоку. Чтобы сравнение с экспериментом было более корректным, принято решение соединить кривые в исходной точке, в которой p/p0 = 1, и согласно этому сместить x0. Значение давления p0 на стенке было выбрано равным минимальному давлению в некоторой окрестности точки отрыва до начала области свободного взаимодействия, аналогично [10]. Результаты сравнения экспериментальных и расчетных данных, представленные на рис. 3б, свидетельствуют об их хорошем согласовании.
4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
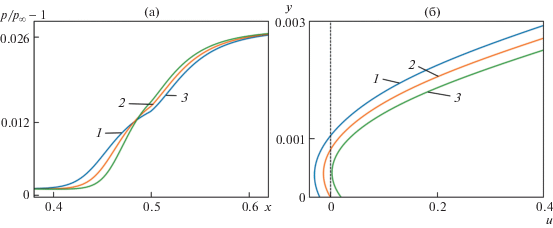
Основные расчетные исследования влияния скорости движения стенки на структуру течения и основные характеристики в области взаимодействия скачка уплотнения с пограничным слоем проведены для M∞ = 3. На рис. 5а изображены графики распределения давления по поверхности пластины для этого случая при различных значениях скорости движения стенки. Видно, что в распределении давления по пластине имеются две характерные особенности: “плато” давления в области отрыва и максимум давления при приближении к точке присоединения потока. При этом увеличение скорости движения стенки вниз по потоку уменьшает размер плато давления, а движение стенки вверх по потоку напротив, расширяет ее. В [10] более протяженная область плато давления связана с более развитой отрывной зоной в пограничном слое. В [6] отмечено, что уменьшение плато соответствует исчезновению возвратного течения в пограничном слое.
Рис. 5.
Распределение нормированного давления в окрестности падения скачка уплотнения (а) и профили продольной компоненты вектора скорости в отрывной зоне при x = 0.5 (б) для различных значений скорости стенки: 1–3 – α = –0.02, 0, 0.2; расчетный вариант 2 (М∞ = 3).
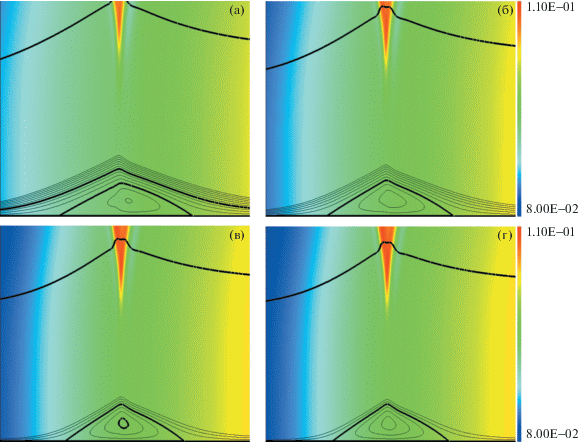
На рис. 6 показана структура течения в отрывной зоне в зависимости от скорости движения стенки. На этих рисунках верхняя выделенная изолиния соответствует, примерно, внешней границе пограничного слоя (u = 0.95). Толстые изолинии в отрывной области соответствуют нулевому значению продольной компоненты вектора скорости (u = 0) и значению скорости стенки (u = α). Для наглядности физическая область рис. 6 растянута по вертикальному направлению. Поле давления совместно с изолиниями продольной компоненты вектора скорости в отрывной области (рис. 5 и рис. 6) наглядно иллюстрируют основные закономерности топологии течения в пограничном слое в зависимости от скорости стенки. В частности, исчезновение “плато” в распределении давления при α = 0.02 соответствует исчезновению изолинии продольной компоненты скорости u = 0 (рис. 6г). Следует отметить, что для выбранных параметров задачи (чисел Маха и Рейнольдса, интенсивности косого скачка уплотнения) толщина отрывной зоны в несколько раз меньше толщины пограничного слоя, а длина отрывной зоны имеет один порядок с толщиной пограничного слоя.
Рис. 6.
Поле давления и изолинии продольной компоненты вектора скорости, изменяющиеся в диапазоне от –0.03 до 0.03 с шагом 0.005, в области отрыва для различных значений скорости движения пластины: а–г – α = = –0.02, 0, 0.015, 0.2; выделенные изолинии соответствуют границе пограничного слоя (u = 0.95), скорости стенки u = α и значению u = 0; x находится в диапазоне от 0.45 до 0.55, y – от 0 до 0.005.
Графики рис. 5б иллюстрируют влияние скорости стенки на профили продольной компоненты вектора скорости в сечении х = 0.5. Данное сечение находится примерно в середине отрывной зоны и соответствует точке, в которой скачок уплотнения попадает на пограничный слой. Из графиков хорошо видно, что при α = 0.02 скорость в отрывной зоне становится всюду положительной, при этом характер поведения профиля такой же, как и при α = 0. Максимальное различие в значении продольной компоненты скорости при изменении α отмечается примерно при u ≈ 0.5. В частности, для u = 0.5 при ∆α = 0.04 получается ∆u ≈ 0.145. Число узлов расчетной сетки по направлению y, по которым были построены профили скорости рис. 5б, равно 480. При этом узлы распределены равномерно по y.
В случае подвижной стенки нельзя определять точку отрыва пограничного слоя как место на поверхности пластины, в которой только трение равно нулю (du/dy = 0). Вместо этого следует использовать другие критерии. В настоящей работе для определения точки отрыва при положительных значениях α используется критерий отрыва Сирса–Мура–Ротта [6]: началу отрыва соответствует точка над стенкой на минимальном расстоянии от передней кромки, в которой du/dy и скорость обращаются в нуль. В случае отрицательных α возвратное течение существует всюду в некоторой окрестности стенки. В связи с этим становится труднее подобрать единый критерий отрыва для сравнения разных типов течений.
На рис. 7а представлена зависимость минимального значения продольной компоненты скорости в пограничном слое (максимальной скорости возвратного течения) от скорости стенки α. Несмотря на то что расстояние между точками на стенке, в которых du/dy = 0 является положительным при любых значениях скорости движения пластинки, при α = 0.02 продольная компонента вектора скорости в пограничном слое всюду больше нуля. Это значит, что по критерию Сирса–Мура–Ротта на данном режиме отсутствует отрыв пограничного слоя. Кроме этого, в распределении давления исчезает характерное плато, что качественно соответствует выводам статьи [6]. Следует отметить, что зависимость от α минимального значения продольной компоненты скорости в пограничном слое близка к линейной. Характер поведения отрывной зоны, полученный на основе численного моделирования, качественно согласуется с результатами асимптотической теории [6, 7].
Рис. 7.
Минимальное значение продольной компоненты вектора скорости u в пограничном слое (а) и длина распространения возмущений давления от скачка уплотнения вверх по потоку λ, отнесенная к значению при α = 0 (б) в зависимости от скорости стенки α.
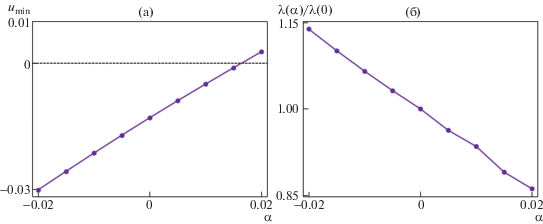
На рис. 7б нанесена зависимость глубины распространения возмущений давления вверх по потоку, отнесенной к своему значению при α = 0, от скорости стенки. Из нее следует, что при движении стенки вниз по потоку возмущения давления от скачка уплотнения локализуются, а при движении стенки вверх по потоку – распространяются выше по пограничному слою. Таким образом, наблюдается качественное соответствие с [6, 7].
ЗАКЛЮЧЕНИЕ
Проведено численное моделирование взаимодействия скачка уплотнения с пограничным слоем на двух режимах: над неподвижной стенкой при параметрах, соответствующих эксперименту, и над подвижной стенкой. Корректность численного метода подтверждена сравнением с теоретическими и экспериментальными данными. Результаты численного моделирования для подвижной стенки качественно согласуются с результатами асимптотической теории. Получена зависимость минимального значения скорости в области отрыва от скорости стенки, близкая к линейной.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-01-00525.
Список литературы
Babinsky H., Harvey J.K. Shock-Wave – Boundary-Layer Interactions. Cambridge University Press, 2011.
Нейланд В.Я. Сверхзвуковое течение вязкого газа вблизи точки отрыва. III Всесоюзный съезд по теоретической и прикладной механике. 25.01–01.02.1968. Сб. аннотаций докладов съезда. М.: Наука, 1968. С. 224.
Нейланд В.Я. К теории отрыва ламинарного пограничного слоя в сверхзвуковом потоке // Изв. АН СССР. МЖГ. 1969. а – № 4. С. 53–57.
Stewartson K., Williams P.G. Self-Induced Separation // Proc. Roy. Soc. Ser. A. 1969. V. 312. № 1509. P. 181–206.
Крапивский П.Л., Нейланд В.Я. Отрыв пограничного слоя от подвижной поверхности тела в сверхзвуковом потоке газа // Ученые записки ЦАГИ. Т. 13. № 3. С. 32–42.
Ruban A.I., Araki D., Yapalarvi R., Gajjar J.S.B. On unsteady boundary-layer separation in supersonic flow. Part 1. Upstream moving separation point // J. Fluid Mech. 2011. V. 678. P. 124–155.
Нейланд В.Я. Асимптотическая теория зарождения отрыва пограничного слоя при взаимодействии с бегущей ударной волной // Ученые записки ЦАГИ. 2020. № 2.
Башкин В.А., Егоров И.В. Численное моделирование динамики вязкого совершенного газа. М.: ФИЗМАТЛИТ, 2012. 372 с.
Егоров И.В., Новиков А.В. Прямое численное моделирование ламинарно-турбулентного обтекания плоской пластины при гиперзвуковых скоростях потока // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 1064–1081.
Chapman D.R., Kuehn D.M., Larson H.K. Investigation of Separated Flows in Supersonic and Subsonic Streams with Emphasis on the Effect of Transition // NACA Report 1356, 1957.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: учеб. пособ.: Для вузов. В 10 т. Т. VI. Гидродинамика. 6-е изд., испр. М. ФИЗМАТЛИТ, 2015. 728 с.
Egorov I.V., Neiland V.Ya., Shvedchenko V.V. Three-dimensional Flow Structures at Supersonic Flow over the Compression Ramp // AIAA Paper, 2011-730, 2011. P. 1–18.
Jiang G.-S., Shu C.-W. Efficient implementation of weighted ENO schemes // Journal of Computational Physics. 1996. V. 126. № 1. P. 202–228.
Динь К.Х., Егоров И.В., Федоров А.В. Влияние волн Маха на ламинарно-турбулентный переход при сверхзвуковом обтекании плоской пластины // Изв. РАН. МЖГ. 2018. № 5. С. 113–124.
Novikov A., Egorov I., Fedorov A. Direct Numerical Simulation of Wave Packets in Hypersonic Compression-Corner Flow // AIAA J. 2016.V. 54. № 7. P. 2034–2050.
Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа