1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2020

Известия РАН. Механика жидкости и газа, 2020, № 4, стр. 3-10

О взаимодействии стационарных возмущений с волнами Толлмина–Шлихтинга в сверхзвуковом пограничном слое

С. А. Гапонов a, *, Н. М. Терехова a, **

a Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Новосибирск, Россия

* E-mail: gaponov@itam.nsc.ru
** E-mail: terekh@itam.nsc.ru

Поступила в редакцию 22.11.2019
После доработки 19.12.2019
Принята к публикации 19.12.2019

Полный текст (PDF)

Аннотация

Изучается возможность управления нестационарными возмущениями, бегущими волнами Толлмина–Шлихтинга, стационарными продольными структурами. Исследования проведены для пограничного слоя на плоской пластине при числе Маха набегающего потока M = 2. Рассмотрена возможность усиления и подавления роста этих волн полосчатыми стационарными структурами собственной задачи устойчивости сверхзвукового пограничного слоя. Задача решается в локально-параллельном приближении в рамках трехволнового резонансного взаимодействия. Волной накачки выступает стационарное почти полосчатое образование. Показано, что даже в устойчивой области под влиянием продольных структур имеет место нарастание волн Толлмина–Шлихтинга. Установлено, что при определенных условиях влияние стационарных возмущений на эти волны заметно и в неустойчивой области, найдены диапазоны чисел Рейнольдса, в которых стационарные возмущения подавляют бегущие волны.

Ключевые слова: пограничные слои сжимаемого газа, гидродинамическая устойчивость, слабонелинейная теория

При малой степени турбулентности внешнего течения в области, предшествующей переходу пограничного слоя в турбулентное состояние, наблюдаются волны, нарастающие вниз по потоку. В случае несжимаемой жидкости эти волны хорошо описываются линейной теорией устойчивости пограничного слоя Толлмина–Шлихтинга, а для сжимаемого газа теорией Лиза–Линя–Дана. Упомянутые теории подробно описаны в [1, 2].

Другой тип перехода связан с присутствием стационарных возмущений в устойчивой области. Интерес к изучению трехмерных возмущений во многом определился [3], где были обнаружены периодические в боковом направлении стационарные изменения продольной скорости, которые слабо изменялись в продольном направлении. Впоследствии аналогичные возмущения стали называть клебановскими модами или продольными структурами. Экспериментально взаимодействие внешней турбулентности с дозвуковым пограничным слоем на плоской пластине исследовалось в ряде работ, обзор которых можно найти в [4, 5]. Во всех этих работах отмечается, что в результате взаимодействия внешней турбулентности с пограничным слоем, в устойчивой относительно малых возмущений области наблюдаются продольные стационарные структуры. Профиль продольной скорости, возбужденный внешней турбулентностью в диапазоне низких частот, имеет колоколообразной вид, максимум которого располагается на расстоянии от стенки ${{y}_{{\max }}} \approx 2.5{\delta }$, где δ – толщина Блазиуса.

Теоретически такое взаимодействие впервые исследовано в [6], где было установлено, что амплитуда толщины пограничного слоя, периодически изменяющаяся в z-направлении с волновым числом β, нарастала линейно вниз по потоку под воздействием продольной внешней завихренности и была пропорциональна β. Можно отметить полное совпадение с зависимостью амплитуды возмущения толщины пограничного слоя, приведенной в [7]. Форма профиля возмущений продольной скорости в нормальном к стенке направлении совпадала с профилем собственных возмущений, полученных в [8] для случая двумерных возмущений (β = 0). Следует заметить, что теория [6] применима только при достаточно малых волновых числах β или больших периодов завихренности. Более точные, с применением параболизованных уравнений устойчивости, результаты были получены в [9, 10]. В результате расчетов [9] было установлено, что форма профиля возмущений продольной скорости практически не зависела от волнового числа β. Его амплитуда росла пропорционально толщине пограничного слоя, то есть $\sqrt {{{{\operatorname{Re} }}_{x}}} $.

Что касается более поздних исследований по возбуждению продольных структур в дозвуковом пограничном слое с использованием численных методов, то можно констатировать хорошую корреляцию с экспериментальными данными. Более того, в некоторых случаях (при специально выбранных параметрах внешней завихренности) получено и количественное совпадение. Достаточно подробную информацию о теоретических работах по взаимодействию вихревых возмущений с дозвуковым пограничным слоем можно найти в [11].

Исследования по порождению продольных структур внешними гидродинамическими (возмущение давления не равно нулю), вихревыми и тепловыми возмущениями в пограничных слоях сжимаемого газа с использованием параболизованных уравнений устойчивости были начаты в [12, 13]. В них было установлено, что возбуждение стационарных возмущений продольной скорости в сверхзвуковом пограничном слое аналогично случаю дозвукового пограничного слоя. Эффективность порождения продольных структур гидродинамическими и вихревыми возмущениями преобладала над эффективностью тепловых волн. Амплитуда возмущений скорости при заданной амплитуде внешних возмущений снижалась с увеличением числа Маха.

Последующие теоретические и численные изучения порождения стационарных возмущений в сверхзвуковом пограничном слое внешними волнами показали хорошее согласие с основными выводами [12, 13]. В той или иной мере взаимодействие внешней турбулентности с пограничным слоем может быть описано сплошным спектром линейных уравнений задачи устойчивости. Впервые связь сплошного спектра с задачей о взаимодействии внешних возмущений (акустических) с параллельным течением в пограничном слое была указана в [14]. По-видимому, наиболее активно возможность описания взаимодействия вихревых возмущений во внешнем потоке с пограничным слоем посредством сплошного спектра стала использоваться после появления статей [15, 16]. Нужно отметить, что сплошной спектр не всегда, в полной мере, описывает такое взаимодействие. В [17] подчеркивается, что в задаче взаимодействия внешней завихренности с пограничным слоем необходимо учитывать непараллельность течения. Продольные структуры, максимально нарастающие на начальном участке продольной координаты, кроме того, были предсказаны в [18–20] на основе теории алгебраического нарастания возмущений [21–23].

Другое объяснение порождения интенсивных возмущений в пограничном слое состоит в квазирезонансном взаимодействии внешних возмущений с собственными волнами пограничного слоя [24]. Исследования проведены как для дозвукового, так и сверхзвукового обтекания пластины, и показано, что структура течения в пограничном слое, возбужденная продольной завихренностью внешнего потока, практически совпадает с собственными стационарными возмущениями. Для сверхзвуковых течений, наряду с продольными стационарными структурами в пограничном слое, имеют место стационарные возмущения, возбуждаемые волнами Маха, которые исследовались в [25].

Стационарные возмущения, как предел нестационарных волн, распространяющихся вверх по потоку, были обнаружены в [26]. В [27] найдено более трех семейств стационарных и квазистационарных волн. Подробно исследованы свойства трех типов возмущений: 1) умеренно затухающие; 2) интенсивно затухающие вниз по потоку с малыми продольными волновыми числами; 3) сильно нарастающие (по-видимому, распространяющиеся вверх по потоку).

Стационарные продольные структуры могут появиться в результате нелинейного взаимодействия двух наклонных нарастающих волн [28], в том числе при наклонном ламинарно-турбулентном переходе [29, 30]. Во всех этих исследованиях на входе в расчетную область амплитуда продольной структуры задавалась более чем на порядок меньше амплитуды наклонной волны Толлмина–Шлихтинга. Однако представляет интерес возможность усиления (замедления) роста бегущих волн полосчатыми стационарными структурами собственной задачи устойчивости сверхзвукового пограничного слоя [27]. Учитывая, что параметры последних возмущений аналогичны параметрам полосчатых структур, возбужденных внешней турбулентностью, результаты по воздействию собственных стационарных возмущений на волны Толлмина–Шлихтинга можно использовать в предсказании влияния внешней турбулентности на ламинарно-турбулентный переход пограничного слоя. Кроме того, эти данные могут применяться для управления нарастанием волн Толлмина–Шлихтинга и тем самым положением перехода. В качестве примера такого управления можно сослаться на статьи [31–33].

Задача решается в рамках трехволнового резонансного взаимодействия [34, 35] в локально-параллельном приближении. Исследования проводились при условии, что одна волна (с наибольшим инкрементом) имела частоту ω, а две другие – ω/2. Однако в пограничном слое, особенно при сверхзвуковых скоростях, волны с другими частотами могут находиться в квазирезонансном взаимодействии с основной волной. Кроме того, в качестве основной волны (волны накачки) могут выступать низкочастотные возмущения. В качестве примера можно сослаться на статью [36], где в качестве волны накачки были колебания с частотой, много меньшей частот волн Толлмина–Шлихтинга, которые могли усиливаться низкочастотными возмущениями. В данной работе волной накачки выступает стационарное почти полосчатое образование. Основное внимание уделяется квазистационарным возмущениям [27] первого типа.

Физическую интерпретацию генезиса полосчатых структур можно связать с наличием на обтекаемой поверхности элементов шероховатости, в качестве которых могут быть рассмотрены различного рода заклепки. От таких элементов вниз по потоку распространяются различного вида стационарные волны. Меняя высоту элементов шероховатости, можно изменять амплитуду стационарной волны, а меняя расстояние между заклепками – их азимутальные волновые числа.

1. ОСНОВНЫЕ УРАВНЕНИЯ

Рассматривается взаимодействие стационарной волны с амплитудой АST и двумя косыми нестационарными волнами, которые симметричны по отношению друг к другу с амплитудами А1 и А–1. Параметры таких бегущих волн пропорциональны $q(y)\exp (i({\theta } + i\int {{{{\alpha }}^{i}}dx} )$, где θ = βz + $\int {{{{\alpha }}^{r}}dx} $ – ωt. Здесь x, z, y – координаты, отнесенные к толщине пограничного слоя ${\delta } = \sqrt {x{{{\nu }}_{e}}{\text{/}}{{u}_{e}}} $ в направлениях: основного потока, в поперечном к нему и нормально к обтекаемой поверхности, t – время, αr и β – значения проекций волнового вектора k на x и z, ω частота бегущей волны. Для любого режима вводились безразмерный параметр частоты волны F, связанный с частотой соотношением F = ω/Re, и безразмерный волновой параметр b = β × 103/Re, где Re – число Рейнольдса, построенное по толщине пограничного слоя.

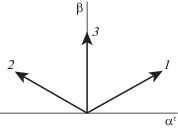
Направления волновых векторов ${{{\mathbf{k}}}_{j}} = {\alpha }_{j}^{r} + {{{\beta }}_{j}}$ показаны на рис. 1.

Рис. 1.

Направления волновых векторов взаимодействующих волн: k1 и –k–1 бегущие волны с азимутальными числами β и –β (1, 2) и kST стационарная волна 2β (3).

В соответствии с теорией [34] соответствующие амплитудные уравнения запишутся как

$\frac{{d{{A}_{{St}}}}}{{d\xi }} = - \alpha _{{{{A}_{{ST}}}}}^{i}{{A}_{{ST}}} + {{S}_{{{{A}_{{ST}}}}}}{{A}_{1}}{{A}_{{ - 1}}}$
$\frac{{d{{A}_{1}}}}{{d\xi }} = - \alpha _{{{{A}_{1}}}}^{i}{{A}_{1}} + {{S}_{{{{A}_{1}}}}}{{A}_{{ST}}}A_{{ - 1}}^{*}$
$\frac{{d{{A}_{{ - 1}}}}}{{d\xi }} = - \alpha _{{{{A}_{{ - 1}}}}}^{i}{{A}_{{ - 1}}} + {{S}_{{{{A}_{{ - 1}}}}}}{{A}_{{ST}}}A_{1}^{*}$

Здесь ${\alpha }_{j}^{i}$ – степени линейного нарастания (затухания) соответствующих волн, $S_{{k,l}}^{j}$ – коэффициенты взаимодействия, $d{\text{/}}d{\xi } = 1{\text{/}}2 \cdot d{\text{/}}d\operatorname{Re} $, ${{{\nu }}_{e}}$, ${{u}_{e}}$ – кинематическая вязкость и скорость на границе пограничного слоя. Звездочкой обозначены комплексно сопряженные величины. Коэффициенты взаимодействия $S_{{k,l}}^{j}$ определяются соотношениями

$S_{{k,l}}^{j} = {{\int\limits_0^\infty {(Z_{j}^{ + } \cdot Q_{{k,l}}^{j})dY} } \mathord{\left/ {\vphantom {{\int\limits_0^\infty {(Z_{j}^{ + } \cdot Q_{{k,l}}^{j})dY} } {\int\limits_0^\infty {(Z_{j}^{ + } \cdot \partial L({{Z}_{j}}){\text{/}}\partial {{{\alpha }}_{j}})dY} }}} \right. \kern-0em} {\int\limits_0^\infty {(Z_{j}^{ + } \cdot \partial L({{Z}_{j}}){\text{/}}\partial {{{\alpha }}_{j}})dY} }}$
где L – линейный дифференциальный оператор уравнений устойчивости, а Zj – вектор-функция решения системы уравнений $L({{Z}_{j}}) = 0$ с однородными граничными условиями, $Z_{j}^{ + }$ – вектор-функция решения уравнений сопряженного оператора L+, Q – вектор нелинейных членов второго порядка. В данной работе для построения решения и нахождения собственных значений αj использовались уравнения Дана–Линя [2]. Подробную информацию о трехволновом взаимодействии для сверхзвукового пограничного слоя можно найти в [35, 36]. Все результаты получены при числе Маха M = 2.

2. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Рассмотрено взаимодействие в двух триплетах с разными азимутальными волновыми параметрами, что служило целью выявления влияния частоты почти продольных полос на рост или затухание бегущих волн. Параметры взаимодействующих волн были следующие. В первом триплете азимутальные параметры волн: b1 = 0.075, b–1 = –0.075, а bST = 0.15; во втором триплете: b1 = = 0.0675, b–1 = –0.0675 и bST = 0.135. Рассмотрены три частоты бегущих волн с разными соотношениями диапазонов их затухания и роста. Частотные параметры следующие: F1 = 0.192 × 10–4; F2 = 0.384 × 10–4; F3 = 0.576 × 10–4.

Также были рассмотрены два семейства стационарных (или почти стационарных) волн. Волны второго семейства из [27] сильно затухают вниз по потоку, их декременты значительно превосходят декременты волн первого семейства.

На рис. 2 показаны зависимости коэффициентов продольного нарастания нестационарных и стационарных волн первого семейства от чисел Рейнольдса, из которых видно, что на низкой частоте F1 очень значителен диапазон затухания, а нижняя ветвь нейтральной кривой достигается при R = 625. Далее следует рост амплитуды волны, с невысоким инкрементом, который достигает максимума в конце рассмотренного диапазона чисел Re (кривая 1). Для частоты с F2 уменьшается диапазон подавления и увеличивается диапазон роста амплитуды по линейной теории (2). На самой высокой из рассмотренных частот F3 был пройден весь диапазон роста внутри нейтральной кривой, достигнута верхняя ветвь и далее переход в диапазон затухания правее верхней ветви (3).

Рис. 2.

Инкременты бегущих волн с |b| = 0.075 на частотах F = (0.192, 0.384, 576) × 10–4 (1–3), 4 – декременты стационарных волн первого семейства (b = 0.15).

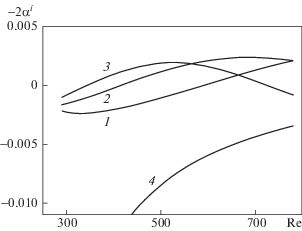
Здесь же приведены декременты стационарной волны первого семейства (4), эти коэффициенты по абсолютной величине невелики, а поэтому соответствующие им амплитуды медленно убывают по продольной координате. Декременты их намного меньше декрементов стационарных волн второго семейства. Из амплитудных уравнений видно, что при интенсивном уменьшении амплитуды стационарной волны (как у второго семейства), нарастание бегущих волн с увеличением продольной координаты стремится к линейному закону со скоростью нарастания ${\alpha }_{{{{A}_{1}}}}^{i}$. Это и явилось причиной в основном акцентировать усилия на изучении влияния стационарных волн первого семейства.

Одна из задач данной работы состояла в изучении возможности усиления бегущих волн Толлмина–Шлихтинга в области их линейного затухания под влиянием стационарной волны. Поэтому предполагалась малость амплитуд бегущих волн в начале расчетной области по сравнению с амплитудой стационарной волны (продольной структуры). Основными расчетными параметрами были следующие: начальные амплитуды бегущих волн А1 = А–1= 0.001 (0.1% от средних величин) и АST = 0.02 (2%), но оценочные расчеты были проделаны и для других амплитуд.

В случае стационарной волны первого семейства, затухание которой слабое, ее влияние на усиление бегущих волн значительное. При этом следует заметить, что усиление амплитуд А1 и А–1 различно при одной и той же частоте и, как отмечено выше, сильно зависит от значения этой частоты, определяющей положение бегущей волны относительно нейтральной кривой.

Изменение амплитуд бегущих волн в нелинейной области, кроме того, зависит от соотношения их начальных фаз. Для удобства физической интерпретации результатов введена тригонометрическая форма записи комплексных амплитуд А = аexp(iψ), где а = |А|, ψ = arctg(Ai/Ar). Амплитудные уравнения решались для модуля амплитуд и взаимной фазы ψ = ψST – ψ1 – ψ–1.

Оказалось, что направление передачи и ее интенсивность полностью определяются значением этой взаимной фазы. Существует фаза максимального усиления бегущих волн (in) и фаза их максимального подавления (d). Эти фазы отличаются на величину π. В рассматриваемых триплетах фаза максимального подавления определена как ψd = π/4, а фаза максимального усиления – ψin = 5π/4. Этот факт отражен на рис. 3, где показаны отношения нелинейных к линейным амплитудам an/alin в фазах максимального подавления (кривые 1) и роста (2). Данные свидетельствуют о том, что бегущие волны положительных (I) и отрицательных (II) азимутальных волновых чисел развиваются при нелинейном взаимодействии по-разному. Таким образом, чтобы грамотно направить процесс в нужную сторону, нужно научиться правильно воздействовать на начальные фазы волн в триплетах.

Рис. 3.

Отношение нелинейных к линейным амплитудам в первом триплете на частоте F2 в фазах максимального подавления ψd = π/4 (1) и усиления ψin = 5π/4 (2) бегущих волн; (I) – волны положительных и (II) – отрицательных азимутальных чисел.

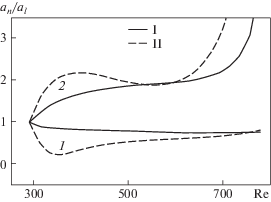
Из рисунка ясно, что в областях линейного затухания волн можно увеличить их амплитуды в два и более раза. Значительный рост амплитуд при Re > 600 связан с пересечением нижней ветви нейтральной кривой и попаданием в область линейного усиления возмущений.

Указанную выше сильную зависимость от рассматриваемой частоты демонстрирует рис. 4, где приведены значения an/alin для фазы максимального усиления ψin = 5π/4 в первом триплете на разных частотах F1–F3 (кривые 1–3). Здесь линиями I показаны волны положительных, II – отрицательных азимутальных чисел. Оказалось, что интенсивности усиления нерегулярны относительно значения F, они зависят от соотношения линейных областей подавления и роста бегущих волн.

Рис. 4.

Отношение нелинейных к линейным амплитудам в первом триплете на разных частотах F1–F3 (1–3) в фазе максимального усиления ψin = 5π/4, I – волны c b1, II – c b–1.

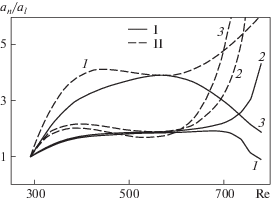
В процессе исследования было проверено влияние разных начальных амплитуд на поведение волн в триплетах. Не иллюстрируя этих расчетов, укажем, что при выбранном начальном значении амплитуды стационарной волны интенсивности усиления an/alin бегущих не зависят (или очень слабо зависят) от начальных амплитуд бегущих волн, в то же время как рост начальной амплитуды стационарной волны напрямую влияет на степени усиления an/alin бегущих. Также не обнаружена значительная разница в интенсивности усиления бегущих волн в первом и втором триплетах. Этот вывод можно трактовать лишь как промежуточный, не претендующий на окончательную закономерность, ибо значения параметров взаимодействующих волн в этих триплетах были довольно близкими.

Приведенные результаты указывают на то, что под влиянием стационарной волны наблюдается активное нарастание нестационарных (бегущих) волн, в несколько раз превышающее линейное. Интенсивные колебания, инициированные бегущими волнами, в свою очередь, способны разрушить исходную стационарную волну и привести к началу ламинарно-турбулентного перехода или формированию турбулентных пятен.

Второй аспект вопроса – можно ли подавить амплитуды бегущих волн в областях их линейного нарастания. Для этого достаточно перенести начало области интегрирования на значение Re с нижней ветви нейтральной кривой для каждой частоты. Физически это можно интерпретировать как постановку источника шероховатости (заклепок) в нужном месте.

Проиллюстрируем этот аспект на интенсивностях усиления бегущих волн во втором триплете (рис. 5). Ищется взаимная фаза, при которой an/alin < 1 как для волны с А1 (кривая 1), так и для волны с А–1 (2). И такой диапазон найден для всех частот, причем взаимная фаза оказалась очень близка к фазе ψin в области их линейного затухания.

Рис. 5.

Степени усиления амплитуд бегущих волн an/alin на частоте F1 = 0.192 × 10–4 во втором триплете для волн с начальными А1 = А–1 (1) и (2) в фазе ψ ∼ 5π/4 при начале интегрирования с нижней ветви нейтральной кривой.

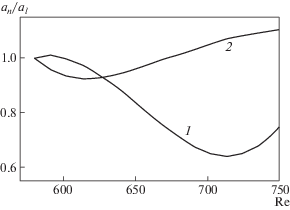
И, наконец, довольно экзотический случай, отвечающий на вопрос – как поведут себя бегущие волны, если установить источник шероховатости в середине области линейного нарастания. Этот пример показан на рис. 6 для второго триплета на F1.

Рис. 6.

Степени усиления амплитуд бегущих волн an/alin на частоте F1 = 0.192 × 10–4 во втором триплете для волн с начальными А1 = А–1 (1) и (2) в фазе ψ ∼ 5π/4 при начале интегрирования в середине области линейного роста.

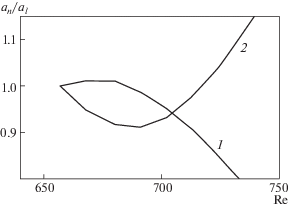
Оказалось, что при некоторых частотах можно найти области одновременного подавления как амплитуды А1, так и амплитуды А–1. Как правило, по протяженности это небольшие области чисел Рейнольдса, но они явно существуют, и их наличие говорит о том, что можно управлять поведением амплитуд бегущих волн, воздействуя на них и в этой области.

В сверхзвуковом пограничном слое фазовая скорость бегущих волн в направлении основного потока слабо зависит от азимутального волнового числа, поэтому условия синхронизма стационарной волны и бегущих волн выполняются для широкой области волновых чисел β (как и в [35]). Как следствие, интенсивность подавления бегущих волн зависит от угла наклона их фронта из-за зависимости коэффициентов нелинейных связей от азимутального волнового числа. Кроме того, коэффициенты связи зависят от свойств основного течения, которые могут сильно отличаться, например, в дву- и трехмерном пограничных слоях. Этим можно объяснить успешное затягивание положения перехода трехмерного пограничного слоя периодическими шероховатостями в [31–33].

ЗАКЛЮЧЕНИЕ

Pассмотрена возможность усиления и подавления роста волн Толлмина–Шлихтинга полосчатыми стационарными структурами, имеющими место в сверхзвуковом пограничном слое. Установлено, что направление и интенсивность передачи энергии от стационарных к бегущим волнам определяются значением взаимной фазы между взаимодействующими волнами, что в области линейного затухания может увеличить амплитуды волн Толлмина–Шлихтинга в два и более раза.

Установлено, что при определенных условиях влияние стационарных возмущений на волны Толлмина–Шлихтинга заметно и в неустойчивой области, что может привести к подавлению амплитуд бегущих волн в области линейного нарастания. В целом можно констатировать, что подобный механизм взаимовлияния может инициировать тип перехода, связанный с присутствием стационарных возмущений в пограничном слое.

Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук на 2013–2020 гг. (проект АААА-22.6.4.) и финансовой поддержке Российского научного фонда (проект № 17-19-01289).

Список литературы

  1. Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1969. 742 с.

  2. Линь Ц.Ц. Теория гидродинамической устойчивости. М.: Изд. ИЛ., 1958. 194 с.

  3. Klebanoff P.S., Tidstrom K.D. Evolution of amplified waves leading to transition in a boundary layer with zero pressure gradient // NASA, TN D-195. 1959.

  4. Saric W.S., Reed H.L., Kerschen E.J. Boundary-layer receptivity to free stream disturbances // Annual Review of Fluid Mechanics. 2002. V. 34. P. 291–319.

  5. Бойко А.В., Грек Г.Р., Довгаль А.В., Козлов В.В. Физические механизмы перехода к турбулентности в открытых течениях. М.: Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2006, 304 с.

  6. Crow S.C. The spanwise perturbation of two-dimensional boundary layers// J. Fluid Mech. 1966. V. 24. P. 153–104.

  7. Bradshaw P. The effect of wind tunnel screens on ‘two-dimensional’ boundary layers // Nat. Phys. Lab. Aero. Rep. 1963. № 1085.

  8. Libby P.A., Fox H. Some perturbation solutions in laminar boundary-layer theory. Part 1. The momentum equation // J. Fluid Mech. 1963. V. 17. P. 433–449.

  9. Bertolotti F.P. Response of the Blasius boundary layer to free-stream vorticity // Ph. Fluids. 1997. V. 9. № 8. P. 2286–2299.

  10. Устинов M.B. Восприимчивость пограничного слоя на плоской пластине к турбулентности набегающего потока // Изв. РАН. МЖГ. 2003. Т. 3. С. 56–68.

  11. Goldstein M.E. Effect of free-stream turbulence on boundary layer transition // Phil. Trans. R. Soc. A. 2014. P. 372.

  12. Гапонов С.А., Юдин А.В. Взаимодействие гидродинамических внешних возмущений с пограничным слоем // ПМТФ. 2002. Т. 43. № 1. С. 100–107.

  13. Gaponov S.A. Interaction of external vortical and thermal disturbances with boundary layer // Int. J. Mech. 2007. V. 1. № 1. P. 15–20.

  14. Гапонов С.А. Взаимодействие сверхзвукового пограничного слоя с акустическими возмущениями // Изв. АН СССР. МЖГ. 1977. № 6. С. 51–56.

  15. Grosch C.E., Salwen H. The continuous spectrum of the Orr-Sommerfeld equation. Part 1. The spectrum and the eigenfunctions // J. Fluid Mech. 1978. V. 87. P. 33–54.

  16. Grosch C.E., Salwen H. The continuous spectrum of the Orr-Sommerfeld equation. Part 2. Eigenfunction expansions // J. Fluid Mech. 1981. V. 104. P. 445–465.

  17. Dong M., Wu X. On continuous spectra of the Orr-Sommerfeld/Squire equations and entrainment of free-stream vortical disturbances // J. Fluid Mech. 2013. V. 732. P. 616–659.

  18. Luchini P. Reynolds-number-independent instability of the boundary layer over a flat surface: optimal perturbations // J. Fluid Mech. 2000. V. 404. P. 289–309.

  19. Andersson P., Berggren M., Henningson D.S. Optimal disturbances in boundary layers // Proc. AFOSR Workshop on Optimal Design and Control. Ed. by J.T. Borggaard, J. Burns, E. Cliff, S. Schreck. Boston, 1998.

  20. Andersson P., Berggren M., Henningson D.S. Optimal disturbances and bypass transition in boundary layers // Phys. Fluids. 1999. V. 11. P. 134–150.

  21. Landahl M.T. A note on an algebraic instability of inviscid parallel shear flows // J. Fluid Mech. 1980. V. 98. P. 243–251.

  22. Hultgren H., Gustavsson. Algebraic growth of disturbances in a laminar boundary layer // Phys. Fluids. 1981. V. 24. P. 1000–1004.

  23. Henningson D.S. An eigenfunction expansion of localized disturbances. In Advances in Turbulence 3 / Ed. by A.V. Johansson, P.H. Alfredsson. 1991. P. 162–169.

  24. Gaponov S.A. Quasi-resonance excitation of stationary disturbances in compressible boundary layer // Int. J. Mech. 2017. V. 11. P. 120–127.

  25. Гапонов С.А., Петров Г.В., Смородский Б.В. Линейное и нелинейное взаимодействие акустических волн со сверхзвуковым пограничным слоем //Аэромеханика и газовая динамика. 2002. № 3. С. 21–30.

  26. Гапонов С.А. О развитии возмущений в сверхзвуковом пограничном слое // ПМТФ. 1991. № 6. С. 98–101.

  27. Гапонов С.А., Терехова Н.М. Стационарные возмущения в сверхзвуковом пограничном слое // Аэромеханика и газовая динамика. 2002. № 4. С. 35–42.

  28. Thumm A., Wolz W., Fasel H. Numerical simulation of spatially growing three-dimensional disturbance waves in compressible boundary layers // Proc. IUTAM Symp. Toulouse, France, 1990. P. 303–308.

  29. Schmid P.J., Henningson D.S. A new mechanism for rapid transition involving a pair of oblique waves // Phys. Fluids A. 1992. V. 4. P. 1986–1989.

  30. Chang C.-L. Malik M.R. Oblique-mode breakdown and secondary instability in supersonic boundary layers // J. Fluid Mech. 1994. V. 273. P. 323–360.

  31. Saric W.S., Carillo R.B., Reibert M.S. Leading edge roughness as a transition control mechanism // AIAA Paper 98-0781. 1998.

  32. Saric W.S., Reed H.L. Supersonic laminar flow control on swept wings using distributed roughness // AIAA Paper 02-0147. 2002.

  33. Семенов Н.В., Косинов А.Д. Метод управления ламинарно-турбулентным переходом сверхзвукового пограничного слоя на скользящем крыле // Теплофизика и аэромеханика. 2007. Т. 14. № 3. С. 353–357.

  34. Craik A.D.D. Non-linear resonant instability in boundary layers // J. Fluid Mech. 1971. V. 50. P. 393–413.

  35. Гапонов С.А., Масленникова И.И. Субгармоническая неустойчивость сверхзвукового пограничного слоя // Теплофизика и аэромеханика. 1997. Т. 4. № 1. С. 1–10.

  36. Гапонов С.А., Масленникова И.И., Тюшин В.Ю. Нелинейное влияние внешней низкочастотной акустики на собственные колебания сверхзвукового пограничного слоя // ПМТФ. 1999. № 5. С. 99–105.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал