1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2020

Известия РАН. Механика жидкости и газа, 2020, № 3, стр. 108-124

СТРУКТУРНЫЙ АНАЛИЗ БИФУРКАЦИЙ КАРТИНЫ ТЕЧЕНИЯ С ПОПЕРЕЧНЫМ ГРАДИЕНТОМ СКОРОСТИ ПРИ ОБТЕКАНИИ НАКЛОННОГО ЦИЛИНДРА С КВАДРАТНЫМ ОСЕВЫМ СЕЧЕНИЕМ: ПРИЛОЖЕНИЕ К ДВУМЕРНОМУ НЕСТАЦИОНАРНОМУ ОТРЫВУ ПОТОКА

А. Кумар a, Р. К. Рэй b, *,

a Факультет фундаментальных наук, Индийский технологический институт
Манди, Индия

b Факультет перспективных научных исследований, технологический институт Веллуру
Бхопал, Индия

* E-mail: rajendra@iitmandi.ac.in

Поступила в редакцию 28.02.2019
После доработки 25.07.2019
Принята к публикации 20.09.2019

Полный текст (PDF)

Аннотация

Рассматривая топологические свойства потока, анализируется структура бифуркаций несжимаемого двумерного (2-D) течения с поперечным градиентом скорости при обтекании наклонного цилиндра с квадратным осевым сечением. Используя этот анализ, показано, каким образом отрыв потока приводит к сложной структуре течения в течение некоторого времени. Задача решается, записывая уравнения Навье–Стокса в переменных функция тока – завихренность ($\Psi - \zeta $) в декартовых координатах и используя компактную конечно-разностную схему высокого порядка. На основании проведенного анализа удалось установить точное положение первой и второй точек бифуркации в соответствующее безразмерное время их появления, как в начальной стадии, так и в полностью развитом течении. На поле течения влияют главным образом число Рейнольдса Re и поперечный градиент скорости (параметр сдвига) κ. Показано, что первая и вторая бифуркации возникают вниз по потоку от верхней и нижней кромок цилиндра в пределах очень маленькой временнóй разности вплоть до κ = 0.1. Численное моделирование выполнено при Re = 100 и 185 при изменении κ в диапазоне от 0.0 до 0.4. Целью настоящего исследования является уточнение влияния параметра сдвига на свойства течения. Временнóе поведение вихреобразования и значимые траектории трассирующих частиц при визуализации течения детально исследованы для всех значений параметров. Для исходного и полностью развитого течений продемонстрированы детали возникновения многократных отрывов течения при изменении $\kappa $. Проведенное сравнение с ранее полученными результатами, описанными в литературе, позволяет проверить точность и обоснованность результатов, полученных в настоящей работе.

В любой картине течения структурное распознавание может быть легко выполнено при использовании топологических подходов. В [22, 23] были изучены топологические аспекты 2-D вязких течений вблизи твердой границы. Были использованы структурные бифуркации, следующие из теории отрыва пограничного слоя и было обнаружено, что структурная бифуркация происходит на твердой стенке всякий раз, когда особая точка с вырожденной завихренностью находится на границе. В [32], используя понятие структурной бифуркации, авторами был описан структурный механизм нестационарного отрыва потока от поверхности прямого цилиндра с квадратным осевым сечением в потоке с поперечным градиентом скорости (сдвиговом потоке). В этом исследовании было описано положение точек бифуркации как функции времени их возникновения, соответствующего вторичным и третичным вихрям. Было также отмечено, что структурная бифуркация не происходит при начальном отрыве течения от задних углов, что приводит к первичным вихрям. При начальном отрыве течения условия структурной бифуркации не выполняются одновременно. Однако в настоящем исследовании сдвигового течения с обтеканием наклонного цилиндра с квадратным осевым сечением можно наблюдать, что структурная бифуркация возникает в результате начального отрыва потока. По мнению авторов, до настоящего момента анализ структурной бифуркации не использовался для исследования механизма отрыва потока с поперечным градиентом скорости при обтекани наклонного цилиндра с квадратным осевым сечением.

В течение длительного времени вязкое обтекание твердого тела высоко оценивалось главным образом из-за его теоретической и практической ценности. Условия отсутствия скольжения на твердой поверхности приводят к генерации завихренности вблизи этой поверхности. Поскольку вихри являются причиной возникновения периодической силы, это приводит к структурным колебаниям. Поэтому в течение последнего столетия многие исследователи уделяли много внимания управлению вихреобразованием (сходом вихрей). Однако бóльшая часть этих исследований, посвященных обтеканию цилиндрических объектов, подобных круговому цилиндру или цилиндру с квадратным осевым сечением, расположенным в однородном потоке, уже опубликованы ранее (см. [2–9]). Однако в случае, когда набегающий поток имеет профиль скорости с поперечным градиентом, след за телом имеет более сложную структуру по сравнению со случаем однородного набегающего потока (см. [10–13]). Однако большинство этих исследований были выполнены для случая обтекания кругового или квадратного цилиндров и только очень немногие исследования были проведены для наклонного цилиндра с квадратным осевым сечением (см. [14–19]). В частности, цилиндр с квадратным осевым сечением, наклоненный относительно направления набегающего сдвигового потока, может вызвать смещение точек отрыва потока на другие грани, что приводит к изменению картины течения в следе за цилиндром.

В экспериментальном исследовании [1] было обнаружено, что величина критического числа Рейнольдса Rec, выше которого происходит вихреобразование (сход вихрей), растет с увеличением параметра сдвига (градиента скорости). В 1997 г. Хванг и Сью [11] проанализировали сход вихрей, индуцированный цилиндром с квадратным осевым сечением, для разных значений параметра сдвига, решив двумерные уравнения Навье–Стокса. Влияние градиента скорости сдвига на картину течения исследовано в зависимости от подъемной силы и силы сопротивления для малых значений параметра сдвига κ на интервале от 0.0 до 0.25 при больших значениях числа Рейнольдса в диапазоне от 500 до 1500. Затем задача обтекания квадратного цилиндра сдвиговым потоком была решена в [24, 29] с использованием сеточного метода Больцмана в диапазоне от малых до умеренных значений числа Рейнольдса. Аэродинамические силы и картина вихреобразования были исследованы для Re = 50–200 и различных значений κ в диапазоне 0.0–0.5. В [12] было исследовано поле течения около двумерного квадратного цилиндра с градиентом скорости сдвига в дипазоне от 0.0 до 0.2 при много меньших значениях чисел Рейнольдса. Было отмечено, что при κ = 0.1 критическое значение числа Рейнольдса находится между 42 и 43, тогда как при κ = 0.2 оно лежит на интервале между 38 и 40. В [28] механизм нестационарного отрыва для плохо обтекаемых тел с гладкими гранями или с острой кромкой был объяснен, рассматривая квадратный и круговой цилиндры. Для квадратного цилиндра точки отрыва потока находятся на передних углах, тогда как для кругового цилиндра они лежат на его части вниз по потоку. В [30] обтекание квадратного цилиндра было исследовано экспериментально при Re = 410 методом измерения скорости по изображениям частиц (PIV методом), методом термоанемометрии. Результаты экспериментов были представлены изображениями картины линий тока, скорости, усредненной по времени, коэффициентом сопротивления, спектрами мощности коэффициента подъемной силы и т.д.

Детальное и тщательное изучение публикаций позволяет предположить, что в большей части предыдущих исследований (как экспериментальных, так и численных), посвященных обтеканию квадратного цилиндра, рассматривались однородные входные условия. Однако течения в окрестности многих конструкций, таких как высотные здания, морские платформы и трубопроводы на морском дне, которые реально находятся внутри течений погранслойного типа, могут быть аппроксимированы сдвиговыми течениями. Кроме того, в вышеупомянутых исследованиях очень небольшое внимание было уделено теоретическому пониманию нестационарного отрыва потока с использованием анализа структурных бифуркаций. В настоящей работе двумерное течение с градиентом скорости, вызванное бесконечно длинным наклонным цилиндром с квадратным осевым сечением в ламинарном вязком несжимаемом потоке, анализируется на начальной и полностью развитой стадиях течения, используя структурные бифуркации. Численное моделирование выполняется с помощью компактной конечно-разностной схемы высокого порядка, использованной ранее в [5, 21, 31, 33]. Результаты исследования изложены следующим образом. В разделе 1 рассматриваются основные уравнения и начальные и граничные условия. В разделе 2 описан метод решения и проводится проверка достоверности результатов, сами результаты и их обсуждение даны в разделе 3. Наконец, в разделе 4 подводятся итоги исследования.

1. ОСНОВНЫЕ УРАВНЕНИЯ

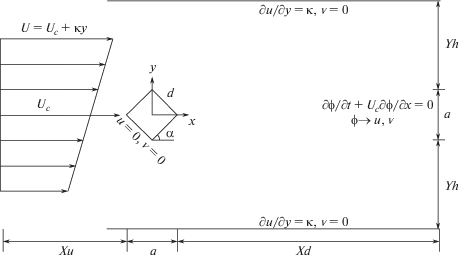
Рассмотрим задачу обтекания нестационарным несжимаемым потоком с исходным сдвигом (градиентом) скорости наклонного цилиндра квадратного сечения. Двумерная схема течения представлена на рис. 1. Набегающий поток с линейным градиентом (сдвигом) скорости обтекает цилиндр квадратного сечения с длиной боковой стороны, равной d. Здесь Xu и Xd обозначают расстояния вверх и вниз по потоку соответственно. Ширина проекции (a) наклонного цилиндра выражается следующим образом

$d = a(\cos \alpha + \sin \alpha ),$
где α – угол наклона цилиндра. В декартовых координатах (x, y) уравнения Навье–Стокса, описывающие течение в переменных безразмерная функция тока – завихренность (Ψ – ζ), записываются в виде
(1.1)
$\frac{{{{\partial }^{2}}\zeta }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\zeta }}{{\partial {{y}^{2}}}} = \operatorname{Re} \left( {u\frac{{\partial \zeta }}{{\partial x}} + v\frac{{\partial \zeta }}{{\partial y}} + \frac{{\partial \zeta }}{{\partial t}}} \right),$
(1.2)
$\frac{{{{\partial }^{2}}\Psi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\Psi }}{{\partial {{y}^{2}}}} = - \zeta $
где $\operatorname{Re} = \frac{{{{U}_{c}}a}}{\nu }$ – число Рейнольдса. Скорости $u,v$ выражаются через функцию тока Ψ в следующем виде
(1.3)
$u = \frac{{\partial \psi }}{{\partial y}},\quad v = - \frac{{\partial \psi }}{{\partial x}},$
а завихренность ζ в виде

(1.4)
$\zeta = \frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}.$
Рис. 1.

Схема течения с поперечным градиентом скорости около наклонного квадратного цилиндра.

В качестве начального условия предполагается, что вычисления начинаются с рассмотрения покоящейся жидкости. На передней границе используется линейный профиль скорости

(1.5)
$u = {{U}_{c}} + \kappa y,\quad v = 0,$
где Uc – начальная скорость на средней линии и κ – градиент скорости сдвига (параметр сдвига). Как видно из недавно проведенного исследования [13], на выходе наиболее подходящим граничным условием при обтекании цилиндра с квадратным осевым сечением сдвиговым потоком является конвективное граничное условие. В настоящем исследовании используется конвективное граничное условие на выходе из расчетной области. Это условие может быть записано в виде

(1.6)
$\frac{{\partial \phi }}{{\partial t}} + {{U}_{c}}\frac{{\partial \phi }}{{\partial x}} = 0.$

Здесь ϕ обозначает $u,\;v,\;\Psi ,\;\zeta $. На поверхности цилиндра рассматриваются граничные условия отсутствия скольжения (условия прилипания), а также условия скольжения, которые реализуются на донной и верхней границах области вычислений, т.е.

(1.7)
$\frac{{\partial u}}{{\partial y}} = \kappa ,\quad v = 0.$

Кроме того, уравнение (1.2) и условие (1.3) могут быть использованы для получения следующего условия на завихренность на гранях цилидра:

(1.8)
$\zeta = - \frac{{{{\partial }^{2}}\Psi }}{{\partial {{x}^{2}}}} - \frac{{{{\partial }^{2}}\Psi }}{{\partial {{y}^{2}}}}.$

2. МЕТОД РЕШЕНИЯ

Следуя [32], для дискретизации на декартовых сетках основных уравнений течения используется компактный конечно-разностный метод высшего порядка точности. Для дискретизации уравнений (1.1) и (1.2) в области $\left[ {{{x}_{1}},{{x}_{2}}} \right] \times \left[ { - {{y}_{1}},{{y}_{1}}} \right]$ используется однородная декартовая сетка. Таким образом, в ${{\left( {i,j} \right)}^{{th}}}$ точке расчетной области компактная дискретизация высшего порядка точности приводит к следующей системе линейных алгебраических уравнений (2.1), (2.2) соответственно, которая может быть решена при использовании бисопряженного градиентного солвера

(2.1)
$\begin{gathered} \text{[}{\text{Re}}\, + \beta {{11}_{{ij}}}\delta _{x}^{2} + \beta {{12}_{{ij}}}\delta _{y}^{2} + \beta {{13}_{{ij}}}{{\delta }_{x}} + \beta {{14}_{{ij}}}{{\delta }_{y}} + \beta {{15}_{{ij}}}{{\delta }_{x}}{{\delta }_{y}} + \\ \, + \beta {{16}_{{ij}}}{{\delta }_{x}}\delta _{y}^{2} + \beta {{17}_{{ij}}}\delta _{x}^{2}{{\delta }_{y}} + \beta {{18}_{{ij}}}\delta _{x}^{2}\delta _{y}^{2}]\zeta _{{ij}}^{{n + 1}} = \\ = [{\text{Re}}\, + \beta {{21}_{{ij}}}\delta _{x}^{2} + \beta {{22}_{{ij}}}\delta _{y}^{2} + \beta {{23}_{{ij}}}{{\delta }_{x}} + \beta {{24}_{{ij}}}{{\delta }_{y}} + \beta {{25}_{{ij}}}{{\delta }_{x}}{{\delta }_{y}} + \\ \, + \beta {{26}_{{ij}}}{{\delta }_{x}}\delta _{y}^{2} + \beta {{27}_{{ij}}}\delta _{x}^{2}{{\delta }_{y}} + \beta {{28}_{{ij}}}\delta _{x}^{2}\delta _{y}^{2}]\zeta _{{ij}}^{n} \\ \end{gathered} $
и
(2.2)
$[\delta _{x}^{2} + \delta _{y}^{2} - (\Gamma 2 + \Lambda 2)\delta _{x}^{2}\delta _{y}^{2}]{{\Psi }_{{ij}}} = [ - 1 + \Gamma 2\delta _{x}^{2} + \Lambda 2\delta _{y}^{2}]{{\zeta }_{{ij}}},$
где коэффициенты в дискретизованных уравнениях (2.1) и (2.2) даны в Приложении 1 . Вкратце дискретизация, приводящая к уравнениям (2.1) и (2.2), и конечно-разностные операторы описаны в [20]. Более подробно конечно-разностные операторы ${{\delta }_{x}},\;\delta _{x}^{2},\;{{\delta }_{y}}$ и $\delta _{y}^{2}$ даны в Приложении 2.

2.1. Обоснование численной схемы

В этом разделе, используя различные размеры сетки и сравнивая полученные результаты с результатами, доступными в литературе, будет проверена точность численной схемы. Возникает очевидный вопрос, касающийся оптимального размера сетки, величины временного шага $\Delta t = 0.01$ и расстояний на входе и выходе из расчетной области. В табл. 1 даны значения $u,\;{v},\;\Psi ,\;\zeta $ в точке (0.75, –0.5) за цилиндром для двух разных значений времени, t = 1.0 и t = 10.0, чтобы продемонстрировать независимость результатов, полученных с использованием рассматриваемой сетки. Из этой таблицы можно видеть, что сетка с размерами (769, 265) вполне достаточна для получения приемлемых результатов, при этом значения переменных $u,\;{v},\;\Psi ,\;\zeta $изменяются приблизительно на 2.0% для сеток с размерами (769, 265) и (1537, 529). Кроме того, чтобы показать точность полученных данных на поверхности цилидра, в табл. 2 приведены значения завихренности в точке (0.04, –0.46) на поверхности цилиндра при κ = 0.1 в разные моменты времени t = = 1.0 и 500.0. Из этой таблицы видно, что в эти моменты времени максимальное отклонение завихренности составляет только 2.1% для сеток (769, 265) и (1537, 529). Кроме того, в табл. 3 даны значения переменных в точке (0.75, –0.5) за цилиндром при трех различных шагах по времени, $\Delta t = 0.001$, 0.005 и $\Delta t = 0.01$, на сетке с размером (769, 265). Для $\Delta t = 0.001,\;0.01$ отличаются приблизительно на 2.4%. Из этих рассмотрений становится очевидным, что сетка с размерами (769, 265) и шаг по времени $\Delta t = 0.01$ достаточны для обеспечения достаточной точности при расчете картины обтекания.

Таблица 1.

Значения компонент скорости, завихренности и фунции тока в точке наблюдений (0.75, –0.5) для четырех размеров сетки при Δt = 0.01, Re = 100 и κ = 0.1

t (I × J) u ${v}$ Ψ ζ
1.0 (385 × 133) 0.39267 0.09872 –0.11389 0.08534
  (641 × 221) 0.41126 0.10614 –0.13212 0.10498
  (769 × 265) 0.43414 0.11639 –0.14350 0.11584
  (1537 × 529) 0.44621 0.12012 –0.14821 0.11874
10.0 (385 × 133) 0.18324 0.02154 0.01249 2.35247
  (641 × 221) 0.21771 0.05318 0.03177 3.11826
  (769 × 265) 0.23179 0.05761 0.03355 3.33159
  (1537 × 529) 0.23827 0.05914 0.03437 3.39624
Таблица 2.

Завихренность в точке (0.04, –0.46) на поверхности цилиндра для сетки одинаковых размеров при Δt = 0.01, Re = 100 и κ = 0.1

(I × J) (385 × 133) (641 × 221) (769 × 265) (1537 × 529)
t = 10        
ζ 0.0855 0.0721 0.0831 0.0932
t = 500.0        
ζ 0.0146 0.0150 0.0162 0.0159
Таблица 3.

Тест на независимость от шага по времени величин $u,\;v,\;\Psi ,\;\zeta $ в точке (0.75, –0.5) во время t = 10.0 при Re = 100 и κ = 0.1

Δt (I × J) u ${v}$ Ψ ζ
0.001 (769 × 265) 0.22536 0.05632 0.03271 3.27215
0.005 (769 × 265) 0.22967 0.05692 0.03310 3.30126
0.01 (769 × 265) 0.23179 0.05761 0.03355 3.33159

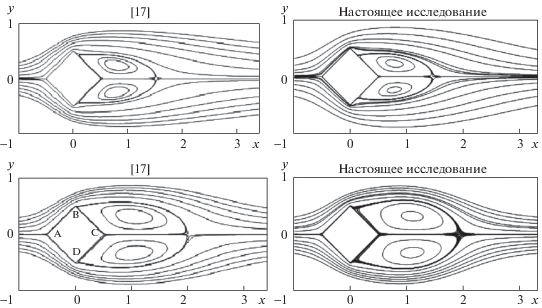
Расссматривая значения компонент скорости, завихренности и функции тока в точке (0.75, –0.5) и значение числа Струхаля (${{S}_{t}}$) для четырех расстояний вверх и вниз по потоку, приведенных в табл. 4, была протестирована зависимость результатов расчетов от размеров сетки. Из этой таблицы можно видеть, что случаи $3a - 5a - 30a$ и $7a - 5a - 30a$ демонстрируют, что число Струхаля почти постоянно и значения других величин отличаются не более чем на 1.3%. Вместе с тем найдено, что $3a - 5a - 30a$ и (769, 265) показывают, что результаты не зависят от области и размеров сетки. Более того, имеется великолепное согласование рассчитанных линий тока с ранее полученными численными результатами [17] для $\operatorname{Re} = 20,\;60$ (рис. 2).

Таблица 4.

Влияние расстояний вверх и вниз по потоку на результаты при Δt = 0.01, t = 100.0, Re = 100 и κ = 0.1

Xu – Yh – Xd (I × J) u ${v}$ Ψ ζ St
3a – 5a – 30a (972 × 315) 0.05198 0.16938 –0.01626 2.79215 0.149
7a – 5a – 30a (1567 × 367) 0.05346 0.17412 –0.01701 2.88021 0.154
3a – 5a – 30a (769 × 265) 0.05265 0.17193 –0.01648 2.83578 0.151
7a – 5a – 30a (1901 × 551) 0.05298 0.18012 –0.01687 0.87821 0.150
Рис. 2.

Сравнение мгновенных линий тока с результатами, полученными в [17]; Re = 20 (а – [17], б – настоящее исследование); Re = 60 (в – [17], г – настоящее исследование).

3. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Детальные расчеты были выполнены для обтекания наклонного квадратного цилиндра потоком с градиентом скорости при числах Рейнольдса Re = 100 и 185, когда параметр сдвига скорости κ изменялся от 0.0 до 0.4, и α = 45°. Сводный анализ нестационарного отрыва потока при обтекании одного наклонного квадратного цилиндра потоком с градиентом скорости может быть найден в предыдущей работе авторов [32].

3.1. Картина начального течения

3.1.1. Структурный анализ бифуркаций. В этом разделе будет описан механизм нестационарного отрыва потока с использованием структурных бифуркаций. Нестационарный отрыв потока, приводящий к образованию вихрей и их последующему сходу с кромок наклонного квадратного цилиндра вниз по потоку, был описан ранее главным образом на основе качественных соображений, хотя для точного описания места и времени появления точек отрыва потока требуются более точные методы. Теория отрыва пограничного слоя [22, 23] основывается на идее структурной бифуркации. Насколько известно авторам, до настоящего времени исследование обтекания наклонного квадратного цилиндра сдвиговым потоком с использованием структурных бифуркаций не проводилось. Анализ структурных бифуркаций течения около наклонного цилиндра аналогичен анализу, описанному в [32], для прямого квадратного цилиндра; поэтому достаточно обсудить влияние наклона на отрыв потока. Условия возникновения структурной бифуркации могут быть заданы следующим образом:

(3.1)
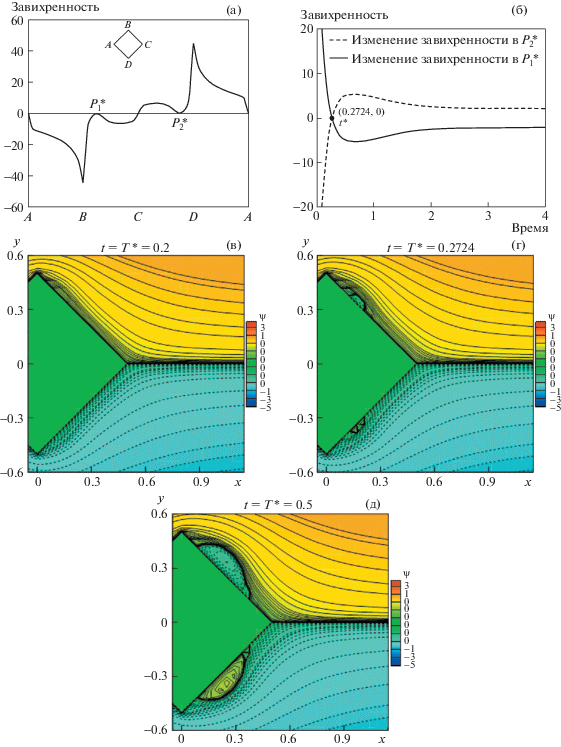
$\zeta \left( {P{\text{*}},T{\text{*}}} \right) = 0,\quad \frac{{\partial \zeta }}{{\partial \tau }}\left( {P{\text{*}},T{\text{*}}} \right) = 0,\quad \frac{{{{\partial }^{2}}\zeta }}{{\partial {{\tau }^{2}}}}\left( {P{\text{*}},T{\text{*}}} \right) < 0,\quad \frac{{\partial \zeta }}{{\partial t}}\left( {P{\text{*}},T{\text{*}}} \right) > 0,$
где $t$ – время и $\tau $ – направление, касательное поверхности цилиндра [32]. В данном исследовании главным образом будет описана структурная бифуркация, соответствующая первичному и вторичному вихрям.

На рис. 3 проиллюстрировано возникновение точек бифуркации, соответствующих первичному отрыву от граней цилиндра вниз потоку для Re = 100 и κ = 0.0. График поверхностной завихренности на рис. 3а ясно показывает существование локального максимума в точке $P_{1}^{*}(x,y) = (0.125,0.375)$ и его дальнейший рост со временем. Математически это означает, что условия $\zeta (P_{1}^{*},T{\text{*}}) = 0,\frac{{\partial \zeta }}{{\partial x}}(P_{1}^{*},T{\text{*}}) = 0,\frac{{{{\partial }^{2}}\zeta }}{{\partial {{x}^{2}}}}(P_{1}^{*},T{\text{*}}) < 0$ верны в точке $P_{1}^{*}(x,y) = (0.125,0.375)$ при $T{\text{*}}$ = 0.2724. Кроме того, на рис. 3б изображено изменение завихренности как функции времени в точке (0.125, 0.375) на верхней грани вниз по потоку, из чего следует, что $\frac{{\partial \zeta }}{{\partial t}}\left( {P{\text{*}},T{\text{*}}} \right) > 0.$ Таким образом, все условия, перечисленные в (3.1), справедливы. Это подтверждает возникновение первой структурной бифуркации в момент времени $t = T{\text{*}} = 0.2724$ из точки $P_{1}^{*}(x,y) = (0.125,0.375)$ на верхней грани наклонного цилиндра вниз по потоку. Течение однородно и симметрично при κ = 0.0. Это демонстрируется на основании того, что вторая структурная бифуркация также происходит в то же самое время $t = T{\text{*}} = 0.2724$ в точке $P_{2}^{*}(x,y) = (0.125, - 0.375)$, показанной на рис. 3а. Условия бифуркации, заданные в (3.1), выполняются в точке $P_{2}^{*}(x,y) = (0.125, - 0.375)$, причем два последних неравенства имеют обратный смысл, поскольку сдвиговое течение направлено вниз. Вдобавок на рис. 3в, 3г и 3д соответственно изображены увеличенные картины линий тока вблизи точек бифуркации на гранях цилиндра вниз по потоку в разные моменты времени. Эти рисунки ясно демонстрируют возникновение нестационарного отрыва потока, вызванного структурной бифуркацией (рис. 3 г).

Рис. 3.

Профиль поверхностной завихренности во время структурной бифуркации при $t = T{\text{*}} = 0.2724$ (а); изменение завихренности в точках $P_{1}^{*}(x,y) = (0.125,0.375)$ и $P_{2}^{*}(x,y) = (0.125, - 0.375)$ с течением времени (б); увеличенный вид линий тока в области $[0.0,0.9] \times [ - 0.6,0.6]$ при значениях времени $t = 0.2$ (в), $t = 0.2724$ (г) и $t = 0.5$ (д) при $\kappa = 0.0$, Re = 100.

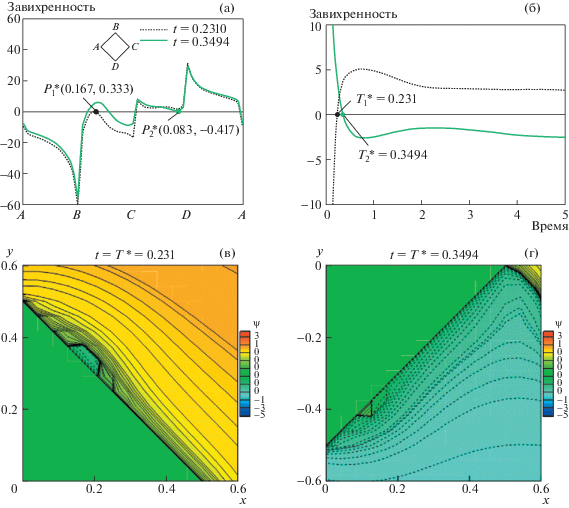
Следуя предыдущей процедуре, на рис. 4 описано возникновение первой и второй структурной бифуркаций при κ = 0.1. Приведенный рисунок наглядно показывает, что первая структурная бифуркация возникает в момент времени $t = T_{1}^{*} = 0.231$ в точке $P_{1}^{*}(x,y) = (0.167,0.333)$ на верхней грани цилиндра вниз по потоку, а вторая бифуркация возникает в момент времени $t = T_{2}^{*}$ = 0.3494 в точке $P_{2}^{*}(x,y) = (0.083, - 0.417)$ на нижней грани цилиндра вниз по потоку. В этом случае первая и вторая структурная бифуркации происходят в разные моменты времени из-за влияния градиента скорости сдвига в набегающем потоке, что находится в противоречии со случаем κ = 0.0. Кроме того, при κ = 0.1 результаты демонстрируют несимметричный характер течения. Рисунки 4в и 4г изображают в увеличенном виде линии тока вблизи первой и второй точек структурной бифуркации.

Рис. 4.

Распределение завихренности по поверхности цилиндра во время первой и второй бифуркаций при t = 0.2310 и 0.3494 (а); изменение завихренности в точках $P_{1}^{*}(x,y) = (0.167,0.333)$ и $P_{2}^{*}(x,y) = (0.083, - 0.417)$ как функция времени (б); увеличенный вид линий тока в окрестности точки бифуркации (в, г) при $\kappa = 0.1$, Re = 100.

При бóльших значениях κ, т.е. при κ = 0.2, 0.3 и 0.4, поведение течения, в котором происходят такие структурные буфуркации, остается прежним. Вкратце, положение первой и второй точек структурной бифуркации вместе с точным временем их возникновения для всех вышеперечисленных значений κ даны в табл. 5. Видно, что данные в табл. 5 следуют некоторой специфической картине в зависимости от времени возникновения точек бифуркации, связанных с первичными и вторичными вихрями для обеих значений Re, что означает более ранний отрыв при большем значении параметра сдвига. Можно также видеть, что при κ = 0.0 эти две бифуркации на верхней и нижней гранях наклонного цилиндра вниз по потоку появляются в одно и то же время из-за симметричного характера течения. Из этой таблицы можно видеть, что время возникновения первой бифуркации уменьшается при увеличении значения κ приблизительно линейно для всех рассмотренных значений Re. Аналогично, время возникновения второй бифуркации постепенно увеличивается при росте κ для двух рассмотренных значений Re. Также можно видеть, что время возникновения обеих структурных бифуркаций постепенно уменьшается при увеличении Re для всех значений κ. Стоит отметить, что точка первой бифуркации возникает на верхней грани вниз по потоку, тогда как точка второй бифуркации возникает на нижней грани цилиндра вниз по потоку для всех рассмотренных значений Re и κ. Сразу же можно увидеть, что первая и вторая бифуркации развиваются в пределах очень маленькой разницы времени на верхней и нижней гранях цилиндра вниз по потоку вплоть до значения κ = 0.1 (табл. 5).

Таблица 5.

Возникновение первой и второй точек структурной бифуркации на грани цилиндра вниз по потоку для Re = 100 и 185

  Первая бифуркация ($P_{1}^{*}$(x, y), $T_{1}^{*}$) Вторая бифуркация ($P_{2}^{*}$(x, y), $T_{2}^{*}$)
Re = 100    
κ = 0.0 ((0.167, 0.375), 0.2724) ((0.125, –0.375), 0.2724)
κ = 0.1 ((0.167, 0.333), 0.2310) ((0.083, –0.417), 0.3494)
κ = 0.2 ((0.167, 0.333), 0.1884) ((0.292, –0.208), 0.7808)
κ = 0.3 ((0.125, 0.333), 0.1451) ((0.208, –0.292), 0.6605)
κ = 0.4 ((0.125, 0.375), 0.1014) ((0.208, –0.292), 0.8231)
Re = 185    
κ = 0.0 ((0.125, 0.375), 0.2154) ((0.125, –0.375), 0.2154)
κ = 0.1 ((0.125, 0.375), 0.1580) ((0.083, –0.417), 0.2852)
κ = 0.2 ((0.125, 0.375), 0.1187) ((0.083, –0.417), 0.7585)
κ = 0.3 ((0.125, 0.375), 0.0888) ((0.208, –0.292), 0.2651)
κ = 0.4 ((0.125, 0.375), 0.0698) ((0.333, –0.167), 0.9330)

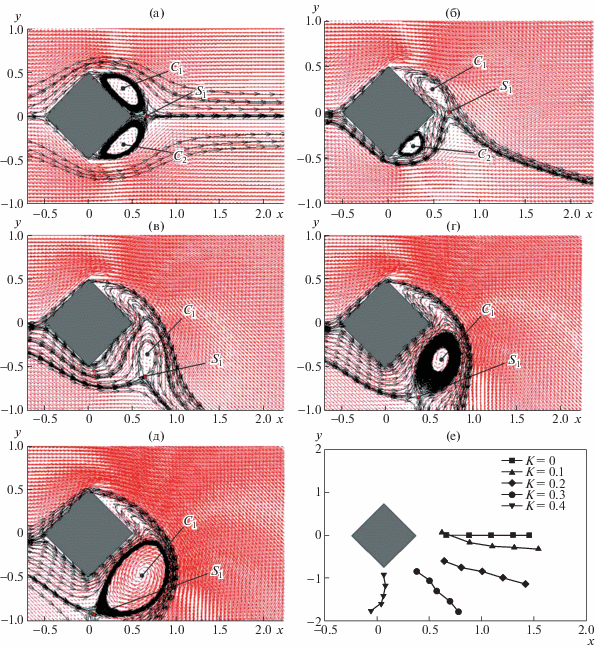
3.1.2. Существование седловых точек. В заключение была проведена частичная оценка центральных и седловых точек вихрей для различных значений параметра сдвига, как это было сделано в [25–27]. Седловые точки существуют в поле скоростей при обтекании наклонного квадратного цилиндра, в случае начального потока с поперечным градиентом скорости. Эти седловые точки ведут себя по-разному во время схода вихрей при разных значениях градиента скорости. На начальной стадии обтекания прямого квадратного цилиндра потоком с поперечным градиентом скорости поведение центров вихрей и седловых точек описано в [32]. В рассмотренном случае описано влияние угла наклона (поперечного градиента скорости) на поведение этих точек. На рис. 5 показано положение седловых точек и отмечены центры вихрей при различных значениях κ. При κ = 0.0 видно, что течение начинается с двух исходных симметричных вихрей с центрами ${{C}_{1}},\;{{C}_{2}}$ на гранях вниз по потоку с общей седловой точкой S1 в следе (рис. 5а). С течением времени размеры вихрей постоянно растут, а седловая точка движется. При κ = 0.1, в начальной стадии может наблюдаться нестационарное поведение картины течения. Как можно видеть, из-за несимметричного характера точек структурной бифуркации при ненулевых значениях κ, на гранях вниз по потоку образуются вихри разных размеров (рис. 6б). Первый вихрь всегда образуется из-за возникновения первой структурной бифуркации, описанной выше, на верхней грани вниз по потоку с центром в точке ${{C}_{1}}$ и далее растет в размерах, будучи закрученным по часовой стрелке при всех значениях κ (рис. 5б–5д). С другой стороны, при κ = 0.1 седловая точка также существует в точке S1 с координатами (0.8, –0.26). Из-за неоднородного характера течения при ненулевых значениях κ, седловая точка смещается в отрицательном направлении оси y при росте κ (рис. 5г). Кроме того, движение этих седловых точек с течением времени показано на рис. 5е при всех значениях κ. На этой фигуре можно видеть, что положение седловых точек постепенно смещается вниз с течением времени для всех ненулевых значений κ из-за более сильно выраженной относительной скорости поля течения на верхней части наклонного цилиндра по сравнению с нижней частью. Можно также видеть, что при увеличении κ вихри постепенно замедляются.

Рис. 5.

Центры вихрей ${{C}_{1}},{{C}_{2}}$ и седловая точка ${{S}_{1}}$ в момент времени $t = 1.0$ при $\operatorname{Re} = 100$, $\kappa = 0.0$ (а), $\kappa = 0.1$ (б), $\kappa = 0.2$ (в), $\kappa = 0.3$ (г), $\kappa = 0.4$ (д) и движение седловой точки (е) как функция времени на временном интервале [1, 3] для всех значений $\kappa $.

Рис. 6.

Картина траекторий частиц, визуализирующих течение, для наклонного квадратного цилиндра при угле α = 45° для Re = 100, (а) $\kappa = 0.0$, (б) $\kappa = 0.1$, (в) $\kappa = 0.2$, (г) $\kappa = 0.3$, (д) $\kappa = 0.4$.

3.2. Картина полностью развитого течения

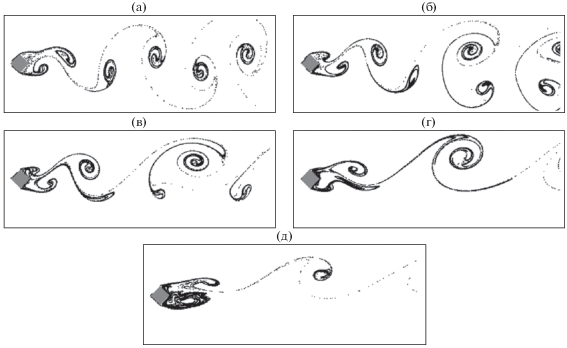
3.2.1. Сход вихрей. В этом разделе поведение течения описывается через картины схода вихрей и изображения траекторий трассирующих частиц, визуализирующих течение, когда течение становится полностью развитым. На рис. 6 изображены траектории частиц, визуализирующих течение, для различных значений κ при $\operatorname{Re} = 100,$ α = 45°. При κ = 0.0 в силу симметричного характера течения вихри близких размеров и интенсивностей сходят поочередно с верхней и нижней граней цилиндра вниз по потоку с определенной периодичностью в ближнем следе (рис. 6а). Этот результат также подтверждает симметричный и периодический характер течения для этого значения κ. Центр цилидра находится в начале координат. При увеличении значения κ, картины траекторий частиц, визуализирующих течение, становятся различными и симметричный характер течения постепенно исчезает. При κ > 0.0 скорость жидкости, движущейся вблизи верхнего угла сечения цилиндра, отличается от скорости жидкости вблизи нижнего угла, что приводит к асимметричному следу за цилиндром относительно центральной линии. Асимметрия в набегающем потоке увеличивает флуктуации в вихревом следе, приводя к более раннему сходу вихрей в течении с поперечным градиентом скорости (сдвигом) по сравнению с однородным потоком. Положительные вихри имеют меньшие размеры, чем отрицательные вихри. Это происходит из-зе того, что относительная скорость жидкости, текущей вблизи нижней поверхности цилиндра, уменьшается при увеличении κ. Можно видеть, что значительное изменение картины течения в ближнем следе имеет место при κ = 0.4, когда положительные вихри растягиваются в направлении основного потока и периодический характер течения полностью исчезает вниз по потоку. В этом случае также отсутствуют положительные вихри, сходящие с цилиндра вниз по потоку, частота схода вихрей убывает с ростом κ.

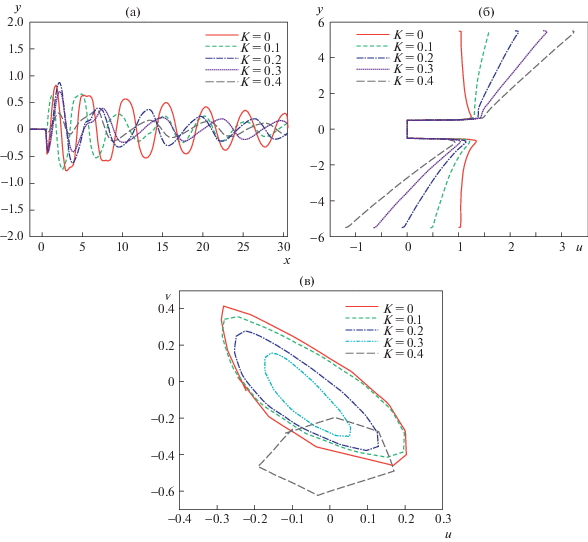
На рис. 7а и 7б изображены осевые профили компонент скорости: $v$ как функции $x$ при $y = 0.0$ и $u$ как функции $y$ при $x = 0.0$ соответственно, при $\operatorname{Re} = 100$ и разных значениях κ. Из построенных графиков видно, что при росте κ значения $u$ увеличиваются в верхней части и убывают в нижней части цилиндра, тогда как максимальные значения и амплитуда флуктуаций $v$ уменьшаются вдоль оси x с ростом κ. Фазовая диаграмма (рис. 7в) зависимости $u$ от $v$ в точке наблюдения (0.75, –0.5) построена для момента, когда течение достигло устойчивого периодического состояния. Эти графики указывают на периодичность решений.

Рис. 7.

Флуктуации скорости на центральной линии при Re = 100 при разных значениях κ: $v$ вдоль оси x (а); $u$ вдоль оси y (б); фазовая диаграмма (в).

3.2.2. Структурная бифуркация. Следуя анализу структурных бифуркаций начального течения, обсудим теперь нестационарный отрыв полностью развитого течения с использованием такого же анализа. Благодаря периодическому характеру течения, который очевиден из картины схода вихрей, описанной выше, достаточно рассмотреть один временной период изменения коэффициента подъемной силы для полностью развитого потока, чтобы продемонстрировать возникновение структурной бифуркации в течение этого периода. На рис. 8 показано возникновение первой и второй структурной бифуркаций в течение одного временного периода при Re = 100, κ = 0.0. Из рисунка видно, что обе бифуркации происходят, когда величина подъемной силы начинает увеличиваться от нулевого значения при значениях времени $t = 0T + 0.337$, $T{\text{/}}2{\text{ }} + 0.385$ в точках (0.333, –0.167) (0.333, 0.167) соответственно. Всегда есть структурная бифуркация, соответствующая каждому вихрю в полностью развитом течении. Характер каждой бифуркации такой же для других значений параметров, приведенных в табл. 6. Из этой таблицы ясно, что точка отрыва на верхней половине цилиндра смещается вверх по потоку при увеличении κ. Однако при увеличении поперечного градиента скорости увеличивается также время между двумя последовательно возникающими отрывами. Из-за этого частота схода вихрей уменьшается при увеличении κ, как было найдено ранее в предыдущем разделе. С другой стороны, точка отрыва с нижней стороны вниз по потоку медленно смещается вверх по потоку при увеличении κ для рассмотренных значений параметров. Однако точной картины, которая может быть описана в терминах времени и положения точек бифуркации, не существует из-за сложной природы течения при больших значениях поперечного градиента скорости (параметра сдвига).

Рис. 8.

Зависимости для Re = 100 и $\kappa = 0.0$: коэффициент подъемной силы на одном временном периоде T (а), распределение завихренности вдоль поверхности цилиндра в момент времени ${{t}_{1}} = 0T + 0.337$ (б), в момент времени ${{t}_{2}} = 0T + 3.359$ (г); изменение во времени завихренности в точке $P_{1}^{*}(x,y) = (0.333, - 0.167)$ (в) и точке $P_{2}^{*}(x,y) = (0.333,0.167)$ (д) на поверхности цилиндра.

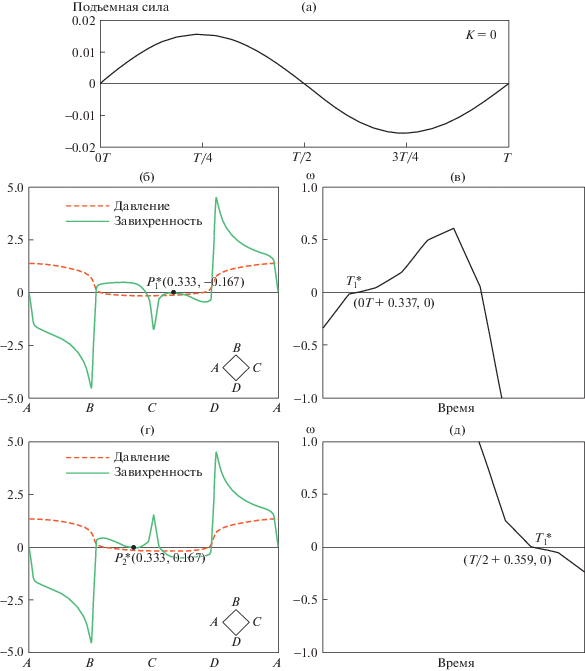
Таблица 6.

Место и время возникновения первой и второй структурных бифуркаций в полностью развитом течении

  Первая бифуркация ($P_{1}^{*}$(x, y, t1) Вторая бифуркация ($P_{2}^{*}$(x, y, t2)
Re = 100    
κ = 0.0 ((0.333, –0.167), 0T + 0.337) ((0.333, 0.167), 0T + 3.359)
κ = 0.1 ((0.333, –0.167), 0T + 0.309) ((0.333, 0.167), 0T + 3.402)
κ = 0.2 ((0.375, –0.125), 0T + 0.292) ((0.333, 0.167), 0T + 3.491)
κ = 0.3 ((0.375, –0.125), 0T + 0.276) ((0.375, 0.125), 0T + 3.579)
κ = 0.3 ((0.333, –0.167), 0T + 0.213) ((0.375, 0.125), 0T + 3.326)

4. ВЫВОДЫ

В настоящем исследовании подробно рассмотрена картина исходного и полностью развитого течения при обтекании наклонного цилиндра с квадратным осевым сечением потоком с поперечным градиентом скорости под углом α = 45° для чисел Рейнольдса $\operatorname{Re} = 100$, 185 и значений параметра сдвига потока от $\kappa = 0.0$ до 0.4. Течение рассчитано при решении уравнений Навье–Стокса в переменных функция тока – завихренность ($\Psi - \zeta $) с использованием компактной конечно-разностной схемы высшего порядка точности. Топологические идеи, основанные на анализе структурных бифуркаций, обеспечивают критерии идентификации возникающих структур течения в рассматриваемой задаче. Используя этот анализ, показано, как происходит отрыв потока в некоторое время в некоторой точке. Расчеты подтвердили, что при $\kappa = 0.0$, т.е. в случае однородного набегающего потока, две точки бифуркации появляются в одно и то же время на верхней и нижней гранях цилидра вниз по потоку, что обнаруживает симметрию течения в этих случаях для двух рассмотренных значений числа Рейнольдса $\operatorname{Re} $. Также отмечено, что при текущих значениях $\operatorname{Re} $ следует точная картина времени возникновения бифуркационных точек при всех значениях κ. Найдено, что время возникновения первой структурной бифуркации уменьшается почти линейно с ростом κ. С другой стороны, время возникновения второй бифуркации растет с ростом κ. Кроме того, используя наличие седловых точек в начальной стадии при Re = 100, показано, что вследствие влияния поперечного градиента скорости (сдвига) потока седловые точки со временем постепенно смещаются вниз при росте κ. Это также подтверждает природу сдвигового течения. Сход вихрей и развитие следа за цилиндром существенно зависят от поперечного градиента скорости (параметра сдвига κ). При росте поперечного градиента скорости частота схода вихрей за цилиндром убывает. Разница в размерах и интенсивности поочередно сходящих вихрей становится более заметной при росте κ.

Список литературы

  1. Kiya M., Tamura M.H., Arie M. Vortex shedding from a circular cylinder in moderate Reynolds number shear flow // Journal of Fluid Mechanics. 1980. V. 141. P. 721–735.

  2. Sohankar A., Norberg C., Davidson L. Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers // Physics of Fluids. 1999. V. 11. P. 288.

  3. Saha A.K., Murlidhar K., Biswas G. Vortex structures and kinetic energy budget in two dimensional flow past a square cylinder // Computers & Fluids. 2000. V. 29. P. 186196.

  4. Ranjan R., Dalal A., Biswas G. A numerical study of fluid flow and heat transfer around a square cylinder at incidence using unstructured grids // Numerical Heat Transfer. 2008. V. 54. P. 890–913.

  5. Kalita J.C., Ray R.K. A transformation-free hoc scheme for incompressible viscous flows past an impulsively started circular cylinder // Journal of Computational Physics. 2009. V. 228. P. 5207–5236.

  6. Chatterjee D., Biswas G., Amiroudine S. Numerical simulation of flow past row of square cylinders for various separation ratios // Computers & Fluids. 2010. V. 39. P. 49–59.

  7. Ray R.K. A transformation-free HOC scheme for incompressible viscous flow past a rotating and translating circular cylinder // Journal of Scientific Computing. 2011. V. 46. P. 265–293.

  8. Kalita J.C., Sen S. Triggering asymmetry for flow past circular cylinder at low Reynolds numbers // Computers & Fluids. 2012. V. 59. P. 44–60.

  9. Kalita J.C., Sen S. Unsteady separation leading to secondary and tertiary vortex dynamics: the sub-α- and sub-β-phenomena // Journal of Fluid Mechanics. 2013. V. 730. P. 19–51.

  10. Ayukawa A., Ochi J., Kawahara G., Hirao T. Effect of shear rate on the flow around a square cylinder in a uniform shear flow // Journal of Wind Engineering and Industrial Aerodynamics. 1993. Vol. 50. P. 97106.

  11. Hwang R.R., Sue Y.C. Numerical simulation of shear effect on vortex shedding behind a square cylinder // International Journal of Numerical Methods in Fluids. 1997. V. 25. P. 1409–1420.

  12. Lankadasu A., Vengadesan S. Onset of vortex shedding in planar shear flow past a square cylinder // International Journal of Heat and Fluid Flow. 2008. Vol. 29. P. 1054–1059.

  13. Kumar A., Ray R.K. Numerical study of shear flow past a square cylinder at Reynolds number 100, 200 // Procedia Engineering. 2015. V. 127. P. 102–109.

  14. Kiya M., Arie M. An inviscid numerical simulation of vortex shedding from an inclined flat plate in shear flow // Journal of Fluid Mechanics. 1977. V. 82. P. 241–253.

  15. Sohankar A., Norberg C., Davidson L. Low-Reynolds number flow around square cylinders at incidence: study of blockage, onset of vortex shedding and outlet boundary condition // International Journal of Numerical Methods in Fluids. 1998. V. 26. P. 39–56.

  16. Tong X.H., Luo S.C., Khoo B.C. Transition phenomena in the wake of an inclined square cylinder // Journal of Fluids and Structures. 2008. V. 24. P. 994–1005.

  17. Yoon D.H., Yang K.S., Choi C.B. Flow past a square cylinder with an angle of incidence // Physics of Fluids. 2010. V. 22. P. 043603.

  18. Yoon D.H., Yang K.S., Choi C.B. Three-dimensional wake structures and aerodynamic coefficients for flow past an inclined square cylinder // Journal of Wind Engineering and Industrial Aerodynamics. 2012. V. 101. P. 34–42.

  19. Piccardo G., Carassale L., Freda A. Critical conditions of galloping for inclined square cylinders // Journal of Wind Engineering and Industrial Aerodynamics. 2011. V. 99. P. 748–756.

  20. Kalita J.C., Dalal D.C., Dass A.K. A class of higher order compact schemes for the unsteady two-dimensional convection-diffusion equation with variable convection coefficients // International Journal for Numerical Methods in Fluids. 2002. V. 38. P. 1111–1131.

  21. Kalita J.C., Dass A.K., Dalal D. A transformation-free hoc scheme for steady-state convection diffusion on non-uniform grids // International Journal for Numerical Methods in Fluids. 2004. V. 44. P. 33–53.

  22. Ghil M., Liu J.G., Wang C., Wang S. Boundary-layer separation and adverse pressure gradient for 2-D viscous incompressible flow // Physica D. 2004. V. 197. P. 149–173.

  23. Ghil M., Ma T., Wang S. Structural bifurcation of 2-d nondivergent flows with Dirichlet boundary conditions applications to boundary-layer separation // SIAM Journal of Applied Maths. 2005. Vol. 65. P. 1576–1596.

  24. Cheng M., Tan S.H., Hung N.K.C. Linear shear flow over a square cylinder at low Reynolds number // Physics of Fluids. 2005. V. 17. P. 078103.

  25. Perry A.E., Chong M.S., Lim T.T. The vortex shedding process behind two-dimensional bluff bodies // Journal of Fluid Mechanics. 1982. V. 116. P. 77–90.

  26. Eton B.E. Analysis of laminar vortex shedding behind a circularcylinder by computer-aided flow visualization // Journal of Fluid Mechanics. 1987. V. 180. P. 117–145.

  27. De A.K., Dalal A. Numerical simulation of unconfined flow past a triangular cylinder // 2006. International Journal for Numerical Methods in Fluids. 2006. V. 52. P. 801–821.

  28. Ozgoren M. Flow structures in the downstream of square and circular cylinders. Fluid Measurement and Instrumentation. 2006. V. 17. P. 225235.

  29. Cheng M., Whyte D.S., Lou J. Numerical simulation of flow around a square cylinder in uniform-shear flow // Journal of Fluids and Structures. 2007. V. 23. P. 207–226.

  30. Dutta S., Panigrahi P.K., Muralidhar K. Experimental investigation of flow past a square cylinder at an angle of incidence // Journal of Engineering Mechanics. 2008. V. 134. P. 788803.

  31. Ray R.K., Kalita J.C. A transformation-free hoc scheme for incompressible viscous flows on nonuniform polar grids // International Journal for Numerical Methods in Fluids. 2010. V. 62. P. 683–708.

  32. Ray R.K., Kumar A. Numerical study of shear rate effect on unsteady flow separation from the surface of the square cylinder using structural bifurcation analysis // Physics of Fluids. 2017. V. 29. P. 083604.

  33. Mittal HVR, Al-Mdallal Q.M., Ray R.K. Locked-on vortex shedding modes from a rotationally oscillating circular cylinder // Ocean Engineering. 2017. V. 146. P. 324–338.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал