Известия РАН. Механика жидкости и газа, 2020, № 3, стр. 141-150

1. ПОСТРОЕНИЕ ТОЧНЫХ АНАЛИТИЧЕСКИХ РЕШЕНИЙ

С использованием массовой лагранжевой переменной $m$ уравнения одномерной нестационарной газовой динамики могут быть сведены к системе с квадратичной нелинейностью [9, 10]

где $x = x(m,t)$ – закон движения, $t$ – время, $p = p(m,t)$ – давление, $\gamma $ – показатель адиабаты, $g(m)$ – массовая сила (например, для газа в однородном поле тяготения $g(m) = - g$, где g – величина ускорения свободного падения; можно также учесть наличие в заряженном газе вмороженного электрического поля в рамках электрогидродинамики [9]). Плотность выражается через закон движения с помощью соотношения $\rho = 1{\text{/}}{{x}_{m}}$. В дальнейшем для функций одной переменной приняты обозначения: точка – производная по времени, штрих – производная по массе.

Важно заметить, что уравнение (1.2) представляет собой закон сохранения

в правой части которого стоит функция $\sigma (m)$, связанная с энтропией.

В уравнениях (1.1), (1.2) можно совершить взаимно-однозначную замену переменной $a = a(t)$. Пусть a удовлетворяет уравнению ${{\dot {a}}^{2}}{\text{/}}2 = U(a)$ (т.к. фактически можно считать, что a определяется гамильтонианом). В этом случае получается система

В уравнение (1.4) входит потенциал U(a), который определяет характер движения. Предполагается, что $a(0) = 0$.

Решение системы (1.4), (1.5) ищется в виде ряда Тейлора по a в окрестности нуля

При этом начальные условия выражаются через члены рядов следующим образом:

Пусть функция $\sqrt {U(a)} $ является гладкой. В этом случае, поскольку $\dot {a} = \sqrt {2U(a)} $ и $a(0) = 0$, в силу теоремы о существовании и единственности решения задачи Коши для $a(t)$, нельзя считать $U(0)$ = 0, что приводит к $a \equiv 0$. Это не пригодно с точки зрения замены переменной. Кроме того, для исследования поведения решения в терминах $a$ отсутствует необходимость определения зависимости $a(t)$ как таковой. При этом теорема гарантирует существование и единственность такой зависимости.

Стоит отметить, что в соответствии со структурой рядов (1.6), (1.7) существует инвариантность относительно растяжения переменной a и коэффициентов разложений. Ясно, что для достаточно малых $a$ ряды будут сходиться при любых ограниченных коэффициентах.

При подстановке (1.6), (1.7) в закон сохранения (1.5) и перемножении рядов по правилу Коши, при одинаковых степенях a получаются рекуррентные соотношения

где $n = 1,2,3,...$ (правая часть равняется нулю при n = 1). Следует сказать, что функция $A_{0}^{'}(m)$, вообще говоря, не может быть тождественно равна нулю в силу ее механического смысла: величина, обратная начальной плотности.

Рекуррентные соотношения, следующие из уравнения движения (1.4), зависят от разложения функции U(a)

и имеют вид где $n = 2,3,4,...$ и δ_ij – символы Кронекера. Важно заметить, что ${{C}_{0}} = U(0) \ne 0$.

Соотношения (1.9) и (1.11) устроены таким образом, что все члены ряда могут быть найдены последовательно исходя из заданных начальными условиями ${{A}_{0}}(m)$, ${{A}_{1}}(m)$ и ${{B}_{0}}(m)$, при этом не нужно решать дифференциальных уравнений и интегрировать

Соотношения (1.12)–(1.14) позволяют точно находить коэффициенты рядов при произвольном разложении (1.10) функции U(a) с помощью любого математического пакета, допускающего символьные преобразования.

Стоит подчеркнуть, что для произвольного момента времени решение при заданном m зависит от вида начальных условий (1.8) и их производных. Кроме того, из вида рекуррентных формул также следует, что равновесные начальные условия, т.е. условия вида

всегда приводят к равновесному решению т.е. равновесие в начальный момент сохраняется во все последующие моменты времени для любого U(a).

Для того чтобы использовать построенные решения в расчетах, необходимо совершить переход от рядов к их частичным суммам. С целью контроля точности такой процедуры, а также с целью проверки необходимого условия сходимости можно вычислить сохраняющуюся во времени энтропийную функцию $\sigma (m)$ (1.3), известную из начальных условий, и сравнить ее точное значение с этой же величиной, но уже вычисленной с помощью построенных частичных сумм рядов. При этом удобно воспользоваться относительной погрешностью

Здесь ряды p и x представлены с помощью своих частичных сумм.

В случае приближения $r(m,t)$ к 0 с ростом числа вычисляемых членов рядов возможность расходимости ряда для $p(m,t)$ можно проверить, проанализировав стремление к 0 ряда для ${{x}_{m}}(m,t)$, и соответственно наоборот.

Граничные условия в рамках данного подхода определяются необходимым для существования решения образом, например, в виде непротекания на поверхностях пары поршней, в области между которыми происходит рассматриваемое движение. Законы движения поршней находятся a posteriori, т.е. после вычисления решения задачи, и представляются функциями $x(0,t)$ и $x(M,t)$ соответственно (если масса m изменяется в пределах [0, M]). В этом смысле можно считать, что для решения конкретных задач применяется полуобратный метод.

Однако можно поставить задачу о равенстве $a(t)$ закону движения одного из поршней. Пусть координате поршня отвечает точка m = 0, и начальные условия, по предположению, согласуются с указанными краевыми условиями при t = 0, так что отсутствуют начальные разрывы. При этом требуется определить подходящее U(a).

В этом случае закон движения поршня имеет вид $x(0,t) = a(t)$. В соответствии с (1.6) получается, что

Данные соотношения можно выполнить, если на каждой итерации рекуррентных соотношений, прежде чем вычислять очередной ${{A}_{n}}(m)$, определять

Таким образом, функция U(a) выстраивается по начальным условиям в процессе решения задачи. В конечном счете она имеет вид

Выбирать ${{C}_{0}}$ следует, если возможно, исходя из неотрицательности U(a). При малых $t$, а значит и малых a в силу $a(0) = 0$, этого добиться несложно. Вообще говоря, возможность выполнения условия неотрицательности при произвольном a зависит от начальных данных и массовой силы. Стоит отметить, что конкретизация ${{C}_{0}}$ также влияет на получаемое решение. Сам вид $a(t)$ определяется через полученную U(a) из соответствующих дифференциального уравнения и начального условия.

2. СРАВНЕНИЕ РЕШЕНИЙ В РЯДАХ С ИЗВЕСТНЫМИ РЕШЕНИЯМИ

Указанные рассуждения оказываются полезными при решении следующей задачи Коши с краевыми условиями. Пусть начальные данные имеют вид

и массовые силы отсутствуют: $g(m) = 0$.

Линейность начальной скорости по $m$ и постоянство начальных плотности и давления в соответствии с (1.12)–(1.14) приводят к тому, что какими бы ни были постоянные ${{C}_{n}}$, x(m, t) = = $m{{q}_{1}}(t)$ и $p(m,t) = {{q}_{2}}(t)$ с некоторыми функциями времени ${{q}_{1}}$ и ${{q}_{2}}$. Отсюда следует, что $x(0,t) \equiv 0$, т.е. поршень в точке m = 0 остается неподвижным во все моменты времени.

Задача нахождения закона движения поршня в точке $m = 1$ в виде a(t) дает, в свою очередь, что ${{C}_{n}}$ = 0 для любого натурального $n$, поскольку $B_{{n - 1}}^{'}(1) = 0$. Следовательно, $U(a) \equiv {{C}_{0}} > 0$ и a(t) = = $\sqrt {2{{C}_{0}}} t$ = Vt. В итоге закон движения второго поршня будет иметь вид $x(1,t) = {{A}_{0}}(1) + {{A}_{1}}(1)a(t)$ = = 1 + αVt, где можно положить V = 1.

Таким образом, с помощью определения в рамках изложенной теории $a(t) = t$ при начальных условиях (2.1) и отсутствии массовых сил, решается точно задача Коши с граничными условиями

которая моделирует процесс расширения газа с однородной деформацией в трубе с подвижной стенкой.

Задача (2.2)–(2.4) имеет точное решение в квадратурах [3]

Решение, получаемое исходя из формул (1.12)–(1.14), в точности представляет собой разложение в ряд Тейлора по времени в окрестности нуля решения (2.5) и представлено на рис. 1.

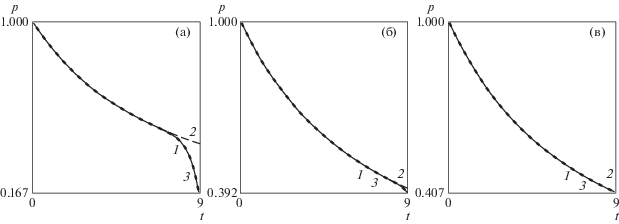
На данном рисунке для $\gamma = 1.4$ и α = 0.1 изображены сравнительные графики давления согласно решению через разложение по степеням функции времени (1), решению в квадратурах (2), разложению решения в квадратурах в ряд Тейлора (3) при 20, 50 и 100 взятых членах рядов соответственно.

Следует отметить, что в данной задаче

т.е. в точности является погрешностью ряда давления относительно его суммы – решения в квадратурах. При $\alpha t < 1$ функция $r(m,t)$ достаточно быстро убывает с ростом числа членов ряда, достигая в точке $\alpha t = 0.9$ значений 0.58981, 0.03597 и 0.00024 при 20, 50 и 100 взятых членов ряда соответственно.

В качестве другого примера можно рассмотреть, наоборот, линейное по $m$ начальное давление и постоянную начальную скорость. В соответствии с рекуррентными соотношениями (1.12)–(1.14) при произвольном U(a) это приводит к решению, которое сходится (вообще говоря в некоторой области) в терминах $a$ к известному решению [3] с постоянной по массе $m$ и линейной по времени $t$ скоростью с сохраняющимися начальными плотностью и давлением, т.е. к твердотельному движению с постоянным ускорением.

Если задать начальные условия в виде

и строить решение с помощью разложения в степенной ряд по функции $a(t) = sint$, где $t \in [ - \pi {\text{/}}2$, π/2], то в терминах a получается решение, в точности представляющее собой разложение в ряд Тейлора следующих функций:

На рис. 2 при $\alpha = 1$ показан график скорости (1) в терминах $t$ для полученного через формулы (1.12)–(1.14) решения с 20, 50 и 100 вычисленными членами ряда соответственно. Хорошо видна сходимость скорости к точному решению $v = - t$ (изображено линией 2). Поведение в окрестности точек $t = \pm \pi /2$ регулярно, несмотря на отсутствие производной арксинуса при $a = \pm 1$.

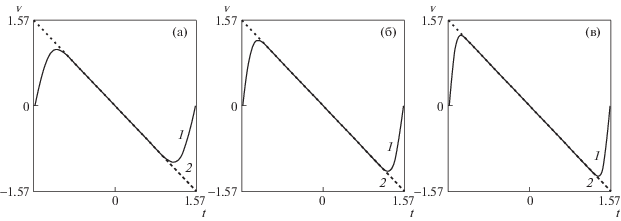
Нужно отметить, что, согласно теории размерности, в приведенных примерах и далее можно выбрать заданным образом только три масштаба. Последний пример показывает, что построенное решение, в некотором смысле, может не зависеть почти во всей области определения от выбора функции $a(t)$.

3. ОГРАНИЧЕННОЕ ДВИЖЕНИЕ

В данном разделе рассматривается более сложная по сравнению с первым примером задача о расширении газа в трубе, одна стенка которой по-прежнему неподвижна, а закон движения второй представляется в терминах монотонно растущих ограниченных функций.

Для моделирования соответствующего процесса можно взять функцию $a(t)$ в виде $a = exp( - t)$ – 1. Задаются те же начальные условия (2.1), чтобы можно было оценить различия решений

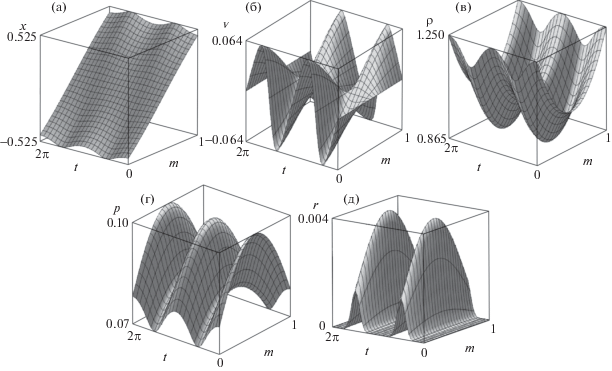
Здесь знак ${{A}_{1}}(m)$ поменялся, поскольку поменялся знак $\dot {a}(0)$. Для этого и всех дальнейших примеров будем также использовать $\gamma = 1.4$ и $g(m) = 0$, кроме последнего примера, в котором учитывается гравитация.

Решение для 20 членов ряда представлено на рис. 3. Здесь и в дальнейшем графики всегда идут в порядке слева направо сверху вниз: закон движения, скорость, плотность, давление, относительная энтропийная погрешность (1.15).

Исходя из рисунка видно, что каждая из функций, входящих в решение, при $t \to \infty $ выходит на свое асимптотическое значение (для каждого m), при этом, как и в предыдущем случае, давление и плотность, а значит и относительная энтропийная погрешность, от $m$ не зависят. Поршень, соответствующий массовой координате m = 0, покоится, закон движения второго поршня изображен на графике $x(m,t)$ при m = 1. Максимальное значение $r(m,t)$ убывает с ростом числа взятых членов рядов. Так, получаются значения порядка 0.016, 0.014 и 0.013 для 20, 50 и 100 членов рядов соответственно. Если вычислить 1000 коэффициентов, то относительная энтропийная погрешность будет составлять менее 1%.

4. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ

Решается задача о распространении возмущений, создаваемых периодическими колебаниями поршня с лагранжевой координатой m = 0, на фоне неоднородно распределенного в начальный момент времени давления.

Для этой цели выбирается $a(t) = sint$ и рассматриваются начальные условия

В данной задаче предполагается, что второй поршень отсутствует.

В соответствии с тригонометрическими формулами, разложение по степеням синуса времени представляет собой комбинацию ряда Фурье [11], взятую с целью справиться с нелинейностью системы уравнений газовой динамики. Прямое использование рядов Фурье оказывается неэффективным, поскольку при перемножении рядов такой подход приводит к бесконечным выражениям, вместо конечных рекуррентных формул.

Для первых 16 взятых коэффициентов решение показано на рис. 4 (в этой и следующей задачах решение изображено на полном периоде с целью наглядности). Колебания поршня изображены на рисунке для закона движения при m = 0.

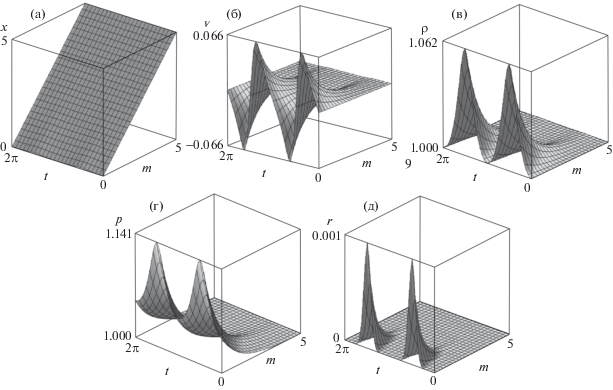
Опираясь на графики, можно утверждать, что при больших m все возмущения затухают. Данное обстоятельство согласуется с упомянутым сохранением изначального равновесия: при больших $m$ начальные условия стремятся к равновесным, а решение в конкретной массовой точке определяется лишь начальными условиями в ее малой окрестности. Поскольку при больших $m$ полученное решение во все моменты времени стремится к равновесному, можно сказать, что в этом смысле равновесие устойчиво.

Порядок относительной энтропийной погрешности убывает с ростом числа взятых членов рядов и составляет 0.0012, 0.0011 и 0.0010 для 8, 12 и 16 коэффициентов соответственно. Число 0.05 в начальных условиях подбиралось именно с той целью, чтобы создаваемое возмущение равновесного давления приводило к регулярному поведению решения в рядах.

В качестве следующего примера решается задача об эволюции зоны высокого давления при сильной неоднородности начальной плотности в трубе с колеблющимися поршнями.

В соответствии с постановкой задачи следует определить начальные условия в виде

Указанная задача представляет интерес в приложениях, однако устройство начальных условий и требования к краевым условиям усложняют процесс поиска аналитического решения. Обойти соответствующие сложности помогает поиск решения в виде разложения по степеням синуса времени $a(t) = sint$.

На рис. 5 показаны графики физических величин, характеризующих рассматриваемый процесс, для 12 членов рядов. Колебания, совершаемые поршнями, изображены на рисунке для закона движения при m = 0 и m = 1. Функционально решение устроено сложно, но при этом порядок относительной энтропийной погрешности остается невысоким и составляет 0.005, 0.004 и 0.003 для 8, 10 и 12 коэффициентов соответственно. Максимум погрешности достигается, как и в прошлом случае, в точках, где косинус времени равен нулю.

5. ДВИЖЕНИЕ С ОБОСТРЕНИЕМ

В настоящем пункте рассматривается задача о движении поршней, описывающемся в терминах неограниченно растущих функций, на неоднородном фоне при наличии гравитации.

Для получения решения такой задачи можно выбрать $a(t) = 1{\text{/}}(1 - t) - 1$, задать $g(m) = - 1$ и положить начальные данные в виде

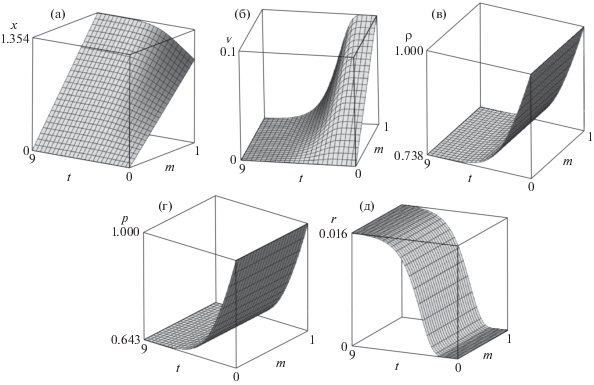
Построенное решение для 10 членов рядов приведено на рис. 6. Функция $a(t)$ является неограниченно растущей при $t \to 1$, поэтому степенные ряды по этой функции начнут расходиться с определенного момента времени. Однако построенное решение хорошо описывается при небольших a: при $t = 0.333$ порядок относительной энтропийной погрешности мал и составляет 0.0012, 0.0007 и 0.0003 для 6, 8 и 10 коэффициентов.

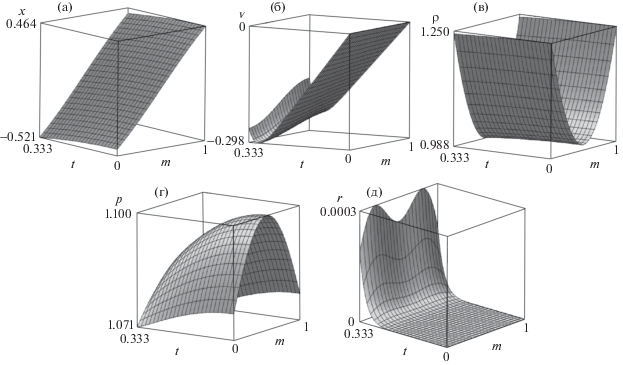
Законы движения поршней изображены на рисунке для $x(m,t)$ при m = 0 и 1. Чтобы перейти от изображения решения в переменных Лагранжа к изображению решения в переменных Эйлера, достаточно построить графики в соответствующих координатах, исключая массу $m$ как параметр.

ЗАКЛЮЧЕНИЕ

В рамках адиабатического движения совершенного идеального газа развита теория построения точных аналитических решений задач Коши с краевыми условиями с помощью разложений в степенные ряды по функции от времени, задающей характер рассматриваемого явления. Для исследования используются уравнения в лагранжевой форме, в частности, записанные с использованием массовой переменной. Рекуррентные соотношения для зависящих от массы коэффициентов устроены так, что все неизвестные величины находятся из начальных условий только с помощью дифференцирования и алгебраических операций. Отсутствие необходимости решать дифференциальные уравнения и интегрировать позволяют использовать символьные вычисления, реализованные в математических пакетах, для точного нахождения коэффициентов рядов при любых заданных наперед начальных данных. Краевые условия определяются после решения задачи, например, в виде непротекания на поверхностях пары поршней, в области между которыми происходит рассматриваемое движение. Закон сохранения энтропии помогает контролировать поведение рядов и судить о погрешности при переходе от рядов к их частичным суммам. Решения, строящиеся на основе разработанного метода, проходят проверку на известных в газовой динамике точных решениях и позволяют распространить результаты на более общие случаи. Также метод позволяет получить новые решения физических задач, связанных, например, с ограниченными и периодическими движениями, течениями с обострением, и другими, задаваемыми заменой времени.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 20-01-00017).