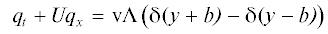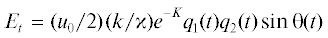Известия РАН. Механика жидкости и газа, 2020, № 2, стр. 28-41
Оптимальные возмущения в развитии неустойчивости свободного слоя сдвига и системы из двух встречных струйных течений
М. В. Калашник a, b, *, О. Г. Чхетиани a, **
a Институт физики атмосферы им. А.М. Обухова РАН
Москва, Россия
b Институт физики Земли им. О.Ю. Шмидта РАН
Москва, Россия
* E-mail: kalashnik-obn@mail.ru
** E-mail: lgg@ifaran.ru
Поступила в редакцию 16.05.2019
После доработки 22.07.2019
Принята к публикации 08.10.2019
Аннотация
Развивается аналитический подход к определению оптимальных возмущений, пригодный для течений с кусочно-постоянным распределением завихренности. Подход опирается на уравнение баланса энергии возмущений и явные выражения для скорости роста энергии или отношения конечной и начальной энергий. Соответствующие выражения являются функциями начальных параметров и из исследования этих функций на экстремум находятся параметры оптимальных возмущений. В рамках подхода рассмотрены классическая задача Релея о неустойчивости свободного слоя сдвига и задача о неустойчивости системы из двух встречных струйных течений во вращающемся слое мелкой воды. Проведено сопоставление параметров оптимальных возмущений с параметрами растущих нормальных мод.
Под оптимальными возмущениями в теории гидродинамической неустойчивости понимают возмущения с максимумом скорости роста энергии или отношения конечной и начальной энергий. Поиск оптимальных возмущений стимулирован осознанием ограниченности классического подхода, основанного на нахождении экспоненциально нарастающих нормальных мод. Так, было показано, что скорость роста суперпозиции растущей и затухающей нормальных мод может превосходить скорость роста одной растущей моды [1, 2]. Даже суперпозиция двух затухающих мод может демонстрировать алгебраический (немодальный) рост энергии на начальном этапе развития. Математическая причина такого поведения связана с отсутствием свойства нормальности у дифференциальных операторов задач теории устойчивости и, как следствие, свойства ортогональности их собственных функций [1, 2]. Важное физическое следствие состоит в возможности реализации различных сценариев подкритического перехода к турбулентности [1–4].
При нахождении оптимальных возмущений, как правило, решается достаточно сложная вычислительная задача на условный экстремум функционала полной энергии. Алгоритм решения задачи использует конечно-разностную аппроксимацию динамического оператора задачи по вертикали с последующим нахождением сингулярного разложения его матрицы (SVD разложения) [1–8]. В настоящей статье развивается аналитический подход к определению оптимальных возмущений, пригодный для течений с кусочно-постоянным распределением завихренности. Он использует уравнение баланса энергии и явные выражения для энергетических функционалов, представляющие собой функции параметров начального возмущения. Из исследования этих функций на экстремум находятся параметры оптимальных возмущений. Применительно к задаче Иди о бароклинной неустойчивости течения с вертикальным сдвигом [9, 10] данный подход был развит в недавней статье [11]. Ниже он применяется к задаче Релея о неустойчивости свободного слоя сдвига [12–14] и задаче о неустойчивости системы из двух встречных струйных течений во вращающемся слое мелкой воды [15]. Следует подчеркнуть физическую значимость этих задач. Так, в отличие от задачи о неустойчивости тангенциального разрыва скорости (неустойчивости Кельвина–Гельмгольца), задача Релея дает предпочтительный горизонтальный масштаб развивающихся возмущений. Системы встречных струйных течений наблюдаются в атмосферах планет и моделируются во вращающихся лабораторных установках.
1. ЗАДАЧА РЕЛЕЯ О НЕУСТОЙЧИВОСТИ СВОБОДНОГО СЛОЯ СДВИГА И ДВА ПРЕДСТАВЛЕНИЯ ЕЕ РЕШЕНИЯ
Динамика малых возмущений двумерного течения несжимаемой жидкости со скоростью $U = U(y)$ и завихренностью $Q(y) = - {{U}_{y}}$ описывается уравнением [3]
(1.1)
${{q}_{t}} + U{{q}_{x}} = - {\text{v}}{{Q}_{y}},\quad q = \Delta {\psi } = {{{\psi }}_{{xx}}} + {{{\psi }}_{{yy}}}$В классической задаче Релея [12] исследуется устойчивость свободного слоя сдвига с профилем скорости
(1.2)
$U = {{u}_{0}}y{\text{/}}b,\quad \left| y \right| < b,\quad U = {{u}_{0}}\operatorname{sgn} (y),\quad \left| y \right| > b,\quad {{u}_{0}} = {\Lambda }b$Для профиля скорости (1.2) уравнение (1.1) принимает вид
где ${\delta }(y)$ – дельта функция. Данному уравнению удовлетворяют периодические по продольной координате решения с завихренностью $q = {{{\psi }}_{{xx}}} + {{{\psi }}_{{yy}}} \equiv 0$. Общая форма таких решений записывается как(1.4)
${\psi } = - \frac{1}{{2k}}({{Q}_{1}}(t){{e}^{{ - k\left| {y + b} \right|}}} + {{Q}_{2}}(t){{e}^{{ - k\left| {y - b} \right|}}}){{e}^{{ikx}}}$На разрывах фоновой завихренности для решений (1.4) должны выполняться условия
(1.5)
$y = \pm b{\text{:}}$ ${{p}_{t}} \pm {{u}_{0}}{{p}_{x}} = \mp {\Lambda }{{{\psi }}_{x}},$ $p = \left[ {{{{\psi }}_{y}}} \right]$Подстановка (1.4), (1.6) в условия (1.5) приводит к системе обыкновенных дифференциальных уравнений для амплитуд
(1.7)
$i\frac{{d{{Q}_{1}}}}{{dt}} = k{{c}_{1}}{{Q}_{1}} + 0.5{\Lambda }{{e}^{{ - 2kb}}}{{Q}_{2}},\quad i\frac{{d{{Q}_{2}}}}{{dt}} = k{{c}_{2}}{{Q}_{2}} - 0.5{\Lambda }{{e}^{{ - 2kb}}}{{Q}_{1}}$(1.9)
$i\frac{{d{\mathbf{q}}}}{{dt}} = S{\mathbf{q}},\quad {\mathbf{q}} = \left( {\begin{array}{*{20}{c}} {{{Q}_{1}}} \\ {{{Q}_{2}}} \end{array}} \right)\quad S = r\left( {\begin{array}{*{20}{c}} { - {\alpha }}&1 \\ { - 1}&{\alpha } \end{array}} \right)$Общее решение системы (1.9) представляется в виде ${\mathbf{q}}(t) = {{C}_{1}}{{e}^{{ - i{{{\omega }}_{1}}t}}}{{{\mathbf{h}}}_{1}} + {{C}_{2}}{{e}^{{ - i{{{\omega }}_{2}}t}}}{{{\mathbf{h}}}_{2}}$, где ${{{\mathbf{h}}}_{{1,2}}}$ – собственные вектора матрицы S, отвечающие собственным значениям
С учетом выражений для собственных векторов ${{{\mathbf{h}}}_{{1,2}}} = {{(1 \pm {\mu },\,\,1 \mp {\mu })}^{T}}$, μ = $\sqrt {({\alpha } - 1){\text{/}}({\alpha } + 1)} $, подстановка q(t) в (1.4) дает представление функции тока возмущений посредством суперпозиции двух нормальных мод с частотами ${{{\omega }}_{1}},\,{{{\omega }}_{2}}$
(1.11)
$\begin{gathered} {\psi } = - \frac{1}{{2k}}({{С}_{1}}{{e}^{{i(kx - {{{\omega }}_{1}}t)}}}{{{\Phi }}_{1}}(y) + {{С}_{2}}{{e}^{{i(kx - {{{\omega }}_{2}}t)}}}{{{\Phi }}_{2}}(y)) \\ {{{\Phi }}_{{1,2}}}(y) = (1 \pm {\mu }){{e}^{{ - k\left| {y + b} \right|}}} + (1 \mp {\mu }){{e}^{{ - k\left| {y - b} \right|}}} \\ \end{gathered} $Входящие в (1.10) произвольные постоянные ${{C}_{{1,2}}}$ однозначно выражаются через начальные амплитуды ${{Q}_{{1,2}}}(0)$, т.е. представление (1.10) дает решение задачи с заданными начальными распределениями скачков на границах $y = \mp b$. Именно эти распределения инициируют развитие возмущений.
Характер поведения во времени возмущений определяется значениями частот. Из (1.10) следует, что частоты ${{{\omega }}_{{1,2}}}$ комплексны, если $ - 1 < {\alpha }(K) < 1$ или, что эквивалентно, $0 < K < {{K}_{b}}$, где граничное значение ${{K}_{b}} = 1.278$ есть корень уравнения $K = 1 + {{e}^{{ - K}}}$ (уравнения ${\alpha }(K) = 1$). Для значений $K = 2bk$ из указанного интервала течение неустойчиво – наряду с затухающей модой существует экспоненциально нарастающая нормальная мода. Инкремент нарастания этой моды
(1.12)
$s(K) = r{{(1 - {{{\alpha }}^{2}})}^{{1/2}}} = 0.5{\Lambda }{{({{e}^{{ - 2K}}} - {{(K - 1)}^{2}})}^{{1/2}}}$Другое представление решения задачи Релея получено в статье [13], содержащей, в частности, критику подхода, основанного на нахождении нормальных мод. Это представление получается из (1.4), если положить ${{Q}_{{1,2}}}(t) = {{q}_{{1,2}}}(t){{e}^{{i{{{\theta }}_{{1,2}}}(t)}}}$, где ${{q}_{{1,2}}}$ – вещественные части комплексных амплитуд, ${{{\theta }}_{{1,2}}}(t)$ – соответствующие фазы. Для функции тока возмущения из (1.4) сразу следует вещественное выражение
(1.13)
${\psi } = - \frac{1}{{2k}}({{q}_{1}}(t){{e}^{{ - k\left| {y + b} \right|}}}\cos (kx + {{{\theta }}_{1}}(t)) + {{q}_{2}}(t){{e}^{{ - k\left| {y - b} \right|}}}\cos (kx + {{{\theta }}_{2}}(t)))$Начальные распределения скачков производной на границах сдвигового слоя даются выражениями $p(y = b) = {{q}_{2}}(0)\cos \left( {kx + {{{\theta }}_{2}}(0)} \right)$, $p(y = - b) = {{q}_{1}}(0)\cos \left( {kx + {{{\theta }}_{1}}(0)} \right)$.
В представлении (1.13) слагаемые, пропорциональные ${{q}_{1}}(t),\;{{q}_{2}}(t)$, описывают краевые волны, локализованные соответственно у границы $y = - b$ и $y = + b$ (в окрестностях скачков фоновой завихренности). Пару таких волн часто называют встречными волнами Россби [13, 14]. Система динамических уравнений, описывающая взаимодействие пары волн, получается подстановкой указанного представления для амплитуд в систему (1.9)
(1.14)
$\frac{{d{{q}_{1}}}}{{dt}} = r{{q}_{2}}\sin {\theta ,}$ $\frac{{d{{q}_{2}}}}{{dt}} = r{{q}_{1}}\sin {\theta }$(1.15)
$\frac{{d{\theta }}}{{dt}} = - 2r({\alpha } - 0.5(m + {{m}^{{ - 1}}})\cos {\theta }),\quad m = {{q}_{1}}{\text{/}}{{q}_{2}}$Здесь ${\theta } = {{{\theta }}_{2}} - {{{\theta }}_{1}}$, ${{{\theta }}_{ + }} = {{{\theta }}_{1}} + {{{\theta }}_{2}}$. Уравнения (1.14), (1.15) образуют замкнутую систему относительно амплитуд ${{q}_{1}},\;{{q}_{2}}$ и сдвига фаз ${\theta } = {{{\theta }}_{2}} - {{{\theta }}_{1}}$.
Хотя система (1.14), (1.15) является нелинейной (в отличие от системы (1.7) или (1.9)), она иллюстрирует принципиальную роль сдвига фаз ${\theta }$ для развития возмущения. Действительно, согласно уравнениям (1.14) амплитуды нарастают, если сдвиг фаз $0 < {\theta } < {\pi }$ $(\sin {\theta } > 0)$. Далее, при ${{q}_{1}} = {{q}_{2}}$ и ${\theta } = {{{\theta }}_{n}}$, где
система имеет точное решение ${{q}_{1}}(t) = {{q}_{1}}(0)\exp (st)$. Данное решение отвечает нормальной моде с инкрементом нарастания (1.12). Растущая нормальная мода, таким образом, всегда имеет равные амплитуды на границах и зависящий от волнового числа сдвиг фаз, определяемый выражением (1.17). Эта информация совершенно теряется в представлении решения суммой нормальных мод.Из системы (1.14), (1.15) вытекают законы сохранения
(1.18)
${{I}_{1}} = q_{1}^{2} - q_{2}^{2} = {\text{const,}}\quad {{I}_{2}} = 0.5\,(q_{1}^{2} + q_{2}^{2}) - {{{\alpha }}^{{ - 1}}}{{q}_{1}}{{q}_{2}}\cos {\theta } = {\text{const}}$2. УРАВНЕНИЕ БАЛАНСА ЭНЕРГИИ И НАЧАЛЬНЫЕ ОПТИМАЛЬНЫЕ ВОЗМУЩЕНИЯ
В рассмотрении проблемы оптимальных возмущений важную роль играет уравнение баланса энергии, следующее из (1.3), (1.5). С использованием операции горизонтального осреднения $\left\langle \phi \right\rangle = \mathop {\lim }\limits_{L \to \infty } \frac{1}{{2L}}\int_{ - L}^L {\phi dx} $, определяется плотность энергии ${\varepsilon } = (1{\text{/}}2)({\psi }_{x}^{2} + {\psi }_{y}^{2})$ и полная энергия возмущения $E = \int_{ - \infty }^{ + \infty } {\left\langle {\varepsilon } \right\rangle \,d} y$. Из определения ${\varepsilon }$ следует тождество
(2.1)
${{{\varepsilon }}_{t}} = {{\left( {{\psi }{{{\psi }}_{{xt}}}} \right)}_{x}} + {{\left( {{\psi }{{{\psi }}_{{yt}}}} \right)}_{y}} - {\psi }{{q}_{t}}$(2.2)
${{E}_{t}} = {{u}_{0}}\left( {\left\langle {\tau } \right\rangle (y = - b) - \left\langle {\tau } \right\rangle (y = + b)} \right),\quad {\tau } = p{{{\psi }}_{x}}$С учетом уравнения (2.2) и представления функции тока (1.13) находятся явные выражения для производной ${{E}_{t}}$ и самой энергии
(2.4)
$E = (b{\text{/}}4K)(q_{1}^{2}(t) + q_{2}^{2}(t) + 2{{e}^{{ - K}}}{{q}_{1}}(t){{q}_{2}}(t)\cos {\theta }(t))$Ключевым параметром в этих выражениях является сдвиг фаз ${\theta }(t) = {{{\theta }}_{2}}(t) - {{{\theta }}_{1}}(t)$. Непосредственно из (2.3) следует, что энергия растет, если сдвиг фаз $0 < {\theta } < {\pi }$. Этот результат, таким образом, может быть получен без привлечения системы (1.14) для описания взаимодействия волн. Только при указанном сдвиге фаз возмущение способно черпать энергию сдвигового потока.
Выражения (2.3), (2.4) позволяют получить простое решение задачи о начальных оптимальных возмущениях – возмущениях с максимальной скоростью энергии в начальный момент времени. Для скорости роста энергии из (2.3), (2.4) следует выражение
(2.5)
${\gamma } = \frac{1}{E}\frac{{dE}}{{dt}} = \frac{{2{\Lambda }K{{q}_{1}}{{q}_{2}}\sin {\theta }}}{{{{e}^{K}}(q_{1}^{2} + q_{2}^{2}) + 2{{q}_{1}}{{q}_{2}}\cos {\theta }}}$Поскольку ${\gamma }$ есть однородная функция амплитуд, она достигает максимального значения при ${{q}_{1}} = {{q}_{2}}$. В этом можно убедиться непосредственно, полагая ${{q}_{1}} = {\rho }\cos \varphi $, ${{q}_{2}} = {\rho }\sin \varphi $. При фиксированных значениях K, θ максимум ${\gamma }$ достигается при $\sin 2\varphi = 1$. Отсюда $\varphi = \pi {\text{/}}4$ и ${{q}_{1}} = {{q}_{2}}$.
При ${{q}_{1}} = {{q}_{2}}$ и фиксированном значении волнового параметра K скорость роста энергии
зависит только от начального сдвига фаз. Поскольку ${\gamma } > 0$ на промежутке $0 < {\theta } < {\pi }$ и на концах промежутка обращается в ноль, существует значение ${\theta } = {{{\theta }}_{{opt}}}$, при котором функция ${\gamma }(K,{\theta })$ достигает максимума. Это значение отвечает начальному оптимальному возмущению. Элементарное исследование (2.6) на экстремум дает(2.7)
$\cos {{{\theta }}_{{opt}}} = - {{e}^{{ - K}}},\quad {{{\gamma }}_{{opt}}} = {{{\gamma }}_{{opt}}}(K) = {\Lambda }K{{({{e}^{{2K}}} - 1)}^{{ - 1/2}}}$Формулы (2.7) определяют зависимости сдвига фаз и скорости роста энергии от волнового числа оптимального возмущения.
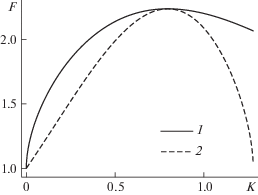
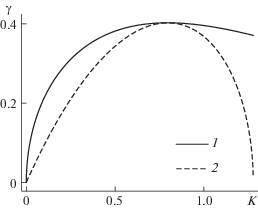
Зависимость ${{{\gamma }}_{{opt}}} = {{{\gamma }}_{{opt}}}(K)$ обращается в ноль при K = 0 и $K \to \infty $, достигая максимума во внутренней точке ${{K}_{{opt}}}$. Важная особенность задачи Релея, не имеющая аналога в других задачах [11], состоит в том, что значение ${{K}_{{opt}}}$ равно значению волнового числа $K = {{K}_{m}}$ для наиболее опасной нормальной моды. Это непосредственно следует из равенства $\cos {{{\theta }}_{{opt}}} = \cos {{{\theta }}_{n}}$, которое с учетом (1.17), (2.7) выполняется, если K удовлетворяет уравнению $K = 1 - {{e}^{{ - 2K}}}$, определяющему значение Km. Таким образом, наиболее опасная нормальная мода есть оптимальное возмущение с максимумом скорости роста энергии. Растущие нормальные моды с $K \ne {{K}_{m}}$ не являются оптимальными возмущениями. Зависимость ${{{\gamma }}_{{opt}}} = {{{\gamma }}_{{opt}}}(K)$ показана на рис. 1 линией 1. Пунктиром показана зависимость ${\gamma } = {{{\gamma }}_{n}}(K) = 2s(K)$ для растущих нормальных мод, определенная с использованием формулы (1.12). В точке $K = {{K}_{m}}$ происходит касание двух кривых.
Рис. 1.
Зависимость ${{\gamma }_{{opt}}}$ (линия 1) и ${{\gamma }_{n}} = 2s(K)$ (2) от безразмерного волнового числа K; значения $\gamma $ нормированы на величину сдвига $\Lambda $.
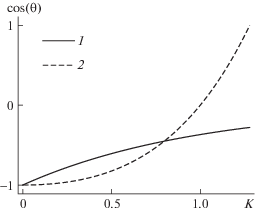
На рис. 2 представлены зависимости $\cos {{{\theta }}_{{opt}}}$ и $\cos {{{\theta }}_{n}}$ от волнового параметра K, пересекающиеся в точке $K = {{K}_{m}}$. В то время как для нормальных мод сдвиг фаз ${{{\theta }}_{n}}$ может быть как острым, так и тупым углом, для оптимальных возмущений всегда ${\pi /}2 < {{{\theta }}_{{opt}}} < {\pi }$. Оптимальному возмущению с $K = {{K}_{m}}$ (наиболее опасной моде) отвечает угол ${{{\theta }}_{{opt}}}\sim 117^\circ $ ($\cos {{{\theta }}_{{opt}}} = - 0.451$). Зависимости (2.7), (1.17) удобно представлять также в терминах тангенса половинного угла
(2.8)
${\text{tg}}(0.5{{{\theta }}_{{opt}}}) = {\text{cth}}(0.5K),\quad {\text{tg}}(0.5{{{\theta }}_{n}}) = {\delta ,}\quad \delta = {{(1 - \alpha )}^{{1/2}}}{{(1 + \alpha )}^{{ - 1/2}}}$Рис. 2
Зависимости $\cos {{\theta }_{{opt}}}$ (линия 1) и $\cos {{\theta }_{n}}$ (2) от волнового числа K.
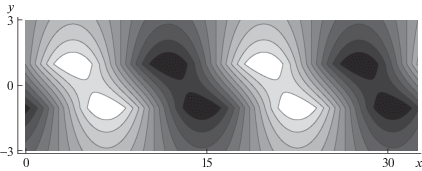
На рис. 3 приведена теневая картина изолиний функции тока оптимального возмущения для $K = {{K}_{m}} = 0.797$ и ${{{\theta }}_{1}} = 0$, ${{{\theta }}_{2}} = {\theta } = {{{\theta }}_{{opt}}}(K)$. На верхней и нижней границах сдвигового слоя формируются системы замкнутых вихревых ячеек, сдвинутые относительно друг друга по горизонтали. Незамкнутые линии тока возмущения внутри слоя имеют характерный наклон, направленный против потока. Этот наклон обусловлен сдвигом фаз ${\theta }$.
3. ОПТИМАЛЬНЫЕ ВОЗМУЩЕНИЯ С МАКСИМУМОМ ОТНОШЕНИЯ КОНЕЧНОЙ И НАЧАЛЬНОЙ ЭНЕРГИЙ
Более общая задача об оптимальных возмущениях формулируется так – для фиксированного момента времени t (времени оптимизации) найти начальное возмущение, для которого функционал $F = E(t){\text{/}}E(0)$ принимает максимальное значение. Данный раздел содержит решения этой задачи в классе возмущений с равными начальными амплитудами ${{q}_{1}}(0) = {{q}_{2}}(0)$ на границах сдвигового слоя. В силу первого закона сохранения (1.18) равенство амплитуд сохраняется в произвольный момент времени. С учетом разложения $F = 1 + {\gamma }(0)\,t$, ${\gamma }(t) = {{E}^{{ - 1}}}dE{\text{/}}dt$, $t \ll 1$, найденные в предыдущем разделе оптимальные возмущения дают решение задачи для значений $t \to 0$. При конечных значениях t решение задачи требует интегрирования системы динамических уравнений (1.14), (1.15).
С учетом (2.4), для возмущений с ${{q}_{1}} = {{q}_{2}}$ отношение конечной и начальной энергий
(3.1)
$F = \frac{{E(t)}}{{E(0)}} = \left( {\frac{{q_{1}^{2}(t)}}{{q_{1}^{2}(0)}}} \right)\left( {\frac{{{{e}^{K}} + \cos {\theta }(t)}}{{{{e}^{K}} + \cos {{{\theta }}_{0}}}}} \right).$Здесь обозначено ${{{\theta }}_{0}} = {\theta }(0)$. Из первого интеграла (1.18) следует равенство
(3.2)
$F = \frac{{E(t)}}{{E(0)}} = \left( {\frac{{{\alpha } - \cos {{{\theta }}_{0}}}}{{{{e}^{K}} + \cos {{{\theta }}_{0}}}}} \right)\,\left( {\frac{{{{e}^{K}} + \cos {\theta }(t)}}{{{\alpha } - \cos {\theta }(t)}}} \right)$В выражении (3.2) сдвиг фаз ${\theta }(t)$ есть решение задачи Коши для уравнения (1.15)
(3.3)
$\frac{{d{\theta }}}{{dt}} = - 2r\left( {{\alpha } - \cos {\theta }} \right),$ ${\theta }(0) = {{{\theta }}_{0}}$Характер поведения решений уравнения (3.3) зависит от значений волнового числа K. В режиме нейтральных мод $K > {{K}_{b}}$ (${\alpha }(K) > 1$) сдвиг фаз ${\theta }$ неограниченно убывает. Ниже рассматривается неустойчивый случай $ - 1 < {\alpha }(K) < 1$. В этом случае сдвиг фаз асимптотически приближается к значению, отвечающему растущей нормальной моде. Стандартное разделение переменных в (3.3) дает точное решение $\,\,\,{\theta } = {\theta }(t,\,K,{{{\theta }}_{0}})$ в форме первого интеграла
(3.4)
$Y = \frac{{X + c(t)}}{{c(t)X + 1}},\quad Y = {{{\delta }}^{{ - 1}}}{\text{tg}}(0.5{\theta }(t)),\quad X = {{{\delta }}^{{ - 1}}}{\text{tg}}(0.5{{{\theta }}_{0}})$Здесь $c(t) = {\text{th}}\left( {s(K)t} \right)$, $s(K)$ – инкремент нарастания нормальной моды (1.12), значение ${\delta } = {\delta }(K)$ определено выражением (2.8).
Использование первого интеграла (3.4) и представление в (3.2) $\cos {\theta }(t)$, $\cos {{{\theta }}_{0}}$ через тангенс половинного угла, после преобразований дает выражение
(3.5)
$F = \frac{1}{{1 - {{c}^{2}}(t)}}\frac{{{{{\left( {X + c(t)} \right)}}^{2}} + n{{{\left( {c(t)X + 1} \right)}}^{2}}}}{{{{X}^{2}} + n}},\quad X = {{{\delta }}^{{ - 1}}}\tan (0.5{{{\theta }}_{0}})$(3.6)
$n = {{{\delta }}^{{ - 2}}}{\text{cth}}(0.5K) = {\text{cth}}(0.5K)\frac{{{{e}^{{ - K}}} + K - 1}}{{{{e}^{{ - K}}} - K + 1}}$Как и ранее, в общем случае нормальные моды не являются оптимальными возмущениями.
Для фиксированных значений t, K, на промежутке $0 < {{{\theta }}_{0}} < {\pi }$ ($0 < X < {{{\delta }}^{{ - 1}}}$) функция F (3.5) имеет единственную точку максимума ${{{\theta }}_{0}} = {{{\theta }}_{{opt}}}$ ($X = {{X}_{{opt}}}$), отвечающую оптимальному возмущению. Нахождение этой точки и соответствующего максимального значения ${{F}_{{opt}}}$ удобно проводить после выделения из (3.5) целой части
(3.8)
$F = 1 + \frac{{(n + 1)c(t)}}{{1 - {{c}^{2}}(t)}}\left( {\frac{{c(t){{X}^{2}} + 2X + c(t)}}{{{{X}^{2}} + n}}} \right)$Дифференцирование (3.8) по X и приравнивание производной нулю дает квадратное урав-нение
С учетом диапазона изменения аргумента отсюда следуют выражения для точки максимума
(3.10)
${{X}_{{opt}}} = {{X}_{{opt}}}(t,K) = {{{\delta }}^{{ - 1}}}\tan (0.5{{{\theta }}_{{opt}}}) = \frac{1}{2}(\sqrt {{{c}^{2}}(t){{{(n - 1)}}^{2}} + 4n} + c(t)(n - 1))$(3.11)
${{F}_{{opt}}} = {{F}_{{opt}}}(t,K) = 1 + \frac{{(n + 1){{c}^{2}}(t)}}{{1 - {{c}^{2}}(t)}}\left( {1 + \frac{1}{{c(t){{X}_{{opt}}}}}} \right)$Формулы (3.10), (3.11) дают аналитическое решение задачи об оптимальных возмущениях.
Согласно (3.10), сдвиг фаз для оптимального возмущения в общем случае зависит от времени оптимизации t. Исключение составляет единственное значение волнового числа K, для которого $n = n(K) = 1$ и ${{X}_{{opt}}} = 1$ (${\text{tg}}({{{\theta }}_{{opt}}}{\text{/}}2) = {\delta }$). С учетом (3.6) легко проверяется, что уравнение $n(K) = 1$ сводится к уравнению $K = 1 - {{e}^{{ - 2K}}}$, определяющему волновое число K = Km наиболее опасной нормальной моды. Таким образом, эта мода является оптимальным возмущением для любого $t \geqslant 0$. Для значений $K \ne {{K}_{m}}$всегда ${\text{tg}}({{{\theta }}_{{opt}}}{\text{/}}2) \ne {\text{tg}}({{{\theta }}_{n}}{\text{/}}2)$, соответственно ${{F}_{{opt}}} > {{F}_{n}}$. Графики зависимостей ${{F}_{{opt}}}$ и ${{F}_{n}}$ от волнового числа K в фиксированный момент времени t = 2 приведены на рис. 4. Как и для начальных оптимальных возмущений, в точке максима $K = {{K}_{m}}$ происходит касание графиков.
Из (3.10), (3.11) следуют асимптотики для максимальных значений
(3.13)
${{F}_{{opt}}} - 1\sim \left( {{{F}_{n}} - 1} \right)\left( {1 + \frac{1}{4}\frac{{{{{(n - 1)}}^{2}}}}{n}} \right),\quad t \to \infty $В приведенном решении задачи об оптимальных возмущениях использовалось представление
(3.5) функции $F = F(t,K,{{{\theta }}_{0}})$, выраженное через тангенс половинного угла. Формула tg(θ/2) = 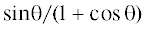 позволяет представить (3.5) в терминах основных тригонометрических функций
позволяет представить (3.5) в терминах основных тригонометрических функций
(3.14)
$F = 1 + \left( {\frac{{c(t)}}{{1 - {{c}^{2}}(t)}}} \right)\,\left( {\frac{{K{{e}^{K}}}}{{1 - {{{\alpha }}^{2}}}}} \right)\,\left( {\frac{{\sqrt {1 - {{\alpha }^{2}}} \sin {{{\theta }}_{0}} + c(t)(1 - {\alpha }\cos {{{\theta }}_{0}})}}{{{{e}^{K}} + \cos {{{\theta }}_{0}}}}} \right)$Для нахождения точек экстремума из (3.14) следует тригонометрическое уравнение
(3.15)
${{(1 - {{{\alpha }}^{2}})}^{{1/2}}}{{e}^{K}}\cos {{{\theta }}_{0}} + c(t)({\alpha }{{e}^{K}} + 1)\sin {{{\theta }}_{0}} + {{(1 - {{{\alpha }}^{2}})}^{{1/2}}} = 0$4. СЛУЧАЙ НЕРАВНЫХ ГРАНИЧНЫХ АМПЛИТУД И ВОЗМОЖНОСТЬ РАСШИРЕНИЯ КЛАССА ДОПУСТИМЫХ ВОЗМУЩЕНИЙ
Выше предполагалось, что оптимальные возмущения принадлежат к классу возмущений с равными граничными амплитудами. В анализе задачи об оптимальных возмущениях, свободной от указанного предположения, используется полная система динамических уравнений (1.14). Подстановка ${{q}_{1}} = {\rho }(t)\cos \varphi (t)$, ${{q}_{2}} = {\rho }(t)\sin \varphi (t)$ сводит эту систему к уравнениям
(4.1)
$\frac{{d\varphi }}{{dt}} = r\sin {\theta }\cos 2\varphi ,\quad \frac{{d{\theta }}}{{dt}} = - 2r({\alpha } - {{\sin }^{{ - 1}}}(2\varphi )\cos {\theta })$С учетом представления амплитуд в полярных координатах отношение энергий (2.4) записывается в виде
(4.2)
$F = \frac{{E(t)}}{{E(0)}} = \left( {\frac{{{{{\rho }}^{2}}(t)}}{{{{{\rho }}^{2}}(0)}}} \right)\,\left( {\frac{{{{e}^{K}} + \sin (2\varphi (t))\cos {\theta }(t)}}{{{{e}^{K}} + \sin (2{{\varphi }_{0}})\cos {{{\theta }}_{0}}}}} \right)$Первые интегралы (1.16) приводят к соотношениям
(4.3)
$\frac{{{{{\rho }}^{2}}(t)}}{{{{{\rho }}^{2}}(0)}} = \frac{{\cos (2{{\varphi }_{0}})}}{{\cos (2\varphi (t))}} = \frac{{{\alpha } - \sin 2{{\varphi }_{0}}\cos {{{\theta }}_{0}}}}{{{\alpha } - \sin 2\varphi (t)\cos {\theta }(t)}}$(4.4)
$F = \frac{{E(t)}}{{E(0)}} = \left( {\frac{{\cos (2{{\varphi }_{0}})}}{{\cos (2\varphi (t))}}} \right)\,\left( {\frac{{{{e}^{K}} + \sin (2\varphi (t))\cos {\theta }(t)}}{{{{e}^{K}} + \sin (2{{\varphi }_{0}})\cos {{{\theta }}_{0}}}}} \right)$В этом выражении ${\theta }(t),\,\,\varphi (t)$ есть решения системы (4.1), зависящие параметрически от волнового числа и начальных условий: ${\theta }(t) = {\theta }(t,\,K,{{{\theta }}_{0}},\,{{\varphi }_{0}})$, $\varphi (t) = \varphi (t,K,{{{\theta }}_{0}},{{\varphi }_{0}})$. С учетом данных зависимостей выражение (4.4) определяет функцию $F = F(t,K,\,{{{\theta }}_{0}},\,{{\varphi }_{0}})$, которая рассматривается для фиксированных значений t, K.
Аналитическое интегрирование системы (4.1) позволяет получить явное выражение для функции $F = F(t,K,\,{{{\theta }}_{0}},\,{{\varphi }_{0}})$. Так, при K = 1, когда ${\alpha }(K) = 0$,
(4.5)
$F = \frac{1}{{\sqrt {1 - {{c}^{2}}(t)} }}\left( {1 + \frac{{d\sin (2{{\varphi }_{0}})}}{{{{e}^{K}} + \sin (2{{\varphi }_{0}})\cos {{{\theta }}_{0}}}}} \right)\,$Следующие два замечания касаются общих возможностей расширения класса допустимых возмущений. Первая возможность состоит в рассмотрении возмущений с ненулевым начальным распределением завихренности ${{q}_{i}}(x,y)$. Если ${{q}_{i}}(x,y)$ отлично от нуля только в пределах сдвигового слоя, то для нахождения функции тока возмущений из уравнения переноса (1.1) следуют уравнения
(4.6)
${{{\psi }}_{{xx}}} + {{{\psi }}_{{zz}}} = {{q}_{i}}(x - {\Lambda }yt,y),$ $\left| y \right| < b$(4.7)
${{{\psi }}^{{({\text{v}})}}} = \exp (ikx)\,\int\limits_{ - b}^{ + b} {G(y,{\xi }){\Phi }({\xi })\exp ( - ik{\Lambda \xi }t)d{\xi }} $Волновой компонент ${{\psi }^{{(w)}}}$ отвечает рассмотренным ранее возмущениям с нулевой завихренностью. Он находится из решения уравнения Лапласа с неоднородными граничными условиями, которые получаются подстановкой представления ${\psi } = {{{\psi }}^{{({\text{v}})}}} + {{{\psi }}^{{(w)}}}$ в условия (1.5). Отыскание волнового компонента в форме (1.4) приводит к неоднородному варианту системы (1.9) для амплитуд $id{\mathbf{q}}{\text{/}}dt = S{\mathbf{q}} + {\mathbf{F}}$. Правая часть F системы зависит от структуры распределения $\Phi (y)$.
Применительно к задаче о бароклинной неустойчивости параметры оптимальных возмущений с учетом вихревого компонента находились в [11]. Было показано, что присутствие этого компонента может существенно увеличивать скорость роста энергии в начальный момент времени. Важно, однако, иметь в виду, что поскольку с течением времени вихревой компонент затухает, на больших временах основной вклад в динамику будет давать экспоненциально нарастающий волновой компонент. Вихревой компонент играет лишь роль катализатора, приводящего к возбуждению волнового компонента.
Вторая возможность расширения основана на рассмотрении трехмерных возмущений в рамках линеаризованных 3D уравнений Эйлера. Известное преобразование Сквайра [3] показывает, что скорость экспоненциального роста трехмерных возмущений меньше скорости роста двумерных возмущений с тем же продольным волновым числом k. Исключение составляет случай k = 0, когда за счет подъемного механизма [3] происходит алгебраическое нарастание поперечного компонента вихря. Этот алгебраический рост не может конкурировать с экспоненциальным ростом.
5. НЕУСТОЙЧИВОСТЬ СИСТЕМЫ ИЗ ДВУХ ВСТРЕЧНЫХ СТРУЙНЫХ ТЕЧЕНИЙ ВО ВРАЩАЮЩЕМСЯ СЛОЕ МЕЛКОЙ ВОДЫ
Рассматривается слой мелкой воды с невозмущенной глубиной $D$, вращающийся вокруг вертикальной оси с угловой скоростью $\Omega $. Движения слоя с малыми значениями числа Россби описываются квазигеострофической формой уравнения переноса потенциальной завихренности $q$ [10, 15, 16]
(5.1)
${{q}_{t}} + u{{q}_{x}} + {\text{v}}{{q}_{y}} = 0,\quad q = {{{\psi }}_{{xx}}} + {{{\psi }}_{{yy}}} - L_{R}^{{ - 2}}{\psi }$Здесь $u = - {{{\psi }}_{y}}$, ${\text{v}} = {{{\psi }}_{x}}$ – компоненты скорости, ${\psi } = (g{\text{/}}f){\eta }$ – геострофическая функция тока, ${\eta } = h - D$ – отклонение полной глубины $h$ от среднего значения, $f = 2\Omega $ – параметр Кориолиса, $g$ – ускорение свободного падения. В выражении для $q$ (5.1) первые два слагаемых описывают относительную завихренность, последнее – эффект деформации свободной поверхности. Фундаментальный масштаб ${{L}_{R}} = \sqrt {gD} {\text{/}}f$ (радиус деформации Россби–Обухова) есть масштаб, на котором слагаемые сопоставимы. Стандартное уравнение переноса завихренности для двумерных течений невращающейся жидкости получается из (1.1) формальным переходом ${{L}_{R}} \to \infty $.
Точное решение $q = Q(y)$ уравнения (5.1) описывает плоскопараллельное (зональное) течение со скоростью $U = - {{{\Psi }}_{y}}$. Функция тока течения находится из уравнения ${{{\Psi }}_{{yy}}} - k_{R}^{2}{\Psi } = \bar {q}(y)$, ${{k}_{R}} = L_{R}^{{ - 1}}$, дополненного условиями регулярности на бесконечности. Для течения с двумя разрывами потенциальной завихренности $Q(y) = - {\Lambda }$, $\left| y \right| < b$, $Q(y) = 0$, $\left| y \right| > b$ решение имеет вид [15]
(5.2)
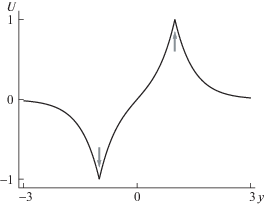
$\begin{gathered} \Psi = \frac{{{{u}_{0}}}}{{{{k}_{R}}}}\left( {1 + \left( {{\text{ch}}({{k}_{R}}b) - {\text{ch}}({{k}_{R}}y)} \right){\text{/sh}}({{k}_{R}}b)} \right), \\ \left| y \right| < b,\quad \Psi = \frac{{{{u}_{0}}}}{{{{k}_{R}}}}{{e}^{{ - {{k}_{R}}(\left| y \right| - b)}}},\quad \left| y \right| > b \\ U = {{u}_{0}}{\text{sh}}({{k}_{R}}y){\text{/sh}}({{k}_{R}}b),\quad \left| y \right| < b,\quad U = {{u}_{0}}\operatorname{sgn} (y){{e}^{{ - {{k}_{R}}(\left| y \right| - b)}}},\quad \left| y \right| > b \\ \end{gathered} $Данное решение описывает систему из двух встречных струйных течений, которая поддерживается локализованным распределением полной глубины (рис. 5). Осевая скорость течений
(5.3)
${{u}_{0}} = \Lambda b{\text{/}}\varphi (R),$ $\varphi (R) = R\left( {1 + {\text{cth}}R} \right)$Рис. 5.
Профиль скорости для системы из двух встречных струйных течений; значения $U$ и $y$ нормированы на ${{u}_{0}}$ и b.
Развитая в [15] линейная теория устойчивости системы струй в математическом плане аналогична теории для свободного слоя сдвига. Функция тока ψ возмущений (используются обозначения без штрихов) удовлетворяет уравнению (1.3), где теперь $q = {{{\psi }}_{{xx}}} + {{{\psi }}_{{yy}}} - k_{R}^{2}{\psi }$. Отыскиваются решения с q = 0 вида
(5.4)
${\psi } = - \frac{1}{{2{\kappa }}}({{Q}_{1}}(t){{e}^{{ - {\kappa }\left| {y + b} \right|}}} + {{Q}_{2}}(t){{e}^{{ - {\kappa }\left| {y - b} \right|}}}){{e}^{{ikx}}}$(5.5)
$i\frac{{d{{Q}_{1}}}}{{dt}} = k{{c}_{1}}{{Q}_{1}} + \frac{{{\Lambda }k}}{{2{\kappa }}}{{e}^{{ - 2{\kappa }b}}}{{Q}_{2}},\quad i\frac{{d{{Q}_{2}}}}{{dt}} = k{{c}_{2}}\,{{Q}_{2}} - \frac{{{\Lambda }k}}{{2{\kappa }}}{{e}^{{ - 2{\kappa }b}}}{{Q}_{1}}$(5.6)
$K = 2b{\kappa ,}\quad {\alpha } = \left( {K{\text{/}}\varphi (R) - 1} \right){{e}^{K}},\quad r = {\Lambda }(k{\text{/}}2{\kappa }){{e}^{{ - K}}}$Вместо волнового числа k далее удобно рассматривать его безразмерное значение $k{\text{'}} = k{\text{/}}{{k}_{R}}$ = = LRk, так что $K = 2b{\kappa } = 2R\sqrt {k{\kern 1pt} {{'}^{2}}\, + 1} $. При фиксированном значении радиуса деформации (характерном для условий лабораторных экспериментов) параметр $K$зависит только от расстояния $2b$ между осями струйных течений.
Как и ранее, частоты нормальных мод (собственные значения матрицы системы (1.9)) ω1, 2 = = $\mu r\sqrt {{{{\alpha }}^{2}} - 1} $ комплексны при $ - 1 < {\alpha } < 1$. С учетом (5.6) отсюда следует существование неустойчивости для значений K из интервала $2R < K < {{K}_{b}}(R)$, где ${{K}_{b}}(R)$ – корень уравнения
Указанному интервалу отвечает интервал неустойчивых волновых чисел $0 < k{\text{'}} < {{k}_{b}}$, где kb = = $\sqrt {{{{({{K}_{b}}{\text{/}}2R)}}^{2}} - 1} $. При $R \to 0$ функция $\varphi (R) \to 1$ и (5.8) сводится к уравнению $K = 1 + {{e}^{{ - K}}}$, определяющему граничное значение волнового числа в задаче Релея. Хорошую аппроксимацию корня (5.8) дает выражение $K = {{K}_{b}}(R) = \varphi (R)(1 + {{e}^{{ - \varphi (R)}}})$, справедливое для всего диапазона изменения R.
В интервале неустойчивости функция тока возмущения (5.4) представляется суммой растущей и затухающей нормальных мод. Инкремент нарастания растущей моды определяется выражением
(5.9)
$s = r\sqrt {1 - {{{\alpha }}^{2}}} = \frac{{\Lambda }}{{1 + {\text{cth}}(R)}}\frac{{k{\text{'}}}}{K}\sqrt {{{\varphi }^{2}}(R){{e}^{{ - 2K}}} - {{{\left( {K - \varphi (R)} \right)}}^{2}}} $При $R \gg 1$ из (5.9) следует асимптотика
(5.10)
$s = ({\Lambda /}4)k{\text{'}}\sqrt {k_{b}^{4} - k{{{\text{'}}}^{4}}} ,\quad {{k}_{b}} = \sqrt 2 {{e}^{{ - R}}}$Согласно (5.10), если расстояние между осями струй много больше радиуса деформации, интервал $0 < k{\text{'}} < {{k}_{b}}$ неустойчивых волновых чисел экспоненциально мал, т.е. неустойчивость носит ярко выраженный длинноволновой характер. Наиболее опасной нормальной моде отвечает волновое число $k_{m}^{'} = \sqrt[4]{{4{\text{/}}3}}{{e}^{{ - R}}}$ и инкремент нарастания ${{s}_{m}} = {{3}^{{ - 3/4}}}\Lambda {{e}^{{ - 3R}}}$.
Как и для задачи Релея, функция тока (5.4) представляется также в виде суперпозиции краевых волн Россби. Взаимодействие волн описывается нелинейной системой, аналогичной (1.14).
6. НАЧАЛЬНЫЕ ОПТИМАЛЬНЫЕ ВОЗМУЩЕНИЯ ДЛЯ СИСТЕМЫ СТРУЙНЫХ ТЕЧЕНИЙ
Теория оптимальных возмущений для рассматриваемой задачи строится аналогично теории для задачи Релея, однако содержит важные качественные отличия. Основное отличие состоит в том, что наиболее опасная нормальная мода уже не является оптимальным возмущением с максимумом скорости роста энергии. Это отличие наглядно иллюстрирует нахождение начальных оптимальных возмущений.
Как и в задаче Релея, выделяется вещественная часть функции тока (5.4) с использованием представления ${{Q}_{{1,2}}}(t) = {{q}_{{1,2}}}(t){{e}^{{i{{{\theta }}_{{1,2}}}(t)}}}$, где ${{q}_{{1,2}}}$ – вещественные части комплексных амплитуд, ${{{\theta }}_{{1,2}}}(t)$ – соответствующие фазы. Далее вводится полная энергия возмущения $E = \int_{ - \infty }^{ + \infty } {\left\langle {\varepsilon } \right\rangle \,d} y$, где плотность энергии ${\varepsilon } = (1{\text{/}}2)({\psi }_{x}^{2} + {\psi }_{y}^{2} + k_{R}^{2}{{{\psi }}^{2}})$ содержит дополнительный член, описывающий потенциальную энергию (обусловленную деформацией свободной поверхности). Прямые вычисления, с использованием аналогичного (2.3) уравнения баланса энергии, дают явные выражения для производной ${{E}_{t}}$ и самой энергии
(6.2)
$E = (1{\text{/}}8{\kappa })(q_{1}^{2}(t) + q_{2}^{2}(t) + 2{{e}^{{ - K}}}{{q}_{1}}(t){{q}_{2}}(t)\cos {\theta }(t))$С учетом (6.1), (6.2) показывается, что максимум скорости роста энергии ${\gamma } = {{E}^{{ - 1}}}dE{\text{/}}dt$ достигается в случае равенства начальных амплитуд ${{q}_{1}} = {{q}_{2}}$. В этом случае
(6.3)
${\gamma } = \frac{{2{\Lambda }}}{{1 + {\text{cth}}(R)}}\frac{{k{\text{'}}\sin {\theta }}}{{{{e}^{K}} + \cos {\theta }}}$Функция (6.3) достигает максимума при ${\theta } = {{{\theta }}_{{opt}}}$, где $\cos {{{\theta }}_{{opt}}} = - {{e}^{{ - K}}}$, соответствующее оптимальное (максимальное) значение
(6.4)
${{{\gamma }}_{{opt}}} = \frac{{2{\Lambda }}}{{1 + {\text{cth}}(R)}}\frac{{k{\kern 1pt} '}}{{\sqrt {\exp (4R\sqrt {1 + k{\kern 1pt} {{'}^{2}}} ) - 1} }}$Выражение для оптимального значения (2.7) в задаче Релея получается из (6.4) предельным переходом $R \to 0$.
Как функция безразмерного волнового числа, зависимость ${{{\gamma }}_{{opt}}}$ (6.4) принимает максимальное значение при некотором $k{\text{'}} = k_{{opt}}^{'}$. Скорость роста энергии нормальной моды ${{{\gamma }}_{n}} = 2s$, равная удвоенному инкременту нарастания (5.9), достигает максимума при $k{\text{'}} = k_{m}^{'}$. Соответствующие зависимости приведены на рис. 6 для двух значений параметра R. Как видно, в отличие от задачи Релея, $k_{m}^{'} \ne k_{{opt}}^{'}$, т.е. наиболее опасная нормальная мода уже не является наиболее опасным оптимальным возмущением. Это прямо следует и из асимптотик, отвечающих случаю $R \gg 1$. При этом из (6.4) асимптотически следует $k_{{opt}}^{'} = 1{\text{/}}\sqrt {2R} $, в то время как согласно предыдущему разделу $k_{m}^{'} = \sqrt[4]{{4{\text{/}}3}}{{e}^{{ - R}}}$. Волновое число оптимального возмущения с максимумом скорости роста энергии даже не принадлежит интервалу неустойчивых волновых чисел. Поскольку $\cos {{{\theta }}_{{opt}}} = - {{e}^{{ - K}}} \to 0$ при $R \gg 1$, сдвиг фаз наиболее опасной оптимальной моды ${{{\theta }}_{{opt}}}$ ~ 90°.
Рис. 6.
Зависимость ${{\gamma }_{{opt}}}$ (линия 1) и ${{\gamma }_{n}} = 2s$ (2) от волнового числа $k{\kern 1pt} '$ для значений $R = 0.5$ (а) и $R = 2$ (б); значения $\gamma $ нормированы на величину сдвига $\Lambda $.
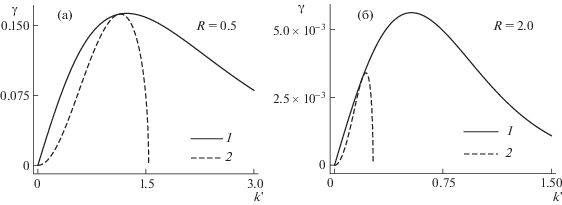
Аналогичные особенности имеют место и для оптимальных возмущений с максимумом отношения конечной и начальной энергий. Алгоритм нахождения этих возмущений аналогичен алгоритму, описанному в разд. 4. Длина волны наиболее быстрорастущего оптимального возмущения всегда меньше длины волны наиболее опасной нормальной моды.
ЗАКЛЮЧЕНИЕ
Поиск оптимальных возмущений, как правило, сводится к численному расчету сингулярных векторов динамического оператора задачи устойчивости. В статье рассмотрен поход, позволяющий найти параметры оптимальных возмущений аналитически. Этот подход, пригодный для течений со скачками завихренности (свободный слой сдвига, система струйных течений) опирается на уравнение баланса энергии возмущений и явные выражения для скорости роста энергии или отношения конечной и начальной энергий. Соответствующие выражения представляют собой функции параметров начального возмущения, в качестве которых выступают амплитуды граничных распределений скачков касательной компоненты скорости и сдвиг фаз между этими распределениями. Параметры оптимальных возмущений находятся из исследования функций на экстремум. Получены аналитические формулы для оптимального сдвига фаз и максимума отношения энергий, определяющие их зависимость от волнового числа и времени оптимизации. Также показано, что оптимальные возмущения всегда имеют равные граничные амплитуды. Следует подчеркнуть, что представленный анализ ограничен классом возмущений с тождественно нулевой завихренностью. В этот важный класс входят экспоненциально нарастающие нормальные моды. Представляет интерес проведение детального анализа для общего случая вихревых и трехмерных возмущений. Некоторые возможности в этом направлении реализованы авторами ранее и отмечены в основном тексте статьи.
Авторы благодарят рецензента за полезные замечания. Работа выполнена при поддержке РНФ (разд. 1–4, Проект № 19-17-00248) и РФФИ (разд. 5–7, Проект № 18-05-00831).
Список литературы
Farrell B.F., Ioannou P.J. Generalized Stability Theory. Part I: Autonomous Operators // J Atm. Sci. 1996. V. 53. P. 2025–2040.
Шарру Ф. Неустойчивость в гидродинамике. М. Ижевск: Ин-т комп. исслед., 2015. 472 с.
Schmidt P.J., Henningson D.S. Stability and transition in shear flows. Springer-Verlag: Berlin and New York, 2001. 551 p.
Leutbecher M. On the representation of initial uncertainties with multiple sets of singular vectors optimized for different criteria // Q. J. Roy. Meteor. Soc. 2007. V. 133. P. 2045–2056.
Diaconescu E.P., Laprise R. Singular vectors in atmospheric sciences: A review // Earth Sci. Rev. 2012. V. 113. P. 161–175.
Раздобурдин Д.Н., Журавлев В.В. Транзиентная динамика возмущений в астрофизических дисках // Успехи физических наук. 2015. Т. 185. № 11. С. 1129–1161.
Боронин С.А. Оптимальные возмущения течения запыленного газа в плоском канале с неоднородным распределением частиц//Изв. РАН. МЖГ. 2012. № 3. С. 74–88.
Farrel B.F., Ioannou P. J. Optimal excitation of three- dimensional perturbations in viscous constant shear flow // Phys. of Fluids A. 1993. V. 5. № 6. P. 1390–1400.
Eady E.T. Long waves and cyclone waves // Tellus. 1949. V. 1. № 3. P. 35–52.
Pedlosky J. Geophysical Fluid Dynamics. Springer-Verlag: Berlin and New York, 1987. 710 p.
Kalashnik M.V., Chkhetiani O.G. An analytical approach to determination of optimal perturbation in the Eady model // J. Atmos. Sci. 2018. V. 75. P. 2741–2761.
Rayleigh L. On the stability, or instability of certain fluid motions // Proc. London Math, Soc. 1880. V. 9. P. 57–70.
Heifetz E., Bishop C.H., Alpert P. Counter-propagating Rossby waves in the barotropic Rayleigh model of the shear instability // Q. J. Roy. Meteor. Soc. 1999. V. 125. P. 2835–2853.
Heifetz E., Methven J. Relating optimal growth to counter-propagating Rossby waves in shear instability //Phys. Fluid. 2005. V. 17. P. 064107.
Калашник М.В., Чхетиани О.Г. Об устойчивости струйных течений во вращающемся слое мелкой воды // Изв. РАН. МЖГ. 2016. № 5. С. 29–42.
Чхетиани О.Г., Калашник М.В., Чагелишвили Г.Д. Динамика и блокирование волн Россби в квазидвумерных сдвиговых течениях //Письма в ЖЭТФ. 2015. Т. 101. Вып. 2. С. 84–89.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа