Известия РАН. Механика жидкости и газа, 2020, № 2, стр. 99-110

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ПОДЪЕМА ПУЗЫРЬКА В ВЕРТИКАЛЬНОМ КЛИНООБРАЗНОМ КАНАЛЕ МОДИФИЦИРОВАННЫМ МЕТОДОМ ФУНКЦИИ УРОВНЯ

Ифу Чжан^a, *, Бин Лян^b, Цзинфэн Ни^c,

^a Department of Safety and Environmental Engineering, Hunan Institute of Technology
421002 Hengyang, China

^b School of Mechanics and Engineering, Liaoning Technical University
123000 Fuxin, China

^c College of Safety Science and Engineering, Key Laboratory of Mine Thermo-motive Disaster and Prevention in Liaoning Technical University
125100 Huludao, China

^* E-mail: zhangyifu_lntu@163.com

Поступила в редакцию 26.11.2018
После доработки 06.05.2019
Принята к публикации 25.06.2019

DOI: 10.31857/S0568528120010156

Полный текст (PDF)

Аннотация

Движение пузырьков в каналах сложной формы моделируется с использованием модифицированного метода функции уровня в сочетании с процедурой локальной повторной инициализации и методом коррекции объема. Последний метод позволяет корректировать потерю массы при моделировании пузырька стандартным методом функции уровня, а локальная повторная инициализация функции уровня исключает численную диссипацию, вызванную неортогональностью сетки на границе. При решении задачи о течении двухфазной среды в области со сложной границей сетка в физической плоскости строится в координатах, связанных с телом. Все параметры физической области преобразуются в вычислительную область, где основные уравнения дискретизируются на соотнесенных сетках с использованием метода конечных объемов и алгоритма SIMPLE для расцепления скоростей и давления. Поверхностное трение пузырька определяется на основе модели континуальной поверхностной силы. Результаты моделирования подъема пузырька в клинообразном канале показывают, что предложенный метод эффективен при решении задач о движении пузырьков в областях сложной формы.

Ключевые слова: метод функции уровня, коррекция объема, локальная повторная инициализация, координаты, связанные с телом, клинообразный канал

Движение пузырьков широко распространено в природе и технике [1]. Оно встречается в энергетических процессах, процессах, связанных с охраной окружающей среды, химической промышленности, охране водных ресурсов и т.д.

Движение пузырьков часто сопровождается сложными процессами деформации, такими как слияние и разрушение в процессе движения, вследствие чего движение пузырька в жидкости представляет собой сложный нелинейный динамический нестационарный процесс [2]. Хвостовой вихрь пузырька оказывает существенное влияние на поля скорости и давления в окружающей пузырек жидкости, а измененные поля скорости и давления в свою очередь влияют на движение и деформацию пузырьков.

В последние десятилетия численные исследования движения пузырьков были сосредоточены, главным образом, на вопросах их подъема, роста, распада, слияния и т.д. в каналах правильной формы [3].

Характеристики движения пузырьков не только связаны с физическими свойствами двухфазной газожидкостной среды, но также зависят от структуры поля течения. В связи со сложностью физических границ в поле течения кинетические характеристики движения пузырьков в сложном канале отличаются от соответствующих характеристик в канале правильной формы [4]. Таким образом, актуальная и практически важная задача состоит в исследовании процесса подъема пузырьков в сложных течениях.

Эффективным методом моделирования потока жидкости со сложной границей является преобразование координат, при котором сложная физическая плоскость превращается в регулярную вычислительную плоскость, в которой и проводятся вычисления. В работе [5] моделируется схлопывание пузырька в бинарном растворе; при этом уравнения Навье–Стокса приводятся к уравнениям для функции тока и завихренности в двумерных осесимметричных подвижных координатах, связанных с телом. В работе [6] моделируется рост пузырька пара при подъеме в равномерно перегретой жидкости.

Для отслеживания поведения резкой межфазной границы в двухфазных течениях предложены различные численные методы, такие как метод слежения за границей [7], метод подвижной сетки [8], метод жидких объемов (VOF) [9, 10], метод функции уровня [11, 12] и другие.

Как метод функции уровня, так и метод жидких объемов используют скалярную величину, несущую в себе информацию о жидкости. При моделировании двухфазных течений эта скалярная величина привязана к самой жидкости, а ее перенос описывается особым уравнением. По этой причине указанные методы могут быть легко и естественным образом реализованы и в настоящее время широко используются при исследовании двухфазных течений.

Метод жидких объемов – это эффективный метод отслеживания межфазной границы в двухфазной жидкости, основанный на кусочно-линейном расчете поверхности раздела (Piecewise Linear Interface Calculation, PLIC). Его преимущество состоит в хорошем выполнении закона сохранения массы. Однако этот метод не обеспечивает высокой точности, существенно сглаживая форму межфазной границы. К тому же его трудно распространить на трехмерные течения, ввиду сложности процесса построения межфазной границы.

Метод функции уровня определяет межфазную границу как нулевое значение функции уровня для расстояния от межфазной границы. Наряду с преимуществами концептуальной простоты и легкости реализации, этот метод может быть распространен на большее число измерений и к нему с высокой точностью может быть применена дискретизация. Метод легко поддается программированию и не требует сложной технологии восстановления. Кроме того, разностная схема с высокой точностью может быть применена к более точному отслеживанию межфазной границы. Однако использование метода функции уровня приводит к большим вычислительным ошибкам в случаях, когда поверхности раздела испытывают сильное растяжение и даже разрыв, что может быть причиной потери или приобретения массы. Поскольку алгоритм слежения за поверхностью раздела в двухфазном течении в этом методе является неконсервативным, постоянство массы или объема пузырька трудно обеспечить ввиду численной диссипации. Помимо того, для того чтобы функция уровня сохраняла свое значение как взятое со знаком расстояние до межфазной границы, требуется прибегать к процедуре повторной инициализации функции уровня. В ходе этой процедуры неортогональность сетки на границе может также привести к численной диссипации, что затрудняет процесс повторной инициализации.

В настоящей работе предложен модифицированный метод функции уровня для моделирования двухфазных течений со сложной границей. В частности, решается проблема несохранения объема пузырька и исключается численная диссипация, вызванная неортогональностью сетки на границе.

1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

В настоящей работе для описания двухфазного течения в канале сложной формы используется модель несмешиваемой двухфазной газожидкостной среды с большими отношениями плотности и вязкости. Газовая и жидкостная фаза считаются несжимаемыми. Движение и деформация пузырьков определяются внешними силами. Динамика пузырька в вертикальном потоке в канале моделируется с использованием метода функции уровня в сочетании с процедурой SIMPLE.

1.1. Основные уравнения

Гидродинамические уравнения в безразмерной форме имеют вид

(1.1)

$\nabla \cdot u = 0$

(1.2)

$\frac{{\partial {\text{(}}\rho {\mathbf{u}}{\text{)}}}}{{\partial t}} + \nabla \cdot {\text{(}}\rho {\mathbf{uu}}{\text{)}} = - \nabla p + \frac{1}{{{\text{Re}}}}\nabla \cdot [\mu {\text{(}}\nabla {\mathbf{u}} + {{\nabla }^{T}}{\mathbf{u}}{\text{)}}] + {\mathbf{B}} + {{{\mathbf{F}}}_{{SF}}}$

где B – вектор силы плавучести, ${\mathbf{B}} = \left( {0,{\text{(}}1 - \rho {\text{)/}}Fr} \right)$, а F_SF – член, описывающий силу поверхностного натяжения.

Поверхность раздела между двумя фазами можно отслеживать при помощи следующего уравнения переноса для функции уровня

(1.3)

$\frac{{\partial \varphi }}{{\partial t}} + {\mathbf{u}} \cdot \nabla \varphi = 0$

где $\varphi $ – функция уровня, означающая взятое со знаком расстояние до поверхности раздела от любой точки в поле течения.

Негладкая форма поверхности раздела в многожидкостной системе может привести к разрывам таких параметров жидкости, как плотность и вязкость, в поле течения. Во избежание численной неустойчивости, обусловленной большими разностями плотности и вязкости, между двумя фазами для сглаживания распределений параметров двухфазной среды по обе стороны поверхности раздела используется модифицированная функция Хевисайда [13] от $\varphi $. Например, безразмерные плотность и вязкость могут быть определены из следующих уравнений

(1.4)

$\left\{ {\begin{array}{*{20}{c}} {{{\rho }_{\varepsilon }}{\text{(}}\varphi {\text{)}} = {{\lambda }_{\rho }} + {\text{(1}} - {{\lambda }_{\rho }}{\text{)}}{{H}_{\varepsilon }}{\text{(}}\varphi {\text{)}}} \\ {{{\mu }_{\varepsilon }}{\text{(}}\varphi {\text{)}} = {{\lambda }_{\mu }} + {\text{(}}1 - {{\lambda }_{\mu }}{\text{)}}{{H}_{\varepsilon }}{\text{(}}\varphi {\text{)}}} \end{array}} \right.$

где $H{\text{(}}\varphi {\text{)}}$ – сглаженная функция Хевисайда

(1.5)

$H(\varphi ) = \left\{ {\begin{array}{*{20}{l}} {0\quad \varphi < - \varepsilon } \\ {\frac{1}{2} + \frac{\varphi }{{2\varepsilon }} + \frac{{{\text{sin(}}\pi \varphi {\text{/}}\varepsilon {\text{)}}}}{{2\pi }}\quad - \varepsilon \leqslant \varphi \leqslant \varepsilon } \\ {1\quad \varphi > \varepsilon } \end{array}} \right.$

где $\varepsilon $ – подгоночный параметр для определения ширины численного сглаживания.

Для описания поверхностного натяжения между фазами в данной работе используется модель континуальной поверхностной силы (Continuum Surface Force, CSF) [14]. В этой модели вводится гладко меняющаяся объемная сила F_SF, действующая на все жидкие элементы. Она заменяет межфазную поверхностную силу поверхностного натяжения и входит в уравнения Навье–Стокса в виде

(1.6)

${{{\mathbf{F}}}_{{SF}}} = - {{\delta }_{\varepsilon }}{\text{(}}\varphi {\text{)}}k{\text{(}}\varphi {\text{)}}{\mathbf{n}}{\text{/}}We$

где ${{\delta }_{\varepsilon }}{\text{(}}\varphi {\text{)}}$ есть функция Дирака, связанная с шириной сглаженной поверхности раздела

(1.7)

${{\delta }_{\varepsilon }}(\varphi ) = \frac{{dH}}{{d\varphi }} = \left\{ \begin{gathered} \left[ {1 + {\text{cos}}\left( {\frac{{\pi \varphi }}{\varepsilon }} \right)} \right]{\text{/}}2\varepsilon \quad \left| \varphi \right| < \varepsilon \hfill \\ 0\quad \left| \varphi \right| \geqslant \varepsilon \hfill \\ \end{gathered} \right.$

Как кривизна поверхности раздела $k{\text{(}}\varphi {\text{)}} = \nabla \cdot {\mathbf{n}}$, так и вектор нормали к этой поверхности определяются при помощи выражения ${\mathbf{n}} = - \nabla \varphi {\text{/}}\left| {\nabla \varphi } \right|$.

В вышеприведенных уравнениях безразмерные числа Рейнольдса, Фруда и Вебера определяются следующим образом

(1.8)

${\text{Re}} = \frac{{{{\rho }_{l}}{{u}_{r}}{{D}_{0}}}}{\mu },\quad {\text{We}} = \frac{{{{\rho }_{l}}u_{r}^{2}{{D}_{0}}}}{\sigma },\quad {\text{Fr}} = \frac{{u_{r}^{2}}}{{g{{D}_{0}}}}$

где D₀ – начальный диаметр пузырька, ${{\rho }_{l}}$ – плотность жидкой фазы, а u_r – характерная скорость, за которую обычно принимается конечная скорость пузырька.

Кроме того, движение пузырька описывается еще двумя безразмерными параметрами, за которые обычно принимаются числа Мортона и Этвеша

(1.9)

${\text{Mo}} = \frac{{g{{\mu }_{l}}^{4}}}{{{{\rho }_{l}}{{\sigma }^{3}}}},\quad {\text{Eo}} = \frac{{{{\rho }_{l}}gD_{0}^{2}}}{\sigma }$

1.2. Локальная повторная инициализация функции уровня

Изменения границы раздела между газовой и жидкой фазами определяются уравнением переноса функции уровня $\varphi {\text{(}}x,t{\text{)}}$. В ходе расчета функция уровня может постепенно потерять свойство представлять взятое со знаком расстояние $\left| \varphi \right| = {\text{1}}$. Внутренние дефекты численных методов могут повлиять на точность отслеживания границы раздела. Для сохранения указанного свойства функции расстояния φ используется схема повторной инициализации функции уровня в соответствии с уравнением

(1.10)

$\frac{{\partial \varphi }}{{\partial \tau }} = {\text{sign}}({{\varphi }_{0}})(1 - \left| {\nabla \varphi } \right|)$

(1.11)

$\varphi {\kern 1pt} (X,\,{\kern 1pt} 0) = {{\varphi }_{0}}{\kern 1pt} (X)$

где ${\text{sign}}({{\varphi }_{0}})$ – гладкая функция сигнала, ${\text{sign}}({{\varphi }_{0}}) = {{S}_{\varepsilon }}({{\varphi }_{0}}) = {{\varphi }_{0}}{\text{/}}\sqrt {\varphi _{0}^{2} + {{\varepsilon }^{2}}} $, а ${{\varphi }_{0}}(X)$ – последнее рассчитанное значение φ на текущем шаге по времени перед повторной инициализацией.

Вообще говоря, при повторной инициализации функции уровня во всем поле течения [15] численная диссипация может исказить форму границы раздела между фазами, что связано с неортогональностью сетки на границе. Аналогично узкополосному методу [16], в методе локальной повторной инициализации функция уровня определяется лишь в малой области ($ - \beta \leqslant \varphi \leqslant \beta $) вблизи границы раздела, что позволяет решить вышеупомянутую проблему. Процедура повторной инициализации проводится только в локальной области в окрестности межфазной границы, благодаря чему сохраняется ее свойство представлять расстояние до границы.

1.3. Метод коррекции объема для сохранения массы пузырька

Вследствие численной диссипации, вызванной неконсервативностью метода функции уровня имеет место некоторая потеря массы пузырька при моделировании его подъема.

Метод коррекции объема вводится для компенсации потери массы (объема) пузырька при расчете стандартным методом функции уровня. При этом подходе положение границы раздела фаз корректируется так, чтобы обеспечить сохранение объема пузырька, компенсируя потерю массы после определения границы раздела в соответствии со стандартным методом функции уровня.

В соответствии с изменением объема пузырька на последнем шаге по времени

(1.12)

$\Delta V = \frac{{V(t) - {{V}_{0}}}}{{{{V}_{0}}}}$

и в предположении сферической формы пузырька приращение его радиуса можно вычислить по формуле

(1.13)

$\Delta r = r - {{r}_{0}} = \left( {{{{(1 - \Delta V)}}^{{\frac{1}{{{{C}_{1}}}}}}} - 1} \right){{r}_{0}}$

где C₁ – измерение пространства. Изменение объема разрывной фазы может быть модифицировано коррекцией функции уровня

(1.14)

$\delta \varphi = {{C}_{2}}\left( {{{{(1 - \Delta V)}}^{{\frac{1}{{{{C}_{1}}}}}}} - 1} \right)$

где C₂ – эмпирический параметр в диапазоне от 0.01 до 0.1.

В результате модификация функции уровня выполняется посредством следующего соотношения

(1.15)

$\varphi = {{\varphi }_{0}} + \delta \varphi $

2. ЧИСЛЕННЫЙ МЕТОД

2.1. Определение поля течения в области со сложной границей

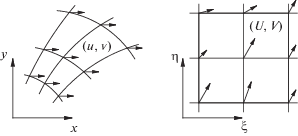
При решении задачи о двухфазном течении в области со сложной границей сетка строится в координатах, связанных с телом, а параметры жидкостей определяются в физической плоскости. Преобразованием координат физическая плоскость со сложной границей поля течения переводится в вычислительную плоскость с регулярной границей. В вычислительной плоскости основные уравнения дискретизируются и соответствующим образом решаются.

Физическая и вычислительная плоскость обозначены (x, y) и (ξ, η) соответственно. Дискретная скорость (U, V) в вычислительной плоскости называется контравариантной скоростью; ее компоненты в направлениях $\xi $ и $\eta $ определяются следующим образом

(2.1)

$U = u\frac{{\partial y}}{{\partial \eta }} - v\frac{{\partial x}}{{\partial \eta }},\quad V = v\frac{{\partial x}}{{\partial \xi }} - u\frac{{\partial y}}{{\partial \xi }}$

Производные в вышеприведенном уравнении вычисляются по формуле

(2.2)

$\left| {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial \eta }}}&{ - \frac{{\partial x}}{{\partial \eta }}} \\ { - \frac{{\partial y}}{{\partial \xi }}}&{\frac{{\partial x}}{{\partial \xi }}} \end{array}} \right| = J\left| {\begin{array}{*{20}{c}} {\frac{{\partial \xi }}{{\partial x}}}&{\frac{{\partial \xi }}{{\partial y}}} \\ {\frac{{\partial \eta }}{{\partial x}}}&{\frac{{\partial \eta }}{{\partial y}}} \end{array}} \right|$

где Якобиан J, представляющий собой степень расширения контрольного объема, вычисляется следующим образом

(2.3)

$J = \frac{{\partial x}}{{\partial \xi }}\frac{{\partial y}}{{\partial \eta }} - \frac{{\partial x}}{{\partial \eta }}\frac{{\partial y}}{{\partial \xi }}$

Преобразование уравнений (1.1)–(1.3) из физической в вычислительную плоскость приводит к следующей записи

(2.4)

$\frac{{\partial \rho }}{{\partial t}} + \frac{1}{J}\frac{{\partial {\text{(}}\rho U{\text{)}}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial {\text{(}}\rho V{\text{)}}}}{{\partial \eta }} = 0$

(2.5)

$\begin{gathered} \frac{{\partial {\text{(}}\rho u{\text{)}}}}{{\partial t}} + \frac{1}{J}\frac{{\partial {\text{(}}\rho Uu{\text{)}}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial {\text{(}}\rho Vu{\text{)}}}}{{\partial \eta }} = - \frac{1}{J}\left( {\frac{{\partial p}}{{\partial \xi }}{{y}_{\eta }} - \frac{{\partial p}}{{\partial \eta }}{{y}_{\xi }}} \right) \\ \frac{1}{{{\text{Re}}}}\left\{ {\frac{\partial }{{\partial \xi }}\left[ {\frac{1}{J}\left( {\alpha \frac{{\partial u}}{{\partial \xi }} + \beta \frac{{\partial u}}{{\partial \eta }}} \right)} \right] + \frac{\partial }{{\partial \eta }}\left[ {\frac{1}{J}\left( { - \beta \frac{{\partial u}}{{\partial \xi }} + \gamma \frac{{\partial u}}{{\partial \eta }}} \right)} \right]} \right\} + {{S}_{u}}{\text{(}}\xi {\text{,}}\eta {\text{)}} \\ \end{gathered} $

(2.6)

$\begin{gathered} \frac{{\partial {\text{(}}\rho v{\text{)}}}}{{\partial t}} + \frac{1}{J}\frac{{\partial {\text{(}}\rho Uv{\text{)}}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial {\text{(}}\rho Vv{\text{)}}}}{{\partial \eta }} = - \frac{1}{J}\left( {\frac{{\partial p}}{{\partial \eta }}{{x}_{\xi }} - \frac{{\partial p}}{{\partial \xi }}{{x}_{\eta }}} \right) + \\ \, + \frac{1}{{{\text{Re}}}}\left\{ {\frac{\partial }{{\partial \xi }}\left[ {\frac{1}{J}\left( {\alpha \frac{{\partial v}}{{\partial \xi }} + \beta \frac{{\partial v}}{{\partial \eta }}} \right)} \right] + \frac{\partial }{{\partial \eta }}\left[ {\frac{1}{J}\left( { - \beta \frac{{\partial v}}{{\partial \xi }} + \gamma \frac{{\partial v}}{{\partial \eta }}} \right)} \right]} \right\} + {{S}_{v}}{\text{(}}\xi {\text{,}}\eta {\text{)}} \\ \end{gathered} $

(2.7)

$\frac{{\partial \varphi }}{{\partial t}} + \frac{1}{J}\frac{{\partial {\text{(}}U\varphi {\text{)}}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial {\text{(}}V\varphi {\text{)}}}}{{\partial \eta }} = 0$

где параметры $\alpha $, $\beta $ и $\gamma $ определены следующим образом

(2.8)

$\alpha = \frac{{\partial x}}{{\partial \eta }}\frac{{\partial x}}{{\partial \eta }} + \frac{{\partial y}}{{\partial \eta }}\frac{{\partial y}}{{\partial \eta }},\quad \beta = \frac{{\partial x}}{{\partial \xi }}\frac{{\partial x}}{{\partial \eta }} + \frac{{\partial y}}{{\partial \xi }}\frac{{\partial y}}{{\partial \eta }},\quad \gamma = \frac{{\partial x}}{{\partial \xi }}\frac{{\partial x}}{{\partial \xi }} + \frac{{\partial y}}{{\partial \xi }}\frac{{\partial y}}{{\partial \xi }}$

Для расцепления скоростей и давления, дискретизированных посредством метода конечных объемов на соотнесенных сетках [18], используется классический алгоритм SIMPLE [17]. Для дискретизации конвективных и диффузионных членов в уравнениях Навье–Стокса используются схема QUICK третьего порядка точности [19] и центральная разностная схема второго порядка точности соответственно.

2.2. Схема высокого порядка для решения уравнения функции уровня в сложном поле течения

Уравнение повторной инициализации имеет вид

(2.9)

${{\varphi }_{\tau }} = {\text{sig}}{{{\text{n}}}_{\varepsilon }}{\text{(}}{{\varphi }_{0}}{\text{)(1}} - \left| {\nabla \varphi } \right|{\text{)}}$

где ${\text{sig}}{{{\text{n}}}_{\varepsilon }}{\text{(}}{{\varphi }_{0}}{\text{)}}$ – функция знака с шириной полосы ε, определяемая как

(2.10)

${\text{sig}}{{{\text{n}}}_{\varepsilon }}{\text{(}}{{\varphi }_{0}}{\text{)}} = \frac{{{{\varphi }_{0}}}}{{\sqrt {\varphi _{0}^{2} + {{\varepsilon }^{2}}} }}$

а $\left| {\nabla \varphi } \right|$ – преобразование из физической в вычислительную плоскость

(2.11)

$\left| {\nabla \varphi } \right| = \sqrt {\frac{\alpha }{{{{J}^{2}}}}\varphi _{\xi }^{2} + \frac{\gamma }{{{{J}^{2}}}}\varphi _{\eta }^{2} - 2\frac{\beta }{{{{J}^{2}}}}{{\varphi }_{\xi }}{{\varphi }_{\eta }}} $

Во избежание численной неустойчивости, связанной с нелинейной конвекцией, уравнение переноса функции уровня решается по противопоточной схеме TVD [20] второго порядка точности с ограничителем потоков. Для повторной инициализации используется модифицированный метод Годунова. Для эффективного и точного определения границы раздела фаз уравнение для повторной инициализации записывается в форме, приводимой ниже, и решается в вычислительном пространстве

(2.12)

$\begin{gathered} {{\varphi }_{\tau }} + \frac{\alpha }{{{{J}^{2}}}}\left[ {\frac{{S({{\varphi }_{0}}){\kern 1pt} {{\varphi }_{\xi }}}}{{\sqrt {\frac{\alpha }{{{{J}^{2}}}}\varphi _{\xi }^{2} + \frac{\gamma }{{{{J}^{2}}}}\varphi _{\eta }^{2} + \left( { - {\kern 1pt} 2\frac{\beta }{{{{J}^{2}}}}} \right){{\varphi }_{\xi }}{{\varphi }_{\eta }}} }}} \right]{{\varphi }_{\xi }} + \frac{\gamma }{{{{J}^{2}}}}\left[ {\frac{{S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} {{\varphi }_{\eta }}}}{{\sqrt {\frac{\alpha }{{{{J}^{2}}}}\varphi _{\xi }^{2} + \frac{\gamma }{{{{J}^{2}}}}\varphi _{\eta }^{2} + \left( { - {\kern 1pt} 2\frac{\beta }{{{{J}^{2}}}}} \right){{\varphi }_{\xi }}{{\varphi }_{\eta }}} }}} \right]{{\varphi }_{\eta }} = \\ \, = S{\kern 1pt} ({{\varphi }_{0}})\left[ {1 - 2\frac{\beta }{{{{J}^{2}}}}\frac{{{{\varphi }_{\xi }}{{\varphi }_{\eta }}}}{{\sqrt {\frac{\alpha }{{{{J}^{2}}}}\varphi _{\xi }^{2} + \frac{\gamma }{{{{J}^{2}}}}\varphi _{\eta }^{2} + \left( { - {\kern 1pt} 2\frac{\beta }{{{{J}^{2}}}}} \right){{\varphi }_{\xi }}{{\varphi }_{\eta }}} }}} \right] \\ \end{gathered} $

где $S({{\varphi }_{0}})$ – сглаживающая функция вида $s = S({{\varphi }_{0}})({\text{|}}\varphi _{\xi }^{ + }{\text{|}}\; - \;{\text{|}}\varphi _{\xi }^{ - }{\text{|}}){\text{/}}(\varphi _{\xi }^{ + } - \varphi _{\xi }^{ - })$, а ${{\varphi }_{x}}$ дискретизируется следующим образом

(2.13)

${{\varphi }_{\xi }} = \left\{ \begin{gathered} \varphi _{\xi }^{ - },\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ + } \geqslant 0,\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ - } \geqslant 0 \hfill \\ \varphi _{\xi }^{ + },\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ + } \leqslant 0,\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ - } \leqslant 0 \hfill \\ 0,\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ + } > 0,\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ - } < 0 \hfill \\ \varphi _{\xi }^{ - },\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ + } < 0,\quad {\kern 1pt} S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ - } > 0,\quad s > 0 \hfill \\ \varphi _{\xi }^{ + },\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ + } < 0,\quad S{\kern 1pt} ({{\varphi }_{0}}){\kern 1pt} \varphi _{\xi }^{ - } > 0,\quad s < 0 \hfill \\ \end{gathered} \right.$

где $\varphi _{\xi }^{ + }$ и $\varphi _{\xi }^{ - }$ – дискретные значения левой и правой производных $\varphi $, которые строятся посредством схемы ENO пятого порядка точности; ${{\varphi }_{\eta }}$ получается при помощи аналогичной процедуры. Интегрирование по времени осуществляется посредством явной TVD схемы Рунге–Кутта третьего порядка точности.

Рис. 1.

Начальное значение функции уровня при β = 0.12.

2.3. Детали численной процедуры

Процедура численного моделирования на основе модифицированного метода функции уровня может быть описана следующим образом:

Рис. 2.

Скорости в различных системах координат.

(1) Сетка в физической плоскости строится в координатах, связанных с телом, в соответствии со сложной границей. В вычислительной плоскости строятся ортогональные сетки с равноотстоящими узлами. Связь между узлами сеток в двух названных плоскостях определяется решением уравнения Пуассона.

(2) Задаются начальные значения функции $\varphi $ как взятые со знаком расстояния от границы раздела фаз, и начальные значения параметров жидкости, таких как плотность, скорость, температура и др.

(3) В вычислительной плоскости гидродинамические уравнения решаются при помощи алгоритма SIMPLE, то есть по решению на слое ${{t}^{n}}$ определяются скорость и давление на слое ${{t}^{{n + 1}}}$.

(4) В вычислительной плоскости решается уравнение для функции уровня и уравнение локальной повторной инициализации, с тем чтобы функция уровня сохраняла свое значение как расстояние со знаком до границы раздела.

(5) Значение функции φ корректируется в соответствии с изменением объема пузырька по сравнению с последним шагом по времени.

(6) Уточняются значения параметров жидкости при ${{t}^{{n + 1}}}$.

(7) На следующем шаге по времени повторяются этапы (3), (4), (5) и (6) до достижения конечного шага по времени.

3. ТЕСТИРОВАНИЕ МЕТОДА

3.1. Анализ чувствительности сетки

Для анализа чувствительности сетки было выполнено моделирование подъема одиночного пузырька в вертикальном канале правильной формы, при одних и тех же значениях параметров Re = 10, We = 30, Fr = 1, ${{\rho }_{g}}{\text{/}}{{\rho }_{l}} = 1{\text{/}}1000$ и ${{\mu }_{g}}{\text{/}}{{\mu }_{l}} = 1{\text{/1}}0$ на различных сетках S1(60 × 120), S2(70 × 140), S3(80 × 160), S4(90 × 180), S5(100 × 200) и S6(110 × 220).

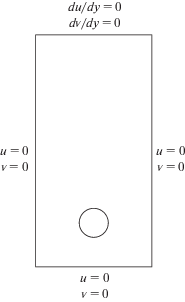
Физическая модель представлена на рис. 3. Феерический пузырек с начальным радиусом 0.5 находится в точке с координатами (0, 1.5) в покоящейся жидкости. Отношение начального радиуса пузырька к ширине канала равно 1:8, а отношение ширины к высоте канала 1:2. Левая и правая стенки канала и его дно представляют собой твердые поверхности, а верхняя граница открытая.

Рис. 3.

Схематическое представление и граничные условия для случая одиночного пузырька, поднимающегося в вертикальном поле течения.

Результаты моделирования движения пузырька в различных случаях приведены на рис. 4. С увеличением количества узлов сетки конечные форма и положение пузырька не претерпевают существенных изменений, а конечная скорость пузырька вырабатывается более устойчиво, особенно в случаях S5 и S6, которые, очевидно, отличаются от других случаев.

Рис. 4.

Влияние размера сетки на результаты моделирования конечных формы, положения и скорости подъема пузырька при τ = 6.4.

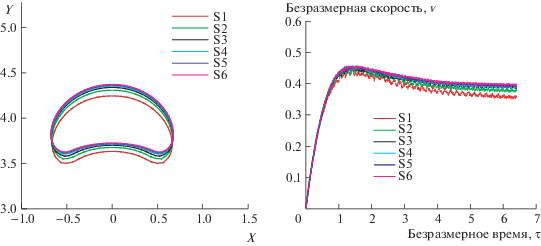
Можно видеть, что результаты моделирования на сетках различных размеров заметно отличаются друг от друга, особенно в случаях S1 до S4. Сравнение с результатами, полученными на мелких сетках S5 и S6, показывает, что скорость поднимающегося пузырька становится более устойчивой, а различия в конечной форме и положении пузырька уменьшаются. Можно заключить, что результаты моделирования не зависят от количества узлов сетки для сеток более мелких, чем S5.

3.2. Верификация процедуры локальной повторной инициализации в сочетании с методом коррекции объема

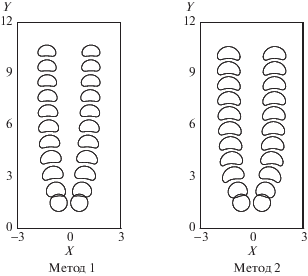
Традиционный метод функции уровня (называемый в дальнейшем методом 1) и модифицированный метод функции уровня (с добавленным процессом локальной повторной инициализации и методом коррекции объема, называемый методом 2) использованы в работе для моделирования подъема двух пузырьков, движущихся рядом друг с другом в регулярном канале. Два первоначально сферических пузырька находятся в точках (–0.6, 1.5) и (0.6, 1.5) и имеют нулевую скорость. На левой и правой границах и на дне ставятся условия прилипания, а верхняя граница является открытой. Расчеты проводятся при значениях параметров Re = 10, We = 20, Fr = 1.0, ${{\rho }_{b}}{\text{/}}{{\rho }_{l}}$ = 1/1000 и ${{\mu }_{b}}{\text{/}}{{\mu }_{l}} = 1{\text{/}}100$. Моделирование проводится на сетке $120 \times 240$.

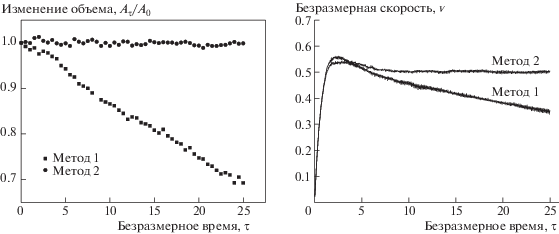
Как следует из рис. 5, результаты, полученные методом 2, безусловно лучше, чем результаты метода 1. После модификации метода функции уровня введением процессов локальной повторной инициализации и коррекции объема сохранение объема пузырька значительно улучшилось.

Рис. 5.

Сравнение форм и положений пузырька при использовании двух методов.

В методе 1 объем газовой фазы постепенно уменьшается вследствие численной диссипации, вызванной неконсервативностью традиционного метода функции уровня. Однако после применения процедуры коррекции объема по методу 2 объем пузырька становится более устойчивым во времени. Сравнение данных на рис. 6 и 7 показывает, что результаты моделирования, полученные методом 2, очевидно лучше, чем в методе 1. Можно видеть, что при моделировании двухфазных течений метод функции уровня в сочетании с процедурой локальной повторной инициализации и методом коррекции объема более консервативен.

Рис. 6.

Сравнение отклонения объема пузырька при моделировании двумя различными методами.

Рис. 7.

Сравнение скорости подъема пузырька при моделировании двумя различными методами.

4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

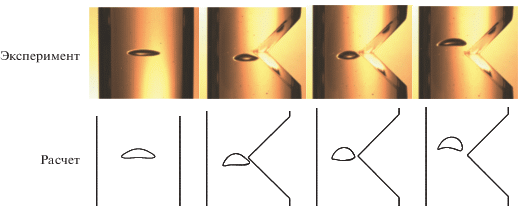
Подъем пузырька в клинообразном канале моделировался при Re = 51.52, Eo = 16.98 и Mo = = 6.94 × 10^–4 при открытой верхней границе, тогда как на остальных границах ставилось условие прилипания. Моделирование проводилось на сетке 100 × 600. На рис. 8 результаты моделирования сравниваются с экспериментом.

Рис. 8.

Сравнение экспериментальных и расчетных результатов по форме пузырька.

Сравнение показывает, что численные результаты в целом согласуются с экспериментальными данными в том, что форма пузырька сильно искажается при прохождении через горло клинообразного канала.

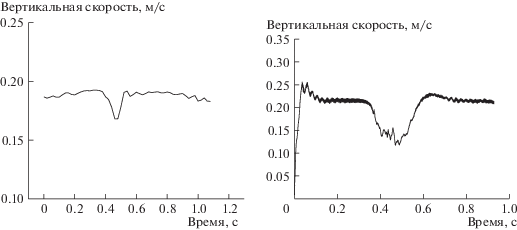
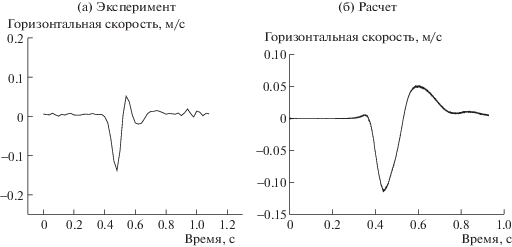
Как показано на рис. 9, и в расчете, и в эксперименте горизонтальная и вертикальная скорости пузырька резко изменяются при прохождении клинообразного угла, причем законы изменения скорости пузырька в обоих случаях близки. Это доказывает, что модифицированный метод функции уровня в сочетании с процедурой локальной повторной инициализации и методом коррекции объема представляет собой эффективный инструмент моделирования движения пузырьков в каналах со сложной границей.

Рис. 9.

Сравнение экспериментальных и расчетных результатов по горизонтальной и вертикальной скорости пузырька.

ЗАКЛЮЧЕНИЕ

Показано, что модифицированный метод функции уровня в сочетании с процедурой локальной повторной инициализации и методом коррекции объема представляет собой эффективный метод, позволяющий исправить неконсервативность объема пузырька и избежать численной диссипации, вызванной неортогональностью сетки на границе. Моделирование подъема пузырька в клинообразном канале при больших отношениях плотности и вязкости успешно осуществлено на основе преобразованных уравнений Навье–Стокса и уравнения для функции уровня в координатах, связанных с телом в вычислительной области. Метод функции уровня в сочетании с методом SIMPLE в системе координат, связанной с телом, является эффективным и точным методом аккуратного отслеживания границы раздела двух фаз при движении пузырька в канале сложной геометрии.

Работа выполнена при поддержке программы State Key Research Development Program Китая (грант № 2016YFC0801404) и фонда Nature Science Foundation провинции Ляонинь, Китай (грант № 20170540412).

Список литературы

Mohanty R.L., Das M.K. A critical review on bubble dynamics parameters influencing boiling heat transfer // Renew. Sust. Energ. Rev. 2017. V. 78. P. 466.
Balcázar N., Lehmkuhl O., Jofre L., Oliva A. Level set simulations of buoyancy-driven motion of single and multiple bubbles // Int. J. Heat Fluid Flow. 2015. V. 56. P. 91.
Safi M.A., Turek S. GPU-based rising bubble simulations using a MRT lattice Boltzmann method coupled with level set interface capturing // Computers Fluids. 2016. V. 124. P. 170.
Sun T., Li W., Dong B. Numerical and experimental study on the motion characteristics of single bubble in a complex channel // Int. J. Comput. Fluid D. 2015. V. 29. P. 346.
Cao J., Christensen R.N. Analysis of moving boundary problem for bubble collapse in binary solutions // Numer. Heat Transfer. A-Appl. 2000. V. 38. P. 681.
Yan Y., Li W. Numerical modelling of a vapour bubble growth in uniformly superheated liquid // Int. J. Numer. Method H. 2006. V. 16. P. 764.
Pivello M.R., Villar M.M., Serfaty R., Roma A.M., Silveira-Neto A. A fully adaptive front tracking method for the simulation of two phase flows // Int. J. Multiphase Flow. 2014. V. 58. P. 72.
Li W., Yan Y. Direct-predictor method for solving steady terminal shape of a gas bubble rising through a quiescent liquid // Numer. Heat Transfer. B-Fund. 2002. V. 42. P. 55.
Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries // J. Comput. Phys. 1981. V. 39. P. 201.
Malgarinos I., Nikolopoulos N., Marengo M., Antonini C., Gavaises M. VOF simulations of the contact angle dynamics during the drop spreading: Standard models and a new wetting force model // Adv. Colloid Interface. 2014. V. 212. P. 1.
Osher S., Setian J.A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton–Jacobi formulations // J. Comput. Phys. 1988. V. 79. P. 12.
Sussman M., Almgren A.S., Bell J.B., Colella P., Howell L.H., Welcome M.L. An adaptive level set approach for incompressible two-phase flows // J. Comput. Phys. 1999. V. 148. P. 81.
Sussman M., Smereka P., Osher S. A level set approach for computing solutions to incompressible two-phase flow // J. Comput. Phys. 1994. V. 114. P. 146.
Brackbill J.U., Kothe D.B., Zemach C. A continuum method for modeling surface tension // J. Comput. Phys. 1992. V. 100. P. 335.
Zhang Y., Li W., Quan S. An exact numerical method for tracking bubble coalescence // Heat Transfer Eng. 2010. V. 31. P. 998.
Peng D., Merriman B., Osher S., Zhao H., Kang M. A PDE-based fast local level set method // J. Comput. Phys. 1999. V. 155. P. 410.
Patankar S.V. Numerical heat transfer and fluid flow // New York: Hemisphere, 1980.
Perić M., Kessler R., Scheuerer G. Comparison of finite-volume numerical methods with staggered and collocated grids // Computers Fluids. 1988. V. 16. P. 389.
Tao W. Numerical heat transfer // Xi’an Jiao Tong University Press, Xi’an, China, 2001.
Osher S., Shu C. High-order essentially nonoscillatory schemes for Hamilton–Jacobi equations // SIAM J. Numer. Anal. 1991. V. 28. P. 907.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал