1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2020

Известия РАН. Механика жидкости и газа, 2020, № 1, стр. 3-8

Гармонические внутренние волны в стратифицированной полубесконечной среде со сдвиговыми течениями

В. В. Булатов a, *, Ю. В. Владимиров a, **

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: internalwave@mail.ru
** E-mail: vladimyura@yandex.ru

Поступила в редакцию 15.04.2019
После доработки 25.06.2019
Принята к публикации 25.06.2019

Полный текст (PDF)

Аннотация

Рассмотрена задача о построении решений, описывающих гармонические внутренние гравитационные волны в стратифицированной полубесконечной среде со сдвиговым течением. Использованы модельное постоянное распределение частоты Брента-Вяйсля и линейная зависимость сдвигового течения по глубине и получено аналитическое решение задачи, которое выражается через модифицированные функции Бесселя мнимого индекса. С помощью дебаевских асимптотик модифицированной функции Бесселя мнимого индекса получены аналитические выражения для дисперсионных соотношений, исследованы фазовые характеристики волновых полей. Исследованы зависимости волновых характеристик возбуждаемых полей от основных параметров использованных моделей стратификации, течений и режимов генерации.

Ключевые слова: стратифицированная среда, внутренние гравитационные волны, частота плавучести, сдвиговые течения, модифицированная функция Бесселя

Среди большого многообразия волновых процессов различной физической природы в океане и атмосфере Земли особый интерес вызывает возбуждение волн в стратифицированных средах с гидродинамическими потоками [1–4]. Движение стратифицированной среды является одним из основных факторов, влияющих на динамику внутренних гравитационных волн (ВГВ) как в естественных условиях, так и в технических устройствах.

В современных научных исследованиях при анализе динамики ВГВ в природных стратифицированных средах с учетом наличия течений применяются асимптотические методы исследования аналитических моделей волновой генерации. В линейном приближении существующие подходы к описанию волновой картины возбуждаемых полей ВГВ основаны на представлении волновых полей интегралами Фурье и их асимптотическом анализе [3–5]. В реальных океанических условиях необходимо рассматривать ВГВ, распространяющиеся на фоне средних течений с вертикальным сдвигом скорости, причем вариация скорости по вертикали составляет десятки см/с, то есть имеет тот же порядок, что и максимальные скорости ВГВ. Такие течения должны существенно сказываться на распространении ВГВ [6–11]. Если пространственный масштаб изменения течений по горизонтали много больше длин ВГВ, а масштаб временной изменчивости много больше периодов внутренних волн, то естественной математической моделью является случай стационарных и горизонтальных однородных сдвиговых течений [1–4, 7, 8, 11–13].

Целью настоящей работы является построение аналитических решений, описывающих поля гармонических ВГВ в стратифицированной полубесконечной среде с учетом сдвиговых течений.

1. ПОСТАНОВКА ЗАДАЧИ И ПОСТРОЕНИЕ АНАЛИТИЧЕСКИХ РЕШЕНИЙ.

Рассматривается вертикально стратифицированная среда бесконечной глубины. Пусть (U(z), $V(z))$ – вектор сдвигового течения на горизонте z. Исходной для дальнейшего анализа является линеаризованная система уравнений гидродинамики относительно невозмущенного состояния, которая имеет вид [1–4, 8, 12]

${{\rho }_{0}}\frac{{D{{U}_{1}}}}{{Dt}} + \frac{{\partial p}}{{\partial x}} = 0,\quad {{\rho }_{0}}\frac{{D{{U}_{2}}}}{{Dt}} + \frac{{\partial p}}{{\partial y}} = 0,\quad {{\rho }_{0}}\frac{{DW}}{{Dt}} + \frac{{\partial p}}{{\partial z}} + \rho g = 0$
$\frac{{\partial {{U}_{1}}}}{{\partial x}} + \frac{{\partial {{U}_{2}}}}{{\partial y}} + \frac{{\partial W}}{{\partial z}} = 0,\quad \frac{{\partial \rho }}{{\partial t}} + W\frac{{\partial {{\rho }_{0}}}}{{\partial z}} = 0$
$\frac{D}{{Dt}} = \frac{\partial }{{\partial t}} + U(z)\frac{\partial }{{\partial x}} + V(z)\frac{\partial }{{\partial y}}$
где (${{U}_{1}}$, ${{U}_{2}}$, $W$) – компоненты возмущенной скорости, ($p$, $\rho $) – возмущения давления и плотности, ${{\rho }_{0}}(z)$ – невозмущенная плотность среды. Воспользовавшись приближением Буссинеска, можно получить уравнение для вертикальной компоненты скорости [1, 4, 12]
(1.1)
$\begin{gathered} \frac{{\mathop D\nolimits^2 }}{{Dt{}^{2}}}\Delta W - \frac{D}{{Dt}}\left( {\frac{{\mathop \partial \nolimits^2 U}}{{\partial z{}^{2}}}\frac{{\partial W}}{{\partial x}} + \frac{{\mathop \partial \nolimits^2 V}}{{\partial z{}^{2}}}\frac{{\partial W}}{{\partial y}}} \right) + {{N}^{2}}(z){{\Delta }_{2}}W = 0 \\ \Delta = {{\Delta }_{2}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}},\quad {{\Delta }_{2}} = \frac{{{{\partial }^{2}}}}{{\partial x{}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}},\quad {{N}^{2}}(z) = - \frac{g}{{{{\rho }_{0}}(z)}}\frac{{d{{\rho }_{0}}(z)}}{{dz}} \\ \end{gathered} $
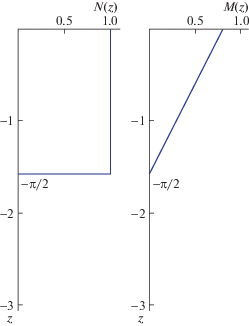
где ${{N}^{2}}(z)$ – квадрат частоты Брента-Вяйсяля (частоты плавучести), $g$ – ускорение свободного падения. Граничные условия берутся в виде (вертикальная ось z направлена вверх)

(1.2)
$\begin{gathered} W = 0\quad {\text{при}}\quad z = 0 \\ W = 0\quad {\text{при}}\quad z \to - \infty \\ \end{gathered} $

Далее используются следующие предположения. Частота Брента-Вяйсяля предполагается постоянной: $N(z) = N = {\text{const}}$ при $ - H \leqslant z \leqslant 0$ (верхний слой), $N(z) = 0$ при $z \leqslant - H$ (нижний слой). Течение предполагается одномерным: $V(z) \equiv 0$. Функция $U(z)$ – линейная функция глубины: $U(z) = {{U}_{0}} + {{U}_{0}}z{\text{/}}H$, при $ - H \leqslant z \leqslant 0$ (верхний слой), $U(z) = 0$ при$z \leqslant - H$ (нижний слой).

Использование данной модельной гидрологии широко применяется в реальных океанологических расчетах и позволяет учитывать основные особенности волновой динамики с учетом реальной изменчивости плотности морской среды, наблюдаемой при натурных измерениях ВГВ в океане, а также исследовать задачу аналитически [7, 8, 12]. В [6–8] в рамках данной модели анализировались результаты натурных измерений внутренних волн, течений, а также их взаимодействие в различных областях Мирового океана. В [9] рассмотрена генерация ВГВ волн сдвиговым течением в проливе Карские Ворота, причем течение меняется с приливной частотой, и пакеты ВГВ появляются с периодичностью, определяемой наличием сдвиговой неустойчивости течений. Аналогичные результаты на примере Гибралтарского пролива получены в [10], где рассмотрены измерения течений и ВГВ, амплитуда которых составляла десятки метров. Многочисленные измерения придонных потоков в глубоководных акваториях Северной Атлантики показывают, что на больших глубинах градиенты сдвиговых скоростей и значения частоты плавучести малы, основные изменения этих гидрофизических параметров наблюдаются в верхних слоях океана на глубинах порядка 100–200 м, что позволяет использовать предложенную модельную гидрологию [8–11].

Решение уравнения (1.1) ищется виде: $W\left( {t,x,y,z} \right) = \varphi (z)exp(i(\omega t - \mu x - \nu y)$. Тогда для определения функции $\varphi (z)$имеем

$\frac{{\mathop \partial \nolimits^2 \varphi }}{{\partial _{z}^{2}}} + ({{k}^{2}}{{\left( {\omega - \mu U(z)} \right)}^{{ - 2}}} - 1) - \frac{{\mu {{U}_{0}}\delta (z + H)}}{{(\omega - \mu U(z))H}})\varphi = 0$
(1.3)
$\mathop k\nolimits^2 = \mathop \mu \nolimits^2 + \mathop \nu \nolimits^2 $
$\begin{gathered} \varphi = 0\quad {\text{при}}\quad z = 0 \\ \varphi = 0\quad {\text{при}}\quad z \to - \infty \\ \end{gathered} $

В безразмерных координатах и переменных $x{\text{*}} = \pi x{\text{/}}2H$, $y{\text{*}} = \pi y{\text{/}}2H$, $z{\text{*}} = \pi z{\text{/}}2H$, $\omega {\text{*}} = \omega {\text{/}}N$, $t{\text{*}} = tN$, $M(z{\text{*}}) = U(z{\text{*}}){\text{/}}C = a + bz{\text{*}}$, $a = \pi \mathop U\nolimits_0 {\text{/}}2NH$, $b = {{U}_{0}}{\text{/}}NH$ (граница $z = - H$ в безразмерных переменных перейдет в $z = - \pi {\text{/}}2$, C – максимальная групповая скорость ВГВ в стратифицированной среде бесконечной глубины без течений $U(z) \equiv 0$ [5]) уравнение (1.3) можно представить в виде (знак “*” далее опускается)

(1.4)
$\begin{gathered} \frac{{\mathop \partial \nolimits^2 \varphi }}{{\partial _{z}^{2}}} + (\mathop k\nolimits^2 {{\left( {\omega - \mu M(z)} \right)}^{{ - 2}}} - 1) - \frac{{\mu b\delta (z + \pi {\text{/}}2)}}{{(\omega - \mu M(z))}})\varphi = 0 \\ \varphi = 0\quad {\text{при}}\quad z = 0,\quad \varphi = 0\quad {\text{при}}\quad z \to - \infty \\ \end{gathered} $

Обозначим через ${{\varphi }_{1}}(z)$ решение задачи (1.4) в верхнем слое $ - \pi {\text{/}}2 \leqslant z \leqslant 0$ с условием ${{\varphi }_{1}}(0) = 0$ и через ${{\varphi }_{2}}(z)$ решение задачи (1.4) в нижнем слое с условием ${{\varphi }_{2}}(z) \to 0$ при $z \to - \infty $. При $z = - \pi {\text{/}}2$ имеем следующее условие сшивки решений

(1.5)
${{\varphi }_{1}}( - \pi {\text{/}}2) = {{\varphi }_{2}}( - \pi {\text{/}}2),\quad \omega (\varphi _{1}^{'}( - \pi {\text{/}}2) - \varphi _{2}^{'}( - \pi {\text{/}}2)) + \mu b{{\varphi }_{1}}( - \pi {\text{/}}2) = 0$

Условия (1.5) получены из уравнения (1.4), однако они также следуют из кинематического (равенство вертикальных скоростей) и динамического (равенства давлений) условий на границе раздела слоев $z = - \pi {\text{/}}2$ [2–4].

Решение в верхнем слое имеет вид

$\begin{gathered} \mathop \varphi \nolimits_1 (z) = i(\mathop f\nolimits_ + (0)\mathop f\nolimits_ - (z) - \mathop f\nolimits_ - (0)\mathop f\nolimits_{ + 1} (z)) \\ \mathop f\nolimits_ \pm (z) = \sqrt {2\beta r(z))} \mathop I\nolimits_{ \pm i\lambda } (\beta r(z)) \\ \end{gathered} $
где согласно [14, 15] $\mathop I\nolimits_{ \pm i\lambda } $ – модифицированная функция Бесселя мнимого индекса $i\lambda $, λ = = $\sqrt {\mathop \beta \nolimits^2 - 1{\text{/}}4} $, $\beta = k{\text{/}}b\mu $.

Функции $\mathop f\nolimits_ \pm (z)$ – комплексно сопряжены, поэтому решение φ1(z) является действительным. Также предполагается, что выполнено условие устойчивости Майлса для числа Ричардсона: $Ri = \mathop N\nolimits^2 {{\left( {\partial U{\text{/}}\partial z} \right)}^{{ - 2}}} > 1{\text{/}}4$, то есть ${{b}^{2}} < 4$ [1–4, 8]. Отсюда в частности следует, что $\mathop \beta \nolimits^2 > 1{\text{/}}4$, и значения $\lambda $ действительны.

Решение в нижнем слое имеет вид: $\mathop \varphi \nolimits_2 (z) = A\exp (kz)$ и условия сшивки при $z = - \pi {\text{/}}2$ дают значение $A = \mathop \varphi \nolimits_1 ( - \pi {\text{/}}2)\exp (\pi k{\text{/}}2)$ и дисперсионное соотношение

(1.6)
$\omega \varphi _{1}^{'}( - \pi {\text{/}}2) + (\mu b - \omega k){{\varphi }_{1}}( - \pi {\text{/}}2) = 0$

В [12] для аналогичной модельной гидрологии (постоянная частота плавучести, линейный профиль сдвигового течения, конечная толщина стратифицированного слоя) получено дисперсионное соотношение в виде, аналогичном (1.6), где было отмечено, что решение этого уравнения представляет большую трудность. Более сложной задачей является исследование аналитических свойств полученного дисперсионного уравнения, так как это дает возможность получить асимптотические выражения для полей ВГВ при различных режимах волновой генерации. Далее будут изучены основные особенности решений дисперсионного уравнения (1.6) и построены асимптотические представления решения этого уравнения.

2. ПОСТРОЕНИЕ АСИМПТОТИЧЕСКИХ РЕШЕНИЙ

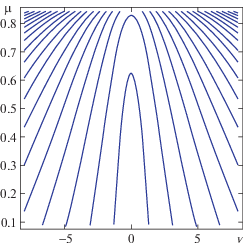
Дисперсионное уравнение (1.6) имеет счетный набор решений $\mathop \mu \nolimits_т (\nu )$, n = 1, 2, … (дисперсионных кривых). Далее будут рассматриваться асимптотические решения (1.6), считая большим параметром $\beta $, в этом случае $\lambda $ можно заменить на $\left| \beta \right|$. Для функции $\mathop \varphi \nolimits_1 (z)$ воспользуемся дебаевской асимптотикой $(\lambda \gg 1)$ модифицированной функции Бесселя мнимого индекса [14, 15]

$\operatorname{Re} {{I}_{{ \pm i\lambda }}}(\lambda r) \approx {{({{r}^{2}} - 1)}^{{ - 1/4}}}\exp (\lambda (\Phi (r) + \pi {\text{/}}2)){\text{/}}\sqrt {2\pi \lambda } $
$\operatorname{Im} {{I}_{{ \pm i\lambda }}}(\lambda r) \approx \mu {{({{r}^{2}} - 1)}^{{ - 1/4}}}\exp ( - \lambda (\Phi (r) - \pi {\text{/}}2)){\text{/}}2\sqrt {2\pi \lambda } $
(2.1)
$\Phi (r) = \sqrt {{{r}^{2}} - 1} - {\text{arctg}}(\sqrt {{{r}^{2}} - 1} ) \pm \pi {\text{/}}2,\quad r > 1$
${{I}_{{ - i\lambda }}}(\lambda r) \approx {{({{r}^{2}} - 1)}^{{ - 1/4}}}\exp (\Theta ){\text{/}}\sqrt {2\pi \lambda } $
$\Theta = \pm i\left( {\lambda \sqrt {1 - {{r}^{2}}} - \frac{1}{2}\ln \frac{{1 + \sqrt {1 - {{r}^{2}}} }}{{1 - \sqrt {1 - {{r}^{2}}} }} - \pi {\text{/}}4} \right) + \pi \lambda {\text{/}}2,\quad 0 < r < 1$

Точка r = 1 является точкой поворота , где асимптотики (2.1) не работают. Если $r < 0$, то имеем

(2.2)
${{I}_{{i\lambda }}}(\lambda r) = \exp ( - \pi \lambda ){{I}_{{i\lambda }}}( - \lambda r),\quad {{I}_{{ - i\lambda }}}(\lambda r) = \exp (\pi \lambda ){{I}_{{ - i\lambda }}}( - \lambda r)$

Интервал изменения переменной $\mu $ разбивается на три части двумя особыми точками: μ0 и μ* (${{\mu }^{0}} > \mu {\text{*}}$). Точка μ0 – корень уравнения $\omega - \mu M(0) = 0$, ${{\mu }^{0}} = \omega {\text{/}}a$. Точка μ* – корень уравнения: $\omega - \mu M(0)$ = 1, $\mu {\text{*}} = (\omega - 1){\text{/}}a$. Точка μ0 – точка ветвления, точка μ* – точка поворота. При $\mu < \mu {\text{*}}$ уравнение (1.6), используя асимптотики (2.1) и соотношения (2.2), можно приближенно представить в виде

(2.3)
$ctg( - k\Theta (r){\text{/}}\mu b - \pi {\text{/}}4) = \omega {\text{/}}\sqrt {1 - {{\omega }^{2}}} $

Решение (2.3) при $\nu > 0$ имеет вид

(2.4)
$\mathop \mu \nolimits_n (\nu ) = - \nu {{({{(\pi n - \pi {\text{/}}4 - arctg\omega {\text{/}}\sqrt {1 - {{\omega }^{2}}} )}^{2}}{{b}^{2}}{{\Theta }^{{ - 2}}}(\omega ) - 1)}^{{ - 1/2}}}$

При $\mu {\text{*}} < \mu < {{\mu }^{0}}$ уравнение (1.6), используя асимптотики (2.1), можно представить в виде

(2.5)
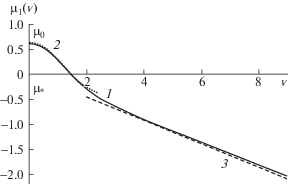
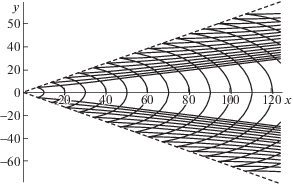
${{\nu }_{n}}(\mu ) = {{B}_{n}}\left| \mu \right|,\quad {{B}_{n}} = {{({{((\pi n - arctg\omega {\text{/}}\sqrt {1 - {{\omega }^{2}}} )b)}^{2}}{{\left( {\Theta (\omega ) - \Theta (\omega - \mu a)} \right)}^{{ - 2}}} - 1)}^{{ - 1/2}}}$

Для получения зависимости ${{\mu }_{n}}(\nu )$ из (2.5) применялись стандартные вычислительные системы типа “Математика”. Для численных расчетов использованы следующие значения параметров: a = 0.8, $b = 2a{\text{/}}\pi $, $\omega = 0.7$. На рис. 1 изображены (в безразмерных переменных) зависимости от глубины частоты плавучести и скорости горизонтального течения. На рис. 2 показана карта дисперсионных кривых при $\mu > 0.1$. На рис. 3 приведены дисперсионная кривая ${{\mu }_{1}}(\nu )$ (кривая 1) и ее приближения. Кривая 2 – приближение с использованием (2.5), кривая 3 – приближение по формуле (2.4). Точка поворота $\mu {\text{*}} = - 0.375$, точка ветвления ${{\mu }^{0}} = 0.875$. На рис. 4 изображены линии равной фазы, сплошные линии – значения $\Phi = {{\mu }_{1}}(\nu ) + \nu y = 2\pi k$, $k = 1,2,..,14$ рассчитанные по формулам

$x = \frac{\Phi }{{{{\mu }_{1}}(\nu ) - \nu \mu _{1}^{'}(\nu )}},\quad y = \frac{{\mu _{1}^{'}(\nu )\Phi }}{{{{\mu }_{1}}(\nu ) - \nu \mu _{1}^{'}(\nu )}}$
Рис. 1.

Зависимости частоты Брента-Вяйсяля N(z) и скорости M(z) горизонтального течения от глубины.

Рис. 2.

Карта дисперсионных кривых первых 16 волновых мод.

Рис. 3.

Дисперсионная кривая (1) первой моды ${{\mu }_{1}}(\nu )$ и ее аппроксимации (2, 3).

Рис. 4.

Фазовая структура волнового поля.

Штриховые линии на рис. 4 – волновые фронты с углом полураствора $\alpha = arctg({{\mu }_{1}}(\nu {\text{*}}))$, где ν* – корень уравнения $\mu _{1}^{{''}}(\nu {\text{*}}) = 0$. Волновая картина возбуждаемых полей ВГВ представляет собой систему продольных и поперечных волн. Поперечные волны занимают всю пространственную область внутри волнового клина с углом полураствора $\alpha $, длина поперечной волны при $y = 0$ равна $2\pi {\text{/}}{{\mu }_{1}}(0)$. Продольные волны ограничены как волновым фронтом с углом полураствора α, так и волновым фронтом (положение которого определяется асимптотикой ${{\mu }_{1}}(\nu )$ при больших ν) с углом полураствора $\vartheta = arctg(B_{n}^{{ - 1}}) < \alpha $.

ЗАКЛЮЧЕНИЕ

Решена задача о поле гармонических внутренних гравитационных волн в полубесконечной стратифицированной среде со сдвиговым течением. Для аналитического решения задачи использованы постоянное распределение частоты плавучести и линейная зависимость сдвигового течения от глубины, на больших глубинах предполагается, что стратификация и сдвиговые течения равны нулю. Используя модельную гидрологию и соответствующие условия сшивки, получены аналитические выражения, описывающие дисперсионные зависимости, которые выражаются через модифицированную функцию Бесселя мнимого индекса. При выполнении условия устойчивости Майлса и больших числах Ричардсона для построения аналитических решений были использованы дебаевские асимптотики модифицированной функции Бесселя мнимого индекса. Изучены свойства дисперсионного уравнения и исследованы основные аналитические свойства дисперсионных кривых. Численно рассчитаны фазовые картины возбуждаемых полей ВГВ для данной модели волновой генерации.

Работа выполнена по теме государственного задания № АААА-А17-117021310375-7.

Список литературы

  1. Miles J.W. On the stability of heterogeneous shear flow // J. Fluid Mech. 1961. V. 10 (4). P. 495–509.

  2. Fabrikant A.L., Stepanyants Yu.A. Propagation of waves in shear flows. World Scientific Publ., 1998. 304 p.

  3. Pedlosky J. Waves in the ocean and atmosphere: introduction to wave dynamics. Berlin-Heildelberg: Springer, 2010. 260 p.

  4. Sutherland B.R. Internal gravity waves. Cambridge: Cambridge Univ. Press, 2010. 394 p.

  5. Булатов В.В., Владимиров Ю.В. Волны в стратифицированных средах. М.: Наука, 2015. 735 с.

  6. Vlasenko V., Stashchuk N., Hutter K. Baroclinic tides. N.Y.: Cambridge Univ. Press, 2005. 372 p.

  7. Morozov E. G. Oceanic internal tides. Observations, analysis and modeling. Berlin: Springer, 2018. 317 p.

  8. Velarde M.G., Tarakanov R.Yu., Marchenko A.V. (Eds.). The Ocean in motion. Springer Oceanography. Springer International Publishing AG, 2018. 625 p.

  9. Morozov E.G., Paka V.T., Bakhanov V.V. Strong internal tides in the Kara Gates Strait // Geoph. Res. Letters. 2008. V. 35. L16603.

  10. Morozov E.G., Parrilla-Barrera G., Velarde M.G., Scherbinin A.D. The Straits of Gibraltar and Kara Gates: A comparison of internal tides // Oceanologica Acta. 2003. V. 26 (3). P. 231–241.

  11. Fraternale F., Domenicale L., Staffilan G., Tordella D. Internal waves in sheared flows: lower bound of the vorticity growth and propagation discontinuities in the parameter space // Phys. Rev. 2018. V. 97. № 6. P. 063102

  12. Гаврильева А.А., Губарев Ю.Г., Лебедев М.П. Теорема Майлса и новые частные решения уравнения Тейлора-Гольдстейна // Уч. Зап. Казанского ун-та. Сер. Физ.-мат. науки. 2016. Т. 158. Кн. 2. С. 156–171.

  13. Булатов В.В., Владимиров Ю.В. Внутренние гравитационные волны, возбуждаемые пульсирующим источником возмущений // Изв. РАН. МЖГ. 2015. № 6. С. 26–34.

  14. Никифоров А.Ф., Уваров В.В. Специальные функции математической физики. М.: ИД Интеллект, 2008. 344 с.

  15. Олвер Ф. Асимптотика и специальные функции. М.: Физматлит, 1990. 528 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал