1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 6, 2019

Известия РАН. Механика жидкости и газа, 2019, № 6, стр. 3-11

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ДЛЯ КРУПНОМАСШТАБНОГО ВРАЩАЮЩЕГОСЯ СЛОЯ ЖИДКОСТИ С ТЕПЛОВОЙ КОНВЕКЦИЕЙ

П. Джалилиан a, *, Т. Лю a, **

a Университет Западного Мичигана, Факультет машиностроения и авиационно-космической техники
MI 49008 Каламазоо, США

* E-mail: pouya76j@gmail.com
** E-mail: tianshu.liu@wmich.edu

Поступила в редакцию 20.02.2019
После доработки 18.03.2019
Принята к публикации 20.04.2019

Полный текст (PDF)

Аннотация

С помощью вспомогательного уравнения Риккати получено солитоноподобное решение для эволюционного уравнения, описывающего деформацию верхней поверхности крупномасштабного вращающегося слоя жидкости с тепловой конвекцией. Полученное решение показывает, что долгоживущая структура вращающегося слоя жидкости зависит от нелинейного слагаемого, связанного с бета-эффектом, и диффузионного члена, обусловленного тепловой конвекцией.

Ключевые слова: крупномасштабный вращающийся слой жидкости, долгоживущая структура, аналитическое решение, солитон, тепловая конвекция

Вращающийся слой жидкости с тепловой конвекцией ранее исследовался как простая модель геофизических течений. Для такого рода течений есть несколько аналитических решений. Первый набор аналитических решений для вращающегося слоя жидкости был получен Чандрасекаром [1]. Нелинейные слагаемые не учитывались, деформация верхней поверхности и бета-эффект не рассматривались. В дальнейшем Чжанг и Робертс [2] развили решения Чандрасекара и получили аналитические решения для вращающегося слоя жидкости при достаточно малых числах Прандтля. Однако в основных уравнениях нелинейные слагаемые по-прежнему не учитывались. Петвиашвили [3] также получил аналитическое решение для слоя невязкой жидкости, подверженного воздействию силы Кориолиса. Это первое решение в виде солитона, которое учитывает поддержание вихревой структуры вращающегося слоя жидкости. Однако в основных уравнениях [3–5] влиянием конвекции и вязкости пренебрегалось. В [6, 7] была предложена модель, известная как глубокая модель, основанная на теореме Тэйлора–Прудмана, и произведен линейный анализ основного уравнения для вращающегося слоя жидкости.

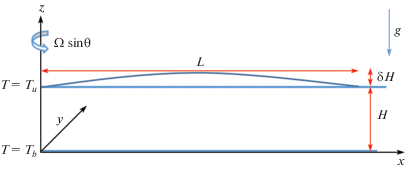
В настоящем исследовании рассматривается крупномасштабный долгоживущий слой жидкости с тепловой конвекцией. На рис. 1 изображен одиночный вращающийся слой жидкости, неограниченный в горизонтальном направлении, причем нижняя граница слоя – недеформируемая ненагруженная изотермическая плоскость, а верхняя граница – деформируемая ненагруженная изотермическая плоскость. На верхней и нижней границах касательные напряжения отсутствуют. Подразумевается, что на нижней недеформируемой поверхности вертикальная компонента скорости равна нулю. Напротив, конвективное движение деформирует верхнюю поверхность, поэтому вертикальное смещение поверхности от невозмущенного положения должно учитываться на верхней границе [8, 9]. Отметим, что в некоторых исследованиях [10–12] деформацией верхней поверхности жидкости пренебрегалось. В математической модели, предложенной Тихомоловым [8, 9] и используемой в настоящем исследовании, сила Кориолиса рассматривается в предположении, что период вращения течения много больше, чем период вращения всей системы. Квазигеострофическое приближение используется вместе с приближением Буссинеска и приближением бета-плоскости. При выводе системы основных уравнений учитываются тепловая конвекция, вязкость жидкости и деформация верхней поверхности. Эволюционное уравнение для деформации верхней поверхности выводится с помощью метода многомасштабных разложений. Цель настоящей работы – получить аналитическое решение нелинейного эволюционного уравнения с помощью вспомогательного уравнения [13–15] и метода разложения Риккати [16, 17]. Получено солитоноподобное решение этого уравнения для деформации верхней поверхности и приведен пример, позволяющий моделировать крупномасштабную долгоживущую структуру в атмосфере Юпитера [8, 9, 18, 19].

Рис. 1.

Модель одиночного слоя жидкости

1. ЭВОЛЮЦИОННОЕ УРАВНЕНИЕ

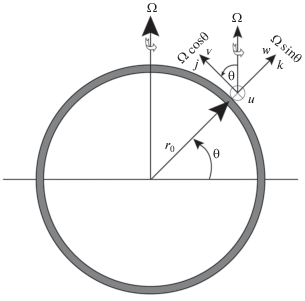
Основное уравнение было выведено Тихомоловым [8, 9] для крупномасштабного долгоживущего вращающегося слоя жидкости в присутствии тепловой конвекции. Перечислим предположения и приближения, лежащие в основе вывода этого уравнения. В соответствии с рис. 1, для одиночного вращающегося слоя жидкости, неограниченного в горизонтальном направлении, характерные масштабы горизонтальных и вертикальных размеров (длин) обозначим L и H соответственно и предположим, что горизонтальный размер много больше вертикального, т.е. $L \gg H$. Предполагается, что нижняя недеформируемая ненагруженная поверхность имеет постоянную температуру Tb, а деформируемая верхняя поверхность имеет температуру Tu. Таким образом, ${\Theta } = {{T}_{b}} - {{T}_{u}}$ есть разность температур между верхней и нижней поверхностями, которая считается постоянной в настоящей работе и $~\delta H$ определяется как отклонение верхней поверхности от невозмущенного состояния. Как показано на рис. 2, вектор угловой скорости вращения всей системы может быть записан в виде ${\mathbf{\Omega }} = {\Omega }\sin {\theta }{\mathbf{k}} + {\Omega }\cos {\theta }{\mathbf{j}}$, где ${\theta }$ – широта, а ${\Omega }\sin {\theta }$ и ${\Omega }\cos {\theta }$ – вертикальная и горизонтальная компоненты ${\mathbf{\Omega }}$ соответственно. При $L \gg H$ горизонтальной компонентой ${\mathbf{\Omega }}$ можно пренебречь [20]. Таким образом, вектор угловой скорости вращения может быть приближенно записан в виде ${\mathbf{\Omega }} = {\Omega }\sin {\theta }{\mathbf{k}}$. Как показано на рис. 2, тонкая оболочка жидкости имеет локальный вертикальный единичный вектор k и компоненту скорости w в этом направлении. Компоненты скорости в северном и восточном направлениях равны ${v}$ и u соответственно (см. рис. 2). Единичные векторы (орты) в северном и восточном направлениях обозначены i и j соответственно. Отметим, что нижняя и верхняя границы жидкости в данной модели соответствуют внутренней и внешней границам сферического тонкого слоя жидкости, показанного на рис. 2.

Рис. 2.

Тонкая оболочка жидкости и локальная система координат на широте $\theta $

Для моделирования течения на сфере используется приближение β-плоскости, в котором разложение в ряд Тэйлора применяется для оценки ${\Omega }\sin {\theta }$ на широте θ0 вдали от экватора [21]. Таким образом, соотношение имеет вид ${\Omega }\sin {\theta } = {\Omega }\sin {{{\theta }}_{0}} + {{{\beta }}_{0}}y{\text{/}}2{\text{\;}}$, где ${{{\beta }}_{0}} = 2{\Omega }\cos {{{\theta }}_{0}}{\text{/}}{{r}_{0}}$, y = ${{r}_{0}}({\theta } - {{{\theta }}_{0}})$ и ${{{\beta }}_{0}}y{\text{/}}2 \ll {\Omega }\sin {{{\theta }}_{0}}$. Приближение β-плоскости может быть записано в виде Ω = Ωsinθk = = ${\Omega }\sin {{{\theta }}_{0}}(1 + {\beta }y){\mathbf{k}}~$, где ${\beta } = {{{\beta }}_{0}}{\text{/}}2{\Omega }\sin {{{\theta }}_{0}}$ (${\beta }y \ll 1$) представляет собой параметр, который характеризует так называемый бета-эффект [18, 20, 22]. Одно из предположений, сделанных в настоящей модели, состоит в том, что ускорение Кориолиса $~2{\mathbf{\Omega }} \times {\mathbf{V}}$ в уравнениях Навье–Стокса становится доминирующим и в основном уравновешивается градиентом давления. Это приводит к квазигеострофическому приближению. Квазигеострофическое приближение было использовано ранее для описания вращающегося слоя жидкости в предыдущих многочисленных численных и экспериментальных исследованиях [23–27]. В настоящей работе квазигеострофическое приближение применяется при выводе эволюционного уравнения для деформации верхней поверхности вращающегося слоя жидкости с тепловой конвекцией. Кроме того, используется приближение Буссинеска, в котором изменение плотности жидкости моделируется слагаемым, обусловленным тепловой конвекцией, когда толщина слоя жидкости много меньше горизонтальной длины.

Следуя [8, 9, 28] и находясь в рамках вышеупомянутых предположений и приближений, выведем нелинейное эволюционное уравнение для деформации верхней поверхности вращающегося слоя жидкости, применяя метод многомасштабных разложений к уравнениям количества движения, энергии и неразрывности. Это уравнение может быть записано в виде

(1.1)
$\begin{gathered} {{\mathcal{H}}_{\tau }} - \frac{\eta }{{\Pr {{D}^{2}}}}{{\Delta }_{{2X}}}{{\mathcal{H}}_{\tau }} - \frac{{~{{\eta }^{2}}}}{{\Pr {{D}^{3}}}}{{J}_{X}}\left( {\mathcal{H},{{\Delta }_{{2X}}}\mathcal{H}} \right) - \frac{{B\eta }}{D}{{\mathcal{H}}_{X}} - \\ - \;{{\varepsilon }^{2}}\frac{{B\eta }}{D}\mathcal{H}{{\mathcal{H}}_{X}} + \frac{\eta }{{{{D}^{2}}}}\Delta _{{2X}}^{2}\mathcal{H} + \frac{{{{{\text{R}}}_{{{\text{cr}}}}}}}{{{{D}^{2}}}}{{\Delta }_{{2X}}}\mathcal{H} = 0 \\ \end{gathered} $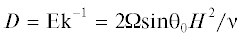
где деформация верхней поверхности характеризуется величиной $\mathcal{H} \approx h{\text{/}}{{{\varepsilon }}^{2}}$, $h = {\delta }H{\text{/}}H$ – относительная деформация (возмущение), $X = {\varepsilon }x$, $Y = {\varepsilon }y~$ и ${\tau } = ~{{{\varepsilon }}^{2}}t$ – масштабированные пространственные и временные координаты, x, y и $t$ – безразмерные пространственные и временные координаты, $B \approx {\beta /}{{{\varepsilon }}^{3}}$ описывает масштабированный безразмерный ${\beta }$-эффект и ${{{\text{R}}}_{{{\text{cr}}}}}$ – критическое значение числа Рэлея ${\text{R}} = g{\alpha \Theta }{{H}^{3}}{\text{/}}\nu \kappa $, определяемое соотношением ${{{\text{R}}}_{{{\text{cr}}}}} \approx 3{{({{\pi }^{2}}{\text{/}}2)}^{{2/3}}}{{D}^{{4/3}}}~$ = = 8.6956D4/3 при $D \to \infty $ [1]. Кроме того, ${\text{Pr}} = {\nu /\kappa }$ – число Прандтля, определяется как обратное число Экмана Ek, ${\eta } \approx {{{\varepsilon }}^{2}}q$ – параметр, в котором q = 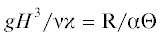= = Re2Pr/Fr ( 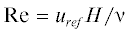– число Рейнольдса на основе характерной скорости течения ${{u}_{{ref}}}$ и ${\text{Fr}} = {{u}_{{ref}}}{\text{/}}\sqrt {gH} $ – число Фруда), R – число Рэлея, ${\nu }$ – кинематическая вязкость жидкости, ${\kappa }$ обозначает коэффициент температуропроводности жидкости и α – коэффициент теплового расширения жидкости. Малый параметр ${\varepsilon } \approx \sqrt {{\text{R}} - {{{\text{R}}}_{{{\text{cr}}}}}} $. Операторы в уравнении (1.1) определены следующим образом: ${{{\Delta }}_{{2X}}} = {{\partial }^{2}}{\text{/}}\partial {{X}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{Y}^{2}}$, ${\Delta }_{{2X}}^{2} = {{\partial }^{4}}{\text{/}}\partial {{X}^{4}} + {{\partial }^{4}}{\text{/}}\partial {{Y}^{4}}$ + $2{{\partial }^{4}}{\text{/}}\partial {{X}^{2}}\partial {{Y}^{2}}$ и ${{J}_{X}}\left( {f,g} \right) = {{f}_{X}}{{g}_{Y}} - {{f}_{Y}}{{g}_{X}}$.

Как указано в разд. 2, наличие нелинейного слагаемого $({{{\varepsilon }}^{2}}B{\eta /}D)\mathcal{H}{{\mathcal{H}}_{X}}$ может иметь следствием солитоноподобное решение для уравнения (1.1). Так как слагаемое $({{{\varepsilon }}^{2}}B{\eta /}D)\mathcal{H}{{\mathcal{H}}_{X}}$ обусловливает ${\beta }$-эффект, рассмотрение сферичности вращающегося слоя жидкости по большей части объяснимо для существования солитоноподобного решения для уравнения (1.1). Диффузионный член $({{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}{{D}^{2}}){{{\Delta }}_{{2X}}}\mathcal{H}$, тесно связанный с тепловой конвекцией, действует как источниковый член, который необходим для поддержания крупномасштабной долгоживущей структуры. Как указано в разд. 2, когда слагаемое $({{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}{{D}^{2}}){{{\Delta }}_{{2X}}}\mathcal{H}$ отсутствует, также отсутствует решение в виде солитона для уравнения (1.1). Наоборот, диффузионный член высшего порядка $({\eta /}{{D}^{2}}){\Delta }_{{2X}}^{2}\mathcal{H}$, являющийся результатом наличия вязких членов в основных уравнениях, и дисперсный член $({\eta /Pr}{{D}^{2}}){{{\Delta }}_{{2X}}}{{\mathcal{H}}_{\tau }}$ играют разные роли, внося вклад в стабилизацию решения уравнения (1.1). В результате, они оба ответственны за затухание деформации. Отметим, что параметр ${\eta }$ отвечает за совместный эффект чисел Фруда, Рейнольдса и Прандтля. Физически допустимое решение уравнения (1.1) должно отражать баланс между энергией, подкачиваемой тепловой конвекцией, и диссипативными потерями энергии на поддержание структуры течения.

2. ДОПУСТИМОЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

2.1. Метод вспомогательного уравнения Рикатти

Разнообразные методы были развиты ранее для реконструкции точных аналитических решений нелинейных уравнений в частных производных, среди них метод вспомогательного уравнения [13–15] и метод разложения Риккати [16, 17]. Используем метод вспомогательного уравнения Рикатти для решения уравнения (1.1). Для простоты уравнение (1.1) преобразуем к виду

(2.1)
${{\mathcal{H}}_{\tau }}~ - a{{\Delta }_{{2X}}}{{\mathcal{H}}_{\tau }} - e{{J}_{X}}\left( {\mathcal{H},{{\Delta }_{{2X}}}\mathcal{H}} \right) - b{{\mathcal{H}}_{X}} - {{\varepsilon }^{2}}b\mathcal{H}{{\mathcal{H}}_{X}} + {\text{Pr}}a\Delta _{{2X}}^{2}\mathcal{H} + c{{\Delta }_{{2X}}}\mathcal{H} = 0$
где $a = \eta {\text{/Pr}}{{D}^{2}}$, $b = B\eta {\text{/}}D$, $c = {{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}{{D}^{2}}$ и $e = {{\eta }^{2}}{\text{/Pr}}{{D}^{3}}$. Предполагается, что в уравнении (2.1) величины a, b, c, e и Pr положительны. Чтобы решить уравнение (2.1), решение записывается в волновом виде $\mathcal{H}\left( {X,Y,\tau } \right) = \mathcal{H}\left( \xi \right)$, где $\xi = X + mY - \lambda \tau $ – переменная бегущей волны, $\lambda $ – скорость волны и $m$ – действительный постоянный параметр. Используя это преобразование, уравнение (2.1) может быть приведено к нелинейному обыкновенному дифференциальному уравнению
(2.2)
$\left( { - \lambda - b} \right)\mathcal{H}{\text{'}} + a\lambda ({{m}^{2}} + 1)\mathcal{H}{\text{'''}} - {{\varepsilon }^{2}}b\mathcal{H}\mathcal{H}{\text{'}} + 4{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}\mathcal{H}{\text{''''}} + c({{m}^{2}} + 1)\mathcal{H}{\text{''}} = 0$
где $\mathcal{H}{\text{'}} = d\mathcal{H}{\text{/}}d\xi $, $\mathcal{H}{\text{''}} = {{d}^{2}}\mathcal{H}{\text{/}}d{{\xi }^{2}}$, $\mathcal{H}{\text{'''}} = {{d}^{3}}\mathcal{H}{\text{/}}d{{\xi }^{3}}$ и $\mathcal{H}{\text{''''}} = {{d}^{4}}\mathcal{H}{\text{/}}d{{\xi }^{4}}$. Интегрируя уравнение (2.2) по $\xi $, получим
(2.3)
$\left( { - \lambda - b} \right)\mathcal{H} + a\lambda ({{m}^{2}} + 1)\mathcal{H}{\text{''}} - ({{\varepsilon }^{2}}b{\text{/}}2){{\mathcal{H}}^{2}} + 4{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}\mathcal{H}{\text{'''}} + c({{m}^{2}} + 1)\mathcal{H}{\text{'}} = A$
где постоянная интегрирования A задается равной нулю после применения асимптотических условий $\mathcal{H} \to 0~$,$~\mathcal{H}{\text{'}} \to 0$, $\mathcal{H}{\text{''}} \to 0$ и $\mathcal{H}{\text{'''}} \to 0$ при $\xi \to \infty $.

При использовании метода вспомогательного уравнения Рикатти предполагается, что решение уравнения (2.3) имеет специальную форму

(2.4)
$\mathcal{H}\left( \xi \right) = ~\mathop \sum \limits_{i = 0}^{n = 3} {{d}_{i}}{{F}^{i}}\left( \xi \right) = {{d}_{0}} + {{d}_{1}}F\left( \xi \right) + ~{{d}_{2}}{{F}^{2}}\left( \xi \right) + {{d}_{3}}{{F}^{3}}\left( \xi \right)$
где ${{d}_{0}}$, ${{d}_{1}}$, $~{{d}_{2}}$ и ${{d}_{3}}$ – коэффициенты, подлежащие определению, и одно из решений для F(ξ) имеет следующий вид [16]:

(2.5)
$F\left( \xi \right) = \left\{ {\begin{array}{*{20}{c}} {{{F}_{1}}\left( \xi \right) = - \sqrt { - {{q}_{0}}} ~{\text{th}}(\sqrt { - {{q}_{0}}} \xi )~} \\ {{{F}_{2}}\left( \xi \right) = - \sqrt { - {{q}_{0}}} ~{\text{cth}}(\sqrt { - {{q}_{0}}} \xi )} \end{array}} \right.~\quad ~{\text{при}}\quad ~{{q}_{0}} < 0$.

Задав $\mathcal{H}\left( \xi \right)$ из уравнения (2.4), можно найти ${{\mathcal{H}}^{2}}$, $\mathcal{H}{\text{'}}$, $\mathcal{H}{\text{''}}$ и $\mathcal{H}{\text{'''}}$. Подставляя выражения для $\mathcal{H}$, $\mathcal{H}{\text{'}}$, $\mathcal{H}{\text{''}}$, $\mathcal{H}{\text{'''}}$ и ${{\mathcal{H}}^{2}}$ в уравнение (2.3) и задавая коэффициенты Fi ($0 \leqslant i \leqslant 6$) равными нулю, получим следующую систему алгебраических уравнений, которую нужно решить:

(2.6)
$\begin{gathered} \left( { - \lambda - b} \right){{d}_{0}} + 2a\lambda (1 + {{m}^{2}}){{d}_{2}}q_{0}^{2} - (b{{\varepsilon }^{2}}{\text{/}}2)d_{0}^{2} + 2{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}{{d}_{1}}q_{0}^{2} + \\ + \;6{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}{{d}_{3}}q_{0}^{3} + c(1 + {{m}^{2}}){{d}_{1}}{{q}_{0}} = 0 \\ \end{gathered} $
(2.7)
$\begin{gathered} \left( { - \lambda - b} \right){{d}_{1}} + a\lambda (1 + {{m}^{2}})(2{{d}_{1}}{{q}_{0}} + 6{{d}_{3}}q_{0}^{2}) - b{{\varepsilon }^{2}}{{d}_{0}}{{d}_{1}} + \\ + \;16{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}{{d}_{2}}q_{0}^{2} + 2c(1 + {{m}^{2}}){{d}_{2}}{{q}_{0}} = 0 \\ \end{gathered} $
(2.8)
$\begin{gathered} \left( { - \lambda - b} \right){{d}_{2}} + 8a\lambda (1 + {{m}^{2}}){{d}_{2}}{{q}_{0}} - (b{{\varepsilon }^{2}}{\text{/}}2)({{d}_{1}}^{2} + 2{{d}_{0}}{{d}_{2}}) + \\ + \;{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}(8{{d}_{1}}{{q}_{0}} + 60{{d}_{3}}q_{0}^{2}) + c(1 + {{m}^{2}})\left( {{{d}_{1}} + 3{{d}_{3}}{{q}_{0}}} \right) = 0 \\ \end{gathered} $
(2.9)
$\begin{gathered} \left( { - \lambda - b} \right){{d}_{3}} + a\lambda (1 + {{m}^{2}})\left( {2{{d}_{1}} + 18{{d}_{3}}{{q}_{0}}} \right) - b{{\varepsilon }^{2}}\left( {{{d}_{0}}{{d}_{3}} + {{d}_{1}}{{d}_{2}}} \right) + \\ + \;40{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}{{d}_{2}}{{q}_{0}} + 2c(1 + {{m}^{2}}){{d}_{2}} = 0 \\ \end{gathered} $
(2.10)
$\begin{gathered} 6a\lambda (1 + {{m}^{2}}){{d}_{2}} - (b{{\varepsilon }^{2}}{\text{/}}2)(d_{2}^{2} + 2{{d}_{1}}{{d}_{3}}) + \\ + \;{\text{P}}ra{{({{m}^{2}} + 1)}^{2}}(6{{d}_{1}} + 114{{d}_{3}}{{q}_{0}}) + 3c(1 + {{m}^{2}}){{d}_{3}} = 0 \\ \end{gathered} $
(2.11)
$12a\lambda (1 + {{m}^{2}}){{d}_{3}} - b{{\varepsilon }^{2}}{{d}_{2}}{{d}_{3}} + 24{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}{{d}_{2}} = 0$
(2.12)
$ - (b{{\varepsilon }^{2}}{\text{/}}2){{d}_{3}}^{2} + 60{\text{Pr}}a{{({{m}^{2}} + 1)}^{2}}{{d}_{3}} = 0$.

Имеется десять наборов решений, полученных при решении семи алгебраических уравнений с помощью пакета Maple 15. Физический смысл имеет решение с гиперболическими функциями при q0 < 0. Такое решение описывает бегущий солитон, как указано в уравнении (2.5). Таким образом, решения с q0 > 0 можно отбросить. Кроме того, допустимое решение должно быть непротиворечиво по отношению ко всем предположениям, сделанным при выводе уравнения (2.3). Набор решений, удовлетворяющий этим требованиям, задается выражениями

(2.13)
$\begin{gathered} {{d}_{0}} = \frac{{15c}}{{{{\varepsilon }^{2}}b}}\sqrt {\frac{{c(1 + {{m}^{2}})}}{{{\text{P}}a}}} ,~\quad ~{{d}_{1}} = - \frac{{30c(1 + {{m}^{2}})}}{{{{\varepsilon }^{2}}b}},\quad ~~{{d}_{2}} = - \frac{{60\sqrt {{\text{Pr}}ac} }}{{{{\varepsilon }^{2}}b}}{{({{m}^{2}} + 1)}^{{\frac{3}{2}}}}~, \\ {{d}_{3}} = \frac{{120{\text{Pr}}a{{{({{m}^{2}} + 1)}}^{2}}}}{{{{\varepsilon }^{2}}b}},~\quad {{q}_{0}} = - \frac{c}{{4{\text{Pr}}a(1 + {{m}^{2}})}},~\quad ~\lambda = - 4\sqrt {\frac{{{\text{Pr}}c(1 + {{m}^{2}})}}{a}} ~,~ \\ a{{b}^{2}} = 16{\text{Pr}}c(1 + {{m}^{2}}){{\left( {\frac{{3c}}{{2P}} - 1} \right)}^{2}}. \\ \end{gathered} $

Для уравнения (2.13) необходимое условие имеет вид $3c{\text{/}}2{\text{Pr}} < 1$, что эквивалентно неравенству $3{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}2{{D}^{2}} < {\text{Pr}}$. Это условие выполнено при $D \gg 1$, где D определено как обратное число Экмана.

Следовательно, задавая значения параметров в соотношениях (2.13), физически допустимое решение для $\mathcal{H}$ мажет быть выражено в виде

(2.14)
$\mathcal{H}\left( \xi \right) = {{A}_{1}}\sec {{{\text{h}}}^{2}}\xi \left( {1 + \operatorname{t} {\text{h}}\xi } \right)$,
с амплитудой ${{A}_{1}} = 15{{R}_{{{\text{cr}}}}}{\text{/}}[2{{\varepsilon }^{2}}(2{\text{P}}r{{D}^{2}} - 3{{{\text{R}}}_{{cr}}})]$ и переменной бегущей волны ξ = $\sqrt {{{{\text{R}}}_{{cr}}}{\text{/}}4(1 + {{m}^{2}})\eta } (X$ + + $mY + 4P\sqrt {{{{\text{R}}}_{{cr}}}(1 + {{m}^{2}}){\text{/}}\eta } ~\tau )$. При ограничении Bη3/2 = $4\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}(1 + {{m}^{2}})} ~D({\text{Pr}} - 3{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}2{{D}^{2}})$ выражение (2.14) задает солитонное решение уравнения (1.1) для деформации верхней поверхности вращающегося слоя жидкости в присутствии тепловой конвекции. Отметим, что при определенных значениях параметров, входящих в систему уравнений, это ограничение может быть удовлетворено либо заданием параметра m, который является вещественной постоянной, или заданием H, т.е. глубины в нашей модели. Далее, чтобы получить выражение для относительной деформации $h\left( {x,y,t} \right) = \delta H{\text{/}}H$ с ограничением $\beta {{q}^{{3/2}}} = 4\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}(1 + {{m}^{2}})} ~D({\text{Pr}} - 3{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}2{{D}^{2}})$, используя соотношения $h\left( {x,y,t} \right) \approx {{\varepsilon }^{2}}\mathcal{H}\left( {X,Y,\tau } \right)$, $B \approx \beta {\text{/}}{{\varepsilon }^{3}}$ и $\eta \approx {{\varepsilon }^{2}}q$, уравнение (2.14) записывается приближенно в виде
(2.15)
$h\left( {x,y,t} \right) = {{A}_{2}}{\text{sec}}{{{\text{h}}}^{2}}\xi \left( {1 + \operatorname{t} {\text{h}}\xi } \right)$
с амплитудой ${{A}_{2}} = 15{\text{/}}[2(2{\text{Pr}}{{D}^{2}}{\text{/}}{{{\text{R}}}_{{{\text{cr}}}}} - 3)]$ и переменной ξ, имеющей вид ξ = $\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}4(1 + {{m}^{2}})q} (x$ + + $my + 4{\text{Pr}}\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}(1 + {{m}^{2}}){\text{/}}q} ~t)$. В уравнении (2.15) присутствуют два параметра: ${{{\text{R}}}_{{{\text{cr}}}}}{\text{/Pr}}{{D}^{2}}$ и $\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}q} $. Параметр ${{{\text{R}}}_{{{\text{cr}}}}}{\text{/Pr}}{{D}^{2}}$ отвечает за совместный эффект чисел Рэлея, Экмана и Прандтля. При заданном числе Прандтля этот параметр по сути описывает соотношение между архимедовой силой, обусловленной тепловой конвекцией, и силой Кориолиса, которая определяет амплитуду солитонноподобного решения. Соотношение (2.15) с соответствующим ограничением справедливо при ${{{\text{R}}}_{{{\text{cr}}}}}{\text{/Pr}}{{D}^{2}} \ll 1~$ и в этом случае эффект плавучести из-за тепловой конвекции сравнительно слабый. Чандрасекар [1] также отметил, что возросшее ${\Omega }$ препятствует возникновению тепловой конвекции. При достаточно больших значениях $D = 2{\Omega }\sin {{{\theta }}_{0}}{{H}^{2}}{\text{/}}\nu ~$ (число Экмана достаточно мало) критическое число Рэлея Rcr можно заменить его асимптотическим выражением ${{{\text{R}}}_{{{\text{cr}}}}} \approx 8.6956{{D}^{{4/3}}}$ (см. раздел 1) и, таким образом, получаем оценку ${{A}_{2}} \approx 15{\text{/}}4({\text{Pr}}{{D}^{2}}{\text{/}}{{{\text{R}}}_{{{\text{cr}}}}})\sim {{D}^{{ - 2/3}}}$. При $D \to \infty $ возмущение $h\left( {x,y,t} \right)$ стремится к нулю глобально. Более того, другое замечание, основывающееся на ограничении $\beta {{q}^{{3/2}}} = 4\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}(1 + {{m}^{2}})} ~D({\text{Pr}} - 3{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}2{{D}^{2}})$, состоит в том, что если β = 0, ограничение уже не будет выполняться, поскольку основное предположение ${{{\text{R}}}_{{{\text{cr}}}}}{\text{/Pr}}{{D}^{2}} \ll 1$ не выполняется. Таким образом, в случае $\beta = 0$ (на полюсах) решение больше не имеет силы.

Другой существенный параметр в уравнении (2.15) – это $\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}q} = \sqrt {{{{\text{R}}}_{{{\text{cr}}}}}{\text{/Pr}}} ~\left( {{\text{Fr/Re}}} \right)$, который олицетворяет совместный эффект чисел Рэлея, Фруда, Рейнольдса и Прандтля. Этот параметр представляет собой выражение соотношения между силой плавучести и силой тяжести при влиянии чисел Рейнольдса и Прандтля. Он также может быть истолкован как так называемая скорость накачки восполнения диссипативных потерь в долгоживущей крупномасштабной структуре из-за тепловой конвекции. Этот параметр определяет скорость солитоноподобной структуры. Очевидно, эффект тепловой конвекции, характеризуемый числом Рэлея Rcr, играет ключевую роль в генерации солитоноподобной структуры в крупномасштабном вращающемся слое жидкости. Отсутствие тепловой конвекции (т.е. Rcr = 0) приводит к тривиальному решению $h(x,y,t) = 0$, в котором как амплитуда, так и скорость равны нулю.

На основе квазигеострофического приближения можно оценить главные члены безразмерных компонент скорости, а именно ${{u}^{{\left( 0 \right)}}}$, ${{{v}}^{{\left( 0 \right)}}}$ и ${{w}^{{\left( 0 \right)}}}$. Оценки ${{u}^{{\left( 0 \right)}}}$, ${{{v}}^{{\left( 0 \right)}}}$ и ${{w}^{{\left( 0 \right)}}}$ имеют вид

(2.16)
${{u}^{{\left( 0 \right)}}} \approx - ~\frac{{~q}}{D}~~\frac{{\partial h}}{{\partial y}}~,\quad {{{v}}^{{\left( 0 \right)}}} \approx - ~\frac{{~q}}{D}~~\frac{{\partial h}}{{\partial x}},\quad {{w}^{{\left( 0 \right)}}} = 0.$

Таким образом, имеем

(2.17)
${{u}^{{\left( 0 \right)}}} = - ~\frac{{~q}}{D}{{A}_{2}}m\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}4(1 + {{m}^{2}})q} (1 - 2{\text{th}}\xi - 3{\text{t}}{{{\text{h}}}^{2}}\xi ){\text{sec}}{{{\text{h}}}^{2}}\xi ,$
(2.18)
${{v}^{{\left( 0 \right)}}} = - ~\frac{{~q}}{D}{{A}_{2}}\sqrt {{{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}4(1 + {{m}^{2}})q} (1 - 2{\text{th}}\xi - 3{\text{t}}{{{\text{h}}}^{2}}\xi ){\text{sec}}{{{\text{h}}}^{2}}\xi ,$
что описывает линию источника в поле скоростей, порожденную тепловой конвекцией вдоль линии бегущей волны ${\xi } = {\text{cosnt}}.$

2.2. Пример: атмосфера Юпитера

Поддержание крупномасштабных структур, таких как Большое Красное Пятно (БКП) в юпитерианской атмосфере является очень интересной задачей [18, 19]. В настоящем исследовании решение уравнения (1.1) в виде бегущей волны применяется к БКП в качестве примера. Солитоноподобная структура, связанная с тепловой конвекцией, может играть некоторую роль в поддержании БКП вместе с другими структурами типа зональных струй. У нас нет намерений дать объяснение такой уникальной структуры течения, поскольку тепловая конвекция сильно локализована в Большом Красном Пятне, так что в этом случае решение (2.15) с постоянной разностью температур (${\Theta }$) не совсем точное. Данные по Юпитеру, взятые из предыдущих исследований [8, 9, 29, 30], следующие: ${v} \approx {{10}^{8}}$ см2/с, ${\text{Pr}} \geqslant 1$, $\alpha \approx 0.01~1{\text{/K}}$, ${\Theta } \approx 10{\text{K}}$, ${\Omega } \approx 1.76 \times {{10}^{{ - 4}}}~$ рад/с, ${{{\theta }}_{0}} \approx 22^\circ $, ${{r}_{0}} \approx 69\,911~$ км и ${{\beta }_{0}} \approx 4.67 \times {{10}^{{ - 14}}}~$ см–1 с–1. Отметим, что широта БКП ${{\theta }_{0}} \approx 22^\circ $ в южном полушарии и $\nu $ представляет собой эффективную турбулентную вязкость для юпитерианской атмосферы.

Чтобы получить приемлемые результаты из решения (2.15), необходимо удовлетворить ограничению, в котором нужно задать достаточно большое значение D. Поэтому в настоящей модели нужно так определить глубину H, чтобы удовлетворить эти требования. Например, задавая вышеупомянутые данные для юпитерианской атмосферы, необходимо предположить, что $H \approx 3 \times {{10}^{5}}~$ м ($H \approx 300~$ км), что дает значение $D \approx 1200$, которое удовлетворяет ограничению при $m = 1$, ${\text{Pr}} \approx 5$ и $q \approx {{q}_{{{\text{cr}}}}} \approx 8.6956{{D}^{{4/3}}}{\text{/}}\alpha \Theta $, где ${{q}_{{{\text{cr}}}}} = {{{\text{R}}}_{{{\text{cr}}}}}{\text{/}}\alpha \Theta $. По этой причине в наших расчетах $m$ и H задаются равными 1 и $3 \times {{10}^{5}}~$ м соответственно. Отметим, что в разных моделях используются разные значения H для БКП. В моделях мелкой воды величина H было задана порядка 25 км [18, 19]. Напротив, в других моделях значение H задается порядка нескольких сотен километров [30]. В нашем случае выбранное значение H должно быть много меньше горизонтального размера БКП, чтобы квазигеострофическое приближение было справедливо.

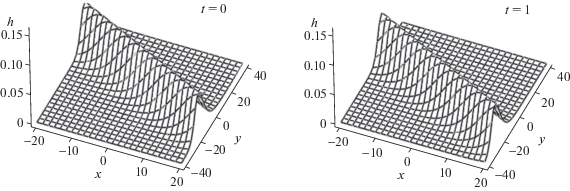
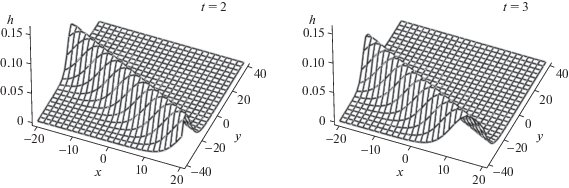
После подстановки данных для атмосферы Юпитера в решение (2.15) относительная деформация $h\left( {x,y,t} \right)$ задается выражением

(2.19)
$h\left( {x,y,t} \right) = {{A}_{3}}(1 + {\text{th}}{{\xi }_{3}} - {\text{t}}{{{\text{h}}}^{2}}{{\xi }_{3}} - {\text{t}}{{{\text{h}}}^{3}}{{\xi }_{3}})$
где ${{A}_{3}} = 0.0595$ и ${{\xi }_{3}} = 0.1118\left( {x + y + 8.94434t} \right)$. Горизонтальные размеры Большого Красного Пятна, которые, как известно [18], составляют $12~\,000~\;{\text{км}} \times 25\,~000$ км, должны быть приведены к безразмерному виду. Таким образом, безразмерная область задается системой неравенств $ - 20 \leqslant x \leqslant 20$ и $ - 41.6 \leqslant y \leqslant 41.6$. Аналогично, безразмерное время t = 1 соответствует 1.43 года. На рис. 3 и 4 показана временная эволюция h(x, y), указывающая на солитоноподобное поведение h(x, y) с медленным затуханием по амплитуде. Результаты, полученные для h(x, y), находятся в близком согласии с одномерными результатами, численно полученными Тихомоловым [8]. Единственное расхождение касается амплитуды h из-за использования разных данных для безразмерных параметров.

Рис. 3.

Временная эволюция относительной деформации $h = \left( {x,y} \right)$ от t = 0 до t = 1 (t = 1 соответствует 1.43 года)

Рис. 4.

Временная эволюция относительной деформации $h = \left( {x,y} \right)$ от t = 2 до t = 3

ВЫВОДЫ

Выведено эволюционное уравнение для деформации верхней границы крупномасштабного вращающегося слоя жидкости при наличии тепловой конвекции. Основной нелинейный член в эволюционном уравнении, связанный с бета-эффектом, определяет существование солитоноподобного решения. Тепловая конвекция является первопричиной диффузии, тесно связанной с накачкой энергии для пополнения диссипативных потерь при поддержании долгоживущей структуры. Диффузионный член высшего порядка и дисперсный член стремятся ослабить развитие деформации верхней границы. На базе метода, использующего вспомогательное уравнение Риккати, получено физически допустимое аналитическое (солитоноподобное) решение, справедливое при достаточно большом значении параметра D, представляющего собой обратное число Экмана E (т.е. при достаточно малом числе Экмана). Тем не менее в предельном случае при $D \to \infty $ деформация верхней границы, возникающая из-за конвекции, стремится к нулю повсюду и, таким образом, увеличение угловой скорости стремится подавить влияние тепловой конвекции. В качестве иллюстративного примера, полученное аналитическое решение использовано для рассмотрения Большого Красного Пятна на Юпитере.

Список литературы

  1. Chandrasekhar S. The instability of layer of fluid heated below subject to Coriolis forces // Proc. R. Soc. London A. 1953. V. 217. P. 306–327.

  2. Zhang K., Roberts P.H. Thermal inertial waves in a rotating fluid layer: exact and asymptotic solutions // Phys. Fluids. 1997. V. 9. P. 1980–1987.

  3. Петвиашвили В.И. Красное пятно Юпитера и дрейфовый солитон в плазме // Письма в ЖЭТФ. 1980. Т. 32. № 11. С. 632–635.

  4. Tan B., Boyd J.P. Dynamics of the Flierl-Petviashvili monopoles in a barotropic model with topographic forcing // Wave Motion. 1997. V. 26. P. 239–251.

  5. Qiang Z., Yuan Z., Shi-Kuo L. Two-dimensional Rossby waves: Exact solutions to Petviashvili equation // Commun. Theor. Phys. 2006. V. 45. P. 414–416.

  6. Busse F.H. Thermal instabilities in rapidly rotating layer systems // J. Fluid Mech. 1970. V. 44. P. 441–460.

  7. Busse F.H. Convection driven zonal flows and vortices in the major planets // Chaos. 1994. V. 4. P. 123–134.

  8. Тихомолов Е.М. Поддержание вихревых структур в подогреваемом снизу вращающемся слое жидкости // Письма в ЖЭТФ. 1994. Т. 59. № 3. С. 155–158.

  9. Tikhomolov E.M. Short-scale convection and long-scale deformationally unstable Rossby wave in a rotating fluid layer heated from below // Phys. Fluids. 1996. V. 8. P. 3329–3337.

  10. Sun Z.P., Schubert G., Glatzmaier G.A., Banded surface flow maintained by convection in a model of rapidly rotating giant planets // Science. 1993. V. 260. P. 661–664.

  11. Gilman P.A. Nonlinear Boussinesq convective model for large scale solar circulations // Sol. Phys. 1972. V. 27. P. 3–26.

  12. Gilman P.A., Miller J. Nonlinear convection of a compressible fluid in a rotating spherical shell // Astrophys. J. Suppl. 1986. V. 61. P. 585–608.

  13. Bekir A. New exact traveling wave solutions for regularized long-wave, Phi-Four and Drinfeld-Sokolov equation // Int. J. Nonlinear Sci. 2008. V. 6. P. 46–52.

  14. Sirendaoreji S. Auxiliary equation method and new solutions of Klein-Gordon equation // Chaos, Solitons & Fractals. 2007. V. 31. P. 943–950.

  15. Pinar Z., Özis T. Solutions of modified equal width equation by means of the auxiliary equation with a sixth-degree nonlinear term // in Proc. Sixth ICMSEM, Lecture Notes in Electrical Engineering. 2013. V. 185. P. 139–148.

  16. Yong C., Biao L., Hong-King Z. Generalized Riccati equation expansion method and its application to the Bogoyavlenskii’s generalized breaking soliton equation // Chin. Phys. Soc. 2003. V. 12. P. 940–946.

  17. Feng D. Exact solutions of Kuramoto-Sivashinsky equation // Int. J. Education and Management Engineering. 2012. V. 2. P. 61–66.

  18. Nezlin M.V., Snezhkin E.N., Rossby Vortices, Spiral Structures, Solitons: Astrophysics and Plasma Physics in Shallow Water Experiments, Berlin: Springer-Verlag, 1993.

  19. Nezlin M.V. Rossby solitary vortices on giant planets and in the laboratory // Chaos. 1994. V. 4. P. 187–202.

  20. Pedlosky J. Geophysical Fluid Dynamics. New York: Springer-Verlag, 1987.

  21. Pokhotelov O.A., Kaladze T.D., Shukla P.K., Stenflo L. Three-dimensional solitary vortex structures in the upper atmosphere // Phys. Scr. 2001. V. 64. P. 245–252.

  22. Kukharkin N., Orszag S.A. Generation and structure of Rossby vortices in rotating fluids // Phys. Rev. E. 1996. V. 54. P. R4524–R4527.

  23. Julien K., Knobloch E., Werne J. A new class of equations for rotationally constrained flows // Theor. Comp. Fluid Dyn. 1998. V. 11. P. 251–261.

  24. King E.M., Stellmach S., Buffett B. Scaling behavior in Rayleigh-Bénard convection with and without rotation // J. Fluid Mech. 2012. V. 717. P. 449–471.

  25. Aubert J., Gillet N., Cardin P. Quasigeostrophic models of convection in rotating spherical shells // Geochem. Geophys. Geosyst. 2003. V. 4. P. 1052–1071.

  26. Cardin P., Olson P. Chaotic thermal convection in a rapidly rotating spherical shell: consequences for flow in the outer core // Phys. Earth Planet. Inter. 1994. V. 82. P. 235–259.

  27. Gillet N., Jones C.A. The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder // J. Fluid Mech. 2006. V. 554. P. 343–369.

  28. Newell A.C., Whitehead J.A. Finite bandwidth, finite amplitude convection // J. Fluid Mech. 1969. V. 38. P. 279–303.

  29. Stone P.H., Baker D.J. Concerning the existence of Taylor columns in atmosphere // Q. J. Royal Meteorol. Soc. 1968. V. 94. P. 576–580.

  30. Flasar F.M., Conrath B.J., Piragila J.A., Clark P.C., French R.G., Gierasch P.J. Thermal structure and dynamics of the Jovian atmosphere. I. The Great Red Spot // J. Geophys. Res. 1981. V. 86. P. 8759–8767.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал