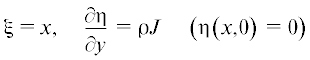Известия РАН. Механика жидкости и газа, 2019, № 6, стр. 145-150

ПОДОБИЕ ТЕЧЕНИЙ МНОГОАТОМНОГО ГАЗА В КИНЕТИЧЕСКОМ УДАРНОМ СЛОЕ

А. Л. Анкудинов^*

Центральный аэрогидродинамический институт (ЦАГИ) им. Жуковского
Московская обл., Жуковский, Россия

Поступила в редакцию 27.12.2018
После доработки 01.03.2019
Принята к публикации 12.03.2019

DOI: 10.1134/S0568528119050025

Аннотация

Рассмотрена двумерная задача высокоскоростного неравновесного обтекания поверхности однородным многоатомным газом, сформулированная на базе макрокинетических 13-моментных уравнений с использованием приближения двуслойного тонкого вязкого ударного слоя (ТВУС) около нетонких тел. Предложен класс переменных подобия, которые позволяют исследуемую сложную кинетическую проблему свести к хорошо изученной навье-стоксовской задаче ТВУС.

Ключевые слова: многоатомный однородный газ, неравновесность по внутренним и поступательным степеням свободы молекул, приближение тонкого вязкого ударного слоя, 13-моментные уравнения кинетической теории газов

Изучение высокоскоростных неравновесных течений разреженного газа является важной для практики проблемой аэротермодинамики высоких скоростей и больших высот. Связано это, прежде всего, с потребностью тепловой защиты гиперзвуковых и воздушно-космических летательных аппаратов (проблема входа в атмосферу, суборбитальный полет и др.).

В [1–3] была показана возможность адекватно описывать неравновесное течение в гиперзвуковом тонком ударном слое (узкой области, расположенной между набегающим высокоскоростным невозмущенным потоком и обтекаемой поверхностью) при посредстве макроскопических моментных уравнений кинетической теории газов в их тонкослойной интерпретации ТВУС (модель гиперзвукового кинетического тонкого вязкого ударного слоя). При этом в статьях [1, 3] рассматривался многоатомный однокомпонентный газ (неравновесность по внутренним и поступательным степеням свободы), а в [2] – одноатомный газ (поступательная неравновесность), для которого там же получена и корреляция решения кинетической задачи ТВУС с решением для навье-стоксовского ТВУС. В [4] для случая многоатомного однородного газа и условий (как в [1]) легкого обмена энергией между внутренними и поступательными степенями свободы его частиц был сформулирован принцип подобия течений в кинетическом и навье-стоксовском ТВУС с использованием переменных Мизеса.

1. КИНЕТИЧЕСКАЯ ЗАДАЧА ТВУС

Макрокинетические 13-моментные уравнения, используемые при изучении высокоскоростного обтекания тел, позволяют описывать течение многоатомного газа с сильным отклонением его состояния от равновесного по внутренним и поступательным степеням свободы. Тонкослойная версия этих уравнений в рамках двуслойного приближения тонкого вязкого ударного слоя и предположения о быстром обмене энергией между внутренними и поступательными степенями свободы частиц, будучи записана (для двумерного течения) в физических переменных ($x,y$), имеет следующий вид ([1–3]):

$\rho u\frac{{\partial u}}{{\partial x}} + \rho v\frac{{\partial u}}{{\partial y}} = \frac{\partial }{{\partial y}}\frac{1}{{\operatorname{Re} }}\frac{{{{P}_{{22}}}}}{p}\mu \frac{{\partial u}}{{\partial y}}$

${\rho }{{u}^{{\text{2}}}}\frac{{\text{1}}}{{{{R}_{w}}}}{\text{ = }}\frac{{\partial {{P}_{{22}}}}}{{\partial y}}$

(1.1)

$\frac{{\partial {{r}^{\nu }}\rho u}}{{\partial x}} + \frac{{\partial {{r}^{\nu }}\rho v}}{{\partial y}}{\text{ = 0}}$

$p = 2{\varepsilon \rho }h$

$\mu = \mu \left( h \right){\text{;}}\quad H = h + \frac{{{{u}^{2}}}}{2}$

$\frac{p}{{{{P}_{{22}}}}} = 1 + \frac{2}{{3\alpha }}{{\left( {\frac{1}{{\operatorname{Re} }}\frac{\mu }{p}\frac{{\partial u}}{{\partial y}}} \right)}^{2}}$

Условия на внешней границе ударного слоя при $y = {{y}_{e}}\left( x \right)$

${{{\rho }}_{\infty }}{{v}_{\infty }}\left( {u - {{u}_{\infty }}} \right){\text{ = }}\frac{{\text{1}}}{{{\text{Re}}}}\frac{{{{P}_{{22}}}}}{p}{\mu }\frac{{\partial u}}{{\partial y}}$

(1.2)

${{P}_{{{\text{22}}}}} = {{{\rho }}_{\infty }}v_{\infty }^{{\text{2}}}$

${{{\rho }}_{\infty }}{{v}_{\infty }}\left( {H - {{H}_{\infty }}} \right){\text{ = }}\frac{{\text{1}}}{{{\text{RePr}}}}\frac{{{{P}_{{22}}}}}{p}{\mu }\frac{\partial }{{\partial y}}\left[ {H + \left( {\Pr - 1} \right)\frac{{{{u}^{{\text{2}}}}}}{2}} \right]$

${\rho }v{\text{ = }}{{{\rho }}_{\infty }}{{v}_{\infty }}$

Условия на поверхности тела при y = 0 (стенка заданной температуры)

(1.3)

$u = v{\text{ = 0,}}\quad H - {{H}_{w}}(x{\text{) = 0}}$

Изначально неизвестная величина отхода скачка ${{y}_{e}}\left( x \right)$ должна определяться в процессе решения задачи.

Здесь приняты обозначения: $xL{\text{*}}$, $yL{\text{*}}$ – расстояния, отсчитываемые в плоскости рассмотрения от передней критической точки затупленного тела вдоль его поверхности и от поверхности вдоль нормали к ней; $uU_{\infty }^{ * }{\text{,}}\,vU_{\infty }^{ * }$ – компоненты скорости в направлениях x и y; ${{R}_{w}}L{\text{*}}$ – радиус продольной кривизны поверхности; $rL{\text{*}}$ – расстояние от оси (плоскости) симметрии осесимметричного (плоского) тела до его поверхности; 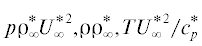– давление, плотность и температура; $hU{{_{\infty }^{{\text{*}}}}^{2}},HU{{_{\infty }^{{\text{*}}}}^{{\text{2}}}}$ – удельные статическая и полная энтальпии; ${\mu \mu }_{0}^{{\text{*}}}$ – коэффициент вязкости; ${{P}_{{22}}} = {\text{ }}p + {{p}_{{{\text{22}}}}}$, где ${{p}_{{{\text{22}}}}}{\rho }_{\infty }^{{\text{*}}}U{{_{\infty }^{{\text{*}}}}^{{\text{2}}}}$ – компонента девиаторной части тензора напряжений ${{p}_{{ij}}}{\rho }_{\infty }^{{\text{*}}}U{{_{\infty }^{{\text{*}}}}^{2}}$ (i, j = 1, 2) при индексах 1 и 2, ассоциируемых с направлениями $x$ и $y$; ${{q}_{2}}{\rho }_{\infty }^{{\text{*}}}U{{_{\infty }^{{\text{*}}}}^{{\text{3}}}}$ – компонента вектора теплового потока в поперечном ($y$) направлении; $\varepsilon = \left( {\gamma - 1} \right){\text{/}}2\gamma $, где $\gamma = c_{p}^{{\text{*}}}{\text{/}}c_{v}^{{\text{*}}}$ – отношение удельных теплоемкостей, $c_{p}^{{\text{*}}}$ и $c_{v}^{{\text{*}}}$ – удельные теплоемкости газа при постоянных давлении и объеме; Re = 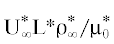– число Рейнольдса; $\Pr = c_{p}^{{\text{*}}}\mu \mu _{0}^{{\text{*}}}{\text{/}}\lambda {\text{*}}$ – число Прандтля; ${\mu }_{0}^{{\text{*}}}$ – значение коэффициента вязкости ${\mu *}$ при температуре торможения $T_{0}^{{\text{*}}}$ набегающего потока; ${\lambda *}$ – коэффициент теплопроводности; $L{\text{*}}$ – характерный линейный размер (например, радиус кривизны носка, т.е. $L* \equiv {{(R_{w}^{{\text{*}}})}_{{x = 0}}}$); $U_{\infty }^{{\text{*}}}$ – скорость набегающего невозмущенного потока; ${\rho }_{\infty }^{{\text{*}}}$ – плотность в набегающем невозмущенном потоке; ${\alpha = \alpha (T)}$ – отношение времен релаксации при упругих и неупругих столкновениях молекул; ${\nu }$ – безразмерный параметр, $\nu {\text{ = 0}}$ и 1 в плоской и осесимметричной задачах. Звездочкой отмечены размерные величины. Индексы $w\,{\text{,}}\,e\,{\text{,}}\,\infty $ относятся к величинам на поверхности тела, на внешней границе ударного слоя и в невозмущенном набегающем потоке.

Введены новые переменные согласно соотношениям

(1.4)

$\frac{{\partial U}}{{\partial y}} = { \rho }u\quad \left( {U\left( {x{\text{,0}}} \right){\text{ = 0}}} \right)$

(1.5)

Здесь ${\xi }$, ${\eta }$ – новые продольная и поперечная координаты; величина J в (1.5) предполагается некоторой функцией от величин $C,\,x,\,u,\,H,\,U$ (где $C{\text{ = const}}$), т.е. функцией вида

(1.6)

$J{\text{ }} = {\text{ }}J\left( {C,x,u,H,U} \right)$

В новых переменных (${\xi ,\eta }$,) ((1.4)–(1.6)) исследуемая кинетическая задача ТВУС (1.1)–(1.3) принимает вид

$\begin{gathered} u\frac{{\partial u}}{{\partial {\xi }}} - \frac{{\partial U}}{{\partial \xi }}\frac{{\partial u}}{{\partial {\eta }}}J - \nu \frac{1}{r}\frac{{dr}}{{dx}}U\frac{{\partial u}}{{\partial {\eta }}}J{\text{ = }}\frac{{\text{1}}}{{{\text{Re}}}}J\frac{\partial }{{\partial {\eta }}}{{P}_{{{\text{22}}}}}{ \mu }\left[ {\frac{{\rho }}{p}} \right]J\frac{{\partial u}}{{\partial {\eta }}} \\ \frac{{\partial {{P}_{{22}}}}}{{\partial {\eta }}}J{\text{ }} = \frac{{{{u}^{2}}}}{{{{R}_{w}}}}. \\ \end{gathered} $

(1.7)

$u\frac{{\partial H}}{{\partial {\xi }}} - \frac{{\partial U}}{{\partial {\xi }}}\frac{{\partial H}}{{\partial {\eta }}}J - \nu \frac{1}{r}\frac{{dr}}{{dx}}U\frac{{\partial H}}{{\partial {\eta }}}J{\text{ = }}\frac{{\text{1}}}{{{\text{Re Pr}}}}J\frac{\partial }{{\partial {\eta }}}{{P}_{{{\text{22}}}}}{ \mu }\left[ {\frac{{\rho }}{p}} \right]J\frac{\partial }{{\partial {\eta }}}\left[ {H + ({\text{Pr}} - 1)\frac{{{{u}^{{\text{2}}}}}}{{\text{2}}}} \right].$

$\frac{{\partial U}}{{\partial {\eta }}}J{\text{ }} = {\text{ }}u$

$\frac{p}{\rho } = 2\varepsilon h;\quad \mu = \mu \left( h \right);\quad H = h + \frac{{{{u}^{2}}}}{2}.$

(1.8)

$\frac{p}{{{{P}_{{22}}}}} = 1 + \frac{2}{{3\alpha }}{{\left( {\frac{1}{{\operatorname{Re} }}\mu \left[ {\frac{\rho }{p}} \right]J{\text{ }}\frac{{\partial u}}{{\partial \eta }}} \right)}^{{\text{2}}}}$

Условия на внешней границе ТВУС при ${\eta = }{{{\eta }}_{{\text{e}}}}$

${{{\rho }}_{\infty }}{{v}_{\infty }}\left( {u - {{u}_{\infty }}} \right) = \frac{{\text{1}}}{{{\text{Re}}}}{{P}_{{{\text{22}}}}}{\mu }\left[ {\frac{{\rho }}{p}} \right]J\frac{{\partial u}}{{\partial {\eta }}};\quad {{P}_{{{\text{22}}}}}{\text{ = }}{{{\rho }}_{\infty }}v_{\infty }^{2}$;

(1.9)

${{{\rho }}_{\infty }}{{v}_{\infty }}\left( {H - {{H}_{\infty }}} \right){\text{ = }}\frac{{\text{1}}}{{{\text{Re}}\,{\text{Pr}}}}{{P}_{{{\text{22}}}}}{\mu }\left[ {\frac{{\rho }}{p}} \right]{\text{J }}\frac{\partial }{{\partial {\eta }}}\left[ {H - \left( {{\text{1}} - {\text{Pr}}} \right)\frac{{{{u}^{{\text{2}}}}}}{{\text{2}}}} \right]$

$\frac{{\partial U}}{{\partial {\xi }}}{\text{ + }}\frac{u}{J}\left( {\frac{{\partial {{{\eta }}_{{\text{e}}}}}}{{\partial {\xi }}}} \right){\text{ + }}{{{\rho }}_{\infty }}{{v}_{\infty }}{\text{ = 0}}$

Условия на стенке при ${\eta = 0}$

(1.10)

$u = {{u}_{w}} = 0;\quad H = {{H}_{w}} = {\text{const;}}\quad {\text{U = 0}}$

2. НАВЬЕ-СТОКСОВСКАЯ ЗАДАЧА ТВУС

Соотношения навье-стоксовской версии ТВУС (уравнения, краевые условия) в физических переменных могут быть получены формально опусканием последнего уравнения в кинетической системе (1.1) и заменой в остальных соотношениях кинетической задачи (1.1)–(1.3) величины $p{\text{/}}{{P}_{{{\text{22}}}}}$ на $p{\text{/}}{{P}_{{{\text{22}}}}} = 1$.

В новых переменных (${\xi ,\eta }$) навье-стоксовская версия ТВУС приобретает вид.

Уравнения

$u\frac{{\partial u}}{{\partial {\xi }}} - \frac{{\partial U}}{{\partial {\xi }}}\frac{{\partial u}}{{\partial {\eta }}}J - \nu \frac{1}{r}\frac{{dr}}{{dx}}U{\text{ }}\frac{{\partial u}}{{\partial {\eta }}}J{\text{ = }}\frac{{\text{1}}}{{{\text{Re}}}}J\frac{\partial }{{\partial {\eta }}}{\mu \rho }J{\text{ }}\frac{{\partial u}}{{\partial {\eta }}}$

$\frac{{\partial p}}{{\partial \eta }}J{\text{ }} = \frac{{{{u}^{2}}}}{{{{R}_{w}}}}$

(2.1)

$\begin{gathered} u\frac{{\partial H}}{{\partial {\xi }}} - \frac{{\partial U}}{{\partial {\xi }}}\frac{{\partial H}}{{\partial {\eta }}}J - \nu \frac{1}{r}\frac{{dr}}{{dx}}U\frac{{\partial H}}{{\partial {\eta }}}J{\text{ = }} \\ = \frac{1}{{\operatorname{Re} \Pr }}J\frac{\partial }{{\partial {\eta }}}{\mu \rho }J\frac{\partial }{{\partial {\eta }}}\left[ {H{\text{ + }}\left( {{\text{Pr}} - {\text{1}}} \right)\frac{{{{u}^{{\text{2}}}}}}{{\text{2}}}} \right] \\ \end{gathered} $

$\frac{{\partial U}}{{\partial {\eta }}}J{\text{ = }}u$

$\frac{p}{\rho } = 2\varepsilon h\,;\quad \mu = \mu \left( h \right);\quad H = h + \frac{{{{u}^{2}}}}{2}$

Условия на внешней границе при ${\eta = }{{{\eta }}_{e}}$

${{{\rho }}_{\infty }}{{v}_{\infty }}\left( {u - {{u}_{\infty }}} \right){\text{ = }}\frac{{\text{1}}}{{{\text{Re}}}}{\mu \rho }J\frac{{\partial u}}{{\partial {\eta }}};\quad p{\text{ = }}{{{\rho }}_{\infty }}v_{\infty }^{2}$;

(2.2)

${{{\rho }}_{\infty }}{{v}_{\infty }}\left( {H - {{H}_{\infty }}} \right) = \frac{{\text{1}}}{{{\text{RePr}}}}{\mu \rho }J\frac{\partial }{{\partial {\eta }}}\left[ {H - \left( {{\text{1}} - {\text{Pr}}} \right)\frac{{{{u}^{{\text{2}}}}}}{{\text{2}}}} \right]$

$\frac{{\partial U}}{{\partial {\xi }}}{\text{ + }}\frac{u}{J}\left( {\frac{{\partial {{{\eta }}_{{\text{e}}}}}}{{\partial {\xi }}}} \right) + {{{\rho }}_{\infty }}{{v}_{\infty }} = 0$

Условия на стенке задачи при ${\eta = 0}$

(2.3)

$u = {{u}_{w}} = 0;\quad H = {{H}_{w}} = {\text{const}};\quad U{\text{ }} = {\text{ }}0$;

В новых переменных (${\xi ,\eta }$), введенных формулами (1.4)–(1.6), задача может быть переписана еще и удобным для анализа, эквивалентным образом, а именно повторяющим трактовку (1.7)–(1.10), где (1.8) заменено на соотношение $p{\text{/}}{{P}_{{{\text{22}}}}} = 1$.

3. ПОДОБИЕ

Представление кинетического ТВУС в переменных (${\xi ,\eta }$,) (см. п. 1) дает возможность сформулировать для вычисления существенной части его неизвестных величин, а именно кинетических величин U, u, H и P₂₂, замкнутую краевую задачу (уравнения и краевые условия), составленную из соотношений (1.7)–(1.10) с отброшенным уравнением (1.8).

Задача навье-стоксовского ТВУС, формализованная под кинетическую ТВУС-задачу, отличается от задачи кинетического ТВУС, как таковой, только лишь уравнением, задающим в полной системе уравнений ТВУС величину $p{\text{/}}{{P}_{{{\text{22}}}}}$.

Аналогично случаю кинетического варианта ТВУС, навье-стоксовский ТВУС позволяет выделить структурно замкнутую задачу для определения своих (т.е. здесь уже навье-стоксовских) величин (U, u, H)_n и ${{{\text{(}}{{P}_{{22}}})}_{n}}$, и эта последняя задача полностью идентична кинетической задаче ТВУС для вычисления кинетических величин (U, u, H)_k и ${{{\text{(}}{{P}_{{22}}})}_{k}}$ (индексы k и n характеризуют принадлежность величин соответственно к кинетической и навье-стоксовской задачам ТВУС).

Отсюда

${{(U,u,H)}_{k}},\quad {{({{P}_{{22}}})}_{k}}~ = {{(U,u,H)}_{n}},\quad {{({{P}_{{22}}})}_{n}}$

а поскольку для навье-стоксовского ТВУС имеет место $p{\text{/}}{{P}_{{{\text{22}}}}} = 1$, т.е. ${{{\text{(}}{{P}_{{22}}})}_{n}}$ = ${{{\text{(}}p)}_{n}}$, то соответственно

(3.1)

${{(U,u,H)}_{k}},\quad {{({{P}_{{22}}})}_{k}}~ = {{(U,u,H)}_{n}},\quad {{(p)}_{n}}$

Неучтенные же в (3.1) такие искомые величины кинетической и навье-стоксовской задач ТВУС, как давление $p$ и плотность ${\rho }$, соответственно оказываются связанными между собой следующим образом:

(3.2)

$\begin{gathered} {{\left( p \right)}_{k}} = \left[ {1 + \frac{2}{{3\alpha }}{{{\left( {\frac{1}{{\operatorname{Re} }}\mu \left[ {\frac{\rho }{p}} \right]{\text{ }}J{\text{ }}\frac{{\partial u}}{{\partial \eta }}} \right)}}^{2}}} \right]{{\left( p \right)}_{n}} \\ {{\left( \rho \right)}_{k}} = \left[ {1 + \frac{2}{{3\alpha }}{{{\left( {\frac{1}{{\operatorname{Re} }}\mu \left[ {\frac{\rho }{p}} \right]{\text{ }}J{\text{ }}\frac{{\partial u}}{{\partial \eta }}} \right)}}^{2}}} \right]{{\left( \rho \right)}_{n}} \\ \end{gathered} $

Соотношения эти получаются из уравнения (1.8), задающего величину $p{\text{/}}{{P}_{{{\text{22}}}}}$ в полной кинетической задаче ТВУС, при использовании уравнений состояния для обеих задач.

В равенствах (3.1) и (3.2) представлены соответствия подобия для компонентов решений кинетической и навье-стоксовской задач ТВУС, имеющих коэффициент подобия, равный 1 (единице) в (3.1), и функциональный коэффициент подобия, равный

$1 + \frac{2}{{3\alpha }}{{\left( {\frac{1}{{\operatorname{Re} }}\mu \left[ {\frac{\rho }{p}} \right]{\text{ }}J{\text{ }}\frac{{\partial u}}{{\partial \eta }}} \right)}^{2}}$

в формуле (3.2). Последний коэффициент подобия (тот, что в (3.2)) построен на основе функций, переходящих из одной задачи в другую с единичным коэффициентом подобия (3.1).

Соотношения подобия (3.1), (3.2) позволяют полностью выстроить решение кинетической задачи ТВУС (1.7)–(1.10), используя решение для навье-стоксовского ТВУС (2.1)–(2.3) (т.е. отправляясь от решения задачи ТВУС, базирующейся на приближении Навье–Стокса).

Соотнесение же кинетического решения ТВУС физическим координатам (до настоящего момента, начиная от формул (1.7), речь шла о представлении задачи ТВУС в переменных подобия (${\xi },{\eta }$)) происходит c привлечением обращенного уравнения (1.5), задающего преобразование подобия задачи

(3.3)

$\frac{{\partial y}}{{\partial \eta }} = {{\left( {\rho {\text{ }}J} \right)}^{{ - 1}}}\quad \left( {y\left( {\eta = 0} \right) = 0} \right)$

где величина ${\rho } = {{\left( {\rho } \right)}_{k}}$.

Помимо (3.1) и (3.2), в переменных подобия имеют место еще и такие соответствия

(3.4)

${{\left( {{{р}_{{12}}}} \right)}_{k}} = {{\left( {{{р}_{{12}}}} \right)}_{n}}{\text{,}}\quad {{\left( {{{q}_{2}}} \right)}_{k}} = {{\left( {{{q}_{2}}} \right)}_{n}}$

Равенства в (3.4) следуют непосредственно из соотношений, попарно связывающих эти величины в физических переменных, вида

${{\left( {{{р}_{{12}}}} \right)}_{k}} = {{\left( {{{р}_{{12}}}} \right)}_{n}}{{\left( {\frac{{{{P}_{{22}}}}}{р}} \right)}_{k}},\quad {{\left( {{{q}_{2}}} \right)}_{k}} = {{\left( {{{q}_{2}}} \right)}_{n}}{{\left( {\frac{{{{P}_{{22}}}}}{р}} \right)}_{k}}.$

Соотношения (3.4), рассматриваемые в переменных подобия для координатной линии η = 0, соответствующей поверхности (здесь p₁₂ – трение на стенке, q₂ – тепловой поток на стенке), свидетельствуют о совпадении на поверхности обтекаемого тела величин трения и теплового потока соответственно для обеих задач кинетического и навье-стоксовского ТВУС. Ранее на такой факт для ТВУС в одноатомном газе (поступательная неравновесность) указывалось Ченгом ([2]).

Кинетический ТВУС по формальным признакам математически более сложен, чем навье-стоксовский: в нем появляется новая (дополнительная) неизвестная, существенно увеличивается нелинейность коэффициента перед старшей производной в основных уравнениях, усиливается взаимосвязь уравнений системы. Потому представляется более естественным и простым заменять решение сложной задачи (кинетического ТВУС) анализом проблемы более простой (навье-стоксовского ТВУС) и через нее выходить на решение сложной.

Установленный принцип подобия дает возможность заменить решение усложненно нелинейной (по сравнению с навье-стоксовским ТВУС) исходной кинетической задачи анализом хорошо апробированной, существенно более простой задачи навье-стоксовского ТВУС. Инструмент подобия в значительной степени упрощает изучение кинетической проблемы ТВУС, представляя собой эффективный способ исследования неравновесных высокоскоростных течений многоатомного газа. Отметим, что предлагаемые переменные подобия задачи, удобные для анализа кинетического ТВУС, включают, как частные случаи, известные переменные Лиза–Дородницына и переменные Мизеса.

Итак, в статье констатируется факт существования широкого класса переменных подобия для рассматриваемой задачи кинетического ТВУС в многоатомном газе, указаны характерные признаки переменных подобия, прописан механизм реализации свойств подобия при переходе от решения навье-стоксовского ТВУС к решению задачи для кинетического ТВУС.

Принцип подобия позволяет в полном объеме выстроить решение задачи кинетического ТВУС на основе навье-стоксовского решения ТВУС ((3.1)–(3.4)).

ЗАКЛЮЧЕНИЕ

Для описания высокоскоростного неравновесного двумерного течения многоатомного однокомпонентного газа в рамках модели кинетического тонкого вязкого ударного слоя, сформулированной на базе кинетического 13-моментного приближения кинетической теории газов, предложены новые переменные, выявляющие связь кинетической интерпретации двуслойной ТВУС-проблемы с навье-стоксовским ее представлением.

В новых переменных реализуется подобие решения задачи кинетического ТВУС для молекулярного газа решению задачи навье-стоксовского ТВУС. Введенные переменные дают возможность существенно упростить анализ новой сложной кинетической задачи ТВУС для многоатомного газа, заменив его (анализ) исследованием вычислительно хорошо освоенной и значительно менее трудной традиционной навье-стоксовской задачи ТВУС.

Сформулировано преобразование подобия для переменных задачи ТВУС в многоатомном газе, важное при практическом конструировании проблемно-ориентированных (т.е. учитывающей специфику конкретной исследуемой проблемы) переменных в различных прикладных задачах приближения ТВУС. Описан механизм реализации подобия при построении решения задачи кинетического ТВУС.

Подтвержден новыми средствами ранее сделанный вывод: учет кинетики неравновесного течения многоатомного газа в ТВУС не сказывается на трении и теплообмене на поверхности обтекаемого тела (имеет место совпадение этих характеристик течения молекулярного газа в кинетическом ТВУС с соответствующими величинами на стенке для навье-стоксовского ТВУС).

Список литературы

Кузнецов М.М., Никольский В.С. Кинетический анализ гиперзвуковых вязких течений многоатомного газа в тонком трехмерном ударном слое // Ученые записки ЦАГИ. 1985. Т. 16, № 3. С. 38–49.
Cheng H.K. The viscous shock layer problem revisited // Int. Conf. of Research in Hypersonic Flows and Hypersonic Technologies. Sept. 19–21, 1994, Zhukovsky.
Кузнецов М.М., Липатов И.И., Никольский В.С. Реология течения разреженного газа в гиперзвуковом ударном и пограничном слоях // Изв. РАН. МЖГ. 2007. № 5. С. 189–196.
Анкудинов А.Л. Тонкий вязкий ударный слой с учетом эффектов разреженности газа // Ученые записки ЦАГИ. 2007. Т. 38. № 3–4. С. 88–93.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал