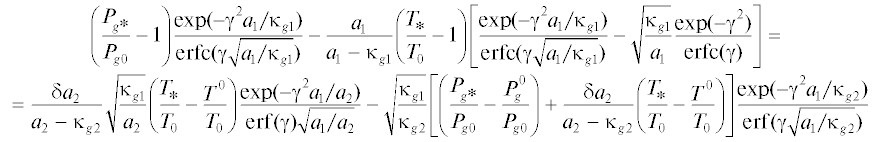Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 93-101

ФАЗОВЫЙ ПЕРЕХОД ВОДА–ЛЕД В НЕНАСЫЩЕННОМ ГРУНТЕ ПРИ НАЛИЧИИ КАПИЛЛЯРНОГО ДАВЛЕНИЯ

Г. Г. Цыпкин^*

Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 04.03.2019
После доработки 04.03.2019
Принята к публикации 06.03.2019

DOI: 10.1134/S0568528119050098

Аннотация

Сформулирована задача образования льда в ненасыщенном грунте при наличии градиента давления и капиллярных сил. Выведена полная система условий на поверхности кристаллизации. Проведено исследование одномерной задачи в автомодельной постановке. Исследована зависимость количества образующегося льда от параметров задачи. Получено, что при снижении давления на охлаждающей стенке, вызывающем подток воды к фронту, а также при более интенсивном режиме охлаждения, насыщенность образующегося льда увеличивается. Увеличение давления приводит к оттоку воды от фронта и уменьшению льдонасыщенности.

Ключевые слова: ненасыщенные грунты, кристаллизация, капиллярное давление, градиент давления, фильтрация, лед

Натурные и лабораторные исследования показывают, что основными физическими механизмами, действующими при фазовых переходах в грунтах, являются перенос тепла, фильтрация компонент, наличие растворенной примеси и поверхностные силы [1, 2]. Первые три механизма достаточно хорошо изучены, математические модели сформулированы и широко используются при расчетах практических задач. Общепринятой теории, описывающей влияние поверхностных сил, в настоящее время не существует, хотя во многих случаях поверхностные силы играют важную роль при движении компонент и фазовых переходах в грунтах.

Экспериментально обнаружено, что при образовании льда в грунте наблюдается течение воды к фронту кристаллизации. Для описания этого явления разрабатывались различные теории миграции влаги (теория пленочной миграции, теория сил кристаллизации, сил всасывания и т.д.), использующие функцию весовой влажности и основанные на формально введенных эффективных уравнениях переноса [1–3]. Параметры, используемые в этих теориях, определяются экспериментально и, зачастую, напрямую не связывались с физико-химическими параметрами грунтов и компонентов, их насыщающих. Такие полуэмпирические теории получили широкое применение при решении практических задач [4, 5].

Однако использование полуэмпирических теорий зачастую приводило к неопределенностям при математической постановке задач. Так, в [2] обсуждались трудности, возникающие при выводе граничных условий на фронте фазового перехода, поскольку подход на основе эффективных уравнений не использует законы сохранения. Итоги развития этого направления исследований были подведены в монографии Н.А. Цытовича [1], где автор пришел к выводу, что дальнейшее развитие теории механики мерзлых грунтов будет происходить на базе новейших достижений общей механики сплошных и многофазных сред.

Включение основных положений перечисленных выше теорий миграции влаги в теорию многофазной фильтрации представляется затруднительным. Развитие получила концепция капиллярного давления, предложенная Левереттом в работе [6], где представлены результаты экспериментов по изучению влияния капиллярного давления на двухфазное течение в песке. Формула Лапласа была обобщена на случай пористых сред и введена функция, зависящая от насыщенности, которая широко используется в теории фильтрации [7].

Влияние капиллярных сил на течения с фазовыми переходами в геотермальных резервуарах исследовались в [8–11] как аналитически, так и численно. В [12] впервые представлена фронтовая модель кристаллизации воды в ненасыщенной пористой среде. Приведена система законов сохранения, учитывающая движение твердых, жидких и газообразных компонент, которая, однако, не является замкнутой. Рассмотренная модель оказалась слишком сложной для исследования, и ни одного решения какой-либо задачи не было построено. В [13, 14] рассматривалась задача о плавлении льда в грунте, изначально насыщенном льдом и воздухом, при наличии капиллярного давления. В нелинейном случае проведено численное исследование зависимости водонасыщенности от вида функции Леверетта, величины капиллярного давления и внешних градиентов давления и температуры.

В настоящей работе рассматривается задача замораживания ненасыщенного грунта. Исследуется влияние капиллярных сил, а также градиентов давления и температуры. Показано, что функция водонасыщенности удовлетворяет диффузионному уравнению с правой частью, зависящей от температуры и давления. Выведены балансовые соотношения на поверхности кристаллизации. Для замыкания системы граничных условий предложено дополнительное условие, предполагающее полное смачивание образующего льда жидкой фазой. Для одномерного случая дан анализ найденного автомодельного решения. Исследовано влияние градиентов давления и температуры на движение воды в окрестности фронта кристаллизации и количество образующегося льда.

1. ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим задачу о кристаллизации воды в ненасыщенном грунте, считая его недеформируемым и несжимаемым. Предположим, что формируется узкая поверхность фазового перехода, разделяющая области, насыщенные водой и воздухом перед фронтом, и льдом и воздухом за фронтом. Считаем, что выполняется условие локального термодинамического равновесия. Тогда, в рамках теории двухфазной фильтрации, система основных уравнений в области перед фронтом имеет вид

(1.1)

$\phi \frac{{\partial {{S}_{w}}}}{{\partial t}} + {\text{div}}{{{\mathbf{v}}}_{w}} = 0$

(1.2)

$\phi \frac{\partial }{{\partial t}}{{\rho }_{g}}(1 - {{S}_{w}}) + {\text{div}}({{\rho }_{g}}{{{\mathbf{v}}}_{g}}) = 0$

(1.3)

${{{\mathbf{v}}}_{j}} = - \frac{{k{{f}_{j}}({{S}_{j}})}}{{{{\mu }_{j}}}}{\text{grad}}{{P}_{j}},\quad j = g,w$

(1.4)

${{P}_{g}} = {{\rho }_{g}}RT$

Здесь P – давление, T – температура, $R$ – газовая постоянная, ${\mathbf{v}}$ – вектор скорости фильтрации, $\rho $ – плотность, $S$ – насыщенность, k – проницаемость, $\phi $ – пористость, $\mu $ – вязкость, f – относительная фазовая проницаемость. Индексы: g – газ (воздух), w – вода.

В области лед–воздух система основных уравнений формально следует из системы (1.1)–(1.4), если заменить индекс w на индекс i, соответствующий льду и считать лед неподвижным ${{{\mathbf{v}}}_{{\mathbf{i}}}}$ = 0.

Учитывая наличие капиллярного давления ${{P}_{c}}$ в области смеси газ–вода, полагаем

(1.5)

${{P}_{w}} = {{P}_{g}} + {{P}_{c}}$

Капиллярное давление отрицательно в смачиваемой среде и положительно в несмачиваемой.

Закон сохранения энергии с учетом капиллярных сил для смеси газ–вода, насыщающей пористую среду, имеет вид [10]

(1.6)

$\begin{gathered} {{(\rho C)}_{m}}\frac{{\partial T}}{{\partial t}} - \phi {{P}_{c}}\frac{{\partial {{S}_{w}}}}{{\partial t}} - \phi (1 - {{S}_{w}})\frac{{\partial {{P}_{g}}}}{{\partial t}} + \\ \; + ({{C}_{p}}{{\rho }_{g}}{{{\mathbf{v}}}_{g}} + {{C}_{w}}{{\rho }_{w}}{{{\mathbf{v}}}_{w}}){\text{grad}}T + {{{\mathbf{v}}}_{{\mathbf{w}}}}{\text{grad}}{{P}_{w}} = {\text{div}}({{\lambda }_{m}}{\text{grad}}T) \\ \end{gathered} $

Исключая плотность газа и скорости фильтрации воды и газа, в области воздух–вода получаем систему четырех уравнений для неизвестных ${{S}_{w}}$, $T$, ${{P}_{w}}$ и ${{P}_{g}}$

(1.7)

$\frac{{\partial {{S}_{w}}}}{{\partial t}} - \frac{k}{{\varphi {{\mu }_{w}}}}{\text{div}}[{{f}_{w}}({{S}_{w}}){\text{grad}}{{P}_{w}}] = 0$

$\frac{{\partial {{S}_{w}}}}{{\partial t}} - (1 - {{S}_{w}})\frac{1}{{{{P}_{g}}}}\frac{{\partial {{P}_{g}}}}{{\partial t}} + (1 - {{S}_{w}})\frac{1}{T}\frac{{\partial T}}{{\partial t}} + \frac{k}{{\phi {{\mu }_{g}}}}\frac{T}{{{{P}_{g}}}}{\text{div}}\left[ {\frac{{{{P}_{g}}}}{T}{{f}_{g}}({{S}_{w}}){\text{grad}}{{P}_{g}}} \right] = 0$

$\begin{gathered} {{(\rho C)}_{1}}\frac{{\partial T}}{{\partial t}} - \phi {{P}_{c}}(S)\frac{{\partial {{S}_{w}}}}{{\partial t}} - \phi (1 - {{S}_{w}})\frac{{\partial {{P}_{g}}}}{{\partial t}} - {\text{div}}\left( {{{\lambda }_{1}}{\text{grad}}T} \right) = \\ = k\left[ {{{\rho }_{w}}{{C}_{w}}\frac{{{{f}_{w}}({{S}_{w}})}}{{{{\mu }_{w}}}}{\text{grad}}{{P}_{w}} + \frac{{{{C}_{P}}}}{R}\frac{{{{P}_{g}}}}{T}\frac{{{{f}_{g}}({{S}_{w}})}}{{{{\mu }_{g}}}}{\text{grad}}{{P}_{g}}} \right]{\text{grad}}T - \frac{k}{{{{\mu }_{w}}}}{{f}_{w}}({{S}_{w}})\mathop {({\text{grad}}{{P}_{w}})}\nolimits^2 \\ \end{gathered} $

${{P}_{w}} = {{P}_{g}} + {{P}_{c}}({{S}_{w}})$

${{\lambda }_{1}} = \phi {{S}_{w}}{{\lambda }_{w}} + \phi (1 - {{S}_{w}}){{\lambda }_{g}} + (1 - \phi ){{\lambda }_{s}}$

${{(\rho C)}_{1}} = \phi {{S}_{w}}{{\rho }_{w}}{{C}_{w}} + \phi (1 - {{S}_{g}}){{\rho }_{g}}{{C}_{p}} + (1 - \phi ){{\rho }_{s}}{{C}_{s}}$

Исключая из первого уравнения системы (1.7) давление воды ${{P}_{w}}$, получаем

(1.8)

$\frac{{\partial {{S}_{w}}}}{{\partial t}} - \frac{k}{{\phi {{\mu }_{w}}}}{\text{div}}\left[ {{{f}_{w}}({{S}_{w}})\frac{{d{{P}_{c}}}}{{d{{S}_{w}}}}{\text{grad}}{{S}_{w}}} \right] + \frac{k}{{\phi {{\mu }_{w}}}}{\text{div}}[{{f}_{w}}({{S}_{w}}){\text{grad}}{{P}_{g}}] = 0$

В пористой среде, насыщенной гетерогенной смесью воды и газа, капиллярное давление зависит от водонасыщенности и определяется соотношением Леверетта

(1.9)

${{P}_{c}}({{S}_{w}}) = \chi \sqrt {\frac{\phi }{k}} J({{S}_{w}}),\quad \chi = - 4\sigma cos\theta $

Здесь $\sigma $ – коэффициент поверхностного натяжения, $\theta $ – контактный угол, $J({{S}_{w}})$ – функция Леверетта. Для смачиваемой среды χ < 0.

Уравнение (1.8) можно записать в виде

(1.10)

$\frac{{\partial {{S}_{w}}}}{{\partial t}} = {\text{div}}({{\kappa }_{S}}{\text{grad}}{{S}_{w}}) + \frac{k}{{\phi {{\mu }_{w}}}}{\text{div}}[{{f}_{w}}({{S}_{w}}){\text{grad}}{{P}_{g}}],\quad {{\kappa }_{S}} = \chi \sqrt {\frac{k}{\phi }} \frac{{{{f}_{w}}({{S}_{w}})}}{{{{\mu }_{w}}}}\frac{{dJ({{S}_{w}})}}{{d{{S}_{w}}}}$

Диффузионное уравнение (1.10) для водонасыщенности, полученное из закона сохранения массы, закона Дарси и выражения для функции капиллярного давления, аналогично эффективному уравнению диффузии влаги [3].

Граничные условия на подвижной поверхности образования льда состоят из условий баланса энергии, масс газа и H₂O и соотношения для капиллярного давления

(1.11)

$\phi \left( {{{S}_{i}}\frac{{{{\rho }_{i}}}}{{{{\rho }_{w}}}} - {{S}_{{w + }}}} \right){{V}_{n}} = \frac{{k{{f}_{w}}({{S}_{{w + }}})}}{{{{\mu }_{w}}}}\mathop {({\text{grad}}{{P}_{w}})}\nolimits_{n + } $

(1.12)

$\phi ({{S}_{{w + }}} - {{S}_{i}}){{V}_{n}} = \frac{{k{{f}_{g}}({{S}_{{w + }}})}}{{{{\mu }_{g}}}}\mathop {({\text{grad}}{{P}_{g}})}\nolimits_{n + } - \frac{{k{{f}_{g}}({{S}_{i}})}}{{{{\mu }_{g}}}}\mathop {({\text{grad}}{{P}_{g}})}\nolimits_{n - } $

(1.13)

$\phi {{S}_{i}}{{\rho }_{i}}q{{V}_{n}} = {{\lambda }_{2}}\mathop {\left( {{\text{grad}}T} \right)}\nolimits_{n + } - {{\lambda }_{1}}\mathop {\left( {{\text{grad}}T} \right)}\nolimits_{n - } $

(1.14)

${{P}_{{w + }}} = {{P}_{{g + }}} + {{P}_{c}}({{S}_{{w + }}})$

${{T}_{ + }} = {{T}_{ - }} = {{T}_{*}},\quad {{P}_{{g + }}} = {{P}_{{g - }}} = {{P}_{{g*}}}$

Здесь q – теплота фазового перехода вода–лед, $V = V(t)$ – скорость фронта кристаллизации. Индексы плюс и минус – значения величин соответственно перед и за фронтом, $n$ – нормаль.

Будем считать, что температура кристаллизации известна ${{T}_{*}} = 273.15$ K, предполагая ее независимость от капиллярных сил.

2. ФОРМУЛИРОВКА ЗАДАЧИ

Пусть в начальном состоянии грунт содержит гетерогенную смесь воды и воздуха с температурой ${{T}_{0}}$, давлением воздуха ${{P}_{{go}}}$ и водонасыщенностью ${{S}_{{w0}}}$. Если температура ${{T}^{0}}$ на некоторой неподвижной границе опускается ниже температуры фазового перехода вода–лед, то возникает фронт образования льда. В общем случае можно полагать, что образующийся лед сосуществует с воздухом и не заполняет поровое пространство целиком.

Рассмотрим процесс кристаллизации в естественных условиях, соответствующих изменениям температуры на десятки градусов и изменениям давления на порядок меньше атмосферного. Тем самым исключаются из рассмотрения случаи искусственного замораживания, например, жидким азотом или при нагнетании холодного воздуха в скважину. Небольшие по сравнению с абсолютными значениями, изменения температуры и давления позволяют применить процедуру линеаризации и системы уравнений в обеих областях существенно упрощаются. Также оценки показывают, что работой капиллярных сил и влиянием сжимаемости газа на баланс энергии можно пренебречь, поскольку основную роль играет теплоперенос по матрице пористой среды. В обеих областях справедливо обычное уравнение теплопроводности

(2.1)

$\frac{{\partial T}}{{\partial t}} = {{a}_{{1,2}}}\Delta T,\quad {{a}_{{1,2}}} = \frac{{{{\lambda }_{{1,2}}}}}{{{{{(\rho C)}}_{{1,2}}}}}$

В талой области перед фронтом кристаллизации перераспределение воды описывается уравнением диффузии влаги (1.10). Рассмотрим задачу в линейном приближении, когда отклонение функции водонасыщенности от невозмущенного состояния невелико. Невозмущенным является состояние, когда вода неподвижна и начальная водонасыщенность равна ${{S}_{{w0}}}$, а для невозмущенного состояния за фронтом насыщенность льда определяется выражением ${{\rho }_{{i0}}} = {{S}_{{w0}}}{{\rho }_{w}}{\text{/}}{{\rho }_{i}}$.

Для простоты аппроксимируем функцию относительной фазовой проницаемости линейной функцией ${{f}_{w}} = {{S}_{w}}$. Тогда в области смеси вода–воздух уравнение для функции водонасыщенности (1.10) в линейном приближении принимает вид

(2.2)

$\frac{{\partial {{S}_{w}}}}{{\partial t}} = {{\kappa }_{S}}\Delta {{S}_{w}} + \kappa \Delta P_{g}^{'},\quad {{\kappa }_{S}} = - 4\sigma cos\theta \sqrt {\frac{k}{\phi }} \frac{{{{S}_{{w0}}}}}{{{{\mu }_{w}}}}\frac{{dJ({{S}_{w}})}}{{d{{S}_{w}}}},\quad \kappa = \frac{{k{{P}_{{g0}}}}}{{\phi {{\mu }_{w}}}}{{S}_{{w0}}},\quad P_{g}^{'} = \frac{{{{P}_{g}}}}{{{{P}_{{g0}}}}}$

В линейном приближении производная функции Леверетта является постоянной величиной, которая может принимать различные значения, в зависимости от выбора начальной водонасыщенности ${{S}_{{w0}}}$.

Второе уравнение системы (1.7), представляющее собой уравнение для давления воздуха, содержит временную производную функции водонасыщенности. Поскольку случаи, близкие к предельным, когда ${{S}_{w}} \to 0$ или ${{S}_{w}} \to 1$ не рассматриваются, то вклад этой производной мал, и уравнение приводится к виду

(2.3)

$\frac{{\partial P_{g}^{'}}}{{\partial t}} = {{\kappa }_{{g1}}}\Delta P_{g}^{'} + {{a}_{1}}\Delta T',\quad {{\kappa }_{{g1}}} = \frac{{k{{P}_{{g0}}}}}{{\phi {{\mu }_{g}}}},\quad T' = \frac{T}{{{{T}_{0}}}}$

В области за фронтом кристаллизации лед считается неподвижным, а невозмущенное состояние характеризуется граничными значениями температуры T⁰ и давления $P_{g}^{0}$. Тогда, в линейном приближении уравнение движения воздуха принимает вид

(2.4)

$\frac{{\partial P_{g}^{'}}}{{\partial t}} = {{\kappa }_{{g2}}}\Delta P_{g}^{'} + \delta {{a}_{2}}\Delta T',\quad {{\kappa }_{{g2}}} = {{\kappa }_{{g1}}}\frac{{P_{g}^{0}}}{{{{P}_{{g0}}}}},\quad \delta = \frac{{{{T}_{0}}P_{g}^{0}}}{{{{T}^{0}}{{P}_{{g0}}}}}$

Аналогичным образом преобразуется условие баланса массы (1.11) на поверхности кристаллизации. Используя соотношение для капиллярного давления и условие равенства насыщенности льда и воды, получаем

(2.5)

$\left( {1 - \frac{{{{\rho }_{i}}}}{{{{\rho }_{w}}}}} \right){{V}_{n}} = \frac{k}{{\phi {{\mu }_{w}}}}\mathop {\left( {{\text{grad}}{{P}_{g}}} \right)}\nolimits_{n + } - \chi \sqrt {\frac{k}{\phi }} \frac{{{{P}_{{g0}}}}}{{{{\mu }_{w}}}}\frac{{dJ({{S}_{w}})}}{{d{{S}_{w}}}}\mathop {\left( {{\text{grad}}{{S}_{w}}} \right)}\nolimits_{n + } $

Сформулированная задача содержит четыре неизвестных параметра: скорость подвижной границы фазового перехода V, давление газа на поверхности кристаллизации ${{P}_{{g*}}}$, насыщенность льда ${{S}_{i}}$ и значение водонасыщености ${{S}_{{w + }}}$ на поверхности раздела. Для их определения имеется три соотношения на границе кристаллизации (1.12), (1.13), (2.5) и задача является недоопределенной. Для замыкания системы соотношений на подвижной границе требуется выставить дополнительное условие, связывающее искомые параметры.

Одним из центральных положений теории двухфазной фильтрации, подтвержденном экспериментально, является гипотеза о том, что вода и газ движутся по разным поровым каналам [15]. В смачиваемой среде каналы меньшего диаметра заняты жидкостью (водой), а в несмачиваемой – газом. При переходе воды в кристаллическое состояние объем увеличивается, что вызывает увеличение давления воды перед фронтом. Это приводит к ее оттоку от фронта по каналам, уже занятым водой. Кроме того, вода, преодолевая сопротивление капиллярных сил, проникает в каналы большего диаметра. Соответственно, водонасыщенность перед фронтом кристаллизации возрастает. Естественно предположить, что лед может образовываться только в тех порах и каналах, которые содержат воду. В той части, где кристалл контактирует не с водой, а с воздухом, лед формироваться не будет. Следовательно, весь растущий кристалл льда в пористой среде должен омываться водой. Из этих соображений следует дополнительное условие равенства насыщенностей воды и льда ${{S}_{i}} = {{S}_{{w + }}}$, которое замыкает систему соотношений на поверхности кристаллизации.

Соотношение ${{S}_{i}} = {{S}_{{w + }}}$ существенно упрощает закон сохранения массы газа (2.6), который сводится к равенству потоков газа на подвижной границе

(2.6)

$\mathop {({\text{grad}}{{P}_{g}})}\nolimits_{n + } = \mathop {({\text{grad}}{{P}_{g}})}\nolimits_{n - } $

3. АВТОМОДЕЛЬНОЕ РЕШЕНИЕ

Рассмотрим задачу в одномерном приближении. Пусть в начальном состоянии талый грунт занимает полупространство $x > 0$, с начальной водонасыщенностью ${{S}_{{w0}}}$. Если температура на неподвижной стенке $x = 0$ опускается ниже температуры фазового перехода вода–лед, то вправо распространяется фронт кристаллизации, двигающийся по закону $x = X(t)$. Если начальная температура, давление и водонасыщенность, а также температура, давление на охлаждающей стенке являются постоянными величинами, то сформулированная задача имеет автомодельное решение вида

$T = T(\xi ),\quad {{S}_{w}} = {{S}_{w}}(\xi ),\quad X(t) = \beta \sqrt t ,\quad \xi = x{\text{/}}\sqrt t $

В области перед фронтом ($\zeta > \gamma $) распределения температуры, давления и водонасыщенности в безразмерной форме ($\zeta = \xi {\text{/}}2\sqrt {{{a}_{1}}} $, $\gamma = \beta {\text{/}}2\sqrt {{{a}_{1}}} $) имеют вид

(3.1)

$\frac{T}{{{{T}_{0}}}} = 1 + \left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right)\frac{{{\text{erfc}}(\zeta )}}{{{\text{erfc}}(\gamma )}}$

(3.2)

$\frac{{{{P}_{g}}}}{{{{P}_{{g0}}}}} = 1 + \left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - 1} \right)\frac{{{\text{erfc}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}} + \frac{{{{a}_{1}}}}{{{{a}_{1}} - {{\kappa }_{{g1}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right)\left[ {\frac{{{\text{erfc}}(\zeta )}}{{{\text{erfc}}(\gamma )}} - \frac{{{\text{erfc}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}}} \right]$

(3.3)

$\begin{gathered} {{S}_{w}} = {{S}_{{w0}}} + \left\{ {{{S}_{{w*}}} - {{S}_{{w0}}} + \frac{\kappa }{{{{\kappa }_{{g1}}} - {{\kappa }_{S}}}}\left[ {\frac{{{{a}_{1}}}}{{{{a}_{1}} - {{\kappa }_{S}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right) - \left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - 1} \right)} \right]} \right\}\frac{{{\text{erfc}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{S}}} )}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{S}}} )}} + \\ \; + \frac{\kappa }{{{{\kappa }_{{a1}}} - {{\kappa }_{S}}}}\frac{{{{a}_{1}}}}{{{{a}_{1}} - {{\kappa }_{{g1}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right)\frac{{{\text{erfc}}(\zeta )}}{{{\text{erfc}}(\gamma )}} - \frac{\kappa }{{{{\kappa }_{{g1}}} - {{\kappa }_{S}}}}\left[ {\frac{{{{a}_{1}}}}{{{{a}_{1}} - {{\kappa }_{{g1}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right) - \left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - 1} \right)} \right]\frac{{{\text{erfc}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}} \\ \end{gathered} $

В области за фронтом ($0 < \zeta < \gamma $) распределение температуры и давления определяется выражениями

(3.4)

$\frac{T}{{{{T}_{0}}}} = \frac{{{{T}^{0}}}}{{{{T}_{0}}}} + \left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - \frac{{{{T}^{0}}}}{{{{T}_{0}}}}} \right)\frac{{{\text{erf}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{a}_{2}}} )}}{{{\text{erf}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{a}_{2}}} )}}$

(3.5)

$\frac{{{{P}_{g}}}}{{{{P}_{{g0}}}}} = \frac{{P_{g}^{0}}}{{{{P}_{{g0}}}}} + \left[ {\left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - \frac{{P_{g}^{0}}}{{{{P}_{{g0}}}}}} \right) + \frac{{\delta {{a}_{2}}}}{{{{a}_{2}} - {{\kappa }_{{g2}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - \frac{{{{T}^{0}}}}{{{{T}_{0}}}}} \right)} \right]\frac{{{\text{erf}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g2}}}} )}}{{{\text{erf}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g2}}}} )}} - \delta \frac{{{{a}_{2}}}}{{{{a}_{2}} - {{\kappa }_{{g2}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - \frac{{{{T}^{0}}}}{{{{T}_{0}}}}} \right)\frac{{{\text{erf}}(\zeta \sqrt {{{a}_{1}}{\text{/}}{{a}_{2}}} )}}{{{\text{erf}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{a}_{2}}} )}}$

Подставляя решения (3.1)–(3.5) в балансовые соотношения на границе кристаллизации (1.13), (2.5), (2.6), записанные для одномерного случая, получаем систему трансцендентных уравнений для определения параметров $\gamma $, ${{P}_{{g*}}}$ и ${{S}_{i}}$

${{S}_{{w0}}}\left( {1 - \frac{{{{\rho }_{i}}}}{{{{\rho }_{w}}}}} \right)\gamma - \frac{\kappa }{{\sqrt {\pi {{a}_{1}}{{\kappa }_{{g1}}}} }}\left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - 1} \right)\frac{{{\text{exp}}( - {{\gamma }^{2}}{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}})}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}} + \frac{1}{{\sqrt \pi }}\frac{\kappa }{{{{a}_{1}} - {{\kappa }_{{g1}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right) \times $

(3.6)

$\begin{gathered} \; \times \left[ {\sqrt {\frac{{{{a}_{1}}}}{{{{\kappa }_{{g1}}}}}} \frac{{{\text{exp}}( - {{\gamma }^{2}}{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}})}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}} - \frac{{{\text{exp}}( - {{\gamma }^{2}})}}{{{\text{erfc}}(\gamma )}}} \right] - \frac{1}{{\sqrt \pi {{P}_{{g0}}}}}\frac{\kappa }{{{{a}_{1}} - {{\kappa }_{S}}}}\frac{\kappa }{{{{a}_{1}} - {{\kappa }_{{g1}}}}}\frac{{d{{P}_{c}}}}{{d{{S}_{w}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right)\frac{{{\text{exp}}( - {{\gamma }^{2}})}}{{{\text{erfc}}(\gamma )}} + \\ \; + \frac{\kappa }{{\sqrt {\pi {{a}_{1}}{{\kappa }_{{g1}}}} {{P}_{{g0}}}}}\frac{\kappa }{{{{\kappa }_{{g1}}} - {{\kappa }_{S}}}}\frac{{d{{P}_{c}}}}{{d{{S}_{w}}}}\left[ {\frac{{{{a}_{1}}}}{{{{a}_{1}} - {{\kappa }_{{g1}}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right) - \left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - 1} \right)} \right]\frac{{{\text{exp}}( - {{\gamma }^{2}}{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}})}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{{g1}}}} )}} - \\ \end{gathered} $

$\; - \frac{\kappa }{{\sqrt {\pi {{a}_{1}}{{\kappa }_{S}}} {{P}_{{g0}}}}}\frac{{d{{P}_{c}}}}{{d{{S}_{w}}}}\left\{ {{{S}_{i}} - {{S}_{{w0}}} + \frac{\kappa }{{{{\kappa }_{{g1}}} - {{\kappa }_{S}}}}\left[ {\frac{{{{a}_{1}}}}{{{{a}_{1}} - {{\kappa }_{S}}}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right) - \left( {\frac{{{{P}_{{g*}}}}}{{{{P}_{{g0}}}}} - 1} \right)} \right]} \right\}\frac{{{\text{exp}}( - {{\gamma }^{2}}{{a}_{1}}{\text{/}}{{\kappa }_{S}})}}{{{\text{erfc}}(\gamma \sqrt {{{a}_{1}}{\text{/}}{{\kappa }_{S}}} )}}$

(3.7)

(3.8)

$\frac{{\sqrt \pi \phi {{S}_{i}}{{\rho }_{i}}q{{a}_{1}}}}{{{{T}_{0}}}}\gamma - {{\lambda }_{2}}\sqrt {\frac{{{{a}_{1}}}}{{{{a}_{2}}}}} \left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - \frac{{{{T}^{0}}}}{{{{T}_{0}}}}} \right)\frac{{{\text{exp}}( - {{\gamma }^{2}}{{a}_{1}}{\text{/}}{{a}_{2}})}}{{{\text{erf}}(\gamma )\sqrt {{{a}_{1}}{\text{/}}{{a}_{2}}} }} - {{\lambda }_{1}}\left( {\frac{{{{T}_{*}}}}{{{{T}_{0}}}} - 1} \right)\frac{{{\text{exp}}( - {{\gamma }^{2}})}}{{{\text{erfc}}(\gamma )}} = 0$

Система (3.6)–(3.7) решалась численно при следующих значениях параметров: $\phi = 0.3$, ρ_s = = $2 \times {{10}^{3}}$ кг/м³, ${{\rho }_{i}} = 0.91 \times {{10}^{3}}$ кг/м³, ${{\rho }_{w}} = {{10}^{3}}$ кг/м³, ${{\lambda }_{s}} = 2$ Вт/(м ⋅ К), ${{\lambda }_{i}} = 2.23$ Вт/(м ⋅ К), ${{\lambda }_{w}}$ = = 0.58 Вт/(м ⋅ К), ${{C}_{s}} = {{10}^{3}}$ Дж/(кг ⋅ К), ${{C}_{i}} = 2 \times {{10}^{3}}$ Дж/(кг ⋅ К), ${{C}_{w}} = 4.2 \times {{10}^{3}}$ Дж/(кг ⋅ К), $q = 3.34 \times {{10}^{5}}$ Дж/кг, ${{\mu }_{w}} = 2 \times {{10}^{{ - 3}}}$ Па ⋅ с, ${{\mu }_{g}} = 2 \times {{10}^{{ - 5}}}$ Па ⋅ c.

Поскольку при кристаллизации объем H₂O возрастает, то при постоянном давлении значение водонащенности на фронте будет больше начального значения. Поскольку функция водонасыщенности удовлетворяет диффузионному уравнению (2.2), жидкая фаза оттекает от фронта и наибольшее значение водонасыщенности не превосходит невозмущенное значение насыщенности льда S_i0, которое определяется из условия неподвижности воды.

Численные эксперименты при ${{P}_{{g0}}} = P_{g}^{0}$ показывают, что увеличение проницаемости приводит к более интенсивной диффузии жидкости перед фронтом и уменьшению количества образующегося льда. На рис. 1 представлены распределения насыщенностей воды и льда при двух значениях проницаемости, которые отличаются на два порядка. Соответственно, коэффициент диффузии ${{\kappa }_{S}}$ отличается на порядок. При низкой проницаемости (кривая 1) диффузия мала и объем образующегося льда больше, чем в случае высокой проницаемости (кривая 2). При этом давление газа снижается из-за охлаждения. При проницаемости $k = {{10}^{{ - 15}}}$ м² давление P_g имеет минимум на фронте и отличается от начального на 4.4 КПа. При высокой проницаемости, соответствующей кривой снижение давления на два порядка меньше. Аналогичным образом влияет изменение угла смачивания, который также входит сомножителем в коэффициент диффузии (рис. 2). Только в этом случае снижение давления из-за охлаждения одинаково. Отметим, что при равенстве начального и граничного давления в рассматриваемом линейном приближении возникает движение воздуха и воды, но скорость фильтрации очень мала, а значение насыщенности льда больше начальной водонасыщенности и меньше невозмущенного значения ${{S}_{{i0}}}$.

Рис. 1.

Характерное распределение насыщенностей воды и льда при различных проницаемостях. $\phi = 0.3$, ${{T}_{0}}$ = 280 К, ${{T}^{0}} = 250$ К, ${{S}_{{w0}}} = 0.5$, ${{P}_{{g0}}} = P_{g}^{0} = {{10}^{5}}$ Па, $cos\theta = 0.02$. 1, 2 – $k = {{10}^{{ - 15}}}$, $k = {{10}^{{ - 13}}}$ м²

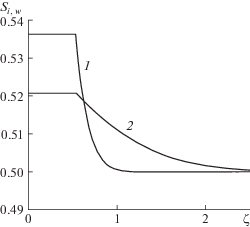
Рис. 2.

Влияние угла смачивания на распределение насыщенностей воды и льда. ${{S}_{{w0}}} = 0.7$, $k = {{10}^{{ - 15}}}$ м². Остальные параметры как рис. 1. 1, 2 – $cos\theta = 0.02,0,01$

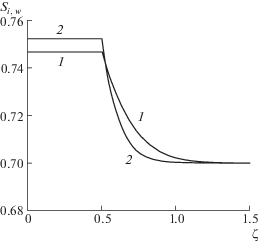
Ситуация радикально изменяется, если давление $P_{g}^{0}$ на замораживающей стенке отличается от начального ${{P}_{{g0}}}$. Отклонение давления воздуха на стенке от начального давления приводит к возникновению градиента давления в воде, и соответственно либо к подтоку жидкости к фронту, либо к оттоку от него. Увеличение $P_{g}^{0}$ вызывает течение жидкой фазы от фронта кристаллизации, что приводит к существенному снижению количество образующегося льда (кривая 1, рис. 3). Если давление $P_{g}^{0}$ достаточно велико, то насыщенность льда ${{S}_{i}}$ может быть меньше начальной водонасыщенности ${{S}_{{w0}}}$ (кривая 2). С увеличением проницаемости эта зависимость усиливается.

Рис. 3.

Распределение насыщенностей при увеличении давления $P_{g}^{0}$ на замораживающей стенке. $k = 0.5 \times {{10}^{{ - 14}}}$ м², ${{T}^{0}} = 260$ К. Остальные параметры как на рис. 1. 1, 2 – $P_{g}^{0} = 1.2 \times {{10}^{5}}$, $1.24 \times {{10}^{5}}$ Па.

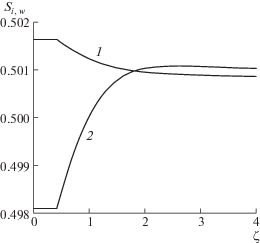
Снижение давления на стенке приводит к возникновению течения воды к поверхности кристаллизации и увеличению объема образующегося льда (рис. 4). Распределение водонасыщенности (кривая 1), соответствующее случаю $P_{g}^{0} = {{P}_{{g0}}}$, характеризуется монотонным поведением. При $P_{g}^{0} < {{P}_{{g0}}}$ имеются два конкурирующих процесса. Диффузия воды преобладает в окрестности фронта фазового перехода, а на удалении от фронта основную роль играет внешний градиент давления воздуха. В точке, где эти процессы уравновешивают друг друга, распределение водонасыщенности имеет минимум. Вид функции водонасыщенности в окрестности точки минимума представлен на рис. 5.

Рис. 4.

Влияние падения давления $P_{g}^{0}$ на распределения насыщенностей. Параметры как на рис. 3. 1, 2 – $P_{g}^{0} = {{10}^{5}}$, $0.75 \times {{10}^{5}}$ Па.

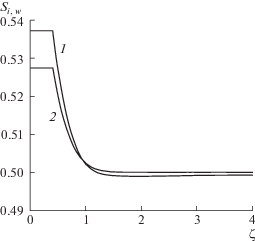
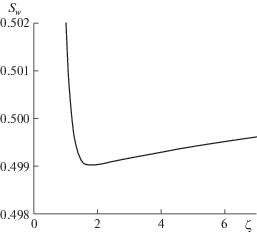
Рис. 5.

Вид функции водонасыщенности в окрестности точки минимума при $P_{g}^{0} = 0.75 \times {{10}^{5}}$ Па. Остальные параметры как на рис. 4.

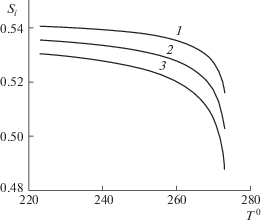
В рассматриваемом линейном приближении скорость фронта кристаллизации существенно зависит только от начальной и граничной температуры. Влияние остальных параметров на скорость незначительно и может привести к изменениям на несколько процентов. С другой стороны, количество образующегося льда существенно зависит от скорости фронта. При слабом охлаждении и медленной кристаллизации характерное время процесса велико и роль диффузии воды и влияние внешнего градиента давления возрастают (рис. 6).

Рис. 6.

Зависимость количества образующегося льда как функция температуры ${{T}^{0}}$ на охлаждающей стенке. Остальные параметры как на рис. 3. 1, 2, 3 – $P_{g}^{0} = 0.8 \times {{10}^{5}}$, ${{10}^{5}}$, $1.2 \times {{10}^{5}}$ Па.

Следует отметить, что капиллярное давление оказывает существенное влияние на течения в грунтах и породах, характерное давление в которых близко к атмосферному [13, 14, 16, 17]. В этом случае капиллярное давление и характерное давление являются величинами одного порядка. Если давление в физической системе, такой, например, как геотермальный резервуар [8–11], значительно превышает капиллярное, то его учет вносит только поправку при расчете течения. Когда капиллярное давление совпадает с высоким характерным давлением, то возникает вопрос о правомерности применения закона фильтрации Дарси.

ЗАКЛЮЧЕНИЕ

Сформулирована математическая модель образования льда в ненасыщенном грунте при наличии капиллярных сил, действующих на границе вода–воздух. На неизвестной подвижной границе кристаллизации предложено условие, замыкающее систему законов сохранения. Это условие состоит в равенстве насыщенностей воды и льда на границе фазового перехода. Предположение о равенстве насыщенностей следует из основного положения теории двухфазной фильтрации, состоящего в том, что течение воды и газа происходит с разной скоростью по различным поровым каналам. Представлено автомодельное решение одномерной задачи. Показано, что рост капиллярных сил уменьшает насыщенность льда из-за диффузии воды перед фронтом, а более интенсивный режим замораживания приводит к росту льдонасыщенности. Найдено, что падение давления на охлаждающей стенке вызывает подток воды к фронту и увеличивает количество образующего льда, а рост давления оказывает обратное воздействие.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А17-117021310375-7).

Список литературы

Цытович Н.А. Механика мерзлых грунтов. М.: Высшая школа, 1973. 446 с.
Жесткова Т.Н. Формирование криогенного строения грунтов. М.: Наука, 1982. 216 с.
Hoekstra P. Moisture movement in soils under temperature gradient with the cold-side temperature below freezing // Water Resources Res. 1966. V. 2. № 2. P. 241–250.
Zhang Y., Carey S.K., Quinton W.L. Evaluation of the algorithms and parametrizations for ground thawing and freezing simulation in permafrost regions // J. Geophys. Research. 2008. V. 113. D17116.
Li Q., Sun S., Dai Q. The numerical scheme development of a simplified frozen soil model // Adv. Apmosph. Sci. 2009. V. 26. № 5. P. 940–950.
Leverett M.C. Capillary behavior in porous solids // Trans. AIME. 1941. V. 142. № 1. 152–169.
Bear J. Dynamics of Fluids in Porous Media. New York: Acad. Press, 1972. 764 p.
Udell K.S. Heat transfer in porous media: considering phase change and capillarity – the heat pipe effect // Int. J. Heat and Mass Transfer 1985. V. 28. 485–495.
Li K., Horne R.N. An experimental and analytical study of steam/water capillary pressure // SPE Reservoir Evaluation and Engineering 2001 V. 4. P. 477–482.
Tsypkin G.G., Calore C. Role of capillary forces in vapour extraction from low permeability, water saturated geothermal reservoir // Geothermics, 2003. V. 32. № 3. 219–237.
Tsypkin G.G., Calore C. Influence of capillary forces on water injection into hot rock, saturated with superheated vapour // Int. J. Heat and Mass Transfer. 2007. V. 20. 3195–3202.
Menot J.M. Equations of frost propagation in unsaturated porous media // Eng. Geology. 1979. V. 13. № 1–4. P. 101–109.
Цыпкин Г.Г. Влияние капиллярных сил на распределение влагонасыщенности при протаивании мерзлого грунта // Известия РАН. МЖГ. 2010. № 6. С. 130–140.
Васильев В.И., Попов В.В., Цыпкин Г.Г. Нелинейная задача протаивания ненасыщенного мерзлого грунта при наличии капиллярных сил // Изв. РАН. МЖГ. 2012. № 1. С. 132–141.
Scheidegger A. E. The physics of flow through porous media / 3d ed. Univ. Toronto Press, 1974. 353 p.
Шаргатов В.А. О неустойчивости фронта фазового перехода жидкость–пар в неоднородных пористых смачиваемых средах // Изв. РАН. МЖГ. 2017. № 1. С. 148–159.
Цыпкин Г.Г. Об устойчивости поверхностей испарения и конденсации в пористой среде // Изв. РАН. МЖГ. 2017. № 6. С. 70–76.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал