Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 6-14

НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ В ПЛАСТЕ С ТРЕЩИНОЙ ГИДРОРАЗРЫВА

И. Л. Хабибуллин^a, *, А. А. Хисамов^a, **

^a Башкирский государственный университет
Уфа, Россия

^* E-mail: habibi.bsu@mail.ru
^** E-mail: khisamovartur@list.ru

Поступила в редакцию 12.07.2018
После доработки 04.03.2019
Принята к публикации 05.03.2019

DOI: 10.1134/S0568528119050050

Аннотация

В настоящее время для интенсификации нефтегазодобычи из коллекторов с трудноизвлекаемыми запасами широко используются технологии гидроразрыва пластов. Моделирование процессов фильтрации в пластах с трещинами гидроразрыва достаточно полно развито в приближении стационарной фильтрации. Нестационарные процессы распределения давления рассмотрены применительно к теории гидродинамических методов исследований скважин, в которой рассматриваются асимптотически ограниченные интервалы изменения координат и времени (расстояния порядка радиуса скважины и времена, намного меньшие, чем характерное время процесса фильтрации). В то же время в коллекторах с трудно извлекаемыми запасами (малые проницаемости пласта и высоковязкие нефти) продолжительность нестационарных процессов распределения давления может быть одного порядка с характерным временем фильтрации в пласте. В данной работе представлены новые аналитические решения задачи о нестационарном распределении давления вокруг скважины, пересеченной вертикальной трещиной. Научная новизна работы заключается в том, что в модели учитывается сжимаемость жидкости в трещине и фильтрация жидкости не только в трещине, но и в пласте. Решения задач построены методом преобразований Лапласа. В частных случаях из полученных решений следуют известные в литературе выражения. Проведен анализ полученных аналитических решений, позволяющий определить основные характерные особенности рассматриваемых процессов фильтрации.

Ключевые слова: вертикальная трещина гидроразрыва, нестационарная фильтрация, билинейный режим, преобразование Лапласа, распределение давления, дебит скважины

Создание в пласте вертикальных трещин, пересекающихся со скважинами, является одним из эффективных методов интенсификации добычи нефти и газа из малопроницаемых коллекторов. Гидродинамическая связь пласта и скважины, как правило, реализуется только через трещину гидроразрыва. В зависимости от соотношений проницаемостей пласта и трещины, соотношений длины трещины и характерного размера пласта меняются геометрия и интенсивность фильтрационного потока в системе пласт-трещина-скважина. Модели таких фильтрационных потоков достаточно полно развиты в приближении стационарной фильтрации [1]. Нестационарные аналитические модели рассматриваются в основном применительно к задачам гидродинамического исследования скважин и пластов, в которых определяются зависимости от времени дебита скважины или давления на забое скважины [1–3], распределения давления в трещине и в пласте не рассматриваются. В работе [4] рассмотрен упругий режим фильтрации в трещине, но фильтрация в пласте также не рассматривается.

В то же время в коллекторах с трудноизвлекаемыми запасами, за счет малой проницаемости пласта и большой вязкости нефти, продолжительность нестационарных процессов распределения давления может быть одного порядка с характерным временем процесса фильтрации [5]. Поэтому актуальным является исследование нестационарных моделей фильтрации в системе пласт-трещина с точки зрения развития общей теории этих процессов [1, 4, 6], а также для развития методов гидродинамических исследований пластов [7], методов оценки дебита скважин с трещиной гидроразрыва [8].

1. ПОСТАНОВКА ЗАДАЧИ

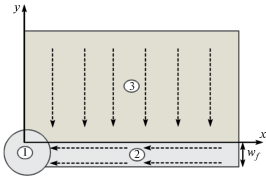
В пласте, насыщенном малосжимаемой однородной жидкостью, имеется скважина, которая пересекается симметричной вертикальной трещиной гидроразрыва по всей толщине пласта. Гидравлическая связь пласта и скважины реализуется только через боковую поверхность трещины, так как ширина (раскрытие) трещины намного меньше, чем ее длина. Предполагается, что вначале давление в пласте и трещине одинаково и при t = 0 скважина запускается в эксплуатацию. Тогда вокруг скважины в трещине и в пласте создается нестационарный фильтрационный поток. С учетом симметрии геометрии задачи относительно скважины и трещины рассматривается одна четвертая часть области фильтрации (рис. 1).

Рис. 1.

Схема области течения: 1 – скважина, 2 – трещина, 3 – пласт

Поскольку ширина трещины намного меньше, чем длина, поток в трещине считается одномерным, направленным по оси x. Поток в пласте направлен по оси y, перпендикулярно к боковой поверхности трещины. Тогда приведенная на рис. 1 схема соответствует так называемому билинейному режиму течения, который представляет собой совокупность одновременно существующих в трещине и в пласте двух линейных взаимно-перпендикулярных потоков [1–3, 6, 9].

Распределения давления в пласте и трещине описываются уравнениями

(1.1)

$\frac{{\partial {{P}_{r}}}}{{\partial t}} = {{\kappa }_{r}}\frac{{{{\partial }^{2}}{{P}_{r}}}}{{\partial {{y}^{2}}}}\quad 0 \leqslant x \leqslant \infty ,~\quad 0 \leqslant y \leqslant \infty ~$

(1.2)

$\frac{{\partial {{P}_{f}}}}{{\partial t}} = {{\kappa }_{f}}\frac{{{{\partial }^{2}}{{P}_{f}}}}{{\partial {{x}^{2}}}} + {{\left. {\frac{{{{\kappa }_{f}}}}{{{{w}_{f}}}}\frac{{{{k}_{r}}}}{{{{k}_{f}}}}\frac{{\partial {{P}_{r}}}}{{\partial y}}} \right|}_{{y = 0}}}\quad 0 \leqslant x \leqslant \infty ,\quad - {{w}_{f}} \leqslant y \leqslant 0$

Здесь P – давление, x и y – координаты, t – время, индексы r и f относятся к пласту и трещине, $\varkappa $ – коэффициент пьезопроводности, k – проницаемость, w_f – полуширина трещины.

Начальное распределение давления

${{P}_{r}}(x,y,t = 0) = {{P}_{f}}(x,t = 0) = {{P}_{0}}.$

На поверхности трещины (линия раздела пласт-трещина) выполняется условие равенства давлений:

(1.3)

${{P}_{r}}(x,y = 0,t) = ~{{P}_{f}}(x,y = 0,t)~$.

Условия на непроницаемых границах имеют вид

(1.4)

$\frac{{\partial {{P}_{r}}(x,y = \infty ,t)}}{{\partial y}} = 0$

(1.5)

$\frac{{\partial {{P}_{f}}(x = \infty ,y,t)}}{{\partial x}} = 0,\quad \frac{{\partial {{P}_{f}}(x,y = - {{w}_{f}},0)}}{{\partial y}} = 0.$

На поверхности пересечения трещины со скважиной выполняется условие, констатирующее работу скважины в режиме заданного давления P_c или заданного дебита Q

(1.6)

${{P}_{f}}(x = 0,t) = {{P}_{c}},$

(1.7)

$\frac{{{{k}_{f}}{{h}_{r}}{{w}_{f}}}}{\mu }\frac{{\partial {{P}_{f}}(x = 0,t)}}{{\partial x}} = Q~$.

Здесь μ – вязкость жидкости, Q – часть дебита, поступающего в скважину из рассматриваемой области фильтрации, x_f – полудлина трещины, h_r – толщина пласта.

Соответственно имеют место первая ((1.1)–(1.6)) или вторая краевые задачи ((1.1)–(1.5), (1.7)). В безразмерных переменных

${{\bar {P}}_{r}} = \frac{{{{P}_{r}} - {{P}_{0}}}}{{P{\text{*}}}},\quad {{\bar {P}}_{f}} = \frac{{{{P}_{f}} - {{P}_{0}}}}{{P{\text{*}}}},\quad P_{1}^{*} = {{P}_{c}} - {{P}_{0}},~\quad P_{2}^{*} = \frac{{Q\mu }}{{{{k}_{r}}{{h}_{r}}}},\quad \bar {y} = \frac{y}{{{{x}_{f}}}},~\quad \bar {x} = \frac{x}{{{{x}_{f}}}},\quad \bar {t} = t\frac{{{{\kappa }_{r}}}}{{x_{f}^{2}}}$

эти задачи имеют вид

(1.8)

$\frac{{\partial {{{\bar {P}}}_{r}}}}{{\partial{ \bar {t}}}} = \frac{{{{\partial }^{2}}{{{\bar {P}}}_{r}}}}{{\partial {{{\bar {y}}}^{2}}}}$

(1.9)

$\frac{{\partial {{{\bar {P}}}_{f}}}}{{\partial{ \bar {t}}}} = a\frac{{{{\partial }^{2}}{{{\bar {P}}}_{f}}}}{{\partial {{{\bar {x}}}^{2}}}} + b{{\left. {\frac{{\partial {{{\bar {P}}}_{r}}}}{{\partial{ \bar {y}}}}} \right|}_{{\bar {y} = 0}}}~$

(1.10)

${{\bar {P}}_{r}}(\bar {x},\bar {y},\bar {t} = 0) = ~{{\bar {P}}_{f}}(\bar {x},\bar {t} = 0) = 0~$

(1.11)

${{\bar {P}}_{r}}(\bar {x},\bar {y} = 0,\bar {t}) = {{\bar {P}}_{f}}(\bar {x},\bar {t})$

(1.12)

${{\bar {P}}_{f}}(\bar {x} = 0,\bar {t}) = 1~~$

(1.13)

$\frac{{\partial {{{\bar {P}}}_{f}}(\bar {x} = 0,\bar {t})}}{{\partial{ \bar {x}}}} = \frac{b}{a}$

(1.14)

${{\bar {P}}_{i}}(\bar {x} \to \infty ,\bar {y} \to \infty ,\bar {t}) = 0~~~(i = r,f).$

Здесь $a = {{\varkappa }_{f}}{\text{/}}{{\varkappa }_{r}}$, $b = a({{k}_{r}}{\text{/}}{{k}_{f}})({{x}_{f}}{\text{/}}{{w}_{f}})$, величина a/b совпадает с безразмерной проводимостью трещины, впервые введенной в [2] и широко используемой в литературе. Величины $P_{1}^{*}$ и $P_{2}^{*}$ относятся соответственно к первой и второй краевым задачам. Приведенная выше модель является инвариантной относительно изменения знаков дебита скважины и депрессии на пласт. Поэтому она позволяет исследовать как процесс отбора жидкости из пласта через трещину и скважину, так и процесс закачки жидкости в пласт через скважину с трещиной гидроразрыва.

Решение первой краевой задачи подробно рассмотрено в [10], поэтому мы здесь приведем только окончательный вид решения. В этой работе получено два вида решения. Первое решение имеет вид

(1.15)

${{\bar {P}}_{f}}\left( {\bar {x},\bar {t}} \right) = 1 - \frac{1}{\pi }\mathop \smallint \limits_0^\infty {\text{exp}}\left( { - \rho \bar {t} - {{f}_{1}}\left( \rho \right)\bar {x}} \right){\text{sin}}\left[ {{{f}_{2}}\left( \rho \right)\bar {x}} \right]\frac{{d\rho }}{\rho }$

(1.16)

${{\bar {P}}_{r}}\left( {\bar {x},\bar {y},\bar {t}} \right) = 1 - \frac{1}{\pi }\mathop \smallint \limits_0^\infty {\text{exp}}\left( { - \rho \bar {t} - {{f}_{1}}\left( \rho \right)\bar {x}} \right){\text{sin}}[{{f}_{2}}\left( \rho \right)\bar {x} + \rho \sqrt {\bar {y}} ]\frac{{d\rho }}{\rho }$

${{f}_{1}}\left( \rho \right) = {{\left[ {\frac{{\sqrt {{{\rho }^{2}} + {{b}^{2}}\rho } - \rho }}{{2a}}} \right]}^{{1/2}}},\quad {{f}_{2}}\left( \rho \right) = {{\left[ {\frac{{\sqrt {{{\rho }^{2}} + {{b}^{2}}\rho } + \rho }}{{2a}}} \right]}^{{1/2}}}$

Другой вид решения выражается формулами

(1.17)

${{\bar {P}}_{f}}\left( {\bar {x},\bar {t}} \right) = \frac{{\bar {x}}}{{\sqrt {\pi a\bar {t}} }}\mathop \smallint \limits_0^1 {\text{exp}}\left( { - \frac{{{{{\bar {x}}}^{2}}}}{{4a\bar {t}{{\rho }^{2}}}}} \right){\text{erfc}}\left( {\frac{{{{\rho }^{2}}b\sqrt {\bar {t}} }}{{2\sqrt {1 - {{\rho }^{2}}} }}} \right)\frac{{d\rho }}{{{{\rho }^{2}}}}$

(1.18)

${{\bar {P}}_{r}}\left( {\bar {x},\bar {y},\bar {t}} \right) = \frac{{\bar {x}}}{{\sqrt {\pi a\bar {t}} }}\mathop \smallint \limits_0^1 {\text{exp}}\left( { - \frac{{{{{\bar {x}}}^{2}}}}{{4a\bar {t}{{\rho }^{2}}}}} \right){\text{erfc}}\left( {\frac{{\bar {y} + {{\rho }^{2}}b\bar {t}}}{{2\sqrt {\bar {t}(1 - {{\rho }^{2}})} }}} \right)\frac{{d\rho }}{{{{\rho }^{2}}}}$

Здесь erfc(ξ) – дополнительная функция ошибок:

${\text{erfc}}(\xi ) = \frac{2}{{\sqrt \pi }}\mathop \smallint \limits_\xi ^\infty {\text{exp}}( - {{u}^{2}})du.$

Выражения (1.17), (1.18) должны быть тождественны (1.15), (1.16), так как они представляют решения одной и той же задачи, построенные методом преобразования Лапласа, но переход от изображений к оригиналу реализован разными методами. При получении выражений (1.15) и (1.16) использована теорема Меллина, а (1.17) и (1.18) получены, используя общие правила преобразования Лапласа.

2. РЕШЕНИЕ ЗАДАЧИ

Решение второй краевой задачи построим методом преобразования Лапласа по переменной t (L – символ преобразования Лапласа)

$L[\bar {P}(\bar {x},\bar {y},\bar {t})] = \bar {\bar {P}}(\bar {x},\bar {y},{\text{s}}){\text{\;}} = \mathop \smallint \limits_0^\infty \bar {P}(\bar {x},\bar {y},\bar {t}){\text{exp}}( - s\bar {t})d\bar {t}$

в изображениях преобразования Лапласа задача (1.8)–(1.14) имеет вид

(2.1)

$\frac{{{{d}^{2}}{{{\bar {\bar {P}}}}_{r}}}}{{d{{y}^{2}}}} = s{{\bar {\bar {P}}}_{r}}$

(2.2)

$\frac{{{{d}^{2}}{{{\bar {\bar {P}}}}_{f}}}}{{d{{x}^{2}}}} - \frac{s}{a}{{\bar {\bar {P}}}_{f}} + \frac{b}{a}{{\left. {\frac{{d{{{\bar {\bar {P}}}}_{r}}}}{{dy}}} \right|}_{{y = 0}}} = 0$

(2.3)

${{\bar {\bar {P}}}_{r}}(x,y = 0,s) = {{\bar {\bar {P}}}_{f}}(x,s)$

(2.4)

$\frac{{d{{{\bar {\bar {P}}}}_{f}}(0,s)}}{{dx}} = \frac{b}{a}\frac{1}{s}$

(2.5)

${{\bar {\bar {P}}}_{i}}(x \to \infty ,y \to \infty ) = 0~~~(i = r,f)$.

Таким образом, в пространстве изображений Лапласа получается система обыкновенных дифференциальных уравнений относительно ${{\bar {\bar {P}}}_{f}}$ и ${{\bar {\bar {P}}}_{r}}$.

Решение этой системы находится стандартными методами и представляется в следующем виде

(2.6)

${{\bar {\bar {P}}}_{f}}\left( {\bar {x},s} \right) = - \frac{b}{a}\frac{{{\text{exp}}\left( { - \bar {x} \cdot \delta } \right)}}{{s\delta }}$

(2.7)

${{\bar {\bar {P}}}_{r}}\left( {\bar {x},\bar {y},s} \right) = - \frac{b}{a}\frac{{{\text{exp}}( - \bar {x} \cdot \delta - \bar {y}\sqrt s )}}{{s\delta }}$

$\delta \equiv {{\left[ {\frac{s}{a} + \frac{b}{a}\sqrt s } \right]}^{{1/2}}}$

Окончательные решения задач получаются посредством перехода в выражениях (2.6), (2.7) к оригиналам.

Для удобства нахождения оригинала выражение (2.6) представим в виде

(2.8)

${{\bar {\bar {P}}}_{f}}\left( {\bar {x},s} \right) = - \frac{1}{{\sqrt a b\sqrt s }}L\left[ {V(\bar {x},\bar {t})} \right],~\quad L\left[ {V(\bar {x},\bar {t})} \right] = \frac{b}{{\sqrt s a}}\frac{{{\text{exp}}\left( { - \bar {x}\delta } \right)}}{\delta }$.

Используя теорему о свертке и формулу обращения преобразования Лапласа [11] (L^–1 – символ обратного преобразования Лапласа)

${{L}^{{ - 1}}}\left( {\frac{1}{{\sqrt s }}} \right) = \frac{1}{{\sqrt {\pi t} }}$

из (2.8) имеем

${{\bar {P}}_{f}}\left( {\bar {x},\bar {t}} \right) = - \frac{1}{{\sqrt a b}}\mathop \smallint \limits_0^{\bar {t}} \frac{1}{{\sqrt {\pi \left( {\bar {t} - \tau } \right)} }}V\left( {\bar {x},\tau } \right)d\tau ~.$

Таким образом, необходимо найти $V(\bar {x},\bar {t})$.

Используя теорему подобия [12] ко второму выражению (2.8), находим

(2.9)

$L[V(\bar {x},{{b}^{2}}\bar {t})] = \frac{1}{{\sqrt s }}\frac{{{\text{exp}}\left[ { - \frac{{b\bar {x}}}{{\sqrt a }}{{{(s + \sqrt s )}}^{{1/2}}}} \right]}}{{\sqrt {s + \sqrt s } }}.$

Для нахождения $V(\bar {x},\bar {t})$, в (2.9) используем следующее правило операционного исчисления [12]

${{L}^{{ - 1}}}\left[ {\frac{{g(s + \sqrt s )}}{{\sqrt s }}} \right] = \frac{1}{{\sqrt \pi }}\mathop \smallint \limits_0^{\bar {t}} \frac{1}{{\sqrt {\bar {t} - u} }}{\text{exp}}\left( { - \frac{{{{u}^{2}}}}{{4\left( {\bar {t} - u} \right)}}} \right)f\left( u \right)du,~\quad f\left( u \right) = {{L}^{{ - 1}}}\left[ {g\left( s \right)} \right].$

Тогда

$V(\bar {x},{{b}^{2}}\bar {t}) = \frac{1}{\pi }\mathop \smallint \limits_0^{{{b}^{2}}\bar {t}} {\text{exp}}\left( { - \frac{{{{u}^{2}}}}{{4({{b}^{2}}\tau - u)}} - \frac{{{{b}^{2}}{{x}^{2}}}}{{4au}}} \right)\frac{{du}}{{\sqrt {{{b}^{2}}\tau - u} \sqrt u }}.$

C учетом этого выражения, (2.9) можно представить в виде

$~{{\bar {P}}_{f}}\left( {\bar {x},\bar {t}} \right) = - \frac{1}{{\sqrt a b\pi \sqrt \pi }}\mathop \smallint \limits_0^{\bar {t}} \frac{1}{{\sqrt {\bar {t} - \tau } }}\mathop \smallint \limits_0^{{{b}^{2}}\tau } {\text{exp}}\left( { - \frac{{{{u}^{2}}}}{{4({{b}^{2}}\tau - u)}} - \frac{{{{b}^{2}}{{{\bar {x}}}^{2}}}}{{4au}}} \right)\frac{{dud\tau }}{{\sqrt {{{b}^{2}}\tau - u} \sqrt u }}.$

Изменяя здесь порядок интегрирования и вычисляя внутренний интеграл

$\mathop \smallint \limits_{u/{{b}^{2}}}^{\bar {t}} \frac{1}{{\sqrt {({{b}^{2}}\tau - u)\left( {\bar {t} - \tau } \right)} }}{\text{exp}}\left( { - \frac{{{{u}^{2}}}}{{4({{b}^{2}}\tau - u)}}} \right)d\tau = \frac{\pi }{b}{\text{erfc}}\left( {\frac{u}{{2\sqrt {{{b}^{2}}\bar {t} - u} }}} \right),$

в итоге получаем выражение для распределения давления в трещине:

(2.10)

${{\bar {P}}_{f}}\left( {\bar {x},\bar {t}} \right) = - \frac{1}{{\sqrt a \sqrt \pi }}\mathop \smallint \limits_0^{{{b}^{2}}\bar {t}} {\text{exp}}\left( { - \frac{{{{b}^{2}}{{{\bar {x}}}^{2}}}}{{4au}}} \right){\text{erfc}}\left( {\frac{u}{{2\sqrt {{{b}^{2}}\bar {t} - u} }}} \right)\frac{{du}}{{\sqrt u }}.$

В (2.10), для удобства численных расчетов, произведем замену переменной интегрирования u на ${{\rho }^{2}}{{b}^{2}}\bar {t}$. Тогда имеем

(2.11)

${{\bar {P}}_{f}}\left( {\bar {x},\bar {t}} \right) = - \frac{{2b\sqrt {\bar {t}} }}{{\sqrt a \sqrt \pi }}\mathop \smallint \limits_0^1 {\text{exp}}\left( { - \frac{{{{{\bar {x}}}^{2}}}}{{4a\bar {t}{{\rho }^{2}}}}} \right){\text{erfc}}\left( {\frac{{{{\rho }^{2}}b\sqrt {\bar {t}} }}{{2\sqrt {(1 - {{\rho }^{2}})} }}} \right)d\rho .$

Выполняя аналогичные операции, из (2.7) получаем выражение для распределения давления в пласте

(2.12)

${{\bar {P}}_{r}}\left( {\bar {x},\bar {y},\bar {t},} \right) = - \frac{{2b\sqrt {\bar {t}} }}{{\sqrt a \sqrt \pi }}\mathop \smallint \limits_0^1 {\text{exp}}\left( { - \frac{{{{{\bar {x}}}^{2}}}}{{4a\bar {t}{{\rho }^{2}}}}} \right){\text{erfc}}\left( {\frac{{{{\rho }^{2}}b\bar {t} + \bar {y}}}{{2\sqrt {\bar {t}(1 - {{\rho }^{2}})} }}} \right)d\rho .$

3. АНАЛИЗ РЕШЕНИЯ

Полагая в (2.12) $\bar {x} = 0$, находим давление на забое скважины

(3.1)

${{\bar {P}}_{f}}(\bar {x} = 0,\bar {t}) = - \frac{1}{{\sqrt {\pi a} }}\mathop \smallint \limits_0^{{{b}^{2}}\bar {t}} {\text{erfc}}\left( {\frac{u}{{2\sqrt {{{b}^{2}}\bar {t} - u} }}} \right)\frac{{du}}{{\sqrt u }}.$

Асимптотическое представление этой формулы, соответствующее большим значениям времени, является одним из основных теоретических выражений, используемых при гидродинамическом исследовании скважин с трещиной гидроразрыва. А именно, это выражение определяет характерную для билинейного режима фильтрации зависимость давления на забое скважины от времени в степени 1/4, и представляет теоретическую формулу для оценки проводимости трещины [2].

В работе [2] отмечается, что ввиду сложности получение соответствующей асимптотики для больших времен из (3.1) является затруднительным. Поэтому эта асимптотика определяется в пространстве изображений Лапласа из выражения (2.6) при x = 0 и малых s (больших t) и последующим переходом от изображения к оригиналу.

Покажем, как можно получить асимптотику (3.1) для больших времен. Для этого случая (b²t → ∞) выражение (3.1) представим в виде

(3.2)

${{\bar {P}}_{f}}(\bar {x} = 0,\bar {t}) \approx - \frac{1}{{\sqrt {\pi a} }}\mathop \smallint \limits_0^\infty {\text{erfc}}\left( {\frac{u}{{2b\sqrt {\bar {t}} }}} \right)\frac{{du}}{{\sqrt u }}.$

Используя подстановку $u{\text{/}}2b\sqrt {\bar {t}} = z$, получаем

(3.3)

${{\bar {P}}_{f}}(\bar {x} = 0,\bar {t}) = - \sqrt {\frac{2}{\pi }} \sqrt {\frac{b}{a}} {{(\bar {t})}^{{\frac{1}{4}}}}\mathop \smallint \limits_0^\infty {\text{erfc}}(z)\frac{{dz}}{{\sqrt z }} = \sqrt {\frac{2}{\pi }} \sqrt {\frac{b}{a}} {{(\bar {t})}^{{\frac{1}{4}}}}\frac{{2Г(0.75)}}{{\sqrt \pi }} = 1.103\sqrt {\frac{b}{a}} {{(\bar {t})}^{{\frac{1}{4}}}}.$

Здесь Г – гамма-функция

$\Gamma \left( \xi \right) = \mathop \smallint \limits_0^\infty {\text{exp}}\left( { - u} \right){{u}^{{\xi - 1}}}du$.

Это выражение можно использовать для определения проводимости трещины так называемым методом типовых кривых, т.е. путем сопоставительного его анализа с кривой изменения давления, экспериментально определяемой на забое скважины.

Представление формулы (3.3) в размерном виде

(3.4)

${{P}_{f}}(x = 0,t) = {{P}_{0}} - 1.103\frac{{Q{{\mu }^{{3/4}}}{{t}^{{1/4}}}}}{{{{h}_{r}}\sqrt {{{w}_{f}}{{k}_{f}}} \beta _{*}^{{1/4}}k_{r}^{{1/4}}}}$

позволяет в явном виде выяснить зависимость давления от основных параметров, характеризующих пласт, трещину и жидкость (в этой формуле ${{\beta }_{*}}$ – коэффициент упругоемкости пласта). Анализ показывает, что наличие трещины качественно меняет характер течения. Так, классическим аналогом (при отсутствии трещины) выражения (3.4) является формула для давления на галерее [13]

(3.5)

$P\left( {x = 0,t} \right) = {{P}_{0}} - 1.128\frac{{Q\sqrt \mu \sqrt t }}{{b{{h}_{r}}\sqrt {{{k}_{r}}} \sqrt {{{\beta }_{*}}} }}$.

Из сравнения (3.4) и (3.5) видно, что наличие трещины гидроразрыва существенным образом влияет на распределение давления, различие между выражениями является качественным, так как принципиально отличаются зависимости давления от времени, вязкости, проницаемости и упругоемкости пласта.

Количество жидкости, поступающее из пласта в трещину, определяется из выражения

$q = \mathop \smallint \limits_0^\infty {{\left. {\frac{{\partial {{{\bar {P}}}_{r}}}}{{\partial{ \bar {y}}}}} \right|}_{{\bar {y} = 0}}}d\bar {x}.$

Тогда, с учетом выражений (1.12), (1.13) и (1.18), можно найти долю в дебите скважины объема жидкости, поступающего в трещину из пласта

$\frac{q}{Q} = 1 - {\text{exp}}({{b}^{2}}\bar {t}){\text{erfc}}(b\sqrt {\bar {t}} ).$

Из этого выражения следует, что в начальной стадии в дебите скважины преобладает доля притока из трещины, со временем увеличивается доля притока из пласта. Так, при $\bar {t} < 0.59{\text{/}}{{b}^{2}}$ больше половины дебита скважины определяется емкостью трещины, в размерном виде это условие имеет вид

$t < 0.59{{\left( {\frac{{{{k}_{f}}}}{{{{k}_{r}}}}} \right)}^{2}}\frac{{{{\kappa }_{r}}w_{f}^{2}}}{{\kappa _{f}^{2}}}.$

Оценки по этому выражению показывают, что проявление емкости трещины в дебите скважины является заметным при малых временах и при малых значениях подвижности k^r/μ жидкости в пласте.

В области определения $0 \leqslant z \leqslant 1$ функция erfc изменяется в пределах от 1 до 0, поэтому, согласно теореме о среднем значении [14], выражение (2.11) можно представить в виде

(3.6)

${{\bar {P}}_{f}}(\bar {x},\bar {t}) = \frac{{2b}}{{\sqrt \pi }}\frac{{\sqrt {\bar {t}} }}{{\sqrt a }}c\mathop \smallint \limits_0^1 {\text{exp}}\left( { - \frac{{{{{\bar {x}}}^{2}}}}{{4a\bar {t}{{z}^{2}}}}} \right)dz,\quad 0 \leqslant c \leqslant 1.$

Очевидно, что значение этого выражения при c = 1 является мажорантой для построенного выше решения (2.11) во всем диапазоне изменения $\bar {x}$ и $\bar {t}$. Вычисляя интеграл в (3.6), полагая c = 1, получаем известную формулу, описывающую распределение давления при плоскопараллельной фильтрации жидкости в полубесконечном пласте, когда при x = 0 задано значение дебита [13]. В размерных переменных эта формула, которая следует так же из полученного выше решения (2.11) при k_r = 0 (отсутствие перетока жидкости из пласта в трещину), имеет вид

${{P}_{f}}\left( {x,t} \right) = {{P}_{0}} + \frac{{\mu Q}}{{{{k}_{f}}{{w}_{f}}{{h}_{r}}}}\left[ {x~{\text{erfc}}\left( {\frac{x}{{2\sqrt {{{\kappa }_{f}}t} }}} \right) - \frac{{2\sqrt {{{\kappa }_{f}}t} }}{{\sqrt \pi }}{\text{exp}}\left( { - \frac{{{{x}^{2}}}}{{4{{\kappa }_{f}}t}}} \right)} \right].$

Рассмотрим некоторые результаты численных расчетов по выражениям (2.11), (2.12) и (3.4). Рассматривается отбор жидкости из пласта при следующих значениях параметров: начальное давление пласта P₀ = 200 × 10⁵ Па, мощность продуктивного пласта h_r = 10 м, дебит Q = 10 м³/сут, ширина трещины w_f = 5 × 10^–3 м, проницаемости пласта и трещины соответственно k_r = 10^–13 м², k_f = 10^–10 м², вязкость жидкости μ = 4 × 10^–3 Па⋅с, коэффициент упругоемкости β = 10^–9 Па^–1.

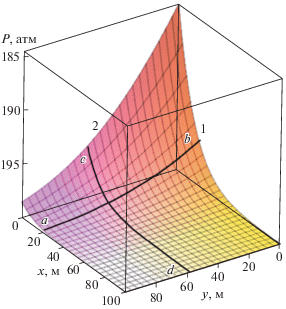
На рис. 2 представлено распределение давления в пласте и в трещине для фиксированного момента времени t = 1 сутки. На этом рисунке кривая 1 описывает изменение давления вдоль трещины P_f(x, t) (формула (2.11)), кривая 2 – изменение давления в пласте P_r (x = 0, y, t) по формуле (2.12). Пересекающиеся линии на этом графике определяют соответствующие значения давления по осям x и y. В частности, линия ab описывает изменение давления в рассматриваемый момент времени на расстоянии x = 20 м от скважины (по трещине) для всех точек пласта 0 < y < < 100 м. Аналогично, линия cd определяет давление P (x, y = 60 м, t = 1 сут).

Рис. 2.

Распределение давления (P) в трещине и в пласте: t = 1 сут; 1 – вдоль трещины – P = P_f(x); 2 – в пласте – P = P_r (x = 0, y); ab – P (x = 20 м, y); cd – P (x, y = 60 м)

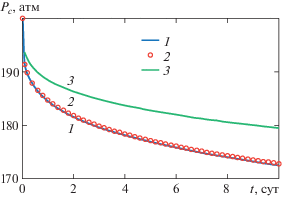
На рис. 3 представлены зависимости давления на забое скважины от времени. Здесь кривые 1 и 2 построены соответственно по точной формуле (3.1) и асимптотической формуле (3.4), кривая 3 – по формуле, полученной в работе [4] в приближении несжимаемости жидкости в трещине. Эта формула с точностью до обозначений совпадает с выражением (33), но имеется количественное различие в численных коэффициентах, в работе [4] этот коэффициент равен 0.83, в формуле (3.4) – 1.103. Расчеты по формулам (3.1) и (3.4) показывают совпадение результатов – во всем практически значимом диапазоне изменения времени разница не превышает 1%. Различие между кривыми 1 и 3 является заметным и увеличивается с ростом времени. При t = 1 сут это различие составляет 2%, при t = 10 сут – 4%. Таким образом, асимптотическое представление точного решения (формула (3.4)) является более приемлемым по сравнению с приближением, когда не учитывается сжимаемость трещины.

Рис. 3.

Распределение давления на забое скважины: 1 – формула (3.1), 2 – формула (3.4), 3 – формула в приближении несжимаемости жидкости в трещине

Отметим, что асимптотическое представление точного решения возможно не только при x = 0, а при любых значениях x. Полагая ${{b}^{2}}\bar {t} \gg u$ и заменяя переменные интегрирования, формулу (2.10) можно привести к асимптотическому виду, в котором явно выделяется зависимость от времени в степени 1/4.

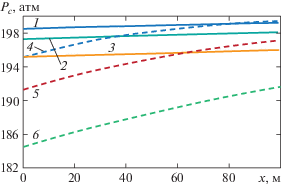
Из рис. 4 (формула (2.11)) видно, что с увеличением проницаемости трещины падение давления вдоль трещины резко уменьшается. Эпюры давления постепенно выпрямляются. Как следует из рисунка, при k_f = 10^–8 м² падение давления в трещине за 100 сут составляет менее 1 атм. Это означает, что при принятых параметрах трещина имеет большую проводимость, поэтому распределение давления вдоль трещины становится практически однородным.

Рис. 4.

Распределение давления в трещине при различных значениях проницаемости трещины (сплошные линии – k_f = 10^–8 м², штриховые линии – k_f = 10^–9 м²): t = 1 сут (1, 4), 10 сут (2, 5), 100 сут (3, 6)

ЗАКЛЮЧЕНИЕ

В работе представлены новые аналитические решения теории нестационарной фильтрации жидкости в пласте с вертикальной трещиной гидроразрыва. Решения получены на основе реализации модели с учетом фильтрации жидкости в пласте и сжимаемости трещины, которая является более общей, чем известные в литературе. Эти решения и их асимптотические представления имеют значимость для теоретического обоснования методов гидродинамических исследований пластов и для оценки дебита скважин с трещиной гидроразрыва. Показано, что при наличии трещины гидроразрыва качественно меняется характер течения в пласте, а именно зависимости давления от времени, вязкости жидкости, проницаемости и упругоемкости пласта. Использование решений в случае нагнетательных скважин позволяет описать динамику заводнения пластов с трещинами гидроразрыва, в частности определить скорость движения жидкости в трещине и в пласте при моделировании трассерных исследований.

Список литературы

Каневская Р.Д. Математическое моделирование разработки месторождений нефти и газа с применением гидравлического разрыва пласта. М.: ООО “Недра-Бизнесцентр”, 1999. 212 с.
Cinco-Ley H., Samaniego V.F. Transient Pressure Analysis for fractured wells // J. Petrol. Techonol. 1981. V. 33. № 9. P. 1749–1766.
Wong D.W., Harrington A.G., Cinco-Ley H. Application of the Pressure-Derivative Function in the Pressure-Transient Testing of Fracture Wells // Paper SPE 13056, SPE formation Evaluation. 1986. P. 470–480.
Нагаева З.М., Шагапов В.Ш. Об упругом режиме фильтрации в трещине, расположенной в нефтяном или газовом пласте // ПММ. 2017. Т. 81. Вып. 3. С. 319–329.
Асалхузина Г.Ф., Давлетбаев А.Я., Хабибуллин И.Л. Моделирование дифференциации пластового давления между нагнетательными и добывающими скважинами на месторождениях с низкопроницаемыми коллекторами // Вестн. Башкирского ун-та. 2016. Т. 21. № 3. С. 537–542.
Хабибуллин И.Л., Евграфов Н.А., Хисамов А.А. Моделирование нестационарного притока жидкости из пласта в скважину через трещину гидроразрыва // Сб. тр. Первой летней школы-конференции “Физико-химическая гидродинамика: модели и приложения”. Уфа: РИЦ БашГУ, 2016. С. 184–192.
Эрлагер Р. Гидродинамические методы исследования скважин. М.–Ижевск: Ин-т компьют. исслед., 2007. 521 с.
Хасанов М.М., Головнева О.Ю. Определение дебита вертикальных скважин с гидроразрывом пласта на неустановившемся режиме фильтрации // Нефтяное хозяйство. 2016. № 12. С. 64.
Хабибуллин И.Л., Хисамов А.А. Моделирование нестационарной фильтрации вокруг скважины с вертикальной трещиной гидроразрыва // Вестн. Башкирского ун-та. 2017. Т. 22. № 2. С. 309–314.
Хабибуллин И.Л., Хисамов А.А. К теории билинейного режима фильтрации в пластах с трещинами гидроразрыва // Вестн. Башкирского ун-та. 2018. Т. 23. № 4. С. 958–963.
Дёч Г. Руководство к практическому применению преобразования Лапласа и z-преобразования. М.: Наука, 1971. 288 с.
Диткин А.В., Прудников А.П. Операционное исчисление. М.: Высшая школа, 1975. 407 с.
Басниев К.С., Дмитриев Н.М., Каневская Р.Д., Максимов В.М. Подземная гидромеханика. М.–Ижевск: Ин-т компьют. исслед., 2006. 488 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. М.: Наука, 2003. 800 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал