Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 63-71
Ламинарное течение степенной жидкости в Т-образном канале при заданных перепадах давления
Е. И. Борзенко a, О. А. Дьякова a, *, Г. Р. Шрагер a
a Томский государственный университет, физико-технический факультет
Томск, Россия
* E-mail: dyakova_o@ftf.tsu.ru
Поступила в редакцию 14.12.2018
После доработки 20.12.2018
Принята к публикации 20.12.2018
Аннотация
Статья посвящена исследованию установившегося ламинарного течения несжимаемой степенной жидкости в плоском Т-образном канале при заданных перепадах давления между граничными сечениями втекания/вытекания. Степенной жидкостью называется неньютоновская жидкость, реологическое поведение которой описывается законом Оствальда-де Виля. Математическая постановка задачи включает уравнения движения и неразрывности. На твердых стенках задается условие прилипания. Для нахождения решения задачи используется конечно-разностный метод с применением процедуры SIMPLE. Проведены параметрические исследования кинематических и динамических характеристик течения в зависимости от основных параметров задачи. Построена диаграмма режимов течения при изменении значений перепадов давления, задаваемых между границами втекания/вытекания канала, для различных показателей нелинейности реологической модели.
Трубопроводные сети, используемые для транспортировки жидкостей и газов в различных технологиях, состоят из множества элементов. Одним из таких элементов является Т-образный канал, который применяется для разветвления и смешения потоков. Исследование течений в подобных конструктивных элементах имеет практическую значимость для технологий орошения и вентиляции, химической, нефтегазовой и других отраслей промышленности [1, 2]. За последнее десятилетие выполнено большое количество исследований движения жидкостей в микроканалах Т-типа [3, 4], которые используются в биомедицине, микробиологии [5], а также в технологии охлаждения микропроцессорной техники [6].
Т-образный канал характеризуется наличием трех границ, через которые жидкость втекает или вытекает. При рассмотрении задач о течениях в каналах с такой геометрией нет общепринятого мнения о предпочтительности вида условий на границах втекания/вытекания как с математической, так и с физической точек зрения [7]. В большинстве случаев такие задачи рассматриваются с заданным профилем скорости на входной границе. К настоящему времени проведены исследования, посвященные изучению течения как ньютоновских [8–13], так и неньютоновских [13–17] жидкостей в Т-образном канале с заданным профилем скорости. Однако во многих случаях скорости на границах неизвестны, поэтому целесообразнее задавать перепады давления между границами втекания и вытекания с последующим определением расхода и направлений течения.
В литературе имеется ограниченное количество работ, посвященных исследованию течения вязкой жидкости с граничными условиями для давления. В [18] проводилось численное моделирование течения ньютоновской несжимаемой жидкости в плоском Т-образном канале, когда на участках границы заданы значения давления и нулевая касательная компонента вектора скорости, с использованием метода расщепления по физическим переменным. Течение степенной жидкости в плоском Т-образном канале с математической постановкой, аналогичной [18], исследовано в [19]. Решение задачи о движении ньютоновской жидкости в Т-образном канале с заданным профилем скорости на входной границе и значениями давления на выходных границах на основе метода конечных элементов представлено в [20]. Решение задачи о течении вязкой жидкости, движущейся под действием заданного перепада давления в канале с несколькими границами втекания/вытекания, выполнено с использованием вариационного подхода в [21]. Задачи тепло- и массопереноса в каналах с различной геометрией, включая Т-образный канал, с заданными граничными условиями для давления численно исследованы с использованием процедуры SIMPLE в [22]. Решение нестационарной трехмерной задачи течения вязкой жидкости с граничными условиями Дирихле для давления, полученное с помощью конечно-разностного метода, представлено в [23]. Течение жидкости Пауэлла-Эйринга в прямой и изогнутой трубах при заданных значениях давления на входе и выходе рассмотрено в [24]. Задача о стационарном течении вязкой несжимаемой жидкости, движущейся под действием заданного перепада давления, при наличии источников/стоков внутри канала численно решена в [25]. Результаты подробного исследования течения ньютоновской несжимаемой жидкости в плоском Т-образном канале при заданных перепадах давления между граничными сечениями представлены в [26]. Построена диаграмма характерных режимов течения, проведен анализ структуры течения и поля давления в области перехода из одного режима в другой.
Целью настоящей работы является исследование установившегося течения степенной жидкости в плоском Т-образном канале при заданных значениях давления на границах втекания/вытекания.
1. ПОСТАНОВКА ЗАДАЧИ
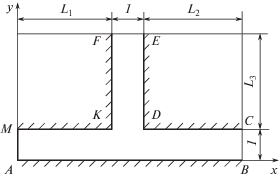
Рассматривается установившееся ламинарное течение неньютоновской несжимаемой жидкости в плоском Т-образном канале. Геометрия канала схематично представлена на рис. 1; начало координат находится в точке А. Область течения ограничена твердыми стенками MKF, EDC и AB. Жидкость втекает или вытекает через граничные сечения AM, FE и BC. Математическую основу задачи образует система уравнений движения и неразрывности, которые в безразмерных переменных записываются в виде
(1.1)
$u\frac{{\partial u}}{{\partial x}} + \text{v}\frac{{\partial u}}{{\partial y}} = - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {{\tau }_{{xx}}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{yx}}}}}{{\partial y}}$(1.2)
$u\frac{{\partial \text{v}}}{{\partial x}} + \text{v}\frac{{\partial v}}{{\partial y}} = - \frac{{\partial p}}{{\partial y}} + \frac{{\partial {{\tau }_{{xy}}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{yy}}}}}{{\partial y}}$Здесь u и $\text{v}$ – компоненты вектора скорости u в декартовой системе координат (x, y), p – давление, ${{\tau }_{{ij}}}$ – компоненты тензора вязких напряжений.
Система уравнений (1.1)–(1.3) замыкается реологическим уравнением Оствальда-де Виля [27]
где ${{e}_{{ij}}}$ – компоненты тензора скоростей деформаций, $A = {{(2{{e}_{{ij}}}{{e}_{{ji}}})}^{{0.5}}}$ – интенсивность тензора скоростей деформаций, m – показатель нелинейности. Величины определяются по формуле:Безразмерная эффективная вязкость определяется выражением
В качестве масштабов обезразмеривания длины и скорости используются величины L (ширина канала в сечении AM) и U0 = (k/ρLm)1/(2 – m) соответственно. Безразмерное давление вычисляется по формуле
Граничные условия в сечениях AM, FE и BC заключаются в задании нулевой поперечной скорости и значения давления и в безразмерном виде записываются следующим образом:
(1.6)
$\begin{gathered} \text{v} = 0,\quad {{p}_{{AM}}} = {{p}_{{\text{1}}}},\quad x = 0,\quad 0 \leqslant y \leqslant 1 \\ u = 0,\quad {{p}_{{FE}}} = 0,\quad {{L}_{1}} \leqslant x \leqslant {{L}_{1}} + 1,\quad y = {{L}_{3}} + 1 \\ \text{v} = 0,\quad {{p}_{{BC}}} = {{p}_{{\text{3}}}},\quad x = {{L}_{1}} + {{L}_{2}} + 1,\quad 0 \leqslant y \leqslant 1 \\ \end{gathered} $Здесь L1, L2 и L3 – безразмерные геометрические характеристики области течения (рис. 1).
На твердых стенках выполняется условие прилипания
2. МЕТОД РАСЧЕТА
Задача решается численно с помощью конечно-разностного метода. Для нахождения стационарных полей скорости и давления используется метод установления [28], который подразумевает добавление производных искомых функций u и v по времени в уравнения (1.1) и (1.2) соответственно. Полученные уравнения дискретизируются на квадратной разнесенной сетке с использованием метода контрольного объема. Для коррекции полей скорости с целью выполнения разностного аналога уравнения неразрывности используется процедура SIMPLE [29].
С целью проверки аппроксимационной сходимости были проведены расчеты на последовательности сеток. Вычисленное распределение продольной скорости в граничном сечении, расход через которое является максимальным, сравнивалось с аналитическим решением задачи о полностью развитом течении степенной жидкости в плоском канале с заданным перепадом давления на единицу длины δp [30]
Значение δp определяется численно в зоне одномерного течения в окрестности рассматриваемой границы. В таблице 1 приведена зависимость значения относительной ошибки Er от шага сетки h при значении показателя нелинейности m = 0.8 и давлениях p1 = 100, p3 = –250. В этом случае максимальный расход жидкости достигается в граничном сечении BC. Величина Er рассчитывается по формуле
Таблица 1.
Зависимость ошибки Er от шага сетки h (m = 0.8, p1 = 100, p3 = –250)
| h | Er, % |
|---|---|
| 1/10 | 1.841 |
| 1/20 | 0.786 |
| 1/40 | 0.286 |
| 1/80 | 0.107 |
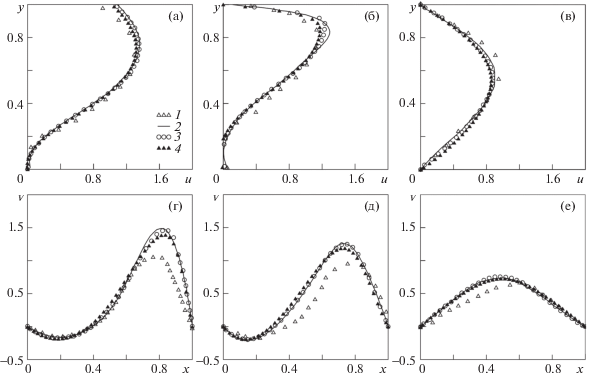
Для тестирования численной методики дополнительно была реализована математическая модель, используемая в [26], и проведено сравнение полученных результатов с данными экспериментальных [8] и численных [13, 26] исследований течения вязкой жидкости в плоском Т-образном канале. Эксперименты в [8] проведены при значении числа Рейнольдса Re = 248 (Re = = ρUavgL/μ, Uavg – среднерасходная скорость во входном сечении AM, μ – динамическая вязкость жидкости) и соотношении расходов через сечения FE и AM β = QFE/QAM = 0.44. В настоящей работе расчеты выполнены в канале с размерами L1 = 2, L2 = 11, L3 = 13. Жидкость втекает в канал через сечение AM, в котором задан профиль скорости $u(y) = 6(y - {{y}^{2}})$, характерный для полностью развитого течения ньютоновской жидкости в плоском канале. В выходном сечении FE задано давление p2 = 0. Для того чтобы выполнить сравнение с результатами работ [8, 13], необходимо задать значение давления p3 = 71.982, которое будет соответствовать значению соотношения расходов β = 0.44. На рис. 2 представлены результаты сравнения профилей скорости, полученные с помощью разработанной численной методики, с данными [8, 13, 26]. Сравнение показывает качественное и количественное согласование.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
В настоящей работе все исследования проведены для Т-образного канала с ответвлениями единичной ширины и одинаковой длины L1 = L2 = L3 = 3 (рис. 1). При фиксированных размерах канала характеристики рассматриваемого течения зависят от показателя нелинейности m и значений давления p1 и p3, задаваемых на границах AM и BC соответственно. В ходе параметрических исследований задачи было установлено, что для степенной жидкости, так же как и для ньютоновской, можно выделить 4 характерных режима течения (I–IV), отличающихся направлением течения в ветвях канала.
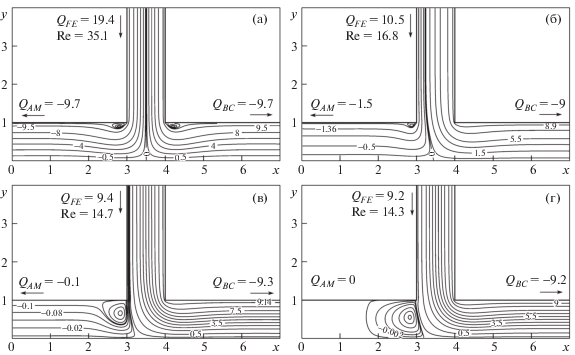
На рис. 3 представлено распределение линий тока для режима I. Рисунок 3а демонстрирует картину течения, которая реализуется при одинаковых значениях давления p1 = p3 = –400. Распределение характеристик симметрично. Втекающий поток делится на две равные части, при этом в окрестности границ AM, FE и BC формируются одномерные движения с профилем скорости, характерным для установившегося течения степенной жидкости в плоском бесконечном канале. Вблизи угловых точек K и D образуются две циркуляционные зоны одинаковых размеров. Увеличение давления p1 при прочих равных приводит к нарушению симметрии. Поток, движущийся в сторону сечения BC, становится интенсивнее потока, движущегося в сторону сечения AM (рис. 3б). Циркуляционная зона вблизи угловой точки D исчезает. При дальнейшем увеличении давления p1 размеры циркуляционной зоны вблизи угловой точки K увеличиваются (рис. 3в). При значении давления p1 = –149.023 циркуляционная зона достигает своих максимальных размеров и перекрывает поперечное сечение, в результате чего расход жидкости через сечение AM становится равным нулю (рис. 3г).
Рис. 3.
Распределение линий тока для режима I: m = 0.8, p3 = –400; p1 = –400, –200, –155, –149.023 (а–г)
Для анализа результатов и возможности использования теории подобия, следуя [26], число Рейнольдса определяется по формуле $\operatorname{Re} = (\rho U_{{avg}}^{{2 - m}}{{L}^{m}}){\text{/}}k$, где Uavg – вычисленное значение размерной среднерасходной скорости на границе с максимальным расходом жидкости. При выбранной характерной скорости с помощью математических преобразований можно прийти к выражению, связывающему число Рейнольдса и безразмерный расход жидкости
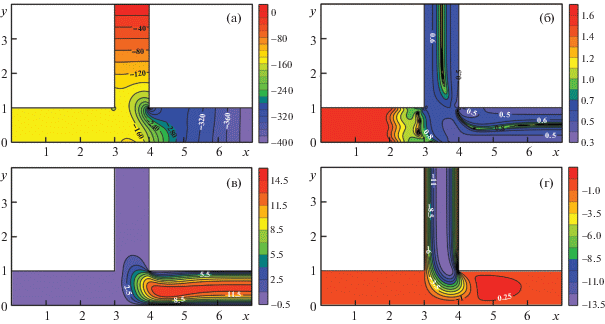
где Qmax – максимальный безразмерный расход жидкости, который рассчитывается при заданных значениях давления p1 и p3. Отрицательные значения расхода соответствуют случаю, когда жидкость вытекает из канала, а положительные – когда жидкость втекает из него.Рисунок 4 демонстрирует распределения характеристик течения при p1 = –149.023, что соответствует случаю, представленному ранее на рис. 3г. Из рис. 4а видно, что в ответвлении, содержащем сечение AM, отсутствует градиент давления, при этом вязкость достигает максимальных значений по всей ширине сечения AM (рис. 4б).
Рис. 4.
Характеристики течения: m = 0.8, p1 = –149.023, p3 = –400; поля давления (а), вязкости (б), компонент скорости u (в) и v (г)
При p1 > –149.023 в ответвлении, содержащем сечение AM, происходит переориентация потока и в канале реализуется режим II (рис. 5а). Число Рейнольдса в этом режиме определяется расходом жидкости через сечение BC. Жидкость втекает через граничные сечения AM и FE и после слияния входных потоков покидает канал через сечение BC. С ростом давления p1 при неизменных значениях остальных параметров циркуляционная зона вблизи угловой точки K уменьшается и смещается в сторону твердой границы AB. Дальнейшее увеличение p1 при прочих равных приводит к исчезновению циркуляционной зоны вблизи твердой границы AB и образованию циркуляционной зоны вблизи угловой точки D. При p1 = 286.693 циркуляционная зона достигает своих максимальных размеров и перекрывает поперечное сечение, а расход жидкости через сечение FE становится равным нулю.
Рис. 5.
Распределение линий тока для различных режимов течения: m = 0.8; (а) – режим II, p1 = –145, p3 = –400; (б) – режим III, p1 = 300, p3 = –400; (в) – режим IV, p1 = 300, p3 = 195
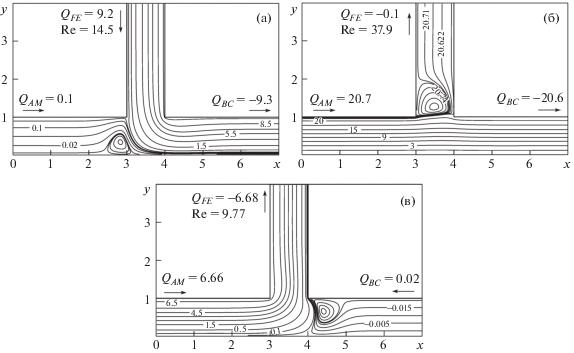
Рисунок 5б демонстрирует распределение линий тока для режима III, в котором происходит переориентация потока в ответвлении, содержащем сечение FE. Жидкость втекает в канал через граничное сечение AM и вытекает через граничные сечения FE и BC. Число Рейнольдса определяется расходом жидкости через сечение AM. С ростом давления p1 > 286.693 при прочих равных циркуляционная зона в ответвлении, содержащем сечение FE, уменьшается и смещается в сторону твердой стенки KF. Далее, чтобы проанализировать возможные картины течения для режима III, значение давления p1 = 300 было зафиксировано, а значение давления p3 варьировалось. В этом случае увеличение давления (p3 > –400) приводит к исчезновению циркуляционной зоны в ответвлении, содержащем сечение FE, и образованию циркуляционной зоны вблизи твердой стенки AB. Образовавшаяся циркуляционная зона достигает максимальных размеров при p3 = 194 и аналогично предыдущим режимам, расход через сечение BC становится нулевым.
При p3 > 194 происходит переориентация потока в ответвлении, содержащем сечение BC. В канале реализуется режим IV, в котором два потока жидкости, втекающие через граничные сечения AM и BC, сливаются в один и покидают канал через граничное сечение FE. Число Рейнольдса в этом режиме определяется расходом жидкости через сечение FE. На рис. 5в представлена картина течения для режима IV. С ростом давления p3 > 194 и остальных неизменных параметрах циркуляционная зона в ответвлении, содержащем сечение BC, уменьшается и смещается в сторону твердой стенки CD. Дальнейшее увеличение p3 приводит к исчезновению циркуляционной зоны.
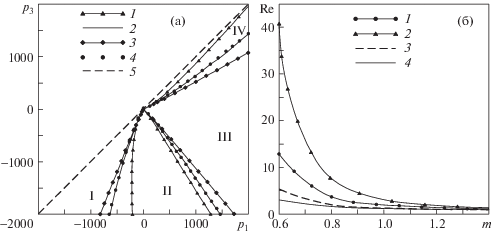
Представленные выше результаты относились к псевдопластичной жидкости (m = 0.8). Параметрические исследования течений ньютоновской (m = 1) и дилатантной (m = 1.2) жидкостей показали, что для этих случаев также можно выделить 4 режима течения. При этом характер изменения картины течения ньютоновской и дилатантной жидкостей аналогичен тому, что реализуется в случае течения псевдопластичной жидкости. На рис. 6а изображена диаграмма режимов течения в плоскости p1 – p3 для жидкостей со значениями показателя нелинейности m = 0.8; 1; 1.2, которая демонстрирует кривые перехода из одного режима в другой. Штриховая линия соответствует случаю, когда p1 = p3. Способ представления результатов в виде диаграммы аналогичен способу, использованному в [26]. Кривые перехода, полученные в [26] для ньютоновской жидкости, так же представлены на рис. 6а. Анализ диаграммы позволяет сделать вывод, что уменьшение показателя нелинейности приводит к увеличению размеров областей диаграммы, в которых реализуются режимы I и III, а следовательно, уменьшению размеров областей, соответствующих режимам II и IV. С помощью построенной диаграммы можно определить значения давления p1 и p3, которые необходимо задать в граничных сечениях AM и BC для реализации того или иного режима течения.
На рис. 6б представлена зависимость числа Рейнольдса Re от показателя нелинейности m для различных режимов течения. Для всех выделенных режимов наблюдается убывающий характер зависимости. Такое поведение можно объяснить реологическими особенностями рассматриваемой жидкости. При этом для псевдопластичной жидкости можно отметить большее влияние показателя нелинейности на расход жидкости, а следовательно, и на число Рейнольдса.
ЗАКЛЮЧЕНИЕ
В настоящей работе проведено исследование установившегося ламинарного течения степенной жидкости, движущейся в плоском Т-образном канале под действием заданных перепадов давления между граничными сечениями.
Представлены результаты численного решения задачи при значениях показателя нелинейности $0.6 \leqslant m \leqslant 1.2$ и давления $ - 2000 \leqslant {{p}_{1}}$, ${{p}_{3}} \leqslant 2000$. Выбранные значения показателя нелинейности соответствуют псевдопластичным (m < 1), ньютоновским (m = 1) и дилатантным (m > 1) жидкостям. Установлено, что в рассматриваемом диапазоне значений давления p1 и p3 для степенной жидкости возможны 4 характерных режима течения. Продемонстрированы распределения кинематических и динамических характеристик для выделенных режимов течения. Выполнена оценка степени влияния основных параметров задачи на картину течения. Построена диаграмма режимов течения в плоскости p1 – p3 для указанных видов жидкостей.
Список литературы
Grace J.L., Priest M.S. Division of flow in open channel junctions. Auburn, Ala.: Engineering Experiment Station, Alabama Polytechnic Institute, 1958. 98 p.
Neofytou P., Housiadas C., Tsangaris S.G., Stubos A.K., Fotiadis D.I. Newtonian and Power-Law fluid flow in a T-junction of rectangular ducts // Theor. Comput. Fluid Dyn. 2014. V. 28. № 2. P. 233–256.
Kovalev A.V., Yagodnitsyna A.A., Bilsky A.B. Flow hydrodynamics of immiscible liquids with low viscosity ratio in a rectangular microchannel with T-junction // Chem. Eng. J. 2018. V. 352. P. 120–132.
Lobasov A.S., Minakov A.V., Rudyak V.Ya. Flow Modes of Non-Newtonian Fluids with Power-Law Rheology in a T-Shaped Micromixer // Theoretical Foundations of Chemical Engineering. 2018. V. 52. № 3. P. 393–403.
Saleh-Lakha S., Trevors J.T. Perspective: Microfluidic applications in microbiology // J. Microbiological Methods. 2010. V. 82. № 1. P. 108–111.
DeMello A.J. Control and detection of chemical reactions in microfluidic systems // Nature Volume. 2016. V. 442. P. 394–340.
Sani R.L., Gresho P.M. Resume and remarks on the open boundary condition minisymposium // Int. J. Numer. Meth. Fluids. 1994. V. 18. P. 983–1008.
Liepsch D., Moravec S., Rastogi A.K., Vlachos N.S. Measurements and calculation of laminar flow in a ninety degree bifurcation // J. Biomechanics. 1982. V. 15. № 7. P. 473–485.
Khodadadi J.M., Nguyen T.M., Vlachos N.S. Laminar forced convective heat transfer in a two-dimensional 90° bifurcation // Numer. Heat Transfer. 1986. V. 9. № 6. P. 677–695.
Neary V.S., Sotiropoulos F. Numerical investigation of laminar flows through 90-degree diversions of rectangular cross-section // Computers & Fluids. 1996. V. 25. № 2. P. 95–118.
Shamloo H., Pirzadeh B. Investigation of characteristics of separation zones in T-Junctions // WSEAS Trans. Math. 2008. V. 7. № 5. P. 303–312.
Benes L., Louda P., Kozel K., Keslerova R., Stigler J. Numerical simulations of flow through channels with T-junction // Applied Mathematics and Computation. 2013. V. 219. P. 7225–7235.
Miranda A.I.P., Oliveira P.J., Pinho F.T. Steady and unsteady laminar flows of Newtonian and generalized Newtonian fluids in a planar T-junction // Int. J. Numer. Meth. Fluids. 2008. V. 57. № 3. P. 295–328.
Khodadadi J.M., Vlachos N.S., Liepsch D., Moravec S. LDA measurements and numerical prediction of pulsatile laminar flow in a plane 90-degree bifurcation // J. Biomech. Eng. 1988. V. 110. № 2. P. 129–136.
Khodadadi J.M. Wall pressure and shear stress variations in a 90-deg bifurcation during pulsatile laminar flow // J. Fluids Eng. 1991. V. 113. № 1. P. 111–115.
Matos H.M., Oliveira P.J. Steady and unsteady non-Newtonian inelastic flows in a planar T-junction // Int. J. Heat Fluid Flow. 2013. V. 39. P. 102–126.
Khandelwal V., Dhiman A., Baranyi L. Laminar flow of non-Newtonian shear-thinning fluids in a T-channel // Computers & Fluids. 2015. V. 108. P. 79–91.
Кузнецов Б.Г., Мошкин Н.П., Смагулов Ш. Численное исследование течения вязкой несжимаемой жидкости в каналах сложной геометрии при задании давления // Сб. науч. тр. Института теоретической и прикладной механики СО АН СССР. 1983. Т. 14. № 15. С. 87–99.
Dyakova O.A., Frolov O.Yu. Pressure driven laminar flow of a power-law fluid in a T-channel // J. Phys. Conf. Ser. 2017. V. 894 № 1. P. 1–7.
Hayes R.E., Nandakumar K., Nasr-El-Din H. Steady laminar flow in a 90 degree planar branch // Computers & Fluids. 1989. V. 17. № 4. P. 537–553.
Heywood J.G., Rannacher R., Turek S. Artificial boundaries and flux and pressure conditions for the incompressible Navier-Stokes equations // Int. J. Numer. Meth. Fluids. 1996. V. 22. № 5. P. 325–352.
Kelkar K.M. Numerical method for the prediction of incompressible flow and heat transfer in domains with specified pressure boundary conditions // Numerical Heat Transfer, Part B. 2000. V. 38. № 1. P. 15–36.
Fernandez-Feria R., Sanmiguel-Rojas E. An explicit projection method for solving incompressible flows driven by a pressure difference // Computers & Fluids. 2004. V. 33. № 3. P. 463–483.
Barth W.L., Carey G.F. On a boundary condition for pressure-driven laminar flow of incompressible fluids // Int. J. Numer. Meth. Fluids. 2007. V. 54. P. 1313–1325.
Гейдаров Н.А., Захаров Ю.Н., Шокин Ю.И. Решение стационарной задачи о течении вязкой жидкости в канале, вызванном заданным перепадом давления, при наличии внутренних источников // Вычислительные технологии. 2010. Т. 15. № 5. С. 14–23.
Moshkin N., Yambangwi D. Steady viscous incompressible flow driven by a pressure difference in a planar T-junction channel // Inter. J. Comput. Fluid Dynamics. 2009. V. 23. № 3. P. 259–270.
Шульман З.П. Конвективный тепломассоперенос реологически сложных жидкостей. М.: Энергия. 1975. 352 с.
Годунов С.К., Рябенький В.С. Разностные схемы. М.: Наука, 1977. 440 с.
Patankar S. Numerical Heat Transfer and Fluid Flow. N.Y.: McGraw-Hill, 1980. 197 p.
Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. М.: Квантум, 1996. 360 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа