Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 119-122

Течение в узком канале с химическими реакциями на стенке

В. В. Лунев^a°, П. С. Тихонычев^a, *

^a Центральный научно-исследовательский институт машиностроения
Московская обл., Королев, Россия

Поступила в редакцию 30.08.2018
После доработки 24.10.2018
Принята к публикации 23.11.2018

DOI: 10.1134/S0568528119030095

Аннотация

Получено решение задачи о течении газа в узком канале, плоском и цилиндрическом с внутренним стержнем на оси, с химическими реакциями на стенках. Задача сводится к решению обыкновенного дифференциального уравнения для поперечного распределения параметров потока. Этот пример моделирует, в некоторой степени, течения в химических реакторах, применяемых иногда для исследования гетерогенных химических реакций.

Ключевые слова: механика сплошной среды, течение многофазной среды, физико-химическая гидромеханика, химический реактор, течение Пуазейля

Эта работа имеет отношение к теории химических реакторов, используемых для определения констант скоростей соответствующих реакций [1, 2]. Рассматриваются два возможных варианта реактора: плоский и цилиндрический. Для измерения констант скоростей реакций через канал прокачивается смесь холодного несущего инертного газа со слабой примесью газа (обычно кислорода), реагирующего с материалом, нанесенным на нагреваемую поверхность одной из стенок в плоском и на центральный стержень в цилиндрическом каналах (реакции горения углерода, гетерогенная рекомбинация атомов и т.д.). По разности входных (в канал) и выходных концентраций реагирующего газа и определяются скорости реакций.

Канал предполагается достаточно длинным по сравнению с его диаметром с тем, чтобы можно было пренебречь концевыми эффектами. Кроме того, для получения обозримых результатов при определении поля скоростей несущего газа будем пренебрегать его нагревом и влиянием примеси, полагая течение в канале вязким, несжимаемым и стационарным с заданным постоянным градиентом давления $\nabla p \leqslant 0.$ Уравнение для реагирующего газа решается уже при заданном поле скоростей.

1. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В КАНАЛЕ

В рамках модели узкого канала продольная скорость u не зависит от продольной координаты x, а уравнения Навье–Стокса сокращаются до уравнения Пуазейля [3]

(1.1)

$\frac{{p'}}{{{\nu \rho }{{u}_{0}}}}R_{0}^{2} = \frac{1}{{{{r}^{{\mu }}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{{\mu }}}\frac{{\partial u}}{{\partial r}}} \right),\quad p' = \frac{{\partial p}}{{\partial x}} \leqslant 0$

Здесь ${\nu , \rho }$ – кинематическая вязкость и плотность газа, R₀ – ширина плоского канала или радиус цилиндрического. Независимая переменная r, обезразмеренная на величину R₀, есть расстояние от реагирующей стенки в плоском канале или от оси симметрии в цилиндрическом. Продольная скорость u отнесена к характерной скорости ${{u}_{0}} = - p'R_{0}^{2}{/\nu \rho }$, обращающей левую часть (1.1) в минус единицу, степени ${\mu } = 0$ и 1 соответствуют плоскому и цилиндрическому каналам, ${{r}_{0}}{{R}_{0}}$ – радиус внутреннего стержня. На стержне и внутренних стенках каналов ставятся граничные условия прилипания

(1.2)

$u = 0{\text{:}}\quad {\mu } = 0,\quad r = 0,\,1;\quad {\mu } = 1,\quad r = {{r}_{0}},\,1$

Проинтегрировав уравнение (1.1) дважды с учетом условий (1.2), получим для плоской задачи обычное решение Пуазейля, где безразмерная координата y отсчитывается от средней линии канала

(1.3)

$u = \frac{1}{8}{{u}_{0}}[1 - 4{{y}^{2}}],\quad y = r - \frac{1}{2}$

Для цилиндра справедлива последовательность формул

(1.4)

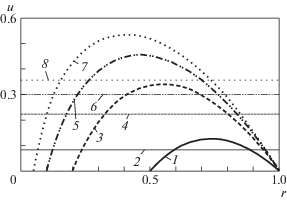
$r\frac{{\partial u}}{{\partial r}} = - \frac{1}{2}{{r}^{2}} - a,\quad u = \frac{1}{4}(1 - {{r}^{2}}) - a\ln r,\quad a = \frac{{1 - r_{0}^{2}}}{{4\ln {{r}_{0}}}}.$

Как следует из (1.4), максимум скорости $u$ достигается в точке ${{r}_{m}} = \sqrt { - a} $, которая смещается к оси с уменьшением r₀. При этом производная скорости неограниченно возрастает на внутреннем цилиндре, но его сопротивление убывает как ${{\left( { - \ln {{r}_{0}}} \right)}^{{ - 1}}}$. Профили скоростей и соответствующие им среднемассовые скорости в таком канале для различных параметров r₀ приведены на рис. 1.

Рис. 1.

Распределение скоростей (линии 1, 3, 5, 7) и средние скорости (2, 4, 6, 8) в цилиндрическом канале с внутренним стержнем при различных параметрах r₀ (0.5, 0.2, 0.1, 0.05 соответственно).

2. УРАВНЕНИЕ ДИФФУЗИИ

Уравнение диффузии для стационарного течения в узком канале с малой примесью с массовой концентрацией c запишем в тех же безразмерных переменных

(2.1)

$D_{0}^{{ - 1}}u\frac{{\partial c}}{{\partial x}} = \frac{1}{{{{r}^{{\mu }}}}}\frac{\partial }{{\partial r}}{{r}^{{\mu }}}\frac{\partial }{{\partial r}}c,\quad {{D}_{0}} = \frac{D}{{{{u}_{0}}{{R}_{0}}}}$

Здесь D – коэффициент диффузии, предполагаемый постоянным, а скорость u определяется формулами (1.3) или (1.4). Граничными условиями при этом будут

(2.2)

$r = 1{\text{:}}\;\frac{{\partial с }}{{\partial r}} = 0\;\;\left( {{\mu } = 0,1} \right);\quad r = {\mu }{{r}_{0}}\;\left( {{\mu } = 0,1} \right){\text{:}}\;\frac{{\partial с }}{{\partial r}} = {\text{Da }}c$

Первое граничное условие соответствует отсутствию реакции на “не реагирующих” стенках канала, второе определяет скорость химической реакции на “реагирующих” поверхностях стержня или стенке плоского канала [4]. Здесь обозначено ${\text{Da}} = k{{R}_{0}}{\text{/}}D$ – число Дамкелера, k – константа скоростей реакции. Так как в процессе течения вдоль канала падение концентрации кислорода за счет пристеночной реакции пропорционально его концентрации, то допустимо искать решение задачи в виде

(2.3)

$c = C\exp \left( { - {\alpha }x'} \right)f(r),\quad x' = x{\text{/}}{{R}_{0}}$

Здесь произвольная константа C определяется лишь расходом примеси в начальном сечении. Уравнение (2.1) в этом случае примет вид

(2.4)

$\frac{d}{{dr}}\left( {{{r}^{{\mu }}}\frac{{df}}{{dr}}} \right) + {\lambda }{{r}^{{\mu }}}uf = 0,\quad {\lambda } = \frac{{\alpha }}{{{{D}_{0}}}}$

В граничных условиях (2.2) при этом следует лишь заменить c на f. В такой постановке профили функций, $f{\text{/}}f\left( 1 \right)$ будут одинаковыми во всех сечениях x = const. В результате, без потери общности, можно в расчетах положить $f(1) = 1,$ включив произвол в константу $C$ в формуле (2.3).

Однородное уравнение (2.4) при однородных граничных условиях (2.2) может иметь нетривиальное решение лишь при некоторых, зависящих от параметра Da собственных числах ${\lambda },$ дискретных или непрерывных. Физически зависимость ${\lambda }\left( {{\text{Da}}} \right)$ обусловлена тем, что, к примеру, с ростом Da будет возрастать и скорость продольного убывания концентрации c, что обеспечивается синхронным увеличением числа α. При этом функция ${\lambda } = {\lambda }\left( {{\text{Da}}} \right)$ будет универсальной для каждого r₀.

Для нахождения зависимости ${\lambda }\left( {{\text{Da}}} \right)$ для каждого r₀ необходимо решить уравнение

(2.5)

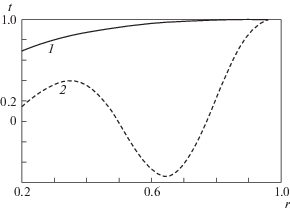
$\frac{d}{{dr}}\left( {{{r}^{{\mu }}}\frac{{df}}{{dr}}} \right) + {\lambda }{{r}^{{\mu }}}uf = 0$

с граничным условием $f_{r}^{'}\;{\text{ = Da }}f$ на реагирующей стенке и заданием $f_{r}^{'} = 0$ на противоположной.

Для этого численно была решена задача Коши: при r = 1 поставлено граничное условие, и для каждого наперед заданного числа λ явным методом движения к реагирующей стенке находилось значение числа Da. При этом можно подобрать несколько чисел λ_i, i = 0, 1, 2, … для одного и того же положительного числа Da, но только наименьшее из них будет иметь физический смысл, так как при остальных функция f меняет знак 2i раз (рис. 2).

Рис. 2.

Два решения распределения концентрации для одного значения числа Da: 1, 2 – λ = 10 и 1815, 1 – pешение физично, 2 – решение не имеет физического смысла.

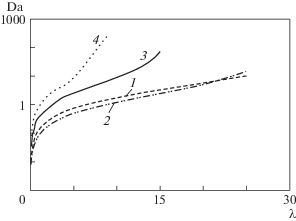
Зависимость ${\text{Da}}({\lambda })$ при различных числах r₀ приведена на рис. 3.

Рис. 3.

Зависимость числа Da от числа λ для различных конфигураций канала: 1, 3, 4 – µ = 1 при r₀ = 0.2, 0.1, 0.05; 2 – µ = 0.

ЗАКЛЮЧЕНИЕ

Представлено численное решение задачи течения газа в модельных химических реакторах разных конфигураций: в осесимметричном и плоском. Из определенной зависимости скорости химической реакции от числа λ можно сделать вывод, что при больших числах λ решение теряет физический смысл. Это соответствует тому, что при больших скоростях реакции вся рассматриваемая примесь газа вступает в реакцию с материалом стенки за несколько калибров R₀. Также показано, что измерения скоростей реакции, проведенные в плоском химическом реакторе, будут приблизительно соответствовать измерениям в осесимметричном реакторе с r₀ = 5.

Список литературы

Rosner D.E., Allendorf H D. Comparative studies of the attack of pyrolytic and isotropic graphite by O and O2 at high temperatures // AIAA J. 1968. № 4. P. 650–654.
Залогин Г.Н., Зябловский В.А., Кусов А.Л., Лунев В.В. Моделирование горения углеродной нити в канальном реакторе // Космонавтика и ракетостроение. 2017. Т. 97. № 4. С. 102–112.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Часть вторая. М.: Изд-во физ.-мат. лит. 1963. 429 с.
Землянский Б.А., Лунев В.В., Власов В.И., Горшков А.Б., Залогин Г.Н., Ковалев Р.В., Маринин В.П., Мурзинов И.Н. Конвективный теплообмен летательных аппаратов // М.: Физматлит, 2014. 241 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал