1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2019

Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 28-37

ОСОБЕННОСТИ ГИДРОДИНАМИЧЕСКИХ ПОЛЕЙ В КАНАЛАХ С ТРЕХЗАХОДНОЙ ШНЕКОВОЙ ВСТАВКОЙ

Е. К. Вачагина a, *, А. И. Кадыйров a, И. А. Конахина b, Э. М. Хуснутдинова b

a ФИЦ КазНЦ РАН
Казань, Россия

b Казанский федеральный университет
Казань, Россия

* E-mail: vachaginae@mail.ru

Поступила в редакцию 28.05.2018
После доработки 14.06.2018
Принята к публикации 14.06.2018

Полный текст (PDF)

Аннотация

Использована винтовая система координат для математического описания ламинарных течений вязкой жидкости в каналах с длинными трехзаходными шнековыми вставками. Разработана математическая модель, в которой уравнения движения записаны в проекции на направления естественного базиса винтовой системы координат. На основе полученных численных результатов проанализированы распределения гидродинамических характеристик в каналах с длинными трехзаходными шнековыми вставками различной геометрией для чисел Рейнольдса до 806.

Ключевые слова: шнековая вставка, винтовая система координат, моделирование

Вопросам интенсификации теплообмена посвящено большое количество работ, например, широко известны работы A.E. Bergles [1], Э.К. Калинина, Г.А. Дрейцера [2], Л.М. Коваленко, А.Ф. Глушкова [3], R.L. Webb [4], Ю.Ф. Гортышова [5], И.А. Попова [6]. Согласно опубликованным обзорным статьям [7–10] наиболее хорошо описаны способы и методы повышения эффективности теплообменных процессов при турбулентных течениях, что объясняется широким использованием маловязких жидкостей (воды) и газов в теплообменных энергетических установках. Однако для случая течения высоковязких жидкостей, например, нефтей и нефтепродуктов, характерным режимом является ламинарный. В этом случае [11] для увеличения эффективности теплообменных аппаратов хорошо себя зарекомендовали пассивные методы. Одним из наиболее распространенных пассивных методов интенсификации является использование различных винтовых оребрений, вставок и накаток [11–14]. В случаях, когда компактность теплообменного оборудования является предпочтительной по сравнению с затратами энергии на прокачку жидкости, наиболее часто в качестве таковых применяются одно и многозаходные шнековые вставки. Общий вид канала с трехзаходной шнековой вставкой представлен на рис. 1. Как показано в [11], в таких каналах появляются поперечные потоки, которые приводят к более интенсивному переносу тепла в поперечных направлениях, по сравнению с каналами без вставок, когда перенос тепла в этом направлении происходит исключительно за счет теплопроводности. Эффективность использования при ламинарных течениях закручивающих устройств, воздействующих на поток по всему сечению канала, также отмечена в работах [7, 10].

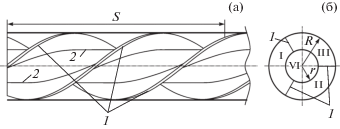
Рис. 1.

Продольное (а) и поперечное (б) сечение канала: $S$ – шаг винтового канала (длина части канала, соответствующая повороту ребер шнека на 360 градусов); R – радиус внешней трубы; r – радиус внутренней трубы; 1 – ребра трехзаходной шнековой вставки; 2 – внутренняя труба; I, II, III – идентичные области течения рабочей жидкости, ограниченные внешней и внутренней трубами и ребрами шнековой вставки; IV – внутренняя область шнековой вставки

В общем случае поле скоростей движущейся жидкости в канале с шнековой вставкой зависит от трех независимых переменных. Обычно для расчетов гидродинамических полей используются математические модели, в которых основная система уравнений записана в декартовой системе координат, ось которой совпадает с осью симметрии канала [10]. Такой подход не основывается на винтовой симметрии, которой обладает как система уравнений совместно с условиями однозначности, так и геометрическая область – винтовой канал, и требует большого объема компьютерной памяти и времени для расчетов. Использование винтовой системы координат позволяет получать распределения гидродинамических полей, зависящих не от трех, а от двух переменных. Это существенно снижает и затраты памяти, и время работы, необходимые для получения результатов.

Введенная в [11, 15] винтовая система координат ${{\xi }^{1}}$, ${{\xi }^{2}}$, ${{\xi }^{3}}$, связанная с цилиндрической системой координат соотношениями, следующими ниже, позволила рассчитать поля скоростей и давлений при течении вязкой жидкости в каналах с однозаходной шнековой вставкой:

(0.1)
${{\xi }^{1}} = r,\quad {{\xi }^{2}} = \varphi \pm Kz,\quad {{\xi }^{3}} = z$
где $K = 2\pi {\text{/}}S$, S – шаг винтового канала (длина части канала, соответствующая повороту ребер шнека на 360 градусов).

В упомянутых работах уравнения движения записаны в проекциях на направление, касательное к винтовым линиям, и на два других перпендикулярных винтовой оси направления, определяемых векторами дуального базиса. Это приводило к тому, что неизвестное заранее постоянное значение градиента давления в проекции на винтовую ось присутствовало в двух уравнениях.

В работе [16] для расчета гидродинамических полей в профилированных трубах предложено использовать декартово-винтовую систему координат ${{x}_{\partial }}$, ${{y}_{\partial }}$, ${{z}_{\partial }}$, связанную с декартовой системой координат следующими соотношениями:

(0.2)
$\begin{array}{*{20}{c}} {{{x}_{\partial }} = x\cos \left( {\frac{z}{S}} \right) - y\sin \left( {\frac{z}{S}} \right)} \\ {{{y}_{\partial }} = x\sin \left( {\frac{z}{S}} \right) + y\cos \left( {\frac{z}{S}} \right)} \\ {{{z}_{\partial }} = z} \end{array}$

Отметим, что для системы координат (0.2) только две компоненты метрического тензора равны нулю. Таким образом, эта система координат существенно неортогональна. В отличие от системы координат (0.1) система координат (0.2) не содержит особых точек, поэтому может быть использована для математического описания течения жидкостей в каналах с винтовым оребрением, ленточными и шнековыми вставками.

В настоящей работе предложена видоизмененная форма системы координат (0.1), а уравнения движения записаны в проекции на направления естественного базиса.

1. ПОСТАНОВКА ЗАДАЧИ

В качестве основных допущений приняты следующие: течение жидкости стационарное, ламинарное, со сформировавшимся профилем скорости, силы тяжести пренебрежимо малы. Вследствие винтовой симметрии поставленной задачи составляющие вектора скорости зависят только от двух переменных ${{\zeta }^{1}}$, ${{\zeta }^{2}}$.

В качестве винтовой системы координат предлагается использовать следующую систему, которая связана с декартовой системой координат соотношениями

(1.1)
$\begin{array}{*{20}{c}} {x = {{\zeta }^{1}}\cos \left( {\frac{{{{\zeta }^{2}}}}{R} + K{{\zeta }^{3}}} \right)} \\ {y = {{\zeta }^{1}}\sin \left( {\frac{{{{\zeta }^{2}}}}{R} + K{{\zeta }^{3}}} \right)} \\ {z = {{\zeta }^{3}}} \end{array}$
где $K = \pm 2\pi {\text{/}}S$, $R$ – радиус внешней трубы, S – шаг винтового канала (длина части канала, соответствующая повороту ребер шнека на 360 градусов). Знак “+” в выражении для K выбирается в случае, когда жидкость движется в винтовом канале, закрученном по часовой стрелке по ходу движения жидкости, а знак “–” – в случае движения в канале, закрученном против часовой стрелки по ходу движения жидкости.

В настоящей работе моделируется течение жидкости в канале с трехзаходной шнековой вставкой, закрученной против часовой стрелки. Таким образом, с учетом предложенной системы координат (1.1) компоненты метрического тензора примут вид

${{g}_{{11}}} = 1,\quad {{g}_{{22}}} = {{({{\zeta }^{1}}{\text{/}}R)}^{2}},\quad {{g}_{{23}}} = \left( {\frac{K}{R}} \right){{({{\zeta }^{1}})}^{2}},\quad {{g}_{{33}}} = 1 + {{K}^{2}}{{({{\zeta }^{1}})}^{2}}$
${{g}^{{11}}} = 1,{\text{ }}{{g}^{{22}}} = \frac{{1 + {{K}^{2}}{{{({{\zeta }^{1}})}}^{2}}}}{{{{{({{\zeta }^{1}}{\text{/}}R)}}^{2}}}},\quad {{g}^{{23}}} = - KR,\quad {{g}^{{33}}} = 1$

Символы Кристоффеля запишутся так

${{\Gamma }_{{22.1}}} = - {{\zeta }^{1}}{\text{/}}{{R}^{2}},\quad {{\Gamma }_{{33.1}}} = - {{K}^{2}}{{\zeta }^{1}},\quad {{\Gamma }_{{23.1}}} = {{\Gamma }_{{32.1}}} = - K{{\zeta }^{1}}{\text{/}}R,\quad {{\Gamma }_{{33.1}}} = {{\Gamma }_{{33.1}}} = - {{K}^{2}}{{\zeta }^{1}}$
${{\Gamma }_{{12.2}}} = {{\Gamma }_{{21.2}}} = {{\zeta }^{1}}{\text{/}}{{R}^{2}},\quad {{\Gamma }_{{13.2}}} = {{\Gamma }_{{31.2}}} = K{{\zeta }^{1}}{\text{/}}R,\quad {{\Gamma }_{{13.3}}} = {{\Gamma }_{{31.3}}} = {{K}^{2}}{{\zeta }^{1}}$
${{\Gamma }_{{12.3}}} = {{\Gamma }_{{21.3}}} = K{{\zeta }^{1}}{\text{/}}R,\quad \Gamma _{{22}}^{1} = {{\Gamma }_{{22.1}}} = - {{\zeta }^{1}}{\text{/}}{{R}^{2}},\quad \Gamma _{{33}}^{1} = {{\Gamma }_{{33.1}}} = - {{K}^{2}}{{\zeta }^{1}}$
$\Gamma _{{23}}^{1} = \Gamma _{{32}}^{1} = {{\Gamma }_{{23.1}}} = = - K{{\zeta }^{1}}{\text{/}}R,\quad \Gamma _{{12}}^{2} = \Gamma _{{21}}^{2} = 1{\text{/}}{{\zeta }^{1}},\quad \Gamma _{{13}}^{2} = \Gamma _{{31}}^{2} = KR{\text{/}}{{\zeta }^{1}}$

Остальные компоненты метрического тензора и символы Кристоффеля равны нулю.

В силу принятых допущений распределения гидродинамических характеристик в трех областях, ограниченных ребрами шнековой вставкой (рис. 1), идентичны. Поэтому далее в качестве исследуемой области рассмотрен кольцевой сектор.

Записывая систему уравнений переноса количества движения и неразрывности в проекциях на направления векторов естественного базиса и переходя к безразмерным переменным ηi = ${{\zeta }^{i}}{\text{/}}R$ ($i = 1,2,3$) и безразмерным контравариантным компонентам скорости ${{\text{v}}^{i}} = {{V}^{i}}{\text{/}}V{\text{*}}$ ($i = 1,2,3$), получим

$\begin{gathered} \operatorname{Re} {\text{*}}\left( {\frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{1}}}}{{\text{v}}^{1}} + \frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{2}}}}{{\text{v}}^{2}} - {{\eta }^{1}}{{\text{v}}^{2}}{{\text{v}}^{2}} + 2\kappa {{\eta }^{1}}{{\text{v}}^{2}}{{\text{v}}^{3}} - {{\kappa }^{2}}{{\eta }^{1}}{{\text{v}}^{3}}{{\text{v}}^{3}}} \right) = \\ = \; - \frac{{\partial p}}{{\partial {{\eta }^{1}}}} + \frac{{\partial E_{1}^{1}}}{{\partial {{\eta }^{1}}}} + \frac{{\partial E_{1}^{2}}}{{\partial {{\eta }^{2}}}} - \frac{1}{{{{\eta }^{1}}}}E_{2}^{2} + \frac{\kappa }{{{{\eta }^{1}}}}E_{2}^{3} + \frac{1}{{{{\eta }^{1}}}}E_{1}^{1} \\ \end{gathered} $
$\begin{gathered} \operatorname{Re} *\left( {{{{({{\eta }^{1}})}}^{2}}\left( {\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{1}}}}{{\text{v}}^{1}} + \frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}}{{\text{v}}^{2}} + \frac{2}{{{{\eta }^{1}}}}{{\text{v}}^{1}}{{\text{v}}^{2}} - \frac{{2\kappa }}{{{{\eta }^{1}}}}{{\text{v}}^{1}}{{\text{v}}^{3}}} \right) - \kappa {{{({{\eta }^{1}})}}^{2}}\left( {\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{1}}}}{{\text{v}}^{1}} + \frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{2}}}}{{\text{v}}^{2}}} \right)} \right) = \\ = \; - \frac{{\partial p}}{{\partial {{\eta }^{2}}}} + \frac{{\partial E_{2}^{1}}}{{\partial {{\eta }^{1}}}} + \frac{{\partial E_{2}^{2}}}{{\partial {{\eta }^{2}}}} + {{\eta }^{1}}E_{1}^{2} - \kappa {{\eta }^{1}}E_{1}^{3} \\ \end{gathered} $
(1.2)
$\begin{gathered} \operatorname{Re} *\left( { - \kappa {{{({{\eta }^{1}})}}^{2}}\left( {\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{1}}}}{{\text{v}}^{1}} + \frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}}{{\text{v}}^{2}} + \frac{2}{{{{\eta }^{1}}}}{{\text{v}}^{1}}{{\text{v}}^{2}} - \frac{{2\kappa }}{{{{\eta }^{1}}}}{{\text{v}}^{1}}{{\text{v}}^{3}}} \right) + (1 + {{\kappa }^{2}}{{{({{\eta }^{1}})}}^{2}})\left( {\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{1}}}}{{\text{v}}^{1}} + \frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{2}}}}{{\text{v}}^{2}}} \right)} \right) = \\ = \; - \frac{{\partial p}}{{\partial {{\eta }^{3}}}} + \frac{{\partial E_{3}^{1}}}{{\partial {{\eta }^{1}}}} + \frac{{\partial E_{3}^{2}}}{{\partial {{\eta }^{2}}}} + \frac{\kappa }{{{{\eta }^{1}}}}E_{2}^{1} - \kappa {{\eta }^{1}}E_{1}^{2} + {{\kappa }^{2}}{{\eta }^{1}}E_{1}^{3} + \frac{1}{{{{\eta }^{1}}}}E_{3}^{1} \\ \end{gathered} $
$\frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{1}}}} + \frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}} + \frac{1}{{{{\eta }^{1}}}}{{\text{v}}^{1}} = 0$
где $\operatorname{Re} {\text{*}} = {{\left( {\rho V{\text{*}}R} \right)} \mathord{\left/ {\vphantom {{\left( {\rho V{\text{*}}R} \right)} \mu }} \right. \kern-0em} \mu }$, $p = {{\left( {PR} \right)} \mathord{\left/ {\vphantom {{\left( {PR} \right)} {\left( {\mu V{\text{*}}} \right)}}} \right. \kern-0em} {\left( {\mu V{\text{*}}} \right)}}$, $\kappa = KR$, $V{\text{*}}$ – характерная скорость. Здесь $\rho $ – плотность жидкости, $\mu $ – коэффициент динамической вязкости, $P$ – давление, $p$ – безразмерное давление, $R$ – радиус внешней трубы (рис. 1). В силу принятых допущений ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial {{\eta }^{3}}}}} \right. \kern-0em} {\partial {{\eta }^{3}}}} = {\text{const}}$.

Безразмерные смешанные компоненты тензора скоростей деформаций $D_{i}^{j}$ имеют вид

$E_{i}^{j} = D_{i}^{j}{\text{/}}\left( {V{\text{*}}R} \right),\quad E_{1}^{1} = 2\frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{1}}}},\quad E_{2}^{1} = \frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{2}}}} + {{({{\eta }^{1}})}^{2}}\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{1}}}} - \kappa {{({{\eta }^{1}})}^{2}}\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{1}}}}$
$E_{3}^{1} = - \kappa {{({{\eta }^{1}})}^{2}}\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{1}}}} + (1 + {{\kappa }^{2}}{{({{\eta }^{1}})}^{2}})\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{1}}}},\quad E_{1}^{2} = \frac{{(1 + {{\kappa }^{2}}{{{({{\eta }^{1}})}}^{2}})}}{{{{{({{\eta }^{1}})}}^{2}}}}\frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{2}}}} + \frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{1}}}}$
$E_{2}^{2} = (2 + {{\kappa }^{2}}{{({{\eta }^{1}})}^{2}})\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}} - \kappa (1 + {{\kappa }^{2}}{{({{\eta }^{1}})}^{2}})\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{2}}}} + \frac{2}{{{{\eta }^{1}}}}{{\text{v}}^{1}}$
$E_{3}^{2} = - \kappa (1 + {{\left( \kappa \right)}^{2}}{{({{\eta }^{1}})}^{2}})\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}} + \frac{{{{{(1 + {{\kappa }^{2}}{{{({{\eta }^{1}})}}^{2}})}}^{2}}}}{{{{{({{\eta }^{1}})}}^{2}}}}\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{2}}}} - \frac{{2\kappa }}{{{{\eta }^{1}}}}{{\text{v}}^{1}}$
$E_{1}^{3} = \kappa \frac{{\partial {{\text{v}}^{1}}}}{{\partial {{\eta }^{2}}}} + \frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{1}}}},\quad E_{2}^{3} = \kappa {{({{\eta }^{1}})}^{2}}\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}} + (1 - {{\kappa }^{2}}{{({{\eta }^{1}})}^{2}})\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{2}}}}$
$E_{3}^{3} = - {{\kappa }^{2}}{{({{\eta }^{1}})}^{2}}\frac{{\partial {{\text{v}}^{2}}}}{{\partial {{\eta }^{2}}}} + \kappa (1 + {{\kappa }^{2}}{{({{\eta }^{1}})}^{2}})\frac{{\partial {{\text{v}}^{3}}}}{{\partial {{\eta }^{2}}}}$

Условия однозначности решения системы уравнений (1.2) состоят в условии прилипания жидкости на стенках канала и поверхностях шнековой вставки и задании объемного расхода жидкости $Q$ через поперечное сечение этого канала.

Численное решение поставленной задачи реализовано в программном комплексе Comsol Multiphysics 3.5, основанном на методе конечных элементов. Программный комплекс позволяет записать уравнения движения и неразрывности в проекциях на направления векторов естественного базиса в новой системе координат ${{\eta }^{i}}{\text{ }}$ ($i = 1,2,3$). Получено, что разбиение расчетной области на 150 000 элементов является достаточным для получения численных результатов, отличающихся от результатов, полученных на более мелкой сетке менее чем на 0.5%.

Для контроля полученных результатов использована винтовая система координат, аналогичная (0.2), приведенная в [17]

(1.3)
$\begin{array}{*{20}{c}} {x = R({{\xi }^{1}}\cos ({{\xi }^{3}}) - {{\xi }^{2}}\sin ({{\xi }^{3}}))} \\ {y = R({{\xi }^{1}}\sin ({{\xi }^{3}}) + {{\xi }^{2}}\cos ({{\xi }^{3}}))} \\ {z = Rw{{\xi }^{3}}} \end{array}$
где $w = 1{\text{/}}\left( {KR} \right)$. Уравнения движения в работе [17] записаны в проекции на направления естественного базиса. В качестве основных неизвестных функций использовались контравариантные компоненты. Данные, полученные с использованием системы координат (1.3), отличаются от данных, полученных с помощью системы координат (1.1) при общей точности расчетов 0.0001 менее чем на 1%.

2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

В данном разделе представлены результаты численных исследований движения вязкой жидкости в канале со шнековой вставкой со следующими геометрическими характеристиками: $r{\text{/}}R$ = 0.3...0.7, $S{\text{/}}D = 4...8$, где $D = 2R$ – диаметр внешней трубы (рис. 1).

Число Рейнольдса вычислено с использованием определяющего размера, равного эквивалентному диаметру ${{D}_{h}}$ поперечного сечения канала по формуле

$\operatorname{Re} = \rho {{V}_{a}}{{D}_{h}}{\text{/}}\mu $
где ${{D}_{h}} = 4F{\text{/}}{{P}_{h}}$ – эквивалентный диаметр поперечного сечения, $F = 2\pi ({{R}^{2}} - {{r}^{2}}){\text{/}}3$ – площадь поперечного сечения, ${{P}_{h}} = 2\left( {R - r} \right) + 2\pi \left( {R + r} \right){\text{/}}3$ – смоченный периметр поперечного сечения, r – радиус внутренней трубы канала (рис. 1). ${{V}_{a}} = Q{\text{/}}F$ – среднерасходная скорость, $Q$ – объемный расход.

Часто используемые на практике в численных расчетах физические компоненты вектора скорости в цилиндрической системе координат (радиальная $\text{v}_{r}^{*}$, окружная $\text{v}_{\varphi }^{*}$ и осевая $\text{v}_{z}^{*}$ компоненты) связаны в компонентами вектора скорости в винтовой системе координат (1.1) соотношениями

$\text{v}_{r}^{*} = {{\text{v}}_{1}}{\text{/}}\sqrt {{{g}_{{11}}}} = {{\text{v}}_{1}} = {{\text{v}}^{1}},\quad \text{v}_{\varphi }^{*} = {{\text{v}}_{2}}{\text{/}}\sqrt {{{g}_{{22}}}} = {{\text{v}}_{2}}{\text{/}}{{({{\zeta }^{1}}{\text{/}}R)}^{2}},\quad \text{v}_{z}^{*} = {{\text{v}}^{3}}{\text{/}}\sqrt {{{g}^{{33}}}} = {{\text{v}}^{3}}$

Здесь и далее все компоненты скорости взяты в безразмерном виде (компоненты отнесены к среднерасходной скорости). Таким образом, радиальная и окружная компоненты вектора скорости выражаются через ковариантные компоненты скорости, а осевая – через контравариантную.

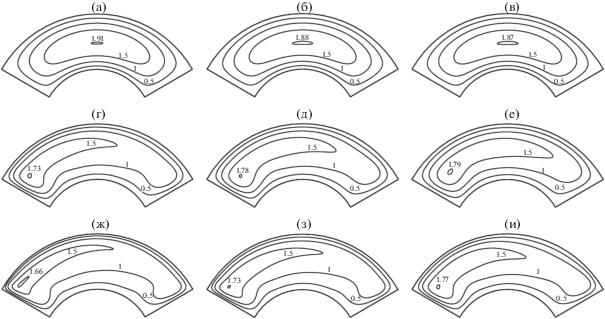
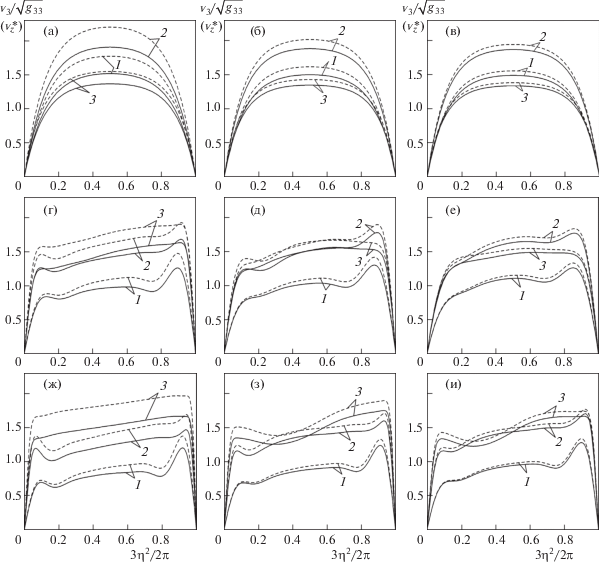
На рис. 2 и 3 представлены линии равных значений (изолинии) распределений винтовой ${{\text{v}}_{3}}{\text{/}}\sqrt {{{g}_{{33}}}} $ (проекция скорости на направление, касательное к винтовым линиям) и осевой $\text{v}_{z}^{*} = {{\text{v}}^{3}}{\text{/}}\sqrt {{{g}^{{33}}}} $ составляющих вектора скорости в поперечном сечении канала. Изолинии позволяют наглядно представить распределение гидродинамических полей сразу во всех частях поперечного сечения канала. Видно, что при малых значениях числа Рейнольдса распределения этих составляющих симметричны, относительно оси симметрии поперечного сечения. Максимальные значения как винтовой, так и осевой составляющих находятся в центре поперечного сечения. Причем, чем больше относительный шаг шнекового канала, тем меньше величина максимума этих составляющих. Такое распределение объясняется пренебрежимо малыми значениями инерционных членов в уравнениях Навье–Стокса (1.2). По мере увеличения числа Рейнольдса инерционные члены уравнений возрастают по величине, и симметрия распределения составляющих скорости нарушается. Максимальное значение становится несколько меньше и смещается в сторону закрутки потока жидкости.

Рис. 2.

Линии равных значений безразмерной винтовой ${{{{\text{v}}_{3}}} \mathord{\left/ {\vphantom {{{{\text{v}}_{3}}} {\sqrt {{{g}_{{33}}}} }}} \right. \kern-0em} {\sqrt {{{g}_{{33}}}} }}$ составляющей вектора скорости ($r{\text{/}}R = 0.5$): S/D = 4 – ((а), (г), (ж)); S/D = 6 – ((б), (д), (з)); S/D = 8 – ((в), (е), (и)); $\operatorname{Re} \to 0$ – ((а), (б), (в)), $\operatorname{Re} = 390.47$ – ((г), (д), (е)), $\operatorname{Re} = 806.34$ – ((ж), (з), (и))

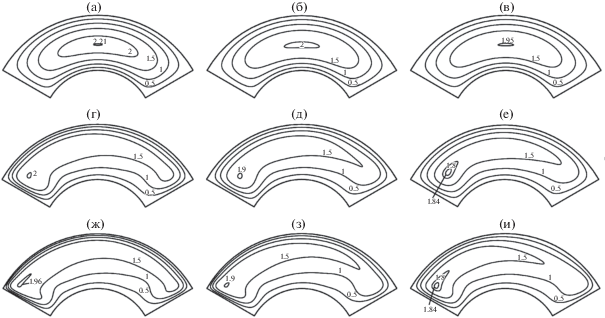
Рис. 3.

Линии равных значений безразмерной осевой $\text{v}_{z}^{*}$ составляющей вектора скорости: остальные обозначения согласно рис. 2

Уменьшение максимального значения винтовой и осевой составляющих вектора скорости с ростом числа Рейнольдса является следствием того, что с его ростом профили скорости становятся более наполненными, приближаясь к почти постоянному значению в центральной области канала, и резко уменьшаясь только около поверхностей ребер, что явно прослеживается на рис. 4. Около боковых стенок канала наблюдается небольшое увеличение как винтовой, так и осевой составляющих вектора скорости (рис. 4), обусловленное резкими изменениями поперечных потоков в этой области. По сравнению с однозаходной шнековой вставкой [18] в трехзаходной шнековой вставке максимальные значения осевой составляющей вектора скорости больше на 10%.

Рис. 4.

Профили винтовой ${{{{\text{v}}_{3}}} \mathord{\left/ {\vphantom {{{{\text{v}}_{3}}} {\sqrt {{{g}_{{33}}}} }}} \right. \kern-0em} {\sqrt {{{g}_{{33}}}} }}$ (пунктирная) и осевой $\text{v}_{z}^{*}$ (сплошная) составляющих вектора скорости: 1 – ${{\eta }^{1}} = 0.625$; 2 – ${{\eta }^{1}} = 0.75$; 3 – ${{\eta }^{1}} = 0.875$; остальные обозначения согласно рис. 2

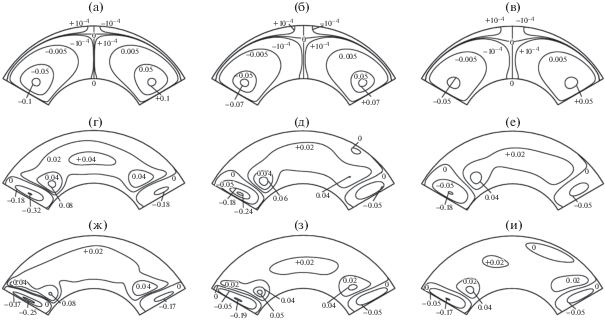
Известно, что одной из причин интенсификации процессов теплообмена в каналах является наличие поперечных потоков. На рис. 5 представлены изолинии одной из поперечных составляющих вектора скорости – радиальной, что позволяет дать оценку ее распределения во всей области поперечного сечения канала. Как следует из рисунка, радиальная составляющая скорости существует даже в предельном случае, когда инерционными членами в уравнениях переноса количества движения можно пренебречь. В этом случае ее значения (при условии $S{\text{/}}D \geqslant 4$) достигают 4.5% от максимального значения винтовой составляющей, и чем меньше относительный шаг, тем больше ее максимальное значение. Все поперечное сечение можно разделить на четыре области, в которых любые две соседние области отличаются по знаку радиальной составляющей вектора скорости: две большие по размеру области в нижней части поперечного сечения и две маленькие области в верхней части поперечного сечения. Эти области отделены друг от друга границами – изолиниями с нулевым значением радиальной составляющей вектора скорости ($\text{v}_{r}^{*}$ = 0). Чем больше относительный шаг канала со шнековой вставкой, тем больше размеры верхних областей и тем меньше абсолютные значения радиальной компоненты вектора скорости. Для канала, закрученного влево по ходу движения жидкости в верхней правой и в нижней левой областях знак радиальной составляющей вектора скорости отрицательный, а в верхней левой и нижней правой ее знак положительный (рис. 5). При увеличении числа Рейнольдса под действием инерционных сил области положительных значений радиальной составляющей вектора скорости сливаются, и, расширяясь, занимают центральную область поперечного сечения, образуя при этом одну центральную область. Верхняя область отрицательных значений оттесняется к ребру винтового канала, перекрывающему поперечное сечение и, расширяясь, примыкает к этому ребру. Правая нижняя область отрицательных значений также под действием инерционных сил уменьшается в размерах и смещается к другому ребру винтового канала. С увеличением инерционных членов происходит и увеличение абсолютных значений радиальной составляющей вектора скорости, которая может достигать 13% от максимального значения винтовой составляющей. Наибольшие по абсолютному значению величины радиальной составляющей вектора скорости имеют отрицательные значения и находятся в боковой области, около винтового ребра (по ходу закрутки винтового ребра). Согласно данным, представленным на рис. 5, области отрицательных значений радиальной составляющей вектора скорости занимают небольшую часть всей площади, поэтому наиболее яркие изменения скоростных полей наблюдаются именно вблизи боковых границ поперечного сечения (винтовых ребер), и наиболее детальное изучение распределения компонент скорости, в этом случае, удобно отслеживать вдоль линий ${{\eta }^{1}} = {\text{const}}$, $0 \leqslant {{\eta }^{2}} \leqslant 1$.

Рис. 5.

Линии равных значений безразмерной радиальной $\text{v}_{r}^{*}$ составляющей вектора скорости: остальные обозначения согласно рис. 2

Как видно из рис. 6, профили поперечных составляющих вектора скорости как радиальной ($\text{v}_{r}^{*} = {{\text{v}}^{1}}{\text{/}}\sqrt {{{g}^{{11}}}} $), так и тангенциальной (${{\text{v}}^{2}}{\text{/}}\sqrt {{{g}^{{22}}}} $ – контравариантной физической составляющей) компонент при Re → 0 существенно отличаются от аналогичных при числах Рейнольдса, равных 390 и 806. При Re → 0 профили радиальной составляющей антисимметричны относительно точки ${{\eta }^{2}}{\text{/}}\left( {2\pi {\text{/}}3} \right) = 0.5$. Профили тангенциальной составляющей симметричны относительно оси симметрии поперечного сечения.

Рис. 6.

Профили радиальной $\text{v}_{r}^{*}$ (сплошная) и тангенциальной ${{\text{v}}^{2}}{\text{/}}\sqrt {{{g}^{{22}}}} $ (пунктирная) составляющих вектора скорости: 1 – ${{\eta }^{1}} = 0.625$; 2 – ${{\eta }^{1}} = 0.75$; 3 – ${{\eta }^{1}} = 0.875$; остальные обозначения согласно рис. 2

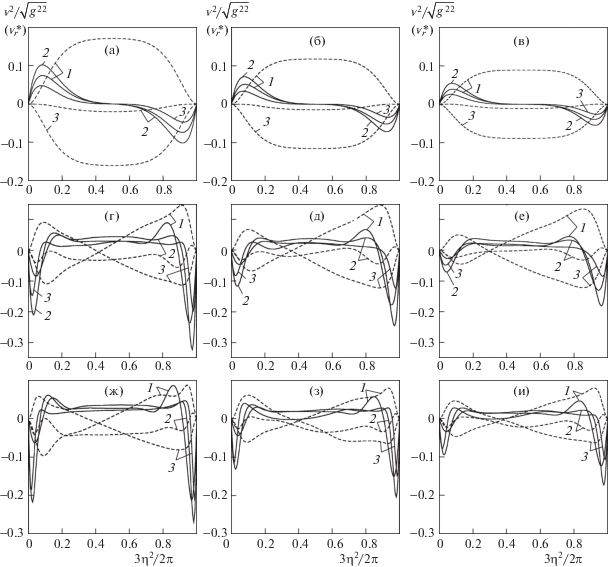
При возрастании числа Re от 390 до 806 симметрия нарушается. Как отмечено выше, в центральной части поперечного сечения радиальная составляющая положительна, а в областях, примыкающих к боковым стенкам, она отрицательна. Центральная область характеризуется также сравнительно небольшими значениями тангенциальной составляющей вектора скорости, причем в данной области эта составляющая меняет знак с положительного на отрицательный. В нижней части области, примыкающей к боковой стенке, тангенциальная составляющая направлена в сторону, противоположную закрутке, а в верхней части – по ходу закрутки. В области, примыкающей к боковой стенке, направление тангенциальной составляющей меняется на противоположное. Как и радиальная составляющая, тангенциальная принимает сравнительно большие значения у боковых стенок и ближе к внешней и внутренней стенкам канала.

На рис. 7 представлены изолинии радиальной и осевой составляющих вектора скорости в поперечном сечении канала для различных отношений радиуса внутренней трубы к радиусу внешней трубы. Видно, что с увеличением этого отношения отрицательные значения радиальной составляющей вектора скорости уменьшаются по модулю. В данном случае действие инерционных сил подавляется расположенными близко относительно друг друга поверхностей внутренней и внешней труб. Напротив, уменьшение отношения радиуса внутренней трубы к радиусу внешней трубы приводит к увеличению абсолютных значений $\text{v}_{r}^{*}$. Увеличение поперечных (радиальных и тангенциальных) составляющих вектора скорости приводит к более интенсивному перемешиванию в поперечном сечении канала. Вне зависимости от величины отношения радиусов внутренней и внешней трубы максимум $\text{v}_{z}^{*}$ расположен вблизи вогнутой поверхности в левой части канала для закрученного влево по ходу движения жидкости.

Рис. 7.

Линии равных значений безразмерных $\text{v}_{r}^{*}$ ((а), (б), (в)) и $\text{v}_{z}^{*}$ ((г), (д), (е)): $\operatorname{Re} = 806.34$; $S{\text{/}}D = 4$; $r{\text{/}}R$ = 0.3 – ((а), (г)); $r{\text{/}}R = 0.5$ – ((б), (д)); $r{\text{/}}R = 0.7$ – ((в), (е))

ЗАКЛЮЧЕНИЕ

Разработанная математическая модель, использующая винтовую систему координат, адекватно описывает установившиеся ламинарные течения вязкой жидкости в каналах со шнековыми вставками, в том числе в канале с трехзаходной шнековой вставкой. Результаты численных исследований показали, что даже в предельном случае исчезающе малых чисел Рейнольдса (приближение Стокса) в канале с трехзаходной шнековой вставкой существуют поперечные потоки. Распределение компонент вектора скорости в этом случае симметрично (антисимметрично для радиальной компоненты) относительно оси симметрии поперечного сечения. По мере увеличения числа Рейнольдса инерционные члены уравнений возрастают по величине, и симметрия распределения компонент вектора скорости нарушается. Максимальные значения осевой составляющей вектора скорости смещаются в сторону закрутки потока. При этом абсолютное значение радиальной составляющей вектора скорости увеличивается до 13% от максимального значения винтовой составляющей. Сравнительный анализ показал, что использование трехзаходной шнековой вставки приводит к более интенсивному перемешиванию в поперечном сечении канала по сравнению с каналом с однозаходной шнековой вставкой.

Список литературы

  1. Bergles A.E., Jensen M.K., Somerscales E.F.C., Manglik R.M. Literature Review of Heat Transfer Enhancement Technology for Heat Exchanges in Gas-Fired Applications, Report GRI 91-0146, Gas Research Institute, Chicago, 1991.

  2. Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена в каналах, 3-е изд. М.: Машиностроение, 1990. 205 с.

  3. Коваленко Л.М., Глушков А.Ф. Теплообменники с интенсификацией теплоотдачи. М.: Энергоатомиздат, 1986. 240 с.

  4. Webb R.L. Principles of Enhanced Heat Transfer. New York: John Wiley & Sons Inc., 1994. 556 p.

  5. Гортышов Ю.Ф. Теплогидродинамическая эффективность перспективных способов интенсификации теплоотдачи в каналах теплообменного оборудования. Интенсификация теплообмена. Казань: Центр инновационных технологий, 2009. 531 с.

  6. Попов И.А., Махянов Х.М., Гуреев В.М. Физические основы и промышленное применение интенсификации теплообмена. Интенсификация теплообмена: монография / Под общ. ред. Гортышова Ю.Ф. Казань: Центр инновационных технологий, 2009. 560 с.

  7. Dewan A., Mahanta P., Sumithra K.R., Kumar S.P. Review of passive heat transfer augmentation techniques // Proc. Inst. Mech. Engrs. Part A: J. Power and Energy. 2004. V. 218. P. 509–527.

  8. Wen-Tao J., Jacobi A.M., Ya-Ling He, Wen-Quan Tao. Summary and evaluation on single-phase heat transfer enhancement techniques of liquid laminar and turbulent pipe flow// Int. J. Heat and Mass Transfer. 2015. № 88. P. 735–754.

  9. Bipin K., Gaurav P.S., Manoj K., Anil K.P. A review of heat transfer and fluid flow mechanism in heat exchanger tube with inserts// Chemical Engineering & Processing: Process Intensification. 2018. № 123. P. 126–137.

  10. Митрофанова О.В. Гидродинамика и теплообмен закрученных потоков в каналах с завихрителями (Аналитический обзор) // ТВТ. 2003. Т. 41. № 4. С. 587–633.

  11. Назмеев Ю.Г. Гидродинамика и теплообмен закрученных потоков реологически сложных жидкостей. М.: Энергоатомиздат, 1996. 304 с.

  12. Назмеев Ю.Г., Конахина И.А. Расчет профиля скорости при течении нелинейной вязкоупругой жидкости в трубах с винтовой накаткой // Инж.-физ. журн. 1992. Т. 62. № 3. С. 373–379.

  13. Назмеев Ю.Г., Конахина И.А. Исследование процесса интенсификации теплообмена при ламинарном течении вязких жидкостей в трубах с винтовой накаткой // Теплоэнергетика. 1993. № 11. С. 59–62.

  14. Назмеев Ю.Г., Конахина И.А. Организация энерготехнологических комплексов в нефтехимической промышленности. М.: Изд-во МЭИ, 2001. 364 с.

  15. Vachagina E.K., Kadyirov A.I. The use of helical coordinate systems// The Quarterly J. Mech. Appl. Math. 2014. V. 67. № 4. P. 553–566.

  16. Комов А.Т., Токарев Ю.H. Численный анализ ламинарных течений закрученных потоков несжимаемой жидкости в декартово-винтовых координатах. Четвертая Российская нац. конф. по теплообмену. 23–27 октября 2006 г. М., 2006.

  17. Kadyirov A.I., Abaydullin B.R., Vachagina E.K. Hydrodynamic characteristics of viscous fluid flow in screw channels formed by two ribs // IOP Conf. Series: J. Phys.: Conf. Ser. 2018. V. 980. P. 012011. https://doi.org/10.1088/1742-6596/980/1/012011

  18. Кадыйров А.И., Халитова Г.Р., Вачагина Е.К. Гидродинамическая структура потока вязкой жидкости в каналах с интенсификаторами в виде шнековой вставки // Тр. Академэнерго. 2016. № 3. С. 7–16.

  19. Щукин В.К., Халатов А.А. Теплообмен, массообмен и гидродинамика закрученных потоков в осесимметричных каналах. М.: Машиностроение, 1982. 200 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал