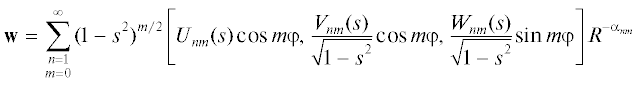Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 48-57

взаимодействие двух противоположно закрученных затопленных струй

А. М. Гайфуллин^a, b, *, В. В. Жвик^a, b, **

^a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Москва, Россия

^b Московский физико-технический институт (государственный университет)
Москва, Россия

^* E-mail: gaifullin@tsagi.ru
^** E-mail: vladzhvick@yandex.ru

Поступила в редакцию 12.07.2018
После доработки 10.09.2018
Принята к публикации 18.10.2018

DOI: 10.1134/S0568528119020063

Полный текст (PDF)

Аннотация

Рассматривается задача о взаимодействии двух противоположно закрученных струй вязкой несжимаемой жидкости, бьющих из параллельных труб в затопленное пространство. С помощью численного решения определен сценарий слияния двух струй в одну. Показано, что на большом расстоянии от источников течение описывается автомодельным осесимметричным решением Ландау для одиночной незакрученной струи. Поле продольной завихренности вдали от источника также является автомодельным с комплексной степенью затухания. Обсуждается асимптотическая структура дальнего поля струи.

Ключевые слова: две струи, закрученная струя, неосесимметричная струя, струя Ландау, затопленная струя

Точное автомодельное решение уравнений Навье–Стокса для несжимаемой жидкости, описывающее бьющую из точечного источника осесимметричную струю, получено Ландау [1] и содержит одну константу, значение которой определяется потоком импульса через сферическую поверхность, в центре которой находится источник. Поток импульса не зависит от радиуса сферы. Если рассмотреть струю, бьющую из источника конечного диаметра, то решение [1] будет главным членом разложения по обратным степеням сферического радиуса вдали от источника. Следующее приближение [2, 3] обеспечивает конечный расход, который также не зависит от радиуса сферы. В струе Ландау расход равен нулю вследствие нулевого размера источника.

Главный член разложения решения [1] по малому обратному числу Рейнольдса совпадает с решением Шлихтинга [4], полученному в приближении пограничного слоя. Следующий член координатного разложения, обеспечивающий конечный расход при истечении из источника, в этом приближении вычислен Лойцянским [5]. В [5] также построено асимптотическое решение для закрученной струи. Продольная и радиальная компоненты скорости в первых двух приближениях по величине обратной продольной координаты соответствуют незакрученной струе. Окружная скорость появляется во втором приближении и зависит от константы, значение которой определяется еще одной сохраняющейся величиной – потоком момента импульса.

Решение уравнений Навье–Стокса для закрученной струи получено Цуккером [6]. При больших значениях числа Рейнольдса решение [6] переходит в решение [5].

Дальнее поле неосесимметричных струй исследовалось в [7]. Асимптотика струи определяется собственным решением уравнений Навье−Стокса, линеаризованных относительно решения Ландау. В этом приближении закон затухания компонент скорости в струе определяется собственными значениями, которые зависят от числа Рейнольдса и могут принимать дробные и даже комплексные значения.

В [8] построено следующее относительно решения [1] приближение для струи, в которой вектор потока момента импульса неколлинеарен вектору потока импульса.

В настоящей работе рассмотрена задача о взаимодействии двух противоположно закрученных струй. Определен сценарий слияния двух струй в одну. При таком слиянии представляет интерес эволюция поля продольной завихренности. Показано, что распределение продольной скорости на больших расстояниях от источника соответствует решению [1]. Исследовано неосесимметричное распределение продольной завихренности. Анализ численного решения показывает, что данное распределение вдали от источника достаточно точно описывается членом мультипольного ряда [7].

1. ПОСТАНОВКА ЗАДАЧИ

Две струи вязкой несжимаемой жидкости бьют из параллельных труб в пространство, затопленное той же жидкостью. Течение в трубах закручивается за счет вращения внутренних поверхностей труб с постоянной угловой скоростью Ω^{. Предполагается, что внутренние поверхности труб вращаются в противоположных направлениях,
а внешние неподвижны. Последнее условие обеспечивает нулевую циркуляцию струй при
выходе из труб. Распределение продольной компоненты скорости u_n на входе в каждую трубу соответствует течению Пуазейля, радиальная компонента скорости
u_r равна нулю, а окружная скорость u_τ соответствует твердотельному вращению}

(1.1)

${{u}_{n}}({{r}_{1}}) = U(1 - r_{1}^{2}{\text{/}}R_{1}^{2}),\quad {{u}_{r}}({{r}_{1}}) = 0,\quad {{u}_{\tau }}({{r}_{1}}) = \pm \Omega {{r}_{1}}$

Здесь r₁ – расстояние от оси трубы, R₁ – радиус трубы, U – максимальная продольная скорость в трубе. Граничные условия (1.1) являются точным решением уравнений Навье–Стокса, описывающим стационарное течение в длинной вращающейся трубе, вызванное перепадом давления на концах трубы.

Для определенности будем считать, что плоскость, в которой лежат оси труб, горизонтальная. Если смотреть со стороны выходного сечения, то вращение жидкости в левой трубе происходит против часовой, а в правой по часовой стрелкам. При удалении от труб на бесконечно большое расстояние скорость стремится к нулю. Течение жидкости предполагается ламинарным и стационарным.

Обезразмерим линейные размеры на радиус трубы, компоненты скорости на максимальную продольную скорость в трубе, давление на удвоенный скоростной напор в трубе

$p = ({{p}_{1}} - {{p}_{{1\infty }}}){\text{/}}\rho {{U}^{2}}$

где p₁ – давление, p_1∞ – давление в невозмущенной области, ρ – плотность жидкости.

Введем декартовую систему координат: начало координат поместим в плоскости выходных сечений труб, ось x определяется пересечением плоскости симметрии и плоскости, в которой лежат оси труб, ось y направим вертикально, а ось z перпендикулярно плоскости симметрии. Проекции вектора скорости на оси координат x, y, z обозначим через u, v, w.

Из уравнений Навье–Стокса следует, что параметрами подобия для данной задачи являются число Рейнольдса Re = UR₁/ν, крутка струи или отношение максимальной окружной скорости в трубе к максимальной продольной скорости S = ΩR₁/U и безразмерное расстояние между осями труб l. Будем решать задачу в предположении $\operatorname{Re} \gg 1$.

В течении за выходными сечениями труб сохраняется поток полного импульса сквозь поперечное сечение струи

(1.2)

$J = \int\limits_{ - \infty }^{ + \infty } {dy\int\limits_{ - \infty }^{ + \infty } {({{u}^{2}} + p)dz} } $

В рамках приближения пограничного слоя также сохраняются поток вертикального импульса и поток момента импульса через поперечное сечение струи. При $\operatorname{Re} \gg 1$ эти интегралы принимают вид

${{J}_{y}} = \int\limits_{ - \infty }^{ + \infty } {dy} \int\limits_{ - \infty }^{ + \infty } {u\text{v}dz} ,\quad L = \int\limits_{ - \infty }^{ + \infty } {dy} \int\limits_{ - \infty }^{ + \infty } {u\left( {yw - z\text{v}} \right)dz} $

В отличие от задачи о диффузии двух вихрей [9], первый интеграл равен нулю, так как равна нулю суммарная циркуляция скорости по контуру вокруг каждой струи непосредственно за выходным сечением из трубы. Второй интеграл равен нулю в силу симметрии задачи относительно плоскости (x, y).

Расчет проводился при следующих значениях безразмерных параметров: Re = 100, S = 0.5, l = 8.

2. ЧИСЛЕННЫЙ МЕТОД

Численное интегрирование уравнений Навье–Стокса проводилось конечно-объемным методом. Использовалась гексаэдральная структурированная сетка объемом 10.3 × 10⁶ ячеек. Расчетная область в направлении распространения струи имела следующий размер: –20 ≤ x ≤ 1060. Размер расчетной области в поперечном направлении в окрестности трубы составлял 60 и возрастал линейно по продольной координате (достигая 520), чтобы избежать взаимодействия боковых границ с расширяющейся из-за вязкой диффузии струей.

Симметрия задачи позволяла моделировать половину течения. На границах расчетной области, везде, кроме входного отверстия трубы и плоскости симметрии, ставились “мягкие” граничные условия, обеспечивающие нулевые нормальные производные компонент вектора скорости.

Применялись схема второго порядка аппроксимации с разностями против потока для интерполяции компонент скорости на гранях ячеек и центрально-разностная схема второго порядка аппроксимации для дискретизации диффузионных членов и давления. Использовался алгоритм совместного решения уравнений имульса и неразрывности. Процедура установления обеспечивалась решением по неявной схеме линеаризованных дискретизованных уравнений переноса, дополненных нестационарной производной с фиксированным значением псевдовременного шага.

Вначале расчет проводился с большим шагом по псевдовремени, чтобы ускорить установление поля течения. При установлении постоянного расхода через дальнее поперечное сечение струи начинался счет с малым шагом для уточнения решения. Максимальное значение невязки наблюдалось по уравнению неразрывности и не превосходило 10^–5.

Верификация (табл. 1) проводилась путем сравнения результатов расчета на сетке 0, которая используется в данной работе, и на более подробных сетках 1, 2. Сетка 1 имеет удвоенное число ячеек в продольном направлении по отношению к сетке 0. Сетка 2 имеет удвоенное число ячеек в поперечной плоскости по отношению к сетке 0, всюду за исключением окрестностей трубы и оси струи. Погрешность определялась по значениям максимальной и минимальной продольной завихренности в ядре струи и максимальной продольной скорости. На используемой в работе сетке погрешность Δ (нижние индексы указывают на номера сеток, которые сравниваются) определения этих величин достигает нескольких процентов, что приемлемо для качественного и приближенного количественного анализа результатов.

Таблица 1.

№ сетки	Число ячеек	x = 4			x = 60			x = 260
№ сетки	Число ячеек	u_x	(ω_x)_max	(ω_x)_min	u_x	(ω_x)_max	(ω_x)_min	u_x × 10²	(ω_x)_max	(ω_x)_min
0	10.3 × 10⁶	0.5598	0.3207	–0.02209	0.1489	5.01 × 10^–3	–1.190 × 10^–3	5.951	9.35 × 10^–5	–6.96 × 10^–5
1	20.7 × 10⁶	0.5612	0.3207	–0.02166	0.1493	5.00 × 10^–3	–1.159 × 10^–3	5.973	9.02 × 10^–5	–7.08 × 10^–5
2	18.8 × 10⁶	0.5602	0.3205	–0.02205	0.1492	5.02 × 10^–3	–1.161 × 10^–3	5.970	9.06 × 10^–5	–7.05 × 10^–5
Δ₀₁, %		0.3	0	2	0.3	0.2	3	0.3	4	2
Δ₀₂, %		0.07	0.06	0.2	0.2	0.2	2	0.3	3	1
Δ₁₂, %		0.2	0.06	2	0.07	0.4	0.2	0.05	0.4	0.4

3. МОДЕЛИРОВАНИЕ ОСЕСИММЕТРИЧНЫХ СТРУЙ

Методика расчета отрабатывалась на моделировании одной осесимметричной струи, бьющей из трубы, внутренняя поверхность которой может вращаться с постоянной угловой скоростью.

Струя моделировалась при Re = 100, S = 0, 1, 1.125. Обозначим $\varepsilon = {{\operatorname{Re} }^{{ - 1}}} \ll 1$. Импульс можно оценить по параметрам потока на выходе из трубы. В безразмерном виде J ∼ O(1). При $x \gg {{\varepsilon }^{{ - 1}}}$ из (1.2) следует, что $J\sim {{u}_{n}}^{2}{{\delta }^{2}}$, где δ – толщина струи. Следовательно, u_n ∼ 1/δ. Условие баланса вязких и инерционных членов в уравнении продольного импульса: ${{u}_{n}}^{2}{\text{/}}x\sim \varepsilon {{u}_{n}}{\text{/}}{{\delta }^{2}}$. Отсюда следует, что δ ∼ εx. Из уравнения неразрывности следует u_n/x ∼ u_r/δ, где u_r – радиальная скорость. Получаем вид решения при $x \gg {{\varepsilon }^{{ - 1}}}$ [4]

(3.1)

${{u}_{n}}^{{(1)}} = \frac{1}{\xi }g(\eta ),\quad {{u}_{r}}^{{(1)}} = \varepsilon \frac{1}{\xi }q(\eta ),\quad \xi = \varepsilon x,\quad \eta = \frac{r}{{\varepsilon x}}$

Отличие решения [4] от решения [1] при ε = Re^–1 = 0.01, ξ > 0, η < 14 не превосходит 1%.

Следующее приближение имеет вид [5]

(3.2)

${{u}_{n}}^{{(2)}} = - \frac{1}{{{{\xi }^{2}}}}h(\eta ),\quad {{u}_{r}}^{{(2)}} = - \varepsilon \frac{1}{{{{\xi }^{2}}}}\eta h(\eta )$

Если струя закручена, то продольная и радиальная скорости в первых двух приближениях по ξ^–1 совпадают с (3.1) и (3.2). Окружная скорость появляется во втором приближении [5]

(3.3)

${{u}_{\tau }}^{{(2)}} = \frac{1}{{{{\xi }^{2}}}}s(\eta )$

В закрученной струе сохраняется поток момента импульса сквозь поперечное сечение

$L = 2\pi \int\limits_0^{ + \infty } {{{u}_{n}}{{u}_{\tau }}{{r}^{2}}dr} $

При $\xi \gg 1$ второе приближение много меньше первого, и струя выходит на автомодельное решение Ландау–Шлихтинга.

Отклонение численного решения от автомодельного при ξ > 3.5 не превышает 2%.

Формулы (3.1)–(3.3) получены в приближении пограничного слоя. Следующие члены координатного разложения (начиная с третьего), полученные в этом приближении, не согласуются с решением полных уравнений Навье–Стокса [10].

Если крутка струи больше или порядка единицы, то на некотором расстоянии от выходного сечения трубы образуется область рециркуляционного течения – “взрыв” вихря в струе. В этом случае также на больших расстояниях от рециркуляционной зоны параметры струи выходят на решение Лойцянского (3.1)–(3.3).

4. БЛИЖНЕЕ ПОЛЕ СТРУИ

Хотя все частицы жидкости внутри каждой струи вращаются в одном направлении, после истечения из труб циркуляция скорости по контуру, охватывающему поперечное сечение струи, равна нулю, что обеспечивается тангенциальным разрывом окружной скорости. Таким образом, внутри каждой струи имеются области с продольной завихренностью разного знака, так чтобы суммарный поток завихренности через поперечное сечение струи был бы равен нулю. Центральную часть струи назовем вихревым ядром, его окружает тангенциальный разрыв скорости.

Исследуем вопрос о слиянии двух струй в одну, суммарная циркуляция которой из-за симметрии также должна быть нулевой. Рассмотрим пространственную эволюцию двух струй по продольной координате x, рис. 1.

Рис. 1.

Эволюция продольной завихренности (по поперечным сечениям): светло-серый цвет – положительная завихренность; темно-серый – отрицательная завихренность; черные точки – точки с максимальной продольной скоростью

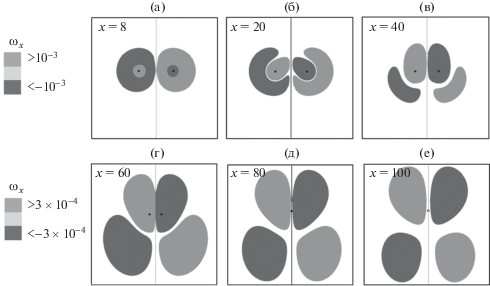
После истечения из трубы тангенциальный разрыв диффундирует в вихревую “шубу”, окружающую вихревое ядро с завихренностью противоположного знака (рис. 1a). Вихревое ядро индуцирует циркуляционное движение вихревой шубы. Струи сближаются вследствие подсасывающего действия и радиальной вязкой диффузии. Из-за сближения струй вихревые шубы перекрываются и частично аннигилируют (рис. 1б). Вследствие циркуляционного движения оставшаяся часть вихревой шубы сползает с вихревого ядра (рис. 1в). После этого вихревые ядра соприкасаются друг с другом и начинают аннигилировать, а шуба сворачивается в отдельный вихрь (рис. 1г). При дальнейшей эволюции можно считать, что две струи сливаются в одну (рис. 1д), так как точка с максимальной продольной скоростью оказывается на плоскости симметрии. Таким образом, на фоне расширяющейся вдоль оси x струи формируется система из четырех продольных вихрей с чередующимися знаками. При дальнейшем увеличении продольной координаты верхние вихри становятся почти симметричными с нижними вихрями (рис. 1е).

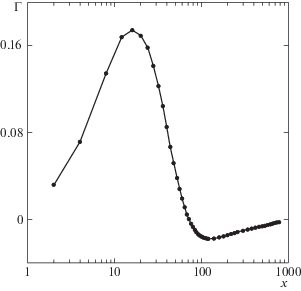
На рис. 2 приведена зависимость от продольной координаты потока завихренности через левую полуплоскость поперечного сечения струи, который равен циркуляции скорости по контуру, охватывающему эту область. Вначале циркуляция равна нулю, так как внешняя поверхность трубы неподвижна. Затем циркуляция растет вследствие аннигиляции вихревой шубы. Циркуляция достигает максимума на расстоянии 16 радиусов и начинает убывать из-за аннигиляции вихревых ядер. На расстоянии примерно 70 радиусов при слиянии двух струй в одну циркуляция обращается в нуль. Затем циркуляция становится отрицательной, достигает минимума на расстоянии 120 и медленно убывает по абсолютной величине.

Рис. 2.

Зависимость потока продольной завихренности через левую полуплоскость поперечного сечения с координатой x

5. ДАЛЬНЕЕ ПОЛЕ СТРУИ

Распределение продольной скорости вдали от источника стремится к осесимметричному, рис. 3.

Рис. 3.

Сравнение расчета продольной скорости (левая полуплоскость) с решением [1] (правая полуплоскость)

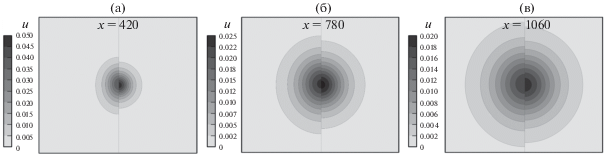
При x = 420 отклонение от решения Ландау составляет 17% (рис. 3а), при x = 780 – 10% (рис. 3б). Это отклонение медленно уменьшается при дальнейшем увеличении расстояния до 8% при x ≈ 1000 (рис. 3в).

При моделировании осесимметричных струй выход на автомодельный режим c точностью 2% наблюдался при меньших значениях приведенной координаты ξ = 3.5. Это связано с тем, что характерный размер источника в осесимметричной задаче порядка радиуса трубы, а в случае двух струй порядка расстояния между трубами (восемь радиусов).

Топология поперечного течения определяется пятью особыми точками: источником на оси струи, двумя седлами на пересечении предельной линии тока и плоскости симметрии и двумя стоками на предельной линии тока по разные стороны от плоскости симметрии, рис. 4. Отличие этой картины от решения [1] наблюдается в тонком слое в окрестности предельной линии тока, где радиальные скорости в решении [1] обращаются в нуль, и становятся существенными следующие члены разложения. При движении поперечной плоскости в сторону увеличения координаты x сток может перемещаться по предельной линии тока.

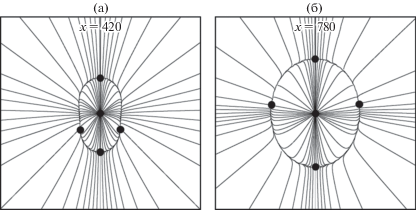
Рис. 4.

Топология поперечного течения: показаны линии тока поперечного течения и особые точки: (а, б) – х = 420, 780

Как отмечено выше, поле продольной завихренности в дальней области представляет собой четыре лепестка с чередующимися знаками. При этом правые лепестки являются зеркальным отражением левых в силу симметрии задачи. На больших расстояниях от источника наблюдается также приближенная симметрия верхних лепестков с нижними. При увеличении продольной координаты лепестки расширяются самоподобно. Закон расширения завихренной области линейный, что подтверждается сравнением распределений завихренности в разных сечениях. На рис. 5 показано сравнение распределений завихренности в сечении х = 780 радиусов и в сечениях х = 420 и 580. Геометрические размеры завихренных областей в сечениях x = 420 и 580 преобразованы растяжением относительно оси струи с коэффициентом, равным отношению координат сечений, а линии равной завихренности соответствуют значениям, полученным из деления диапазона между максимальной и минимальной величинами завихренности в данном сечении на 10 равных интервалов.

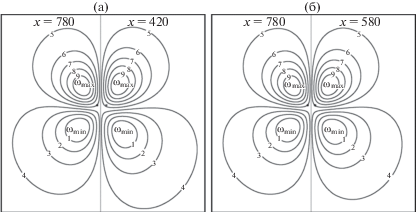
Рис. 5.

Подобие изолиний продольной завихренности в разных сечениях: в правой полуплоскости показаны изолинии завихренности в соответствующем сечении, отраженные относительно плоскости симметрии; завихренность на контуре с номером n равна ω_x = ω_min + 0.1(ω_max – ω_min)n, где ω_min, ω_max – минимальная и максимальная по сечению продольная завихренность

Установленное свойство автомодельности поля продольной завихренности по продольной координате выразим формулой

${{\omega }_{x}} = \frac{1}{{{{x}^{k}}}}F(\eta ,\varphi )$

где F – функция от автомодельной переменной η и азимутального угла φ.

Закон затухания завихренности по продольной координате можно определить по зависимости максимальной и модуля минимальной продольной завихренности в левой полуплоскости от продольной координаты. Из анализа, приведенного на рис. 6а, имеем k ≈ 3.5÷3.6. Закон затухания можно также определить по зависимости циркуляции положительного и отрицательного вихрей от продольной координаты. Соответствующий анализ (рис. 6б) дает показатель затухания циркуляции k_Γ ≈ 1.5÷1.6, что согласуется с приведенным выше значением k.

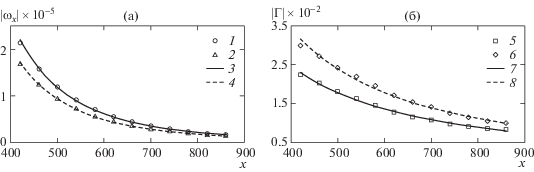
Рис. 6.

Определение показателя затухания по зависимости завихренности (а) и циркуляции (б) от продольной координаты х: 1 – максимальная по сечению продольная завихренность; 2 – модуль минимальной продольной завихренности; 3 – аппроксимация данных 1 зависимостью 56801 × x^–3.59, 4 – аппроксимация данных 2 зависимостью 28783 × x^–3.52; 5 – поток положительной продольной завихренности; 6 – модуль потока отрицательной продольной завихренности, 7 – аппроксимация данных 5 зависимостью 172 × x^–1.48; 8 – аппроксимация данных 6 зависимостью 544 × x^–1.61

Исследовалась зависимость продольной завихренности от азимутального угла. Для этой цели рассматривалась зависимость продольной завихренности ω_x от угла на девяти эквидистантных окружностях (рис. 7) в сечении x = 780. Расстояние между соседними окружностями равно десяти радиусам трубы. Начиная с третьей окружности, зависимость от угла довольно точно описывается функцией sin2φ

(5.1)

${{\omega }_{x}} = \frac{1}{{{{x}^{k}}}}f(\eta )\sin 2\varphi $

Рис. 7.

Зависимость продольной завихренности от азимутального угла: 1–9 –номер окружности; сплошные линии (б, в) – распределение продольной завихренности на окружности; пунктирные линии (б, в) – аппроксимация численных данных функцией (5.1)

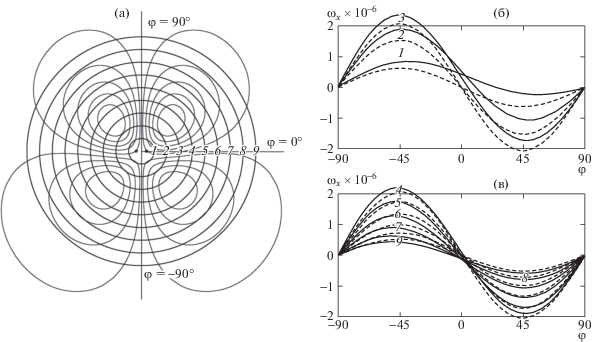
Функция f(η) определяется по численному распределению |ω_x| интегрированием вдоль окружности η = const

$f(\eta ) = \frac{1}{4}\int\limits_0^{2\pi } {{\text{|}}{{x}^{k}}{{\omega }_{x}}{\text{|}}d\varphi } $

Для сравнения отметим, что продольная завихренность в струе Ландау–Шлихтинга равна нулю, а в закрученной струе Лойцянского имеет осесимметричное распределение: вихревое ядро, окруженное вихревой шубой, при нулевой суммарной циркуляции.

Полученная структура зависимости завихренности от пространственных координат (5.1) соответствует члену мультипольного ряда [7], построенного для описания асимптотического поведения неосесимметричных струй.

Собственное решение уравнений Навье–Стокса, линеаризованных на решении [1], разыскивается в виде ряда гидродинамических мультиполей [7]

(5.2)

Здесь s = cosθ, (R, θ, φ) – сферические координаты, α_nm – собственное значение, обеспечивающее существование регулярного решения линейной однородной системы обыкновенных дифференциальных уравнений относительно функций U_nm(s), V_nm(s), W_nm(s).

Поскольку зависимость завихренности от угла описывается функцией sin2φ, выберем главный член ряда (5.2) при m = 2, n = 1

(5.3)

${\mathbf{w}} = (1 - {{s}^{2}})\left[ {U(s)\cos 2\varphi ,\;\frac{{V(s)}}{{\sqrt {1 - {{s}^{2}}} }}\cos 2\varphi ,\;\frac{{W(s)}}{{\sqrt {1 - {{s}^{2}}} }}\sin 2\varphi } \right]{{R}^{{ - \alpha }}}$

Определим составляющую завихренности ω_R

(5.4)

${{\omega }_{R}} = [({{s}^{2}} - 1)W{\text{'}}(s) + 2\left( {sW(s) + V(s)} \right)]{{R}^{{ - (\alpha + 1)}}}\sin 2\varphi $

Численный анализ затухания завихренности в двух струях дает k = α + 1 ≈ 3.5÷3.6, т.е. α ≈ 2.5÷2.6. Анализ [7] при m = 2 дает комплексное собственное значение с наименьшей вещественной частью α ≈ 2.77 + 0.92i. Затухание скорости определяется вещественной частью Re(α) ≈ 2.77, которая хорошо согласуется с численным решением. Следующее собственное число, определенное в [7], действительное и равно 3.37, что намного больше полученного в расчете взаимодействия двух струй. Такое сравнение указывает на реализуемость именно комплексного собственного числа в законе затухания компонент скорости и продольной завихренности.

Наличие мнимой части в собственном значении α = α₁ + iα₂ требует уточнения формулы (5.4). В этом случае функции U(s), V(s), W(s) также будут комплексными: U(s) = U₁(s) + iU₂(s), V(s) = V₁(s) + iV₂(s), W(s) = W₁(s) + iW₂(s). Тогда вещественная часть продольной завихренности имеет вид

(5.5)

$\begin{gathered} {{\omega }_{R}} = \frac{{\sin 2\varphi }}{{{{R}^{{{{\alpha }_{1}} + 1}}}}}[\{ ({{s}^{2}} - 1)W_{1}^{'} + 2(s{{W}_{1}} + {{V}_{1}})\} \cos \left( {{{\alpha }_{2}}\ln (R)} \right) + \\ + \;\{ ({{s}^{2}} - 1)W_{2}^{'} + 2(s{{W}_{2}} + {{V}_{2}})\} \sin \left( {{{\alpha }_{2}}\ln (R)} \right)] = \frac{{\sin 2\varphi }}{{{{R}^{{{{\alpha }_{1}} + 1}}}}}A(s)\cos \left( {{{\alpha }_{2}}\ln (R) + \delta (s)} \right) \\ \end{gathered} $

Решение (5.5) имеет медленно осциллирующий множитель – косинус логарифма R. При увеличении расстояния от источника этот множитель приведет к изменению знака у продольных вихрей.

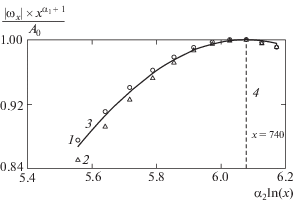
На рис. 6а была показана аппроксимация численных данных с помощью зависимости (5.4) с вещественной величиной α, которая оказалась близкой к значению 2.5÷2.6. Аппроксимация этих же данных с помощью соотношения (5.5) при α ≈ 2.77 + 0.92i показана на рис. 8. Здесь изображена функция ${{\omega }_{R}}{{R}^{{{{\alpha }_{1}} + 1}}}$ для максимальной и модуля минимальной продольной завихренности. Данные величины сначала растут, потом достигают максимума и начинают уменьшаться. Ограничения вычислительной мощности не позволили авторам проследить дальнейшую эволюцию струи, но из аппроксимации результатов, представленных на рис. 8, следует, что знак продольной завихренности изменится при R ≈ 4080.

Рис. 8.

Численная оценка масштаба смены знака продольных вихрей: 1, 2 – максимальная и минимальная завихренность в поперечном сечении x = const; 3 – аппроксимирующая функция cos(α₂ln(x) + δ₀); 4 – поперечное сечение α₂ln(x) + δ₀ = 0, α₁ = 2.77, α₂ = 0.92

ЗАКЛЮЧЕНИЕ

Рассмотрено ближнее и дальнее поле двух противоположно закрученных струй. Показано, что две струи притягиваются, диффундируют и на некотором расстоянии сливаются в одну, причем поле продольной скорости вдали от источника описывается в главном приближении осесимметричной незакрученной струей Ландау. Поскольку второе приближение также осесимметрично, продольная завихренность возникает не раньше, чем в третьем приближении.

Обнаружено, что поле продольной завихренности вдали от источника автомодельно по продольной координате и представляет собой четыре вихря с чередующимися знаками, при этом зависимость продольной завихренности от азимутального угла описывается функцией sin2φ.

Описан механизм формирования автомодельного поля завихренности. Установлено, что главный неосесимметричный член асимптотики поля скоростей является членом мультипольного ряда c азимутальным числом m = 2 и комплексным законом затухания по продольной координате.

Авторы выражают благодарность А.В. Зубцову за обсуждение результатов работы.

Работа выполнена при поддержке РФФИ (проект № 16-01-00128).

Список литературы

Ландау Л.Д. Об одном новом точном решении уравнений Навье–Стокса // Докл. АН СССР. 1944. Т. 43. № 7. С. 299–301.
Румер Ю.Б. Задача о затопленной струе // ПММ. 1952. Т. 16. Вып. 2. С. 255–256.
Гольдштик М.А., Яворский Н.И. О затопленных струях // ПММ. 1986. Т.50. Вып. 4. С. 573–583.
Schlichting H. Laminare Strahlausbreitung // Z. Angew. Math. Mech. 1933. Bd 13. № 4. S. 260–263.
Лойцянский Л.Г. Распространение закрученной струи в безграничном пространстве, затопленном той же жидкостью // ПММ. 1953. Т. 17. Вып. 1. С. 3–16.
Цуккер М.С. Закрученная струя, распространяющаяся в пространстве, затопленном той же жидкостью // ПММ. 1955. Т. 19. Вып. 4. С. 500–503.
Яворский Н.И. Неосесимметричные затопленные струи // ПММ. 1988. Т. 52. Вып. 5. С. 760–772.
Мулляджанов Р.И., Яворский Н.И. Решение задачи об истечении неосесимметричной закрученной затопленной струи // ПМТФ. 2013. Т. 54. № 2. С. 46–51.
Гайфуллин А.М., Зубцов А.В. Диффузия двух вихрей // Изв. РАН. МЖГ. 2004. № 1. С. 126–142.
Яворский Н.И. Теория затопленных струй и следов. Новосибирск: Наука, 1998. 243 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал