Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 113-122

Распространение ударной волны в вязком теплопроводном газе в длинном микроканале

О. А. Азарова^a, *, Е. М. Шахов^a, **

^a Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия

^* E-mail: olga_azarova@list.ru
^** E-mail: shakhov@ccas.ru

Поступила в редакцию 24.09.2018
После доработки 18.10.2018
Принята к публикации 18.10.2018

DOI: 10.1134/S0568528119020038

Аннотация

На основе полной системы уравнений Навье–Стокса численно решается задача о нестационарном течении газа в канале между параллельными пластинами, вызванном начальным разрывом давления и плотности в поперечном сечении канала при больших перепадах давления и умеренно малых числах Кнудсена. Применяется разностная схема второго порядка точности по пространственным переменным и по времени. Изучается влияние вязкости и теплопроводности газа на скорость распространения ударной волны и характер потока за ней в условиях длинного канала и низкой плотности газа в отсеке низкого давления. Построенное численное решение сопоставляется с известными экспериментальными и расчетными данными.

Ключевые слова: ударная волна, пограничный слой, молекулярный пучок, разреженный газ, распад разрыва, комплексно-консервативная разностная схема

Проблема генерации и исследования высокоскоростных молекулярных пучков представляет интерес не только как одна из фундаментальных проблем механики газов, но и с точки зрения широких возможностей практического применения молекулярных пучков в промышленности и аэрокосмической инженерии. В работе [1] предложен способ применения малогабаритных бездиафрагменных ударных труб для генерации высокоскоростных молекулярных пучков. Получены зависимости чисел Маха ударной волны на всей длине испытательного отсека (превышающей его ширину в 250 раз) при изменении перепада давления в резервуаре и в измерительном отсеке от 20 до 10 000 раз. При этом полученные зависимости существенно отличаются от зависимостей, предписываемых одномерной теорией идеальной ударной трубы.

Численному моделированию нестационарных газодинамических процессов в каналах и трубах посвящен ряд работ, из которых отметим статьи [2–6]. Во всех цитированных работах исследования выполнены в предположении разреженного газа, т.е. при достаточно больших числах Кнудсена (Kn₁ > 0.01) для относительно малых перепадов давлений (p₄/p₁ = 0.1) и относительно коротких каналов. Исследования проводились на основе кинетических уравнений.

Некоторое исключение составляет работа [2], в которой дан сравнительный анализ течений тремя методами: двумя методами (алгоритмами, программными кодами) решения уравнений Навье–Стокса с граничными условиями скольжения и температурного скачка на стенках канала, методом Монте–Карло и конечно-разностным методом решения модельного кинетического уравнения (S-модель) [7]. Вычисления проводились для условий, когда толкающим и испытуемым газом был один и тот же газ–аргон при начальной температуре T = 300° K. Результаты вычислений по трем методам оказались очень близкими и показали сильное затухание ударной волны. Более того, в ряде случаев число Маха M_s, регистрируемое в численном эксперименте, оказалось меньше единицы.

Цель данной работы – изучение диссипативных свойств потока в длинных каналах с отношением длины к ширине 50 < L/H < 250 на основе уравнений Навье–Стокса в диапазоне чисел Кнудсена Kn₁ < 0.03. Термин “микроканал”, использованный в заголовке, означает, что ширина канала соизмерима со средней длиной свободного пробега. Необходимым условием, которому должна удовлетворять разностная схема, является хорошее воспроизводство одномерного невязкого течения на больших расстояниях от места разрыва. Поэтому в данной работе для численного решения полной системы уравнений Навье–Стокса использовалась консервативная схема [8], обладающая низкой схемной вязкостью, которая дополнялась учетом диссипативных слагаемых, предложенным в [9].

1. ОПИСАНИЕ ПРОБЛЕМЫ

В статье проводится численное моделирование фрагментов экспериментальных результатов работы [1]. Установка [1] представляет собой длинную трубку с внутренним диаметром H = 2 мм и длиной L = 500 мм, присоединенную на одном из концов (левом) через электромагнитный клапан к резервуару высокого давления и закрытую пробкой отверстием на правом конце. Через отверстие трубка соединяется с вакуумной камерой и с устройством по формированию молекулярного пучка. Клапан играет роль диафрагмы в обычной ударной трубе и работает в циклическом режиме с временем раскрытия менее 100 мкс [1]. Перед каждым новым открытием клапана трубка освобождается от остатков имеющегося в ней газа и вновь заполняется испытуемым газом, для чего используется специальная система очистки – накачки. Периодическая работа клапана обеспечивает периодическую работу установки.

Эксперименты [1] проводились в условиях, когда толкающим газом был гелий, а испытуемым азот. Во всех опытах давление в резервуаре было одним и тем же и равнялось p₄ = 1 МПа, в то время как давление в измерительном отсеке (и во всей трубке) изменялось от опыта к опыту в диапазоне p₁ = (10²–5 × 10⁴) Па, что соответствует диапазону отношения давлений p₄/p₁ = (20–10 000). При этом температура воздуха была комнатной, т.е. приближенно Т₄ = Т₁ = 300° K. Максимальное число Кнудсена в измерительном отсеке в невозмущенном состоянии можно оценить как Kn₁ = λ₁/H = 0.032, а минимальное – как Kn₁ = 6.4 × 10^–5. Таким образом, диапазон рассматриваемых течений охватывает режимы от сплошной среды до истечения в вакуум. Однако основной режим течения в трубе близок к течению сплошной среды.

В экспериментах [1] для одного рабочего цикла получено семейство зависимостей чисел Маха M_s(x) ударной волны от координаты x вдоль оси трубы, которая отсчитывается от положения пускового клапана для диапазона отношений давлений p₄/p₁ = (20–10 000) (рис. 3б из [1]). На начальном участке трубы отмечается подъем кривых до максимального значения M_f при некотором значении x = x_f. Интервал возрастания числа Маха M_s (0 < x < x_f) соответствует временному интервалу, на котором происходит формирование фронта ударной волны. Значение x_f зависит от отношения давлений p₄/p₁ и возрастает вместе с ним. Для p₄/p₁ = 20; 100 и 200 значения x_f соответственно равны 120 мм; 150 мм и 180 мм. Интервал x > x_f интерпретируется как интервал сформировавшегося фронта ударной волны. На этом интервале происходит процесс падения M_s, обусловленный затуханием ударной волны из-за трения на стенках трубы. Таким образом, поведение числа Маха вдоль трубы существенно отличается от его распределения, предписываемого теорией идеальной трубы.

Данная работа посвящена исследованию второго из этих процессов, а именно, влиянию торможения газа на стенках трубы на число Маха ударной волны. При этом работа установки [1] в рамках рабочего цикла моделируется как обычная ударная труба в предположениях отсутствия влияния размеров бака высокого давления, мгновенного раскрытия диафрагмы и одного и того же одноатомного газа справа и слева от нее.

2. ФОРМУЛИРОВКА ЗАДАЧИ

Рассматривается течение вязкого, теплопроводного газа в плоском канале между двумя параллельными пластинами, расположенными в плоскостях y = 0 и у = H, возникающее вследствие квазиодномерного распада разрыва давления и плотности газа при t < 0 по разные стороны от диафрагмы, расположенной в точке x = x₀. Слева и справа от диафрагмы, при x = 0 и x = x₀ + L газ ограничен вертикальными стенками. В начальный момент t = 0 газ покоится с параметрами p₁, ρ₁, T₁, u₁ = 0, ${{v}_{1}}$ = 0 (давление, плотность, температура и компоненты скорости газа) справа от диафрагмы и с параметрами p₄, ρ₄, T₄, u₄ = 0, ${{v}_{4}}$ = 0 слева от нее. Полагается, что температура газа в начальный момент одинакова для всего газа, т.е. T₁ = T₄, и совпадает с постоянной температурой стенок канала T_w = T₁.

В дальнейшем полагаем, что p₄$ \gg $ p₁. В экспериментах [1] в отсеке высокого давления (0 < x < x₀) расположен толкающий газ – гелий, в отсеке низкого давления (x₀ < x < L) располагается толкаемый (или испытуемый) газ – азот (используется терминология из [10]). При моделировании считается, что толкающий и испытуемый газы совпадают, т.е. рассматривается один и тот же совершенный газ с постоянными теплоемкостями, уравнение состояния которого имеет вид:

(2.1)

$p = n{{k}_{B}}T = mn({{k}_{B}}{\text{/}}m)t = \rho RT,\quad \rho = mn,\quad R = {{k}_{B}}{\text{/}}m$

Здесь k_B = 1.38 × 10^–16 эрг/град – универсальная газовая постоянная [11], n – числовая плотность газа, R – газовая постоянная, своя для каждого газа, m – масса молекулы. В дальнейшем для простоты рассматриваются только одноатомные газы.

В начальный момент времени t = 0 диафрагма мгновенно убирается, и в газе возбуждается движение, вызванное распадом разрыва параметров. Сразу после устранения диафрагмы возникает практически одномерный невязкий распад разрыва, осложненный вязкими эффектами. Возбуждается движение газа слева–направо. По испытуемому газу распространяется волна сжатия, практически газодинамическая ударная волна, а по толкающему газу – звуковая волна, распространяющаяся со скоростью с₄ = (γRT)^0.5, где γ = 5/3 для одноатомного газа. Между этими двумя волнами располагается контактный разрыв (в газодинамическом приближении), на котором происходит изменение плотности и температуры.

Вязкие эффекты приводят к размыванию контактного разрыва и сокращению (по сравнению с теорией идеальной трубы) области постоянных параметров газа, сжатого ударной волной (области “пробки”). Этот эффект низких противодавлений был давно известен [12, 13]. Возможно, вопрос об удлинении пробки постоянных параметров испытуемого газа был одним из факторов в пользу выбора длинной трубы. Однако не очевидно, что удлинение трубы ведет к удлинению пробки, т.к. одновременно происходит падение скорости головной волны, так что этот вопрос требует дополнительного исследования.

У горизонтальных стенок движение газа тормозится и происходит нарастание пограничного слоя, который возбуждает движение газа не только в горизонтальном, но и в вертикальном направлении. Картина движения сложная и заслуживает отдельного подробного рассмотрения. В данной работе изучается движение газа на больших расстояниях от места разрыва диафрагмы (при x $ \gg $ x₀), однако и не настолько больших, при которых пограничные слои от противоположных стенок можно считать слившимися. Ведущую роль в формировании течения на рассматриваемом этапе играет движение, возбуждаемое перепадом давления, а эффекты вязкости и теплопроводности – вторичную, ведущую к затуханию процесса.

Движение газа описывается уравнениями Навье–Стокса. Вязкость газа µ и коэффициент теплопроводности k считаются зависящими от температуры по степенному закону:

(2.2)

$\begin{gathered} \mu (T) = \mu {\text{*}}{{(T{\text{/}}T*)}^{S}},\quad \mu * = \mu (T*) \\ k(T) = k{\text{*}}{{(T{\text{/}}T*)}^{S}},\quad k* = k(T*) \\ \end{gathered} $

Здесь звездочками отмечены характерные значения величин, соответствующие характерному значению температуры T*.

Средняя длина свободного пробега λ определяется через вязкость µ [14, 2 ]:

(2.3)

$\lambda = \sqrt {0.5\pi } \frac{\mu }{{\sqrt {p\rho } }}$

Это определение средней длины свободного пробега незначительно в числовом коэффициенте отличается от принятого в [11], но более часто используется в теории движения разреженных газов в каналах. Число Кнудсена определяется как

(2.4)

${\text{Kn}} = \lambda {\text{/}}H$

Скорость звука в газе c равна

$c = \sqrt {\gamma RT} $

Внутренняя энергия газа ε равна

$\varepsilon = {{C}_{v}}T$

где ${{C}_{v}}$ – теплоемкость газа при постоянном объеме.

Безразмерные величины (отмеченные штрихами) для времени, пространственных переменных, составляющих скорости и скорости звука, плотности газа, давления, температуры и коэффициентов вязкости и теплопроводности водятся следующим образом:

$\begin{gathered} t' = t{\text{/}}t*,\quad x' = x{\text{/}}l*,\quad y' = y{\text{/}}l*,\quad u' = u{\text{/}}u*,\quad v' = v{\text{/}}v*,c' = c{\text{/}}v{\text{*}} \\ \rho ' = \rho {\text{/}}\rho *,\quad p' = p{\text{/}}p*,\quad T' = T{\text{/}}T{\text{*}}\mu ' = \mu {\text{/}}\mu {\text{*}}k' = k{\text{/}}k{\text{*}} \\ \end{gathered} $

В работе приняты следующие масштабы величин:

$\begin{gathered} \rho * = {{\rho }_{1}},\quad p* = {{p}_{1}},\quad l* = H,T* = {{T}_{1}},\quad v* = \sqrt {{{p}_{1}}{\text{/}}{{\rho }_{1}}} \\ t* = l{\text{*/}}u*,\quad \mu * = {{\mu }_{1}},\quad k* = {{k}_{1}} \\ \end{gathered} $

В дальнейшем штрихи над безразмерными переменными опускаются.

При переходе к безразмерным переменным уравнение состояния (2.1) переписывается в виде p = ρT, или p = nT. При этом выражение для удельной внутренней энергии газа имеет вид $\varepsilon = p{\text{/}}(\rho (\gamma - 1))$, который справедлив для газов с постоянным отношением удельных теплоемкостей γ. Выражения для вязкости и теплопроводности (2.2) запишутся как µ = T^s и k = T^s.

Численно решается система уравнений Навье–Стокса в безразмерном виде для идеального равновесного газа с γ = 5/3 [15]:

(2.5)

$\frac{{\partial U}}{{\partial t}} + \frac{{\partial (F + {{F}_{v}})}}{{\partial x}} + \frac{{\partial (G + {{G}_{v}})}}{{\partial y}} = 0$

$U = \left( {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho v} \\ E \end{array}} \right),\quad F = \left( {\begin{array}{*{20}{c}} {\rho u} \\ {p + \rho {{u}^{2}}} \\ {\rho uv} \\ {u(E + p)} \end{array}} \right),\quad G = \left( {\begin{array}{*{20}{c}} {\rho v} \\ {\rho uv} \\ {p + \rho {{v}^{2}}} \\ {v(E + p)} \end{array}} \right)$

${{F}_{v}} = - \left( {\begin{array}{*{20}{c}} 0 \\ {\mu {\text{/Re}}(4{\text{/}}3{{u}_{x}} - 2{\text{/}}3{{v}_{y}})} \\ {\mu {\text{/Re}}({{v}_{x}} + {{u}_{y}})} \\ {\mu {{\pi }_{1}}{\text{/Re}} - (1{\text{/}}N)k{{T}_{x}}} \end{array}} \right),\quad {{G}_{v}} = - \left( {\begin{array}{*{20}{c}} 0 \\ {\mu {\text{/}}\operatorname{Re} ({{v}_{x}} + {{u}_{y}})} \\ {\mu {\text{/Re}}(4{\text{/}}3{{v}_{y}} - 2{\text{/}}3{{u}_{x}})} \\ {\mu {{\pi }_{2}}{\text{/Re}} - (1{\text{/}}N)k{{T}_{y}}} \end{array}} \right)$

${{\pi }_{1}} = u(4{\text{/}}3{{u}_{x}} - 2{\text{/}}3{{v}_{y}}) + v({{v}_{x}} + {{u}_{y}}),\quad {{\pi }_{2}} = v(4{\text{/}}3{{v}_{y}} - 2{\text{/}}3{{u}_{x}}) + u({{v}_{x}} + {{u}_{y}})$

$E = \rho (\varepsilon + 0.5({{u}^{2}} + {{v}^{2}})),\quad {\text{N}} = \operatorname{Re} \Pr (\gamma - 1){\text{/}}\gamma $

Здесь Re – число Рейнольдса, Pr – число Прандтля, N – Нуссельта. Для одноатомного газа Pr = 2/3. Число Рейнольса связано с числом Кнудсена соотношением (с учетом (2.3), (2.4)):

$\operatorname{Re} = \sqrt {0.5\pi } {\text{K}}{{{\text{n}}}^{{ - 1}}}$

На горизонтальных стенках ставились граничные условия прилипания: u = 0, $v$ = 0; полагалось, что температура газа, примыкающего к стенке, совпадает с температурой стенки. Для учета торможения газа на стенке это условие является наиболее жестким по сравнению с условиями скольжения для скорости и температурного скачка на стенке.

В расчетах использовалcя усовершенствованный пакет программ для расчета полной системы уравнений Навье–Стокса, основанный на комплексно-консервативных разностных схемах второго порядка аппроксимации по пространству и времени [8] с аппроксимацией диссипативных слагаемых по типу [9] на ортогональной шахматной сетке с одинаковыми шагами по пространству. Для повышения порядка аппроксимации без расширения шаблона схемы применялся подход [16] с использованием систем для пространственных производных по x и по y системы (2.5). Усовершенствование пакета программ касалось учета диссипативных свойств газа (вязкости и теплопроводности) применительно к условиям длинного канала.

3. АНАЛИЗ РЕЗУЛЬТАТОВ

Решение задачи зависит от двух безразмерных параметров, – отношения давлений p₄/p₁ и числа Кнудсена Kn₁, а также от зависимости вязкости и теплопроводности от температуры. Основные расчеты были выполнены p₄/p₁ = 20, 100 и 200 для различных Kn₁ с коэффициентами вязкости и теплопроводности µ = T^s и k = T^s с s = 0.5, что соответствует молекулярной модели твердых шаров для одноатомного газа.

3.1. Перепад давлений p₄/p₁ = 20

В расчетах для p₄/p₁ = 20 длина трубы равнялась 40 000h_y (что соответствовало 500H), на ширину трубы H приходилось 80h_y; распад разрыва происходил в точке x_o = 20 000 (что соответствовало 250H). Здесь и далее для нахождения координаты ударной волны наравне с критерием, связанным с maxp_x(x, 0.5H) в расчетном узле, использовался также другой критерий: если p(x_i, 0.5H) > 1.1p₁, то значение x_i принималось за координату ударной волны. Оба критерия давали практически совпадающие результаты. Заметим, что используемый критерий на основе оценки давления аналогичен предложенному в [2], где подобные оценки применяются на основе изменения плотности.

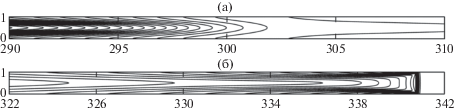
Изолинии плотности в окрестности ударной волны и волны разрежения для p₄/p₁ = 20 приведены на рис. 1. Видно, что используемый алгоритм дает абсолютно симметричную картину течения.

Рис. 1.

Изолинии плотности в окрестности (а) волны разрежения (расстояние между изохорами 0.2) и (б) ударной волны (расстояние между изохорами 0.02), p₄/ p₁ = 20, Kn₁ = 0.01, t = 46

На рис. 2 представлены профили плотности на оси симметрии y = H/2 в различные моменты времени при p₄/p₁ = 20 и Kn₁ = 0.01. Видно, что ударная волна вырождается (в простую волну сжатия), не доходя до конца трубы. Длина пробки хорошо видна на распределениях плотности: это область постоянных параметров за фронтом ударной волны. Отметим, что давление в области пробки вследствие действия вязкости и теплопроводности является монотонно (почти линейно) возрастающей функцией (считая от фронта ударной волны к левой границе пробки), причем ее наклон относительно оси x является постоянным по времени.

Рис. 2.

Распределения плотности (а) и давления (б) на оси симметрии y = H/2, p₄/p₁ = 20 , Kn₁ = 0.01, t = 46, 92, 140 (1–3)

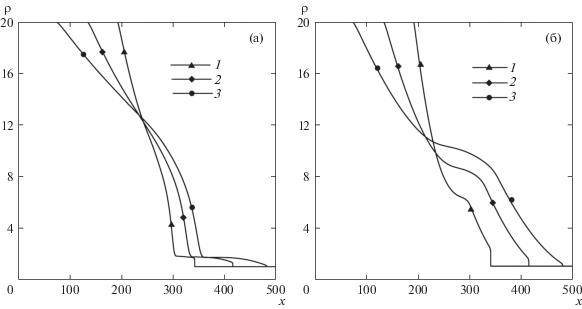
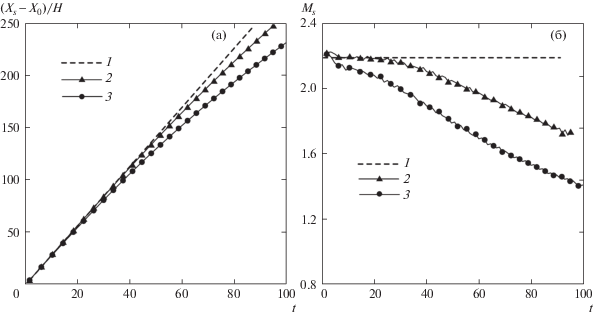
Рис. 3.

Динамика координаты (а) и числа Маха ударной волны (б), p₄/p₁ = 20: 1 – значения из задачи о невязком распаде разрыва; Kn₁ = 0.005, 0.01, 0.015 (2–4), 5 – Kn₁ = 0.0025

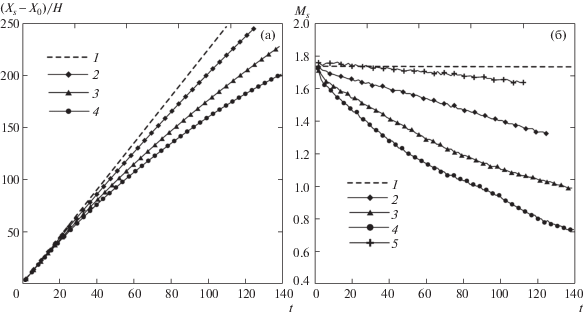
На рис. 3 представлены результаты расчетов динамики ударной волны и числа Маха ударной волны при p₄/p₁ = 20. Видно, что ударная волна проходит всю длину канала L = 250H только при достаточно малых числах Кнудсена, Kn₁ < 0.005. При больших числах Кнудсена ударная волна вырождается в простую волну сжатия (при этом M_s < 1). Зависимость от Kn₁ достаточно резкая, так что уже при Kn₁ = 0.01 эксперимент по разгону газа ударной волной для генерации молекулярного пучка теряет смысл. Чтобы это было возможно, необходимо повышать отношение давлений p₄/p₁.

3.2. Перепад давлений p₄/p₁ = 100 и 200

В расчетах для p₄/p₁ = 100 длина трубы равнялась 32 000h_y (что соответствовало 400H), в расчетах для p₄/p₁ = 200 длина трубы равнялась 32400h_y (что соответствовало 405H). В обоих случаях на ширину канала H приходилось 80h_y; распад разрыва происходил в точке x_o = 12 000 (что соответствовало 150H). Начальные условия задавались из соответствующих расчетов по схеме первого порядка на интервале времени t₁ ~ o(t_k), где t_k – время окончания счета. Значение t₁ выбиралось расчетным образом, здесь t₁ = 0.2. Некоторое нефизичнное поведение M_s(t) в самом начале процесса (превышение невязкого значения, найденного из задачи о распаде разрыва) можно объяснить влиянием “сшивки” решений, полученных по схемам первого и второго порядков.

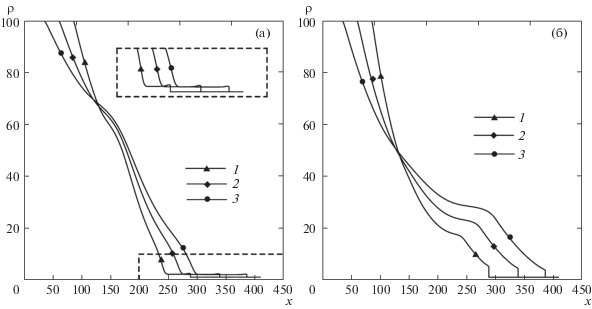
На рис. 4 представлены профили плотности на оси симметрии y = H/2 в различные моменты времени при p₄/p₁ = 100 и Kn₁ = 0.01. Видно, что область пробки также характеризуется постоянными параметрами плотности за фронтом ударной волны и наличием линейных отрезков давления с неизменяющимися по времени наклонами по x.

Рис. 4.

Распределения плотности (а) и давления (б) на оси симметрии y = H/2, p₄/p₁ = 100 , Kn₁ = 0.01, t = 50, 70, 90 (1–3), увеличенная область (пунктир) (а)

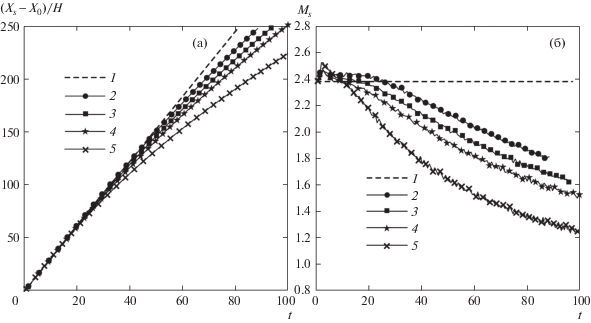
На рис. 5 и 6 представлены результаты расчетов динамики ударной волны и числа Маха ударной волны при p₄/p₁ = 100 и 200. Эти фигуры показывают, что только сильное повышение отношения давлений p₄/p₁ позволяет сжать и разогнать более разреженный газ (p₄/p₁ = 100 для Kn₁ = 0.01 и p₄/p₁ = 200 для Kn₁ = 0.02).

Рис. 5.

Динамика координаты (а) и числа Маха ударной волны (б), p₄/p₁ = 100: 1 – значения из задачи о невязком распаде разрыва; Kn₁ = 0.01, 0.015 (2, 3)

Рис. 6.

Динамика координаты (а) и числа Маха ударной волны (б), p₄/p₁ = 200: 1 – значения из задачи о невязком распаде разрыва; Kn₁ = 0.015, 0.0175, 0.02, 0.03 (2–5)

3.3. Обсуждение результатов

Представленные результаты получены без учета воздействия толкающего газа на испытуемый в процессе раскрытия клапана и качественно согласуются с результатами [1] в средней части трубы. Детальное сравнение результатов невозможно из-за различия условий задачи и эксперимента, в особенности, различия в геометрии течения (в экспериментах – течение в ударной трубе цилиндрически симметричное, в расчетах рассматривается двумерное плоское течение между параллельными стенками). Различие также связано с приближением проистекающих процессов в резервуаре и в измерительном отсеке одним и тем же (одноатомным) газом.

Тем не менее было проведено сопоставление результатов по наклонам кривых (M_s)_x, заимствованным из рис. 3б работы [1], и полученных расчетных кривых при одних и тех же отношениях давлений p₄/p₁ = 20, 100 и 200 и установлено соответствие между числами Кнудсена в расчетах Kn₁ и экспериментах ${\text{Kn}}_{1}^{*}$. В табл. 1 представлены результаты расчетов и обработки экспериментальных данных по наклонам (M_s)_x при различных числах Кнудсена. Наклоны экспериментальных кривых (абсолютные величины), выражающих зависимость M_s(x), оценивались на интервале 200–400 мм, при этом использовалась линейная интерполяция. Наклоны соответствующих численных кривых (абсолютные величины) рассматривались на интервалах по x (x $ \gg $ x₀), на которых зависимость M_s(x) близка к линейной. Двумя звездочками отмечены те значения наклонов, которые наилучшим образом отвечают эксперименту.

Таблица 1.

Сравнение значений наклонов кривых M_s(x) с результатами [1]

p₄/p₁	20	100	200
$abs{{({{{\text{M}}}_{s}})}_{x}}$, эксперимент [1]	0.000893	0.00143	0.00268
$abs{{({{{\text{M}}}_{s}})}_{x}}$, расчет Kn₁ = 0.005	0.00085**
$abs{{({{{\text{M}}}_{s}})}_{x}}$, расчет Kn₁ = 0.01	0.00156	0.00140**
$abs{{({{{\text{M}}}_{s}})}_{x}}$, расчет Kn₁ = 0.015	0.00212	0.00198	0.00184
$abs{{({{{\text{M}}}_{s}})}_{x}}$, расчет Kn₁ = 0.0175			0.00193
$abs{{({{{\text{M}}}_{s}})}_{x}}$, расчет Kn = 0.02			0.00254**
$abs{{({{{\text{M}}}_{s}})}_{x}}$, расчет Kn₁ = 0.03			0.00297

** наилучшее приближение для экспериментальной кривой

Видно, что для p₄/p₁ = 20 экспериментальному значению ${\text{Kn}}_{1}^{*}$ = 0.000064 отвечает расчетное число Kn₁ = 0.005, для p₄/p₁ = 100 экспериментальному значению ${\text{Kn}}_{1}^{*}$ = 0.00032 отвечает расчетное значение Kn₁ = 0.01 и для p₄/p₁ = 200 значению ${\text{Kn}}_{1}^{*}$ = 0.00064 отвечает Kn₁ = 0.02. Таким образом, экспериментальные значения ${\text{Kn}}_{1}^{*}$ для p₄/p₁ = 100 и p₄/p₁ = 200 в 31 раз меньше полученных расчетных значений по двумерной модели течения в плоском канале и в 78 раз меньше для p₄/p₁ = 20.

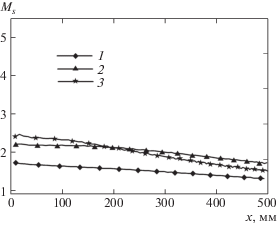
Зависимости, наилучшим образом приближающие экспериментальные кривые, полученные в [1] для p₄/p₁ = 20, 100 и 200, представлены на рис. 7. Здесь взяты масштабы по осям координат такие же, как в [1]. Отметим, что имеющееся повышение полученных в эксперименте значений числа Маха на начальной стадии процесса (x < 180 мм) можно объяснить происходящим процессом формирования фронта ударной волны в результате срабатывания клапана. Эта стадия при численном моделировании не рассматривалась и полученные расчетные зависимости M_s(x) не содержали интервала первоначального возрастания (поэтому, в отличие от эксперимента, расчетные кривые для p₄/p₁ = 100 и p₄/p₁ = 200 пересекаются). Далее в эксперименте наблюдается монотонное (близкое к линейному) уменьшение числа Маха ударной волны на исследуемом интервале (200 мм < x < 400 мм) с наклонами кривых, близкими к полученным с помощью обработки расчетных данных.

Рис. 7.

Численные зависимости, наилучшим образом приближающие экспериментальные кривые из [1]: 1 – p₄/p₁ = 20, Kn₁ = 0.005; 2 – p₄/p₁ = 100, Kn₁ = 0.01; 3 – p₄/p₁ = 200, Kn₁ = 0.02

ЗАКЛЮЧЕНИЕ

На основе численного решения полной системы уравнений Навье–Стокса для длинной ударной трубы (канала) при низких значениях противодавления и при больших отношениях давлений в отсеках канала установлено, что течение с ударными волнами в длинных каналах реализуется при достаточно малых (пороговых) числах Кнудсена. С увеличением отношения давлений в отсеках пороговое число Кнудсена может быть увеличено.

Работа выполнена при частичной финансовой поддержке РФФИ, Проекты № 16-01-00489 и № 16-08-01228.

Список литературы

Mioshi N., Nagata S., Rinefuchi I., Shimizu K., Takagi S., Matsumoto Y. Development of ultra small shock tube for high energy molecular beam source // 26^th Internat. Symp. Rarefied Gas Dynamics. AIP Conf. Proc. 1084, Melville, New York, 2009. P. 557–562.
Zeiton D.E., Graur I.A., Burtschell Y., Ivanov M.S., Kudrayvtsev A.N., Bondar Ye.A. Continuum and kinetic simulation of shock wave propogation in long microchannel // 26^th Internat. Symp. Rarefied Gas Dynamics. AIP Conf. Proc. 1084, Melville, New York, 2009. P. 464–469.
Клосс Ю.Ю., Черемисин Ф.Г., Шувалов П.В. Решение уравнения Больцмана для нестационарных течений с ударными волнами в узких каналах // Журн. вычисл. матем. и матем. физ. 2010. Т. 50. № 6. С. 1148–1158.
Конопелько Н.А., Титарев В.А., Шахов Е.М. Нестационарное течение разреженного газа в микроканале из-за распада разрыва давления // Журн. вычисл. матем. и матем. физ. 2016. Т. 56. № 3. С. 476–486.
Титарев В.А., Шахов Е.М. Нестационарное течение разреженного газа с ударной волной в канале // Изв. РАН. МЖГ. 2018. № 1. С. 147–155.
Ларина И.Н., Рыков В.А., Шахов Е.М. Развитие течения разреженного газа между параллельными пластинами из-за начального разрыва давления // Докл. АН РАН. 1995. Т. 343. № 7. С. 482–485.
Шахов Е.М. Об обобщении релаксационного кинетического уравнения Крука // Изв. РАН, МЖГ. 1968. № 5. С. 142–145.
Азарова О.А. Комплексно-консервативные разностные схемы в задачах сверхзвукового обтекания простых аэродинамических форм // Журн. вычисл. матем. и матем. физ. 2015. Т. 55. № 12. С. 2057–2092.
Azarova O.A. Modeling of instabilities and contact structures on the base of minimum-stencil difference schemes using viscous and inviscid approaches // Proc. Int. Conf. “Numerical geometry, grid generation and high performance computing (NUMGRID2010)”. Russia, Moscow, CC RAS, 2010. P. 78–85.
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978. 736 с.
Чепмен С., Каулинг Г. Математическая теория неоднородных газов. М.: ИЛ, 1960. 510 с.
Duff R.E. Shock-tube performance at low initial pressure // Phys. Fluids. 1959. V. 2. P. 207–216.
Roshko A. On flow duration in low pressure shock tube // Phys. Fluids. 1960. V. 3. P. 835–842.
Шарипов Ф.М., Селезнев В.Д. Движение разреженных газов в каналах и микроканалах. Екатеринбург: УО РАН, 2008. 230 с.
Роуч П. Вычислительная гидромеханика. М.: Мир, 1980. 616 с.
Грудницкий В.Г., Прохорчук Ю.А. Один прием построения разностных схем с произвольным порядком аппроксимации дифференциальных уравнений в частных производных // Докл. АН СССР. 1977. Т. 234. № 6 . С. 1249–1252.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал