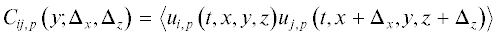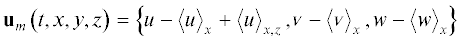Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 72-93
ХАРАКТЕРИСТИКИ НЕУСТОЙЧИВОСТИ, РАЗВИВАЮЩЕЙСЯ В ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ПЛОСКОМ КАНАЛЕ
Н. В. Никитин a, *, Н. В. Попеленская a, **
a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
* E-mail: nvnikitin@mail.ru
** E-mail: aero.natap@mail.ru
Поступила в редакцию 04.06.2018
После доработки 14.06.2018
Принята к публикации 27.06.2018
Аннотация
Проведено численное исследование эволюции возмущений в развитых турбулентных течениях в плоском канале при числах Рейнольдса до ${\text{R}}{{{\text{e}}}_{{\tau }}} = 586$. Рассчитанные на основе решения несжимаемых уравнений Навье–Стокса установившиеся турбулентные течения используются затем в качестве основных течений для изучения процесса развития возмущений. Найдены значения старшего показателя Ляпунова (СПЛ) ${{\lambda }_{1}}$, определены мгновенные и статистические свойства соответствующего старшего ляпуновского вектора (СЛВ). При произвольных начальных условиях выход возмущений на режим экспоненциального роста $ \sim {exp\;}({{\lambda }_{1}}t)$ происходит за время ${\Delta }{{t}^{ + }} < 50$. Обнаружено, что значение СПЛ увеличивается с ростом числа Рейнольдса от $\lambda _{1}^{ + } \approx 0.021$ при ${\text{R}}{{{\text{e}}}_{{\tau }}} = 180$ до $\lambda _{1}^{ + } \approx 0.026$ при ${\text{R}}{{{\text{e}}}_{\tau }} = 586$. СЛВ проявляется в виде локализованных во времени и пространстве пятен повышенной интенсивности пульсаций, концентрирующихся в области буферного слоя. Распределения среднеквадратичных интенсивностей пульсаций скорости и завихренности в СЛВ качественно близки к соответствующим распределениям в основном течении с искусственно удаленными из него пристенными полосами. Отличием является бóльшая концентрация возмущений в окрестности буферного слоя ${{y}^{ + }}$ = 10–30 и относительно бóльшая (примерно на 80%) амплитуда пульсаций завихренности. Основываясь на энергетических спектрах пульсаций скорости и завихренности, определены интегральные пространственные масштабы структур в поле СЛВ. Обнаружено, что структуры СЛВ в среднем вдвое ýже и вдвое короче соответствующих структур основного течения. Определен вклад каждого из слагаемых, входящих в выражение для производства кинетической энергии возмущений. Показано, что процесс развития возмущений существенным образом диктуется неоднородностью основного течения, а также присутствием в нем трансверсального движения. Пренебрежение этими факторами ведет к значительной недооценке скорости роста возмущений. Наличие пристенных полос в основном течении наоборот не играет заметной роли в развитии возмущений СЛВ. Искусственное удаление полос из поля основного течения не меняет характера роста возмущений.
Поведение пространственно-временных хаотических систем остается трудным для объяснения и предсказания, несмотря на значительные усилия, затраченные на их изучение. Турбулентные течения относятся к числу таких труднопредсказуемых систем. Даже простейшие статистические закономерности, детально изученные экспериментально, вроде закона сопротивления в круглой трубе, не имеют до сих пор теоретического объяснения. Серьезным остается вопрос, насколько хаотическое поведение системы во времени связано с пространственной неупорядоченностью и является ли знание пространственной структуры достаточным для предсказания временнóй динамики. Степень предсказуемости пространственно-временной системы ассоциируется с характеристиками ее устойчивости – насколько быстро меняется пространственная структура под действием малых случайных возмущений.
Развитие мелкомасштабных возмущений в пристенных турбулентных течениях обычно связывается с наличием пристенных полосчатых структур. Полосчатые структуры – непременный атрибут пристенных сдвиговых течений. Они наблюдаются как в естественных, так и контролируемых условиях, лабораторных экспериментах, численных расчетах. Полосы возникают в пограничных слоях на стадии перехода от ламинарного режима движения к турбулентному [1] и сохраняются в развитых турбулентных течениях [2]. Возникновение крупномасштабных неоднородностей в распределении продольной скорости объясняется наличием в сдвиговом потоке продольных вихрей и происходит под действием так называемого “лифт-ап” эффекта [3]. В переходных пограничных слоях продольные вихри отбираются из случайных возмущений набегающего потока. Высокочастотные и соответственно коротковолновые вихри быстро затухают без заметного влияния на основное течение, а низкочастотные, длинноволновые вихри за время своего затухания вниз по потоку успевают произвести заметные искажения в распределении продольной скорости. Искажение пограничного слоя под действием вихревых возмущений набегающего потока может вызывать вторичную неустойчивость полосчатого движения и переход к турбулентности, минуя стадию развития волн Толмина–Шлихтинга (“байпасный” переход) [4, 5].
В развитых (постпереходных) пристенных турбулентных течениях полосчатые структуры сохраняются, однако становятся быстро меняющимися как в пространстве, так и во времени. По большей части они концентрируются в области буферного слоя. Их средняя протяженность вдоль потока составляет около 103, а средний интервал в направлении размаха – около 102 вязких длин [6]. Согласно общепринятой точке зрения эти нестационарные пристенные полосчатые структуры вовлечены в процесс поддержания пристенной турбулентности [7–12]. Предложено множество моделей, призванных обосновать повторяющееся появление полосчатых структур в пристенных турбулентных течениях и, в частности, объяснить известные из экспериментов и численных расчетов универсальные линейные размеры этих структур [13–18].
Неустойчивость пристенных полос в турбулентных течениях исследуется, начиная с первых работ по их визуализации в [2, 7]. Было предположено, что основной причиной осцилляции и последующего разрушения полос может быть неустойчивость типа Кельвина–Гельмгольца, развивающаяся в областях полос замедления, где локальный профиль скорости $U\left( y \right)$ может иметь точку перегиба. В исследованиях устойчивости двумерных распределений скорости $U\left( {y,z} \right)$, в которых на одномерный профиль скорости $U\left( y \right)$ накладываются периодические по z полосы [12], [19–21], выявлено два основных типа неустойчивости: синусовый и варикозный. Им отвечает соответственно антисимметричное и симметричное по z распределение возмущений. В большинстве случаев синусовая неустойчивость оказывается доминирующей по сравнению с варикозной. Более того, в [20] делается вывод, что при типичной интенсивности полосчатого движения в турбулентных течениях варикозная неустойчивость едва ли может развиваться. Что касается синусовой неустойчивости, то даже если она и возникает, то соответствующие коэффициенты нарастания ограничены сравнительно небольшими значениями из-за вязкой диффузии полос. В качестве альтернативного, более выраженного фактора в [10] предложен немодальный механизм роста возмущений на фоне полосчатого движения.
Отметим, что в большинстве теоретических исследований предполагаются стационарность и прямолинейность полос, тогда как в реальных турбулентных течениях полосы нестационарны и непрямолинейны, имеют конечную длину и нерегулярное распределение в боковом направлении, переменную амплитуду как в пространстве, так и во времени. Каждый из перечисленных факторов может иметь важное значение. В работе [22] показано, что при исследовании устойчивости нестационарных решений линейных несамосопряженных систем фактор нестационарности может иметь решающее значение и приводить, в частности, к асимптотической неустойчивости. В [23] делается вывод, что нестационарность полос в турбулентном течении является определяющим фактором установления процесса самоподдержания турбулентности (см. также [24]). Заметим, что в [23] рассматривалась модельная постановка, в которой нестационарное полосчатое движение предполагается однородным в направлении движения. В настоящей работе показано, в частности, что изменчивость течения в направлении движения также является существенным фактором при оценке степени его устойчивости.
При исследовании устойчивости систем с хаотическим поведением классические определения утрачивают свое значение. Им на смену приходит понятие орбитальной устойчивости, характеризуемое ляпуновскими показателями и соответствующими им ляпуновскими векторами. Ляпуновские показатели и векторы характеризуют устойчивость хаотических аттракторов аналогично тому, как собственные значения и векторы характеризуют устойчивость стационарных решений. Описание турбулентных течений жидкости с позиций поведения хаотических динамических систем на сегодняшний день не является общепринятым. Наибольшее развитие это направление исследований получило в приложении к задачам турбулентной конвекции Рэлея–Бенара [25–27]. В настоящей работе численно изучаются свойства устойчивости развитых турбулентных течений в плоском канале. Известно несколько алгоритмов расчета ляпуновских показателей и векторов [28, 29]. Расчет ляпуновского спектра с соответствующими векторами представляет собой довольно ресурсоемкую процедуру и поэтому затруднителен для многомерных ($N \sim {{10}^{8}}$) систем, подобных рассматриваемым в настоящей работе. Мы ограничиваемся исследованием свойств старшего ляпуновского вектора, отвечающего наибольшему показателю ${{\lambda }_{1}}$. Для этой цели используется подход, разработанный в предыдущих публикациях [30, 31]. Линеаризованные уравнения Навье–Стокса для возмущений, развивающихся на фоне развитого турбулентного течения, интегрируются параллельно с уравнениями для основного турбулентного течения. С течением времени амплитуда возмущений выходит на экспоненциальный режим развития, что соответствует выходу решения на старший ляпуновский вектор. Аналогичный метод расчета эволюции возмущений в сверхзвуковой струе недавно был применен в [32]. Отметим, что формально старший ляпуновский вектор выделяется среди других возмущений лишь при $t \to \infty $. Однако, как показывают наши результаты, даже стартуя с достаточно произвольных случайных начальных условий, асимптотическое поведение амплитуды возмущения достигается за сравнительно короткое время ${\Delta }{{t}^{ + }} \lesssim 50.$ Для сравнения, характерное время изменения крупномасштабных структур в пристенном турбулентном слое (“eddy turnover time”) составляет бóльшую величину ${{\tau }^{ + }} \approx 80$ ([15]).
Численные исследования эволюции возмущений в развитых турбулентных течениях в трубах были начаты в [33]. Обнаружено, что малые возмущения скорости во входном сечении турбулентного течения экспоненциально нарастают вниз по потоку. В [30] показано, что в диапазоне чисел Рейнольдса ${\text{R}}{{{\text{e}}}_{\tau }}$ от 140 до 320 в круглой трубе и плоском канале скорость экспоненциального роста возмущений соответствует универсальному значению показателя экспоненты $\sigma _{1}^{ + } \approx 0.0021$. Рост возмущений вниз по потоку можно интерпретировать как рост возмущений во времени при их сносе по течению. Если ${{c}_{f}}$ – скорость сноса возмущений, то скорость экспоненциального роста во времени можно оценить как ${{\lambda }_{1}} = {{c}_{f}}{{\sigma }_{1}}$. Из анализа характера распространения возмущений в [30] найдено $c_{f}^{ + } \approx 10$, таким образом, для скорости роста во времени получена оценка $\lambda _{1}^{ + } \approx 0.021$. Это значение согласуется с результатами [34], где рассчитывался ляпуновский спектр, соответствующий турбулентному течению в плоском канале при предельно низком числе Рейнольдса ${\text{R}}{{{\text{e}}}_{{\tau }}} = 80$. Старший показатель Ляпунова, характеризующий наибольшую скорость временнóго роста малых возмущений, оказался равным $\lambda _{1}^{ + } \approx 0.02$, что близко к оценке, полученной в [30]. Выводы об универсальности (т.е. независимости от числа Рейнольдса и вида течения) величины $\lambda _{1}^{ + }$, сделанные в [30], подтверждены в [31] непосредственными расчетами временного развития возмущений. В [31, 34] турбулентные течения рассчитывались в традиционной временной постановке, предусматривающей условие периодичности в направлении основного потока. Условие пространственной периодичности обеспечивает замкнутость системы, что оправдывает применимость подходов теории динамических систем. В численных экспериментах [30, 33] система не являлась замкнутой, поскольку на входе в трубу/канал задавался нестационарный турбулентный поток. Тем более интересно, что два принципиально отличающихся с математической точки зрения подхода дают совпадающие оценки для максимальной скорости роста возмущений. Это, в частности, лишний раз подтверждает уместность использования периодических граничных условий в численных расчетах установившихся турбулентных течений в трубах и каналах.
В [35] рассчитаны показатели Ляпунова для плоского течения Куэтта при предельно низком числе Рейнольдса Re $ = 400$ (Re$_{\tau } = 34$) в области минимального размера ${{L}_{x}} = 1.75\pi ,\quad{{L}_{z}} = 1.2\pi $, ранее рассматривавшемся в [8] (${{L}_{x}},{{L}_{z}}$ – размеры расчетной области в продольном и боковом направлении, отнесенные к полуширине канала соответственно). Для старшего показателя Ляпунова получено $\lambda _{1}^{ + } \approx 0.007$, что втрое меньше значений, найденных в [30, 31] и [34]. Авторы предполагают, что причиной такого значительного расхождения может служить предельно низкое значение числа Рейнольдса в их работе. Это предположение противоречит выводу [30, 31] о независимости $\lambda _{1}^{ + }$ от числа Рейнольдса в пристенных турбулентных течениях и ставит под сомнение гипотезу об универсальности этой характеристики для любых пристенных течений. Мы повторили вычисления [35] и обнаружили, что заметное отличие в значении $\lambda _{1}^{ + }$ объясняется не малостью числа Рейнольдса, а недостаточностью размеров расчетной области [36]. Даже при минимальном числе Рейнольдса Re = 400 увеличение размера расчетной области приводит к увеличению $\lambda _{1}^{ + }$ от 0.007 до 0.023, что близко к оценке $\lambda _{1}^{ + } \approx 0.021$, полученной в [30, 31].
В настоящей работе вычисление значений старшего показателя Ляпунова в турбулентном течении в плоском канале распространено на область бо́льших чисел Рейнольдса (до ${\text{R}}{{{\text{e}}}_{{\tau }}} = 586$). Определены мгновенные проявления и статистические характеристики старшего ляпуновского вектора. Насколько нам известно, это первая работа по исследованию свойств старшего вектора Ляпунова в реалистически рассчитанном пристенном турбулентном течении.
1. ПОСТАНОВКА И РАСЧЕТНЫЕ ВАРИАНТЫ
Рассмотрим турбулентное поле скорости $u\left( {t,x} \right)$ и близкое к нему в начальный момент времени $t = 0$ поле ${{u}_{1}}\left( {t,x} \right)$. Например, $u\left( {0,x} \right)$ может быть мгновенным распределением скорости в турбулентном течении, рассчитанном численно методом прямого численного моделирования, а ${{u}_{1}}(0,x)$ есть $u\left( {0,x} \right)$ плюс некоторое малое возмущение
(1.1)
${{u}_{1}}\left( {0,x} \right) = u\left( {0,x} \right) + {{u}_{p}}\left( {0,x} \right),\quad \left\| {{{u}_{p}}\left( {0,x} \right)} \right\| \ll \left\| {u\left( {0,x} \right)} \right\|$Решая уравнения Навье–Стокса параллельно с начальными условиями $u\left( {0,{\mathbf{x}}} \right)$ и ${{u}_{1}}(0,x)$, можно проследить процесс расхождения изначально близких турбулентных полей. Эволюцию разности двух решений при $t > 0$ можно интерпретировать как эволюцию возмущения
В данной работе нас интересует именно эволюция возмущения, поэтому вместо уравнений Навье–Стокса для поля ${{u}_{1}}$ удобно сразу выписать уравнения для возмущения (1.2) и решать их параллельно с уравнениями для $u$
(1.3)
$\frac{{\partial u}}{{\partial t}} + \left( {u\nabla } \right)u = - \frac{1}{\rho }\nabla p + \nu {{\nabla }^{2}}u,\quad \nabla u = 0$(1.4)
$\frac{{\partial {{u}_{p}}}}{{\partial t}} + \left( {{{u}_{p}}\nabla } \right)u + \left( {u\nabla } \right){{u}_{p}} + \left( {{{u}_{p}}\nabla } \right){{u}_{p}} = - \frac{1}{\rho }\nabla {{p}_{p}} + \nu {{\nabla }^{2}}{{u}_{p}},\quad\quad \nabla {{u}_{p}} = 0$В (1.4) ${{p}_{p}}$ – возмущение давления. Уравнения (1.4) – нелинейные уравнения для возмущения, развивающегося на фоне основного течения $u\left( {t,x} \right)$, которое в рассматриваемом случае представляет собой нестационарное трехмерное поле, рассчитываемое параллельно решением уравнений (1.3).
В настоящей работе рассматривается турбулентное течение в плоском канале. Уравнения (1.3), (1.4) решаются в прямоугольной области $\left( {x,y,z} \right) \in \left[ {0,{{L}_{x}}} \right] \times \left[ { - h,h} \right] \times \left[ {0,{{L}_{z}}} \right]$ с условием периодичности в однородных направлениях $x$ и $z$ и условием прилипания на твердых стенках канала $y = \pm h$. Используется алгоритм [37], сочетающий конечноразностный консервативный метод второго порядка аппроксимации по пространству и полунеявную схему третьего порядка интегрирования по времени. Средняя скорость ${{U}_{b}}$ (а следовательно, и число Рейнольдса Re = = $2h{{U}_{b}}{\text{/}}\nu $) сохраняется постоянной в процессе расчета. Всего в рамках исследования было рассчитано более двадцати вариантов течения в диапазоне $140 \leqslant {\text{R}}{{{\text{e}}}_{{\tau }}} \leqslant 590$. Кроме числа Рейнольдса варьировались размеры расчетной области и расчетной сетки, величина шага интегрирования по времени. Для представления в настоящей работе выбраны три основных варианта при ${\text{Re}} = 5600$, 13 764 и 21 907 (соответствующие значения ${\text{R}}{{{\text{e}}}_{{\tau }}}$ составляют 178, 391 и 586). Течения при этих значениях Re рассчитывались ранее в [38], результаты этих расчетов подробно опубликованы в сети Интернет по адресу http://turbulence.ices.utexas.edu/MKM_1999.html. Список расчетных вариантов, включающий значения числа Рейнольдса ${\text{R}}{{{\text{e}}}_{{\tau }}} = {{u}_{\tau }}h{\text{/}}\nu \equiv {{h}^{ + }}$, размеры расчетной сетки, величины пространственных периодов течений ${{L}_{x}},{{L}_{z}}$, размеры ячеек сетки ${{h}_{x}},{{h}_{y}},{{h}_{z}}$ в каждом пространственном направлении, приведен в таблице 1.
Таблица 1.
| Расчет | ${Re\;}\left( {{\text{R}}{{{\text{e}}}_{{\tau }}}} \right)$ | Сетка | ${{L}_{x}}{\text{/}}h\quad(L_{x}^{ + })$ | ${{L}_{z}}{\text{/}}h\quad(L_{z}^{ + })$ | $h_{x}^{ + }$ | $h_{y}^{ + }$ | $h_{z}^{ + }$ | ${{{\Delta }}_{{Cf}}}$ |
|---|---|---|---|---|---|---|---|---|
| R178 | 5600 (178) | $256 \times 128 \times 256$ | 12 (2140) | 6 (1070) | 8.3 | 1.1–4.3 | 4.2 | –0.2% |
| R391 | 13 764 (391) | $256 \times 256 \times 256$ | 6 (2350) | 3 (1170) | 9.2 | 0.9–4.7 | 4.6 | –0.4% |
| R586 | 21 907 (586) | $512 \times 384 \times 512$ | 6 (3520) | 3 (1780) | 6.9 | 1.0–5.0 | 3.4 | –0.2% |
| R391s | 13 764 (392) | $64 \times 256 \times 256$ | 1.5 (590) | 3 (1180) | 9.2 | 0.9–4.7 | 4.6 | –0.26% |
Как обычно, нормировка на пристенные (вязкие) масштабы скорости ${{u}_{\tau }} = \sqrt {{{\tau }_{w}}{\text{/}}\rho } $ и длины ${{l}_{\tau }} = \nu {\text{/}}{{u}_{\tau }}$, где ${{\tau }_{w}}$ – среднее трение на стенке, $\rho $ и $\nu $ – плотность и кинематическая вязкость жидкости, обозначается верхним индексом “+”. Во всех расчетах размеры сеток адекватны для надежного воспроизведения основных статистических характеристик рассчитываемых течений. Шаг сетки в продольном направлении составляет от 7 до 9, а в боковом – от 3 до 5 вязких длин. В нормальном к стенке направлении шаг сетки у стенки составляет около одной вязкой длины. Размеры расчетной области во всех основных вариантах превышают (иногда значительно) значения в 2000 и 1000 вязких длин в продольном и боковом направлении соответственно, что является достаточным для воспроизведения основных энергосодержащих структур, присутствующих в течении. Для представления о степени точности настоящих расчетов в последнем столбце таблицы 1 показаны отличия рассчитанных коэффициентов сопротивления от значений, полученных в [38]. Максимальная погрешность в 0.4% свидетельствует о высоком качестве данных расчетов. Отметим, что хорошее согласие с результатами [38] наблюдается по всем характеристикам, представленным в их статье.
В качестве примера на рис. 1, 2 приведены профили средней скорости, а также профили среднеквадратичных интенсивностей пульсаций скорости и завихренности при максимальном числе Рейнольдса ${\text{R}}{{{\text{e}}}_{{\tau }}} = 586$. Результаты, полученные в настоящей работе, с графической точностью совпадают с результатами [38], что служит дополнительным свидетельством точности проведенных расчетов. На рис. 1, 2 и далее по тексту компоненты векторов скорости u и завихренности $\nabla \times u$ основного течения обозначаются как $\left( {{{u}_{1}},{{u}_{2}},{{u}_{3}}} \right) \equiv \left( {u,v,w} \right)$ и $\left( {{{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}}} \right) \equiv \left( {{{\omega }_{x}},{{\omega }_{y}},{{\omega }_{z}}} \right)$ соответственно. Аналогично компоненты векторов скорости и завихренности возмущений ${{u}_{p}}$ и $\nabla \times {{u}_{p}}$ обозначаются как $\left( {{{u}_{{1,p}}},{{u}_{{2,p}}},{{u}_{{3,p}}}} \right) \equiv \left( {{{u}_{p}},{{v}_{p}},{{w}_{p}}} \right)$ и $\left( {{{\omega }_{{1,p}}},{{\omega }_{{2,p}}},{{\omega }_{{3,p}}}} \right) \equiv \left( {{{\omega }_{{x,p}}},{{\omega }_{{y,p}}},{{\omega }_{{z,p}}}} \right)$.
Рис. 1.
Профиль средней скорости: 1 – [38], 2 – результаты настоящей работы; ${{\operatorname{Re} }_{\tau }} = 586$
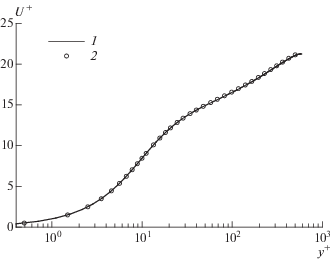
Рис. 2.
Профили среднеквадратичных интенсивностей пульсаций скорости (a) и завихренности (б): линии – [38], символы – результаты настоящей работы; ${\text{R}}{{{\text{e}}}_{{\tau }}} = 586$
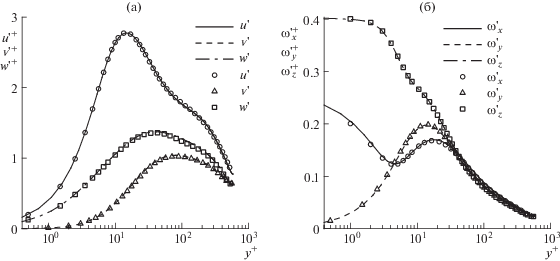
Кроме основных трех вариантов, в работе будут использоваться результаты расчета R391s, параметры которого отличаются от варианта R391 укороченной в четыре раза длиной расчетной области $L_{x}^{ + } \approx 590$ с пропорциональным уменьшением числа узлов сетки в направлении $x$. Укороченная область используется для условного разделения течения на длинноволновую и коротковолновую компоненты. К первой относится не зависящая от $x$ составляющая, которая получается осреднением поля течения по всей длине расчетной области. Все остальное относится к коротковолновой составляющей.
В дальнейшем изложении по большей части будут представляться результаты, полученные в расчете R391, исследованном наиболее подробно. Результаты при меньшем и большем числе Рейнольдса использовались в основном для подтверждения качественных выводов. Отметим, что результаты всех проведенных расчетов, не вошедших в данную публикацию, качественно, а в большинстве случаев и количественно согласуются с выводами, формулируемыми ниже.
2. ХАРАКТЕРИСТИКИ РАСТУЩИХ ВОЗМУЩЕНИЙ
Численные исследования развития возмущений в развитых турбулентных течениях были начаты в работе [33]. В этой и последующих работах [30, 31] было показано, что малые возмущения турбулентного течения в круглой трубе и плоском канале растут в среднем экспоненциально как вдоль потока при расчете пространственного развития, так и во времени, когда задача решается в традиционной временнóй постановке с условиями пространственной периодичности. Отметим, что сама процедура принятого подхода подразумевает выделение из всех возможных лишь наиболее быстро растущего возмущения. Для хаотических систем это возмущение соответствует старшему вектору Ляпунова (отвечающему наибольшему ляпуновскому показателю ${{\lambda }_{1}}$). В отличие от собственных векторов задачи устойчивости стационарных решений ляпуновские векторы хаотически меняются во времени, так что их свойства определяются лишь статистически. Таким образом, в настоящей работе изучаются свойства одного лишь старшего вектора Ляпунова. Вопрос о наличии и количестве других растущих ляпуновских векторов (т.е. числе положительных ляпуновских показателей) в работе не рассматривается.
Скорость роста
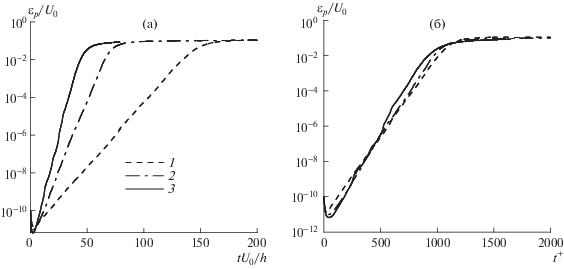
Настоящие расчеты согласуются с результатами [30, 31, 33]. Малые возмущения в турбулентном потоке после этапа начальной перестройки растут в среднем экспоненциально. Экспоненциальный тренд сохраняется до наступления этапа насыщения на определенном конечно-амплитудном уровне. Конкретная форма начального возмущения сказывается лишь на начальном перестроечном этапе и не влияет на скорость экспоненциального роста. В настоящей работе начальные возмущения задавались случайным образом (с помощью датчика случайных чисел) с последующим приведением поля скорости к бездивергентному виду и нормировкой. На рис. 3 приведены графики изменения со временем интегральной амплитуды возмущений
(2.1)
$\varepsilon _{p}^{2}\left( t \right) = \frac{1}{{\left| V \right|}}\mathop \smallint \limits_V {\text{|}}{{u}_{p}}\left( {t,x} \right){{{\text{|}}}^{2}}dx$Интегрирование в (2.1) проводится по всей расчетной области объемом $\left| V \right|$.
На рис. 3(а) время измеряется в глобальных единицах $h{\text{/}}{{U}_{0}}$, где $h$ – полувысота канала, а U0 = $1.5{{U}_{b}}$ – максимальная скорость в течении Пуазейля, соответствующего данной средней скорости ${{U}_{b}}$. Результатом случайного выбора начального возмущения является их заметное затухание (на порядок и более) на начальном этапе эволюции. Во всех вариантах при начальной амплитуде ${{\varepsilon }_{p}}\left( 0 \right){\text{/}}{{U}_{0}} = {{10}^{{ - 10}}}$ затухание возмущений на перестроечном этапе сменяется экспоненциальным ростом, который продолжается до насыщения на уровне ${{\varepsilon }_{p}}{\text{/}}{{U}_{0}} \approx {{10}^{{ - 1}}}$. Скорость экспоненциального роста заметно увеличивается с числом Рейнольдса.
В работах [30, 31] обнаружено, что в диапазоне чисел Рейнольдса ${\text{R}}{{{\text{e}}}_{{\tau }}}$ от 140 до 320 скорость роста малых возмущений, будучи выраженной в пристенных масштабах, оказывается близкой к постоянному значению $\lambda _{1}^{ + } \approx 0.021$. Результаты настоящей работы, согласуясь с наблюдениями [30, 31] о постоянстве ${{\lambda }^{ + }}$ в диапазоне ${\text{R}}{{{\text{e}}}_{{\tau }}}$ от 140 до 320, показывают увеличение $\lambda _{1}^{ + }$ при бо́льших числах Рейнольдса. На рис. 3(б) представлены графики ${{\varepsilon }_{p}}({{t}^{ + }})$, демонстрирующие некоторое изменение наклона кривых линейного роста с увеличением Re.
Структура поля возмущений после завершения этапа нелинейного насыщения
В начальный момент времени возмущенное поле ${{u}_{1}} = u + {{u}_{p}}$ отличается от исходного поля u на малую величину, но по мере роста возмущения растет и степень расхождения двух полей. Достижение амплитудой возмущения предельной величины свидетельствует о том, что этап расхождения двух полей завершен, и поле ${{u}_{1}}$ выходит на состояние статистической независимости от исходного поля u. Другими словами, поля u и ${{u}_{1}}$ на этой стадии представляют собой две статистически независимые реализации одного и того же стационарного турбулентного течения и имеют совпадающие статистические характеристики. Отсюда следует, в частности, что средние значения компонент поля ${{u}_{p}}$ тождественно равны нулю: $\left\langle {{{u}_{{i,p}}}} \right\rangle (y) = 0$. Здесь и далее угловые скобки обозначают осреднение по времени и двум однородным координатам $x$ и $z$.
Для определения вторых моментов поля возмущений рассмотрим кросс-корреляцию двух компонент скорости возмущений ${{u}_{{i,p}}}$ и ${{u}_{{j,p}}}$
Подставим в последнее выражение определение возмущения (1.2), которое с учетом равенства средних $\langle {{u}_{1}}\rangle = \langle u\rangle $ запишем в виде разности пульсационных составляющих полей u и ${{u}_{1}}$
Принимая во внимание статистическую независимость и совпадение статистических характеристик полей u и u1, после несложных манипуляций получим
(2.3)
${{C}_{{ij,p}}}\left( {y;{{{\Delta }}_{x}},{{{\Delta }}_{z}}} \right) = 2{{C}_{{ij}}}\left( {y;{{{\Delta }}_{x}},{{{\Delta }}_{z}}} \right),$(2.4)
$\left\langle {{{u}_{{i,p}}}{{u}_{{j,p}}}} \right\rangle \left( y \right) = 2\left\langle {\left( {{{u}_{i}} - \left\langle {{{u}_{i}}} \right\rangle } \right)\left( {{{u}_{j}} - \left\langle {{{u}_{j}}} \right\rangle } \right)} \right\rangle \left( y \right);\quad u_{{i,p}}^{'}\left( y \right) = \sqrt 2 u_{i}^{'}\left( y \right)$Очевидно, что аналогичные тождества выполняются и для компонент завихренности. Полученные в расчетах вторые моменты компонент скорости и завихренности, соответствующие полю возмущений после его установления на постоянном конечно-амплитудном уровне, с высокой точностью удовлетворяют соотношениям (2.4), что доказывает предположение о статистической независимости полей u и u1 на этом этапе.
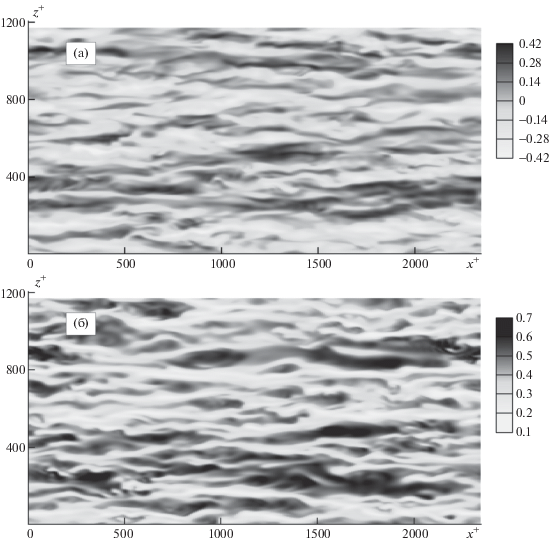
Корреляционные функции линейно связаны с пространственными спектрами колебаний формулой Винера–Хинчина. Таким образом, совпадение (с точностью до множителя) кросс-корреляционных функций, соответствующих колебаниям в поле возмущений и в поле основного течения, означает аналогичное совпадение пространственных спектров. Все это указывает на присутствие в поле возмущений тех же структур, что имеются в поле основного течения. На рис. 4 изображены мгновенные распределения продольной компоненты скорости в горизонтальной плоскости ${{y}^{ + }} = 14$ в предельном поле возмущений и в поле основного течения. В полном соответствии со сделанными предсказаниями представленные поля имеют качественно совпадающий вид с доминирующими вытянутыми вдоль потока полосчатыми структурами. При этом, в соответствии с (2.4), разброс значений в поле возмущений в $\sqrt 2 $ раз превышает аналогичный разброс в основном течении.
Пространственная локализация малых возмущений
Наблюдение за процессом развития малых возмущений, предшествующим нелинейному установлению, показывает, что вспышки активности спорадически возникают в той или иной части канала, как правило на высоте ${{y}^{ + }}$ = 10–20, т.е. в области буферного слоя основного течения, где максимален уровень пульсаций и, в частности, наиболее выражены полосчатые структуры. Пятно возмущения, появившись в одном месте, сносится потоком, разрастаясь в размере и интенсивности, увеличивая интегральную амплитуду возмущений. Следующий за ним всплеск возникает уже на повышенном амплитудном фоне, таким образом обеспечивается общий экспоненциальный рост. Распределения интенсивности возмущений $\sqrt {{\text{|}}{{u}_{p}}{{{\text{|}}}^{2}}} $ в плоскости ${{y}^{ + }} = 14$ в два случайных момента времени, изображенные на рис. 5, демонстрируют степень пространственной неоднородности поля возмущений, а также некоторые характерные геометрические черты возбуждающихся структур. В частности, обращает на себя внимание то, что, несмотря на некоторую вытянутость возмущений вдоль потока, в поле возмущений отсутствуют крупномасштабные структуры с длиной $l_{x}^{ + } \sim {{10}^{3}}$, аналогичные пристенным полосам в основном турбулентном потоке или полосам, возникающим в поле возмущений на этапе нелинейного насыщения (см. рис. 4).
Рис. 5.
Распределения интенсивности возмущений $\sqrt {{\text{|}}{{u}_{p}}{{{\text{|}}}^{2}}} $ в плоскости $\left( {x,z} \right)$ в два случайных момента времени на линейной стадии развития, ${{y}^{ + }} = 14;$ ${\text{R}}{{{\text{e}}}_{{\tau }}} = 391$
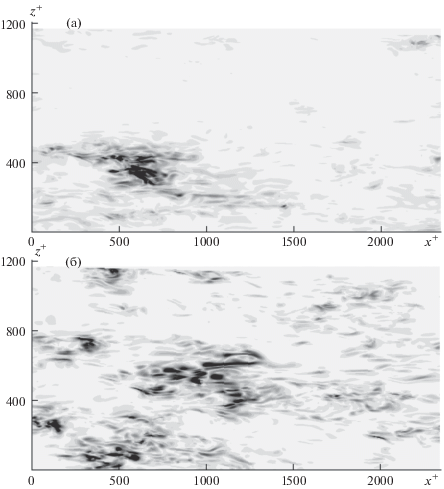
В работе [25] численно изучался так называемый хаотический режим спиральных дефектов в конвекции Рэлея–Бенара. Обнаружено, что ляпуновские векторы, отвечающие положительным показателям, крайне локализованы как в пространстве, так и во времени. Наоборот, ляпуновские векторы, соответствующие отрицательным показателям, более равномерно распределены в пространстве. Делается вывод, что возникновение хаоса в исследованном режиме связано со вспышками активности пульсаций, описываемыми старшим ляпуновским вектором. В погран-слойных течениях пространственно-локализованные турбулентные пятна встречаются на стадии ламинарно-турбулентного перехода. Недавно в [39] обнаружены пространственно-локализованные образования с повышенной пульсационной активностью в буферном слое развитого турбулентного пограничного слоя. По своим свойствам они напоминают турбулентные пятна в переходных течениях. Интересно, что пристенные полосы при этом выглядят неактивными по отношению к развивающимся на их фоне локализованным структурам. Обнаруженная в настоящей работе пространственно-временная локализация возмущений, соответствующих старшему ляпуновскому вектору, согласуется с наблюдениями и выводами работы [25] и напоминает локализованные турбулентные структуры развитого пограничного слоя, обнаруженные в [39]. В рамках данного исследования предпринимались попытки установления связи обстоятельств внезапных вспышек активности возмущений с особенностями поля основного течения, в частности, с деталями крупномасштабных полосчатых структур. Пока определенных выводов на этом пути сделать не удалось. Как и в численных экспериментах [39], мгновенное распределение пристенных полос не выглядит важным фактором роста возмущений. Вероятно, существенное влияние на условия роста возмущений оказывает не только пространственная неоднородность, но и нестационарность основного течения, как это отмечалось в работах [23, 24]. Кроме того, как будет показано ниже, коротковолновая составляющая основного течения, а также и движение в поперечной к направлению основного потока плоскости вносят серьезный вклад в развитие возмущений.
Статистические характеристики малых возмущений
Выше было показано, что статистические свойства возмущения после его выхода на этап нелинейного насыщения элементарным образом связаны со свойствами основного турбулентного течения. Для определения характеристик малых растущих возмущений можно пренебречь нелинейным относительно ${{u}_{p}}$ членом в левой части первого из уравнений (1.4). Во избежание путаницы c решениями уравнений (1.4), обозначим решения получающегося таким образом линейного уравнения через ul
(2.5)
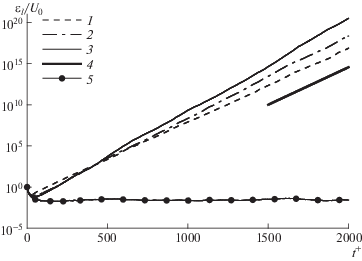
$\frac{{\partial {{u}_{l}}}}{{\partial t}} + \left( {{{u}_{l}}\nabla } \right)u + \left( {u\nabla } \right){{u}_{l}} = - \frac{1}{\rho }\nabla {{p}_{l}} + \nu {{\nabla }^{2}}{{u}_{l}},\quad \nabla {{u}_{l}} = 0$Решения этого уравнения на начальном этапе совпадают с решениями (1.4), но, выйдя на экспоненциальный режим, остаются на нем без насыщения бесконечно долго. Больший период развития позволяет, в частности, более точно оценить скорость роста возмущений. Графики зависимости от времени интегральной амплитуды возмущений ${{\varepsilon }_{l}}({{t}^{ + }})$, определенной аналогично (2.1) через ${{u}_{l}}$, полученные в трех основных вариантах, изображены на рис. 6. Решения линейной задачи определяются с точностью до произвольного множителя, поэтому нормировка начального возмущения может быть выбрана произвольно. В этих расчетах нормировка выбрана из условия ${{\varepsilon }_{l}}\left( 0 \right){\text{/}}{{U}_{0}} = 1$. Приведенные на рис. 6 графики отчетливо показывают увеличение скорости экспоненциального роста амплитуды возмущения от $\lambda _{1}^{ + } = 0.021$ при ${\text{R}}{{{\text{e}}}_{{\tau }}} = 178$ до $\lambda _{1}^{ + } = 0.026$ при ${\text{R}}{{{\text{e}}}_{{\tau }}}$ = 586. При ${\text{R}}{{{\text{e}}}_{{\tau }}} = 391$ лучшей оценкой оказывается $\lambda _{1}^{ + } = 0.023$, что подтверждается отсутствием заметного экспоненциального тренда на графике ${{\varepsilon }_{l}}({{t}^{ + }}){exp\;}( - 0.023{{t}^{ + }}){\text{/}}{{U}_{0}},$ приведенном на рис. 6. Заметим, что выход на экспоненциальную зависимость ${{\varepsilon }_{l}} \sim {exp\;}({{\lambda }_{1}}t)$ происходит во всех вариантах уже при ${{t}^{ + }} < 50$, несмотря на случайность начального возмущения.
Рис. 6.
Эволюция амплитуды возмущений в линейном приближении: 1 – $R178$, 2 – $R391$, 3 – $R586$, 4 – $( - \exp (0.021\quad{{t}^{ + }}))$, 5 – ${{\varepsilon }_{l}}({{t}^{ + }})\exp \quad( - 0.023{{t}^{ + }}){\text{/}}{{U}_{0}},$ $R391$
Выглядит естественным предполагать, что качественные свойства малых возмущений остаются неизменными во все время экспоненциального нарастания, а поведение во времени нормированного поля
(2.6)
$u_{l}^{*}\left( {t,x} \right) = {{u}_{l}}\left( {t,x} \right)\exp \quad( - {{\lambda }_{1}}t)$Полученные описанным способом профили интенсивностей колебаний скорости $u_{{i,l}}^{'}$ приведены на рис. 7(a). Там же для сравнения изображены аналогичные характеристики колебаний в основном течении $u_{i}^{'}$. Нормировка интенсивности возмущений выбирается из условия равенства максимальных интенсивностей колебаний в поперечной к потоку плоскости в поле возмущений и в поле основного течения
(2.7)
$\mathop {\max }\limits_y \{ {{(v_{l}^{'})}^{2}} + {{(w_{l}^{'})}^{2}}\} = \mathop {\max }\limits_y \{ {{(v{{'}^{ + }})}^{2}} + {{(w{{'}^{ + }})}^{2}}\} $Рис. 7.
Профили интенсивностей пульсаций скорости (a) и завихренности (б): линии – возмущения на линейном этапе развития, символы – основное течение; нормировка возмущений – (2.7); ${{\operatorname{Re} }_{{\mathbf{\tau }}}} = 391$
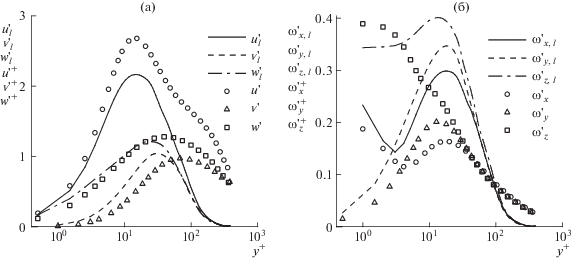
Максимальные пульсации в поле возмущений сконцентрированы в области ${{y}^{ + }} \approx 14$, где, в частности, наиболее выражено полосчатое движение в основном течении. Последнее может означать, что рост возмущений является следствием неустойчивости полосчатого движения. Однако, как будет показано ниже, неустойчивость полос не является непосредственной причиной роста возмущений ведущего ляпуновского вектора. В соответствии с выбранной нормировкой максимальные интенсивности пульсаций боковой и нормальной компонент скорости возмущений близки к соответствующим величинам в основном течении. При этом интенсивность продольных пульсаций в основном течении оказывается заметно большей, чем в поле возмущений. Мы полагаем, что это объясняется наличием крупномасштабных полос в основном течении, вносящих заметный вклад в интенсивность пульсаций продольной скорости в пристенном слое. В целом возмущения оказываются гораздо более концентрированными по толщине канала. Интенсивности колебаний всех компонент скорости в поле возмущений гораздо быстрее затухают при удалении от области максимальных значений, чем в поле основного течения.
Профили интенсивностей пульсаций завихренности, изображенные на рис. 7(б), обладают несколькими интересными особенностями. Профили, соответствующие колебаниям продольной и нормальной компонент завихренности в поле возмущений, качественно близки аналогичным профилям, построенным для основного течения. А вот профиль $\omega _{{z,l}}^{'}$ существенно отличается от $\omega _{z}^{'}$. Интенсивность пульсаций ${{\omega }_{z}}$ в основном течении достигает максимума непосредственно на стенке и монотонно убывает с удалением от нее. Напротив, интенсивность колебаний ${{\omega }_{{z,l}}}$ максимальна на том же расстоянии от стенки, ${{y}^{ + }}$ = 10–20, что и для других компонент завихренности. Непосредственно на стенке ${{\omega }_{z}} = - \partial u{\text{/}}\partial y$, поэтому большие флуктуации продольной скорости, обусловленные наличием полосчатых структур в пристенном слое, очевидно вызывают флуктуации ${{\omega }_{z}}$ непосредственно на стенке и вблизи нее. Таким образом, качественное различие $\omega _{{z,l}}^{'}$ и $\omega _{z}^{'}$ вблизи стенки также можно объяснить наличием полосчатого движения в основном течении и его отсутствием в поле возмущений.
Справедливость предположений о вкладе полосчатых структур в профили интенсивности пульсаций скорости и завихренности можно проверить, используя результаты расчета в укороченной расчетной области (R391s в таблице 1). Длина расчетной области в этом варианте $L_{x}^{ + } \approx 590$ меньше, чем типичная протяженность полосчатых структур в турбулентном пристенном слое. Поэтому большинство полос простираются на всю длину расчетной области. Таким образом, коротковолновая составляющая течения ${{u}_{s}} = \left( {{{u}_{s}},{{v}_{s}},{{w}_{s}}} \right)$, получаемая удалением из поля скорости не зависящей от x компоненты: ${{u}_{s}} = u - {{\left\langle u \right\rangle }_{x}}$ (${{\left\langle \cdot \right\rangle }_{x}}$ означает осреднение по $x$), может считаться свободной от полос. На рис. 8 интенсивности возмущений из расчета R391 сравниваются с интенсивностями пульсаций скорости и завихренности $(u_{s}^{{' + }},v_{s}^{{' + }},w_{s}^{{' + }},)$ и $(\omega _{{x,s}}^{{' + }},\omega _{{y,s}}^{{' + }},\omega _{{z,s}}^{{' + }})$ коротковолновой (“бесполосной”) компоненты течения, полученной в расчете R391s. Возмущения нормируются аналогично (2.7):
(2.8)
$\mathop {\max }\limits_y \{ {{(v_{l}^{'})}^{2}} + {{(w_{l}^{'})}^{2}}\} = \mathop {\max }\limits_y \{ {{(v_{s}^{{' + }})}^{2}} + {{(w_{s}^{{' + }})}^{2}}\} $Рис. 8.
Профили интенсивностей пульсаций скорости (a) и завихренности (б); линии – возмущения на линейном этапе развития, символы – коротковолновая составляющая основного течения расчета R391s; нормировка возмущений – (2.8); ${{\operatorname{Re} }_{\tau }} = 391$
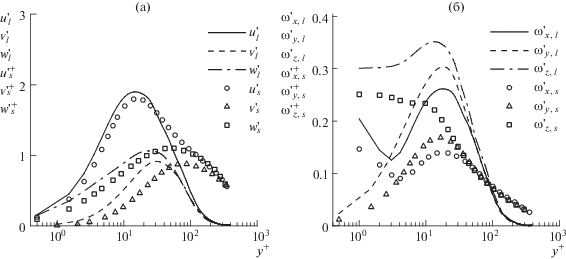
Как и ожидалось, исключение длинноволновой составляющей отражается в первую очередь в уменьшении уровня продольных пульсаций в области ${{y}^{ + }}$ = 10–20 и пульсаций ${{\omega }_{z}}$ в непосредственной близости от стенки. В результате получается более близкое количественное согласие профилей $u_{l}^{'}$ и $u_{s}^{{' + }}$ и качественное согласие профилей $\omega _{{z,l}}^{'}$ и $\omega _{{z,s}}^{{' + }}$ Это подтверждает предположение об отсутствии крупномасштабных полос большой амплитуды в поле возмущений на линейном этапе развития.
При нормировках (2.7), (2.8) характерные значения пульсаций завихренности в поле возмущений оказываются примерно на 80% бóльшими соответствующих значений в основном течении. Повышенный уровень пульсаций завихренности в поле возмущений при сопоставимом уровне пульсаций скорости может объясняться тем, что эти пульсации ассоциированы с меньшими по линейному масштабу структурами. Косвенно это подтверждается большей локализацией по $y$ профилей интенсивностей пульсаций скорости и завихренности на рис. 7 и 8. Более убедительные аргументы в пользу доминирования меньших по размеру структур в поле возмущений следуют из анализа пространственных спектров колебаний.
На рис. 9 изображены полученные в расчете R391 модифицированные двумерные спектры колебаний трех компонент скорости ${{k}_{x}}{{k}_{z}}{{E}_{{{{u}_{i}}{{u}_{i}}}}}\left( {{{k}_{x}},{{k}_{z}}} \right)$ в поле основного течения и в поле возмущения на расстоянии ${{y}^{ + }} = 14$ от стенки, т.е. в области максимальных уровней пульсаций в обоих полях. Спектры представлены как функции логарифмов длин волн ${{{\lambda }}_{x}} = 2\pi {\text{/}}{{k}_{x}},{{{\lambda }}_{z}} = 2\pi {\text{/}}{{k}_{z}}$. При таком представлении энергия колебаний, приходящаяся на площадку заданной площади ${\text{d}}({ln\;}{{{\lambda }}_{x}}){\text{d}}({ln\;}{{{\lambda }}_{z}}),$ пропорциональна уровню изображенной величины ${{k}_{x}}{{k}_{z}}{{E}_{{{{u}_{i}}{{u}_{i}}}}}$, поскольку
Рис. 9.
Модифицированные двумерные спектры мощности колебаний компонент скорости ${{k}_{x}}{{k}_{z}}{{E}_{{{{u}_{i}}{{u}_{i}}}}}$ на расстоянии ${{y}^{ + }} = 14$ от стенки в основном течении – (а–в) и в возмущении – (г–е): $u$ – ((а), (г)), $v$ – ((б),(д)) и $w$ – ((в),(е)); • – точка максимума, ее координаты: (а) – $\lambda _{x}^{ + } = \;\quad800,\quad\quad\lambda _{z}^{ + }\;\quad = \;\quad110,\;\quad\left( {\text{б }} \right)$ – $\lambda _{x}^{ + }\;\quad = \;\quad300,\quad\quad\lambda _{z}^{ + }\quad\; = \;\quad65$, (в) – $\lambda _{x}^{ + } = \quad\,350,\quad\quad\lambda _{z}^{ + }$ = 130, (г) – $\lambda _{x}^{ + }\quad\; = \quad\;200,\quad\quad\lambda _{z}^{ + }\; = \quad\;60$, (д) – $\lambda _{x}^{ + }\quad\; = \quad\;130,\quad\quad\lambda _{z}^{ + }\; = \quad\;40$, (e) – $\lambda _{x}^{ + }\quad\; = \quad\;130,\quad\quad\lambda _{z}^{ + }\; = \quad\;80$; $\quad{{\operatorname{Re} }_{\tau }} = 391$
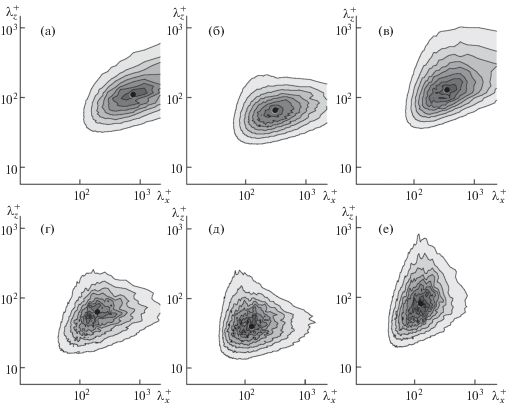
В частности, координаты максимальных уровней модифицированных спектров указывают на характерные размеры (длины волн) наиболее энергонесущих структур. Эти координаты приведены в подписи к рис. 9.
Двумерные спектры пульсаций скорости показывают, что протяженность расчетной области $L_{x}^{ + } = 2350$ не вполне достаточна для точного воспроизведения всех энергосодержащих структур в основном потоке. В наибольшей степени это относится к продольной компоненте скорости. Это, впрочем, не означает, что длинные структуры не представлены в расчетах. Им отвечают не зависящие от $x$ структуры, т.е. спектральные компоненты, соответствующие ${{k}_{x}} = 0$. Возмущения лучше укладываются в параметры расчетной сетки как по максимальным, так и по минимальным разрешаемым размерам. В целом наиболее энергонесущие структуры в поле возмущений ýже и короче наиболее энергонесущих структур в основном потоке.
Для более объективной оценки размеров различных структур, присутствующих в поле основного течения и в поле возмущений, для каждой компоненты скорости определим характерные линейные масштабы в продольном и боковом направлениях ${{l}_{{x,{{u}_{i}}}}}\left( y \right)$ и ${{l}_{{z,{{u}_{i}}}}}\left( y \right)$, отвечающие координатам центров тяжести соответствующих двумерных спектров в плоскости волновых чисел ${{k}_{x}},{{k}_{z}}$
(2.9)
$2\pi l_{{x,{{u}_{i}}}}^{{ - 1}}\left( y \right) = \frac{{\iint {{k}_{x}}{{E}_{{{{u}_{i}}{{u}_{i}}}}}\left( {{{k}_{x}},{{k}_{z}};y} \right)d{{k}_{x}}d{{k}_{z}}}}{{\iint {{E}_{{{{u}_{i}}{{u}_{i}}}}}\left( {{{k}_{x}},{{k}_{z}};y} \right)d{{k}_{x}}d{{k}_{z}}}}$(2.10)
$2\pi l_{{z,{{u}_{i}}}}^{{ - 1}}\left( y \right) = \frac{{\iint {{k}_{z}}{{E}_{{{{u}_{i}}{{u}_{i}}}}}\left( {{{k}_{x}},{{k}_{z}};y} \right)d{{k}_{x}}d{{k}_{z}}}}{{\iint {{E}_{{{{u}_{i}}{{u}_{i}}}}}\left( {{{k}_{x}},{{k}_{z}};y} \right)d{{k}_{x}}d{{k}_{z}}}}$Аналогично определим характерные линейные масштабы компонент завихренности ${{l}_{{x,{{\omega }_{i}}}}}\left( y \right),{{l}_{{z,{{\omega }_{i}}}}}\left( y \right)$ через спектры мощности пульсаций завихренности ${{E}_{{{{\omega }_{i}}{{\omega }_{i}}}}}\left( {{{k}_{x}},{{k}_{z}};y} \right)$. Рассчитанные в соответствии с определениями (2.9), (2.10) характерные масштабы, отвечающие различным компонентам скорости и завихренности в поле основного течения и в поле возмущений, приведены на рис. 10–13 как функции расстояния от стенки в пристенном слое ${{y}^{ + }} \leqslant {{10}^{2}}$.
Рис. 10.
Характерные продольные масштабы пульсаций компонент скорости в основном течении (a) и в возмущении (б): 1 – ${{l}_{{x,u}}}$, 2 – ${{l}_{{x,v}}}$, 3 – ${{l}_{{x,w}}}$; ${{\operatorname{Re} }_{\tau }} = 391$
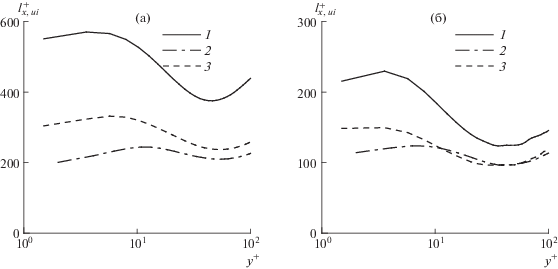
Приведенные на рис. 10–13 графики открывают удивительные геометрические свойства, присущие пульсациям в двух полях. Для всякой компоненты скорости или завихренности распределение поперек канала каждого из двух масштабов в поле возмущений оказывается удивительно близким по форме к соответствующему распределению в поле основного течения. При этом величина каждого масштаба в поле возмущений оказывается вдвое меньшей соответствующего масштаба в поле основного течения. В области максимального уровня пульсаций ${{y}^{ + }}$ = 10–20 продольный масштаб в поле возмущений составляет 100–150, а в основном течении – 200–300 вязких длин. Для поперечного масштаба аналогичные значения для разных компонент скорости и завихренности в несколько (2–3) раз меньше. Из этого правила выбивается разве что продольный масштаб пульсаций продольной компоненты скорости, который в основном течении оказывается существенно бо́льшим, что безусловно является отражением наличия полосчатых структур. По той же причине продольный масштаб боковой компоненты завихренности в основном течении в непосредственной близости от стенки также заметно превышает аналогично удвоенную величину для поля возмущений.
Рис. 11.
Характерные продольные масштабы пульсаций компонент завихренности в основном течении (a) и в возмущении (б): 1 – ${{l}_{{x,\omega x}}}$, 2 – ${{l}_{{x,\omega y}}}$, 3 – ${{l}_{{x,\omega z}}}$; ${{\operatorname{Re} }_{\tau }} = 391$
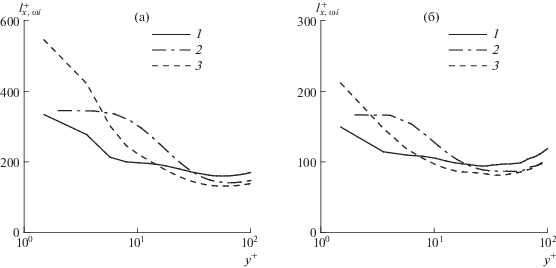
Рис. 12.
Характерные поперечные масштабы пульсаций компонент скорости в основном течении (a) и в возмущении (б): 1 – ${{l}_{{z,u}}}$, 2 – ${{l}_{{z,v}}}$, 3 – ${{l}_{{z,w}}}$; ${{\operatorname{Re} }_{\tau }} = 391$
Определенные в (2.9), (2.10) интегральные масштабы, вычисленные через энергетические спектры, не следует воспринимать буквально как геометрические размеры имеющихся в потоке структур. Отметим, однако, что, например, вычисленный по формуле (2.9) продольный масштаб осевой завихренности $l_{{x,{{\omega }_{x}}}}^{ + }$ в основном течении в области концентрации полосчатых структур ${{y}^{ + }}$ = 10–20, составляет около 200 единиц, что совпадает с длиной преобладающих в пристенном слое продольных вихрей, определенной в [40] с помощью ${{\lambda }_{2}}$-метода идентификации вихрей [41]. Это указывает на то, что формально введенные в (2.9), (2.10) величины действительно имеют определенные основания считаться линейными масштабами турбулентных структур.
3. О МЕХАНИЗМЕ ГЕНЕРАЦИИ ВОЗМУЩЕНИЙ
Определенное представление о важности тех или иных механизмов генерации возмущений в турбулентном потоке дает анализ баланса кинетической энергии. Для вывода уравнения баланса энергии малых возмущений умножим уравнение (2.5) скалярно на ${{u}_{l}} = \left( {{{u}_{l}},{{v}_{l}},{{w}_{l}}} \right) \equiv \left( {{{u}_{{1,l}}},{{u}_{{2,l}}},{{u}_{{3,l}}}} \right)$. После несложных преобразований получим
(3.1)
$\frac{\partial }{{\partial t}}\left( {\frac{1}{2}{{u}_{{i,l}}}{{u}_{{i,l}}}} \right) = - {{u}_{{i,l}}}{{u}_{{j,l}}}{{s}_{{ij}}} - \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{1}{2}{{u}_{{i,l}}}{{u}_{{i,l}}}{{u}_{j}} + \frac{1}{\rho }{{u}_{{j,l}}}{{p}_{l}} - 2\nu {{u}_{{i,l}}}{{s}_{{ij,l}}}} \right) - 2\nu {{s}_{{ij,l}}}{{s}_{{ij,l}}}$Здесь
(3.2)
${{s}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right),\quad {{s}_{{ij,l}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{{i,l}}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{{j,l}}}}}{{\partial {{x}_{i}}}}} \right)$Здесь ${{P}_{l}}\left( y \right),{{T}_{l}}\left( y \right)$ и ${{D}_{l}}\left( y \right)$ – генерация, перенос и диссипация кинетической энергии возмущений ${{K}_{l}}\left( y \right)$, определяемые следующими формулами [42]:
Звездочками обозначена нормировка в соответствии с (2.6).
Распределение по толщине канала всех членов уравнений баланса энергии в основном течении и в поле возмущений представлено на рис. 14. Для возмущений дополнительно выбрана нормировка, при которой максимальное значение энергии равно 1, а время нормируется на ${{l}_{\tau }}{\text{/}}{{u}_{\tau }}$. При такой нормировке максимум величины ${{P}_{l}} + {{T}_{l}} - {{D}_{l}}$ при ${\text{R}}{{{\text{e}}}_{\tau }} = 391$ составляет $2\lambda _{1}^{ + } \approx 0.046$, что согласуется с представленными на рис. 14(б) данными. Распределение генерации энергии по толщине канала в поле возмущений качественно совпадает с ситуацией в основном течении. Максимальная генерация происходит при ${{y}^{ + }} = 16$ (в основном течении при ${{y}^{ + }} = 12$). Перенос энергии из области максимальной генерации в основном происходит в сторону стенки в наибольшей степени посредством вязкой диффузии. Интересно, что вязкая диссипация в поле возмущений максимальна не на стенке, как в основном течении, а в области максимальной генерации.
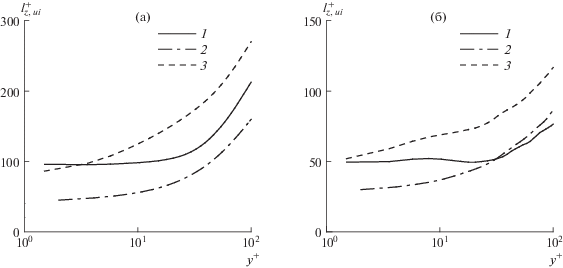
Рис. 13.
Характерные поперечные масштабы пульсаций компонент завихренности в основном течении (a) и в возмущении (б): 1 – ${{l}_{{z,\omega x}}}$, 2 – ${{l}_{{z,\omega y}}}$, 3 – ${{l}_{{z,\omega z}}}$; ${{\operatorname{Re} }_{\tau }} = 391$
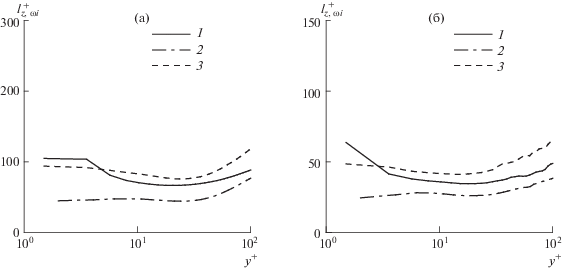
Рис. 14.
Баланс кинетической энергии пульсаций в основном течении (a) и в поле возмущений (б): P, Pl – генерация, D, Dl – диссипация, $T,{{T}_{l}}$ – перенос; ${{\operatorname{Re} }_{\tau }} = 391$
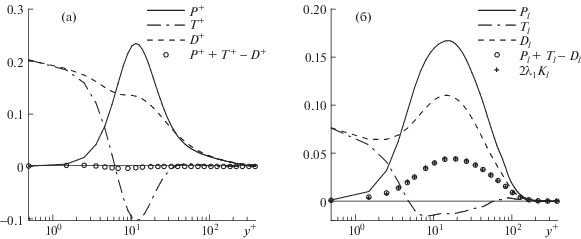
Генерация кинетической энергии в основном течении описывается выражением P = $ - \left\langle {uv} \right\rangle dU{\text{/}}dy$, где $U\left( y \right) = \langle u\rangle $ – профиль средней скорости. Выражение для генерации энергии в поле возмущений выглядит следующим образом:
(3.4)
$\begin{gathered} {{P}_{l}} = {{P}_{{11}}} + {{P}_{{12}}} + {{P}_{{13}}} + {{P}_{{22}}} + {{P}_{{23}}} + {{P}_{{33}}}, \\ {{P}_{{11}}} = - \left\langle {{{u}_{l}}{{{^{*}}}^{2}}\frac{{\partial u}}{{\partial x}}} \right\rangle ,{\;}\quad {{P}_{{12}}} = - \left\langle {{{u}_{l}}^{*}{{v}_{l}}^{*}\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)} \right\rangle ,\quad\quad {{P}_{{13}}} = - \left\langle {{{u}_{l}}^{*}{{w}_{l}}^{*}\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)} \right\rangle , \\ {{P}_{{22}}} = - \left\langle {{{v}_{l}}{{{^{*}}}^{2}}\frac{{\partial v}}{{\partial y}}} \right\rangle ,\quad\quad\quad{{P}_{{23}}} = - \left\langle {{{v}_{l}}^{*}{{w}_{l}}^{*}\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)} \right\rangle ,\quad\quad\quad {{P}_{{33}}} = - \left\langle {{{w}_{l}}{{{^{*}}}^{2}}\frac{{\partial w}}{{\partial z}}} \right\rangle . \\ \end{gathered} $На рис. 15 представлено распределение каждого из слагаемых суммы (3.4), показывающее роль различных механизмов в процессе генерации энергии возмущений. Максимальный вклад величиной в 37% предсказуемо дает слагаемое ${{P}_{{12}}},$ соответствующее генерации энергии возмущений на поперечном градиенте продольной скорости $\partial u{\text{/}}\partial y$. Вторым по величине вклада (21%) оказывается ${{P}_{{13}}}$, отвечающее генерации энергии в слоях смешения в боковом направлении: $\partial u{\text{/}}\partial z$. Максимальное значение ${{P}_{{13}}}$ достигается в области наибольшей амплитуды пульсаций в основном течении ${{y}^{ + }} \approx 15$, тогда как максимум ${{P}_{{12}}}$ достигается ближе к стенке при ${{y}^{ + }} \approx 7$. Следующим по величине вклада оказывается ${{P}_{{11}}}$ (13%). Существенная величина ${{P}_{{11}}}$ вскрывает важность нового механизма генерации возмущений, проявляющегося в областях замедления ($\partial u{\text{/}}\partial x < 0$) основного потока. Интересно, что все слагаемые (3.4) дают положительный вклад, причем не только суммарный, но и локальный при каждом y.
Рис. 15.
Генерация кинетической энергии пульсаций в поле возмущений. Распределения каждого из слагаемых выражения (3.4) и их процентный вклад в сумму по всей толщине канала: 1 – ${{P}_{{11}}},\quad13\% ;$ 2 – ${{P}_{{12}}},\quad37\% $; 3 – ${{P}_{{13}}},\quad21\% $; 4 – ${{P}_{{22}}},\quad11\% $; 5 – ${{P}_{{23}}},\quad11\% $; 6 – ${{P}_{{33}}},\quad7\% $; ${{\operatorname{Re} }_{\tau }} = 391$
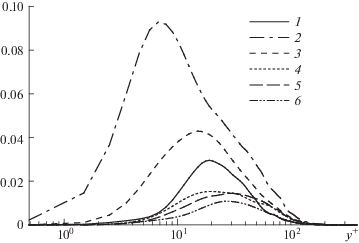
В соответствии с наиболее популярной точкой зрения пульсации в пристенном турбулентном течении возникают в результате неустойчивости крупномасштабного полосчатого движения. Доминирование членов ${{P}_{{12}}}$ и ${{P}_{{13}}}$ в уравнении производства энергии возмущений свидетельствует, что основной и боковой сдвиги в поле скорости основного течения являются важными факторами роста возмущений, соответствующих главному ляпуновскому вектору. Однако заметный вклад других членов указывает на то, что изменение основного течения в направлении x и наличие движения в трансверсальной плоскости также являются важными. Для оценки вклада этих факторов мы исследовали развитие малых возмущений на фоне поля скорости u расчета R391s, модифицированного несколькими способами. В этих экспериментах поведение возмущений определяется из решения уравнений
(3.5)
$\frac{{\partial {{u}_{l}}}}{{\partial t}} + \left( {{{u}_{l}}\nabla } \right){{u}_{m}} + \left( {{{u}_{m}}\nabla } \right){{u}_{l}} = - \frac{1}{\rho }\nabla {{p}_{l}} + \nu {{\nabla }^{2}}{{u}_{l}},\quad \nabla {{u}_{l}} = 0,$В расчете R391s длина расчетной области выбрана столь малой, что осреднение по x, как мы надеемся, лишь отфильтрует из основного течения малозначимые короткие волны и не повлияет серьезно на характеристики его устойчивости. Результаты вычислений, однако, не подтверждают сделанные предположения – в реальности скорость роста возмущений уменьшается более, чем в пять раз до $\lambda _{1}^{ + } \approx 0.004$ (2 на рис. 16).
Рис. 16.
Расчет R391s. Эволюция амплитуды возмущений на фоне исходного и модифицированных полей скорости основного течения; 1 – исходное основное течение $u$, $\lambda _{1}^{ + } \approx 0.023$; 2 – ${{u}_{m}} = \left( {{{{\left\langle u \right\rangle }}_{x}},{{{\left\langle v \right\rangle }}_{x}},{{{\left\langle w \right\rangle }}_{x}}} \right)$, $\lambda _{1}^{ + } \approx 0.004$; 3 – ${{u}_{m}} = \left( {{{{\left\langle u \right\rangle }}_{x}},0,0} \right)$, $\lambda _{1}^{ + } \approx 0$; 4 – ${{u}_{m}} = \left( {u - {{{\left\langle u \right\rangle }}_{x}} + {{{\left\langle u \right\rangle }}_{{x,z}}},v - {{{\left\langle v \right\rangle }}_{x}},w - {{{\left\langle w \right\rangle }}_{x}}} \right)$
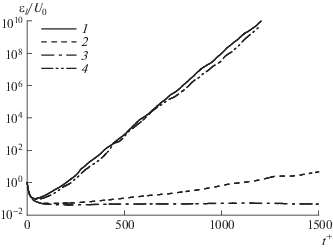
Отметим, что поле скорости ${{\left\langle u \right\rangle }_{x}}$ в (3.6) содержит все три компоненты. Если в тестируемом основном течении ${{u}_{m}}$ оставить лишь продольную компоненту скорости, удалив трансверсальное движение, то рост возмущений и вовсе прекращается (3 на рис. 16). Наоборот, оказывается, что длинноволновая составляющая движения не играет существенной роли в генерации возмущений старшего ляпуновского вектора. Кривой 4 на рис. 16 показана эволюция возмущений на фоне основного течения, из которого удалена длинноволновая составляющая
Удаление длинных волн из основного течения практически не сказывается на характере эволюции возмущений.
Таким образом, рост возмущений главного ляпуновского вектора решающим образом определяется коротковолновой составляющей (в рассмотренном случае с длиной волны $ \leqslant 590\nu {\text{/}}{{u}_{\tau }}$). Длинные волны, к которым обычно относят и пристенные полосы, в данном случае не оказывают заметного влияния. Обнаруженный факт перекликается с наблюдениями [39], где были обнаружены пристенные пространственно-локализованные структуры с повышенным уровнем пульсаций – турбулентно-турбулентные пятна, спорадически возникающие на фоне развитого турбулентного течения в пограничном слое. По мнению авторов [39], пристенные полосы неактивны по отношению к этим структурам. Можно предположить, что причиной возникновения турбулентно-турбулентных пятен является особенность коротковолновой составляющей течения. Исследованный в данной работе старший ляпуновский вектор также проявляется в виде локализованных в пространстве и времени пятен, что дает основания предполагать наличие связи между этими двумя объектами.
ЗАКЛЮЧЕНИЕ
В настоящей работе проведено численное исследование эволюции возмущений развитого турбулентного течения в плоском канале при числах Рейнольдса до ${\text{R}}{{{\text{e}}}_{\tau }} = 586.$ Уравнения Навье–Стокса для несжимаемой жидкости решаются конечноразностным методом [37]. Результаты расчетов турбулентных течений с высокой точностью совпадают с результатами [38]. Рассчитанные установившиеся турбулентные течения используются затем в качестве основных течений для изучения процесса развития на их фоне возмущений.
Показано, что в согласии с результатами предыдущих исследований [30, 31], амплитуда малых возмущений после непродолжительного начального перестроечного этапа (${\Delta }{{t}^{ + }} \lesssim 50$) выходит на режим экспоненциального роста, что отвечает выходу решения на старший ляпуновский вектор (СЛВ). Вопреки ранее сделанным выводам о постоянстве старшего ляпуновского показателя $\lambda _{1}^{ + } \approx 0.021$ при изменении числа Рейнольдса, зафиксировано некоторое увеличение $\lambda _{1}^{ + }$ при наибольших ${{\operatorname{Re} }_{\tau }}$ (до $\lambda _{1}^{ + } \approx 0.026$ при ${{\operatorname{Re} }_{\tau }} = 586$).
Рост возмущений, соответствующих СЛВ, можно связать с наличием крупномасштабных полосчатых структур, присутствующих в пристенном слое турбулентного течения. Это подтверждается тем, что наибольший уровень возмущений достигается на расстоянии ${{y}^{ + }}$ = 10–20 от стенки, т.е. в области буферного слоя основного течения, где наблюдается наибольший уровень пульсаций в основном течении и, в частности, наиболее выражены полосчатые структуры. Однако генерация возмущений СЛВ не связана непосредственно с неустойчивостью полос, а диктуется нестационарностью и неоднородностью коротковолновой составляющей основного течения. Всплески активности возмущений происходят спорадически в разных частях потока, где локально возникают подходящие условия для их роста. Пятно возмущения, появившись в одном месте, сносится потоком, разрастаясь в размере и интенсивности, увеличивая интегральную амплитуду возмущений. Следующий за ним всплеск возникает уже на повышенном амплитудном фоне, таким образом обеспечивается общий экспоненциальный рост.
Проведен анализ и определен вклад каждого из слагаемых, входящих в выражение для производства кинетической энергии возмущений. Наибольший вклад предсказуемо вносят слагаемые, отражающие генерацию возмущений на поперечном градиенте продольной скорости $\partial u{\text{/}}\partial y$, а также в слоях сдвига в боковом направлении. Однако остальные слагаемые, отражающие эффект продольной неоднородности и наличие трансверсального движения в основном течении, также вносят существенный вклад в генерацию возмущений. Пренебрежение этими эффектами ведет к существенной недооценке скорости роста возмущений.
Основываясь на форме двумерных спектров мощности в плоскости волновых чисел ${{k}_{x}},{{k}_{z}}$, определены и вычислены характерные линейные масштабы, отвечающие пульсациям различных компонент скорости и завихренности в поле возмущений и в поле основного течения. В целом полученные результаты указывают на то, что структуры СЛВ оказываются вдвое уже и короче характерных структур основного течения.
Проведенные в работе исследования не дают ответа на вопрос о существовании и количестве других положительных показателей Ляпунова в турбулентном течении в плоском канале. Исследование турбулентных течений с позиций динамики хаотических систем не является устоявшимся подходом. Связь растущих ляпуновских векторов с наблюдаемыми структурами турбулентных потоков еще предстоит установить. В этой связи уместно упомянуть работу [25], в которой рассчитаны ляпуновские показатели и изучены свойства ляпуновских векторов в конвекции Рэлея–Бенара. Обнаружено, что ляпуновские векторы, отвечающие положительным показателям, крайне локализованы как в пространстве, так и во времени. Наоборот, ляпуновские векторы, соответствующие отрицательным показателям, более равномерно распределены в пространстве. Результаты данной работы, касающиеся пространственно-временной локализации структур СЛВ, согласуются с выводами [25]. Локализованные в пространстве и времени структуры наблюдаются также и в пристенных турбулентных течениях. Отметим в этой связи так называемые турбулентно-турбулентные пятна, возникающие в пристенной области развитого пограничного слоя на плоской пластине [39]. Интересно, что пристенные полосы оказываются неактивными по отношению к этим структурам. В этом отношении возмущения СЛВ, рассмотренные в настоящей работе, аналогичны турбулентно-турбулентным пятнам, обнаруженным в [39].
Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ им. М.В. Ломоносова при финансовой поддержке РФФИ, проект № 17-01-00140-a.
Список литературы
Klebanoff P.S., Tidstrom K.D., Sargent L.M. The three-dimensional nature of boundary-layer instability // J. Fluid Mech. 1962. V. 12. № 1. P. 1–34.
Kline S.J., Reynolds W.C., Schraub F.A., Runstadler P.W. The structure of turbulent boundary layers // J. Fluid Mech. 1967. V. 30. № 4. P. 741–773.
Landahl M.T. A note on an algebraic instability of inviscid parallel shear flows // J. Fluid Mech. 1980. V. 98. № 2. P. 243–251.
Zaki T.A. From streaks to spots and on to turbulence: exploring the dynamics of boundary layer transition // Flow Turbul. Combust. 2013. V. 91. № 3. P. 451–473.
Козлов В.В., Грек Г.Р., Литвиненко Ю.А., Толкачев С.Н., Чернорай В.Г. Экспериментальные исследования локализованных возмущений и их вторичной высокочастотной неустойчивости в пограничном слое плоской пластины, прямого и скользящего крыла (обзор) // Вестник НГУ. Сер. Физика. 2014. Т. 9. № 4. С. 39–64.
Smith C.R., Metzler S.P. The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer // J. Fluid Mech. 1983. V. 129. P. 27–54.
Kim H.T., Kline S.J., Reynolds W.C. The production of turbulence near a smooth wall in a turbulent boundary layers // J. Fluid Mech. 1971. V. 50. P. 133–160.
Hamilton K., Kim J., Waleffe F. Regeneration mechanisms of near-wall turbulence structures // J. Fluid Mech. 1995. V. 287. P. 317–348.
Jimenez J., Pinelli A. The autonomous cycle of near wall turbulence // J. Fluid Mech. 1999. V. 389. P. 335–359.
Schoppa W., Hussain F. Coherent structure generation in near-wall turbulence // J. Fluid Mech. 2002. V. 453. P. 57–108.
Waleffe F. Hydrodynamic stability and turbulence: Beyond transients to a self-sustaining process // Stud. Appl. Maths. 1995. V. 95. № 3. P. 319–343.
Waleffe F. On a self-sustaining process in shear flows // Phys. Fluids. 1997. V. 9. № 4. P. 883–900.
Jang P.S., Benney D.J., Gran R.L. On the origin of streamwise vortices in a turbulent boundary layer // J. Fluid Mech. 1986. V. 169. P. 109–123.
Brooke J.W., Hanratty T.J. Origin of turbulence producing eddies in a channel flow // Phys. Fluids A. Fluid Dynamics. 1993. V. 5. № 4. P. 1011–1021.
Butler K.M., Farrell B.F. Optimal perturbations and streak spacing in wall-bounded turbulent shear flows // Phys. Fluids A. Fluid Dynamics. 1993. V. 5. № 3. P. 774–777.
Никитин Н.В., Чернышенко С.И. О природе организованных структур в турбулентных пристенных течениях // Изв. РАН. МЖГ 1997. № 1. С. 24–30.
Schoppa W., Hussain F. Formation of near-wall streamwise vortices by streak instability // AIAA Paper. 1998. P. 61–78.
Chernyshenko S.I., Baig M.F. The mechanism of streak formation in near-wall turbulence // J. Fluid Mech. 2005. V. 544. P. 99–131.
Waleffe F., Kim J. How streamwise rolls and streaks self-sustain in a shear flow // In Self-Sustaining Mechanisms of Wall Turbulence / Ed. R. Panton. Computational Mechanics Publications. 1997. P. 309–332.
Schoppa W., Hussain F. Genesis and dynamics of coherent structures in near-wall turbulence: A new look // In Self-Sustaining Mechanisms of Wall Turbulence (ed. R. Panton). Computational Mechanics Publications. 1997. P. 385–422.
Kawahara G., Jiménez J., Uhlmann M., Pinelli A. The instability of streaks in near-wall turbulence // CTR Annu. Res. Briefs, Stanford University. 1998. P. 155–170.
Farrell B.F., Ioannou P.J. Generalized stability. Part II. Non-autonomous operators // J. Atmos. Sci. 1996. P. 2041–2053.
Farrell B.F., Ioannou P.J. Dynamics of streamwise rolls and streaks in turbulent wall-bounded shear flow // J. Fluid Mech. 2012. V. 708. P. 149–196.
Farrell B.F., Ioannou P.J., Jiménez J., Constantinou N.C., Lozano-Durán A., Nikolaidis M.-A. A statistical state dynamics-based study of the structure and mechanism of large-scale motions in plane Poiseuille flow // J. Fluid Mech. 2016. V. 809. P. 290–315.
Egolf D.A., Melnikov I.V., Pesch W., Ecke R.E. Mechanisms of extensive spatiotemporal chaos in Rayleigh–Bénard convection // Nature, London. 2000. V. 404. P. 733–736.
Jayaraman A., Scheel J.D., Greenside H.S., Fischer P.F. Characterization of the domain chaos convection state by the largest Lyapunov exponent // Phys. Rev. E. 2006. V. 74. № 1. 016209.
Xu M., Paul M.R. Covariant Lyapunov vectors of chaotic Rayleigh–Bénard convection // Phys. Rev. E. 2016. V. 93. № 6. 062208.
Parker T.S., Chua L.O. Practical Numerical Algorithms for Chaotic Systems. New York, Springer-Verlag. 1989. 347 p.
Ginelli F., Poggi P., Turchi A., Chatґe H., Livi R., Politi A. Characterizing dynamics with covariant Lyapunov vectors // Phys. Rev. Lett. 2007. V. 99. № 13. 130601.
Nikitin N. On the rate of spatial predictability in near-wall turbulence // J. Fluid Mech. 2008. V. 614. P. 495–507.
Никитин Н.В. О скорости роста возмущений в пристенных турбулентных течениях // Изв. РАН. МЖГ. 2009. № 5. С. 27–32.
Unnikrishnan S., Gaitonde D.V. A high-fidelity method to analyze perturbation evolution in turbulent flows // J. Comput. Phys. 2016. V. 310. 45–62.
Nikitin N. Spatial periodicity of spatially evolving turbulent flow caused by inflow boundary condition // Physics of Fluids. 2007. V. 19. № 9. 091703.
Keefe L., Moin P., Kim J. The dimension of attractors underlying periodic turbulent Poiseuille flow // J. Fluid Mech. 1992. V. 242. P. 1–29.
Inubushi M., Takehiro S-I, Yamada M. Regeneration cycle and the covariant Lyapunov vectors in a minimal wall turbulence // Phys. Rev. E. 2015. V. 92. № 2. 023022.
Никитин Н.В., Пивоваров Д.Е. О скорости роста возмущений в турбулентном течении Куэтта // Изв. РАН. МЖГ. 2018. № 6. С. 3–8.
Nikitin N. Finite-difference method for incompressible Navier-Stokes equations in arbitrary orthogonal curvilinear coordinates // J. Comput. Phys. 2006. V. 217. P. 759–781.
Moser R.D., Kim J., Mansour N.N. Direct numerical simulation of turbulent channel flow up to ${\text{R}}{{{\text{e}}}_{\tau }} = 590$ // Physics of Fluids. 1999. V. 11. № 4. P. 943–945.
Wu X., Moin P., Wallace J.M., Skarda J., Lozano-Duran A., Hickey J.-P. Transitional-turbulent spots and turbulent-turbulent spots in boundary layers // PNAS. 2017. V. 114. № 27. E5292–E5299.
Jeong J., Hussain F., Schoppa W., Kim J. Coherent structures near the wall in a turbulent channel flow // J. Fluid Mech. 1997. 185–214.
Jeong J., Hussain F. On the identification of a vortex // J. Fluid Mech. 1995. V. 285. P. 69–94.
Tennekes H., Lumley J.L. A First Course in Turbulence. M.I.T. Press, 1972. 300 p.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа