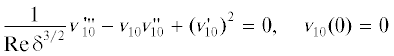Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 99-111

CТАЦИОНАРНОЕ ВТОРИЧНОЕ ТЕЧЕНИЕ В ПЛОСКОЙ ТУРБУЛЕНТНОЙ СВОБОДНОЙ СТРУЕ

А. Р. Горбушин^{a, b, *, **}, В. Б. Заметаев^a, b, ***, И. И. Липатов^a, b, ****

^a Московский физико-технический институт (государственный университет)
Долгопрудный, Россия

^b Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Россия

^* E-mail: gorbushin.ar@mipt.ru
^** E-mail: gorbushin@tsagi.ru
^*** E-mail: zametaev.vb@mipt.ru
^**** E-mail: igor_lipatov@mail.ru

Поступила в редакцию 15.10.2018
После доработки 18.10.2018
Принята к публикации 18.10.2018

DOI: 10.1134/S0568528119020075

Полный текст (PDF)

Аннотация

Асимптотическими методами изучена турбулентная плоская струя вязкой несжимаемой жидкости, истекающая через узкую щель в заполненное жидкостью пространство. Рассматриваются полные уравнения Навье–Стокса. Характерное число Рейнольдса потока считается большим, а толщина струи малой. Для анализа задачи применен метод многих масштабов, позволивший найти и исследовать стационарное вторичное течение внутри турбулентной струи. Получены аналитически вторичные стационарные решения для поперечной и продольной составляющих скорости и давления. Показано, что самоиндуцированный отток жидкости из ядра струи на периферию является основным вторичным течением, обеспечивающим подачу кинетической энергии из зоны максимальной скорости в зону генерации турбулентности. Полученные решения удовлетворительно согласуются с имеющимися экспериментальными данными.

Ключевые слова: турбулентность, вязкая струя, асимптотический анализ

Целью данной статьи является изучение свойств турбулентной, в осредненном смысле, двухмерной струи, без дополнительных, даже физически обоснованных гипотез замыкания, с помощью асимптотического анализа полных уравнений Навье–Стокса. Такие струи являются классическим объектом исследований, и к настоящему времени выполнено множество экспериментов, например [1–5], написаны монографии [6, 7], описавшие основные свойства струй. В частности, установлено, что турбулентные струи расширяются по линейному закону, профиль осредненной скорости имеет автомодельный характер, и течение само себе подобно на различных расстояниях. Максимальная скорость на оси струи убывает обратно пропорционально корню из расстояния, по мере ее распространения в покоящейся жидкости, в соответствии с законом сохранения импульса. Известно свойство у подобных струй подсасывать жидкость из зоны покоя благодаря турбулентному перемешиванию.

Теория тонких турбулентных струй, пограничных слоев и течений в каналах, основанная на решении осредненных уравнений Рейнольдса с использованием различных концепций замыкания, давно построена и неплохо совпадает с экспериментальными данными, например, [8–10]. Однако гипотезы, заложенные в структуру уравнений Рейнольдса, недостаточно строги, что и подталкивает к поиску альтернативных подходов к анализу турбулентных течений.

Авторы предлагают в определенном смысле сделать шаг назад, во времена до активного использования осредненных уравнений Навье–Стокса (RANS) и проанализировать полные уравнения Навье–Стокса. Таким образом, мы не изучаем уравнения RANS с некоторыми гипотезами замыкания, используя асимптотические методы, а рассматриваем именно полные уравнения Навье–Стокса, предполагая число Рейнольдса большим, толщину струи малой и малую амплитуду пульсаций.

Статья использует результаты работ [11, 12], но применительно к рассматриваемому типу течений со свободной турбулентностью. В последней из них выполнено асимптотическое исследование двухмерных вязких пульсаций в несжимаемом турбулентном пограничном слое, развивающемся вдоль плоской пластины. Изложение в [12] коснулось только локальной задачи в зоне генерации турбулентности и в вязком подслое вблизи обтекаемой поверхности. В данной же работе описывается решение, справедливое во всей толщине турбулентной струи и на длинах развитого турбулентного течения. Для анализа полных нестационарных уравнений Навье–Стокса используется метод многих масштабов при стремлении числа Рейнольдса к бесконечности, а толщины струи к нулю. В работе предполагается существование аналогии между турбулентной струей и течениями, обусловленными быстрым пульсирующим движением самого обтекаемого тела в покоящейся жидкости, или наличием малых пульсаций во внешнем стационарном потоке. Хорошо известно так называемое стационарное вторичное течение, генерируемое быстро колеблющимся цилиндром в покоящейся жидкости, описанное в [13]. Детальные эксперименты с таким цилиндром выполнены в работе [14]. Случаи, когда внешний поток содержит малую быстро осциллирующую составляющую и, как следствие, появляются вторичные стационарные движения, описаны в [15, 16]. Другой пример появления вторичных стационарных течений найден в [17]. Подробные обзоры таких течений сделаны, например, в [18, 19].

Несмотря на, казалось бы, существенную разницу между приведенным примером течения с действующей внешней периодической силой и турбулентной струей, самостоятельно генерирующей пульсации, в ней также возможны вторичные стационарные течения, хотя и другой природы. В работе выводятся уравнения и ищутся решения для нормальной к направлению распространения струи вторичной стационарной скорости. Она является основной скоростью и представляет собой отток жидкости из центрального ядра струи на ее периферию в зону генерации турбулентности. Анализируется продольная вторичная стационарная скорость. Во всех случаях удается найти решения, удовлетворительно совпадающие с имеющимися экспериментальными данными.

1. ОСНОВНАЯ ЧАСТЬ СТРУИ

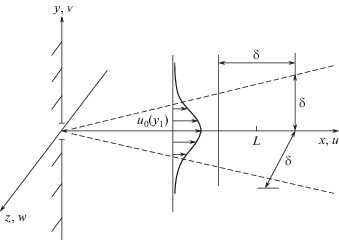
Рассматривается истечение вязкой несжимаемой турбулентной струи из двухмерной щели в затопленное пространство на характерном размере $L$, рис. 1. Характерные время и максимальная скорость струи равны $L{\text{/}}{{V}_{c}},\,{{V}_{c}}$ соответственно, а безразмерная малая полутолщина струи равна $\delta $ на указанной длине. Давление вводится по формуле $p' = {{p}_{\infty }} + \rho V_{c}^{2}p$, где $\rho $ – плотность жидкости, а ${{p}_{\infty }}$ – давление в покоящейся жидкости. Все гидродинамические функции, длины и время обезразмериваются традиционным способом, используя указанные параметры потока.

Рис. 1.

Схема истечения плоской турбулентной струи в затопленное пространство

Дальнейшее изложение в статье предполагает только безразмерные величины и уравнения. Число Рейнольдса является большой величиной в данном асимптотическом исследовании, и вводится как $\operatorname{Re} = {{\rho {{V}_{c}}L} \mathord{\left/ {\vphantom {{\rho {{V}_{c}}L} \mu }} \right. \kern-0em} \mu }$, где $\mu $ – коэффициент вязкости жидкости. Сама струя полагается турбулентной, учитывая быстрые пульсации давления и скоростей относительно некоторого базового профиля продольной скорости течения ${{u}_{0}}(x,{{y}_{1}})$.

Безразмерные полные уравнения Навье–Стокса удобно записать для введенного приращения давления p, нормальной к плоскости симметрии струи скорости $v$, поперечной скорости w, а продольная компонента скорости u, в результате, найдется из уравнения неразрывности

(1.1)

${{\nabla }^{2}}p = - 2\frac{{\partial u}}{{\partial y}}\frac{{\partial v}}{{\partial x}} - 2{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^{2}} - 2\frac{{\partial v}}{{\partial y}}\frac{{\partial w}}{{\partial z}} - 2{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^{2}} - 2\frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}} - 2\frac{{\partial w}}{{\partial y}}\frac{{\partial v}}{{\partial z}}$

(1.2)

$\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} = - \frac{{\partial p}}{{\partial y}} + \frac{1}{{\operatorname{Re} }}{{\nabla }^{2}}v$

(1.3)

$\frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}} = - \frac{{\partial p}}{{\partial z}} + \frac{1}{{\operatorname{Re} }}{{\nabla }^{2}}w$

(1.4)

$\frac{{\partial u}}{{\partial x}} + \frac{{\partial \text{v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$

Для поиска решения системы (1.1)–(1.4) используется метод многих масштабов. Поскольку метод асимптотический, то немедленно возникает принципиальный вопрос о виде пригодного асимптотического разложения решения уравнений Навье–Стокса. Обычно предполагается, в соответствии с экспериментами, что можно ввести в рассмотрение двухмерный осредненный профиль скорости в основной части струи, по отношению к которому имеются пульсации. Средняя величина пульсаций, вычисленная по некоторому большому периоду времени, равна нулю. Однако такой подход не кажется самым общим, если решение заметно меняется по координатам, да и период осреднения, вообще говоря, неизвестен. Поэтому в данной работе, в качестве базового профиля скорости рассматривается и ищется стационарный регулярный профиль ${{u}_{0}}(x,{{y}_{1}})$, а осредненный можно получить, если добавить к нему пульсации, средняя величина которых, вообще говоря, не нулевая. Теория подобных пульсаций в пограничном слое, имеющих особенность вблизи обтекаемой поверхности, предложена в статье [12]. Далее предполагается, следуя гипотезе [20], что квадраты пульсаций должны влиять на базовое течение

$\begin{gathered} v'{{\partial u'} \mathord{\left/ {\vphantom {{\partial u'} {\partial y'}}} \right. \kern-0em} {\partial y'}}\sim {{u}_{0}}{{\partial {{u}_{0}}} \mathord{\left/ {\vphantom {{\partial {{u}_{0}}} {\partial x}}} \right. \kern-0em} {\partial x}}\sim 1 \\ v'\sim u'\sim w'\sim {{\delta }^{{1/2}}},\quad x'\sim y'\sim z'\sim \delta \\ \end{gathered} $

Также следует учесть, что согласно экспериментам и теории [21], основная кинетическая энергия пульсаций содержится в так называемых крупномасштабных невязких вихрях. Характерные размеры вихрей по всем осям одинаковы по порядку величины и сопоставимы с толщиной струи $\delta $, рис. 1. Исходя из перечисленных фактов и предположений, асимптотические разложения решения в турбулентной части струи следует искать при $\delta \to 0,\operatorname{Re} \to \infty $ в следующем виде

(1.5)

$\begin{gathered} u = {{u}_{0}}(x,{{y}_{1}}) + {{\delta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{u}_{1}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) + \delta {{u}_{2}} + ... \\ v = {{\delta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{v}_{1}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) + \delta {{v}_{2}} + ... \\ w = {{\delta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{w}_{1}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) + \delta {{w}_{2}} + ... \\ p = {{\delta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{p}_{1}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) + \delta {{p}_{2}} + ... \\ {{y}_{1}} = \frac{y}{\delta },\quad {{x}_{1}} = \frac{x}{\delta },\quad {{z}_{1}} = \frac{z}{\delta },\quad {{t}_{1}} = \frac{t}{\delta } \\ \end{gathered} $

Искомые функции зависят от медленной переменной $x$ и от быстрых переменных с подстрочным индексом 1.

Подставляя асимптотические разложения (1.5) в (1.1)–(1.4) и выделяя последовательно главные члены в уравнениях, получим задачи для возмущений первого порядка ${{v}_{1}},\;{{p}_{1}}$ и ${{w}_{1}},\,\,{{u}_{1}}$

(1.6)

$\begin{gathered} O\left( {\frac{{{{\delta }^{{1/2}}}}}{{{{\delta }^{2}}}}} \right){\text{:}}\;\frac{{{{\partial }^{2}}{{p}_{1}}}}{{\partial x_{1}^{2}}} + \frac{{{{\partial }^{2}}{{p}_{1}}}}{{\partial y_{1}^{2}}} + \frac{{{{\partial }^{2}}{{p}_{1}}}}{{\partial z_{1}^{2}}} + 2\frac{{\partial {{u}_{0}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{1}}}}{{\partial {{x}_{1}}}} = 0 \\ O\left( {\frac{{{{\delta }^{{1/2}}}}}{\delta }} \right){\text{:}}\;\frac{{\partial {{v}_{1}}}}{{\partial {{t}_{1}}}} + {{u}_{0}}\frac{{\partial {{v}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{p}_{1}}}}{{\partial {{y}_{1}}}} = 0 + O\left( {\frac{1}{{\operatorname{Re} \delta }}} \right) \\ {{y}_{1}} = 0\,{\text{:}}\;{{v}_{1}} = 0,\quad \frac{{\partial {{p}_{1}}}}{{\partial {{y}_{1}}}} = 0;\quad y_{1}^{2} + x_{1}^{2} + z_{1}^{2} \to \infty {\text{:}}\;{{p}_{1}} = 0 \\ \end{gathered} $

$\begin{gathered} O\left( {\frac{{{{\delta }^{{1/2}}}}}{\delta }} \right){\text{:}}\;\frac{{\partial {{w}_{1}}}}{{\partial {{t}_{1}}}} + {{u}_{0}}\frac{{\partial {{w}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{p}_{1}}}}{{\partial {{z}_{1}}}} = 0 + O\left( {\frac{1}{{\operatorname{Re} \delta }}} \right) \\ O\left( {\frac{{{{\delta }^{{1/2}}}}}{\delta }} \right){\text{:}}\;\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{v}_{1}}}}{{\partial {{y}_{1}}}} + \frac{{\partial {{w}_{1}}}}{{\partial {{z}_{1}}}} = 0 \\ \end{gathered} $

В результате найдена невязкая система уравнений, введенная ранее Рэлеем [22] для описания эволюции малых возмущений в канале; для справки в уравнениях указаны порядки величин отброшенных малых вязких членов. Следует отметить, что в случае плоского базового профиля скорости ${{u}_{0}}(x,{{y}_{1}})$ уравнения для пульсаций ${{v}_{1}},\,{{p}_{1}}$ отделились и представляют замкнутую задачу, в которой только лапласиан давления является трехмерным. Если имеется направленное трехмерное турбулентное течение струи с профилем скорости ${{u}_{0}}(x,{{y}_{1}})$, то именно пульсации ${{v}_{1}},\,{{p}_{1}}$ являются основными. Зная возмущенное давление ${{p}_{1}}$, можно затем вычислить поперечную пульсацию ${{w}_{1}}$ из соответствующего уравнения импульса, а продольную пульсацию ${{u}_{1}}$ – из уравнения неразрывности.

Решения невязкой линейной задачи (1.6) традиционно ищутся в виде бегущих волн ${{v}_{1}}\,\sim \,{\text{exp}}(i\alpha ({{x}_{1}}$ – ct₁)), см., например, монографию [23]. Отметим, что согласно экспериментальным данным величина пульсаций в турбулентной струе, отнесенная к скорости в плоскости симметрии, не нарастает по амплитуде при развитии течения вдоль оси $x$.

В системе уравнений (1.6) содержатся производные только по быстрым переменным ${{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}}$, и в общем случае пульсации ${{v}_{1}},\,{{p}_{1}},\,{{u}_{1}}$ должны содержать стационарные слагаемые, зависящие от медленной переменной x. Что касается пульсации ${{w}_{1}}$, то если физические причины для появления стационарной составляющей в поперечном течении отсутствуют (например, заданное перетекание), то и такого слагаемого не должно быть

(1.7)

$\begin{gathered} {{v}_{1}} = {{v}_{{10}}}(x,{{y}_{1}}) + {{v}_{{11}}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x),\quad {{p}_{1}} = {{p}_{{10}}}(x) + {{p}_{{11}}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) \\ {{w}_{1}} = {{w}_{{11}}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x),\quad {{u}_{1}} = {{u}_{{10}}}(x,{{y}_{1}}) + {{u}_{{11}}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) \\ \end{gathered} $

Подстановка формул (1.7) в систему (1.6) показывает, что медленные функции с индексом, содержащим “0”, исключаются при дифференцировании и никак не влияют на решение системы (1.6). В результате эта система уравнений может быть переписана без изменений для быстрых возмущений ${{v}_{{11}}},{{p}_{{11}}}$. Медленные же функции ${{v}_{{10}}},{{p}_{{10}}}$ остаются произвольными. Возмущения давления вне струи создаются турбулентным подсосом и определяются квадратом скорости подсоса, поэтому в линейном приближении возмущенное давление должно быть нулем ${{p}_{{10}}} = 0$.

Задачу для второго приближения можно представить в следующем виде

$\begin{gathered} O\left( {\frac{\delta }{{{{\delta }^{2}}}}} \right){\text{:}}\;{{\nabla }^{2}}{{p}_{2}} + 2\frac{{\partial {{u}_{0}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{2}}}}{{\partial {{x}_{1}}}} = - 2\frac{{\partial {{u}_{1}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{1}}}}{{\partial {{x}_{1}}}} - 2{{\left( {\frac{{\partial {{v}_{1}}}}{{\partial {{y}_{1}}}}} \right)}^{2}} - \\ - \;2\frac{{\partial {{v}_{1}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{w}_{1}}}}{{\partial {{z}_{1}}}} - 2{{\left( {\frac{{\partial {{w}_{1}}}}{{\partial {{z}_{1}}}}} \right)}^{2}} - 2\frac{{\partial {{u}_{1}}}}{{\partial {{z}_{1}}}}\frac{{\partial {{w}_{1}}}}{{\partial {{x}_{1}}}} - 2\frac{{\partial {{w}_{1}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{1}}}}{{\partial {{z}_{1}}}} \\ \end{gathered} $

(1.8)

$\begin{gathered} O\left( {\frac{\delta }{\delta }} \right){\text{:}}\;\frac{{\partial {{v}_{2}}}}{{\partial {{t}_{1}}}} + {{u}_{0}}\frac{{\partial {{v}_{2}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{p}_{2}}}}{{\partial {{y}_{1}}}} = - {{u}_{1}}\frac{{\partial {{v}_{1}}}}{{\partial {{x}_{1}}}} - {{v}_{1}}\frac{{\partial {{v}_{1}}}}{{\partial {{y}_{1}}}} - {{w}_{1}}\frac{{\partial {{v}_{1}}}}{{\partial {{z}_{1}}}} + \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}{{\nabla }^{2}}{{v}_{1}} \\ O\left( {\frac{\delta }{\delta }} \right){\text{:}}\;\frac{{\partial {{w}_{2}}}}{{\partial {{t}_{1}}}} + {{u}_{0}}\frac{{\partial {{w}_{2}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{p}_{2}}}}{{\partial {{z}_{1}}}} = - {{u}_{1}}\frac{{\partial {{w}_{1}}}}{{\partial {{x}_{1}}}} - {{v}_{1}}\frac{{\partial {{w}_{1}}}}{{\partial {{y}_{1}}}} - {{w}_{1}}\frac{{\partial {{w}_{1}}}}{{\partial {{z}_{1}}}} + \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}{{\nabla }^{2}}{{w}_{1}} \\ O\left( {\frac{\delta }{\delta }} \right){\text{:}}\;\frac{{\partial {{u}_{2}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{u}_{0}}}}{{\partial x}} + \frac{{\partial {{v}_{2}}}}{{\partial {{y}_{1}}}} + \frac{{\partial {{w}_{2}}}}{{\partial {{z}_{1}}}} = 0 \\ \end{gathered} $

В уравнениях (1.8) для возмущений второго порядка линейные операторы совпадают с таковыми в (1.6), но появляются неоднородные квадратичные члены, аналогично выводу уравнений Рейнольдса. В (1.8) оставлены также вязкие члены в соответствии с результатами статьи [12], в которой установлено, что величина параметра ${{Z}_{i}} = \operatorname{Re} {{\delta }^{{3/2}}}$ может принимать конечные, хотя и большие значения в турбулентной области течения на конечном расстоянии от области перехода в пограничных слоях. Авторы полагают, что и в свободных турбулентных течениях данный параметр может принимать конечные значения, на конечных расстояниях от щели. В отличие от традиционного метода многих масштабов в системе (1.8) не появились производные по медленной переменной $x$, исключением является уравнение неразрывности. Это объясняется тем фактом, что разложения искомых функций идут по степеням ${{\delta }^{{1/2}}}$, а медленные производные убывают по степеням $\delta $. Соответственно дифференциальные уравнения по медленной переменной для амплитуд пульсаций могут быть получены только из третьего приближения, а система (1.8) служит для определения медленных стационарных вторичных возмущений ${{v}_{{10}}}$.

Подстановка (1.7) в систему уравнений (1.8) формулирует задачу для ${{v}_{2}},\;{{p}_{2}}$

$\begin{gathered} {{\nabla }^{2}}{{p}_{2}} + 2\frac{{\partial {{u}_{0}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{2}}}}{{\partial {{x}_{1}}}} = - \underbrace {2{{{\left( {\frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}}} \right)}}^{2}}}_G - \\ - \;\underbrace {2\frac{{\partial {{u}_{1}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{{11}}}}}{{\partial {{x}_{1}}}} - 2\left( {2\frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{{11}}}}}{{\partial {{y}_{1}}}} + {{{\left( {\frac{{\partial {{v}_{{11}}}}}{{\partial {{y}_{1}}}}} \right)}}^{2}}} \right) - 2\frac{{\partial {{v}_{1}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{w}_{1}}}}{{\partial {{z}_{1}}}} - 2{{{\left( {\frac{{\partial {{w}_{1}}}}{{\partial {{z}_{1}}}}} \right)}}^{2}} - 2\frac{{\partial {{u}_{1}}}}{{\partial {{z}_{1}}}}\frac{{\partial {{w}_{1}}}}{{\partial {{x}_{1}}}} - 2\frac{{\partial {{w}_{1}}}}{{\partial {{y}_{1}}}}\frac{{\partial {{v}_{1}}}}{{\partial {{z}_{1}}}}}_{} \\ \end{gathered} $

(1.9)

$\begin{gathered} \frac{{\partial {{v}_{2}}}}{{\partial {{t}_{1}}}} + {{u}_{0}}\frac{{\partial {{v}_{2}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{p}_{2}}}}{{\partial {{y}_{1}}}} = \underbrace { - {{v}_{{10}}}\frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}} + \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}\frac{{{{\partial }^{2}}{{v}_{{10}}}}}{{\partial {{y}_{1}}^{2}}}}_E - \\ - \;\underbrace {{{u}_{1}}\frac{{\partial {{v}_{{11}}}}}{{\partial {{x}_{1}}}} - ({{v}_{{10}}} + {{v}_{{11}}})\frac{{\partial {{v}_{{11}}}}}{{\partial {{y}_{1}}}} - {{v}_{{11}}}\frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}} - {{w}_{1}}\frac{{\partial {{v}_{1}}}}{{\partial {{z}_{1}}}} + \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}{{\nabla }^{2}}{{v}_{{11}}}}_{} \\ \end{gathered} $

В полученных уравнениях (1.9) слева выписаны линейные операторы, зависящие от быстрых переменных, а справа скомпонованы стационарные медленные (G, E) и нестационарные быстрые неоднородные члены. Вклад в стационарные, неоднородные члены дает только ${{v}_{1}}$, поэтому только она и разложена на составляющие в (1.9). В силу линейности решение задачи (1.9) можно представить в виде суммы быстрого нестационарного и медленного стационарного частных решений. Детальный анализ нестационарных решений можно выполнить, зная первое приближение, однако это выходит за рамки представленного исследования. Достаточно потребовать, чтобы быстрое нестационарное неоднородное решение задачи (1.9) не нарастало по пространственной координате ${{x}_{1}}$. Такое требование является типичным в методе многих масштабов при выводе уравнения эволюции амплитуд пульсаций по координате, а также соответствует экспериментам, в которых найдено, что в турбулентных струях относительная амплитуда пульсаций не нарастает в направлении основного потока.

Что касается частного решения задачи (1.9), обусловленного стационарной неоднородностью, то оно имеет вид

(1.10)

$\begin{gathered} {{v}_{2}} = {{x}_{1}}{{V}_{m}}({{y}_{1}}),\quad {{p}_{2}} = {{p}_{{20}}}({{y}_{1}}) \\ {{V}_{m}} = \frac{{E - p_{{20}}^{'}}}{{{{u}_{0}}}},\quad p_{{20}}^{'} = - u_{0}^{2}\int\limits_{{{y}_{1}}}^{ + \infty } {\left( {\frac{G}{{u_{0}^{2}}} - \frac{{2u_{0}^{'}}}{{u_{0}^{3}}}E} \right)} d\eta \\ \end{gathered} $

Если стационарные правые части G и E уравнений (1.9) произвольны, то формулы (1.10) означают появление линейно растущего по ${{x}_{1}}$, а значит секулярного члена в вертикальной скорости. Чтобы исключить не физические растущие решения (1.10), надо приравнять нулю ${{V}_{m}}({{y}_{1}})$, откуда следует необходимое условие отсутствия секулярных членов

(1.11)

Это условие сводится к обычному нелинейному дифференциальному уравнению третьего порядка для вертикальной вторичной стационарной скорости, причем для нее имеется только одно граничное условие непротекания в плоскости симметрии струи. Следует отметить независимость условия (1.11) от продольной скорости ${{u}_{0}}$, причем медленная переменная $x$ оказывается лишь параметром в этой задаче. Уравнение (1.11) не меняется при аффинном преобразовании

(1.11а)

${{y}_{1}} = Y{\text{/}}{{V}_{e}}(x),\quad {{v}_{{10}}} = {{V}_{e}}(x)V$

и допускает преобразование сдвига по аргументу. Вторичное возмущенное давление должно удовлетворять уравнению

(1.12)

$\frac{{\partial {{p}_{{20}}}}}{{\partial {{y}_{1}}}} = - {{v}_{{10}}}\frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}} + \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}\frac{{{{\partial }^{2}}{{v}_{{10}}}}}{{\partial y_{1}^{2}}}$

Получен важный результат: чтобы решения пульсационных уравнений (1.9) не содержали стационарных секулярных членов, должно выполняться условие (1.11). Этого можно добиться двумя способами: положить нулем вертикальную стационарную скорость ${{v}_{{10}}} = 0$, либо удовлетворить уравнение (1.11) при ненулевой скорости ${{v}_{{10}}} \ne 0$. Удалось найти четыре точных решения уравнения (1.11) в полубесконечной области

(1.13)

$\begin{gathered} {{v}_{{10}}} = {\text{const,}}\quad {{v}_{{10}}} = - \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}\frac{6}{{{{y}_{1}}}} \\ {{v}_{{10}}} = \frac{{{{V}_{e}}(x)}}{{\operatorname{Re} {{\delta }^{{3/2}}}}}\left( {1 - \exp ({{V}_{e}}{{y}_{1}})} \right),\quad {{V}_{e}}(x) < 0 \\ {{v}_{{10}}} = \frac{{{{V}_{e}}(x)}}{{\operatorname{Re} {{\delta }^{{3/2}}}}}\left( {1 + \exp ({{V}_{e}}{{y}_{1}})} \right),\quad {{V}_{e}}(x) < 0 \\ \end{gathered} $

Третье решение, удовлетворяющее условию непротекания в плоскости симметрии течения, а при сдвиге и на любом заданном расстоянии от плоскости симметрии есть вязкий стационарный распределенный подсос жидкости в струю из области покоя. Однако полученные точные решения не пригодны для центральной части струи, так как интуитивно ожидается, что жидкие частицы, имеющие максимальную кинетическую энергию, должны передаваться из ядра в зону генерации турбулентности на склоне струи. Это возможно только при положительной скорости ${{v}_{{10}}} > 0$ вблизи оси, и подобные решения могут быть найдены только численно.

Важно отметить нетрадиционное действие вязкости в данном случае. Обычно эффект вязкости сказывается поперек направления движения основного потока, как это происходит в ламинарной струе, в которой коэффициент вязкости непосредственно определяет толщину слоя и входит показателем затухания в экспоненциально малые члены решения. При умеренных же числах Рейнольдса уже лапласиан скорости определяет вязкие эффекты. В рассмотренном случае ситуация иная, основное медленное вторичное течение – это самоиндуцированный вертикальный отток жидкости из ядра струи, и от лапласиана вертикальной скорости остается вторая производная в том же направлении. В результате, как видно из решений (1.13), коэффициент молекулярной вязкости определяет амплитуду скорости оттока жидкости из ядра струи и подсоса жидкости из области покоя, но не толщину струи. Следует отметить, что описанная ситуация соответствует физическому понятию “турбулентная вязкость”, т.к. определяет в качестве вязкого размера всю толщину струи, но при этом никаких искусственных гипотез не используется. Аналитическое решение найдено с точностью до произвольной функции ${{V}_{e}}(x) < 0$, которая представляет собой нормированную скорость подсоса безвихревой жидкости на внешней границе струи. Подчеркнем полную независимость найденного подсоса жидкости от скорости продольного течения, что означает принципиальное изменение свойств вязкой струи при переходе к турбулентному состоянию. Если в ламинарной фазе течение в струе параболично, а развитие малых возмущений демонстрирует отдельные эллиптические свойства, то после ламинарно-турбулентного перехода в области развитой турбулентности параболичность пропадает. Начинают доминировать пульсации вертикальной скорости и давления над плавным изменением осредненных величин, что определяет очередность постановки и решения возникающих задач.

Сначала необходимо решить быструю задачу эволюции пульсаций (1.6) в первом приближении – она главная, затем вычислить неоднородности во втором приближении (1.9) и решить соответствующие линейные уравнения, затем третье приближение и т.д. Устранение возможных секулярных членов на каждом этапе порождает медленное стационарное вторичное течение и определяет условия на амплитуды пульсаций. В результате основным стационарным вторичным течением становится самоиндуцированный, вязкий и распределенный отток жидкости из ядра струи на периферию. Самоиндуцированность заключается в том, что ненулевая скорость оттока жидкости от плоскости симметрии уменьшает давление (1.12) на склоне струи, что, в свою очередь, повышает скорость оттока, а это еще более увеличивает падение давления и так далее, пока нелинейные эффекты не сбалансируют течение. Важно отметить, что вторичное стационарное решение может совпадать (а в зоне генерации турбулентности не совпадать!) с осредненными скоростями и давлением в струе.

В общем случае ${{v}_{2}},\,{{p}_{2}}$ также содержат слагаемые, зависящие от медленной переменной $x$

(1.14)

$\begin{gathered} {{v}_{2}} = {{v}_{{20}}}(x,{{y}_{1}}) + {{v}_{{21}}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) \\ {{p}_{2}} = {{p}_{{20}}}(x,{{y}_{1}}) + {{p}_{{21}}}({{x}_{1}},{{y}_{1}},{{z}_{1}},{{t}_{1}},x) \\ \end{gathered} $

Следующий этап – это вычисление вторичной стационарной продольной скорости течения в струе на фоне сформированного оттока жидкости из ядра струи на ее склон и на фоне сформированного подсоса жидкости из зоны покоя. Из уравнения неразрывности в первом приближении можно найти быструю пульсацию горизонтальной скорости

(1.15)

$O\left( {\frac{{{{\delta }^{{1/2}}}}}{\delta }} \right){\text{:}}\;\frac{{\partial {{u}_{{11}}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{v}_{{11}}}}}{{\partial {{y}_{1}}}} + \frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}} + \frac{{\partial {{w}_{{11}}}}}{{\partial {{z}_{1}}}} = 0 \to {{u}_{{11}}} = - \frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}}{{x}_{1}} + {{u}_{{12}}}$

Пульсационная составляющая продольной скорости в (1.15) содержит быстрый стационарный член, зависящий от вертикальной скорости. Это вынужденное, физически обоснованное решение, обусловленное законом сохранения массы. Оно напоминает секулярный член, однако, следует указать, что u и $v$ в турбулентном слое поменялись ролями по сравнению с ламинарным случаем. В ламинарном случае: u – главная скорость, а $v$ можно найти из уравнения неразрывности и при ${{y}_{1}} \to \infty ,\,v\sim - u'(x){{y}_{1}}$ (по форме напоминает секулярный член, но не является им). В турбулентном течении получается ровно наоборот: ${{v}_{{10}}}$ – главная индуцированная скорость, а u находится из уравнения неразрывности (1.15), и линейный член также не является секулярным. К тому же устранять секулярные члены надо в первую очередь у вертикальной составляющей скорости – так как она теперь основной поток, что уже сделано. Поведение же продольного течения должно подстроиться под сформированный подсос жидкости. Отметим, что линейно растущее возмущение продольной скорости не может повлиять на свойства решений задачи (1.9) и вывод уравнения (1.11).

Для нахождения базового профиля скорости ${{u}_{0}}$ обратимся к стандартному уравнению продольного импульса в системе Навье–Стокса. Это уравнение не выписано в (1.1)–(1.4), но имеет хорошо известный вид

(1.16)

$\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} = - \frac{{\partial p}}{{\partial x}} + \frac{1}{{\operatorname{Re} }}{{\nabla }^{2}}u$

Подставив асимптотические разложения решения (1.5) в (1.16) и выделяя последовательно главные члены, можно получить для возмущений первого порядка уравнение

(1.17)

$O\left( {\frac{{{{\delta }^{{1/2}}}}}{\delta }} \right){\text{:}}\;\frac{{\partial {{u}_{{12}}}}}{{\partial {{t}_{1}}}} + {{u}_{0}}\frac{{\partial {{u}_{{12}}}}}{{\partial {{x}_{1}}}} = \underbrace {{{u}_{0}}\frac{{\partial {{v}_{{10}}}}}{{\partial {{y}_{1}}}} - {{v}_{{10}}}\frac{{\partial {{u}_{0}}}}{{\partial {{y}_{1}}}} + \frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}\frac{{{{\partial }^{2}}{{u}_{0}}}}{{\partial {{y}_{1}}^{2}}}}_{} - \underbrace {{{v}_{{11}}}\frac{{\partial {{u}_{0}}}}{{\partial {{y}_{1}}}} - \frac{{\partial {{p}_{{11}}}}}{{\partial {{x}_{1}}}}}_{}$

Как и в уравнении для вертикальных пульсаций, слева скомпонован оператор, зависящий от быстрых переменных, а в правой части собраны стационарный медленный (первый) и нестационарный быстрый (второй) неоднородные члены. В уравнении (1.17) оставлены вязкие члены в соответствии с результатами статьи [12], в которой установлено, что величина параметра Z_i = = ${\text{Re}}{{\delta }^{{3/2}}}$ может принимать конечные значения в турбулентной области течения после ламинарно-турбулентного перехода. Более того, из решений (1.13) следует, что этот параметр определяет только амплитуду скорости подсоса, но не поведение решения, и поэтому можно рассматривать и его очень большие значения, что не приводит к вырождению задачи.

Пульсация продольной скорости ${{u}_{{12}}}$ не должна содержать стационарный линейный член по ${{x}_{1}}$ (так как он уже выделен), что возможно, если приравнять нулю медленную правую часть в (1.17)

(1.18)

$\frac{1}{{\operatorname{Re} {{\delta }^{{3/2}}}}}u_{0}^{{''}} - {{v}_{{10}}}u_{{10}}^{'} + v_{{10}}^{'}{{u}_{0}} = 0$

Следует отметить, что параметр ${{Z}_{i}} = \operatorname{Re} {{\delta }^{{3/2}}}$ исключается из (1.18) при подстановке любого точного решения ${{v}_{{10}}}$ из (1.13). Задаваясь третьим точным решением, можно найти два линейно независимых решения задачи (1.18) для продольной вторичной скорости в рассматриваемой полубесконечной области

(1.19)

$\begin{gathered} {{u}_{{01}}} = {{e}^{{ - Y}}},\quad {{u}_{{02}}} = {{e}^{{ - Y}}}\int\limits_0^Y {\exp (\eta - {{e}^{{ - \eta }}}} )d\eta \\ {{u}_{{02}}}(Y \to 0) = \frac{Y}{e} + ...,\quad Y = ( - {{V}_{e}}){{y}_{1}} \\ \end{gathered} $

Первое из них имеет конечное значение в точке $Y = 0$ и экспоненциально затухает, а второе начинается с нуля и стремится к единице в бесконечности. Оба решения определены с точностью до произвольной функции ${{V}_{e}}(x) < 0$. Важно отметить, что решение зависит от автомодельной переменной $Y = ( - {{V}_{e}}){{y}_{1}}$. Из найденного решения следует, что толщина струи обратно пропорциональна нормированной скорости подсоса жидкости на внешней границе. Найденное решение является несомненно вязким, но имеет большой “турбулентный вязкий размер”, в отличие от малого масштаба вязкости в зоне генерации турбулентности.

На фундаментальное явление подсоса жидкости в турбулентный пограничный слой указано в статье [24], собравшей множество экспериментальных данных. В частности в ней найдено, что толщина турбулентного пограничного слоя зависит именно от скорости подсоса. На важность явления подсоса жидкости с обеих сторон в турбулентный слой смешения указано в работе [25].

2. РЕШЕНИЕ В СТРУЕ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

2.1. Течение в ядре струи

Чтобы найти для струи решения фундаментальных уравнений (1.11, 1.18), уместно обратиться вначале к экспериментальным результатам статьи [2], представленным на рис. 2а. На указанном графике приведены два распределения осредненной вертикальной скорости в разных сечениях по оси $x$. Скорость ведет себя немонотонно по толщине струи: ноль в плоскости симметрии, затем становится положительной, достигает максимума, затем убывает и в некоторой точке обращается в ноль. Далее она отрицательна и стремится к константе при выходе из струи.

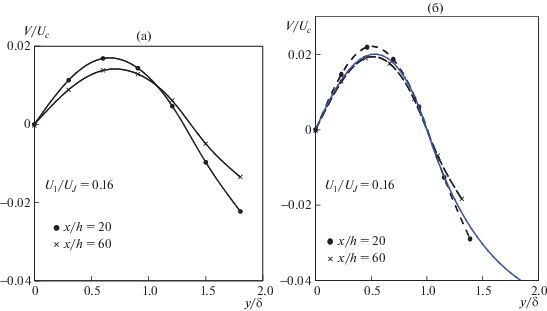
Рис. 2.

(а) Экспериментальные кривые [2] для вертикальной осредненной скорости в турбулентной струе; (б) те же кривые, преобразованные согласно (1.11а), с добавленным теоретическим решением

Такое поведение скорости вполне объяснимо с физической точки зрения, ведь максимальная кинетическая энергия струи содержится в ядре и должна подаваться из зоны максимума скорости в зону генерации турбулентности, расположенную на склоне струи. Этот эффект и является, по-видимому, причиной расширения турбулентных струй при распространении вниз по потоку – для передачи массы на периферию вектор скорости не должен быть параллелен оси основного движения.

Указанная картина течения позволяет предположить, что и искомая вторичная вертикальная скорость должна быть нулевой в плоскости симметрии течения, затем возрастать до положительных величин в основной части струи и далее убывать до нуля на некотором расстоянии от оси, как это указано на рис. 2.

Для расчета удобно ввести нормированные скорости и переменные в виде

$\begin{gathered} {{u}_{0}} = {{U}_{c}}U(Y),\quad {{v}_{{10}}} = \frac{{( - {{V}_{e}})}}{{\operatorname{Re} \cdot {{\delta }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}V(Y),\quad {{p}_{{20}}} = {{\left( {\frac{{{{V}_{e}}}}{{\operatorname{Re} {{\delta }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right)}^{2}}P(Y) \\ Y = ( - {{V}_{e}}){{y}_{1}},\quad {{U}_{c}} = {{U}_{c}}(x),\quad {{U}_{c}}(1) = 1 \\ \end{gathered} $

(2.1)

$\begin{gathered} V''' - VV'' + V{{'}^{2}} = 0,\quad V(0) = V(1) = 0,\quad V'(0) = \gamma \\ U'' - VU' + V'U = 0,\quad U(0) = 1,\quad U'(0) = 0 \\ \end{gathered} $

Для вторичной вертикальной скорости в задаче (2.1) выставлены условия нулевого значения в плоскости симметрии (функция $V$ должна быть антисимметрична в ней) и в точке $Y = 1$. В качестве третьего условия выбрана величина производной в нуле. Для вторичной горизонтальной скорости в плоскости симметрии можно выставить в качестве условий ее единичное значение и условие симметрии. Численный расчет (сплошная кривая на рис. 2, б, $\gamma = 2.338$, ${{U}_{\infty }} = 0.16$) показывает, что подходящие решения задачи существуют в некотором диапазоне параметра $\gamma > 0$. Для любой посчитанной скорости V можно найти соответствующую продольную скорость U. Она оказывается симметричной убывающей функцией, принимающей некоторое положительное значение в точке Y = 1. Нужно подчеркнуть принципиально нелинейный характер найденных решений, что означает самоиндуцированный нелинейный процесс передачи кинетической энергии из ядра струи на ее склон. Давление вычисляется по формуле (1.12) и оказывается убывающей функцией при отходе от плоскости симметрии. Изучая область ядра, не представляется возможным отобрать единственное решение задачи (2.1) и это понятно, ведь не выполнено условие затухания продольной скорости вне струи в области подсоса покоящейся жидкости.

2.2. Течение в периферийной области струи

Точка нулевой вторичной скорости Y = 1 является особой для уравнения (2.1), так как она разделяет область самоиндуцированного оттока высокоэнергетической жидкости из ядра струи и пассивную полубесконечную область подсоса безвихревой жидкости из окружающего пространства. Этот процесс подсоса происходит благодаря наличию точки минимального давления при Y = 1. Задача в периферийной области имеет вид

(2.2)

$\begin{gathered} V{\text{'''}} - VV{\text{''}} + V{{'}^{2}} = 0,\quad V(1) = 0,\quad V'(1) = V_{{inner}}^{'}(1),\quad V'( + \infty ) = 0 \\ U{\text{''}} - VU{\text{'}} + V'U = 0,\quad U(1) = {{U}_{{inner}}},\quad U'(1) = U_{{inner}}^{'},\quad U( + \infty ) = 0 \\ \end{gathered} $

Задача для скорости $U$ переопределена и имеет решение не при всяких граничных условиях, а значит не при всяком $\gamma $. В полубесконечной области единственное решение задачи (2.2), удовлетворяющее условию нулевой скорости $V(1) = 0$, это третье точное решение из (1.13). Чтобы его полностью определить, достаточно задать $V(1) = 0$ и величину $V'(1) = V_{{inner}}^{'}(1)$, которая известна из расчета задачи (2.1) в области ядра струи при заданном $\gamma $. При этом однозначно отберется величина скорости подсоса жидкости в струю из области покоя, обусловленная нелинейным подтеканием к точке минимума давления. Зная такую составную вертикальную вторичную скорость, можно найти решение для продольной вторичной скорости, интегрируя уравнение для U от точки Y = 1 с заданными $U(1) = {{U}_{{inner}}},\;U'(1) = U_{{inner}}^{'}$.

Для любой известной скорости подсоса можно, в результате, найти дважды непрерывно дифференцируемую продольную скорость в струе. Однако при задании произвольной величины $\gamma $ в (2.1) продольная скорость в бесконечности будет выходить на какое-то не нулевое значение, что означает смешение струи со спутным потоком. Например, при $\gamma = 2.338$ продольная скорость вне струи принимает значение ${{U}_{\infty }} = 0.16$, что соответствует экспериментальным данным на рис. 2а. На рис. 2б значками обозначены экспериментальные данные для вертикальной осредненной скорости, а сплошная кривая взята из построенной теории. Для сравнения с теорией координаты точек нулевой скорости были трансформированы в единицу, а величины скоростей пропорционально увеличены в соответствии с аффинным преобразованием (1.11а).

Удалось найти единственное решение $\gamma = 2.425,\,\,V(Y)$, для которого продольная скорость U выходит на нулевое значение в бесконечности – рис. 3.

Рис. 3.

Численное решение в зоне ядра струи и аналитическое в зоне подсоса, сопряженные в точке нулевой вертикальной вторичной скорости

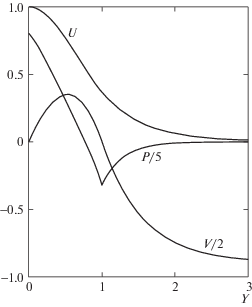
Именно на фоне такого вторичного стационарного профиля скорости и могут поддерживаться пульсации в турбулентной струе, а отток жидкости из ядра струи обеспечивает турбулентные пульсации кинетической энергией. Ведь зона генерации турбулентности находится на склоне струи и высокоэнергетическую жидкость надо подать именно туда, это принципиальный момент снабжения энергией. Отметим, что основной профиль продольной скорости найден из уравнения для линейных возмущений, т.е. процедуры осреднения при анализе турбулентных течений надо использовать осторожно.

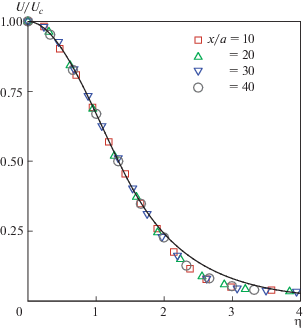
Сравнение построенных решений с экспериментальными данными [1] приведено на рис. 4. Следует отметить хорошее совпадение осредненной скорости с вторичным стационарным профилем скорости в ядре струи, тогда как в зоне малых скоростей имеется расхождение, что связано, вероятно, с распределенной генерацией на склоне струи и невозможностью точного измерения скорости.

Рис. 4.

Сравнение осредненной скорости в струе [1] с вторичной стационарной скоростью. Теоретическая сплошная кривая нанесена на экспериментальные данные с совмещением точек максимальной и половинной скоростей

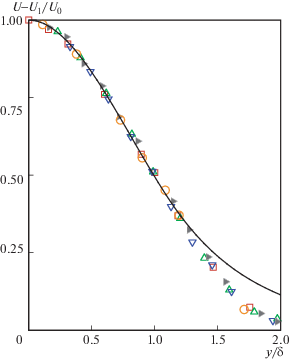
Вторым для сравнения взят профиль продольной осредненной скорости из экспериментальной работы [2]. Результаты сопоставления с теорией представлены на рис. 5. Сравнение также выглядит удовлетворительным за исключением зоны малых скоростей.

Рис. 5.

Сопоставление данных (символы) эксперимента [2] для осредненной скорости в струе с вторичной стационарной скоростью, полученной теоретически (сплошная кривая)

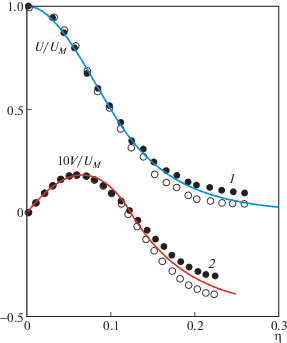
Следующее сравнение проведено с экспериментальными данными из работы [4]; сопоставление с теорией представлено на рис. 6. На оцифрованный оригинальный график удалось нанести и совместить как продольную, так и вертикальную вторичные стационарные скорости. Как и в предыдущих экспериментах, продольная скорость совпадает с теорией, за исключением зоны малых скоростей. Похожим образом ведет себя и скорость подсоса, совпадающая с теоретической кривой в основной части струи и слегка отклоняясь к краю.

Рис. 6.

Сопоставление продольной (${U \mathord{\left/ {\vphantom {U {{{U}_{M}}}}} \right. \kern-0em} {{{U}_{M}}}}$, символы) и поперечной (${{10V} \mathord{\left/ {\vphantom {{10V} {{{U}_{M}}}}} \right. \kern-0em} {{{U}_{M}}}}$, символы) осредненных скоростей, измеренных в эксперименте [4], с аналитическими кривыми (сплошные линии)

ЗАКЛЮЧЕНИЕ

В работе построена асимптотическая теория вторичных стационарных течений в свободных плоских турбулентных струях. Обнаружено, что в отличие от ламинарных течений первичным явлением в рассмотренных задачах являются быстрые пульсации нормальной к плоскости симметрии скорости и давления, порождающие стационарный отток высокоскоростной жидкости из области ядра струи в область генерации турбулентности (зону самоподдержания пульсаций).

Показано, что вторичное стационарное течение является вязким на всей толщине струи, что позволяет говорить о крупномасштабной вязкости, и обосновывает хорошо известное физическое понятие турбулентной вязкости.

Найденное стационарное решение можно рассматривать как нелинейный механизм передачи кинетической энергии в зону генерации турбулентности, вообще говоря, независимо от типа генерации. Известное явление подсоса жидкости в турбулентную струю из зоны покоя объясняется, помимо турбулентного перемешивания, наличием минимума давления внутри струи по сравнению с давлением вне струи. В результате подсос оказывается нелинейным процессом, но пассивным по своей природе.

Найденные решения удовлетворительно совпадают с экспериментальными данными различных авторов почти на всей толщине изучаемых струй, что позволяет говорить о распределенном характере генерации турбулентности в зоне малых скоростей.

Авторы выражают благодарность Вик. В. Сычеву и Г.Н. Дудину за активные обсуждения во время выполнения исследования и Т.В. Хохловой за помощь в оформлении графиков.

Список литературы

Miller D.R., Comings E.W. Static pressure distributionin the free turbulent jet // J. Fluid Mech. 1957. V. 3. № 1. P. 1–16.
Bradbury L.J.S. The structure of a self-preserving turbulent plane jet // J. Fluid Mech. 1965. V. 23. № 1. P. 31–64.
Rodi W. A Review of Experimental Data on Uniform Density, Free Turbulent Boundary Layers / 1975. Studies in Convection 1. Launder B. E. (Ed.).
Gutmark E., Wygnanski I. The planar turbulent jet // J. Fluid Mech. 1976. V. 3. № 3. P. 465–495.
Deo R.C., Mi J., Nathan G.J. The influence of nozzle aspect ratio on plane jets // Experimental Thermal and Fluid Science. 2007. V. 31. P. 825–838.
Гиневский А.С. Теория турбулентных струй и следов. М.: Машиностроение, 1969. 400 с.
Абрамович Г.Н., Гиршович Т.А., Крашенинников С.Ю., Секундов А.Н., Смирнова И.П. Теория турбулентных струй / Под ред. Г.Н. Абрамовича. М.: Наука, 1984. 717 с.
Schneider W. Boundary-layer theory of free turbulent shear flows // Z. Flugwiss. Weltraumforsch. (J. Flight Sci. Space Res.). 1991. V. 15. № 3. P. 143–158.
Вигдорович И.И. Тепловой турбулентный пограничный слой на пластине. Аналогия Рейнольдса и закон теплопередачи во всем диапазоне числа Прандтля // Изв. РАН. МЖГ. 2018. № 5. С. 38–52.
Scheichl B. Time-mean Turbulent Shear Flows: Classical Modelling–Asymptotic Analysis–New Perspectives // May 2016, In book: Fluid and Solid Mechanics. P. 71–108. doi 10.1142/9781786340276_0003
Zametaev V.B., Gorbushin A.R. Evolution of vortices in 2D boundary layer and in the Couette flow // AIP Conf. Proc. 2016. 1770. 030044. doi 10.1063/1.4963986
Горбушин А.Р., Заметаев В.Б. Асимптотический анализ вязких пульсаций в турбулентном пограничном слое // Изв. РАН. МЖГ. 2018. № 1. С. 11–22.
Schlichting H. Berechnung ebener periodischer Grenzschichtstromungen // Physikal. Z. 1932. Bd. 33. P. 327–335.
Tatsuno M. Secondary flow induced by a circular cylinder performing unharmonic oscillations // J. Phys. Soc. Jpn. 1981. 50. P. 330–337.
Lin C.C. Motion in the boundary layer with a rapidly oscillating external flow // Proc. 9^th Intern. Congress Appl. Mech. 1957. Brussels. V. 4. P. 155–167.
Pedley T.J. Two-dimensional boundary layers in a free stream which oscillates without reversing // J. Fluid Mech. 1972. V. 55. P. 359–383.
Юдович В.И. Пример рождения вторичного стационарного или периодического течения при потере устойчивости ламинарного течения вязкой несжимаемой жидкости // ПММ. 1965. Т. 29. № 3. С. 453–467.
Stewartson K. The theory of unsteady laminar boundary layers // Advances in Appl. Mechanics. 1960. V. 6. P. 1–37.
Riley N. Unsteady laminar boundary layers // SIAM Review. 1975. V. 17. P. 274–297.
Reynolds O. On the dynamic theory of incompressible viscous fluids and the determination of the criterion // Phil. Trans. Roy. Soc. 1895. V. 186. A 123.
Колмогоров А.Н. Локальная структура турбулентности в несжимаемой жидкости при очень больших числах Рейнольдса // Докл. АН СССР. 1941. Т. 30. № 4. С. 299–303.
Rayleigh L. On the stability, or instability, of certain fluid motions // Sci. Papers. Cambridge: Univ. Press. 1880. V. 1. P. 474–487.
Drazin P.G., Reid W.H. Hydrodynamic_Stability / Second Ed. Cambridge Univ. Press, 2004.
Head M.R. Entrainment in the Turbulent Boundary Layer // R. & M. № 3152. 1960. ARC Technical Report.
Brown G.L., Roshko A. On density effects and large structure in turbulent mixing layers // J. Fluid Mech. 1974. V. 64. № 4. P. 775–816.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал