Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 59-71
стоксово течение в микроканале с супергидрофобными стенками
А. И. Агеев a, А. Н. Осипцов a, *
a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
* E-mail: osiptsov@imec.msu.ru
Поступила в редакцию 18.10.2018
После доработки 18.10.2018
Принята к публикации 19.10.2018
Аннотация
Проведено численное моделирование медленного течения вязкой жидкости в плоском микроканале, обе стенки которого являются текстурированными супергидрофобными поверхностями. Полосчатая текстура супергидрофобных поверхностей образована периодически расположенными бесконечными прямоугольными микрокавернами, ориентированными перпендикулярно течению и полностью либо частично заполненными газом. Рассмотрены случаи как симметричного, так и несимметричного расположения микрокаверн на нижней и верхней стенках канала. Для решения уравнений Стокса в области, соответствующей одному периоду течения, использован метод граничных интегральных уравнений. Построены картины течения и проведено параметрическое численное исследование влияния газовых пузырьков, удерживаемых супергидрофобными стенками, на интенсивность эффективного проскальзывания жидкости и снижение трения (перепада давления) в микроканале.
Супергидрофобные поверхности обладают важными для практических приложений свойствами, связанными с их очень низкой смачиваемостью, способностью к самоочистке и снижению гидродинамического сопротивления. Многочисленные эксперименты свидетельствуют, что при напорном течении вязкой жидкости в микроканале с одной или двумя супергидрофобными стенками происходит заметное снижение осредненного трения (или перепада давления) по сравнению с течением в таком же канале с обычными стенками [1]. Снижение трения наблюдается как при ламинарном, так и при турбулентном режимах течения вдоль супергидрофобных поверхностей [2]. Такие поверхности имеют шероховатость (текстуру), образованную системой микрокаверн либо микровыступов, внутри (или между) которых стабильно удерживаются пузырьки воздуха или жидкость с меньшей динамической вязкостью [3, 4]. Характерные линейные размеры элементов текстуры поверхности составляют от одного до сотен микрометров, поэтому пузырьки воздуха в микрокавернах могут стабильно удерживаться за счет сил поверхностного натяжения. На образующейся устойчивой межфазной границе между жидкостью и газом (форма которой, как правило, совпадает со статической формой) трение практически отсутствует. Поэтому осредненное макроскопическое трение на супергидрофобной поверхности заметно снижено, а эффективная скорость проскальзывания жидкости на ней не равняется нулю. Столь необычные свойства делают текстурированные супергидрофобные поверхности предметом интенсивных междисциплинарных исследований.
Для описания важных для гидродинамики эффективных свойств супергидрофобных поверхностей используется тензор эффективной длины скольжения $b_{{ij}}^{*}$. Компоненты тензора скольжения имеют размерность длины. Для большинства используемых на практике супергидрофобных поверхностей с периодической текстурой тензор скольжения есть симметричная матрица второго порядка. Тензор эффективной длины скольжения входит в эффективное граничное условие проскальзывания типа Навье [5]
Здесь $u_{{\tau j}}^{*}$ – компоненты вектора осредненной скорости жидкости, касательные к поверхности, $n{\text{*}}$ – направление внешней нормали к поверхности. Это соотношение записано в локальном ортонормированном базисе, связанном с рассматриваемой точкой поверхности. Такое граничное условие применяется при осредненном описании течения вязкой жидкости на масштабе, значительно превышающем размер шероховатости текстуры [6]. В случае одномерного течения поперек или вдоль полосчатой текстуры существенен единственный коэффициент тензора скольжения $(b_{{ii}}^{*} = b{\text{*}})$, часто называемый эффективной длиной скольжения. Естественно ожидать, что влияние проскальзывания будет изменять осредненный профиль скорости потока на расстояниях от поверхности порядка $b{\text{*}}$. Для практических приложений необходимо уметь вычислять значения компонент тензора эффективной длины скольжения для заданного режима течения и проводить оценку снижения осредненного трения или перепада давления за счет использования супергидрофобных поверхностей. Для однородных супергидрофобных поверхностей с периодической текстурой математическая задача о стоксовом течении жидкости под некоторым углом к текстуре поверхности разделяется на две задачи, соответствующие течениям вдоль главных направлений тензора эффективной длины скольжения. В таком случае достаточно вычислить только главные значения тензора скольжения, соответствующие собственным направлениям. Главные значения тензора скольжения можно вычислить из решения задачи на микромасштабе, то есть задачи обтекания вязкой жидкостью элемента периодической текстуры супергидрофобной поверхности, и последующего осреднения рассчитанного поля скорости. В основном, в литературе рассматриваются текстуры, образованные периодической системой бесконечных прямоугольных микрокаверн, полностью занятых газом или другой маловязкой жидкостью, при этом межфазная граница для простоты принимается плоской. Решение такой задачи для скорости в приближении Стокса с периодическими граничными условиями удается получить разложением в ряд Фурье или с использованием теории функций комплексного переменного [7–10]. Однако вычисленная величина эффективной длины скольжения и снижение трения, полученные при таких предположениях, дают слишком завышенные значения по сравнению с результатами имеющихся экспериментальных измерений. Экспериментальные наблюдения течения на масштабе каверн показывают, что форма поверхности пузырька искривлена, а каверна может быть лишь частично заполнена газом, то есть положение мениска может не совпадать с угловыми точками микрокаверны. Эти факторы могут приводить к заметному снижению эффективного скольжения, а для пузырьков, выступающих в область жидкости, даже к увеличению трения на супергидрофобных поверхностях [11–14]. В расчетах при вычислении эффективной длины скольжения кривизну поверхности пузырька и/или смещение мениска в каверну стали учитывать сравнительно недавно.
Асимптотические решения задач продольного и поперечного обтекания сдвиговым потоком очень разреженной полосчатой текстуры супергидрофобной поверхности с учетом кривизны поверхности газовых пузырьков получены в [15, 16]. Эффективная длина скольжения в [15, 16] найдена как функция статического угла смачивания или, что эквивалентно, радиуса кривизны межфазной границы. Результаты численного моделирования течения вязкой жидкости в микроканале, имеющем супергидрофобную стенку с искривленными границами пузырьков [17], на основе полных уравнений Навье–Стокса качественно подтверждают найденную зависимость эффективной длины скольжения от статического угла смачивания, полученную в [15, 16]. Одновременный учет кривизны мениска и сдвига межфазной границы в каверну для течения в микроканале и сдвигового течения Куэтта вблизи супергидрофобной стенки в приближении Стокса проведен в [18, 19].
Сложность численного решения гидродинамических задач на масштабе текстуры супергидрофобной поверхности с помощью конечно-разностных методов заключается в необходимости дискретизации уравнений движения и смешанных граничных условий в области со сложной геометрией, содержащей межфазную границу. Дополнительные трудности возникают при аппроксимации граничных условий в точках сопряжения граничных условий прилипания и проскальзывания, где производные искомых функций могут иметь сингулярности. В связи с этим для моделирования течения вязкой жидкости вблизи супергидрофобной поверхности и вычисления поля скорости жидкости необходимо разрабатывать альтернативные методы расчета. Как отмечалось, размер неоднородности текстуры супергидрофобной поверхности не превосходит несколько десятков микрометров. Поэтому числа Рейнольдса, характеризующие локальное течение вязкой жидкости в окрестности элементов текстуры, малы, и для моделирования течений на микромасштабе практически всегда можно использовать приближение Стокса.
Настоящая работа является продолжением исследований [18, 19], в которых для медленных течений вязкой жидкости вблизи супергидрофобных поверхностей применен метод граничных интегральных уравнений [20] и разработаны соответствующие численные алгоритмы. В [18, 19] продемонстрирована эффективность метода граничных интегральных уравнений для вычисления эффективной длины скольжения, в том числе, для оценки снижения трения в микроканале с одной супергидрофобной стенкой. Кроме того, в [19] было показано, что в течениях с существенными продольными градиентами давления учет сжимаемости газа может приводить к неоднородному сдвигу менисков в микрокаверны и значительному ухудшению гидродинамических свойств супергидрофобных поверхностей. В самые последние годы метод граничных интегральных уравнений стал применяться для исследования обтекания элементов микроструктуры супергидрофобных поверхностей и в работах других авторов (см., например, [21, 22]).
В настоящей работе рассматривается течение вязкой жидкости в микроканале, образованном двумя супергидрофобными стенками, имеющими, в общем случае, различные геометрические параметры полосчатой текстуры и различные формы и положения менисков. Численно исследованы поля скоростей и картины линий тока в области, соответствующей одному периоду течения, и изучено взаимное влияние двух супергидрофобных стенок канала на величины эффективного проскальзывания и перепада давления. Исследование течений вязкой жидкости в микроканалах с двумя супергидрофобными стенками представляет практический интерес для управления течениями в различных устройствах микрофлюидики, сепараторах микрочастиц, биомеханичеких и медицинских приложениях.
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается установившееся стоксово течение вязкой жидкости в плоском канале, обе стенки которого являются текстурированными супергидрофобными поверхностями, содержащими бесконечные прямоугольные микрокаверны, частично или полностью заполненные газом. На каждой стенке канала текстура является периодической, но геометрические характеристики текстуры (ширина и глубина каверн, расстояние между кавернами, радиусы кривизны менисков межфазной поверхности и глубина смещения менисков в каверну) могут быть различными. В общем случае каверны на верхней и нижней стенках канала расположены несимметрично, однако расстояния между кавернами на противоположных стенках канала отличаются не очень сильно, так что можно выделить масштаб длины L, соответствующий одному периоду течения, на котором имеется по одной каверне внизу и вверху. Расход жидкости в канале считается фиксированным и известным, поверхности газовых пузырей могут быть выпуклы как внутрь каверн, так и внутрь жидкости. Так как отношение динамических вязкостей газа и жидкости мало ${{{{\mu }_{g}}} \mathord{\left/ {\vphantom {{{{\mu }_{g}}} {{{\mu }_{f}}}}} \right. \kern-0em} {{{\mu }_{f}}}} \ll 1$, трением между жидкостью и газом пренебрегается. Схема течения показана на рис. 1, где $H$ – толщина канала, ${{d}_{{1,2}}}$ – ширина микрокаверн на нижней и верхней стенках канала, $R_{{1,2}}^{*}$ и ${{\delta }_{{1,2}}}$ – размерный радиус кривизны поверхности пузырька и смещение точек закрепления мениска в микрокаверну. Величины ${{\delta }_{{1,2}}}$ определяются массой газа, удерживаемого в микрокаверне, и статическим давлением в жидкости [19]. Положение точек закрепления мениска ${{\delta }_{{1,2}}}$ на рассматриваемом масштабе считается фиксированным. Изменение давления вдоль мениска, обусловленное движением жидкости, значительно меньше, чем разность статических давлений в жидкости и пузырьке воздуха в каверне [18]. Поэтому форма поверхности газового пузыря такая же, как в статике. С высокой точностью она может быть аппроксимирована элементом дуги окружности. Размерный радиус кривизны $R_{{1,2}}^{*}$ элемента дуги окружности определяется статическим углом смачивания ${{\theta }_{{1,2}}}$ в точках закрепления мениска со стенками микрокаверны, для конкретной супергидрофобной поверхности этот угол может быть определен экспериментально.
Рис. 1.
Схема течения вязкой жидкости в области, соответствующей одному периоду течения в микроканале, образованном двумя супергидрофобными поверхностями с прямоугольными кавернами
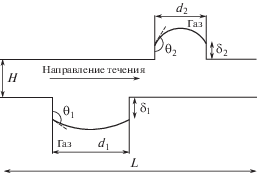
Для описания течения жидкости вводится декартова система координат $xOy$ с началом координат, расположенным на нижней стенке в середине области периодического течения, имеющей длину $L$. Через $r* = (x*,y{\text{*}})$ обозначим размерный радиус-вектор точки относительно выбранной системы координат. При обезразмеривании все величины, имеющие размерность длины, отнесены к длине периода $L$. После процедуры обезразмеривания уравнение линии, описывающей форму поверхности пузырька, расположенного на нижней стенке, принимает вид:
Уравнение для формы поверхности пузырька, расположенного на верхней стенке:
Здесь ${{R}_{{1,2}}}$ – безразмерный (отнесенный к L) радиус кривизны поверхности пузырька, c1, 2 = = ${{{{d}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{d}_{{1,2}}}} {2L}}} \right. \kern-0em} {2L}}$ – безразмерная половина ширины каверны с газом, ${{s}_{{1,2}}} = {{{{\delta }_{{1,2}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{1,2}}}} L}} \right. \kern-0em} L}$ – безразмерный сдвиг мениска в каверну, ${{x}_{{1,2}}}$ – безразмерное смещение центра каверны относительно середины области периодического течения в канале. Значения ${{x}_{{1,2}}} = 0$ соответствуют “стандартному” расположению каверны в середине выбранного периода течения, обычно рассматриваемому в литературе. Выбор верхних или нижних знаков в полученных уравнениях зависит от направления выпуклости поверхностей пузырьков: внутрь каверны или в сторону основного потока жидкости. Заметим, что в зависимости от химических свойств верхней и нижней стенок канала возможны ситуации, когда газовые пузырьки на верхней и нижней стенках выпуклы как в одном, так и в противоположном направлениях.
Пусть $Q{\text{*}}$ – заданный размерный объемный расход жидкости на единицу “ширины” канала. В качестве масштаба скорости $U$ выберем ${{12Q{\text{*}}{{L}^{2}}} \mathord{\left/ {\vphantom {{12Q{\text{*}}{{L}^{2}}} {{{H}^{3}}}}} \right. \kern-0em} {{{H}^{3}}}}$, для давления выберем масштаб ${{\rho \nu U} \mathord{\left/ {\vphantom {{\rho \nu U} L}} \right. \kern-0em} L}$, где $\rho $ – плотность, а $\nu $ – кинематическая вязкость жидкости. Масштаб скорости выбран из условия, чтобы безразмерный перепад давления на длине $L$ в канале с обычными стенками (в течении Пуазейля) был равен единице. Число Рейнольдса для рассматриваемого класса течений в микроканале записывается в виде $\operatorname{Re} = {{UL} \mathord{\left/ {\vphantom {{UL} \nu }} \right. \kern-0em} \nu }$. После процедуры обезразмеривания уравнений Навье-Стокса с использованием выбранных масштабов в пределе при $\operatorname{Re} \to 0$ получаем линейные уравнения Стокса:
(1.1)
$\begin{array}{*{20}{c}} {{{\nabla }^{2}}u - \nabla p = 0,\quad }&{\nabla \cdot u = 0} \end{array}$Здесь $u = \left( {u,v} \right)$ – двумерное поле скорости жидкости, $p$ – поле давления, $\nabla $ – оператор набла в декартовой системе координат. Для устройств микрофлюидики, в которых эффект снижения трения с использованием СГП наиболее заметен, число Рейнольдса составляет доли единицы.
Математическая постановка задачи о течении вязкой жидкости в рассматриваемой двумерной области, соответствующей одному периоду течения, завершается заданием необходимых граничных условий на всей границе области течения, показанной на рис. 1. На твердых стенках ставится условие прилипания для скорости $u = 0$; на входном и выходном сечениях расчетной области при $x = \mp 0.5$ задаются периодические граничные условия для вектора скорости
Равенство производных по x на входе и выходе обеспечивает гладкость искомого периодического решения. На поверхности пузырька требуется выполнение кинематического условия непротекания для скорости $u \cdot n = 0$ и динамического условия отсутствия касательных напряжений ${{\sigma }_{{ij}}}{{n}_{j}}{{\tau }_{i}} = 0$, где ${{n}_{j}}$ и ${{\tau }_{i}}$ – компоненты единичной нормали к межфазной границе, направленной в жидкость, и касательного вектора на межфазной границе, ${{\sigma }_{{ij}}}$ – тензор напряжений в жидкости. Для определения периодического профиля скорости, вырабатывающегося при течении в канале с двумя супергидрофобными стенками, применяется следующая итерационная процедура. Сначала на входном сечении расчетной области задается стандартный профиль Пуазейля $({{u}_{0}}(y),{{v}_{0}}(y)) = ( - {{y}^{2}}{\text{/}}2 + {{yH} \mathord{\left/ {\vphantom {{yH} {2L}}} \right. \kern-0em} {2L}}$, 0), а на выходе – условие равенства нормальных производных соответствующим производным во входном сечении. Решается полученная математическая задача и определяется профиль скорости на выходе из расчетной области. Затем вычисленный профиль скорости задается во входном сечении расчетной области, а на выходном – условие для производных. Итерации продолжаются до тех пор, пока не будет достигнуто равенство профилей скорости во входном и выходном сечениях с заданной точностью.
В [18] показано, что для течения вязкой жидкости в канале с одной супергидрофобной стенкой, имеющей разреженную систему каверн, задание на входе и выходе из расчетной области стандартного профиля скорости Пуазейля дает удовлетворительное согласие с расчетами. Имеются ввиду расчеты, в которых задавался корректный периодический профиль скорости, полученный из решения задачи обтекания нескольких последовательно расположенных каверн. Использование в расчетах профиля Пуазейля во входном и выходном сечениях расчетной области, по-видимому, также допустимо для разреженных текстур супергидрофобной поверхности и каверн, не смещенных относительно середины периода $x = 0$ (для рассматриваемого случая двух супергидрофобных стенок канала). Однако периодический профиль скорости необходимо предварительно определять численно, когда относительная ширина каверн ${{d{}_{{1,2}}} \mathord{\left/ {\vphantom {{d{}_{{1,2}}} L}} \right. \kern-0em} L} > 0.5$ и/или каверны смещены относительно $x = 0$.
Как и в [18, 19], для решения сформулированной математической задачи в области, содержащей межфазную границу, с заданными на границе расчетной области смешанными граничными условиями применяется метод граничных интегральных уравнений (МГИУ) [20]. Данный метод имеет существенные преимущества по сравнению с конечно-разностными методами решения уравнений Стокса, поскольку позволяет снизить на единицу размерность исходной задачи и избежать проблем, связанных с конечно-разностной аппроксимацией бесконечных производных параметров вблизи точек сопряжения граничных условий прилипания и проскальзывания. Согласно методу граничных интегральных уравнений [20] поле скорости жидкости $u$, удовлетворяющее уравнениям (1.1), может быть получено сверткой фундаментальных решений оператора Стокса с некоторыми их заранее неизвестными плотностями, распределенными по границе области течения:
(1.2)
$\begin{array}{*{20}{c}} {\Lambda {{u}_{j}}\left( {{{x}_{0}}} \right) = - \frac{1}{{4\pi }}\int\limits_\Gamma {{{f}_{i}}\left( x \right){{G}_{{ij}}}\left( {x,{{x}_{0}}} \right)dl\left( x \right)} + \frac{1}{{4\pi }}\int\limits_\Gamma {{{u}_{i}}\left( x \right){{T}_{{ijk}}}\left( {x,{{x}_{0}}} \right){{n}_{k}}\left( x \right)dl\left( x \right)} } \\ {\begin{array}{*{20}{c}} {{{G}_{{ij}}} = - {{\delta }_{{ij}}}\ln r + \frac{{{{\xi }_{i}}{{\xi }_{j}}}}{{{{r}^{2}}}},}&{{{T}_{{ijk}}} = - 4\frac{{{{\xi }_{i}}{{\xi }_{j}}{{\xi }_{k}}}}{{{{r}^{4}}}}} \end{array}} \\ {\begin{array}{*{20}{c}} {\xi = x - {{x}_{0}},}&{r = {\text{|}}\xi {\text{|}}} \end{array}} \end{array}$Здесь ${{G}_{{ij}}}\left( {x,{{x}_{0}}} \right)$ и ${{T}_{{ijk}}}\left( {x,{{x}_{0}}} \right)$ – фундаментальные решения “стокслет” и “стресслет” [20]; $x$ и ${{x}_{0}}$ – точки, лежащие на границе или внутри расчетной области соответственно; $\Lambda $ равняется 1/2 или 1 для граничных или внутренних точек расчетной области; $\Gamma $ – граница расчетной области; $f = {{\sigma }_{{ij}}}{{n}_{j}}{{e}_{i}}$ – вектор напряжений; $i$, $j$ и $k$ равняются 1 или 2; по повторяющимся индексам производится суммирование.
Помимо [18, 19], в последнее время метод граничных интегральных уравнений начал применяться и в других работах для численного моделирования течения вязкой жидкости вблизи супергидрофобных поверхностей. Например, в [21] использован вариант метода граничных уравнений для бигармонического уравнения, решение для которого строится в переменных “функция тока – завихренность”. В [21] рассмотрен только случай плоской межфазной границы, закрепленной в углах каверны. В [22] метод граничных интегральных уравнений применен для исследования стоксова течения жидкости над каверной, заполненной другой вязкой жидкостью при конечном отношении вязкостей.
Формула (1.2) позволяет по заданным плотностям фундаментальных решений, распределенным по границе расчетной области, вычислить скорости жидкости в любой точке области течения. Неизвестные значения плотностей, распределенные по границе области, определяются из решения интегральных уравнений, записанных для граничных точек при $\Lambda = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, с использованием заданных граничных условий. Граничные интегральные уравнения могут быть решены только численно. Для их решения применяется метод коллокаций. Согласно методу коллокаций исходная граница расчетной области заменяется замкнутой ломаной, образованной прямолинейными элементами. Интегралы, входящие в (1.2), с использованием метода коллокаций заменяются дискретной суммой интегралов по всем элементам, образующим границу области, а интегральные уравнения сводятся к системе линейных алгебраических уравнений относительно неизвестных значений компонент векторов $u$ и $f$, заданных на элементах разбиения границы. В использованном при расчетах варианте метода коллокаций предполагалось, что искомые функции (компоненты векторов $u$ и $f$) постоянны на длине элемента и равны их значениям в серединах элементов. Компоненты касательного вектора и внутренней нормали к межфазной границе также вычислялись в середине элементов. При решении граничных интегральных уравнений, соответствующих граничным точкам, при $\left| {x - {{x}_{0}}} \right| \to 0$ под интегралами возникают сингулярности логарифмического типа и типа 1/r. С помощью введения локальной системы координат, связанной с серединой элемента, вклад окрестностей сингулярных точек вычисляется аналитически (см. детали в [23]). К полученной системе линейных алгебраических уравнений необходимо добавить уравнения, соответствующие граничным условиям, заданным на межфазной границе [18] и на входном/выходном сечениях канала, которые понимаются в смысле уравнений, записанных для граничных точек. Периодические граничные условия для точек, лежащих на входном/выходном сечениях расчетной области, с использованием формулы (1.2) и $\Lambda = 1$ заменяются разностным аналогом. Он записывается для каждой точки входного/выходного сечения расчетной области и добавляется к системе линейных алгебраических уравнений в качестве дополнительных уравнений для неизвестных компонент вектора скорости $u$. Получаемая в итоге система линейных алгебраических уравнений (СЛАУ) высокого порядка решается стандартным методом Гаусса. После нахождения неизвестных компонент векторов $u$ и $f$ поле скорости жидкости во внутренних точках вычисляется по формуле (1.2) с $\Lambda = 1$. При численной реализации метода граничных интегральных уравнений (МГИУ) использовались разбиения границы расчетной области, при которых суммарное количество прямолинейных элементов было порядка 500. Для вычисления интегралов вдоль элементов при $\left| {x - {{x}_{0}}} \right| \ne 0$ использовалась квадратурная формула пятого порядка точности. Периодические граничные условия, содержащие производные по координате $x$, аппроксимировались направленными разностями со вторым порядком точности. Шаг дискретизации производных $\Delta h$ равнялся 0.005. Отметим, что все производные, возникающие при численном решении сформулированной математической задачи, аппроксимировались со вторым порядком точности. Это позволило проводить расчеты с точностью до двух значащих цифр.
Безразмерная (отнесенная к L) осредненная длина скольжения для случая одинаковых каверн, симметрично расположенных относительно x = 0, может быть вычислена двумя способами. Когда пузырьки выпуклы внутрь каверн, осредненную длину скольжения можно вычислить непосредственно по формуле $b = {{\left\langle {{{u}_{w}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{u}_{w}}} \right\rangle } {\left( {{{{\left\langle {{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}} \right\rangle }}_{w}}} \right)}}} \right. \kern-0em} {\left( {{{{\left\langle {{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}} \right\rangle }}_{w}}} \right)}}$. Здесь $\left\langle \cdot \right\rangle $ обозначает операцию осреднения по длине периода текстуры, содержащего каверны, индекс $w$ соответствует параметрам, вычисляемым на линии, проходящей через углы каверн. В ситуации, когда поверхность пузырьков выпукла в направлении основного потока жидкости, можно привлечь решение задачи о течении вязкой жидкости в плоском канале длиной $L$ с условием проскальзывания Навье и получить связь между перепадом давления и величиной $b{\text{*}}$. В безразмерной форме эта связь имеет вид (длина проскальзывания отнесена к L):
Здесь $\Delta p = {{p}_{{in}}} - {{p}_{{out}}}$, а ${{p}_{{in}}}$ и ${{p}_{{out}}}$ суть безразмерные значения давления во входном и выходном сечениях расчетной области.
В общем случае, когда микрокаверны, полностью или частично заполненные газовыми пузырьками разной формы, несимметрично расположены относительно $x = 0$, говорить об эффективной длине скольжения не имеет смысла. Однако из решения сформулированной математической задачи можно определить величину снижения трения (перепада давления), обусловленного проскальзыванием жидкости на поверхностях пузырьков.
В случае, когда пузырьки выпуклы в глубь каверн, для вычисления перепада давления можно использовать интегральное условие сохранения импульса. Для установившегося течения вязкой жидкости в рассматриваемой области закон сохранения импульса записывается в виде
В качестве контрольного объема рассмотрим прямоугольную область, образованную входным и выходным сечениями, прямолинейными участками твердых стенок канала и прямыми, соединяющими угловые точки микрокаверн. После разбиения границы контрольного объема на участки входного сечения, верхней стенки, выходного сечения и нижней стенки, а также использования выражения для компонент тензора напряжений вязкой жидкости, можно записать в безразмерной форме интегральный закон сохранения продольной компоненты количества движения жидкости для выбранного контрольного объема
(1.3)
$\begin{array}{*{20}{c}} {\int\limits_{botwall} {\left( {\frac{{\partial u}}{{\partial y}}} \right)dl} + \int\limits_{botcavity} {\left( {\frac{{\partial v}}{{\partial x}}} \right)dl} + \int\limits_{botcavity} {\left( {uv} \right)dl} - } \\ { - \int\limits_{upwall} {\left( {\frac{{\partial u}}{{\partial y}}} \right)dl} - \int\limits_{upcavity} {\left( {\frac{{\partial v}}{{\partial x}}} \right)dl} - \int\limits_{upcavity} {\left( {uv} \right)dl} = \left( {{{p}_{{in}}} - {{p}_{{out}}}} \right)\frac{H}{L}} \end{array}$Здесь botcavity и upcavity – прямолинейные участки границы контрольного объема, проходящие через угловые точки микроскопических каверн. Области botwall и upwall – прямолинейные участки между кавернами (на нижней и верхней стенках канала). Интегрируя рассчитанные значения компонент скорости и их производных по соответствующим линиям, получаем безразмерный перепад давления (${{p}_{{in}}} - {{p}_{{out}}}$) на одном периоде течения в микроканале. При наличии поперечных градиентов давления во входном и выходном сечениях ${{p}_{{in}}}$ и ${{p}_{{out}}}$ обозначают средние по соответствующим сечениям значения безразмерного давления. Такой подход позволяет оценить снижение перепада давления, обусловленное наличием пузырьков воздуха в микрокавернах, при заданном фиксированном расходе жидкости. В расчетах производные под интегралами аппроксимировались со вторым порядком точности с использованием центральных или направленных разностей.
Средний перепад давления (${{p}_{{in}}} - {{p}_{{out}}}$) может быть также вычислен после нахождения поля скорости с помощью интегрирования уравнения импульса в проекции на ось $Ox$ вдоль средней линии канала с заданным значением давления на левой границе
Интегрируя указанное уравнение от $x = - 0.5$ до 0.5 при $y = {H \mathord{\left/ {\vphantom {H {2L}}} \right. \kern-0em} {2L}}$, получаем значение ${{p}_{{out}}}$ на выходе. Такой подход применим и в случае, когда пузырьки выпуклы внутрь канала в общем случае их несимметричного расположения, при наличии вертикальных градиентов давления во входном и выходном сечениях. В принципе, интегрирование здесь можно вести по любой линии $y = const$, не пересекающей поверхность пузырьков, поскольку интегралы от давления по $y$, вычисленные по одинаковым отрезкам входного и выходного сечений, для любой длины отрезка отличаются на одну и ту же константу (равную ${{p}_{{in}}} - {{p}_{{out}}}$) в силу периодичности профиля скорости и ее производных.
2. РЕЗУЛЬТАТЫ РАСЧЕТОВ ДЛЯ СИММЕТРИЧНО РАСПОЛОЖЕННЫХ ОДИНАКОВЫХ КАВЕРН
В данном разделе рассматривается случай одинаковых каверн, симметрично расположенных на верхней и нижней стенках канала (${{x}_{{1,2}}} = 0$). Для такой геометрии текстуры супергидрофобных стенок канала можно вычислить интенсивность снижения перепада давления $\Delta p$ и осредненную безразмерную длину скольжения $b = {{b{\text{*}}} \mathord{\left/ {\vphantom {{b{\text{*}}} L}} \right. \kern-0em} L}$ для обеих стенок.
На рис. 2 представлены результаты расчетов безразмерного перепада давления $\Delta p$ (а) и осредненной безразмерной длины скольжения $b$ (б) в канале с двумя супергидрофобными стенками, соответствующие одинаковым пузырькам, выпуклым внутрь каверн, когда ${{\theta }_{1}} = {{\theta }_{2}}$ и ${{s}_{1}}_{{,2}} = 0$ (для ряда значений геометрических параметров текстуры). Здесь также показаны результаты расчетов, соответствующие течению в канале с текстурированными стенками, имеющими каверны, полностью заполненные жидкостью. Предполагается, что нижняя граница каверн в этом случае является твердой стенкой с условием прилипания, форма нижней стенки каверны совпадает с формой пузырьков в первом случае. Как видно на рис. 2а, наличие каверн одновременно на верхней и нижней супергидрофобных стенках канала, содержащих газовые пузырьки, приводит к значительному снижению приложенного перепада давления (в случае гладких плоских стенок с условием прилипания перепад давления равен единице). Интересно, что величина снижения перепада давления в канале, образованном двумя супергидрофобными поверхностями, содержащими газовые пузырьки с минимальным радиусом кривизны поверхности ${{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}} = {{{{R}_{2}}} \mathord{\left/ {\vphantom {{{{R}_{2}}} {{{c}_{2}} = 1}}} \right. \kern-0em} {{{c}_{2}} = 1}}$, и в канале с кавернами, полностью заполненными жидкостью и имеющими форму границы пузырьков, принимает практически одинаковые значения. Таким образом, снижения сопротивления в микроканале (перепада давления) в десятки процентов можно достичь лишь за счет создания микрорельефа на стенках канала в отсутствие газовых пузырьков. Дополнительная гидрофобизация поверхности и наличие в кавернах газовых пузырьков, как следует из рис. 2а, приводит к дальнейшему снижению перепада давления. Видно, что при выпрямлении межфазной границы происходит дополнительное снижение перепада давления в канале с супергидрофобными стенками, а при выпрямлении поверхности каверн в канале с обычными стенками перепад давления возрастает до значения, соответствующего каналу с плоскими стенками. В расчетах было получено, что при увеличении ширины канала H/L влияние проскальзывания на интенсивность снижения перепада давления для двух типов текстур уменьшается.
Рис. 2.
Зависимость безразмерного перепада давления $\Delta p$ в микроканале (а) и осредненной длины скольжения $b$ (б) для обеих стенок от кривизны межфазной границы: ${d \mathord{\left/ {\vphantom {d L}} \right. \kern-0em} L} = 0.5$, ${{\theta }_{1}} = {{\theta }_{2}}$, ${{x}_{{1,2}}} = 0$, ${{s}_{{1,2}}} = 0$ сплошные линии; ${H \mathord{\left/ {\vphantom {H L}} \right. \kern-0em} L}$ = 0.5, 1.0 (1, 2). Пунктирные линии соответствуют расчетам для случая текстурированной поверхности с кавернами, полностью заполненными жидкостью и совпадающими по форме с поверхностью пузырьков; на поверхности каверн ставилось условие прилипания
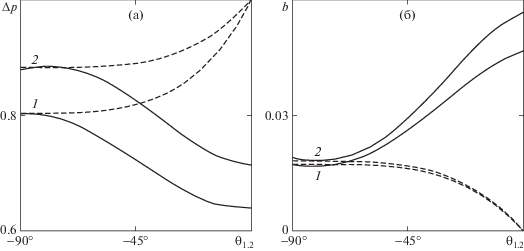
На рис. 2б представлены аналогичные расчеты осредненной длины скольжения b в канале с супергидрофобными стенками, содержащими газовые пузырьки, и в канале с полукруглыми кавернами, полностью заполненными жидкостью. Полученная зависимость длины скольжения для двух каверн, содержащих газовые пузырьки, качественно совпадает с результатами, опубликованными ранее для течения в канале с одной супергидрофобной стенкой. Видно, что значение эффективной длины скольжения, вычисленное для канала, содержащего каверны с пузырьками с минимальным радиусом кривизны, совпадает с соответствующим значением для канала с кавернами, полностью заполненными жидкостью. На основе параметрического исследования зависимости величины эффективной длины скольжения от формы межфазной границы было установлено, что значение длины скольжения для канала с двумя одинаковыми супергидрофобными стенками меньше соответствующего значения для канала с одной супергидрофобной стенкой.
Рисунок 3 иллюстрирует влияние смещения менисков, имеющих большой радиус кривизны, внутрь каверн. На этом рисунке представлены расчеты величины безразмерного перепада давления $\Delta p$ (а) и осредненной длины скольжения $b$ (б) в канале с двумя одинаковыми супергидрофобными стенками и со стенками, имеющими прямоугольные каверны, полностью заполненные жидкостью. В последнем случае величина $s$ есть просто глубина каверны, полностью заполненной жидкостью. Видно, что при наличии пузырьков смещение менисков внутрь каверн приводит к заметному ухудшению супергидрофобных свойств поверхности – происходят увеличение перепада давления и снижение эффективной длины скольжения по сравнению со случаем межфазной границы, закрепленной в верхних углах каверны. Кроме того, из представленных результатов следует, что увеличение глубины каверн, полностью заполненных жидкостью, приводит к снижению требуемого перепада давления и возникновению осредненного проскальзывания по сравнению с обычным каналом, имеющим гладкие стенки. При этом предельные (для $s \geqslant 0.15$) значения $\Delta p$ и $b$ для каверн, содержащих пузырьки газа, и каверн, полностью заполненных жидкостью, практически совпадают. Аналогичный результат был обнаружен ранее для канала с одной супергидрофобной стенкой в [18, 19].
Рис. 3.
Зависимость безразмерного перепада давления $\Delta p$ в микроканале (а) и осредненной длины скольжения $b$ (б) для обеих стенок от смещения менисков ${{s}_{{1,2}}} = s$ в каверны; параметры и обозначения такие же, как на рис. 2
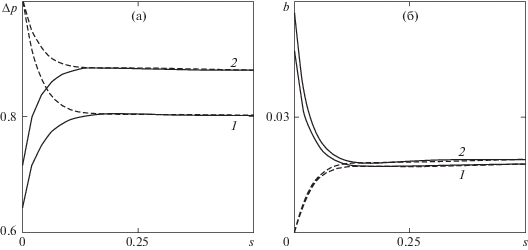
Для других форм поверхности газового пузырька (с меньшими радиусами кривизны) результаты расчетов качественно совпадают с представленными данными, однако при этом происходит заметное повышение перепада давления и уменьшение эффективной длины скольжения.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ ДЛЯ РАЗЛИЧНОЙ ГЕОМЕТРИИ КАВЕРН НА ПРОТИВОПОЛОЖНЫХ СТЕНКАХ КАНАЛА
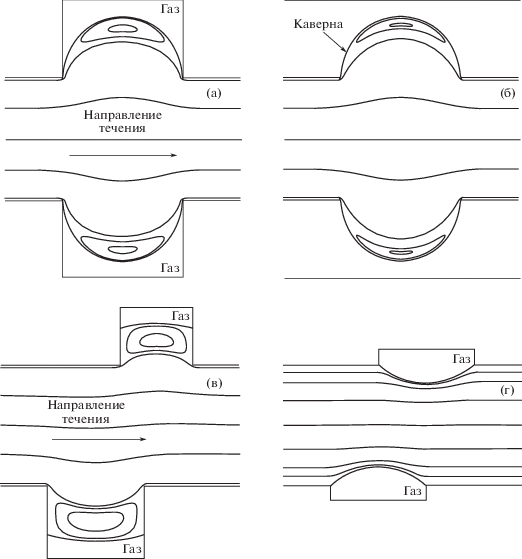
На рис. 4 для некоторых значений геометрических параметров каверн представлены картины линий тока в плоском канале, стенки которого образованы различными типами текстурированных поверхностей. На рис. 4а, б показаны соответственно картины линий тока в канале с двумя одинаковыми супергидрофобными стенками, содержащими газовые пузырьки, и в канале с кавернами, полностью заполненными жидкостью, совпадающими по форме с поверхностью пузырьков в первом случае. Видно, что в каверне с газовым пузырьком и в каверне, полностью заполненной жидкостью, образуются вихревые зоны. Параметрический численный анализ картин течения жидкости в канале показывает, что при увеличении ширины канала H/L вихревые зоны в обоих случаях увеличиваются и занимают практически всю область над межфазной границей или над нижней искривленной стенкой каверны [18]. Наличие проскальзывания на межфазной границе приводит к увеличению размера вихря по сравнению с каверной, заполненной жидкостью. Установлено, что так же, как и в случае одной каверны на нижней стенке [18], при выпрямлении межфазной границы вихри исчезают и жидкость движется вдоль стенок канала. Качественно похожие картины течения жидкости получены и для других значений доли газового участка. На рис. 4в, г для некоторых значений параметров представлены картины линий тока течения в канале с двумя различными супергидрофобными поверхностями. Для смещенных каверн также возможно образование вихревых зон в жидкости над газовыми пузырьками (рис. 4в).
Рис. 4.
Картины линий тока в канале с двумя текстурированными стенками: (а) – супергидрофобные стенки, содержащие одинаковые газовые пузырьки; (б) – каверны полностью заполнены жидкостью и имеют форму границы пузырьков, на всей границе каверны ставится условие прилипания, ${{{{d}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{d}_{{1,2}}}} L}} \right. \kern-0em} L} = 0.5$, ${{{{R}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{R}_{{1,2}}}} {{{c}_{{1,2}}}}}} \right. \kern-0em} {{{c}_{{1,2}}}}} = 1$, ${{x}_{{1,2}}} = 0$; (в) – супергидрофобные стенки с различными пузырьками, ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} L}} \right. \kern-0em} L} = 0.4$, ${{x}_{1}} = 0.1$, ${{s}_{1}} = 0.2$, ${{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} L}} \right. \kern-0em} L} = 0.3$, ${{x}_{2}} = 0.15$, ${{s}_{2}} = 0.15$, ${{{{R}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{R}_{{1,2}}}} {{{c}_{{1,2}}}}}} \right. \kern-0em} {{{c}_{{1,2}}}}} = 4$; (г) – супергидрофобные поверхности с одинаковыми пузырьками, выступающими в поток жидкости, ${{{{d}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{d}_{{1,2}}}} L}} \right. \kern-0em} L} = 0.4$, ${{{{R}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{R}_{{1,2}}}} {{{c}_{{1,2}}} = 1.5}}} \right. \kern-0em} {{{c}_{{1,2}}} = 1.5}}$, ${{x}_{{1,2}}} = 0.1$, ${{s}_{{1,2}}} = 0$; ${H \mathord{\left/ {\vphantom {H L}} \right. \kern-0em} L} = 0.5$
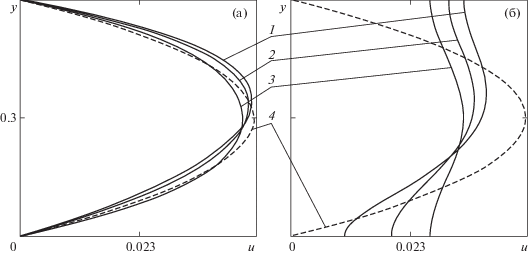
Проведено численное исследование формы периодического профиля скорости, вырабатывающегося на границах области периодичности в канале с различными супергидрофобными стенками. В качестве примера на рис. 5а представлен периодический профиль скорости в плоском канале, образованном двумя идеализированными супергидрофобными поверхностями, содержащими каверны, полностью заполненные газовыми пузырьками с плоской межфазной границей ${{\theta }_{{1,2}}} = 0^\circ $. Видно, что для выбранных значений параметров периодический профиль скорости, вырабатывающийся в канале, заметно отличается от стандартного профиля Пуазейля. В данном случае происходит отклонение профиля скорости в сторону стенки с большей каверной ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} L}} \right. \kern-0em} L} < {{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} L}} \right. \kern-0em} L}$, содержащей газовый пузырек. Для случая, представленного на рис. 5а, это соответствует каверне, расположенной на верхней стенке канала. Для бóльших долей газовых участков ${{{{d}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{d}_{{1,2}}}} L}} \right. \kern-0em} L}$ отклонение вырабатывающегося периодического профиля скорости от параболического становится более выраженным. При выравнивании ширины каверн с газовыми пузырьками на обеих стенках канала профиль скорости становится симметричным относительно линии ${{y = H} \mathord{\left/ {\vphantom {{y = H} {2L}}} \right. \kern-0em} {2L}}$, но при этом все еще заметно отличается от параболического. На рис. 5б показано распределение продольной компоненты скорости $u$ вдоль линии x = 0. Видно сильное влияние газовых пузырьков на форму профиля скорости в выбранном сечении. При малых долях газовых участков периодический профиль скорости на входном/выходном сечениях слабо отличается от стандартного параболического профиля скорости.
Рис. 5.
Периодический профиль скорости $u\left( y \right)$, вырабатывающийся в канале с двумя супергидрофобными стенками (а), и распределение продольной компоненты скорости в сечении $x = 0$ (б): ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} L}} \right. \kern-0em} L} = 0.2,\,\,0.4,\,\,0.6$ (1–3), ${{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} L}} \right. \kern-0em} L} = 0.6$, ${H \mathord{\left/ {\vphantom {H L}} \right. \kern-0em} L} = 0.6$, ${{\theta }_{{1,2}}} = {{0}^{ \circ }}$, ${{x}_{{1,2}}} = 0$, ${{s}_{{1,2}}} = 0$. Пунктир – стандартный профиль Пуазейля
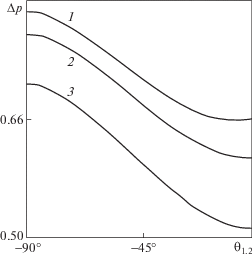
Результаты расчетов зависимости безразмерного перепада давления $\Delta p$ от статического угла смачивания в канале с двумя супергидрофобными стенками, содержащими каверны, полностью заполненные газом ${{s}_{{1,2}}} = 0$, представлены на рис. 6. Рассматривался случай, когда каверны имеют разную (или одинаковую) ширину и расположены одна над другой: ${{x}_{{1,2}}} = 0$. Одновременно варьировался статический угол смачивания для обеих каверн при ${{\theta }_{1}} = {{\theta }_{2}}$. Из представленных результатов видно, что при выпрямлении межфазной границы (${{\theta }_{{1,2}}} \to 0^\circ $) происходит значительное снижение перепада давления. Имеется в виду снижение по сравнению со случаем, когда межфазная граница имеет форму сегмента окружности с минимальными радиусами кривизны ${{{{R}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{R}_{{1,2}}}} {{{c}_{{1,2}}}}}} \right. \kern-0em} {{{c}_{{1,2}}}}}$ = 1. Кроме того, интенсивность снижения перепада давления в канале увеличивается, если каверны на обеих стенках геометрически совпадают: ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} L}} \right. \kern-0em} L} \to {{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} L}} \right. \kern-0em} L}$.
Рис. 6.
Зависимость перепада давления в микроканале с двумя супергидрофобными стенками от кривизны межфазной границы: ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} L}} \right. \kern-0em} L} = 0.6$, ${{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} L}} \right. \kern-0em} L} = 0.2,\,\,0.4,\,\,0.6$ (1–3), ${H \mathord{\left/ {\vphantom {H L}} \right. \kern-0em} L} = 0.5$, ${{\theta }_{1}} = {{\theta }_{2}}$, ${{x}_{{1,2}}} = 0$, ${{s}_{{1,2}}} = 0$
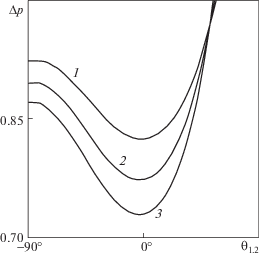
На рис. 7 представлены результаты расчетов перепада давления в микроканале с двумя супергидрофобными стенками, содержащими смещенные каверны. Видно, что представленные кривые качественно совпадают с результатами, полученными ранее для несмещенных относительно x = 0 каверн. Также как и в предыдущих случаях, максимальное снижение перепада давления достигается, когда форма поверхности пузырьков близка к плоской. Видно, что при выпучивании пузырьков в направлении основного потока жидкости ${{\theta }_{{1,2}}} > 0^\circ $ происходит резкое ухудшение свойств супергидрофобной поверхности, и существует предельное значение угла смачивания, при достижении которого перепад давления совпадает со значением, соответствующим течению в плоском канале с прямыми стенками и заданными условием прилипания, то есть эффект снижения сопротивления супергидрофобных стенок исчезает.
Рис. 7.
Зависимость перепада давления от кривизны поверхности пузырька в микроканале с двумя супергидрофобными стенками, имеющими каверны, смещенные относительно середины периода течения; ${{{{d}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{d}_{{1,2}}}} L}} \right. \kern-0em} L}$ = 0.3, ${{x}_{{1,2}}} = 0.15$ (1); ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} L}} \right. \kern-0em} L} = 0.3$, ${{x}_{1}} = 0.15$, ${{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} L}} \right. \kern-0em} L} = 0.4$, ${{x}_{2}} = 0.1$ (2); ${{{{d}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{d}_{{1,2}}}} L}} \right. \kern-0em} L} = 0.4$, ${{x}_{{1,2}}} = 0.1$ (3); ${H \mathord{\left/ {\vphantom {H L}} \right. \kern-0em} L} = 0.6$, ${{\theta }_{1}} = {{\theta }_{2}}$, ${{s}_{{1,2}}}$ = 0.
ЗАКЛЮЧЕНИЕ
С использованием метода граничных интегральных уравнений для оператора Стокса проведено параметрическое численное исследование медленного течения вязкой жидкости в микроканале, образованном различными типами текстурированных стенок, имеющих периодическую полосчатую структуру. Рассмотрены полосчатые супергидрофобные поверхности, каверны которых содержат газовые пузырьки, а также поверхности, содержащие периодически расположенные бесконечные микрокаверны, полностью заполненные жидкостью. В наиболее общей постановке сформулирована математическая задача о двумерном стоксовом течении жидкости в таком микроканале. Математическая постановка включает случаи различной геометрии текстуры стенок канала, а также различные положения и радиусы кривизны межфазной поверхности. В том числе рассмотрены случаи, когда пузырьки выпуклы внутрь каверн и внутрь жидкости.
Разработанный численный алгоритм применен для параметрического численного исследования величины перепада давления в микроканале с текстурированными стенками и для вычисления осредненной длины скольжения, характеризующей гидродинамические свойства стенок микроканала. Установлено, что снижение перепада давления в микроканале происходит не только при использовании супергидрофобных стенок, содержащих газовые пузырьки, но и в случае стенок канала, имеющих микрокаверны, полностью заполненные вязкой жидкостью. При этом текстура стенок должна быть организована так, чтобы в жидкости, заполняющей микрокаверны, образовывался вихрь, приводящий к снижению осредненного трения. Так как течение в микроканале происходит при очень малых числах Рейнольдса, вихри могут устойчиво удерживаться в кавернах и не вымываться основным потоком жидкости. При этом заметный эффект снижения перепада давления с использованием текстурированной стенки наблюдается в случае, когда толщина канала сопоставима с шириной каверны. При увеличении толщины канала эффект снижения трения быстро уменьшается.
Показано, что гидрофобизация обеих стенок микроканала, то есть наличие газовых пузырьков, приводит к значительному снижению перепада давления по сравнению со случаем стандартных гладких стенок с условием прилипания. Исследованы зависимости перепада давления в микроканале от комбинации геометрических параметров текстуры стенок канала. Показано, что максимального снижения перепада давления в микроканале можно достигнуть, когда каверны на обеих стенках имеют одинаковую ширину, а форма поверхности пузырьков близка к плоской. Для всех значений параметров подобия обнаружено наличие предельного значения статического угла смачивания, при котором происходит значительное ухудшение свойств супергидрофобных поверхностей, а эффект снижения сопротивления исчезает.
Полученные в работе результаты могут быть использованы для разработки оптимального дизайна текстурированных поверхностей, используемых для снижения гидродинамического сопротивления при течениях вязкой жидкости в устройствах микрофлюидики.
Работа выполнена при поддержке гранта РФФИ № 17-01-00057.
Список литературы
Rothstein J.P. Slip on superhydrophobic surfaces // Annu. Rev. Fluid Mech. 2010. V. 42. P. 89–109.
Ou J., Perot B., Rothstein J.P. Laminar drag reduction in microchannels using ultrahydrophobic surface // Phys. Fluids. 2004. V. 16. P. 4635–4643.
Lafuma A., Quere D. Superhydrophobic states // Nature Materials. 2003. V. 2. P. 457–460.
Lee C., Choi C.-H., Kim C.-J. Structured surfaces for a giant liquid slip // Phys. Rev. Let. 2008. V. 101. № 6. 064501.
Bazant M.Z., Vinogradova O.I. Tensorial hydrodynamic slip // J. Fluid Mech. 2008. V. 613. P. 125–134.
Агеев А.И., Осипцов А.Н. Автомодельные режимы растекания тонкого слоя жидкости вдоль супергидрофобной поверхности // Изв. РАН. Механика жидкости и газа. 2014. № 3. С. 37–51.
Philip J.R. Flows satisfying mixed no-slip and no-shear conditions // J. Appl. Math. Phys. 1972. V. 23. P. 353–372.
Vinogradova O.I., Belyaev A.V. Wetting, roughness and flow boundary conditions // J. Phys.: Condens. Matter. 2011. V. 23. P. 184104.
Teo C.J., Khoo B.C. Analysis of Stokes flow in microchannels with superhydrophobic surfaces containing periodic array of micro-grooves // Microfluid and Nanofluid. 2009. V. 7. P. 353–382.
Schonecker C., Hardt S. Longitudinal and transverse flow over a cavity containing a second immiscible fluid // J. Fluid Mech. 2013. V. 717. P. 376–394.
Steinberger A., Cottin-Bizonne C., Kleimann P. Charlaix E. High friction on a bubble mattress // Nature Material. 2007. V. 6. P. 665–668.
Bolognesi G., Cottin-Bizonne C., Pirat C. Evidence of slippage breakdown for a superhydrophobic microchannel // Phys. Fluids. 2014. V. 26. P. 082004.
Xiang Y., Xue Y., Lv P., Li D., Duan H. Influence of fluid flow on the stability and wetting transition of submerged superhydrophobic surfaces // Soft Matter. 2016. V. 12. № 18. P. 4241–4246.
Lee C., Choi C.-H., Kim C.-J. Superhydrophobic drag reduction in laminar flows: a critical review // Experim. in Fluids. 2016. V. 57. № 12. P. 176.
Davis A.M.J., Lauga E. Geometric transition in friction for flow over a bubble mattress // Phys. Fluids. 2009. V. 21. P. 011701.
Crowdy D. Slip length for longitudinal shear flow over a dilute periodic mattress of protruding bubbles // Phys. Fluids. 2010. V. 22. P. 121703.
Teo C.J., Khoo B.C. Effects of interface curvature on Poiseuille flow through microchannels and microtubes containing superhydrophobic surfaces with transverse grooves and ribs // Microfluid Nanofluid. 2014. V. 17. P. 891–905.
Агеев А.И., Осипцов А.Н. Стоксово течение над каверной супергидрофобной поверхности, содержащей пузырек газа // Изв. РАН. МЖГ. 2015. № 6. С. 35–49.
Ageev A.I., Golubkina I.V., Osiptsov A.N. Application of boundary element method to Stokes flows over a striped superhydrophobic surface with trapped gas bubbles // Phys. Fluids. 2018. V. 30. 012102.
Pozrikidis C. Boundary integral and singularity methods for linearized viscous flow. N.Y.: Cambridge Univ. Press, 1992. 272 p.
Nishad C.S., Chandra A., Sekhar G.P.R. Flows in slip-patterned micro-channels using boundary element methods // Engineering Analysis with Boundary Elements. 2016. V. 73. P. 95–102.
Alinovi E., Bottaro A. A boundary element method for Stokes flows with interfaces // J. Comput. Physics. 2018. V. 356. P. 261–281.
Якутенок В.А. Численное моделирование медленных течений вязкой жидкости со свободной поверхностью методом граничных элементов // Математическое моделирование. 1992. Т. 4. № 10. С. 62–70.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


