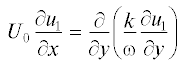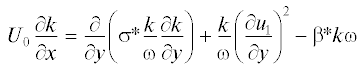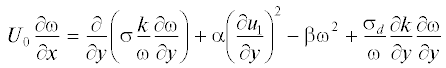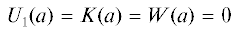1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 2, 2019

Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 94-98

АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ $k - \omega $-МОДЕЛИ ДАЛЬНЕГО ТУРБУЛЕНТНОГО СЛЕДА

А. В. Шмидт a, *

a Институт вычислительного моделирования СО РАН
Красноярск, Россия

* E-mail: schmidt@icm.krasn.ru

Поступила в редакцию 13.03.2018
После доработки 16.07.2018
Принята к публикации 16.07.2018

Полный текст (PDF)

Аннотация

Рассмотрена полуэмпирическая модель турбулентности $k - \omega $ в приближении дальнего следа. Искомыми величинами в данной модели являются дефект продольной осредненной компоненты скорости, турбулентная кинетическая энергия, удельная скорость диссипации энергии. Выполнен теоретико-групповой анализ модели, получена редуцированная автомодельная система обыкновенных дифференциальных уравнений, которая решена численно. Показано, что результаты расчетов согласуются с имеющимися экспериментальными данными.

Ключевые слова: модель турбулентности, дальний след, автомодельность

Модель $k - \omega $, предложенная в основополагающей статье [1], является первой двухпараметрической моделью турбулентности с двумя дифференциальными уравнениями переноса, записанными для масштабов скорости и длины, хотя и уступает по широте применения моделям типа $k - \varepsilon $. Значительный вклад в совершенствование модели $k - \omega $ внес Уилкокс (например, [2–4]). Классическая версия модели $k - \omega $ [2] успешно применяется для моделирования пристенных турбулентных течений. Причем, в отличие от модели $k - \varepsilon $, не требуется введения дополнительных пристенных функций. Тем не менее значительный недостаток модели $k - \omega $ – наличие чувствительности к внешнему уровню удельной скорости диссипации $\omega $ [5]. Включение слагаемого перекрестной диффузии в уравнение на $\omega $ [6] позволяет устранить зависимость от граничных условий. С целью улучшения прогностических свойств в расчетах свободных сдвиговых течений предложена [3, 4] версия модели $k - \omega $, включающая слагаемое перекрестной диффузии, а также модифицированные значения эмпирических постоянных модели.

В статьях [7, 8] на основе теоретико-группового анализа построены согласующиеся с экспериментальными данными автомодельные решения ряда полуэмпирических моделей свободных сдвиговых турбулентных течений, включающих уравнение для скорости диссипации энергии турбулентности $\varepsilon $. Цель данной работы заключается в применении развиваемого в [7, 8] подхода к модели $k - \omega $ [3, 4] для построения автомодельных решений задачи о течении в дальнем плоском турбулентном следе за телом, которая имеет прикладное значение и является одной из классических задач гидродинамики.

1. МОДЕЛЬ ДАЛЬНЕГО ТУРБУЛЕНТНОГО СЛЕДА

Для описания течения в дальнем плоском турбулентном следе за телом привлекается модель $k - \omega $ [4] в приближении дальнего следа

(1.1)
(1.2)
(1.3)
где x – продольная координата, ${{U}_{0}}$ – скорость набегающего на тело невозмущенного потока, ${{u}_{1}} = {{U}_{0}} - U$ – дефект продольной осредненной компоненты скорости ($U$ – продольная компонента скорости осредненного движения), k – кинетическая энергия турбулентности, $\omega $ – удельная скорость диссипации кинетической энергии. Эмпирические постоянные, входящие в уравнения (1.1)–(1.3), принимают следующие значения [3, 4]:

$\sigma = \frac{1}{2},\quad \sigma * = \frac{3}{5},\quad \beta = 0.0708,\quad \beta * = \frac{9}{{100}},\quad \alpha = \frac{{13}}{{25}},\quad {{\sigma }_{d}} = \frac{1}{8}$

Основное отличие данной версии модели $k - \omega $ от классической версии [2] заключается в наличии слагаемого перекрестной диффузии (последнее слагаемое в уравнении (1.3)) и модифицированных значениях эмпирических постоянных $\sigma {\text{*}}$, $\beta $ и $\alpha $.

Предполагается, что течение установившееся. Кроме того, в дальнейшем скорость набегающего на тело невозмущенного потока ${{U}_{0}}$ считается равной единице.

2. ТЕОРЕТИКО-ГРУППОВОЙ АНАЛИЗ МОДЕЛИ

Известные экспериментальные данные [9–11] свидетельствуют о том, что течение в дальнем турбулентном следе можно считать близким к автомодельному, следовательно, естественно интересоваться автомодельными редукциями уравнений (1.1)–(1.3). Базис алгебры Ли [12] рассматриваемой модели составляют пять операторов

${{X}_{1}} = \tfrac{\partial }{{\partial x}},\quad {{X}_{2}} = \tfrac{\partial }{{\partial y}},\quad {{X}_{3}} = \tfrac{\partial }{{\partial {{u}_{1}}}},\quad {{X}_{4}} = x\tfrac{\partial }{{\partial x}} + y\tfrac{\partial }{{\partial y}} - \omega \tfrac{\partial }{{\partial \omega }}$
${{X}_{5}} = y\tfrac{\partial }{{\partial y}} + {{u}_{1}}\tfrac{\partial }{{\partial {{u}_{1}}}} + 2k\tfrac{\partial }{{\partial k}}$

Составляется следующая линейная комбинация операторов X4, X5:

$Y = x\frac{\partial }{{\partial x}} + \gamma y\frac{\partial }{{\partial y}} - \omega \frac{\partial }{{\partial \omega }} + (\gamma - 1){{u}_{1}}\frac{\partial }{{\partial {{u}_{1}}}} + 2(\gamma - 1)k\frac{\partial }{{\partial k}}$
где $\gamma $ – произвольная постоянная. Решение системы уравнений (1.1)–(1.3), инвариантное относительно преобразования, порожденного оператором Y, имеет вид
(2.1)
${{u}_{1}}(x,y) = {{x}^{{\gamma - 1}}}{{U}_{1}}(t),\quad k(x,y) = {{x}^{{2\gamma - 2}}}K(t),\quad \omega (x,y) = {{x}^{{ - 1}}}W(t),\quad t = \frac{y}{{{{x}^{\gamma }}}}$
где $t$ – автомодельная переменная.

Пусть выполняется следующее условие:

$\frac{k}{\omega }\frac{{\partial {{u}_{1}}}}{{\partial y}} \to 0,\quad y \to \pm \infty $

Тогда, интегрируя уравнение (1.1) по y в пределах от $ - \infty $ до $\infty $, находим закон сохранения импульса

$\frac{d}{{dx}}\int\limits_{ - \infty }^\infty {{{u}_{1}} = 0} ,\quad {\text{и л и }}\quad \int\limits_{ - \infty }^\infty {{{u}_{1}} = {\text{const}}} $
откуда с помощью представления (2.1) для функции ${{u}_{1}}$ имеем

$\int\limits_{ - \infty }^\infty {{{x}^{{2\gamma - 1}}}} {{U}_{1}}(t)dt = {\text{const}}$

Для того, чтобы левая часть последнего равенства не зависела от x, необходимо положить $\gamma = 1{\text{/}}2$. Такая автомодельность согласуется с экспериментальными данными [9–11].

Подставляя (2.1) в уравнения (1.1)–(1.3), получаем следующую систему обыкновенных дифференциальных уравнений:

(2.2)
$U_{1}^{{''}} + \left( {\frac{{K{\text{'}}}}{K} - \frac{{W{\text{'}}}}{W} + \gamma t\frac{W}{K}} \right)U_{1}^{'} - (\gamma - 1)\frac{{{{U}_{1}}W}}{K} = 0$
(2.3)
$\sigma {\text{*}}K{\text{''}} + U_{1}^{{}} + \sigma {\text{*}}\frac{{{{K}^{{'2}}}}}{K} + \left( { - \sigma {\text{*}}\frac{{W{\text{'}}}}{W} + \gamma t\frac{W}{K}} \right)K{\text{'}} - (2(\gamma - 1) + \beta {\text{*}}W)W = 0$
(2.4)
$\sigma W{\text{''}} + \alpha \frac{W}{K}U_{1}^{{'2}} - \sigma \frac{{\mathop W\nolimits^{'2} }}{W} + \left( {(\sigma + {{\sigma }_{d}})\frac{{K{\text{'}}}}{K} + \gamma t\frac{W}{K}} \right)W{\text{'}} - (\beta W - 1)\frac{{{{W}^{2}}}}{K} = 0$

Для системы уравнений (2.2)–(2.4) ставятся краевые условия

(2.5)
$U_{1}^{'}(0) = K{\text{'}}(0) = W{\text{'}}(0) = 0$
(2.6)
что соответствует симметрии течения относительно оси $Ox$ и равенству нулю функций ${{u}_{1}}$, k и $\omega $ вне зоны турбулентного следа. Значение a, связанное с полушириной турбулентного следа, в расчетах можно полагать равным единице, в силу инвариантности системы уравнений (2.2)–(2.4) относительно преобразования растяжения, либо задавать это значение исходя из экспериментальных данных. Следует также отметить то обстоятельство, что коэффициенты системы уравнений (2.2)–(2.4) имеют особенности в краевых условиях.

Используя уравнение (2.2), находим первый интеграл

(2.7)
$\frac{K}{W}{{U}_{1}} + \frac{t}{2}U_{1}^{'} = {\text{const}}$
где равенство нулю константы, стоящей в правой части, следует из краевых условий. Наличие первого интеграла позволяет при дальнейших расчетах использовать обыкновенное дифференциальное уравнение первого порядка на функцию ${{U}_{1}}$.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Система обыкновенных дифференциальных уравнений (2.7), (2.3), (2.4), удовлетворяющая условиям (2.5), (2.6), решалась численно. Для решения задачи использовался модифицированный метод стрельбы и асимптотическое разложение решения в окрестности особой точки

${{U}_{1}}(t) = {{c}_{1}}{{\left| {t - a} \right|}^{{\kappa \sigma {\text{*}}}}} + o({{\left| {t - a} \right|}^{{\kappa \sigma {\text{*}}}}}),\quad K(t) = {{c}_{2}}{{\left| {t - a} \right|}^{\kappa }} + o({{\left| {t - a} \right|}^{\kappa }})$
$W(t) = \tfrac{{{{c}_{2}}\kappa \sigma {\text{*}}}}{{a\gamma }}{{\left| {t - a} \right|}^{{\kappa - 1}}} + o({{\left| {t - a} \right|}^{{\kappa - 1}}}),\quad \kappa = \sigma {\text{/}}(\sigma - \sigma {\text{*}} + {{\sigma }_{d}})$

Заметим, что показатели степени, входящие в асимптотическое разложение, представлены в [3, 4] и принимают значения, большие единицы, что свидетельствует о гладком приближении решений рассматриваемой краевой задачи к границе турбулентного следа.

В результате расчетов были получены следующие значения функций ${{U}_{1}}$, K и W при t = 0:

${{U}_{1}}(0) = 3.9,\quad K(0) = 3.4902,\quad W(0) = 14.45$

Сопоставление автомодельных профилей решений, полученных методом стрельбы, с экспериментальными данными [9] представлено на рисунке 1. Имеет место достаточно хорошее соответствие результатов проведенных расчетов экспериментальным данным по дефекту осредненной продольной компоненты скорости ${{u}_{1}}$ и нормальному рейнольдсову напряжению $\left\langle {u{\text{'}}u{\text{'}}} \right\rangle $ (угловые скобки означают осреднение по времени, $u{\text{'}}$ – пульсационная составляющая продольной компоненты скорости). Для устранения имеющегося несоответствия по касательному рейнольдсову напряжению $\left\langle {u{\text{'}}\text{v}{\text{'}}} \right\rangle $ ($\text{v}{\text{'}}$ – пульсационная составляющая поперечной компоненты скорости), по всей видимости, следует привлекать более сложные модели турбулентности, включающие дифференциальные уравнения переноса на компоненты тензора рейнольдсовых напряжений.

Рис. 1.

Результаты расчетов: 1 – экспериментальные данные [9], 2 – автомодельные решения, ${{u}_{{10}}}$ – осевое значение дефекта скорости, (а) нормированный профиль ${{u}_{1}}$, (б) нормированный профиль $\left\langle {u{\text{'}}u{\text{'}}} \right\rangle $, (в) профиль удельной диссипации, нормированный на ${{W}_{0}} = W(0)$, (г) нормированный профиль $\left\langle {u{\text{'}}\text{v}{\text{'}}} \right\rangle $

ЗАКЛЮЧЕНИЕ

Построены автомодельные решения уравнений $k - \omega $ модели дальнего турбулентного следа. Выполненное сопоставление с экспериментальными данными свидетельствует о применимости модифицированной версии $k - \omega $ модели к расчетам свободных сдвиговых турбулентных течений.

Автор выражает благодарность О.В. Капцову и Г.Г. Черных за предоставленные материалы и внимание к работе. Работа выполнена при финансовой поддержке РФФИ (проект № 17-01-00332).

Список литературы

  1. Колмогоров А.Н. Уравнения турбулентного движения несжимаемой жидкости // Изв. АН СССР. физ. сер. 1942. Т. 6. № 1–2. С. 56–58.

  2. Wilcox D.C. Reassessment of the scale-determining equation for advanced turbulence models // AIAA J. 1988. V. 26. № 11. P. 1299–1310. doi.org/10.2514/3.10041

  3. Wilcox D.C. Turbulence modeling for CFD. La Canada, California: DCW Industries, 2006. 522 p.

  4. Wilcox D.C. Formulation of the $k - \omega $ turbulence model revisited // AIAA J. 2008. V. 46. № 11. P. 2823–2838. doi.org/10.2514/1.36541

  5. Kok J.C. Resolving the dependence on freestream values for the $k$ω-turbulence model // AIAA J. 2000. V. 38. № 7. P. 1292–1295. doi.org/10.2514/2.1101

  6. Speziale C.G., Abid R., Anderson E.C. Critical evaluation of two-equation turbulence models for near-wall turbulence // AIAA J. 1992. V. 30. № 2. P. 324–331. doi.org/10.2514/3.10922

  7. Капцов О.В., Ефремов И.А., Шмидт А.В. Автомодельные решения модели второго порядка дальнего турбулентного следа // ПМТФ. 2008. Т. 49. № 2. С. 74–78.

  8. Шмидт А.В. Автомодельное решение задачи о турбулентном течении круглой затопленной струи // ПМТФ. 2015. Т. 56. № 3. С. 82–88. doi.org/10.15372/PMTF20150310

  9. Wygnanski I., Champagne F., Marasli B. On the large-scales structures in two-dimensional small-deficit, turbulent wakes // J. Fluid Mech. 1986. V. 168. P. 31–71. doi.org/10.1017/S0022112086000289

  10. Fage A., Falkner V.M. Note on experiments on the temperature and velocity in the wake of a heated cylindrical obstacle // Proc. Royal Soc. London, Ser. A: Math. and Phys. Sci., 1932. V. 135. № 828. P. 702–705.

  11. Weygandt J.H., Mehta R.D. Three-dimensional structure of straight and curved plane wakes // J. Fluid Mech. 1995. V. 282. P. 279–311. doi.org/10.1017/S0022112095000140

  12. Овсянников Л.В. Групповой анализ дифференциальных уравнений. М.: Наука, 1978.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал