Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 145-149

Структурный вариант уравнения Освальда-Вейля: фрактальная трактовка

И. В. Долбин^a, *, Г. В. Козлов^a

^a Кабардино-Балкарский государственный университет им. Х.М. Бербекова
Нальчик, Россия

Поступила в редакцию 12.01.2018
После доработки 27.03.2018
Принята к публикации 27.03.2018

DOI: 10.1134/S0568528119010055

Аннотация

Предложена структурная трактовка уравнения Освальда–Вейля с привлечением представлений фрактального анализа для описания реологических свойств систем каучук/дисперсный наполнитель. Показано, что величина вязкости и тип течения системы определяются структурой частиц (агрегатов частиц) наполнителя, характеризуемой их фрактальной размерностью. В свою очередь, указанную размерность определяет механизм формирования агрегатов. Предложенная модель позволяет прогнозировать вязкость систем каучук/дисперсный наполнитель при разных содержаниях наполнителя и скоростях сдвига.

Ключевые слова: каучук, дисперсный наполнитель, вязкость, структура, фрактальная размерность, скорость сдвига

Зависимость вязкости суспензий η от скорости сдвига γ* часто описывается с помощью уравнения Освальда–Вейля [1]

$\eta = {{\eta }_{0}}\gamma {{{\text{*}}}^{n}}$

где η₀ – коэффициент, зависящий от химической природы суспензии, n – индекс текучести.

При n = 0 течение суспензии подчиняется закону Ньютона и параметр η₀ совпадает со значением ньютоновской вязкости. Для дилатантных систем n > 0, т.е. вязкость растет с повышением скорости сдвига и значения параметра η₀ не равны вязкости. Для псевдопластичных систем при n < 0 вязкость с ростом скорости сдвига снижается и значения параметра η₀ также не соответствуют значениям вязкости.

Отметим, что существует большое количество соотношений, сходных по форме с уравнением Освальда–Вейля, которые описывают разные свойства полимеров в различных состояниях. Наиболее типичным примером служит хорошо известное уравнение Куна–Марка–Хаувинка, связывающее характеристическую вязкость [η] и молекулярную массу М для полимерных растворов [2]

$\left[ \eta \right] = {{К }_{\eta }}{{М }^{{{{а }_{\eta }}}}}$

где К_η и а_η – константы для полимера в выбранном растворителе при данной температуре в определенном интервале значений М.

Общим и очень существенным недостатком уравнений такого типа является наличие в них эмпирических констант, не связанных со структурой, что не позволяет прогнозировать нужные свойства. В то же время такие уравнения легко поддаются параметризации в рамках фрактального анализа. Так, авторы [3] предложили следующий фрактальный вариант уравнения Куна–Марка–Хаувинка:

(0.1)

$\left[ \eta \right] = с (\alpha )\frac{{{{М }^{{(3 - {{D}_{f}})/{{D}_{f}}}}}}}{{m_{0}^{{3/{{D}_{f}}}}}}$

где с – некоторая константа, зависящая от коэффициента набухания макромолекулярного клубка, D_f – фрактальная размерность этого клубка, физически строго характеризующая его структуру, m₀ – средний вес элементарного звена полимера (без заместителей).

Аналогичные фрактальные варианты были получены и для ряда других характеристик полимеров: коэффициентов поступательной диффузии и скоростной седиментации [4].

Авторы [5] предложили следующее соотношение для определения вязкости η при течении битого льда

(0.2)

$\eta = {{\eta }_{0}}{{l}^{{2 - {{D}_{f}}}}}$

где η₀ – еще одна константа, l – характерный линейный масштаб течения.

Уравнение (0.2) хорошо описывает аномальное поведение расплавов полимерных нанокомпозитов разных классов, тогда как классические модели, разработанные для этой цели, не в состоянии это сделать [6]. Наиболее важной особенностью фрактальных соотношений, подобных (0.1) и (0.2), является то, что они включают в анализ проблемы структурный фактор (структуру макромолекулярного клубка, нанонаполнителя), характеризуемый той или иной фрактальной размерностью. Исходя из указанного выше, целью настоящей работы является разработка структурного варианта уравнения Освальда–Вейля с привлечением представлений фрактального анализа.

1. ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ

Использованы два типа суспензий на основе полидиметилфенилсилоксана (ПДМФС) с наполнителями двух типов – технический углерод (ТУ) с массовым содержанием 5–25% и карбонильное железо (КЖ) с содержанием 10–60%. Характеристики наполнителей приведены в таблице.

Таблица 1.

Наполнитель	Диаметр, мкм	Удельная поверхность, м²/г	Плотность, кг/м³	Элементный состав, (масс. %)
Наполнитель	Диаметр, мкм	Удельная поверхность, м²/г	Плотность, кг/м³	С	О	Fe
Технический углерод (ТУ)	0.40	15.0	1900	98.7	0.13	–
Карбонильное железо (КЖ)	4.30	27.3	3420	19.4	11.2	68.0

Реологические свойства изучали на ротационном вискозиметре “Реотест-2” при температуре 293 ± 2 К и различных скоростях сдвига, измеряя напряжение сдвига при последовательном увеличении скорости вращения рабочего цилиндра.

В процессе измерений вязкости полимерных суспензий наблюдается агрегация наполнителя, оценить уровень которой можно с помощью следующего соотношения [6]:

(1.1)

$\eta \sim \frac{{R_{{ag}}^{3}}}{{\gamma {\text{*}}}}$

где R_ag – радиус агрегата частиц наполнителя, γ* – скорость сдвига.

Для определения коэффициента в соотношении (1.1) использована следующая методика. Сначала была определена величина R_ag при наименьшем значении γ* согласно уравнению [6]

${{R}_{{ag}}} = с \varphi _{n}^{{1/2}}$

где с – постоянная, равная 48.5 мкм, φ_n – объемное содержание наполнителя, которое определяется следующим образом [7]:

${{\varphi }_{н }} = {{\left[ {1 + \left( {\frac{{{{\rho }_{n}}}}{{{{\rho }_{p}}}}} \right)\left( {\frac{{1 - {{W}_{n}}}}{{{{W}_{n}}}}} \right)} \right]}^{{ - 1}}}$

где ρ_n и ρ_p – плотность наполнителя и полимера соответственно, W_n – массовое содержание нанонаполнителя. Величина ρ_n для рассматриваемых наполнителей приведена в таблице, а величина ρ_p принята равной 1200 кг/м³ [1].

2. РЕЗУЛЬТАТЫ

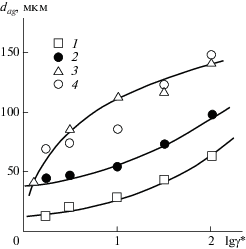
На рис. 1 приведены зависимости диаметра агрегатов наполнителя d_ag от скорости сдвига γ* в логарифмических координатах для трех из рассматриваемых суспензий. Как и следовало ожидать, снижение φ_n существенно ослабляет агрегацию, а КЖ агрегируется слабее, чем ТУ. Это наблюдение можно объяснить двумя факторами. Во-первых, поверхности исследуемых наполнителей различаются – для ТУ она является лиофобно-лиофильной, а для КЖ – лиофильно-лиофобной [8]. Вторым фактором может быть различие плотностей ρ_ec и ρ_ci наполнителей ТУ и КЖ соответственно. Так, значения d_ag для суспензии ПДМФС/КЖ (кривая 2) можно нормализовать введением фактора K_c = (ρ_ciφ_ec/ρ_ecφ_ci), где φ_ec и φ_ci – объемное содержание технического углерода и карбонильного железа соответственно. На рис. 1 показана зависимость K_cd_ag(γ*) для КЖ, которая хорошо согласуется с полученной аналогично зависимостью d_ag(lgγ*) для суспензий ПДМФС/ТУ (кривая 1).

Рис. 1.

Зависимости диаметра агрегатов наполнителя d_ag от скорости сдвига γ* для суспензий: ПДМФС/КЖ с W_n = 10% (1); ПДМФС/КЖ с W_n = 60% (2) и ПДМФС/ТУ с W_n = 25% (3); 4 – зависимость (2), нормализованная по плотности и объемному содержанию наполнителя

Далее для определения вязкости η рассматриваемых суспензий можно использовать уравнение (0.2), в котором для определения фрактальной размерности кластеров (агрегатов) наполнителя D_f использована модель формирования таких кластеров на множественных местах роста [9] в следующем виде [10]:

${{R}_{{ag}}} = 3.4\varphi _{n}^{{ - 1/\left( {d - {{D}_{f}}} \right)}}$

где d – размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d = 3).

Для описания зависимости η(γ*) соотношение (0.2) было переписано в виде

(2.1)

$\eta = k{{\left( {\gamma {\text{*}}} \right)}^{{2 - {{D}_{f}}}}}$

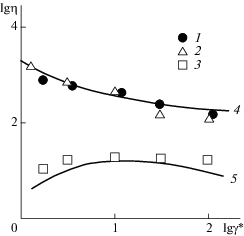
поскольку изменение γ* влияет на величину η так же, как вариация характерного линейного масштаба течения l.

На рис. 2 приведено сравнение рассчитанных согласно уравнению (2.1) и полученных экспериментально зависимостей η(γ*) для трех суспензий: ПДМФС/КЖ с массовым содержанием наполнителя W_n = 10 и 60%, а также ПДМФС/ТУ с W_n = 25%. Величина коэффициента k в уравнении (2.1) подобрана методом наилучшего совмещения теории и эксперимента. Как следует из приведенного сравнения, уравнение (2.1) хорошо описывает изменение вязкости исследуемых суспензий по мере вариации скорости сдвига. Это означает, что вязкость суспензий η определяется следующими факторами: содержанием наполнителя, уровнем его агрегации и скоростью сдвига, что и следовало ожидать из самых общих соображений.

Рис. 2.

Полученные экспериментально (1–3) и рассчитанные согласно уравнению (2.1) (4, 5) зависимости вязкости η от скорости сдвига γ* для суспензий ПДМФС/КЖ с W_n = 60% (1, 4), ПДМФС/ТУ с W_n = 25% (2, 4) и ПДМФС/ЖУ с W_n = 10% (3, 5)

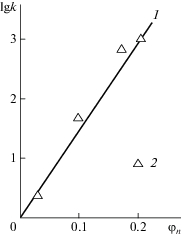
Последующее изучение поведения коэффициента k в уравнении (2.1) показало его систематическое изменение по мере вариации объемного содержания наполнителя φ_n, а именно, рост φ_n приводит к увеличению k. На рис. 3 приведена зависимость k(φ_n) в логарифмических координатах, подтверждающая эту корреляцию, что аналитически можно выразить следующим эмпирическим уравнением:

(2.2)

$\lg k = 14.7{{\varphi }_{n}}$

Рис. 3.

Зависимость коэффициента k в уравнении (2.2) от объемного содержания наполнителя φ_n для рассматриваемых суспензий: 1 – теоретический расчет; 2 – экспериментальные данные

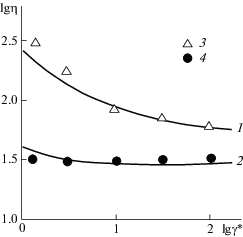
Это обстоятельство позволяет прогнозировать зависимость η(γ*), по крайней мере, для рассматриваемых суспензий. На рис. 4 приведено сравнение рассчитанных согласно уравнениям (2.1) и (2.2) и полученных экспериментально зависимостей η(γ*) в двойных логарифмических координатах для двух суспензий на основе ПДМФС: с содержанием ТУ W_n = 15% и содержанием КЖ W_n = 35%. Как можно видеть, получено хорошее соответствие результатов прогнозирования и эксперимента.

Рис. 4.

Сравнение рассчитанных согласно уравнениям (2.1) и (2.2) (1, 2) и полученных экспериментально (3, 4) зависимостей вязкости η от скорости сдвига γ* для суспензий ПДМФС/ТУ с W_n = 15% (1, 3) и ПДМФС/КЖ с W_n = 35% (2, 4)

И в заключение отметим, что согласно уравнению (2.1) режим течения суспензий определяется только структурой агрегатов наполнителя, характеризуемой их фрактальной размерностью D_f. При D_f = 2 течение суспензии подчиняется закону Ньютона, т.е. η = η₀ = const. При D_f < 2 вязкость растет с повышением скорости сдвига, что означает реализацию дилатантного режима, а при D_f > 2 вязкость снижается по мере роста скорости сдвига, т.е. реализуется псевдопластичный режим. Отметим, что размерность кластеров (агрегатов) D_f = 2 является условной границей между механизмами формирования кластеров – при D_f < 2 реализуется механизм кластер-кластер (Cl–Cl), а при D_f > 2 – механизм частица–кластер (Р–Cl) [11]. Это предполагает, что режим течения суспензий определяется механизмом роста кластеров (агрегатов) наполнителя.

3. ЗАКЛЮЧЕНИЕ

Результаты настоящей работы продемонстрировали, что увеличение скорости сдвига приводит к повышению и размера агрегатов наполнителя, и фрактальной размерности их структуры. Предложенное фрактальное соотношение позволяет корректное количественное описание зависимости вязкости от скорости сдвига. Режим течения полностью контролируется структурой кластеров (агрегатов) наполнителя. Определяющую роль в этом смысле играет механизм формирования указанных кластеров. Предложенная модель позволяет корректное количественное прогнозирование поведения суспензий полимер/дисперсный наполнитель.

Список литературы

Nelyub V.A., Borodulin A.S., Kobets L.P., Malysheva G.V. Capillary hydrodynamics of oligomer binder // Polymer Sci.-Series D. 2016. V. 9. № 3. P. 322–325.
Будтов В.П. Физическая химия растворов полимеров. СПб.: Химия, 1992. 384 с.
Козлов Г.В., Долбин И.В. Фрактальный вариант уравнения Марка–Куна–Хаувинка // Высокомолекулярные соединения. Сер. Б. 2002. Т. 44. № 1. С. 115–118.
Карманов А.П., Монаков Ю.Б. Фрактальная структура bulk- и end-wise-дегидрополимеров // Высокомолекулярные соединения. Сер. Б. 1995. Т. 37. № 2. С. 328–331.
Гольдштейн Р.В., Мосолов А.Б. Течение фрактально-битого льда // Докл. РАН. 1992. Т. 324. № 3. С. 576–581.
Козлов Г.В., Долбин И.В. Фрактальная физическая химия полимерных растворов и расплавов. М.: Изд-во “Спутник+”, 2016. 352 с.
Blond D., Barron V., Ruether M., Ryan K.P., Nicolosi V., Blau W.J., Coleman J.N. Enhancement of modulus, strength, and toughness in poly(methyl methacrylate)-based composites by the incorporation of poly(methyl methacrylate)-functionalized nanotubes // Adv. Funct. Mater. 2006. V. 16. № 6. P. 1608–1614.
Кобец Л.П., Бородулин А.С. Реологические свойства системы полимерное связующее–дискретный металлический наполнитель // Энциклопедия инженера-химика. 2015. № 6. С. 9–14.
Witten T.A., Meakin P. Diffusion-limited aggregation at multiple growth sites // Phys. Rev. B. 1983. V. 27. № 5. P. 2616–2623.
Микитаев А.К., Козлов Г.В. Зависимость степени усиления нанокомпозитов полимер/углеродные нанотрубки от размерности нанонаполнителя // Докл. РАН. 2015. Т. 462. № 1. С. 41–44.
Meakin P. Formation of fractal clusters and networks by irreversible diffusion-limited aggregation // Phys. Rev. Lett. 1983. V. 51. № 13. P. 1119–1122.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал