Известия РАН. Механика жидкости и газа, 2019, № 1, стр. 99-114

Расчет неравновесного излучения ударных волн в воздухе с использованием двух моделей

С. Т. Суржиков^{a, b, *}

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^b Всероссийский научно-исследовательский институт автоматики им. Н.Л. Духова,
Москва, Россия

^* E-mail: surg@ipmnet.ru

Поступила в редакцию 14.06.2018
После доработки 20.09.2018
Принята к публикации 20.09.2018

DOI: 10.1134/S0568528119010146

Полный текст (PDF)

Аннотация

Представлены результаты численного моделирования спектральной излучательной способности ударно-нагретого воздуха, полученные с использованием двух моделей неравновесного излучения, испускаемого из релаксационной зоны за фронтом сильной ударной волны. Первая модель основана на уравнениях Эйлера и сформулирована для одномерной задачи кинетических процессов за фронтом ударной волны. Вторая модель основана на двумерных уравнениях Навье–Стокса для вязкого ударного слоя вблизи лобовой поверхности затупленного тела в гиперзвуковом потоке. Обсуждаются проблемы интерпретации данных летного эксперимента Fire-II с использованием указанных расчетных моделей.

Ключевые слова: неравновесное излучение, ударные волны в воздухе, релаксационные процессы, модель ударной волны Эйлера, модель ударной волны Навье−Стокса, летный эксперимент Fire-II

Успех развития фундаментальных направлений физической механики во многом базируется на экспериментальных данных по излучению сильных ударных волн, получаемых уже более 50 лет на ударных трубах. Последнее десятилетие отмечено появлением значительного количества экспериментальных работ по измерению абсолютных величин спектральной интенсивности излучения в воздухе, смесях CO₂–N₂ и CH₄–N₂, что стало возможным с использованием высокоскоростных оптико-электронных камер. Обзор экспериментальных данных, полученных с использованием ударных труб, и используемых в настоящее время для валидации расчетно-теоретических моделей приведен в работах [1–3]. Результаты первых экспериментов [4–6] также остаются в поле внимания специалистов, развивающих теоретические и экспериментальные методы исследования структуры сильных ударных волн.

Среди развиваемых расчетных моделей наибольшее распространение получили многотемпературные и так называемые гибридные радиационно-столкновительные (РС) модели [7, 8], как упрощенные версии поуровневых моделей определения заселенностей возбужденных квантовых состояний без использования понятия температуры, в которых задаются константы скоростей возбуждения отдельных квантовых состояний, определяющих тепловое излучение газа за фронтом ударной волны (ФУВ). Важно, что использование РС-моделей стимулирует развитие квантово-механических, квантово-химических и квантово-статистических моделей элементарных физико-химических процессов в плазме применительно к задачам физической механики.

Значительная область исследования физики излучающих ударных волн приходится на задачи аэрофизики высокотемпературных сжатых слоев, образующихся у поверхности спускаемых космических аппаратов, входящих в плотные слои атмосферы. Актуальность этих задач определяется работами по проектному анализу всех типов высокоскоростных летательных аппаратов и пилотируемых спускаемых аппаратов (СА), возвращаемых на Землю с орбитальными и, в особенности, со сверхорбитальными скоростями, когда радиационный нагрев поверхности становится превалирующим.

В работе [9] выполнено численное исследование закономерностей изменения спектральной и интегральной интенсивности излучения, испускаемого релаксационной зоной за ФУВ в воздухе для условий, моделирующих сжатый слой у лобовой поверхности спускаемого аппарата в летном эксперименте Fire-II [10]. Однако, как и в предшествующих работах, исследовавших специфику излучения ударных волн в атмосфере Марса [7, 11], эта задача решалась в классической постановке, отвечающей наблюдению релаксационной зоны за ФУВ через окно в боковой поверхности ударной трубы (УТ) [12], поэтому остается открытым вопрос об использовании получаемых экспериментальных и соответствующих расчетных данных для оценки радиационного нагрева поверхности реального СА.

В данной работе предлагается методика сопоставления экспериментальных и расчетных данных, отвечающих классическому эксперименту на УТ, с экспериментальными и расчетными данными по радиационному нагреву поверхности СА. С этой целью задача о спектральном тепловом излучении сильных ударных волн решается с использованием двух подходов.

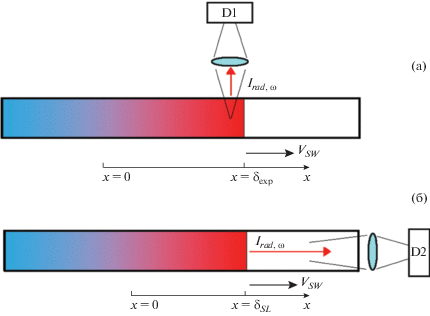
На фиг. 1а схематически показана постановка задачи о спектральном излучении ударной волны, регистрируемом через боковое окно в экспериментах на УТ. При интерпретации получаемых экспериментальных данных спектральная интенсивность теплового излучения рассчитывается в приближении объемного высвечивания (приближение оптически тонкого слоя) из единичного физического объема в приосевой области ударной трубы. Учет движения фронта ударной волны позволяет получить временные зависимости концентраций химических компонент и заселенностей электронных состояний атомов и молекул, определяющих высвечивание газа из высокотемпературной области за фронтом ударной волны. Интегрирование по времени от момента прихода ФУВ в поле зрения детектора D1 до задаваемого в эксперименте ${{t}_{{\exp }}}$ дает спектральную и интегральную интенсивность излучения, покидающего нагретый газ от ФУВ до границы ${{\delta }_{{\exp }}}$, которая достигает боковое окно за время ${{t}_{{\exp }}}$.

Фиг. 1.

Схема измерения излучения в задаче об ударной волне

Из ударно-волновых экспериментов удается также извлечь временную зависимость излучения на заданной длине волны (реально: в узком спектральном диапазоне). Указанные данные представляют особенную ценность для тестирования моделей физической и химической кинетики возбуждения и дезактивации электронно-возбужденных состояний, ответственных за спускание излучения на данной длине волны. В мировой практике такое тестирование называется валидацией расчетных моделей.

Однако одномерная задача об излучении ударной волны может также решаться в иной постановке. Если предположить, что излучение регистрируется на правом торце ударной трубы при наблюдении вдоль оси симметрии (фиг. 1б), то в предположении об установившемся движении ФУВ вдоль УТ некоторое время будет наблюдаться квазистационарная картина теплового излучения (вплоть до образования отраженной ударной волны). Интенсивность излучения ${{I}_{{rad,\omega }}}$, достигающего в этом случает детектора D2, будет формироваться всей областью нагретого газа за ФУВ, толщина которой может быть чрезмерно большой. В этом случае дополнительная погрешность в результаты сопоставления расчетных и экспериментальных данных будет вноситься точностью описания процессов остывания газа на большом расстоянии от ФУВ, которые обычно в одномерной задаче об УТ не рассматриваются.

Тем не менее решение такой одномерной задачи об ударной волне можно использовать для оценки радиационного нагрева поверхности реального СА. В последнем случае толщина сжатого слоя ${{\delta }_{{SL}}}$ можно определить с удовлетворительной точностью из корреляционных соотношений. Поэтому если пренебречь относительно тонким пограничным слоем, то можно положить толщину области горячего газа за ФУВ (в схеме фиг. 1а), совпадающей с величиной отхода ФУВ от поверхности обтекаемого тела (в схеме задачи на фиг. 1б). В этом случае результаты ударно-волновых экспериментов и соответствующих расчетов физико-химической и радиационной кинетики за ФУВ можно использовать для расчета радиационного нагрева поверхности СА. В данной работе такая модель используется для интерпретации опытных данных экспериментального СА Fire-II на участке траектории t = 1634–1639 с, которые отвечают высоте полета H ∼ 80–60 км, то есть в неравновесной области течения.

Кроме решения одномерной задачи, радиационная газовая динамика СА Fire-II рассчитывалась с использованием двумерного компьютерного кода, что позволяет более точно учесть структуру сжатого слоя и тем самым выяснить степень различия расчетных данных, отвечающих одномерной модели движения газа в УТ и двухмерной модели осесимметричного обтекания лобовой поверхности СА.

1. МОДЕЛЬ ЭЙЛЕРА ДВИЖЕНИЯ РЕЛАКСИРУЮЩЕГО ГАЗА ЗА ФРОНТОМ УДАРНОЙ ВОЛНЫ

Газовая динамика физически и химически неравновесного газа за фронтом ударной волны описывается уравнениями Эйлера в одномерной постановке. Предполагается, что давление, плотность, поступательная температура атомов и молекул скачком изменяются в фронте ударной волны (при x = 0), но при этом молярные доли газовых компонентов набегающего воздуха ${{x}_{i}}$ не меняются. После скачка уплотнения начинают протекать процессы физической и химической кинетики, обусловленные постепенной передачей кинетической энергии сталкивающихся частиц внутренним степеням свободы с последующей диссоциацией и ионизацией. Газовая смесь, образующаяся за фронтом ударной волны, состоит из следующих $i = 1,\; \ldots ,\;{{N}_{s}} = 11$ компонент: N₂, O₂, NO, N, O, N$_{2}^{ + }$, O$_{2}^{ + }$, NO⁺, N⁺, O⁺, e^–, в которых выделяются ${{N}_{\text{v}}} = 3$ колебательных моды двухатомных молекул N₂ (m = 1), O₂ (m = 2) и NO (m = 3).

Уравнения для определения газодинамических параметров за ФУВ имеют следующий вид:

(1.1)

$\frac{d}{{dx}}\left( {\rho u} \right) = 0$, $\frac{d}{{dx}}(p + \rho {{u}^{2}}) = 0$, $\frac{d}{{dx}}\left( {h + \frac{{{{u}^{2}}}}{2}} \right) = 0$

(1.2)

$\frac{d}{{dx}}\left( {\frac{3}{2}{{T}_{e}}{{n}_{e}}u} \right) + {{T}_{e}}{{n}_{e}}\frac{{du}}{{dx}} = {{Q}_{{ei}}} + {{Q}_{{ea}}} + {{Q}_{{ai}}} + {{Q}_{{ion}}} + {{Q}_{{e\text{v}}}}$

(1.3)

$\begin{gathered} \frac{{d{{X}_{i}}}}{{dt}} = \sum\limits_{n = 1}^{{{N}_{r}}} {\left[ {\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)k_{n}^{f}\prod\limits_{j = 1}^{{{N}_{s}}} {X_{j}^{{{{a}_{{j,n}}}}}} + \left( {{{a}_{{i,n}}} - {{b}_{{i,n}}}} \right)k_{n}^{r}\prod\limits_{j = 1}^{{{N}_{s}}} {X_{j}^{{{{b}_{{j,n}}}}}} } \right]} = \\ = \;\sum\limits_{n = 1}^{{{N}_{r}}} {[({{b}_{{i,n}}} - {{a}_{{i,n}}})(S_{n}^{f} - S_{n}^{r})]} ,\quad i = 1,2,\; \ldots ,\;{{N}_{s}} \\ \end{gathered} $

(1.4)

$\frac{{d{{e}_{{\text{v},m}}}}}{{dt}} = {{\dot {e}}_{{\text{v},m}}} = Q_{{\text{v}T}}^{m} + Q_{{\text{vv}}}^{m} + Q_{{c\text{v}}}^{m},\quad m = 1,2,\quad {{N}_{\text{v}}} = 3$

где x – эйлерова координата вдоль направления распространения ФУВ; $\rho $, $u$, $p$ – плотность, скорость и давление смеси газов; $h$, $T$, ${{T}_{e}}$ – энтальпия, температура поступательных степеней свободы смеси газов и электронов; ${{n}_{e}}$, ${{X}_{i}}$, ${{a}_{{i,n}}}$, ${{b}_{{i,n}}}$ – концентрация электронов, объемная молярная концентрация i-го химического компонента, а также стехиометрические коэффициенты реагентов в n-й химической реакции, записанной в символической форме

$\sum\limits_{j = 1}^{{{N}_{s}}} {{{a}_{{j,n}}}\left[ {{{X}_{j}}} \right]} \mathop \Leftrightarrow \limits_{k_{j}^{r}}^{k_{j}^{f}} \sum\limits_{j = 1}^{{{N}_{s}}} {{{b}_{{j,n}}}\left[ {{{X}_{j}}} \right]} ,\quad n = 1,2, \ldots ,\;{{N}_{r}};$

[X_j] – химические символы реагентов и продуктов реакций; $Q_{{\text{v}T}}^{m}$, $Q_{{\text{vv}}}^{m}$, $Q_{{c\text{v}}}^{m}$ – источниковые слагаемые в уравнении сохранения энергии в колебательных модах молекул, обусловленные энергообменом между колебательными и поступательными степенями свободы (VT-релаксация), между колебательными степенями свободы (VV-релаксация) и в результате протекания химических реакций (VC-релаксация); ${{e}_{{\text{v},m}}}$, ${{\dot {e}}_{{\text{v},m}}}$ – удельная энергия и источник колебательной энергии в m-ой моде; $k_{n}^{f}$, $k_{n}^{r}$ – константы скоростей прямых и обратных химических реакций; N_r – число химических реакций; ${{Q}_{{ei}}}$, ${{Q}_{{ea}}}$, ${{Q}_{{ai}}}$, ${{Q}_{{ion}}}$, ${{Q}_{{e\text{v}}}}$ – источниковые слагаемые в уравнении сохранения энергии электронного газа (1.2), обусловленные энергообменом в элементарных процессах в частично ионизованном газе, соответственно при столкновении электронов с ионами и нейтралами, ассоциативная и ударная ионизация, резонансные взаимодействия с колебаниями молекул (в K/см³ с) [13, 14]

${{Q}_{{ei}}} = 1.21 \times {{10}^{{20}}}{{X}_{e}}{{X}_{i}}\frac{{T - {{T}_{e}}}}{{T_{e}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}\ln \Lambda $

${{Q}_{{ea}}} = 3.378 \times {{10}^{{10}}}{{X}_{e}}{{X}_{a}}\sqrt {{{T}_{e}}} \left( {T - {{T}_{e}}} \right)\left[ {1 - {{{\left( {1 + \frac{{{{T}_{e}}}}{{T_{a}^{ * }}}} \right)}}^{{ - 1}}}} \right],\quad a = {\text{N}},\;{\text{O}}$

${{Q}_{{ai}}} = T\sum\limits_{q = 1}^3 {{{\alpha }_{q}}k_{q}^{f}{{X}_{{{{a}_{q}}}}}{{X}_{{{{b}_{q}}}}}} - {{T}_{e}}\sum\limits_{q = 1}^3 {{{\beta }_{q}}k_{q}^{r}{{X}_{e}}{{X}_{{{{{({{a}_{q}}{{b}_{q}})}}^{ + }}}}}} $

${{Q}_{{ion}}} = - {{\gamma }_{i}}Tk_{{{\text{N}},e}}^{f}{{X}_{{\text{N}}}}{{X}_{e}} - {{\delta }_{i}}Tk_{{{\text{O}},e}}^{f}{{X}_{{\text{O}}}}{{X}_{e}} + {{\gamma }_{r}}Tk_{{{\text{N}}_{2}^{ + },r}}^{f}{{X}_{{{\text{N}}_{2}^{ + }}}}X_{e}^{2} + {{\delta }_{r}}Tk_{{{\text{O}}_{2}^{ + },r}}^{f}{{X}_{{{\text{O}}_{2}^{ + }}}}X_{e}^{2}$

где $\ln \Lambda = 7.47 + 1.5\lg (T) - 0.5\lg ({{n}_{e}})$ – кулоновский логарифм; ${{T}_{e}}$ – температура электронов; $T_{{\text{N}}}^{ * }$ = 31 000 K, $T_{{\text{O}}}^{ * }$ = 12 000 K; q – признак реакции ассоциативной ионизации ($q = 1$: ${\text{N}} + {\text{O}} \to {\text{N}}{{{\text{O}}}^{ + }} + e$; $q = 2$: ${\text{N}} + {\text{N}} \to {\text{N}}_{2}^{ + } + e$; $q = 3$: ${\text{O}} + {\text{O}} \to {\text{O}}_{2}^{ + } + e$); ${{\alpha }_{q}}$, ${{\beta }_{q}}$ – коэффициенты преобразования энергии (эти значения изменялись в интервале 0.05–0.1); $k_{q}^{f}$, $k_{g}^{r}$ – коэффициенты скорости реакции ассоциации и диссоциации; ${{k}_{{{\text{N}},e}}}$, ${{k}_{{{\text{O}},e}}}$, ${{k}_{{{\text{N}}_{2}^{ + },r}}}$, ${{k}_{{{\text{O}}_{2}^{ + },r}}}$ – константы ударной ионизации электронов и ионно-ионной диссоциативной рекомбинации; коэффициенты ${{\gamma }_{i}}$, ${{\gamma }_{r}}$ и ${{\delta }_{i}}$, ${{\delta }_{r}}$ позволяют учитывать эффективность ионизационных и рекомбинационных процессов (эти коэффициенты оцениваются величиной 0.1–1);

${{Q}_{{e\text{v}}}} = 2 \times {{10}^{{ - 16}}}{{n}_{e}}{{n}_{{{{{\text{N}}}_{2}}}}}{{\omega }_{e}}{{P}_{{1,{\text{0}}}}} \times \left[ {\frac{{{{E}_{e}}}}{{{{{\left( {1 - {{E}_{e}}} \right)}}^{2}}}} - \frac{{{{E}_{\text{V}}}}}{{{{{\left( {1 - {{E}_{\text{V}}}} \right)}}^{2}}}}} \right]$

${{\omega }_{e}} = 2358.57\,\,{\text{c}}{{{\text{m}}}^{{ - 1}}},\quad {{P}_{{1,0}}} = 0.45 \times {{10}^{{ - 10}}}\exp \left( { - \frac{{10\,000}}{{{{T}_{e}}}}} \right)$

${{E}_{e}} = \exp \left( { - \frac{{1.44{{\omega }_{e}}}}{{{{T}_{e}}}}} \right)$, ${{E}_{\text{V}}} = \exp \left( { - \frac{{1.44{{\omega }_{e}}}}{{{{T}_{v}}}}} \right)$

Использованная в расчетах кинетическая модель приведена в [8]. Заметим, что для численного интегрирования уравнений (1.1)–(1.4) используется модель установившегося движения ФУВ.

2. МОДЕЛЬ НАВЬЕ−СТОКСА ДВИЖЕНИЯ ВЯЗКОГО ТЕПЛОПРОВОДНОГО ХИМИЧЕСКИ РЕАГИРУЮЩЕГО ГАЗА С УЧЕТОМ ФИЗИЧЕСКОЙ КИНЕТИКИ

Эта модель основана на двумерных осесимметричных уравнениях Навье–Стокса для вязкого ударного слоя вблизи затупленного тела в гиперзвуковом потоке (см. фиг. 2). Задача решается методом установления. На каждом временном (итерационном) шаге интегрируются следующие группы уравнений с дополнительными внутренними итерациями для учета радиационно-газодинамического (РадГД) взаимодействия

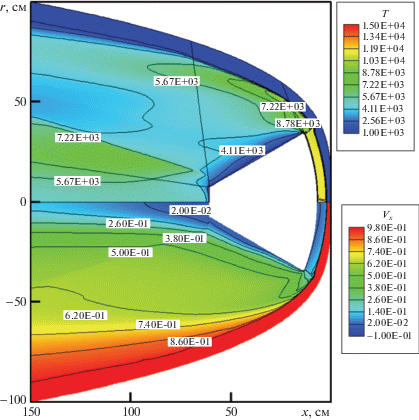
Фиг. 2.

Поле температур поступательных степеней свободы (в K) и проекции скорости на осевое направление ${{V}_{x}} = u{\text{/}}{{V}_{\infty }}$: Fire-II, t = 1634 с

– уравнение неразрывности

(2.1)

$\frac{{d\rho }}{{dt}} + \rho {\text{div}}\left( {\mathbf{V}} \right) = 0$

– уравнения Навье–Стокса

$\frac{{d\rho u}}{{dt}} + \rho u{\text{div}}\left( {\mathbf{V}} \right) = - \frac{{\partial p}}{{\partial x}} - \frac{2}{3}\frac{\partial }{{\partial x}}\left( {\mu {\text{div}}{\mathbf{V}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r\mu \left( {\frac{{\partial \text{v}}}{{\partial x}} + \frac{{\partial u}}{{\partial r}}} \right)} \right] + 2\frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right)$

(2.2)

$\begin{gathered} \frac{{d\rho \text{v}}}{{dt}} + \rho \text{v}{\text{div}}\left( {\mathbf{V}} \right) = - \frac{{\partial p}}{{\partial r}} - \frac{2}{3}\frac{\partial }{{\partial r}}\left( {\mu {\text{div}}{\mathbf{V}}} \right) + \frac{\partial }{{\partial x}}\left[ {\mu \left( {\frac{{\partial \text{v}}}{{\partial x}} + \frac{{\partial u}}{{\partial r}}} \right)} \right] + \\ + \;2\frac{\partial }{{\partial r}}\left( {\mu \frac{{\partial \text{v}}}{{\partial r}}} \right) + 2\mu \frac{\partial }{{\partial r}}\left( {\frac{\text{v}}{r}} \right) \\ \end{gathered} $

– уравнение сохранения энергии в виде уравнения Фурье–Кирхгофа для температуры поступательных степеней свободы

(2.3)

$\rho {{c}_{p}}\frac{{dT}}{{dt}} = \operatorname{div} \left( {\lambda \operatorname{grad} T - \sum\limits_{i = 1}^{{{N}_{s}}} {{{h}_{i}}{{{\mathbf{J}}}_{i}}} - {{{\mathbf{q}}}_{r}}} \right) + \frac{{dp}}{{dt}} + {{\Phi }_{\mu }} + {{Q}_{{vib}}} - \sum\limits_{i = 1}^{{{N}_{s}}} {{{h}_{i}}{{{\dot {w}}}_{i}}} $

– уравнения сохранения энергии в колебательных модах

(2.4)

$\frac{{d\rho {{e}_{{\text{v},m}}}}}{{dt}} + \rho {{e}_{{v,m}}}\operatorname{div} \left( {\mathbf{V}} \right) = \operatorname{div} \left( { - {{{\mathbf{J}}}_{m}}{{e}_{{\text{v},m}}}} \right) + {{\dot {e}}_{{\text{v},m}}},\quad m = 1,2,\; \ldots ,\;{{N}_{V}}$

– уравнения неразрывности для компонент смеси газов

(2.5)

$\frac{{d{{\rho }_{i}}}}{{dt}} + {{\rho }_{i}}\operatorname{div} {\mathbf{V}} = - \operatorname{div} {{{\mathbf{J}}}_{i}} + {{\dot {w}}_{i}},\quad i = 1,2,\; \ldots ,\;{{N}_{s}}$

Здесь $d{\text{/}}dt = \partial {\text{/}}\partial t + {\mathbf{V}} \times \nabla $; t – время; V, $u$, $\text{v}$ – вектор скорости и его компоненты вдоль осей x и r; c_p, $\mu $, $\lambda $ – удельная теплоемкость при постоянном давлении, вязкость, теплопроводность; ${{\rho }_{i}}$, ${{h}_{i}}$, ${{{\mathbf{J}}}_{i}}$, ${{\dot {w}}_{i}}$ – плотность, энтальпия, диффузионный массовый поток и массовая скорость образования i-го компонента газовой смеси

${{\dot {w}}_{i}} = {{M}_{i}}\frac{{\partial {{X}_{i}}}}{{\partial t}} = {{M}_{i}}\sum\limits_{n = 1}^{{{N}_{r}}} {{{{\left( {\frac{{\partial {{X}_{i}}}}{{\partial t}}} \right)}}_{n}}} = {{M}_{i}}\sum\limits_{n = 1}^{{{N}_{r}}} {\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)(S_{n}^{f} - S_{n}^{r})} ,\quad i = 1,2,\; \ldots ,\;{{N}_{s}}$

Величины ${{\Phi }_{\mu }}$, ${{Q}_{{vib}}}$, ${{{\mathbf{q}}}_{r}}$, M_i – диссипативная функция, источник тепла, связанный с процессами колебательной релаксации, вектор плотности интегрального радиационного теплового потока, молекулярный вес i-ой компоненты соответственно.

Диссипативная функция рассчитывается по формуле

${{\Phi }_{\mu }} = \mu \left[ {2{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}}^{2}} + } \right.\left. {{{{\left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)}}^{2}} - \frac{2}{3}{{{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right)}}^{2}}} \right]$

В обеих моделях используется термическое уравнение состояния идеального газа

$p = \frac{{\rho {{R}_{0}}T}}{{{{M}_{\Sigma }}}} = nkT$

а средние для смеси газов функции рассчитываются по соотношениям

${{M}_{\Sigma }} = \sum\limits_{i = 1}^N {{{M}_{i}}{{x}_{i}}} = {{\left( {\sum\limits_{i = 1}^N {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}} } \right)}^{{ - 1}}},\quad n = \sum\limits_i^{{{N}_{s}}} {{{n}_{i}},\quad } {{x}_{i}} = \frac{{{{n}_{i}}}}{n} = \frac{{{{p}_{i}}}}{p},\quad {{Y}_{i}} = \frac{{{{\rho }_{i}}}}{\rho }$

$h = \left[ {(T - {{T}^{0}})\left( {\frac{5}{2} + \sum\limits_{i = 1}^{{{L}_{2}}} {{{x}_{i}}} } \right) + \sum\limits_{m = 1}^{{{N}_{\text{v}}}} {{{x}_{{i(m)}}}} \frac{{{{\theta }_{m}}}}{{\exp \left( {{{{{\theta }_{m}}} \mathord{\left/ {\vphantom {{{{\theta }_{m}}} {{{T}_{{\text{v,}m}}}}}} \right. \kern-0em} {{{T}_{{\text{v,}m}}}}}} \right) - 1}} + \sum\limits_{i = 1}^{{{N}_{s}}} {{{\Delta }_{f}}H_{i}^{0}{{x}_{i}}} } \right]\frac{{{{R}_{0}}}}{{{{M}_{\Sigma }}}}$

где ${{T}_{{\text{v},m}}}$ – колебательная температура в m-ой моде; ${{\tau }_{{\text{v},m,i}}}$ – время колебательной VT-релаксации для молекулы с колебательной модой m при столкновениях с i-ми частицами; L₂ = 6 – число двухатомных компонент; характерные колебательные температуры нейтральных двухатомных молекул: ${{\theta }_{1}} = 3396$ K (N₂), ${{\theta }_{2}} = 2275$ K (О₂) и ${{\theta }_{3}} = 2742$ K (NО); ${{\Delta }_{f}}H_{i}^{0}$ – тепловой эффект образования i-й компоненты при стандартной температуре T⁰.

Коэффициенты скорости для прямой и обратной реакций моделируются модифицированным уравнением Аррениуса

$k_{i}^{{f(r)}} = {{A}_{{i,f(r)}}}{{T}^{{{{n}_{{i,f(r)}}}}}}\exp \left( { - {{E}_{{i,f(r)}}}{\text{/}}T} \right)$

Они связаны между собой константой равновесия, аппроксимируемой также аррениусовской зависимостью

${{K}_{{i,eq}}} = {{k}_{{i,f}}}{\text{/}}{{k}_{{i,r}}}$, ${{K}_{{i,eq}}} = {{A}_{{i,eq}}}{{T}^{{{{n}_{{i,eq}}}}}}\exp \left( {{{E}_{{i,eq}}}{\text{/}}T} \right)$

где ${{E}_{{i,eq}}}$ – энергия активации в K.

Коэффициенты скорости диссоциации молекул, для которых учитывалась колебательная энергия в m-й моде, модифицировались в соответствии с моделью Мерроуна–Тринора [15]

$k\left( {{{T}_{{\text{v,}m}}},T} \right) = k_{d}^{{(f,r),0}}\left( T \right)Z\left( {{{T}_{{\text{v,}m}}},T} \right)$

$Z\left( {T,{{T}_{v}}} \right) = \frac{{Q\left( T \right)Q\left( {{{T}_{F}}} \right)}}{{Q\left( {{{T}_{v}}} \right)Q\left( { - U} \right)}}$, $Q\left( {{{T}_{\alpha }}} \right) = \frac{{1 - \exp \left( { - {{D}_{0}}{\text{/}}{{T}_{\alpha }}} \right)}}{{1 - \exp \left( { - \theta {\text{/}}{{T}_{\alpha }}} \right)}}$

${{T}_{\alpha }} = \{ T,\;{{T}_{\text{v}}},\;{{T}_{F}},\; - U\} ;\quad T_{F}^{{ - 1}} = {{T}_{\text{v}}}^{{ - 1}} - {{T}^{{ - 1}}} - {{U}^{{ - 1}}},\quad U = {{D}_{0}}{\text{/}}3;\quad {{T}_{\text{v}}} < T$

где: $k_{d}^{{(f,r),0}}$ – равновесный коэффициент скорости диссоциации, ${{D}_{0}}$ – энергия диссоциации в K.

Источниковые слагаемые в уравнениях сохранения колебательной энергии (1.4), (2.4) и энергии поступательных степеней свободы (2.3) имеют вид

${{Q}_{{vib}}} = - \sum\limits_{m = 1}^{{{N}_{\text{v}}}} {(Q_{{\text{v}T}}^{m} + Q_{{\text{vv}}}^{m} + Q_{{\text{cv}}}^{m})} ,\quad Q_{{\text{v}T}}^{m} = \frac{{e_{{\text{v},m}}^{0} - {{e}_{{\text{v},m}}}}}{{{{\tau }_{{\text{v},m}}}}},\quad {{\tau }_{{\text{v},m}}} = {{\left( {\sum\limits_{i = 1}^{{{N}_{s}}} {\frac{{{{x}_{i}}}}{{{{\tau }_{{\text{v},m,i}}}}}} } \right)}^{{ - 1}}}$

${{e}_{{\text{v},m}}} = \frac{{{{R}_{0}}{{\theta }_{m}}}}{{{{M}_{{i(m)}}}\left[ {\exp \left( {{{\theta }_{m}}{\text{/}}{{T}_{{\text{v},m}}}} \right) - 1} \right]}},\quad e_{{\text{v},m}}^{0} = \frac{{{{R}_{0}}{{\theta }_{m}}}}{{{{M}_{{i(m)}}}\left[ {\exp \left( {{{\theta }_{m}}{\text{/}}T} \right) - 1} \right]}}$

$Q_{{\text{vv}}}^{m} = {{k}_{{\text{v},m,n}}}\left[ {{{e}_{{\text{v},n}}}\left( {{{e}_{{\text{v},m}}} + 1} \right)\exp \left( {\frac{{{{\theta }_{n}}}}{T} - \frac{{{{\theta }_{m}}}}{T}} \right) - {{e}_{{\text{v},m}}}\left( {{{e}_{{\text{v},n}}} + 1} \right)} \right]$

$\begin{gathered} Q_{{c\text{v}}}^{m} = - \left[ {\frac{1}{{{{X}_{{i(m)}}}}}\sum\limits_{n = 1}^{{{N}_{r}}} {\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)S_{{i,n}}^{f}} } \right](e_{{\text{v},m}}^{*}(T,{{T}_{{\text{v},m}}}) - {{e}_{{\text{v},m}}}) + \\ + \;\left[ {\frac{1}{{{{X}_{{i(m)}}}}}\sum\limits_{n = 1}^{{{N}_{r}}} {\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)S_{{i,n}}^{r}} } \right](e_{{\text{v},m}}^{*}(T,T) - {{e}_{{\text{v},m}}}) \\ \end{gathered} $

где ${{\tau }_{{\text{v},m,i}}}$ – время колебательной VT-релаксации для молекулы с колебательной модой m при столкновении с i-й частицей, определяемая по [16]; ${{k}_{{\text{v},m,n}}}$ – константа реакции межмодового обмена колебательной энергией, рассчитываемая по [9, 14]. Здесь и далее индексы вида i(m) обозначают i-ю компоненту, обладающую колебательной модой m.

В работе [15] показано, что при использовании модели преимущественной диссоциации с возбужденных колебательных уровней, средняя энергия колебаний, теряемой при диссоциации равна

$e_{{\text{v},m}}^{*}(T,{{T}_{{\text{v},m}}}) = {{e}_{{\text{v},m}}}({{T}_{F}})$

а приобретенная при рекомбинации –

$e_{{\text{v},m}}^{*}(T,T) = {{e}_{{\text{v},m}}}( - U)$

Расчеты неравновесной спектральной излучательной способности (в Вт/(см³ ср)) нагретого воздуха за фронтом ударной волны проводились по следующей зависимости:

${{\varepsilon }_{{J{\text{'}},J{\text{''}}}}} = 2.303 \times {{10}^{{ - 23}}}{{N}_{{J'}}}\omega _{{J{\text{'}}J{\text{''}}}}^{4}\frac{{{{S}_{{\text{v}{\text{'}}\text{v}{\text{''}}}}}}}{{\left( {2 - {{\delta }_{{0,\Lambda {\text{'}} + \Lambda {\text{''}}}}}} \right)\left( {2S + 1} \right)}}\frac{{{{S}_{{J{\text{'}},J{\text{''}}}}}}}{{\left( {2J{\text{'}} + 1} \right)}}$

где ${{S}_{{\text{v}{\text{'}}\text{v}{\text{''}}}}} = \left( {2 - {{\delta }_{{0,\Lambda {\text{'}} + \Lambda {\text{''}}}}}} \right)\left( {2S + 1} \right){{\left| {{{R}_{{\text{v}{\text{'}}\text{v}{\text{''}}}}}} \right|}^{2}}$, ${{R}_{{v{\text{'}}v{\text{''}}}}}$ – сила и матричный элемент вибронного (электронно-колебательного) перехода, см^–1, ${{S}_{{J{\text{'}}J{\text{''}}}}}$, ${{\omega }_{{J{\text{'}}J{\text{''}}}}}$ – сила и волновое число вращательной линии; ${{N}_{{J{\text{'}}}}}$ – заселенность верхнего энергетического уровня; $\Lambda $, $S$, $J$, $\text{v}$ – квантовые числа проекции орбитального и спинового момента электронов на межъядерную ось, вращательного и колебательного состояний; один и два штриха фиксируют соответственно верхнее и нижнее квантовые состояния; ${{\delta }_{{0,\Lambda {\text{'}} + \Lambda {\text{''}}}}}$ – дельта-символ Кронекера. Квадрат матричного элемента вибронного перехода представлялся в виде

${{\left| {{{R}_{{\text{v}{\text{'}}\text{v}{\text{''}}}}}} \right|}^{2}} = \frac{{3h}}{{64{{\pi }^{4}}a_{0}^{2}{{e}^{2}}}}\frac{{2 - {{\delta }_{{0,\Lambda {\text{'}}}}}}}{{2 - {{\delta }_{{0,\Lambda {\text{'}} + \Lambda {\text{''}}}}}}}\frac{1}{{\omega _{{\text{v}{\text{'}}\text{v}{\text{''}}}}^{3}}}{{A}_{{\text{v}{\text{'}}\text{v}{\text{''}}}}}$

где ${{A}_{{\text{v}{\text{'}}\text{v}{\text{''}}}}}$ – коэффициент Эйнштейна вибронного перехода.

И, наконец, спектральная излучательная способность в узких спектральных полосах (∼$\Delta \omega $ ~ ~ 20 см^–1) рассчитывалась по формуле

(2.6)

${{I}_{{rad,\Delta \omega }}} = \sum\limits_{\text{v}{\text{'}}} {\sum\limits_{J'} {{{\varepsilon }_{{J{\text{'}}J{\text{''}}}}}} } $

Для расчета источника тепловыделения ${\text{div}}{{{\mathbf{q}}}_{r}}$ в уравнении (2.3), связанного с процессами лучистого теплообмена, решалось уравнение переноса селективного теплового излучения

(2.7)

$\Omega \frac{{\partial {{J}_{\omega }}\left( {{\mathbf{r}},\Omega } \right)}}{{\partial {\mathbf{r}}}} + {{\kappa }_{\omega }}({\mathbf{r}}){{J}_{\omega }}\left( {{\mathbf{r}},\Omega } \right) = {{j}_{\omega }}({\mathbf{r}}),$

где ${{J}_{\omega }}\left( {{\mathbf{r}},\Omega } \right)$ – спектральная интенсивность теплового излучения; ${{\kappa }_{\omega }}({\mathbf{r}})$ – коэффициент спектрального поглощения; ${{j}_{\omega }}({\mathbf{r}})$ – коэффициент спектральной эмиссии, который рассчитывается в случае локального термодинамического равновесия по формуле Кирхгофа ${{j}_{\omega }}({\mathbf{r}}) = {{\kappa }_{\omega }}({\mathbf{r}}){{J}_{{b,\omega }}}({\mathbf{r}})$, ${{J}_{{b,\omega }}}({\mathbf{r}})$ – спектральная интенсивность излучения абсолютно черного тела (функция Планка); r – координата точки на поверхности; Ω – вектор направленности.

Метод полумоментов использовался для расчета радиационного переноса внутри неоднородных ударных слоев в многогрупповом приближении. Этот метод позволял рассчитывать однонаправленные интегральные радиационные тепловые потоки от поверхности ($M_{1}^{ + }$) и к поверхности ($M_{1}^{ - }$). Спектральные оптические свойства рассчитывались с помощью кода ASTEROID [17], который основан на квазиклассических и квантово-механических моделях и использует только исходную спектроскопическую информацию, поэтому фактически все спектральные оптические свойства вычислялись с помощью ab-initio подхода.

Будучи решенным, это уравнение позволяет рассчитать полный поток радиационного тепла на элементе с локальной нормалью n:

${{q}_{R}} = M_{1}^{ - } = \left( {{\mathbf{n}} \cdot {{{\mathbf{q}}}_{R}}} \right) = \int\limits_{{\text{4}}\pi } {{\text{d}}\Omega } \int\limits_{\Delta {{\omega }_{{tot}}}} {{{J}_{\omega }}\left( {{\mathbf{r}},\Omega } \right)\left( {{\mathbf{n}} \cdot \Omega } \right){\text{d}}\omega } $

где $\Delta {{\omega }_{{tot}}} = {{\omega }_{{\max }}} - {{\omega }_{{\min }}} = 150\,{\kern 1pt} 000\, - \,1000$ см^–1.

Коэффициенты вязкости, теплопроводности и эффективного коэффициента диффузии газовых смесей рассчитываются в системе СГС (соответственно: г/см⋅с, эрг/см ⋅ с ⋅ K, см²/с) по следующим формулам [18]:

$\mu = \frac{1}{{\sum\limits_{i = 1}^{{{N}_{c}}} {\left( {{{Y}_{i}}{\text{/}}{{\mu }_{i}}} \right)} }}$, $\lambda = \frac{1}{2}\left[ {\sum\limits_{i = 1}^{{{N}_{c}}} {{{x}_{i}}{{\lambda }_{i}}} + \frac{1}{{\sum\limits_{i = 1}^{{{N}_{c}}} {\left( {{{x}_{i}}{\text{/}}{{\lambda }_{i}}} \right)} }}} \right]$

${{\mu }_{i}} = 2.67 \times {{10}^{{ - 5}}}\frac{{\sqrt {{{M}_{i}}T} }}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2)*}}}}$, ${{\lambda }_{i}} = 8330\sqrt {\frac{T}{{{{M}_{i}}}}} \frac{1}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2)*}}}}$, ${{D}_{i}} = \frac{{1 - {{x}_{i}}}}{{\sum\limits_{j \ne i}^{{{N}_{c}}} {\left( {{{x}_{j}}{\text{/}}{{D}_{{ij}}}} \right)} }}$

${{D}_{{i,j}}} = 1.858 \times {{10}^{{ - 3}}}\sqrt {{{T}^{3}}\frac{{{{M}_{i}} + {{M}_{j}}}}{{{{M}_{i}}{{M}_{j}}}}} \frac{1}{{p\sigma _{{i,j}}^{2}\Omega _{{i,j}}^{{(1,1)*}}}}$

где ${{\sigma }_{i}}$ – диаметр столкновения, А; $\Omega _{i}^{{(2,2)*}}$, $\Omega _{{i,j}}^{{(1,1)*}}$ – интегралы столкновений; ${{\sigma }_{{i,j}}}$ – диаметр бинарного столкновения, А; ${{D}_{{i,j}}}$ – коэффициент бинарной диффузии.

Граничные условия для псевдокаталитической поверхности использовались в следующем виде:

${{\left( {{{Y}_{i}}} \right)}_{w}} = {{Y}_{{i,\infty }}},\quad i = 1,2,3,\; \ldots ,\;{{N}_{s}}$

где ${{Y}_{{i,\infty }}}$ – массовые доли в потоке встречного газа.

Температура поверхности рассчитывается по модели равновесной излучающей поверхности:

$\varepsilon \sigma T_{w}^{4} = {{q}_{w}}$

где ε степень черноты поверхности ($\varepsilon = 0.8$); $\sigma = 5.67 \times {{10}^{{ - 12}}}$Вт/(см² ⋅ K⁴) – постоянная Стефана-Больцмана; ${{q}_{w}} = {{q}_{c}} + M_{1}^{ - }$ – полная плотность теплового потока, включающая конвективную и лучистую составляющие.

Двухмерная задача радиационной газовой динамики СА Fire-II решалась с использованием авторского компьютерного кода NERAT [17] на структурированной трехблочной сетке, границы блоков которой показаны на фиг. 2.

3. СРАВНЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ И РАСЧЕТНЫХ ДАННЫХ

Одномерные расчеты физико-химической кинетики за ФУВ и двухмерные расчеты РадГД СА Fire-II выполнены для 4-х траекторных точек, параметры которых даны в таблице ниже. На фиг. 2 показаны двумерные поля поступательной температуры и продольной скорости в первой из полученных траекторных точек. Видно, что фронт головной ударной волны, ограничивающий сжатый слой со стороны набегающего потока, эквидистантен поверхности СА. Температура в сжатом слое составляет ∼11 000 K. За боковой кромкой лобового аэродинамического щита температура падает до ∼5000 K, а затем, в следе, газ опять нагревается до температуры ∼7500 K. Вблизи заднего аэродинамического щита наблюдается возвратно-вихревое движение.

Таблица.

Траекторные параметры Fire-II

t, s	1634	1636	1637	1639
ρ_∞ × 10⁺⁷, г/см³	0.372	0.857	1.47	2.41
p_∞, эрг/см³	20.8	51.7	96.2	167.4
T_∞, К	195	210	228	242
T_w, К	615	810	1030	1325
V_∞, км/с	11.36	11.31	11.25	11.14

Данные, приведенные на фиг. 2, отвечают первой из рассмотренных траекторных точек, в которой реализуются неравновесные условия течения в сжатом слое. По мере спуска СА в атмосфере значительно возрастает плотность набегающего потока, а торможение СА еще незначительно, поэтому сильно возрастают скоростной напор и объемная энергия набегающего потока. В результате наблюдается более эффективная термализация внутренних степеней свободы газа в сжатом слое.

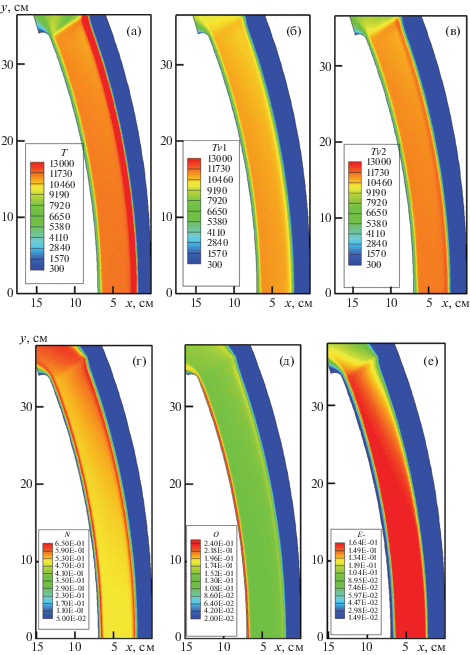
Распределения поступательной и колебательных температур N₂ и O₂ в сжатом слое за фронтом ударной волны и относительные мольные концентрации атомов N и O, а также электронов при t = 1634 с показаны на фиг. 3. Расчеты выполнены на сетке с числом узлов 121 × 137 по нормали к поверхности и вдоль нее. На фиг. 3 хорошо идентифицируются пограничный слой вблизи обтекаемой поверхности и фронт головной ударной волны.

Фиг. 3.

Температуры (в K) поступательных степеней свободы (а) и колебательного возбуждения N₂ (б) и O₂ (в). Мольные доли N (г), O (д) и электронов (е): Fire-II, t = 1634 с

Распределения поступательной и колебательных температур, рассчитанные с учетом и без учета радиационно-газодинамического (РадГД) взаимодействия, показаны на фиг. 4а, 4б для двух траекторных точек Fire-II: t = 1634 и 1639 с. При учете РадГД взаимодействия принимаются в учет потери энергии на тепловое излучение и реабсорбция испущенного излучения в самом слое. Как правило, наблюдаются два эффекта: падение температуры сжатого слоя и дополнительный нагрев пограничного слоя за счет поглощения излучения в нем (в основном, в области вакуумного ультрафиолета, при длине волны излучения $\lambda $ < 200 нм). Из указанных рисунков хорошо видно, насколько быстро термализуется область сжатого слоя для более поздней траекторной точки при t = 1639 с.

Фиг. 4.

Осевое распределение поступательных и колебательных температур вдоль критической линии тока при t = 1634 с (а), (в) и при t = 1639 с (б), (г) в одномерной модели (в), (г) и в двухмерной модели (а), (б) с учетом РадГД взаимодействия (кружки) и без учета РадГД взаимодействия (квадратики)

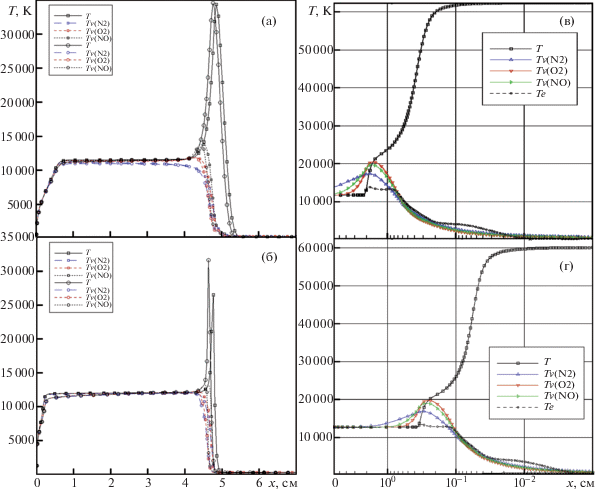
На фиг. 4в, 4г показаны результаты одномерных расчетов поступательной, электронной и колебательных температур за фронтом ударной волны по модели Эйлера для тех же траекторных точек. Поступательная температура в сжатом слое получилась одинаковой при использовании обеих моделей. Колебательные температуры в значительной части сжатого слоя в одномерной модели превосходят получаемые в двухмерной модели. Обратим внимание, что температурные профили на фиг. 4в, 4г даны в логарифмической шкале, позволяющей проанализировать в деталях изменение газодинамических функций за ФУВ. В этом одно из преимуществ одномерной модели, в которой расчет ведется с очень малым шагом по времени (по пространству), гарантирующим практически точное решение жесткой системы кинетических уравнений. Результаты решения одномерной задачи являются важным дополнением к результатам решения двухмерной задачи, решаемой методом сквозного счета, когда максимальная поступательная температура разрешается со значительной погрешностью ввиду того, что пространственное разрешение в окрестности ФУВ оказывается существенно грубее. Вместе с тем отметим, что указанная погрешность не приводит к заметным негативным последствиям для решения двухмерной задачи в сжатом слое.

Сравнение относительных мольных концентраций в сжатом слое при t = 1634 и 1639 с дано на фиг. 5. Отметим хорошее совпадение мольных концентраций в сжатом слое и хорошее соответствие толщин зон химической релаксации за ФУВ.

Фиг. 5.

Осевое распределение мольных долей компонент частично ионизованного воздуха вдоль критической линии тока в двухмерной (а), (б) и одномерной (в), (г) моделях при t = 1634 с (а), (в) и t = 1639 с (б), (г). Отдельно обозначены электронно-возбужденные состояния: ${{N}_{2}}$ (${{A}^{3}}{{\Sigma }_{u}}$, ${{B}^{3}}{{\Pi }_{g}}$, ${{C}^{3}}{{\Pi }_{u}}$, ${{D}^{3}}\Sigma _{u}^{ + }$, ${{b}^{1}}{{\Pi }_{u}}$, $b{{{\text{'}}}^{1}}{{\Sigma }_{u}}$), $NO$ (${{A}^{2}}{{\Sigma }^{ + }}$, ${{D}^{2}}\Pi $, ${{C}^{2}}\Pi $, ${{D}^{2}}{{\Sigma }^{ + }}$), $N_{2}^{ + }$ (${{A}^{2}}{{\Pi }_{u}}$, ${{B}^{2}}\Sigma _{u}^{ + }$, ${{C}^{2}}\Sigma _{u}^{ + }$) и ${{O}_{2}}$ (${{B}^{3}}\Sigma _{u}^{ - }$)

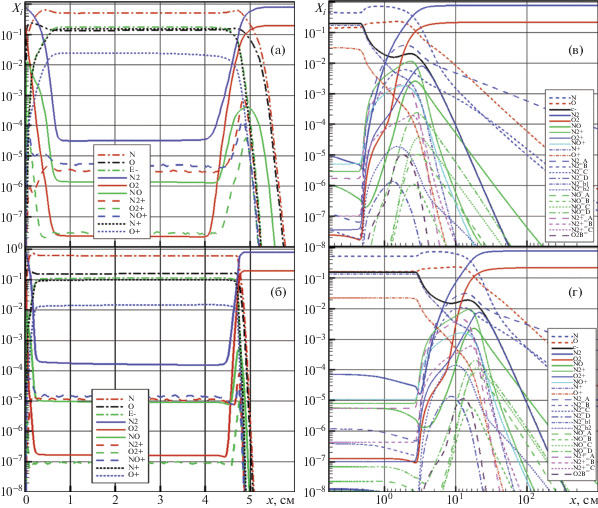
По аналогии с температурными распределениями на фиг. 5в, 5г показаны мольные доли компонент в логарифмической зависимости от величины отхода от ФУВ. Здесь, кроме 11 компонент частично ионизованного воздуха, даны заселенности наиболее важных электронно-возбужденных состояний, которые, в соответствии с гибридной РС моделью, в одномерной модели считались отдельными компонентами газовой смеси. Для остальных компонент, представленных на фиг. 5в, 5г, даны заселенности основного и всех возбужденных состояний. Константы скоростей реакций для них и для отдельных электронно-возбужденных состояний взяты из [8]. При использовании многотемпературной двухмерной модели для расчета переноса излучения и определения заселенностей электронно-возбужденных состояний молекул применялась модель Больцмана с температурой ${{T}_{e}}$, которая близка средневзвешенной колебательной температуре (см. фиг. 4в, 4г).

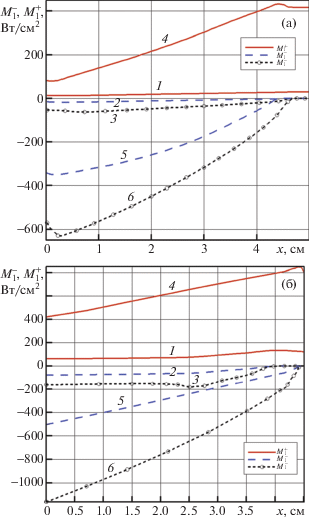
С использованием полученных температурных распределений и мольных концентраций были рассчитаны распределения односторонних радиационных тепловых потоков к поверхности и от поверхности. Толщина высокотемпературной области в одномерной задаче задавалась $\delta = 4.5$ см, что соответствует результатам двухмерных расчетов. На фиг. 6а, 6б показаны распределения указанных интегральных радиационных тепловых потоков по толщине сжатого слоя в окрестности критической линии тока. Радиационные потоки на поверхности рассчитаны без и с учетом атомных линий, вклад которых оказывается весьма значительным. Хорошо видно поглощение излучения в пограничном слое в двухмерной задаче (кривые 3 и 6 на фиг. 6а). Плотность интегральных радиационных тепловых потоков на обтекаемой поверхности в расчетах по двухмерной модели оказывается значительно ниже, чем в одномерных расчетах. Это же хорошо видно на распределениях кумулятивных функций спектральных радиационных тепловых потоков

(3.1)

${{Q}_{r}} = \int\limits_{{{\omega }_{{\min }}}}^\omega {M_{{1,\omega }}^{ - }d\omega } $

представленных на фиг. 7 и соответствующих плотностей спектральных радиационных тепловых потоков. Исходя из определения кумулятивной функции (3.1) интегральная плотность радиационного теплового потока, достигающего поверхности (величина $M_{1}^{ - }$ $(x = 0)$ на фиг. 6), определяется по величине ${{Q}_{r}}({{\omega }_{{\max }}})$.

Фиг. 6.

Осевое распределение вдоль критической линии тока плотностей однонаправленных от поверхности ($M_{1}^{ + }$) и к поверхности ($M_{1}^{ - }$) интегральных радиационных тепловых потоков в двухмерной (а) и одномерной (б) задачах при t = 1634 с (кривые 1–3) и t = 1639 с (4–6); 2, 5 – без учета атомных линий, 3, 6 – с учетом атомных линий. Без учета РадГД взаимодействия

Фиг. 7.

Плотность спектральных радиационных тепловых потоков в критической точке в двухмерной (а), (б) и одномерной (в), (г) задачах с учетом (кривые 1 и 3) и без учета (2, 4) атомных линий при t = 1634 с (а), (в) и t = 1639 с (б), (г). Без учета РадГД-взаимодействия.

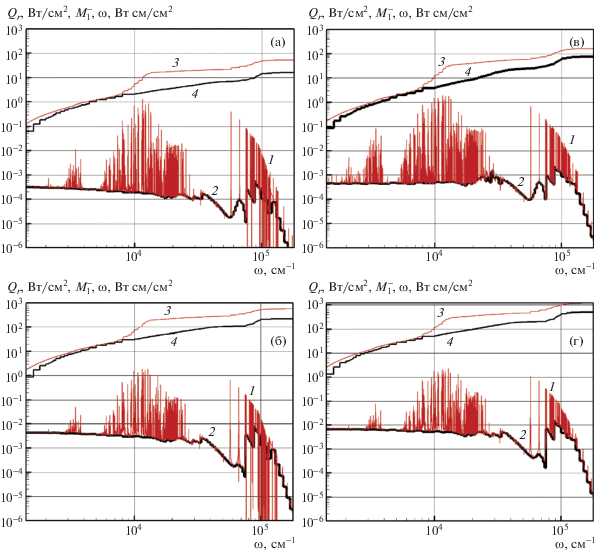
Из распределений плотностей спектральных радиационных тепловых потоков на фиг. 7а, 7б хорошо видно, что в двухмерной модели наблюдается систематическое снижение плотности потока в ультрафиолетовой области спектра, где расположены атомные линии, образованные при квантовых переходах между основными и нижними возбужденными состояниями, в то время, как в одномерной модели (фиг. 7в, 7г) значительного поглощения не наблюдается. Причина этого обсуждалась выше и связана с поглощением излучения в пограничном слое в двухмерном случае. В видимой и ближней инфракрасной области ($\omega $ < 20 000 см^–1) реабсорбция в центрах атомных линий не наблюдается.

Сравнивая температурные распределения на фиг. 4а, 4б в два момента времени, отметим, что зона релаксации за фронтом ударной волны уменьшилась более, чем на порядок (см. фиг. 4в, 4г). Уменьшилась также толщина пограничного слоя у поверхности в расчетах по двухмерной модели. Соответственно уменьшилась протяженность области химической релаксации. Расчеты по одномерной и двухмерной моделям дают близкие температуры в сжатом слое.

Относительные мольные концентрации атомарного азота и кислорода, электронов, ионов азота и кислорода остаются практически неизменными. Максимальная концентрация заряженных частиц (N⁺ и e^–) составляет несколько более 10%.

За счет увеличения скоростного напора и объемной энергии набегающего потока заметно возрастает давление газа в сжатом слое, следствием чего являются увеличение оптической толщины и возрастание плотностей радиационных тепловых потоков. Плотность интегральных радиационных тепловых потоков к поверхности возрастает от $M_{1}^{ - }\sim 80$ Вт/см² (t = 1634 с) до $M_{1}^{ - }$ ~ ~ 600 Вт/см² (t = 1639 с). Из анализа кумулятивных функций на фиг. 7 следует, что атомные линии обеспечивают более чем двукратное возрастание радиационных потоков. Первый скачок плотности радиационных тепловых потоков приходится на область $\Delta \omega \sim 8000{\kern 1pt} - {\kern 1pt} 14\,000$ см^–1, где расположены атомные линии, образованные при квантовых переходах между возбужденными состояниями. Второй скачок приходится на ультрафиолетовую область спектра, где расположены атомные линии, образованные при переходах в основные состояния.

При использовании результатов ударно-волновых экспериментов в ударных трубах для валидации физико-химических моделей РадГД аэрофизики СА следует иметь в виду следующее. В ударно-волновых экспериментах измерения проводятся в ограниченном спектральном диапазоне. Например, в работе [7] анализируются экспериментальные данные в диапазоне $\Delta \lambda $ = 200–800 нм. Однако в работах по сверхорбитальному входу СА показано [17], что значительный вклад в радиационный нагрев поверхности вносят спектральные диапазоны в инфракрасной области спектра $\lambda $ > 800 нм и, в особенности, в вакуумной ультрафиолетовой области спектра ($\lambda $ < 200 нм). Известно, что сложность экспериментального измерения спектральных радиационных потоков в ВУФ области спектра состоит в малой длине свободного пробега фотонов. В этой области спектра постановка экспериментов по измерению спектральной интенсивности излучения требует использования специального спектрального оборудования, размещенного в вакуумированных камерах. Следует также учитывать, что измеряемая спектральная интенсивность излучения может формироваться из периферийных, а не приосевых объемов высокотемпературной области.

Таким образом, главной информацией извлекаемых из ударно-волновых экспериментов являются не данные по полному радиационному нагреву, а по физико-химической кинетике в газе за фронтом ударной волны. Здесь проявляется особая ценность сопряжения физического и численного моделирования, поскольку использование подтвержденных экспериментом физико-химических данных в расчетных моделях РадГД СА позволяет получить достоверные данные о радиационном нагреве поверхности.

В случае расчета нагрева поверхности СА с использованием двухмерной модели использование приближения плоского бесконечного слоя вполне оправдано. Интуитивно это ясно из анализа фиг. 2, где толщина сжатого слоя у лобовой поверхности значительно меньше его размеров в касательном направлении. Количественная оценка погрешности использования модели бесконечного плоского слоя была выполнена ранее.

Использование модели плоского слоя при решении задачи об ударной трубе по схеме фиг. 1б менее обосновано вследствие относительно малого радиуса высокотемпературной пробки. Однако это вопрос скорее методического характера, поскольку построение модели испускания излучения с торца цилиндрического объема не представляет в настоящее время принципиально сложной проблемы.

ЗАКЛЮЧЕНИЕ

Таким образом, в данной работе продемонстрирована расчетная методика использования экспериментальных данных по спектральному излучению сильных ударных волн, получаемых в классической постановке ударно-волновых экспериментов в ударных трубах, с пространственными радиационно-газодинамическими расчетами, направленными на повышение достоверности данных по конвективному и радиационному нагреву спускаемых аппаратов. Суть этой методики состоит в отработке модели физико-химической кинетики на примере одномерной задачи, получении подробного разрешения релаксационной зоны за ФУВ, с последующим использованием этих данных в пространственной задаче РадГД.

Оценка радиационного нагрева поверхности СА посредством решения одномерной задачи в осевом направлении распространения излучения требует дополнительного анализа по выбору толщины излучающего слоя и более точного решения задачи об излучении цилиндрического объема.

Еще одна постановка одномерной задачи об излучении пробки нагретого газа за отраженной ударной волной осталась нерассмотренной. Однако эта постановка требует дополнительного анализа для получения данных по неравновесной релаксационной зоне.

Работа поддержана грантом РФФИ № 16-01-00379.

Список литературы

Surzhikov S.T. Spectral Emissivity of Shock Waves in Martian and Titan Atmospheres // AIAA Paper 2010-4527. 32 p.
Surzhikov S.T. Comparison of Two Hybrid CR-Models for Prediction of Nonequilibrium Radiation from Strong Shock Waves // AIAA 2015-2513. 2015. 41 p.
Дикалюк А.С., Суржиков С.Т. Расчетное исследование модели неравновесного излучения за фронтом ударных волн в марсианской атмосфере // Изв. РАН. МЖГ. 2013. № 1. С. 141−160.
Keck C.K., Camm J.C., Kivel B. and Wentink T. Jr. Radiation from Hot Air Part II. Shock Tube Study of Absolute Intensities // Annals of Physics. 1959. V. 7. P. 1−38.
Thomas G.M., Menard W.A. Experimental Measurements of Nonequilibrium and Equilibrium Radiation from Planetary Atmospheres // AIAA J. 1966. V. 4. № 2. P. 227−237.
Collins D.J., Livingston F.R., Babineaux T.L., Morgan N.R. Hypervelocity Shock Tube // JPL Technical Report.1964. № 32-620.
Залогин Г.Н., Козлов П.В., Кузнецова Л.А., Лосев С.А., Макаров В.Н., Романенко Ю.В., Суржиков С.Т. Излучение смеси СО₂–N₂–Ar в ударных волнах: эксперимент и теория // ЖТФ. 2001. Т. 46. № 6. С. 254–661.
Surzhikov S., Shang J. eRC Model for Prediction of Molecular Bands Radiation for Stardust Entry Conditions // AIAA 2014-2490. 45th AIAA Plasmadynamics and Lasers Conf., 2014. 42 p.
Surzhikov S.T., Sharikov I., Capitelli M., Colonna G. Kinetic Models of Non-Equilibrium Radiation of Strong Air Shock Waves // AIAA 2006-0586. 2006. 11 p.
Cauchon D.L. Radiative Heating Results from the Fire II Flight Experiment at a Reentry Velocity of 11.4 km/s // NASA TM X-1402, 1967.
Kudryavtsev N.N., Kuznetsova L.A., Surzhikov S.T. Kinetics and nonequilibrium radiation of CO2-N2 shock waves // AIAA 2001-2728. 19 p.
Ступоченко Е.В., Лосев С.А., Осипов А.И. Релаксационные процессы в ударных волнах. М.: Наука, 1965. 484 с.
Железняк М.Б., Мнацаканян А.Х., Якубов И.Т. Релаксация и неравновесное излучение за ударными волнами в воздухе // Изв. РАН. МЖГ. 1970. № 4. С. 161−174.
Лосев С.А., Макаров В.Н., Погосбекян М.Ю. Модель физико-химической кинетики за фронтом очень сильной ударной волны в воздухе // Изв. РАН. МЖГ. 1995. № 2. С. 169−182.
Marronne P.V., Treanor C.E. Chemical Relaxation with Preferential Dissociation from Excited Vibrational Levels // Phys. Fluids. 1963. V. 6. № 9. P. 1215−1221.
Millikan R.C., White D.R. Systematic of Vibrational Relaxation // J. Chem. Phys. 1963. V. 39. № 12. P. 3209–3212.
Суржиков С.Т. Компьютерная аэрофизика спускаемых космических аппаратов. Двухмерные модели. М.: Физматлит, 2018. 544 с.
Берд Р., Стьюарт В., Лайтфут Е. Явления переноса. М.: Химия, 1974. 687 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал