Известия РАН. Механика жидкости и газа, 2019, № 1, стр. 36-43
Двумерное плоское стационарное термокапиллярное течение
a Институт вычислительного моделирования СО РАН
Красноярск, Россия
b Институт математики и фундаментальной информатики СФУ
Красноярск, Россия
* E-mail: cher@icm.krasn.ru
Поступила в редакцию 16.03.2018
После доработки 10.05.2018
Принята к публикации 20.06.2018
Аннотация
Изучается задача о двумерном стационарном течении жидкости в плоском канале со свободной границей, вдоль которой поверхностное натяжение линейно зависит от температуры, а на дне поддерживается ее заданное распределение. Температура в жидкости распределена по квадратичному закону, что согласуется с полем скоростей типа Хименца. Возникающая краевая задача является сильно нелинейной и обратной относительно градиента давления вдоль канала. Применение к ней тау-метода показывает, что она имеет три различных решения, а в случае теплоизолированной свободной границы – одно. Для каждого из решений построены характерные структуры течения.
Интерес к исследованию влияния капиллярных сил на равновесие и движение жидкости в условиях пониженной гравитации связан с развитием космических технологий [1, 2]. Выращивание кристаллов и создание композитов с новыми свойствами в невесомости, получение в космосе особо чистых металлов и стекол в результате термокапиллярного осаждения капель и пузырей инородной фазы – вот далеко не полный перечень технологических применений капиллярных эффектов. Температурная зависимость коэффициента поверхностного натяжения – один из важных факторов, обусловливающих многообразие динамики межфазной поверхности при наличии в системе неоднородного поля температур.
В статьях [1, 3] изучена задача о термокапиллярной конвекции невесомой жидкости в плоском слое со свободной теплоизолированной поверхностью и подогреваемым дном в случае квадратичной зависимости коэффициента поверхностного натяжения от температуры в рамках уравнений Навье–Стокса и теплопроводности. В случае полупространства подобная задача исследована в [4], только, в отличие от [1, 3], на свободной границе поддерживается линейное распределение температуры.
Данная работа посвящена исследованию решений стационарной задачи, которая возникает при описании двумерного течения вязкой теплопроводной жидкости, находящейся в открытом плоском канале. Течение возникает под действием термокапиллярных сил, приложенных вдоль свободной границы, которые вызывают конвекцию Марангони, причем, в отличие от [1, 3, 4], коэффициент поверхностного натяжения линейно зависит от температуры. Такая конвекция может преобладать в условиях микрогравитации или при движении тонких пленок жидкостей.
1. ПОСТАНОВКА ЗАДАЧИ
Двумерное стационарное движение вязкой теплопроводной жидкости в отсутствие внешних сил описывается уравнениями
(1.1)
$\begin{array}{*{20}{c}} {{{u}_{1}}{{u}_{{1x}}} + {{u}_{2}}{{u}_{{1y}}} + \frac{1}{\rho }{{p}_{x}} = \nu ({{u}_{{1xx}}} + {{u}_{{1yy}}})} \\ {{{u}_{1}}{{u}_{{2x}}} + {{u}_{2}}{{u}_{{2y}}} + \frac{1}{\rho }{{p}_{y}} = \nu ({{u}_{{2xx}}} + {{u}_{{2yy}}})} \\ {{{u}_{{1x}}} + {{u}_{{2y}}} = 0} \\ {{{u}_{1}}{{\theta }_{x}} + {{u}_{2}}{{\theta }_{y}} = \chi ({{\theta }_{{xx}}} + {{\theta }_{{yy}}})} \end{array}$Пусть ${{u}_{1}} = w(y)x$, ${{u}_{2}} = v(y)$, $p = p(x,y)$, $\theta = \theta (x,y)$ есть решение системы (1.1). Данное представление для скоростей имеет название поле скоростей типа Хименца [5]. Подстановка решения в первые три уравнения (1.1) приводит к соотношениям
(1.2)
$\begin{array}{*{20}{c}} {w + {{v}_{y}} = 0,\quad v{{w}_{y}} + {{w}^{2}} = f + \nu {{w}_{{yy}}}} \\ {\frac{1}{\rho }p\; = \;d(y)\; - \;\frac{{f{{x}^{2}}}}{2},\quad {{d}_{y}}\; = \;\nu {{v}_{{yy}}}\; - \;v{{v}_{y}}} \end{array}$Последнее уравнение в (1.1) для температуры примет вид
Среди его решений имеет место квадратичное по переменной $x$
Далее, для простоты, предполагается, что $m(y) \equiv 0$. Это означает, что температурное поле имеет в точке x = 0 экстремум: максимум при $a(y) < 0$ и минимум при $a(y) > 0$ для всех $y \in [0,1]$, в частности, и на твердой стенке y = 0. Для описания течения вязкой теплопроводной жидкости в плоском канале с нижней твердой неподвижной стенкой $y = 0$ и верхней свободной границей $y = l = {\text{const}} > 0$ применяется решение вида (1.2), (1.3). Тогда при $0 < y < l$ неизвестные $w(y)$, $v(y)$, $a(y)$ и $b(y)$ удовлетворяют уравнениям
(1.4)
$\begin{array}{*{20}{c}} {v{{w}_{y}} + {{w}^{2}} = \nu {{w}_{{yy}}} + f,\quad w + {{v}_{y}} = 0,\quad v{{v}_{y}} + {{d}_{y}} = \nu {{v}_{{yy}}}} \\ {2wa\; + \;v{{a}_{y}}\; = \;\chi {{a}_{{yy}}},\quad v{{b}_{y}}\; = \;\chi {{b}_{{yy}}}\, + \;2\chi a} \end{array}$Предполагается, что коэффициент поверхностного натяжения $\sigma $ линейно зависит от температуры
${{\sigma }^{0}},\unicode{230} ,{{\theta }^{0}} = {\text{const}} > 0$. На свободной границе $y = l$ выполнены условия [6]Условия (1.5) есть следствия кинематического и динамического условий соответственно. В условии теплового контакта (1.6) $k > 0$ – коэффициент теплопроводности, Q(x) – заданный поток тепла, $\gamma \geqslant 0$ – коэффициент межфазного теплообмена, далее $\gamma = {\text{const}}$. Из условия для нормальных напряжений получается, что свободная поверхность остается плоской. Данное предположение может выполняться, например, при действии достаточно большого капиллярного давления (величина ${{\sigma }^{0}}$ достаточно велика) [7]. В соответствии с представлением температуры (1.3) в условии (1.6) необходимо считать в общем случае, что
с заданными постоянными ${{a}_{k}},{{b}_{k}}$, $k = 1,2.$ Следовательно, на свободной границе выполнены условия для $a(y)$, $b(y)$Граничные условия на твердой стенке имеют вид
с известными постоянными ${{a}_{{10}}}$, ${{b}_{{10}}}$.Стоит отметить следующие особенности поставленной задачи. Она нелинейная и обратная, так как постоянная f является искомой. Действительно, если из уравнения сохранения массы исключить $v(y)$, то получается задача для функций $w(y)$, $a(y)$. Задача для функции $b(y)$ при известных $v(y)$ и $a(y)$ отделяется. Функция $d(y)$ восстанавливается квадратурой из третьего уравнения (1.4) с точностью до константы.
Замечание 1. Если решение задачи (1.4)–(1.6), (1.9) искать в виде
2. ВЫВОД СИСТЕМЫ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Выпишем полностью полученную нелинейную задачу в безразмерном виде для функций $w(y)$, $a(y)$ и постоянной f, учитывая что из второго уравнения (1.4)
Она имеет вид
(2.2)
${{L}_{1}}(W,F) \equiv {\text{Pr}}{{W}_{{\xi \xi }}} + {{W}_{\xi }}\left( {\int\limits_0^\xi {W(z)dz} } \right) - {{W}^{2}} + F = 0,\quad 0 < \xi = y{\text{/}}l < 1$(2.3)
${{L}_{2}}(W,A) \equiv {{A}_{{{{{_{\xi }}}_{\xi }}}}} + {{A}_{{_{\xi }}}}\left( {\int\limits_0^{_{\xi }} {W(z)dz} } \right) - 2AW = 0,\quad 0 < \xi < 1$(2.6)
$\begin{array}{*{20}{c}} {{{A}_{0}}(\xi ) = - \frac{{{\text{Bi}}}}{{1 + {\text{Bi}}}}\xi + 1,\quad {{W}_{0}}(\xi ) = \frac{{{{F}_{0}}}}{{6{\text{Pr}}}}(2\xi - 3{{\xi }^{2}}),\quad {{F}_{0}} = \frac{{3{\text{MPr}}}}{{1 + {\text{Bi}}}}} \end{array}$В статьях [1, 3] рассматривалась задача о течении жидкости в плоском канале, на дне которого поддерживается заданное распределение температуры, а свободная поверхность теплоизолирована (Bi = 0). В результате разделения переменных была получена нелинейная двухточечная краевая задача, описывающая движение жидкости в слое, где постоянная $F$ играет роль собственного значения, а числа Прандтля и Марангони – параметры. Установлена неединственность решения этой задачи (от одного до трех решений) в зависимости от параметра M (Pr = 0, т.е. рассмотрен предельный случай идеально теплопроводной жидкости). В данной работе для решения задачи (2.2)–(2.5) применяется тау-метод, представляющий модификацию метода Галеркина [9]. Приближенное решение ищется в виде сумм
(2.7)
${{W}_{n}}(\xi ) = \sum\limits_{k = 0}^{n + 1} {{W}^{k}}{{R}_{k}}(\xi ),\quad {{A}_{n}}(\xi ) = \sum\limits_{k = 0}^{n + 1} {{A}^{k}}{{R}_{k}}(\xi )$(2.8)
$\begin{array}{*{20}{c}} {\int\limits_0^1 {{L}_{1}}({{W}_{n}},F){{R}_{m}}(\xi )d\xi = 0,\quad \int\limits_0^1 {{L}_{2}}({{W}_{n}},{{A}_{n}}){{R}_{m}}(\xi )d\xi = 0,\quad m = 0,\;...,\;n - 1} \end{array}$Последнее уравнение в (2.9) получается из интегрального условия (2.5), учитывая ортогональность полиномов Лежандра на отрезке [0, 1] с весом 1 [10]. Таким образом уравнения (2.8) и (2.9) образуют замкнутую систему алгебраических нелинейных уравнений на коэффициенты ${{W}^{k}}$, ${{A}^{k}}$ и постоянную F.
3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
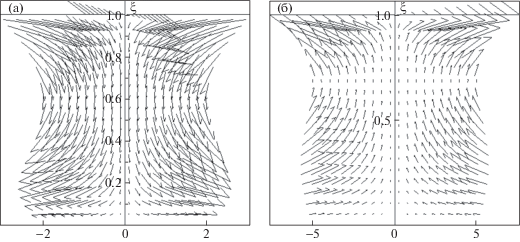
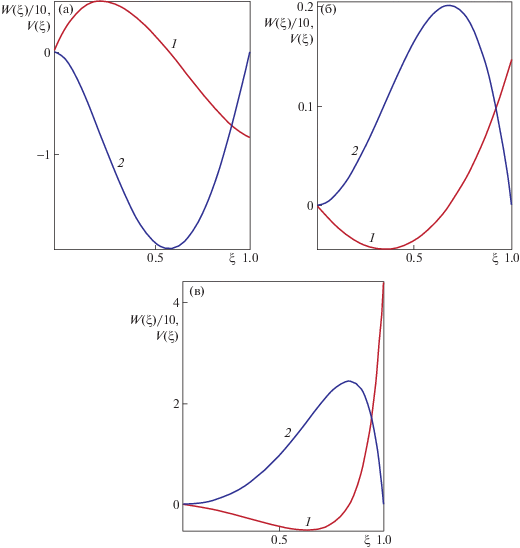
Расчеты проводились для ${\text{Pr}} = 0.2$, ${\text{Bi}} = 2$, ${\text{M}} = 10$ (${{a}_{{10}}} > 0$, то есть температура в точке x = 0, y = 0 минимальна) и n = 17. Было установлено три различных значения безразмерной постоянной $F$: ${{F}_{1}} = 14.1397$, ${{F}_{2}} = 4.5359$ и ${{F}_{3}} = 4.4877$. При этом разность значений полученных при $n = 16$ и 17 составляет порядка 10–11, 10–14 и 10–6 для ${{F}_{1}}$, ${{F}_{2}}$ и ${{F}_{3}}$ соответственно, что говорит о хорошей сходимости τ – метода при решении данной краевой задачи. Стоит также отметить,что при ${\text{M}} \ll 1$ решения стремятся к единственному решению линейной задачи (2.6), описывающей ползущее движение в слое. Например, при M = 0.01 найдено ${\text{|}}{{F}_{0}} - {{F}_{{1,2,3}}}{\text{|}}$ $ \approx {{10}^{{ - 6}}}$. На фиг. 1 приведены профили безразмерной функции W(ξ) и поперечной скорости $V(\xi )$ (2.1) для значений ${{F}_{1}}$, ${{F}_{2}}$ и ${{F}_{3}}$ соответственно. Профили для ${{F}_{1}}$ и ${{F}_{2}}$ схожи, но стоит отметить, что течение, отвечающее параметру ${{F}_{1}}$, является более интенсивным, так $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}W(\xi ,{{F}_{1}}){\text{|}} = 4.65$, $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}V(\xi ,{{F}_{1}}){\text{|}} = 0.9$, а $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}W(\xi ,{{F}_{2}}){\text{|}} = 2.37$, $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}V(\xi ,{{F}_{2}}){\text{|}}$ = 0.4. На фиг. 2 изображены профиль функции $A(\xi )$ и поле скоростей для ${{F}_{1}}$ и ${{F}_{3}}$. В первом случае функция $A(\xi )$ на свободной границе $\xi = 1$ положительна, следовательно температура при x = 0 минимальная и возрастает в направлении оси x. Поскольку жидкость течет в сторону большего поверхностного натяжения, то вблизи поверхности раздела возникает возвратное течение, что и изображено на фиг. 2,а. Во втором случае $A(1) < 0$ и температура при x = 0 максимальна, следовательно, жидкость вблизи свободной границы течет в направлении оси $x$ (фиг. 2,б). Видно, что в обоих случаях более интенсивное движение формируется вблизи свободной границы $\xi = 1$.
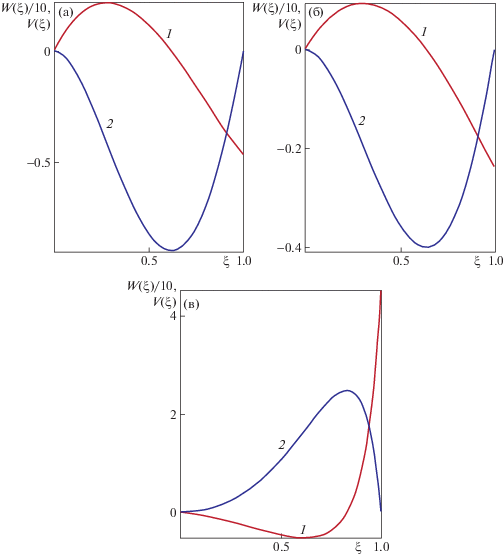
Фиг. 1.
Профили безразмерной функции $W(\xi )$ (1) и поперечной скорости $V(\xi )$ (2) для ${{F}_{1}}$ (а), ${{F}_{2}}$ (б) и ${{F}_{3}}$ (в)
Фиг. 2.
Профиль безразмерной функции $A(\xi )$ и линии тока в слое для ${{F}_{1}}$ (а, б) и ${{F}_{3}}$ (в, г)
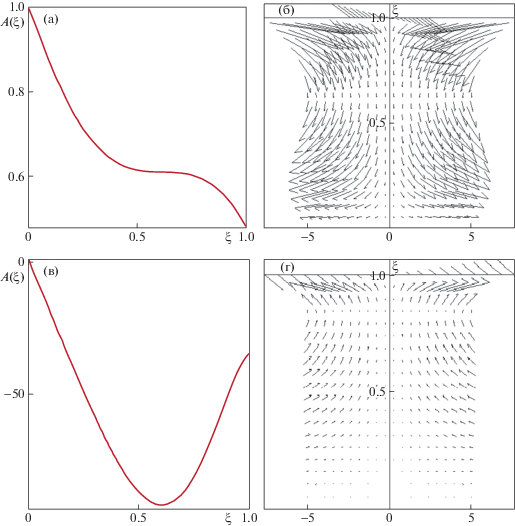
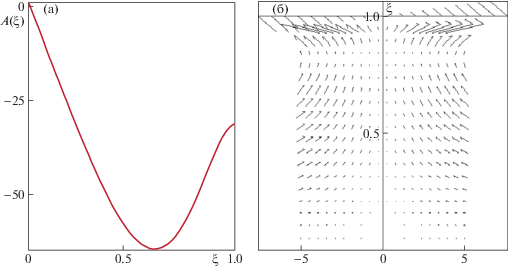
В случае, когда ${\text{M}} = - 10$ (${{a}_{{10}}} < 0$ и температура в точке x = 0, y = 0 максимальна) для параметра F получим значения ${{F}_{1}} = 50.08$, ${{F}_{2}} = - 1.3368$ и ${{F}_{3}} = 4.271$. На фиг. 3 изображены профили безразмерной функции $W(\xi )$ и поперечной скорости $V(\xi )$ для значений ${{F}_{1}}$, ${{F}_{2}}$ и ${{F}_{3}}$ соответственно. Профили для $F = 4.271$ аналогичны профилям как при M = 10, $F = 4.4877$ (см. фиг. 1в), причем $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}W(\xi $, F = 4.4877)| = 43.962, $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}V(\xi ,F = 4.4877){\text{|}} = 2.44$, а $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}W(\xi ,F = 4.271){\text{|}}$ = 45.174, $\mathop {max}\limits_{\xi \in [0,1]} {\text{|}}V(\xi ,F = 4.271){\text{|}}$ = 2.476. На фиг. 4 изображены линии тока в слое для ${{F}_{1}}$ и ${{F}_{2}}$. Видно, что течение, отвечающее параметру ${{Z}_{1}}$, наиболее интенсивно. В обоих случаях более интенсивное движение формируется вблизи свободной границы $\xi = 1$.
Фиг. 3.
Профили безразмерной функции $W(\xi )$ (1) и поперечной скорости $V(\xi )$ (2) для ${{F}_{1}}$ (а), ${{F}_{2}}$ (б) и ${{F}_{3}}$ (в), ${\text{M}} = - 10$
В случае теплоизолированной свободной границы (Bi = 0) получено одно значение безразмерной постоянной $F = 3.97$. Это решение при малых числах Марангони также стремится к единственному решению линейной задачи (2.6). На фиг. 5 изображены профиль функции $A(\xi )$ и линии тока в слое. Поскольку $A(1) < 0$, то жидкость вблизи свободной границы течет в направлении оси $x$. Видно, что наиболее интенсивное течение формируется вблизи $\xi = 1$, т.е. свободной границы.
Стоит также сказать о влиянии безразмерных параметров на интенсивность возникающих течений: с ростом числа Марангони M скорость движения увеличивается, а с увеличением числа Прандтля Pr – уменьшается.
Замечание 2. Для оценки точности полученных решений можно использовать следующие равенства:
(3.1)
$\begin{array}{*{20}{c}} {W(1)W'(1) - \int\limits_0^1 {{{(W')}}^{2}}d\xi - \frac{3}{{2{\text{Pr}}}}\int\limits_0^1 {{W}^{3}}d\xi = 0} \\ {{\text{Pr}}\left[ {W'(0) - W'(1)} \right] + 2\int\limits_0^1 {{W}^{2}}d\xi - F = 0} \end{array}$Первое равенство в (3.1) следует из умножения уравнения (2.2) на $W(\xi )$ и интегрирования по $\xi \in [0,1]$, с учетом первого условия (2.4) и интегрального условия (2.5), а второе – интегрирования уравнения (2.2) по области определения. Так, подставляя решения, полученные для всех рассмотренных выше случаев в равенства (3.1), устанавливается их выполнение с точностью до порядка 10–10 и 10–50 соответственно.
ЗАКЛЮЧЕНИЕ
Изучена задача о двумерном стационарном течении жидкости в плоском канале со свободной границей, вдоль которой поверхностное натяжение линейно зависит от температуры, а на дне поддерживается заданное распределение температуры. Установлена неединственность решения этой задачи: для ${\text{Bi}} \ne 0$ найдено три различных решения, а для Bi = 0 – одно. Все найденные решения при малых числах Марангони стремятся к единственному нетривиальному решению линейной задачи, описывающей ползущее движение жидкости в открытом канале. Для каждого из решения построены характерные структуры течения.
Автор благодарит В.К. Андреева за обсуждение результатов работы.
Работа выполнена при поддержке проекта РФФИ № 17-01-00229.
Список литературы
Гупало Ю.П., Рязанцев Ю.С. О термокапиллярном движении жидкости со свободной поверхностью при нелинейной зависимости поверхностного натяжения от температуры // Изв. АН СССР. МЖГ. 1988. № 5. С. 132–137.
Legros J.C., Limbourg-Foutaine M.C., Petre G. Influence of a surface tension minimum as a function of temperature on the Marangoni convection // Acta Astrounat. 1984. V. 11. № 2. P. 143–147.
Бобков Н.Н., Гупало Ю.П. Структура течения в жидком слое и спектр краевой задачи при нелинейной зависимости поверхностного натяжения от температуры // Прикладная математика и механика. Т. 60. Вып. 6. 1996. С. 1021–1028.
Гупало Ю.П., Рязанцев Ю.С., Скворцова А.В. Влияние термокапиллярных сил на движение жидкости со свободной поверхностью // Механика жидкости и газа. 1989. № 5. С. 3–7.
Hiemenz K. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Poliytech. J. 1911. V. 326. P. 321–440.
Андреев В.К., Захватаев В.Е., Рябицкий Е.А. Термокапиллярная неустойчивость. Новосибирск: Наука, 2000. 279 с.
Зейтунян Р.Х. Проблема термокапиллярной неустойчивости Бенара–Марангони // УФН. 1998. Т. 168. № 3. С. 259–286.
Andreev V.K. Influence of the Interfacial Internal Energy on the Thermocapillary Steady Flow // J. Siberian Federal Univ. Mathematics & Physics. 2017. V. 10. № 4. P. 537–547.
Флетчер К. Численные методы на основе метода Галеркина. М.: Мир, 1988. 352 с.
Сеге Г. Ортогональные многочлены. М.: Физматлит, 1962. 500 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа