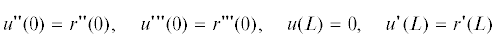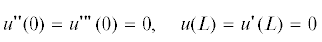Известия РАН. Механика твердого тела, 2022, № 6, стр. 114-126
УТОЧНЕННАЯ МОДЕЛЬ ИЗГИБА БАЛКИ ПРИМЕНИТЕЛЬНО К МЕТОДУ ЗАЛИПШЕГО КАНТИЛЕВЕРА
И. А. Солдатенков a, *, А. А. Яковенко a, В. Б. Световой b
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия
* E-mail: iasoldat@hotmail.com
Поступила в редакцию 14.02.2022
После доработки 20.03.2022
Принята к публикации 21.03.2022
- EDN: HYBEHU
- DOI: 10.31857/S0572329922060162
Аннотация
Предложена математическая модель, описывающая изгиб кантилевера и с учетом факторов его неидеальности (исходный прогиб, изменение толщины), а также податливости подложки применительно к методу залипшего кантилевера. На основе предложенной модели выполнен численный анализ изгиба кантилевера и даны оценки энергии адгезии. Полученные результаты свидетельствуют о важности учета факторов неидеальности кантилевера, а также податливости подложки.
Введение. В последние десятилетия значительно повысился интерес к изучению адгезионного взаимодействия твердых тел, что обусловлено, в частности, широким применением микроэлектромеханических систем (MEMS) [1, 2]. Адгезионное взаимодействие тел обуславливается силами различной природы (электростатической, капиллярной, химической и др.), среди которых выделяются дисперсионные силы (ДС). Эти силы действуют между незаряженными телами и их существование связано с флуктуациями электромагнитного поля [3]. На расстояниях между телами h ~ 1 нм ДС носят название ван-дер-ваальсовых сил, при больших расстояниях (свыше 10 нм), когда существенным становится запаздывание электромагнитных волн, они называются силами Казимира. Общая макроскопическая теория ДС была построена Лифшицем с коллегами [4].
С увеличением расстояния h между телами ДС быстро убывают ($\sim {\kern 1pt} {{h}^{{ - \alpha }}},$ $\alpha = 3{\kern 1pt} - {\kern 1pt} 4$). Однако, несмотря на это, ДС играют важную роль в производстве и функционировании различных микромеханических устройств, т.к. они являются причиной крайне нежелательного явления – адгезионного залипания подвижных элементов подобных устройств [5]. В отличие от других сил (например, электростатических или капиллярных), ДС не могут быть устранены выбором материалов, модификацией поверхности и т.п., поскольку природа ДС связана с фундаментальными свойствами электромагнитного поля.
Указанные обстоятельства обуславливают актуальность задачи измерения ДС. Использование для этого традиционных систем с упругим подвесом представляется проблематичным из-за потери устойчивости и спонтанного залипания. Особенно остро такая проблема стоит для диапазона расстояний 3 нм $ < h < $ 30 нм, характерного для многих микромеханических устройств. Предложенный ранее метод залипшего кантилевера (МЗК) лишен подобного недостатка, при этом МЗК позволяет измерять также и энергию адгезии исследуемых поверхностей [6–9].
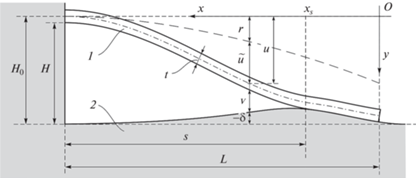
МЗК предполагает использование упругой балки (кантилевера), один конец которой консольно закреплен на высоте H над подложкой. Характерная длина и толщина кантилевера составляют L ~ 10 мм и t ~ 10 мкм, высота крепления кантилевера H ~ 10 мкм. Свободный конец кантилевера приводится в контакт с подложкой, в результате чего происходит адгезионное залипание части кантилевера (рис. 1). Остальная (свободная) часть кантилевера находится под действием ДС, которые вызывают изменение прогиба кантилевера относительно его классической формы. Как показывают оценки, подобное изменение составляет ~100 нм. Оно может быть измерено при помощи сканирующего интерферометра с точностью ~1 нм и служит в качестве исходных данных для оценки ДС с привлечением теории изгиба балок [10, 11].
Для экспериментальных исследований обычно используется кремниевый кантилевер, а на подложку наносится покрытие. Это обусловлено тем, что стандартная технология производства микромеханических устройств предполагает использование кремния, как базового материала, и тонких покрытий, для нанесения которых применяются известные способы – магнетронное напыление, термическое осаждение и др. [12]. Как показывают эксперименты [13, 14], получаемая в результате шероховатость покрытия часто описывается негауссовым распределением и характеризуется значительным числом неровностей (пиков), которые имеют высоту ~10 нм, существенно превышающую среднеквадратичное отклонение шероховатости ~1 нм. Такое избыточное количество высоких пиков приводит к ощутимой податливости подложки, что, в свою очередь, оказывает влияние на измеряемый прогиб кантилевера.
Вследствие погрешностей технологии изготовления, форма кантилевера не является идеальной. Это проявляется в существовании исходного (остаточного) прогиба кантилевера и отклонения его толщины от постоянного значения [15]. Указанные факторы неидеальности кантилевера также влияют на его прогиб и требуют учета.
Следует отметить существование и других факторов, влияющих на изгиб кантилевера. Примерами тому служат факторы капиллярных явлений и растяжения кантилевера [16] или податливости консольного закрепления кантилевера, которая исследовалась применительно к атомно-силовому микроскопу [17].
В данной работе предлагается модель изгиба кантилевера, учитывающая исходный прогиб и изменение толщины кантилевера, а также податливость подложки применительно к МЗК. Предложенная модель позволяет производить уточненный расчет прогиба кантилевера и энергии адгезии кантилевера к подложке. Целью работы является анализ влияния факторов неидеальности кантилевера (исходный прогиб, изменение толщины) и податливости подложки на результирующий прогиб кантилевера и оценку энергии адгезии применительно к МЗК.
1. Постановка задачи и основные уравнения. Рассмотрим изгиб балки (кантилевера) длины $L$ и ширины $w$ в поле ДС при ее консольном закреплении на расстоянии ${{H}_{0}}$ от подложки и наличии участка $[0,{{x}_{s}}]$ адгезионного сцепления с подложкой (участок залипания) (рис. 1). Здесь и далее ${{x}_{s}} = L - s$, причем длина s свободного (незалипшего) участка считается заданной. Рассмотрение проводится на макромасштабе, что позволяет пренебречь шероховатостью кантилевера и подложки на микро- и наноуровне. На свободном участке $({{x}_{s}},L]$ кантиллевер и подложка разделены положительным зазором ${v}$. Прогиб кантилевера задается ординатой $u$ его оси в системе координат $Oxy$. Допускаются существование исходного (до залипания) прогиба $r$ кантилевера и изменение толщины $t$ кантилевера по его длине. Подложка считается податливой (деформируемой), что обуславливает существование перемещения $\delta $ ее границы. Между указанными величинами имеет место соотношение (рис. 1):
Используя положения теории изгиба балок со слабоизменяющейся толщиной, можно вывести следующее соотношение между прогибом $u$ балки и внешней нагрузкой $q$, распределенной по длине балки [10, 11]:
где $J(x) = w{{t}^{3}}(x){\text{/}}12$ – момент инерции сечения балки, E – модуль упругости, штрих у символа функции означает производную по координате x. Для слабоискривленной в исходном состоянии балки величину $u$ в равенстве (1.2) следует заменить разностью $\tilde {u} = u - r$ [10, 11].Принимая во внимание вышесказанное, можно прийти к следующему дифференциальному уравнению, описывающему прогиб кантилевера:
(1.3)
$\mathcal{K}(\tilde {u})(x) \equiv [D(x)\tilde {u}_{{}}^{{''}}(x)]_{{}}^{{''}} = \beta (x),\quad x \in [0,L]$Для описания деформационного поведения подложки будет использоваться модель Винклера [18, 19]:
где ${{\sigma }_{y}}(x)$ – граничное напряжение, $0 < A$ – коэффициент податливости, который определяется деформационными свойствами шероховатого контакта кантилевера и подложки [15, 20].Присутствующее в уравнении (1.3) изгибающее напряжение $\beta $ обусловлено реакцией подложки (участок залипания) или действием ДС (свободный участок), однако в любом случае справедливо равенство
Исключив из этого равенства напряжение ${{\sigma }_{y}}$ с помощью равенств (1.1) и (1.4), можно получить следующее выражение:
(1.6)
$\beta (x) = {{A}^{{ - 1}}}\left[ {{{H}_{0}} - u(x) - t(x){\text{/}}2 - {v}(x)} \right],\quad x \in [0,L]$На участке залипания имеем ${v}(x) = 0$, поэтому из выражения (1.6) следует, что
причемНа свободном участке зазор ${v}$ отличен от нуля, поэтому справедливо равенство
в котором функция $\Pi $ – удельная сила притяжения друг к другу поверхностей кантилевера и подложки, обусловленная наличием ДС. Для рассматриваемого случая можно использовать выражение в котором параметр ${{\Pi }_{0}}$ задает силу притяжения при ${v} = 0$, а величина h0 характеризует равновесный зазор шероховатого контакта кантилевера и подложки на наноуровне [20, 21].Если, с помощью цепочки равенств (1.4), (1.5), выразить в правой части соотношения (1.1) величину $\delta $ через $\beta $ и подставить полученное выражение для зазора ${v}$ в правую часть равенства (1.9), то можно получить алгебраическое уравнение для изгибающего напряжения на свободном участке:
(1.11)
$\beta (x) = \Pi \left( {{{H}_{0}} - u(x) - t(x){\text{/}}2 - A{\kern 1pt} \beta (x)} \right),\quad x \in ({{x}_{s}},L]$Решение этого уравнения имеет вид
при условии, что функция ${{\beta }_{2}}(X)$ удовлетворяет уравнениюОтметим, что уравнение (1.11) отвечает самосогласованному по Дерягину подходу к постановке контактной задачи для деформируемых тел при наличии межмолекулярного взаимодействия [22]. Действительно, это уравнение предполагает существование зазора ${v}$ между телами (кантилевер и подложка), величина которого обеспечивает равенство ДС и сил деформации подложки.
Подставим полученные выражения (1.7), (1.12) в правую часть уравнения (1.3) и заменим в нем перемещение $\tilde {u}$ разностью $u - r$. В результате придем к следующему дифференциальному уравнению для прогиба $u$ рассматриваемого кантилевера:
(1.14)
$\mathcal{K}(u)(x) = {{\beta }_{r}}(x) + \left\{ \begin{gathered} {{\beta }_{1}}\left( {u(x) + t(x){\text{/}}2} \right),\quad x \in [0,{{x}_{s}}] \hfill \\ {{\beta }_{2}}\left( {u(x) + t(x){\text{/}}2} \right),\quad x \in ({{x}_{s}},L] \hfill \\ \end{gathered} \right.$Граничные условия для уравнения (1.14) имеют вид
из которых первые два отвечают отсутствию изгибающего момента и поперечной силы на свободном конце кантилевера (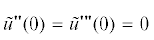 ), а два последних – консольному закреплению кантилевера.
), а два последних – консольному закреплению кантилевера.
Замечание 1. В работе [15] использовалось дополнительное условие относительно способа консольного закрепления кантилевера (рис. 1). А именно, считалось, что его нижняя грань при $x > L$ сцеплена с горизонтальной плоскостью ступеньки высотой H. В этом случае имеет место равенство $r_{{}}^{'}(L) = - t_{{}}^{'}(L){\text{/}}2$ и, поэтому, последнее граничное условие (1.15) принимает вид [15]: $u_{{}}^{'}(L) = - t_{{}}^{'}(L){\text{/}}2$.
Прогиб кантиливера $u(x)$, полученный в результате решения краевой задачи (1.14), (1.15), позволяет с помощью цепочки равенств (1.4), (1.5), (1.7), (1.12) найти граничные напряжение ${{\sigma }_{y}}(x)$ и перемещение $\delta (x)$ на отрезке $[0,L]$. После этого, воспользовавшись соотношением (1.1), можно определить зазор ${v}(x)$.
Конкретизируем краевую задачу (1.14), (1.15) для двух частных случаев рассмотренной выше постановки задачи об изгибе кантилевера.
1. Случай абсолютно жесткой подложки описывается представленными выше формулами, если в них выполнить предельный переход $A \to 0$ и положить $\delta (x) \equiv 0$.
На участке залипания прогиб $u$ кантилевера известен и определяется по формуле
вытекающей из соотношения (1.1) при ${v}(x) = \delta (x) = 0$.На свободном участке прогиб кантилевера описывается уравнением
(1.17)
$\mathcal{K}(u)(x) = {{\beta }_{r}}(x) + \Pi \left( {{{H}_{0}} - u(x) - t(x){\text{/}}2} \right),\quad x \in ({{x}_{s}},L]$Граничные условия для уравнения (1.17) имеют вид
(1.18)
$u({{x}_{s}}) = {{H}_{0}} - t({{x}_{s}}){\text{/}}2,\quad u_{{}}^{'}({{x}_{s}}) = - t_{{}}^{'}({{x}_{s}}){\text{/}}2,\quad u(L) = 0,\quad u_{{}}^{'}(L) = r_{{}}^{'}(L)$Пример. Допустим, что ДС пренебрежимо малы ($\Pi ({v}) = 0$), а кантилевер имеет постоянную толщину ($t(x) = {\text{const}}$). Тогда решение краевой задачи (1.17), (1.18) представляется выражением
(1.19)
$u(x) = H + {{a}_{3}}{{\xi }^{3}} + {{a}_{2}}{{\xi }^{2}} - r_{{}}^{'}({{x}_{s}})s{\kern 1pt} \xi + r(x) - r({{x}_{s}})$Отметим, что решение (1.20) остается в силе и при наличии исходного прогиба, описываемого степенными функциями
– в этом нетрудно убедиться прямой подстановкой выражений (1.21) в решение (1.19).2. Случай деформируемой подложки и идеального кантилевера описывается приведенными выше общими формулами, если в них положить $r(x) = 0,$ $t(x) = {\text{const}}$. В этом случае имеет место соотношение $H = {{H}_{0}} - t{\text{/}}2$ (рис. 1), поэтому уравнению (1.14) и граничным условиям (1.15) можно придать следующий вид:
(1.22)
$D{\kern 1pt} {\kern 1pt} {{u}^{{({\text{IV}})}}}(x) = \left\{ \begin{gathered} {{b}_{1}}\left( {u(x)} \right),\quad x \in [0,{{x}_{s}}] \hfill \\ {{b}_{2}}\left( {u(x)} \right),\quad x \in ({{x}_{s}},L] \hfill \\ \end{gathered} \right.$На участке $[0,{{x}_{s}}]$ решение уравнения (1.22), удовлетворяющее первой паре граничных условий (1.23), находится в аналитическом виде [11]
(1.24)
$\begin{gathered} u\left( x \right) = H + {{e}^{{k{\kern 1pt} x}}}\left( {a\cos kx + b\sin kx} \right) + {{e}^{{ - k{\kern 1pt} x}}}\left( {\left( {a - 2b} \right)\cos kx + b\sin kx} \right), \\ x \in [0,{{x}_{s}}] \\ \end{gathered} $На участке $[{{x}_{s}},L]$ решение уравнения (1.22) строится численно с начальными условиями (задача Коши)
в которых значения ${{u}^{{(n)}}}({{x}_{s}} - 0)$ определяются с помощью выражения (1.24), при этом параметры a и b подбираются таким образом, чтобы удовлетворить второй паре граничных условий (1.23).2. Энергетические аспекты МЗК. Данный раздел посвящен выводу формулы, связывающей энергию адгезии $\Gamma $ с состоянием рассматриваемой системы кантилевер–подложка. Для этого введем в рассмотрение полную энергию $\mathcal{E}$ этой системы, которая складывается из потенциальных энергий ${{U}_{1}}$ и ${{U}_{2}}$ изогнутого кантилевера и деформированной подложки, а также из энергии ${{U}_{3}}$ межмолекулярного взаимодействия кантилевера и подложки:
Определим вклады ${{U}_{1}},\;{{U}_{2}},\;{{U}_{3}}$ в полную энергию $\mathcal{E}$.
Согласно теории изгиба балок [10, 11]
(2.2)
${{U}_{1}} = \int\limits_0^L {\frac{{{{M}^{2}}(x)dx}}{{2EJ(x)}}} = \frac{w}{2}\int\limits_0^L {D(x){{{[u_{{}}^{{''}}(x) - r_{{}}^{{''}}(x)]}}^{2}}dx} $Энергия U2 определяется работой напряжения ${{\sigma }_{y}}$ при перемещении границы подложки на величину $\delta $. С учетом соотношения (1.4), это позволяет установить, что
Энергия U3 определяется работой, которую надо совершить для разведения залипших поверхностей кантилевера и подложки на расстояние ${v}(x),\;x \in [{{x}_{s}},L]$ (рис. 1). При подсчете этой работы необходимо учитывать, что, наряду с ДС вида (1.10), между кантилевером и подложкой могут действовать короткодействующие силы, обусловленные, например, перекрытием электронных облаков или капиллярными эффектами. Короткодействующий характер таких сил позволяет представить работу по их преодолению при разведении кантилевера и подложки на расстояние ${v}(x)$ в виде произведения $w{\kern 1pt} s{\kern 1pt} {{\Gamma }_{{sf}}}{\kern 1pt} $, где ${{\Gamma }_{{sf}}}$ – энергия адгезии короткодействующих сил. Учитывая указанные обстоятельства, для энергии U3 можно получить выражение:
(2.4)
${{U}_{3}} = U_{{df}}^{ + } + {{C}_{0}}{\kern 1pt} s + w{\kern 1pt} {\kern 1pt} {{\Gamma }_{{sf}}}{\kern 1pt} {\kern 1pt} s$(2.5)
$U_{{df}}^{ + } = - {{C}_{0}}\int\limits_{{{x}_{s}}}^L {{{{\left( {\frac{{{{h}_{0}}}}{{{{h}_{{{\kern 1pt} 0}}} + {v}(x)}}} \right)}}^{{\alpha - 1}}}dx} ,\quad {{C}_{0}} = \frac{{w{{h}_{0}}{{\Pi }_{0}}}}{{\alpha - 1}}$Нетрудно убедиться, что присутствующий в равенствах (2.4) и (2.5) коэффициент C0 связан с энергией адгезии ${{\Gamma }_{{df}}}$ ДС: ${{C}_{0}} = w{\kern 1pt} {\kern 1pt} {{\Gamma }_{{df}}}$. Если принять это во внимание и учесть равенство
то выражению (2.4) можно придать следующий вид:Замена в соотношении (2.1) энергии U3 правой частью равенства (2.6) приводит к выражению
в которомК выражению (2.7) применима известная процедура определения величины $\Gamma $ путем минимизации полной энергии $\mathcal{E}$ по параметру $s$ [7, 16]. В результате можно получить искомую формулу
Формула (2.9) используется для оценки энергии адгезии $\Gamma $ в МЗК. Величина U* в этой формуле определяется равенством (2.8), правая часть которого рассчитывается на основе формул (2.2), (2.3) и (2.5). Присутствующие в этих формулах функции $u(x)$, ${v}(x)$ и ${\kern 1pt} \delta (x)$, как указывалось выше, известны из решения краевой задачи (1.14), (1.15). Отметим также, что правая часть равенства (2.9) не зависит от ширины w кантилевера – это непосредственно следует из определения (2.8) величины U* и формул (2.2), (2.3) и (2.5).
В случае, когда ДС и податливость подложки пренебрежимо малы ($\Pi ({v}) = 0$, $A = 0$), а контилевер является идеальным ($r(x) = 0$, $t(x) = {\text{const}}$), формула (2.9) приводит к известному выражению для энергии адгезии [7, 15]
Выражение (2.10) остается справедливым, если допустить существование исходного прогиба $r(x) = {{k}_{2}}{{(L - x)}^{2}}$. Несмотря на то, что в этом случае исходный прогиб не влияет на оценку энергии адгезии $\Gamma $, потенциальная энергия U1 изогнутого кантилевера зависит от исходного прогиба – в силу равенств (1.20) и (2.2):
3. Расчеты. Выполним численные анализ поведения системы кантилевер – подложка на основе решения краевой задачи (1.14), (1.15). Это решение находилось при помощи метода стрельбы, предполагающего построение численного решения дифференциального уравнения (1.14) известными методами (Рунге–Кутты, Эйлера–Коши) [23]. Энергия адгезии $\Gamma $ рассчитывалась по формуле (2.9) с использованием найденного решения краевой задачи (1.14), (1.15).
Целью численного анализа является демонстрация возможного влияния неидеальной формы кантилевера (исходный прогиб, изменяющаяся толщина) и податливости подложки на результирующий прогиб кантилевера и оценку энергии адгезии. Для этого результаты расчетов сравниваются с референсными прогибом $u^\circ (x)$ и энергией адгезии $\Gamma ^\circ $, отвечающих случаю идеального кантилевера (отсутствие исходного прогиба, постоянная толщина) и абсолютно жесткой подложки при наличии ДС.
Расчеты проводились при следующих значениях параметров: $L = 10$ мм, $s = 0.3L$, ${{H}_{0}} = 15$ мкм, $E = 160$ ГПа, ${{\Pi }_{{0}}} = 1.5577$ × 104 Па, ${{h}_{0}} = 10$ нм, $\alpha = 3.5$. Значения остальных параметров указываются ниже для каждого конкретного примера. Отметим, что среди указанных значений отсутствует значение ширины $w$ кантилевера, т.к. этот параметр не влияет на решение краевой задачи (1.14), (1.15) и на величину энергии адгезии $\Gamma $, определяемой по формуле (2.9).
1. Случай абсолютно жесткой подложки, как указывалось выше (раздел 1), реализуется путем предельного перехода $A \to 0$ в уравнениях задачи. Для такого случая был рассмотрен неидеальный кантилевер, исходный прогиб и толщина которого имеют волнистую форму:
(3.1)
$\begin{gathered} r(x) = {{R}_{a}}\sin {{\omega }_{R}}(L - x),\quad t(x) = {{T}_{0}} + {{T}_{a}}\sin {{\omega }_{T}}(L - x) \\ {{\omega }_{R}} = 2\pi {\text{/}}{{L}_{R}},\quad {{\omega }_{T}} = 2\pi {\text{/}}{{L}_{T}} \\ \end{gathered} $Расчеты проводились при следующих значениях параметров: ${{T}_{0}} = 10$ мкм, Ra = = ${{C}_{R}}{{H}_{0}}$, ${{T}_{a}} = {{C}_{T}}{{T}_{0}}$, ${{L}_{R}} = {{L}_{T}} = s = 0.3L$, причем значения коэффициентов ${{C}_{R}},\;{{C}_{T}}$ приводятся ниже для каждого примера. Для удобства представления результатов используется введенная ранее безразмерная координата $\xi = x_{{}}^{'}{\text{/}}s$, $x_{{}}^{'} = x - {{x}_{s}}$.
На рис. 2 изображен прогиб $u$ кантилевера на свободном участке при разных значениях параметров ${{C}_{R}}$ и ${{C}_{T}}$: 0 и 0 (0), $ - 0.05$ и $ - 0.05$ (1), 0.05 и $ - 0.05$ (2). Отметим, что нулевые значения параметров ${{C}_{R}}$ и ${{C}_{T}}$ (кривая 0) отвечают случаю идеального кантилевера, имеющего референсный прогиб $u^\circ $. Как видно, имеет место существенное отличие прогиба $u$ неидеального кантилевера (кривые 1 и 2) от прогиба $u^\circ $.
Рис. 2.
Прогиб $u$ кантилевера как функция координаты $\xi $ при разных значениях параметров ${{C}_{R}}$ и ${{C}_{T}}$: 0 и 0 (0), $ - 0.05$ и $ - 0.05$ (1), 0.05 и $ - 0.05$ (2). Кривая 0 отвечает референсному прогибу $u^\circ $.
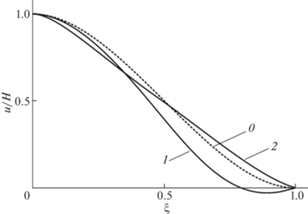
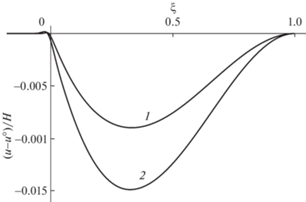
Более наглядно эффекты неидеальности кантилевера демонстрирует рис. 3, на котором показано, как меняется разность $u - u^\circ $ на свободном участке при разных значениях параметров ${{C}_{R}}$ и ${{C}_{T}}$: $ - 0.05$ и $ - 0.05$ (1), 0.05 и $ - 0.05$ (2), 0.05 и 0 (3).
Рис. 3.
Разность $u - u^\circ $ прогибов кантилевера как функция координаты $\xi $ при разных значениях параметров ${{C}_{R}}$ и ${{C}_{T}}$: $ - 0.05$ и $ - 0.05$ (1), 0.05 и $ - 0.05$ (2), 0.05 и 0 (3).
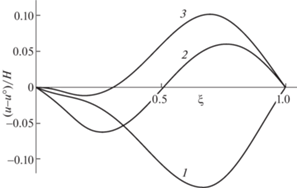
Оценки энергии адгезии $\Gamma $ при разных значениях параметров ${{C}_{R}}$, ${{C}_{T}}$ представлены в табл. 1.
Таблица 1.
Оценки энергии адгезии $\Gamma $ в мкДж/м2 при разных значениях параметров ${{C}_{R}}$ и ${{C}_{T}}$.
| CT CR | $ - 0.05$ | 0 | 0.05 |
|---|---|---|---|
| –0.05 | 111.8 | 262.8 | 482.9 |
| 0 | 142.7 | $\Gamma ^\circ $ = 297.2 | 511.7 |
| 0.05 | 167.0 | 317.6 | 516.1 |
2. Случай деформируемой подложки и идеального кантилевера, рассмотренный в разделе 1, отвечает ненулевым значениям коэффициента податливости A и $r(x) = 0,$ $t(x)$ = const. В этом случае полагалось $t = 10$ мкм, а значение коэффициента A определялось на основе известной модели шероховатого контакта при наличии межмолекулярного взаимодействия [15, 20]. Для примера был взят контакт Si (кантилевер) – Au (покрытие подложки) с двумя вариантами распределения высот шероховатости покрытия: нормальное (гауссово) распределение и негауссово распределение, которое имеет место в реальном эксперименте и характеризуется значительным числом высоких неровностей [13]. Для этих вариантов расчетные значения коэффициента A составили 15.2 мкм/ГПа и 113 мкм/ГПа, соответственно.
Как видно, учет высоких неровностей шероховатости подложки (негауссово распределение) значительно увеличивает коэффициент податливости A, что, в свою очередь, приводит к существенному изменению прогиба $u$ кантилевера (рис. 4 и 5 ).
Рис. 4.
Прогиб $u$ кантилевера как функция координаты $\xi $ при разных значениях параметра A, ГПа: 0 (0), 15.2 (1), 113 (2). Кривая 0 отвечает референсному прогибу $u^\circ $.
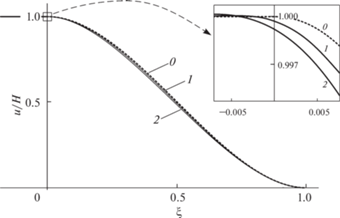
Оценки энергии адгезии $\Gamma $ при разных значениях коэффициента податливости A представлены в табл. 2.
Таблица 2.
Оценки энергии адгезии $\Gamma $ в мкДж/м2 при разных значениях параметра A
| A = 0 | $A = 15.2$ мкм/ГПа | $A = 113$ мкм/ГПа |
|---|---|---|
| $\Gamma ^\circ $ = 297.2 | 285.3 | 277.9 |
4. Обсуждение результатов. Показанные на рис. 2 и 3 графики свидетельствуют о том, что форма изогнутого кантилевера может претерпевать существенные количественные и качественные изменения при учете факторов неидеальности кантилевера (исходный прогиб, изменение толщины). Обращает на себя внимание то, что влияние факторов неидеальности кантилевера на его прогиб носит неоднозначный характер – это выражается в изменении знака разности $u - u^\circ $ по длине кантилевера (рис. 3, кривые 2 и 3). Как и следовало ожидать, отрицательные значения параметра ${{C}_{R}}$ приводят к появлению отрицательного прогиба кантилевера вблизи места его закрепления (рис. 2, кривая 1). Сравнение кривых 2 и 3 на рис. 3 позволяет установить, что при одинаковом исходном прогибе наличие фактора изменения толщины кантилевера приводит к росту величины ${\text{|}}u - u^\circ {\text{|}}$ при относительно малых значениях координаты $\xi $ ($\sim {\kern 1pt} 0.25$), но уменьшает эту величину при больших $\xi $ ($\sim {\kern 1pt} 0.75$).
Согласно рис. 4 и 5 , учет податливости подложки приводит к изменению прогиба $u$ кантилевера по всей его длине L, причем на свободном участке ($0 < \xi \leqslant 1$) прогиб уменьшается с увеличением коэффициента податливости A. Максимальное значение величина ${\text{|}}u - u^\circ {\text{|}}$ достигает в области значений $\xi \sim 0.3$.
Как показывают расчеты, отклонение прогиба $u$ кантилевера от референсного прогиба $u^\circ $ может достигать величины $0.14{\kern 1pt} {\kern 1pt} H$ = 1.4 мкм при изменении амплитуд исходного прогиба и толщины кантилевера в пределах всего 5% от значений ${{H}_{0}}$ и ${{T}_{0}}$, соответственно (рис. 3, кривая 1). Даже незначительная податливость подложки ($A = $ 15.2 мкм/ГПа) приводит к разности прогибов $u$ и $u^\circ $ в $0.009{\kern 1pt} {\kern 1pt} H$ = 0.09 мкм (рис. 5 , кривая 1). Указанные величины (1.4 мкм и 0.09 мкм) отклонений измеряемого прогиба кантилевера за счет факторов его неидеальности и податливости подложки сравнимы с отклонением ~0.1 мкм кантилевера за счет ДС, поэтому эти факторы требуют учета при обработке экспериментальных данных в МЗК [9].
Согласно данным табл. 1 и 2, учет факторов неидеальности кантилевера и податливости подложки может приводить к существенному изменению оценки энергии адгезии $\Gamma $ по сравнению с референсным значением $\Gamma ^\circ $. Особенно чувствительна эта оценка оказывается к фактору исходного прогиба кантилевера волнистой формы (3.1) – изменение амплитуды функции $r(x)$ в пределах всего 5% от значения ${{H}_{0}}$ может приводить к многократному изменению оценки энергии адгезии (табл. 1). Учет податливости подложки приводит к снижению оценки энергии адгезии (табл. 2).
Замечание 2. При реализации МЗК длина $s$ свободного участка подлежит измерению, будучи зависимой от факторов исходного прогиба и изменения толщины кантилевера, а также от податливости подложки. Напротив, энергия адгезии $\Gamma $ является свойством контактирующих поверхностей кантилевера и подложки и, поэтому, не зависит от указанных факторов. Тем не менее, полученные выше результаты представляют интерес для МЗК, т.к. они свидетельствуют о необходимости учета неидеальности формы кантилевера (исходный прогиб, изменяющаяся толщина) и податливости подложки при обработке экспериментальных данных в МЗК.
Выводы. 1. Предложена математическая модель, описывающая изгиб кантилевера и энергию адгезии при наличии ДС с учетом факторов неидеальности кантилевера (исходный прогиб, изменение толщины), а также податливости подложки применительно к МЗК.
2. На основе предложенной модели выполнен численный анализ изгиба кантилевера и даны оценки энергии адгезии. Полученные результаты свидетельствуют о важности учета реальной формы кантилевера, обладающей в общем случае исходным прогибом и изменяющейся толщиной, а также учета податливости подложки.
Работа выполнена при финансовой поддержке Российского научного фонда, грант № 20-19-00214.
Список литературы
Zhao Y.-P., Wang L.S., Yu T.X. Mechanics of adhesion in MEMS – a review // J. Adhesion Sci. Technol. 2003. V. 17. № 4. P. 519–546. https://doi.org/10.1163/15685610360554393
Mishra M.K., Dubey V., Mishra P.M., Khan I. MEMS technology: a review // J. Eng. Res. Rep. 2019. V. 4. № 1. P. 1–24. https://doi.org/10.9734/jerr/2019/v4i116891
Лифшиц Е.М., Питаевский Л.П. Статистическая физика. Часть 2. М.: Наука, 1978. 447 с.
Дзялошинский И.Е., Лифшиц Е.М., Питаевский Л.П. Общая теория ван-дер-Ваальсовых сил // УФН. 1961. Т. 73. № 3. С. 381–422. https://doi.org/10.3367/UFNr.0073.196103b.0381
Tas N., Sonnenberg T., Jansen H., Legtenberg R., Elwenspoek M. Stiction in surface micromachining // J. Micromech. Microeng. 1996. V. 6. P. 385–397. https://doi.org/10.1088/0960-1317/6/4/005
Maboudian R., Howe R.T. Critical review: Adhesion in surface micromechanical structures // J. Vacuum Sci. Technol. B. 1997. V. 15. № 1. P. 1–20. https://doi.org/10.1116/1.589247
de Boer M.P., Michalske T. A. Accurate method for determining adhesion of cantilever beams // J. Appl. Phys. 1999. V. 86. № 2. P. 817–827. https://doi.org/10.1063/1.370809
Svetovoy V.B., Melenev A.E., Lokhanin M.V., Palasantzas G. Global consequences of a local Casimir force: Adhered cantilever // Appl. Phys. Lett. 2017. V. 111. P. 011603. https://doi.org/10.1063/1.4991968
Svetovoy V.B., Postnikov A.V., Uvarov I.V., Stepanov F.I., Palasantzas G. Measuring the dispersion forces near the van der Waals–Casimir transition // Phys. Rev. Appl. 2020. V. 13. P. 064057. https://doi.org/10.1103/PhysRevApplied.13.064057
Тимошенко С.П. Курс теории упругости. Киев: Наукова думка, 1972. 506 с.
Феодосьев В.И. Сопротивление материалов. М.: Наука, 1986. 512 с.
Gudmundsson J.T. Physics and technology of magnetron sputtering discharges // Plasma Sources Sci. Technol. 2020. V. 29. P. 113001. https://doi.org/10.1088/1361-6595/abb7bd
van Zwol P.J., Svetovoy V.B., Palasantzas G. Distance upon contact: Determination from roughness profile // Phys. Rev. B. 2009. V. 80. P. 235401. https://doi.org/10.1103/PhysRevB.80.235401
Muravyeva T.I., Uvarov I.V., Naumov V.V., Palasantzas G., Svetovoy V.B. Excessive number of high asperities for sputtered rough films // Phys. Rev. B. 2021. V.104. P. 035415. https://doi.org/10.1103/PhysRevB.104.035415
Soldatenkov I.A., Yakovenko A.A., Svetovoy V.B. Measuring the Casimir forces with an adhered cantilever: analysis of roughness and background effects // Universe. 2021. V. 7. № 3. P. 64. https://doi.org/10.3390/universe7030064
Mastrangelo C.H., Hsu C.H. Mechanical stability and adhesion of microstructures under capillary forces. I. Basic theory // J. Microelectromech. Syst. 1993. V. 2. P. 33–43. https://doi.org/10.1109/84.232593
Устинов К.Б. Об уточнении граничных условий для балочной модели кантилевера атомно-силового микроскопа и их влиянии на интерпретацию результатов измерений // Изв. РАН. МТТ. 2008. № 3. С. 182–188.
Механика контактных взаимодействий / Под ред. И.И. Воровича и В.М. Александрова. М.: Физматлит, 2001. 670 с.
Dillard D.A., Mukherjee B., Karnal P., Batra R.C., Frechette J. A review of Winkler’s foundation and its profound influence on adhesion and soft matter applications // Soft Matter. 2018. V. 14. № 19. P. 3669–3683. https://doi.org/10.1039/C7SM02062G
Soldatenkov I.A., Stepanov F.I., Svetovoy V.B. Dispersion forces and equilibrium distance between deposited rough films in contact // Phys. Rev. B. 2022. V. 105. № 7. P. 075401. https://doi.org/10.1103/PhysRevB.105.075401
Palasantzas G., Svetovoy V.B., van Zwol P.J. Optical properties and kinetic roughening influence on dispersive Casimir and van der Waals forces // Int. J. Modern Phys. B. 2010. V. 24. № 31. P. 6013–6042. https://doi.org/10.1142/S0217979210057456
Muller V.M., Yushchenko V.S., Derjaguin B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane // J. Colloid Interface Sci. 1980. V. 77. № 1. P. 91–101. https://doi.org/10.1016/0021-9797(80)90419-1
Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела