Известия РАН. Механика твердого тела, 2022, № 6, стр. 18-27

РЕАЛИЗАЦИЯ ЗАДАННЫХ ОТНОСИТЕЛЬНЫХ СФЕРИЧЕСКИХ И ВИНТОВЫХ ДВИЖЕНИЙ ДВУХ ТВЕРДЫХ ТЕЛ ДВУРУКИМ РОБОТОМ

Е. И. Воробьёв^a, *

^a Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

Поступила в редакцию 10.08.2020
После доработки 03.02.2021
Принята к публикации 26.04.2021

EDN: AJYZXC
DOI: 10.31857/S0572329922050142

Аннотация

В работе решается задача реализации заданного относительного движения двух твердых тел двуруким роботом, содержащим два манипулятора с вращательными и поступательными приводами. Тела считаются жестко связанными с рабочими звеньями манипуляторов. Движение этих тел по отношению друг к другу соответствует общему случаю движения твердого тела и также разделяется на переносное и относительное. Движение этих тел по отношению друг к другу задается двумя способами. В первом случае за переносное движение принимается движение некоторой точки тела, а за относительное – движение тела вокруг этой точки. Во втором случае за переносное движение принимается движение некоторой прямой тела, а за относительное – движение тела вдоль этой прямой. На основе использования уравнений связей между параметрами, задающими движение тел относительно друг друга и обобщенными координатами манипуляторов робота, получены выражения для обобщенных координат, которые принимаются за управляющие воздействия. Показано применение данного метода к построению движений двурукого робота при сборке цилиндрических соединений. Приводится циклограмма движений робота при осуществлениях сборки.

Ключевые слова: двурукий робот, твердое тело, относительное движение, управляющие функции, сборка, алгоритм управления

Введение. Двуруким роботом будем называть совокупность манипуляторов, работающих в одной рабочей зоне и имеющих единую систему управления. Манипуляторы могут размещаться на одной подвижной платформе или на неподвижном основании. Исполнительная система двуруких роботов состоит из двух рук-манипуляторов, которые при совместном выполнении операций оказываются связанными программными связями между рабочими звеньями. При этом образуется единый механизм с несколькими степенями свободы. Такие механизмы известны под названием “механизмов относительного манипулирования” [1]. Функционирование таких механизмов подобно функционированию двух рук человека, так как основной задачей движения, необходимого для выполнения сложных операций, является реализация заданных относительного движения рабочих звеньев. Важным свойством этих механизмов является также возможность получения в относительном движении рабочих звеньев числа степеней свободы, равной сумме числа степеней свобод, взаимодействующих манипуляторов. Это приводит к повышению точности относительного манипулирования при выполнении операций по сравнению с однорукими роботами.

В [2, 3] отмечены особенности устройств относительного манипулирования и решены отдельные вопросы их структуры и кинематики. В [3] показана возможность создания таких систем на основе механизмов с параллельной структурой и решена задача о положениях одного из таких механизмов. В [4] решена задача реализации заданного относительного движения двух твердых тел двуруким роботом, у которых один из манипуляторов имеет только поступательные кинематические пары.

Ниже рассматриваются задачи реализации заданного сферического и винтового относительного движения двух твердых тел двуруким роботом с шестью степенями свободы, и построение алгоритмов управления движениями двуруких роботов на операциях сборки цилиндрических соединений.

1. Реализация относительного движения двух твердых тел двуруким роботом. При решении различных технологических и научных задач необходимо рассматривать движение твердого тела относительно неподвижной или подвижной системы координат. Наиболее распространенным методом является метод рассмотрения движения общего вида твердого тела как суммы двух движений, переносного движения тела со скоростью некоторой точки тела-полюса и относительного движения тела вокруг полюса [5]. При решении задач сборки и монтажа конструкций с цилиндрическими и винтовыми соединениями одним из основных требований является обеспечение совпадения некоторых осей, прямых линий, принадлежащих соединяемым объектам. В этом случае целесообразно целевое относительное положение объектов задавать в виде заданного относительного положения некоторой прямой и перемещения объекта вдоль этой прямой. Такой метод определения положения прямых и тел используется в винтовом исчислении и линейчатой геометрии [6]. Сборочные операции цилиндрических соединений широко распространены в машиностроении. Для осуществления таких операций в производстве применяются автоматические сборочные центры, содержащие роботы и специальные сборочные устройства [7, 8]. Некоторые задачи управления двурукими роботами с учетом динамики рассматривались в [9–11].

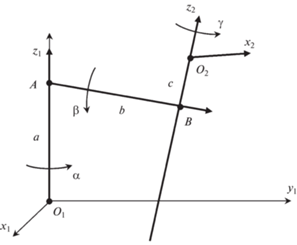
1.1. Винтовой способ задания движения твердого тела. Известно, что движение твердого тела в любой момент времени является винтовым, то есть имеет место мгновенная ось вращения и вращение тела относительно этой оси. При конечных перемещения твердого тела аналогично существует ось конечного поворота и угол поворота, переводящий тело из начального положения в конечное. Рассмотрим вопрос об определении положения твердого тела и прямой линии при совершении трех винтовых движений относительно перпендикулярных осей. Положение прямой относительно декартовой системы координат будем определять четырьмя независимыми параметрами a, α, b, β. (рис. 1).

Рис. 1.

Винтовой способ задания положения твердого тела.

Среди которых a, α – соответственно линейное перемещение прямой вдоль некоторой оси системы координат (например, оси Oz) и угол поворота вокруг этой оси и b, β – перемещение прямой по линии кратчайшего расстояния между прямой и осью Oz и угол поворота вокруг этой линии. Перемещение тела, относительно прямой будем определять перемещением “с” и поворотом “γ” тела вдоль этой прямой. Перемещение тела, связанного с этой прямой, является винтовым, состоящим из перемещения прямой и перемещения тела вдоль этой прямой. Для задания относительно движения двух твердых тел, с каждым из них свяжем декартову систему координат, причем одну из них O₁x₁y₁z₁ можно считать неподвижной, а положение второй относительно первой будем определять шестью параметрами: a, α, b, β, с, γ.

1.2. Матрица относительного положения двух твердых тел. В соответствии с введенными параметрами, определяющими винтовое движение твердого тела, можно составить матрицу, определяющую относительное положение двух твердых тел, в виде матрицы четвертого порядка как произведение матриц трех винтовых перемещений.

(1.1)

${{M}_{{12}}} = {{M}_{\alpha }}{{M}_{\beta }}{{M}_{\gamma }}~$

где M₁₂ – матрица определяющая относительное положение систем координат связанных с телами; M_αM_βM_γ – соответственно матрицы винтовых перемещений. Эти матрицы имеют вид:

(1.2)

$\begin{gathered} {{M}_{\alpha }} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos {{\alpha }}}&{ - \sin {{\alpha }}} \\ {\sin {{\alpha }}}&{\cos {{\alpha }}} \end{array}}&{\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}} \\ {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}}&{\begin{array}{*{20}{c}} 1&a \\ 0&1 \end{array}} \end{array}} \right],\quad {{M}_{\beta }} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&0 \\ 0&{\cos {{\beta }}} \end{array}}&{\begin{array}{*{20}{c}} 0&b \\ { - \sin {{\alpha }}}&0 \end{array}} \\ {\begin{array}{*{20}{c}} 0&{\sin {{\beta }}} \\ 0&0 \end{array}}&{~~~\begin{array}{*{20}{c}} {\cos {{\beta }}}&0 \\ 0&1 \end{array}} \end{array}} \right] \\ {{M}_{\gamma }} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos {{\gamma }}}&{ - \sin {{\gamma }}} \\ {\sin {{\gamma }}}&{\cos {{\gamma }}} \end{array}}&{\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}} \\ {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}}&{\begin{array}{*{20}{c}} 1&c \\ 0&1 \end{array}} \end{array}} \right] \\ \end{gathered} $

Перемножением матриц в (1.1) с учетом (1.2) получим матрицу относительного положения двух тел в виде определяющую положение твердого тела после трех винтовых поворотов.

(1.3)

${{M}_{{12}}} = \left[ {\begin{array}{*{20}{c}} {\left[ {{{L}_{z}}} \right]}&{\left[ x \right]} \\ 0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{{\alpha }}}_{{11}}}}&{{{{{\alpha }}}_{{12}}}} \\ {{{{{\alpha }}}_{{21}}}}&{{{{{\alpha }}}_{{22}}}} \end{array}}&{\begin{array}{*{20}{c}} {{{{{\alpha }}}_{{13}}}}&{{{a}_{1}}} \\ {{{{{\alpha }}}_{{23}}}}&{{{b}_{1}}} \end{array}} \\ {\begin{array}{*{20}{c}} {{{{{\alpha }}}_{{31}}}}&{{{{{\alpha }}}_{{32}}}} \\ 0&0 \end{array}}&{\begin{array}{*{20}{c}} {{{{{\alpha }}}_{{33}}}}&{{{c}_{1}}} \\ 0&1 \end{array}} \end{array}} \right]$

где $\left[ {{{L}_{z}}} \right]$ – матрица третьего порядка направляющих косинусов осей координат, связанных с телами, [x] – матрица координат начала одной системы в другой

Произведя перемножение матриц, получим

(1.4)

$\left[ {{{L}_{z}}} \right] = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos {{\alpha }}\cos {{\gamma }} - } \\ { - \sin {{\alpha }}\cos {{\beta }}\sin {{\gamma }}} \end{array}}&{\begin{array}{*{20}{c}} { - \cos {{\alpha }}\sin {{\gamma }} - } \\ { - \sin {{\alpha }}\cos {{\beta }}\cos {{\gamma }}} \end{array}}&{\sin {{\alpha }}\sin {{\beta }}} \\ {\begin{array}{*{20}{c}} {\sin {{\alpha }}\cos {{\gamma }} + } \\ { + \cos {{\alpha }}\cos {{\beta }}\sin {{\gamma }}} \end{array}}&{\begin{array}{*{20}{c}} { - \sin {{\alpha }}\sin {{\gamma }} + } \\ { + \cos {{\alpha }}\cos {{\beta }}\cos {{\gamma }}} \end{array}}&{ - \cos {{\alpha }}\sin {{\beta }}} \\ {\sin {{\beta }}\sin {{\gamma }}}&{\sin {{\beta }}\cos {{\gamma }}}&{\cos {{\beta }}} \end{array}} \right]$

(1.5)

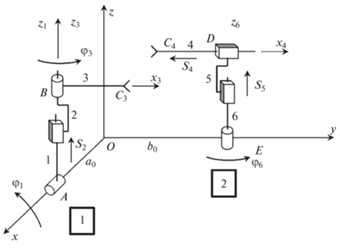
$\left[ x \right] = \left[ {\begin{array}{*{20}{c}} {{\text{c}}\sin {{\beta }}\sin {{\alpha }} + {\text{b}}\cos {{\alpha }}} \\ { - {\text{c}}\sin {{\beta }}\cos {{\alpha }} + {\text{b}}\sin {{\alpha }}} \\ {{\text{c}}\cos {{\beta }} + a} \end{array}} \right]$

1.3. Реализация переносного и сферического относительного движения двух твердых тел двуруким роботом. Будем считать, что манипуляционная система двурукого робота содержит два манипулятора, каждый с тремя степенями свободы (рис. 2). Общее число степеней свободы манипуляционной системы равно шести.

Рис. 2.

Схема двурукого робота ВПВ – ВПП.

Манипуляторы содержат вращательные (В) и поступательные (П) кинематические пары. Положения манипуляторов определяется шестью обобщенными координатами q_i (i = 1, 2, …, 6). Определению подлежат обобщенные координаты манипуляторов: S_i (i = 2, 4, 5); φ_i (i = 1, 2, 6), которые являются управляющими функциями. Эти перемещения реализуются системой управления робота. Рабочими звеньями манипуляторов является звенья 3 и 4. В этом случае положение звена 3 по отношению к звену 4 определяется матрицей ориентации. Mатрицу ориентации относительного положения рабочих звеньев 3 и 4 используем для определения положения звена 3 в неподвижной системе координат.

Переходя к системе C₃x₃y₃z₃ от системы Oxyz через звенья манипулятора “1” получим матрицу ориентации

(1.6)

$\begin{gathered} L_{{03}}^{{\left( 1 \right)}} = \left[ {\begin{array}{*{20}{c}} {\cos {{{{\varphi }}}_{6}}}&{ - \sin {{{{\varphi }}}_{6}}}&0 \\ {\sin {{{{\varphi }}}_{6}}}&{\cos {{{{\varphi }}}_{6}}}&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{{\alpha }}}_{{11}}}}&{{{{{\alpha }}}_{{12}}}}&{{{{{\alpha }}}_{{13}}}} \\ {{{{{\alpha }}}_{{21}}}}&{{{{{\alpha }}}_{{22}}}}&{{{{{\alpha }}}_{{23}}}} \\ {{{{{\alpha }}}_{{31}}}}&{{{{{\alpha }}}_{{32}}}}&{{{{{\alpha }}}_{{33}}}} \end{array}} \right] = \\ = \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{{11}}}\cos {{\varphi }_{6}} - {{\alpha }_{{21}}}\sin {{\varphi }_{6}}}&{{{\alpha }_{{12}}}\cos {{\varphi }_{6}} - {{\alpha }_{{22}}}\sin {{\varphi }_{6}}}&{{{\alpha }_{{13}}}\cos {{\varphi }_{6}} - {{\alpha }_{{23}}}\sin {{\varphi }_{6}}} \\ {{{\alpha }_{{11}}}\sin {{\varphi }_{6}} + {{\alpha }_{{21}}}\cos {{\varphi }_{6}}}&{{{\alpha }_{{12}}}\sin {{\varphi }_{6}} + {{\alpha }_{{22}}}\cos {{\varphi }_{6}}}&{{{\alpha }_{{13}}}\sin {{\varphi }_{6}} + {{\alpha }_{{23}}}\cos {{\varphi }_{6}}} \\ {{{\alpha }_{{31}}}}&{{{\alpha }_{{32}}}}&{{{\alpha }_{{33}}}} \end{array}} \right] \\ \end{gathered} $

Переходя к системе C₃x₃y₃z₃ от системы Oxyz через звенья манипулятора “2” получим

(1.7)

$\begin{gathered} L_{{03}}^{{\left( 2 \right)}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {{{{\varphi }}}_{1}}}&{ - \sin {{{{\varphi }}}_{1}}} \\ 0&{\sin {{{{\varphi }}}_{1}}}&{\cos {{{{\varphi }}}_{1}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos {{{{\varphi }}}_{3}}}&{ - \sin {{{{\varphi }}}_{3}}}&0 \\ {\sin {{{{\varphi }}}_{3}}}&{\cos {{{{\varphi }}}_{3}}}&0 \\ 0&0&1 \end{array}} \right] = \\ = \left[ {\begin{array}{*{20}{c}} {\cos {{{{\varphi }}}_{3}}}&{ - \sin {{{{\varphi }}}_{3}}}&0 \\ {\cos {{{{\varphi }}}_{1}}\sin {{{{\varphi }}}_{3}}}&{\cos {{{{\varphi }}}_{1}}\cos {{{{\varphi }}}_{3}}}&{ - \sin {{{{\varphi }}}_{1}}} \\ {\sin {{{{\varphi }}}_{1}}\sin {{{{\varphi }}}_{3}}}&{\sin {{{{\varphi }}}_{1}}\cos {{{{\varphi }}}_{3}}}&{\cos {{{{\varphi }}}_{1}}} \end{array}} \right] \\ \end{gathered} $

Из условия $L_{{03}}^{{\left( 1 \right)}} = L_{{03}}^{{\left( 2 \right)}}$ имеем

${{{{\varphi }}}_{1}} = \arccos {{{{\alpha }}}_{{33}}}$

${{{{\varphi }}}_{3}} = {\text{arctg}}\frac{{{{{{\alpha }}}_{{31}}}}}{{{{{{\alpha }}}_{{32}}}}}$

${{{{\varphi }}}_{6}} = {\text{arctg}}\frac{{{{{{\alpha }}}_{{13}}}}}{{{{{{\alpha }}}_{{23}}}}}$

Приравнивая координаты С₃ в неподвижной системе координат при переходе через звено манипулятора 1 и 2 получим

${{l}_{{\text{3}}}}{\text{cos}}{{{{\varphi }}}_{{\text{3}}}} + {{a}_{{\text{0}}}} = ({{a}_{{\text{1}}}} + {{S}_{{\text{4}}}}){\text{cos}}{{{{\varphi }}}_{{\text{6}}}} - {{b}_{1}}\sin {{{{\varphi }}}_{6}} + {{b}_{{\text{0}}}}$

(1.8)

${{l}_{{\text{3}}}}\sin {{{{\varphi }}}_{3}}{\text{cos}}{{{{\varphi }}}_{{\text{1}}}} - {{S}_{{\text{2}}}}\sin {{{{\varphi }}}_{1}} = \left( {{{a}_{{\text{1}}}} + {{S}_{{\text{4}}}}} \right)\sin {{{{\varphi }}}_{6}} - {{b}_{1}}{\text{cos}}{{{{\varphi }}}_{{\text{6}}}}$

${{l}_{{\text{3}}}}\sin {{{{\varphi }}}_{3}}\sin {{{{\varphi }}}_{1}} - {{S}_{{\text{2}}}}\sin {{{{\varphi }}}_{1}}{\text{ = \;}}{{C}_{1}} + {{S}_{5}}$

Из последних уравнений линейные перемещения S₂, S₄ и S₅ найдем, решая линейную систему уравнений (1.8).

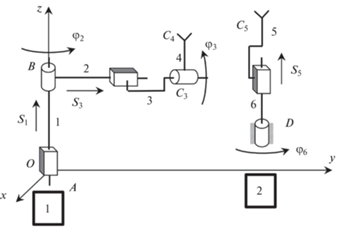
1.4. Реализация относительного винтового движения двух твердых тел. Для реализации заданного относительного винтового движения двух твердых тел используем двурукий робот, состоящий из двух манипуляторов с четырьмя и двумя степенями свободы (рис. 3).

Рис. 3.

Схема двурукого робота ПВПВ – ВП.

Первый манипулятор содержит две поступательные и две вращательные кинематические пары, а второй манипулятор содержит одну вращательную и одну поступательную кинематическую пары. Управляющими функциями манипулятора 1 являются углы поворота звеньев 2 и 4 относительно предыдущих φ₂, φ₄ и относительные линейные перемещения звеньев 1 и 3 относительно предыдущих S₁ и S₃. Управляющими функциями у манипулятора 2 являются поворот звена 6 – φ₆ и линейное перемещение звена 6 – S₅. Эти функции подлежат определению. Заданными будем считать относительные положения звеньев 4 и 5. Это относительное положение задается положением прямой звена 4 в системе звена 5, определяемое параметрами a, α, b, и перемещением звена 5 вдоль этой прямой, определяемое параметрами с, γ. За прямую линию звена 4 примем прямую С₃С₄. Эта прямая должна совпасть с прямой С₅D, принадлежащей звену 5. Для совпадения этих прямых должны совпасть также координаты точки С₃ прямой С₃С₄ и точки D прямой С₅D, а также направляющие косинусы прямых. Условие совпадения точек можно записать в виде

${{S}_{3}}\cos {{{{\varphi }}}_{2}} = {{x}_{d}}$

(1.9)

${{S}_{3}}\sin {{{{\varphi }}}_{2}} = {{y}_{d}}$

${{S}_{1}} = {{z}_{d}}$

где x_d, y_d, z_d – координаты точки D в неподвижной системе координат Oxyz, считаем заданными. Условие совпадения направляющих косинусов прямых имеет вид

$\sin {{{{\varphi }}}_{2}}\sin {{{{\varphi }}}_{4}} = {{l}_{6}}$

(1.10)

$ - \cos {{{{\varphi }}}_{2}}\sin {{{{\varphi }}}_{4}} = {{m}_{6}}$

$\cos {{{{\varphi }}}_{4}} = {{n}_{6}}$

где l₆, m₆, n₆ – направляющие косинусы оси С₅D, считаем заданными. Из уравнения (1.10) найдем

${{{{\varphi }}}_{2}} = {\text{arctg}}\left( { - \frac{{{{l}_{6}}}}{{{{m}_{6}}}}} \right)$

(1.11)

${{{{\varphi }}}_{4}} = {\text{arccos}}~{{n}_{6}}$

Из уравнений (1.9) найдем

(1.12)

${{S}_{1}} = {{z}_{d}}$

${{S}_{3}} = \pm \sqrt {(x_{d}^{2} + y_{d}^{2})} $

При выполнении условий (1.11) и (1.12) прямые С₃С₄ и С₅D совпадают.

После этого перемещения S₅ и φ₆ равны соответственно

${{S}_{5}} = c$

(1.13)

${{{{\varphi }}}_{6}} = \gamma $

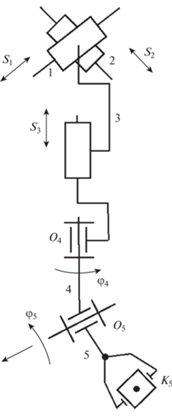
1.5. Определение относительных положений звеньев манипуляторов сборочной системы (рис. 5). Для построения программных движений манипуляторов в сборочной системе решим вначале задачу об определении относительных положений звеньев манипулятора с пятью степенями свободы при захвате цилиндрической детали.

Рис. 4.

Система сборки цилиндрических соединений.

Рис. 5.

Манипулятор.

Манипулятор содержит три поступательных и две вращательных кинематические пары (рис. 5).

Со звеньями манипулятора свяжем системы координат следующим образом: оси системы координат звеньев 1, 2, 3 параллельны осям неподвижной системы координат $~OXYZ$, со звеном 4 свяжем систему координат ${{O}_{{4~}}}{{X}_{4}}{{Y}_{4}}{{Z}_{4}}$, направив ось ${{Z}_{4}}$ параллельно оси OZ, а ось X₄ параллельна оси пары ${{O}_{5}}$, со звеном 5 свяжем систему координат ${{O}_{{5~}}}{{X}_{5}}{{Y}_{5}}$ ${{Z}_{5}}$, направив ось X₅ по оси пары ${{O}_{{5~}}}$, а ось ${{Z}_{5}}$ по оси звена 5 – схвата манипулятора. Положение цилиндрической детали будем задавать координатами точки, расположенной на оси детали и направляющими косинусами оси детали в неподвижной системе координат. При решении обратной задачи о положениях манипулятора будем иметь в виду, что захват цилиндрической детали может производиться схватом робота двумя разными способами, с торца и сбоку. Будем считать, что цилиндрические детали для сборки, втулка и цилиндрический штифт в загрузочном устройстве подаются в положении, когда ось детали параллельна оси OZ, неподвижной системы координат. Координаты контролируемой точки схвата робота ${{O}_{{5~}}}$ могут быть найдены по формуле:

(1.14)

$\left[ {{{x}_{5}}} \right] = {{L}_{{03}}} + {{L}_{{34}}}{{l}_{4}} + {{L}_{{45}}}{{l}_{5}}$

где l₄, l₅ – длины звеньев 4 и 5, ${{L}_{{34}}}$, ${{L}_{{45}}}$ – матрица перехода от системы i к системе $i - 1$ ($i = 3,4$), ${{L}_{{03}}}$ – единичная матрица перехода от системы ${{X}_{3}}{{Y}_{3}}$${{Z}_{3}}$ к системе $OXYZ$.

Причем,

(1.15)

${{L}_{{45}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {{{{\varphi }}}_{5}}}&{ - \sin {{{{\varphi }}}_{5}}} \\ 0&{\sin {{{{\varphi }}}_{5}}}&{\cos {{{{\varphi }}}_{5}}} \end{array}} \right];\quad {{L}_{{34}}} = \left[ {\begin{array}{*{20}{c}} {\cos {{{{\varphi }}}_{4}}}&{ - \sin {{{{\varphi }}}_{4}}}&0 \\ {\sin {{{{\varphi }}}_{4}}}&{\cos {{{{\varphi }}}_{4}}}&0 \\ 0&0&1 \end{array}} \right]$

Произведя перемножение матриц в выражении (1.12) с учетом (1.11) получим координаты точки K₅ схвата в неподвижной системе координат.

${{X}_{5}} = {{S}_{1}} + {{l}_{5}}\sin {{{{\varphi }}}_{4}}\sin {{{{\varphi }}}_{5}}$

(1.16)

${{Y}_{5}} = {{S}_{2}} - {{l}_{5}}\cos {{{{\varphi }}}_{4}}\sin {{{{\varphi }}}_{5}}$

${{Z}_{5}} = {{S}_{3}} + {{l}_{5}}\cos {{{{\varphi }}}_{5}}$

Ориентация схвата определяется матрицей ориентации, связанной с ним системы координат ${{K}_{{5~}}}{{X}_{5}}{{Y}_{5}}$ ${{Z}_{5}}$.

(1.17)

${{L}_{{05}}} = {{L}_{{04}}}{{L}_{{05}}}$

Используя выражения матриц (1.15) и, производя перемножение, получим:

(1.18)

$~~{{L}_{{05}}} = \left[ {\begin{array}{*{20}{c}} {\cos {{{{\varphi }}}_{4}}}&{ - \sin {{{{\varphi }}}_{4}}\cos {{{{\varphi }}}_{5}}}&{~~~~\sin {{{{\varphi }}}_{4}}\sin {{{{\varphi }}}_{5}}} \\ {\sin {{{{\varphi }}}_{4}}}&{~~~~~\cos {{{{\varphi }}}_{4}}\cos {{{{\varphi }}}_{5}}}&{ - \cos {{{{\varphi }}}_{4}}\sin {{{{\varphi }}}_{5}}} \\ 0&{\sin {{{{\varphi }}}_{5}}}&{\cos {{{{\varphi }}}_{5}}} \end{array}} \right]$

$L = \left[ {\begin{array}{*{20}{c}} {{{{{\alpha }}}_{{11}}}}&{{{{{\alpha }}}_{{12}}}}&{{{{{\alpha }}}_{{13}}}} \\ {{{{{\alpha }}}_{{21}}}}&{{{{{\alpha }}}_{{22}}}}&{{{{{\alpha }}}_{{23}}}} \\ {{{{{\alpha }}}_{{31}}}}&{{{{{\alpha }}}_{{32}}}}&{{{{{\alpha }}}_{{33}}}} \end{array}} \right]$

При захвате детали с торца, ось Z₅ схвата становится направленной по оси OZ, т.е. элементы третьего столбца матрицы (1.15) соответственно равны:

${{\alpha }_{{13}}} = 0,\quad {{\alpha }_{{33}}} = 1$

откуда $\cos {{{{\varphi }}}_{5}}$ = 1, ${{{{\varphi }}}_{5}}$ = 0, $\sin {{{{\varphi }}}_{4}}$ = 0, ${{{{\varphi }}}_{4}}$ – 0. При захвате детали сбоку ось Z₅ перпендикулярна оси $OZ$, ${{{{\alpha }}}_{{33}}}$= 0. Следовательно, $\cos {{{{\varphi }}}_{5}}$ = 0, ${{{{\varphi }}}_{5}}$ = ${{\pi /}}2$. Значение S₁, S₂, S₃ определяются из линейной системы уравнений (1.16).

1.6. Циклограммы движения манипуляторов. Циклограмма движения манипулятора 1:

– Переход из начального положения в опорную точку A₁ на оси втулки.

– Движение в точку A₂ захвата втулки.

– Зажим втулки.

– Возврат схвата со втулкой в точку A₁.

– Перенос втулки в положение сборки, в точку A₃.

Циклограмма движения манипулятора 2:

– Переход из начального положения в опорную точку A₄, на линию оси штифта.

– Движение по оси штифта в точку A₅, захвата штифта.

– Захват штифта.

– Перенос штифта в точку A₄ на оси штифта.

– Перенос штифта в точку A₆, на линию сборки, на оси втулки.

– Перемещение штифта по линии сборки до соединения со втулкой.

– Освобождение штифта манипулятором.

– Перенос схвата манипулятора в точку A₄.

Перемещение собранного изделия манипулятором 1 на конвейер.

Перемещение втулки манипулятором 1 в точки A₁, A₂, A₃ и перемещение штифта в точки A₄, A₅, A₆ может быть осуществлено одновременно, при этом сокращается общее время цикла и повышается производительность сборочного комплекса. Однако, при этом следует обеспечить отсутствие пересечения звеньев манипуляторов.

Заключение. Предложен метод реализации относительного движения общего вида двух твердых тел двуруким роботом с шестью степенями свободы. Особенностью метода является разделение в уравнениях связи линейных и угловых перемещений. Получены в явном виде выражения для управляющих функций при реализации относительного движения общего вида двух твердых тел двуруким роботом, с вращательными и поступательными приводами. Показано применение предложенного метода построения движений двуруких роботов к выполнению операций сборки цилиндрических соединений.

Список литературы

Крайнев Ф.Ф., Глазунов В.А. Новые механизмы относительного манипулирования // Проблемы машиностроения и надежности машин. 1994. № 5. С. 106–117.
Глазунов В.А., Ласточкин А.Б., Терехова Ф.Н., Ву Нгок Бик Об особенностях устройств относительного манипулирования // Проблемы машиностроения и надежности машин. 2007. № 2. С. 77–85.
Глазунов В.А., Ласточкин А.Б., Шалюхин К.А., Данилин П.О. К анализу и классификации устройств относительного манипулирования // Проблемы машиностроения и надежности машин. 2009. № 4. С. 81–85.
Воробьев Е.И. Осуществление заданного относительного движения двух твердых тел двуруким роботом // Изв. РАН. МТТ. 2018. № 2. С. 122–128.
Лурье А.И. Аналитическая механика. М.: ГИФМЛ, 1961. 824 с.
Дименберг Ф.М. Теория винтов и ее приложения. М.: Наука, 1978. 328 с.
Козырев Ю.Г. Установка захватных устройств и инструментов на конечном звене манипулятора при сборке изделий // Сборка в машиностроении, приборостроении. 2016. № 12. С. 19–21.
Козырев Ю.Г. Применение промышленных роботов. M.: КноРус, 2011, 488 с.
Chiacchio P., Chiaverini S., Silciliano B. Direct and inverse kinematics for coordinated motion tasks of a two-manipulator system // J. Dyn. Syst. Meas. Control. 1996. V. 118. № 4. P. 691–697. https://doi.org/10.1115/1.2802344
Caccavale F., Chiacchio P., Chiaverini S. Task-Space regulation of cooperative manipulators // Automatica. 2000. V. 36. № 6. P. 879–887. https://doi.org/10.1016/S0005-1098(99)00215-0
Luh J.Y.S., Zheng Y.F. Constrained relations between two coordinated industrial robots for motion control // Int. J. Robot. Res. 1987. V. 6. № 3. P. 60–70. https://doi.org/10.1177/027836498700600304

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал