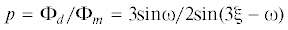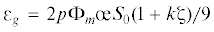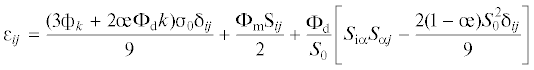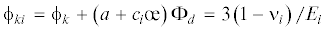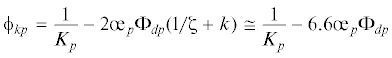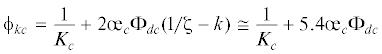Известия РАН. Механика твердого тела, 2022, № 6, стр. 3-17
О ВЛИЯНИИ ДИЛАТАНСИИ НА ХАРАКТЕРИСТИКИ ФОРМОИЗМЕНЕНИЯ И ОБЪЕМНОЙ УПРУГОСТИ РАЗНОСОПРОТИВЛЯЮЩИХСЯ СРЕД
a Военно-технический университет
Балашиха, Россия
* E-mail: 06kfk38@mail.ru
Поступила в редакцию 17.12.2020
После доработки 03.11.2021
Принята к публикации 23.11.2021
- EDN: KORUCS
- DOI: 10.31857/S0572329922050087
Аннотация
Данная работа является продолжением исследований автора по практическому использованию математических моделей на основе тензорно-нелинейных уравнений, с помощью которых показано, что количественную меру тензорной нелинейности в них выполняет отношение материальных функций при тензорных аргументах, названное параметром тензорной нелинейности. Являясь независимой величиной от угла вида напряженного состояния, параметр определяет изменение фазы подобия девиаторов, способствуя формулированию соотношений для описания деформаций: формоизменения, объемной деформации и дополнительной деформации – дилатансии, а также показывает, что деформации, как формоизменения, так и объемные можно представить в виде двух частей. Первую часть связать с деформацией жестких элементов структуры, а вторую часть, включающую в себя этот параметр, отнести к утрате упругости межструктурных связей при пропорциональном росте напряжений. Поведение разносопротивляющихся сред существенно зависит не только от уровня деформаций, но и их знака, которые способствуют или препятствуют росту дилатансии. В направлении большей положительной деформации дилатансия дополняет ее, создает коэффициенты поперечных деформаций со значениями, меньшими начального их значения, а, являясь поперечной для других направлений, может вызывать коэффициенты, которые растут, превышая иногда число 0.5, существенно влияя на другие характеристики. Допущение дилатансии к упругим деформациям является неизбежным шагом, необходимым для объяснения поведения всех коэффициентов и характеристик упругости по трем направлениям. Исследования этих деформаций в разных квадрантах позволили установить, что утрата связей и рост дилатансии является основной причиной деформационной анизотропии теоретических коэффициентов поперечных деформаций, помогающей выявить эффект влияния дилатансии на характеристики объемной упругости при пропорциональном росте напряжений. Для точной оценки возникающей анизотропии в направлении главных напряжений предлагается использовать параметр изменяющейся упругости, значения которого при двухосном сжатии становятся отрицательными с отрицательным значением параметра разрыхления и отрицательной дилатансией.
1. Введение. В настоящее время в нелинейной теории упругости разносопротивляющихся сложных сред, в группу которых входят зернистые композиты, чугуны, графиты, строительные материалы, в том числе и грунты, для описания их свойств наиболее распространенным направлением являются теории, основанные на выборе потенциала деформаций. Они позволяют установить определяющие уравнения и характеристики упругости для решения краевых задач, к которым следует отнести работы [1, 2] и другие, где о разрушении связей часто не упоминается. Подробный анализ исследований по данному направлению проведен в работах Трещева А.А. [2], где можно найти обзор литературы, как по персоналиям, так и по хронологии. Поскольку число публикаций по данному вопросу нелинейной теории упругости достаточно велико, в том числе и обзорных, например, работа Трещева А.А. [2], поэтому нет веских причин останавливаться на этом вопросе более подробно. С нашей точки зрения перспективным направлением для решения проблем механики разносопротивляющихся материалов, является разработка моделей, использующих подзабытый математический аппарат уравнений, вывод которых был дан В.В. Новожиловым [3]. В отечественной и зарубежной литературе еще весьма мало работ, в которых применялись бы тензорно-нелинейные уравнения для решения практических задач. Одной из причин такого отношения к ним следует назвать отсутствие более глубокого анализа и исследований их свойств и, в частности, материальных функций, которые отвечали бы реальным свойствам отмеченных сред. Используя концепцию тензорно-нелинейных уравнений, в работе [6, с. 189] разработана методика определения дилатансии и характеристик объемной упругости, показано существенное различие значений модулей: высокие при растяжении, но низкие при сжатии, зависящих от уровня нагрузки и от вида напряженного состояния. Методика, включающая в себя процедуры наложения теоретических кривых для коэффициентов поперечных деформаций с кривыми, полученными при испытаниях на растяжение и сжатие, позволила определять значения теоретических модулей объемной упругости и параметры разрыхления для напряженных состояний второго квадранта. Она раскрыла механизм изменения дополнительной объемной деформации – дилатансии, состоящей в том, что положительные деформации, как формоизменения, так и объемные, сопровождаются потерей упругости и утраты связей, создавая заметную деформационную анизотропию коэффициентов поперечных деформаций и характеристик объемной упругости.
Целью данной работы является вывод соотношений для описания деформаций формоизменения и объемных деформаций при использовании общего выражения для фазы подобия девиаторов, как законов связи инвариантов тензора деформаций с инвариантами тензора напряжений, учитывающих дилатансию, в результате последовательного накопления изменений упругости межструктурных связей, – основной причины взаимосвязи упомянутых деформаций. Провести исследования по изучению влияния дилатансии на характеристики упругости в трех квадрантах плоских напряженных состояний, чтобы показать, что концепция на основе тензорно-нелинейных уравнений способна более наглядно и точнее описывать деформации и нелинейные эффекты разносопротивляющихся сред.
2. Метод решения. После замены вторых инвариантов на интенсивности напряжений и деформаций, уравнения [3, 4] связи девиатора деформаций с девиатором напряжений Новожилова В.В. можно привести к виду:
(2.1)
${{{\text{e}}}_{{ij}}} = {{{{\Phi }}}_{m}}{{S}_{{ij}}}{\text{/}}2 + {{{{\Phi }}}_{d}}({{S}_{{i\alpha }}}{{S}_{{\alpha j}}} - 2S_{0}^{2}{\text{/}}9{{{{\delta }}}_{{ij}}}){\text{/}}{{S}_{0}}$(2.2)
${{{{\Phi }}}_{m}} = {{{{\Phi }}}_{{{\xi }}}}{\text{sin}}(3{{\xi }} - {{\omega }}){\text{/}}\sin 3{{\xi }} = {{{{\varphi }}}_{i}}{\text{/}}3$(2.3)
${{{{\Phi }}}_{d}} = 3{{{{\Phi }}}_{{{\xi }}}}{\text{sin}}({{\omega }}){\text{/}}(2\sin 3{{\xi }}) = {{\{ 3{\text{/}}8[{{({{{{\Phi }}}_{m}} - {{{{\varphi }}}_{i}})}^{2}}]\} }^{{1/2}}}$3. О фазе подобия девиаторов. Определение параметра и анализ тригонометрического выражения (2.4), дают общее выражение для фазы подобия девиаторов:
а для частного случая, ${{\omega }} = {\text{const}}$, впервые предложенного в работе Новожилова В.В. [4, с. 712], в качестве характеристики упругости, как связь между третьими инвариантами. Исследование параметра на экстремум выявило, что производная тригонометрического выражения (2.4) по углу ξ равна нулю, а, следовательно, его независимость от вида напряженного состояния. Этот вывод утверждает, что функции (2.2) и (2.3) подобны при постоянном уровне напряжений для всех состояний:Именно эта связь функций позволяет рассматривать деформации, как формоизменения, так и объемные деформации в виде двух частей. Первую часть связывать с деформацией жестких элементов структуры, а вторую часть деформации, включающей в себя параметр тензорной нелинейности, отнести к утрате упругости структурных связей [7, 8]. Эти деформации, несмотря на их физическое отличие, в математическую модель входят как упругие.
Графики для фазы подобия девиаторов, исходя из (3.1), незначительно отличаются от полуволны синусоиды с изменением угла ξ от нуля до π/3, а нулевые ее значения соответствуют состояниям растяжения и сжатия. При значениях фазы, отличной от нуля, отношения компонент девиаторов, принадлежащих одному и тому же напряженному состоянию не равны: ${{e}_{1}}{\text{/}}{{S}_{1}} \ne {{e}_{2}}{\text{/}}{{S}_{2}} \ne {{e}_{3}}{\text{/}}{{S}_{3}}$, что соответствует условию их непропорциональности. Тем не менее, для состояний обобщенного растяжения и сжатия неравенства становятся равенствами: ${{S}_{1}}{\text{/}}{{{\text{S}}}_{2}} = {{e}_{1}}{\text{/}}{{e}_{2}} = 1$, так как для них реализуются условия подобия, поскольку ${{S}_{2}} = {{S}_{3}}$ и ${{e}_{2}} = {{e}_{3}}$, а фаза равна нулю независимо от свойств материала, что согласуется с соотношением (3.1). Его анализ дает значения угла ξ, при котором достигается максимум фазы ${{{{\omega }}}_{{{\text{max}}}}}$. Структура практически всех упомянутых выше сред, ярким примером которых являются зернистые композиты [8, с. 15], содержит множество равномерно распределенных межструктурных связей. Рост параметра p указывает на последовательную утрату упругости связей возрастающей прочности.
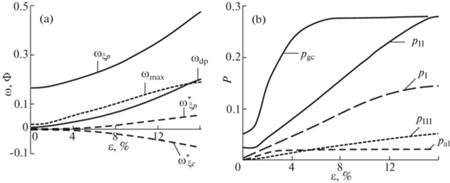
Значение характеристики упругости ${{\omega }} = {\text{const}}$, как это принято в работе [4] вместо (3.1), при сохранении вида функции Φm приводит к тому, что параметр становится величиной со снижающимися значениями, что расходится с неравенством p < 1. К тому же при растяжении и сжатии нарушается условие нулевого значения фазы ω, как функции угла ${{\xi }}$. На рис. 1,a показана кривая (мелкий штрих) для фазы подобия девиаторов ${{{{\omega }}}_{{{\text{max}}}}}$, как функции деформации ε. Графики для параметров p трех разных квадрантов и других материалов, представлены на рис. 1,b.
Рис. 1.
(a) Кривая (мелкий штрих) для фазы ${{{{\omega }}}_{{{\text{max}}}}}$, как функции деформации ${{\varepsilon }}$; также показаны кривые для функций с символами ${{\Phi }}_{{{{\xi }}p}}^{*}$ и ${{\Phi }}_{{{{\xi }}c}}^{*}$, для состояний растяжения и сжатия, которые относятся ко второму квадранту. (b) Графики для параметров трех разных квадрантов и других материалов: серого чугуна pgc и алюминиевого сплава pal.
4. О деформациях формоизменения. Отказ от постоянства фазы приводит к отказу и от постоянства модулей упругости. Уравнения (2.3) для главных деформаций и общее выражение для интенсивности деформаций приводят к закону формоизменения:
где основной характеристикой становится обобщенная податливость, как обратная величина обобщенного модуля сдвига [6, с. 709]:(4.2)
${{{{\Phi }}}_{{{\xi }}}} = {{{{\Phi }}}_{m}}{{[1 + (4{\text{/}}3)p\cos 3{{\xi }} + (4{\text{/}}9){{p}^{2}}]}^{{1/2}}}$Первую часть деформации с функцией Φm, а вторую часть, вызванную утратой связей, найти с помощью алгоритма: $e_{0}^{*} = {{\Phi }}_{\xi }^{*}{{S}_{0}}{\text{/}}3$. Отношение этой части, принятой за “дилатансию при формоизменении”, к найденной деформации по (4.1) показывает, что она имеет малые значения – это иллюстрируется графиками на рис. 1,a.
Анализ соотношения (4.2) для частных случаев растяжения и сжатия при известных функциях Φm и параметра p, приводит к виду:
где $i = p,~c$; (p – растяжение, c – сжатие). Эти выражения показывают, что материальная функция ${{{{\Phi }}}_{d}}$ не принимает нулевого значения при состояниях, соответствующих углам ξ = 0 и ${{\xi }} = {{\pi /}}3$ даже при отсутствии разномодульности, поэтому и параметр тензорной нелинейности имеет здесь ненулевые значения. Для определения функций ${{{{\Phi }}}_{{mi}}}$ и ${{{{\Phi }}}_{{di}}}$, как характеристик формоизменения, для этих состояний, используется первый признак Коши [14]. По этому признаку их значения следуют из соотношений (2.2) и (2.3), если сместиться на ${{\Delta \xi }} \approx \pm 0.1^\circ $ от исходных углов. Выражения (4.4) дают второй вариант определения параметра тензорной нелинейности: где $\kappa = {{{{\Phi }}}_{{{{\xi }}p}}}{\text{/}}{{{{\Phi }}}_{{{{\xi }}c}}}$ – отношение обобщенных и ${{\kappa }_{m}} = {{{{\Phi }}}_{{{\text{m}}p}}}{\text{/}}{{{{\Phi }}}_{{{\text{m}}c}}}$ – средних податливостей. На рис. 1,a верхняя кривая (сплошная линия) иллюстрирует обобщенную податливость для растяжения, а для последующих состояний кривизна графиков постепенно снижается. Третья кривая тоже (сплошная линия) для функции ${{{{\Phi }}}_{{dp}}}$ показана с ординатами, увеличенными вдвое.5. О постулатах и исходных данных. Трудности использования тензорно-нелинейных уравнений начинались вследствие отсутствия простых формул для определения функций ${{{{\Phi }}}_{m}}$, ${{{{\Phi }}}_{d}}$ и фазы ω. Расчет материальных функций по функциям ${{{{\varphi }}}_{i}} = {{{{\gamma }}}_{i}}{\text{/}}{{\tau }_{i}}$, где $i = 1,~2,~3$, входящим в соотношения (2.2) и (2.3) невозможно выполнить, вследствие отсутствия о них исходной информации. Это препятствие можно преодолеть, если воспользоваться следующими постулатами: первый утверждает, что значениями функций ${{{{\varphi }}}_{i}}$ можно считать значения податливостей ${{\Upsilon }_{i}} = 3{{e}_{0}}{\text{/}}{{S}_{0}} = {{{{\Phi }}}_{{{{\xi }}i}}}$ для трех напряженных состояний: растяжения, чистого сдвига и сжатия. Согласно второму постулату: – функции ${{{{\varphi }}}_{i}}$ и ${{\Upsilon }_{i}}$ равны, то есть ${{{{\varphi }}}_{i}} \cong {{\Upsilon }_{i}}$, что подтверждают расчеты по формулам (2.4) и (4.5) при сравнении их результатов. Расчет параметра тензорной нелинейности вначале проводится по формуле (2.4), используя опытные данные и для чистого сдвига. Недостаток исходных данных при чистом сдвиге, которые, как правило, получаются испытаниями на другом оборудовании и другими средствами измерения деформаций, можно восполнить алгоритмами, которые выводятся из преобразованных уравнений, описанных в работах [6, 7].
Результаты расчетов по двум вариантам: – по (2.4) и (4.5), показали, что они отличаются только пятой значащей цифрой после запятой для любой ступени нагружения. Это указывает на то, что введенные постулаты вполне приемлемы для практического использования.
Далее выполняется расчет функций для любых состояний в следующей последовательности: сначала определяется функция Φm, а затем функция ${{{{\Phi }}}_{d}} = p{{{{\Phi }}}_{m}}$ для состояний каждого квадранта. Значения параметра тензорной нелинейности, возрастая с ростом интенсивности напряжений до предельного значения, представляют диаграмму связующей матрицы в виде кривой с символом pII на рис 1,b. Также показаны графики для параметров с символами pI и pIII для первого и третьего квадрантов, а символами pgc – для серого чугуна, по данным работы [9] и pal – для алюминиевого сплава, по результатам испытаний работы [12]. Все графики отчетливо показывают интенсивность процессов утраты внутренних связей. А графики для зернистого композита дают представление о влиянии условий нагружения на этот процесс в разных квадрантах. Сравнение нижних двух графиков показывает, что при двухосном сжатии зернистый композит по интенсивности утраты связей сближается с алюминиевым сплавом. А интенсивность потери связей серого чугуна протекает весьма неравномерно: – после небольшого сопротивления происходит резкий подъем, занимающий примерно треть его диаграммы, после которого интенсивность принимает постоянное значение на участке, занимающем больше половине диаграммы.
Опытные данные, полученные испытаниями на растяжение и сжатие квазиизотропного композита,
имеющего предельную деформацию при сжатии ${{{{\varepsilon }}}_{{\text{c}}}} = 16{\text{\% }}$ в виде первичных диаграмм 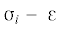 и графиков для коэффициентов поперечных деформаций, ${{{{\nu }}}_{i}} - {{\varepsilon }}$, ${{\nu }_{i}} = - {{\varepsilon }_{n}}{\text{/}}\varepsilon $, необходимо уточнять. Это выполняется для напряжений и деформаций по формулам работы
[4], которым можно придать следующий вид:
и графиков для коэффициентов поперечных деформаций, ${{{{\nu }}}_{i}} - {{\varepsilon }}$, ${{\nu }_{i}} = - {{\varepsilon }_{n}}{\text{/}}\varepsilon $, необходимо уточнять. Это выполняется для напряжений и деформаций по формулам работы
[4], которым можно придать следующий вид:
(5.1)
${{\sigma *}} = {{\sigma }}{{[{{(1 + 2{{\varepsilon }}_{n}^{{\text{*}}})}^{2}}{\text{/}}(1 + 2{{\varepsilon *}})]}^{{1/2}}}$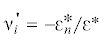 νi – коэффициенты поперечных деформаций; i = p, c; индекс n – указывает на поперечную деформацию. Напряжения σ* и деформации ε* называются приведенными
[6]. Далее звездочка над приведенными напряжениями и деформациями снимается.
νi – коэффициенты поперечных деформаций; i = p, c; индекс n – указывает на поперечную деформацию. Напряжения σ* и деформации ε* называются приведенными
[6]. Далее звездочка над приведенными напряжениями и деформациями снимается.
Для исследования свойств конкретных разносопротивляющихся материалов, обладающих особенностями по-разному сопротивляться приобретению и развитию дополнительной деформации – дилатансии, как предвестника потери прочности, требуются опытные данные. В их качестве были приняты четыре диаграммы и четыре графика зависимости коэффициентов поперечных деформаций. На рис. 2,a показаны графики (диаграммы), полученные по испытаниям зернистого композита на растяжение и сжатие для работ [7, 11]. После приведения по алгоритму (5.1) они используются, как для квадранта ІІ, так и квадрантов І и ІІІ. Кривые с символами S0p – для растяжения и ${{S}_{{0c}}}$ – для сжатия, ограничивают квадрант ІІ. Кривые с символом – ${{S}_{{0{\text{pp}}}}}$ – для двухосного растяжения вместе с кривой ${{S}_{{0p}}}$ ограничивают квадрант І; а диаграмма с символом ${{S}_{{0{\text{cc}}}}}$ – для двухосного сжатия вместе с диаграммой для сжатия ${{S}_{{0{\text{c}}}}}$ ограничивают квадрант ІII. Значения напряжений по оси ординат на рис. 2,a в МПа. Некоторые сведения о диаграммах для двухосного растяжения и двухосного сжатия получены с учетом результатов испытаний аналогичных материалов, например, работы [8, 10] и других работ [12] путем их сравнения с результатами испытаний серого чугуна [9] и грунтов [13].
Рис. 2.
Исходные данные; (a) графики (диаграммы испытаний), полученные после отмеченного выше приведения по алгоритму (5.1), по испытаниям зернистого композита на растяжение и сжатия не только для состояний второго квадранта, но и для первого и третьего квадрантов. (b) Показаны графики зависимости коэффициентов поперечных деформаций с аналогичными символами и такими же линиями, что и для диаграмм.
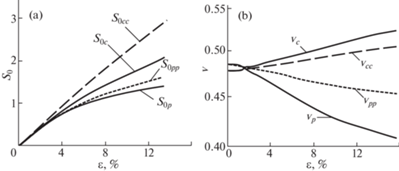
Графики для коэффициента поперечной деформации при растяжении и сжатии получены по результатам испытаний, изложенных в [7, 11]. Отсутствующие опытные данные для двухосного растяжения и двухосного сжатия были получены, используя идею [7] о связи “зазора” между прямой E0 = const и реальной диаграммой с “зазором” между прямой ${{{{\nu }}}_{0}} = {\text{const}}$ и реальной кривой для соответствующего коэффициента поперечной деформации, принимая во внимание исходные данные о растяжении и сжатии. В данной работе уравнение для объемной деформации учитывает среднее напряжение σ0, связанное с параметром ${{\zeta }} = {{\sigma }_{0}}{\text{/}}{{S}_{0}}$. Его значения при пропорциональном изменении напряжений определяются зависимостью: ${{\zeta }} = - (2{\text{/}}3)\cos {{\Theta }}$, где Θ – угловая координата, изменяющаяся в пределах $0 \leqslant {{\Theta }} \leqslant {{\pi }}$, значения которой изменяются от –2/3 при двухосном сжатии до +2/3 при двухосном растяжении. Значения в первом квадранте в пределах $1{\text{/}}3 \leqslant {{\zeta }} \leqslant 2{\text{/}}3$; во втором $ - 1{\text{/}}3 \leqslant {{\zeta }} \leqslant 1{\text{/}}3$; в третьем, $ - 2{\text{/}}3 \leqslant {{\zeta }} \leqslant - 1{\text{/}}3$. Термин “квадрант” [15] еще редко встречается в теории упругости, но здесь возникла такая необходимость.
6. Об уравнении для объемной деформации. Вывод равенства (4.3), как дополнительной части деформации формоизменения, и высказанная ранее мысль, что параметр p делит деформации разносопротивляющихся сред на две части, явились основанием того, чтобы объемную деформацию представить в виде:
Первая часть, линейно зависимая от среднего напряжения, унаследована от линейной теории упругости, относится к деформации жестких элементов структуры:
Величина Kξ является теоретическим модулем объемной упругости, которая определяется методикой совмещения теоретических кривых коэффициентов поперечных деформаций с кривыми, полученными опытами. А вторая часть, включающая в себя параметр тензорной нелинейности, относится к утрате упругости связей:
то есть является дилатансией, включающей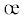 – параметр разрыхления, определяемый вместе с теоретическим модулем объемной упругости.
Функция ${{{{\Phi }}}_{m}}$ отражает взаимосвязь объемной деформации с формоизменением. Коэффициент k в формулу (6.3) введен для учета влияния среднего напряжения на процесс образования
дилатансии, а так же для удобства проверки предлагаемого соотношения. Так при k = 0 формула для дилатансии принимает тот вид, который использовался уже в работах
автора, например, в [6, 7], поскольку при k = 0.3 кривые для объемных деформаций при растяжении и сжатии лучше накладываются
на опытные кривые. Процесс преобразования тензорно-нелинейных уравнений, о котором
упоминалось выше, достаточно подробно оcвещен в работе [6, с. 60], и, возможно, впервые
реализован в [11]. Уравнения связи девиатора деформаций с девиатором напряжений (2.1) вместе с уравнением
для средней деформации с инвариантами тензора напряжений (6.1), приводят к уравнениям
связи тензора деформаций с тензором напряжений:
– параметр разрыхления, определяемый вместе с теоретическим модулем объемной упругости.
Функция ${{{{\Phi }}}_{m}}$ отражает взаимосвязь объемной деформации с формоизменением. Коэффициент k в формулу (6.3) введен для учета влияния среднего напряжения на процесс образования
дилатансии, а так же для удобства проверки предлагаемого соотношения. Так при k = 0 формула для дилатансии принимает тот вид, который использовался уже в работах
автора, например, в [6, 7], поскольку при k = 0.3 кривые для объемных деформаций при растяжении и сжатии лучше накладываются
на опытные кривые. Процесс преобразования тензорно-нелинейных уравнений, о котором
упоминалось выше, достаточно подробно оcвещен в работе [6, с. 60], и, возможно, впервые
реализован в [11]. Уравнения связи девиатора деформаций с девиатором напряжений (2.1) вместе с уравнением
для средней деформации с инвариантами тензора напряжений (6.1), приводят к уравнениям
связи тензора деформаций с тензором напряжений:
Эти уравнения, приведенные к главным деформациям, используются для матричного преобразования: ${{{{\varepsilon }}}_{i}} = {{a}_{{ij}}}{{{{\sigma }}}_{i}}$, которые затем можно привести к виду уравнений, характерному для анизотропных сред:
(6.5)
${{{{\varepsilon }}}_{i}} = {{{{\sigma }}}_{i}}{\text{/}}{{E}_{i}} - {{{{\nu }}}_{{ji}}}{{{{\sigma }}}_{j}}{\text{/}}{{E}_{j}} - {{{{\nu }}}_{{{{\alpha }}i}}}{{{{\sigma }}}_{{{\alpha }}}}{\text{/}}{{E}_{{{\alpha }}}}$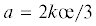 . Свертка уравнений (6.5) приводит к уравнению связи средней деформации с главными
напряжениями:
. Свертка уравнений (6.5) приводит к уравнению связи средней деформации с главными
напряжениями:
(6.6)
${{\varepsilon }_{0}} = ({{\sigma }_{1}}{{\phi }_{{k1}}} + {{{{\sigma }}}_{2}}{{\phi }_{{k2}}} + {{\sigma }_{3}}{{\phi }_{{k3}}}){\text{/}}3$ вместе с теоретическим модулем объемной упругости ${{K}_{{{\xi }}}} = 1{\text{/}}{{\phi }_{k}}$, с помощью которого проводится расчет линейной части объемной деформации. Эта задача
возлагается на процедуру совмещения теоретических кривых для коэффициентов поперечных
деформаций с опытными кривыми, решение которой можно найти в [6, 7].
вместе с теоретическим модулем объемной упругости ${{K}_{{{\xi }}}} = 1{\text{/}}{{\phi }_{k}}$, с помощью которого проводится расчет линейной части объемной деформации. Эта задача
возлагается на процедуру совмещения теоретических кривых для коэффициентов поперечных
деформаций с опытными кривыми, решение которой можно найти в [6, 7].
Высокие значения теоретического модуля объемной упругости при растяжении, но низкие при сжатии, можно объяснить путем простого преобразования уравнения (6.1). Если из него выделить линейную объемную деформацию, εyi = ε0i – εgi = ${{{{\sigma }}}_{0}}{{\phi }_{{ki}}}{\text{/}}3$, то можно найти податливости ${{\phi }_{{ki}}}$ для растяжения и сжатия. Объемные деформации ε0i связаны с модулями ${{K}_{i}} = {{E}_{i}}{\text{/}}3(1 - 2{{{{\nu }}}_{i}})$ и устанавливаются с этими значениями с помощью упомянутой процедуры совмещения. Принимая: ${{{{\zeta }}}_{c}} = - {{{{\zeta }}}_{p}}$, $1{\text{/}}{{{{\zeta }}}_{i}} \cong \pm 3$; 1/ζ = = 3.0009; i = p, c; (p – растяжение, c – сжатие), действия с выражением (6.1) приводят к формулам:
Из соотношения (6.8) следует, что второе слагаемое понижает податливость для растяжения,
а значение теоретического модуля, наоборот, повышает. Во второй формуле (6.9) второе слагаемое повышает податливость для сжатия. Вторые слагаемые в этих соотношениях
позволяют количественно оценивать его влияние на значения теоретической податливости.
Среднее напряжение при чистом сдвиге равно нулю, но, учитывая, что ${{{{\zeta }}}_{p}} + {{{{\zeta }}}_{c}} = 0$, как и для значения параметра ${{{{\zeta }}}_{{{\tau }}}}$, то подсказывается алгоритм, как ответ на вопрос о значении теоретического модуля
и для этого состояния: 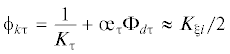 . Формулы (6.8) и (6.9) содержат ответ на причины большого различия значений теоретического модуля. Рассмотренная
методика позволила найти такие значения теоретических модулей упругости, которые приводят
к более точным значениям не только линейно–упругой объемной деформации, но и коэффициентов
поперечных деформаций.
. Формулы (6.8) и (6.9) содержат ответ на причины большого различия значений теоретического модуля. Рассмотренная
методика позволила найти такие значения теоретических модулей упругости, которые приводят
к более точным значениям не только линейно–упругой объемной деформации, но и коэффициентов
поперечных деформаций.
7. О деформационной анизотропии коэффициентов поперечных деформаций. Линейная теория упругости обходится тремя модулями и одним коэффициентом поперечных деформаций, взаимосвязанных между собой. Нелинейная теория упругости разносопротивляющихся материалов не может себе этого позволить, поскольку эти материалы не только проявляют нелинейность с уровнем нагрузки, но и проявляют тензорную нелинейность, с накоплением дилатансии, сопровождающейся деформационной анизотропией. Об этом явлении, для описания которого может быть использован математический аппарат тензорно-нелинейных уравнений, В.В. Новожилов в своей [3] высказал свое мнение, как о “важном явлении”. При отсутствии экспериментальных исследований не акцентировал, на каких характеристиках она проявляется, учитывая только тот факт, что материальные функции его уравнений содержат тригонометрические коэффициенты. Расчеты, по приведенным выше соотношениям, показывают незначительное влияние дилатансии на модули продольной упругости Ei. Расхождение значений этих модулей с разными индексами составляет менее 5%, но ведет к заметной деформационной анизотропии коэффициентов поперечных деформаций.
В истории механики материалов, описанной в [14], много места уделено исследованиям его начального значения, то есть коэффициента Пуассона, однако значениям при разрушающих напряжениях, не уделено должного внимания, тем более по другим направлениям главных напряжений. В данной работе, возможно, впервые, даны графики теоретических коэффициентов поперечных деформаций. Их легче описать не формулами, а графиками. Линия, представленная точками на рис. 3,$a$ повторяет теоретические кривые для ${{{{\nu }}}_{{12}}} = {{{{\nu }}}_{{13}}}$, которые совмещаются со значениями коэффициента νp. Отклонение кривой для коэффициента νp от начального ее значения следует считать основной причиной роста дилатансии и положения кривых для всех других коэффициентов. Если бы значения этой кривой для коэффициента νp совпадали бы с коэффициентом Пуассона, то все кривые, представленные на рис. 3,$a$, слились бы в одну прямую, а дилатансия отсутствовала бы. Чем ниже опускаются точки кривой νp от начального значения, тем больше дилатансия, выше поднимаются значения коэффициентов ν21 и ν31, так как дилатансия, как дополнение к основной деформации ${{{{\varepsilon }}}_{1}}$, по направлению ${{{{\sigma }}}_{1}}$, для деформаций других направлений 2 и 3, является поперечной в соответствии с индексами. И тем больше поведение материала отличается от линейной теории упругости. Значения кривой для коэффициента ν23 опускаются, так как по направлению 3 дилатансия отсутствует, но значения двух пар, ν2 и ν3, накладывающиеся друг на друга, снижаются. Коэффициенты первой пары имеют одинаковые значения, ${{{{\nu }}}_{{12}}} = {{{{\nu }}}_{{13}}}$, отличаясь от значений двух других пар, ν2 и ν3, которые на большей части оси абсцисс превышают число 0.5.
Рис. 3.
Изменение коэффициентов поперечных деформаций: $a$ – при растяжении; $b~$ – при сжатии; с – изменение последних значений коэффициентов при растяжении для всех состояний II квадранта от растяжения до сжатия.
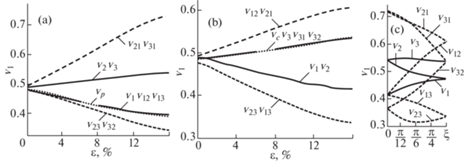
На рис. 3,b приводятся подобные же графики для коэффициентов поперечных деформаций при сжатии. Линия, показанная точками, относится к коэффициентам с символами νc, ν31 и ν32. Значения дилатансии в этом направлении наименьшие или полностью отсутствуют. Рост значений коэффициента νc согласуется с показаниями результатов испытаний и связан с дилатансией по осям 1 и 2. Вместе с ним растут значения коэффициента пары ν3 и ее составляющих ν31 и ν32, что выполняет методика. Рост коэффициента νc следует считать основной причиной роста дилатансии по направлениям 1 и 2, имеющих положительные деформации, относительно которых откланяются вниз пары ν1 и ν2, а еще ниже ν13 и ν23, поскольку деформация по оси 3 является поперечной, а по осям 1 и 2 деформация с дилатансией, продольной.
И чем выше поднимаются значения последних точек кривой для коэффициента νc, тем больше дилатансии на осях 1 и 2, тем выше поднимаются значения коэффициентов ν21 и ν12, как равноправные, имеющие одинаковые дилатансии. Хотя по направлению 3 дилатансия отсутствует, но значения двух пар ν2 и ν3, совпадая друг с другом, снижаются. Расстановка кривых для состояния сжатия сложнее, чем для состояния растяжения, но необходимо обязательно принимать во внимание положение дилатансии. Если при растяжении кривая с коэффициентом νp, опускаясь, отталкивает от себя другие кривые, то при сжатии кривая с коэффициентом νc сама притягивается к кривым с коэффициентами ν21 и ν12, “содержащими” дилатансию.
На рис. 3,c приводятся кривые для всех перечисленных выше коэффициентов по оси ξ для предельной деформации ${{\varepsilon }} = 16\% .$ С изменением этого угла значения коэффициентов: ν21, ν31, ν13, ν2 уменьшаются. А значения коэффициентов: ν32, ν12, ν1 увеличиваются, только значение коэффициента ν3 остается почти неизменным. Значения ν23, снижаясь до состояния чистого сдвига, затем почти восстанавливаются. Все эти изменения объясняются значениями дилатансии на соответствующих осях. Началом всех кривых на рис. 3,c являются последние значения кривых рис. 3,a, которые заканчиваются последними значениями кривых рис. 3,b для всех состояний II квадранта от растяжения до сжатия.
8. О дилатансии. Наличие параметра тензорной нелинейности p, параметра разрыхления $\unicode{230} $ и функции Φm – дает возможность определить дилатансию по формуле (6.3) при всех напряженных состояниях. На рис. 4 представлены кривые для дилатансии, чтобы оценить ее влияние на коэффициенты поперечных деформаций в других квадрантах. Каждому состоянию, характеризующемуся значением угла ${{\xi }}$, соответствует своя кривая. В квадранте ІІ, рис. 4,b, шесть кривых, которые охватывают состояния от простого растяжения, ξ = 0, до простого сжатия, ${{\xi }} = {{\pi /}}3$. Шестая кривая совпадает с пятой. В каждом подрисунке кривая, показанная линиями с мелкими штрихами, соответствует чистому сдвигу, то есть углу ${{\xi }} = {{\pi /}}6$, (во втором квадранте она совпадает с осью абсцисс). Верхняя кривая рис. 4,b с самым большим значением дилатансии, относится к состоянию простого растяжения, ${{\xi }} = 0$, а нижняя к простому сжатию, ${{\xi }} = {{\pi /}}3$. Как показал анализ, резкого изменения положений кривых для коэффициентов не происходит, но при сжатии, согласно результатам на рис. 3,c, дилатансия в виде нижней кривой (большой штрих) на рис. 4,b, привела к тому, что все коэффициенты уже существенно изменили свое положение. Этот факт говорит о том, что положение коэффициентов зависит не от значений дилатансии, а больше от осей, в которых она реализуется. В квадранте І – состояния от простого растяжения до двухосного растяжения, верхние три кривых 4,a практически повторяют кривые рис. 4,b и относятся они к простому растяжению, следовательно, графики рис. 3,a будут для них повторяться. А нижняя кривая (большой штрих) к двухосному растяжению, ${{\xi }} = {{\pi /}}3$, подсказывающему, что вторая ось с индексом 2 и с положительной деформацией, содержит эту дилатансию, должна сохранить положение коэффициентов, как на рис. 3,b. В квадранте ІІI – от простого сжатия до двухосного сжатия, отличаясь между собой приращением ${{\Delta \xi }} = {{\pi /}}9$. Верхняя кривая рис. 4,c с самым большим значением дилатансии, относится к оси с индексом 1 с нулевым напряжением, но при отрицательных значениях напряжений по осям 3 и 2 имеет положительную деформацию, которая содержит эту дилатансию. Следует ожидать, что положение коэффициентов повторит рис. 3,a при их значениях, незначительно отличающихся от коэффициента Пуассона.
Рис. 4.
Семейства кривых дилатансии при напряженных состояниях трех квадрантов; в каждом квадранте I рис. 4,a; II рис. 4,b и III рис. 4,c семь кривых. Кривая, показанная линией с мелкими штрихами, соответствует чистому сдвигу, то есть состоянию ${{\xi }} = {{\pi /}}6$; сплошные линии относятся к состояниям $0 \leqslant {{\pi /}}6$, штриховые линии к состояниям от ${{\pi /}}6 \geqslant {{\pi /}}3$.
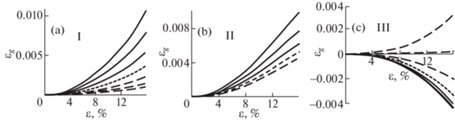
Графики, иллюстрирующие дилатансию, можно разделить на две части. Начальную криволинейную часть, отображающую постепенное накопление повреждений вследствие утраты связей, соответствующую деформации $\varepsilon = \sim 8 \div 10\% $. Вторая часть, близкая по форме к прямой линии, представляет наиболее интенсивный заключительный процесс ее возрастания перед разрушением. Проведенные исследования дилатансии дают возможность высказать следующие выводы: эта деформация возникает при всех состояниях, при которых происходит формоизменение элементарного объема, то есть отклонение от трехосного сжатия или растяжения равными по трем осям напряжениями. Чем большее значение имеет положительная деформация по одной оси с присутствием отрицательных напряжений по двум другим осям, тем больших значений может достигать дилатансия разносопротивляющихся материалов. При двухосном сжатии наблюдается уплотнение объема, то есть “дилатансия” с отрицательным знаком. Дилатансия снижает значения коэффициентов поперечных деформаций на оси наибольшей положительной деформацией, но повышает ее на взаимно перпендикулярных осях с нулевыми или отрицательными напряжениями. Последовательным изменением значения k > 0 установлено, что при k = 0.3 достигается наилучшее согласие теоретических значений полной объемной деформации со значениями, найденными по данным о коэффициентах поперечных деформаций при растяжении и сжатии. Вывод – учет среднего напряжения повышает точность расчета дилатансии. Модули сдвига Gξi и их податливости формоизменения ${{Ф}_{{{{\xi }}i}}}$ не приобретают таких особенностей, как коэффициенты поперечных деформаций и характеристики объемной деформации, поэтому отношения интенсивностей деформаций, найденных, как по начальным данным, связанным с опытными результатами, к интенсивностям деформаций, найденных после матричного преобразования уравнений (6.5), равны единице. Причем это значение (единица с тремя нулями после запятой) практически сохраняется, как с ростом напряжений до предельных значений, так и при смене состояний от ξ = 0 до ${{\xi }} = {{\pi /}}3$. Высокие значения коэффициентов ν2 и ν3 не оказывают заметного влияния на это значение.
9. О деформационной анизотропии податливостей (модулей) объемной упругости. Деформационная анизотропия коэффициентов поперечных деформаций проявляет себя весьма заметно и по всем направлениям, а поскольку с их значениями связаны значения всех модулей или податливостей упругости, то полезно иметь представление и об их изменениях. Более наглядно деформационная анизотропия проявляется на графиках для податливостей объемной упругости в направлении главных напряжений, которая определяется по формуле (6.6). Податливости или (коэффициенты) объемной упругости, определяются по первому равенству (6.7), а второе равенство, повторяя эти результаты, предназначено для расчета средней деформации по трем направлениям. Податливости, как величины обратные модулю, являются плавными неразрывными функциями, не одинаково изменяющиеся с ростом напряжений. В линейной теории упругости находит применение только один модуль объемной упругости – “классический” или податливость $\phi = 1{\text{/}}K$, которые определяются по начальным данным о модуле продольной упругости и коэффициенте Пуассона, в нелинейной теории упругости тоже можно ограничиться начальными значениями податливостей ${{\phi }_{{ki}}}$. Они позволяют для любого состояния найти значения трех параметров изменяющейся упругости:
(9.1)
${{\vartheta }_{{\xi i}}} = \frac{\phi }{{{{\phi }_{{ki}}}}} = \frac{{{{K}_{{{{\xi }}i}}}}}{K}$Рис. 5.
Графики изменения значений параметров ${{\vartheta }_{{\xi i}}}$ с изменением напряженных состояний от 0 до π/3 в каждом квадранте I, II и III; четыре кривые, линии 1, 2 и 3 – их начальные значения при ${{\sigma }_{i}} = 0$; кривая для параметра ${{\vartheta }_{K}}$ в каждом квадранте представляет отношение “классической” податливости к теоретической, то есть $\phi {\text{/}}{{\phi }_{{ki}}}$.
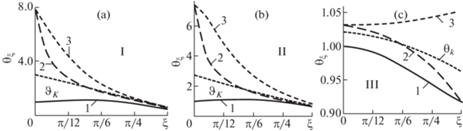
Эти параметры, имея вначале значения большие числа 6, быстро снижаются, что вызвано существенным изменением значения дилатансии на оси 1 и снижением коэффициента поперечных деформаций ν2 и ν3 с изменением угла ${{\xi }}$, рис. 3,c. Быстрое уменьшение ординат между кривыми 1 и 3, а также между кривыми 1 и 2, свидетельствует о снижении дилатансии, а их различие указывает на то, что напряжение ${{{{\sigma }}}_{3}} > 0$, как “поджатие” усиливает процесс накопления дилатансии.
Значения параметров ${{\vartheta }_{{{{\xi }}i}}}$ квадранта I отличаются от параметров квадранта II, если судить о них по оси ординат, принимая во внимание три первые кривые для дилатансии рис. 4,a, тогда как по форме они почти повторяются, так же как по снижению дилатансии от простого растяжения до двухосного растяжения. Значения параметров ${{\vartheta }_{{{{\xi }}i}}}$ квадранта III существенно отличаются от параметров соседних квадрантов, как по форме кривых, так и по их начальным и конечным значениям. Если при двухосном сжатии (ξ = 0), начальные значения всех кривых, отличаются в пределах 3%, то в конце их расхождение достигает более 10%. Кривая 1, представляя значения параметров ${{\vartheta }_{{k1}}}$ (не напряженного направления), с приближением к простому сжатию, снижается примерно на 8%. Следовательно, при простом сжатии модуль меньше, чем при двухосном сжатии. Все по той же причине, – изменения дилатансии в этом направлении. Расхождение кривых для параметров ${{\vartheta }_{{ki}}}$ можно связывать с поведением межструктурных связей, участвующих в создании дилатансии для каждого состояния. Числовые значения параметров могут быть полезными для сравнения поведения разных материалов, что является важной процедурой при их анализе и практическом выборе материалов, отличающихся, например, связующей матрицей. Материал при этом более наглядно оказывает деформационную анизотропию [8, с. 58].
Кривые для параметра ${{\vartheta }_{{\text{K}}}} = {{\vartheta }_{{{{\xi }}i}}}{\text{/}}3$ в каждом квадранте имеют среднее значение трех параметров. Это значение параметра указывает на связь теоретической податливости ϕk с податливостями в направлениях главных напряжений ϕki, хотя приемы и алгоритмы их определения существенно отличаются. С изменением внешних условий, например, значительное охлаждение материала, – дилатансия может снизиться до нулевого значения. При сохранении нелинейности по напряжениям, параметр разрыхления примет нулевое значение, кривые с номерами сольются в одну кривую с символом ${{\vartheta }_{K}}$. Если нелинейность по напряжениям тоже исчезнет, то все кривые примут значение $~\phi {\text{/}}{{\phi }_{{ki}}}$ = 1, а все модули примут значение K, и среда станет линейно-упругой.
10. Заключение. Заканчивая свою работу, Новожилов В.В. предусмотрительно высказался о деформационной анизотропии, что изложенная им “теория является подходящим математическим аппаратом для описания таких деформаций, при которых в теле происходят структурные изменения, различные в разных направлениях”, способные привести к упомянутой анизотропии. В настоящее время эти тела выделились в отдельную группу, названную разносопротивляющимися средами. В развитие его теории упругости в данной работе предлагается использовать новые свойства материальных функций тензорно-нелинейных уравнений, которые проявляют себя характеристиками, способствующими найти соотношения связи между тремя инвариантами. Последние помогают сформулировать законы формоизменения и объемной деформации, включающей в себя дилатансию, точное определение которой позволяет выявить особенности поведения материалов, содержащих равномерно распределенную систему внутренних связей со свойствами по-разному сопротивляться положительным и отрицательным деформациям.
Исследования с привлечением разработанной методики определения теоретического модуля, дали возможность изучить эффект влияния дилатансии на значения коэффициентов поперечных деформаций и на параметры изменяющейся упругости, представляющих собой отношение классической податливости к податливостям по направлениям главных напряжений. Отказ от второй материальной функции ведет не только к потере точности расчетов, но и потере эффектов, связанных со структурными изменениями, которые не следует считать эффектами второго порядка малости. Допущение дилатансии к упругим деформациям является неизбежным шагом, чтобы проследить за поведением всех деформаций по трем направлениям. Точное совпадение полной объемной деформации, как суммы ее составляющих в направлении главных напряжений, или, как сумму линейно-упругой деформации и дилатансии, указывают на то, что аппарат предлагаемых уравнений может явиться основным направлением в нелинейной теории упругости.
Каких бы концепций другие теории упругости не придерживались, точный учет реальных значений коэффициентов поперечных деформаций при растяжении и сжатии требует учета дилатансии, а, следовательно, и различия значений характеристик объемной упругости. Приступая к изучению свойств новых материалов, исследователь должен обратить внимание на поведение коэффициента поперечных деформаций при растяжении. Чем ниже опускаются значения последующих точек кривой от начального (коэффициента Пуассона), тем больше поведение материала отличается от линейной теории упругости и тем в большей мере происходит процесс накопления дилатансии.
Список литературы
Мясников В.П., Олейников А.И. Основы механики гетерогенно-сопротивляющихся сред. Владивосток: Дальнаука, 2007. 171 с.
Трещев A.A. О дилатации и разносопротивляемости изотропных материалов // Эксперт: теория и практика 2021. № 3 (12). С. 53–58.
Новожилов В.В. О связи между напряжениями и деформациями в нелинейно-упругой среде // ПММ. 1951. Т. 15. Вып. 2. С. 183–194.
Новожилов В.В. О принципах обработки результатов статических испытаний изотропных материалов // ПММ. 1951. Т. 15. Вып. 6. С. 709–722.
Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.
Комков К.Ф. О методике определения модуля объемной упругости и параметров, учитывающих разрыхление и изменение упругости композитов, основанной на тензорно-нелинейных уравнениях // Изв. РАН. МТТ. 2019. № 1. С. 50–62. https://doi.org/10.1134/S0572329919010057
Комков К.Ф. О тензорной нелинейности сред, проявляющих существенное различие в сопротивлении растяжению и сжатию // Электронный журн. № 10, октябрь 2013. https://doi.org/10.7463/0513.0571202
Мошев В.В. Структурная механика зернистых композитов на эластомерной основе. М.: Наука, 1992. 79 с.
Леонов М.Я., Поняев В.А., Русинко К.Н. Зависимость между деформациями и напряжениями для полухрупких тел // Инж. журнал. МТТ. 1967. № 6. С. 26–32.
Schwarzs F.R. On mechanical properties of unfilled and filled elastomers. Mechanics and chemistry of sold propellants // Proc. of the fourth symposium of naval structural mechanics. Held at Purdue University: Lafayette, Indiana, 1965. P. 19–21.
Комков К.Ф. Описание анизотропии изотропных материалов, вызванной пластической деформацией // Изв. РАН. МТТ. 2008. № 1. С. 147–153.
Надаи А. Пластичность и разрушение твердых тел. Т. 2. М.: Изд-во иностр. лит., 1969. 863 с.
Роу П. Теоретический смысл и наблюдаемые величины деформационных параметров грунта // Новое в зарубежной науке. Механика. Вып. 2. Определяющие законы механики грунтов. М.: Мир, 1975. С. 76–143.
Бел Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. М.: Наука, 1984. Часть I. 596 с.; Часть II. 431 с.
Корн Г. Справочник по математике. М.: Наука, 1977. 831 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела