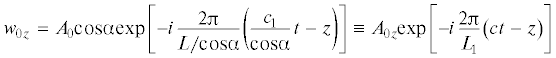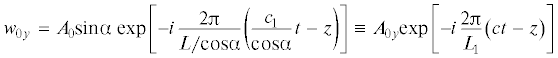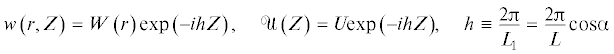Известия РАН. Механика твердого тела, 2022, № 5, стр. 58-69

1. Введение. Впервые задача о действии продольной сейсмической волны на бесконечно протяженный трубопровод рассмотрена А. Сакураи и Т. Такахаши [1]. Считается, что волна распространяется вдоль трубопровода и является стационарной, то есть периодической функцией времени. Тогда амплитуды ускорений и деформаций в трубопроводе находятся из простых алгебраических уравнений в предположении, что действие грунта заменяется силой, пропорциональной разности между перемещениями в волне и трубопроводе в одном и том же сечении, перпендикулярном оси трубопровода. Эти амплитуды (при различных значениях коэффициента взаимодействия в указанной пропорциональной зависимости) не превышают амплитуд соответствующих величин, определяемых из простейшей инженерной теории “жесткого защемления” трубопровода в грунте, согласно которой перемещения, а значит, и деформации трубопровода совпадают с перемещениями и деформациями грунта в сейсмической волне [2–4].

В дальнейшем А.А. Ильюшин и Т.Р. Рашидов [5, 6] рассмотрели нестационарный режим распространения волн вдоль бесконечного трубопровода, когда нестационарное динамическое состояние трубопровода (перемещения, деформации и напряжения) в разные моменты времени на равном расстоянии от фронта волны одинаково. Иными словами, названные характеристики являются функциями расстояния до фронта волны. В этом случае задача является автомодельной и волновое уравнение нестационарных продольных колебаний трубопровода приводится к обыкновенному дифференциальному уравнению второго порядка, что позволяет получить аналитическое решение задачи. Основной результат работы состоит в том, что в ней впервые вводится в рассмотрение названный “сверхзвуковым” режим распространения сейсмической волны вдоль трубопровода, когда ее скорость больше скорости распространения продольных возмущений в трубопроводе. Появление сверхзвукового режима объясняется наличием демпфирующих стыков, соединяющих сегменты трубопровода и гасящих скорость волн в трубопроводе. Из результатов настоящего исследования следует, что такой режим может возникнуть и в более простой ситуации падения наклонной волны на однородный трубопровод.

Следует отметить, что в постановках задач в [1] и [5, 6] не конкретизируется заглублен ли трубопровод на некоторую глубину в полупространстве, занятом грунтом, или же он расположен в неограниченной упругой среде (грунте); второй случай рассматривается для упрощения задачи, когда глубина залегания трубопровода значительно превышает его диаметр. Эта конкретизация зависит от физических соображений или опытных данных, исходя из которых определяется коэффициент в линейной зависимости между силой взаимодействия грунта и трубопровода и относительным смещением трубопровода, принятой в этих работах при выводе дифференциального уравнения движения трубопровода. Указанное обстоятельство, связанное с тем, что грунт отбрасывается и его действие на трубопровод заменятся силой взаимодействия, является основным допущением подхода к постановке задач сейсмодинамики для трубопровода, предложенного в работах [1, 5, 6]. Этот подход в дальнейшем многократно использовался, принимая различные гипотезы (законы) для зависимости между силой взаимодействия и относительным смещением трубопровода.

Другая, более строгая постановка задачи о действии сейсмической волны на трубопровод состоит в том, что исследуются совместные (связанные) движения грунта и трубопровода. Впервые такая постановка задач сейсмодинамики трубопровода дана в наших работах [7–10]. В них считалось, что падающая продольная волна распространяется вдоль трубопровода, что упрощало решение внешней задачи для грунта, сводя ее к краевой задаче для обыкновенного дифференциального уравнения. В настоящей работе рассматриваются постановки и решения связанных задач о совместных стационарных движениях грунта и трубопровода при произвольном угле падения плоской сейсмической волны. Ввиду теоретической и практической важности задачи указаны или исправлены неточности, допущенные в постановке и решении подобной задачи по “модели взаимодействия” в работах [5, 6], когда сейсмическая волна движется вдоль трубопровода.

2. Разложение наклонной волны в сумму нескольких волн, распространяющихся вдоль трубопровода. Предположим сначала, что падающая на трубопровод плоская сейсмическая волна является продольной волной и что она распространяется в вертикальной плоскости (плоскости, проходящей через ось трубопровода и центр Земли или через ось трубопровода перпендикулярно поверхности Земли). Последнее означает, что в декартовой системе координат, с осью $z$, направленной по оси трубы и осями $y$ и x, лежащими соответственно в вертикальной и горизонтальной плоскостях, фронт падающей волны перпендикулярен вертикальной плоскости $Oyz$. Этот фронт (вернее, его след в вертикальной плоскости) изображен прямой $FF'$ на рис. 1. Предположение же, что волна является продольной означает, что перемещения частиц грунта в возмущенной волной области (за ее фронтом) происходят в перпендикулярных фронту направлениях. Такая волна описывается уравнением

если она является стационарной. В (2.1) ${{A}_{0}}$ есть амплитуда волны, $L - $ ее длина, ${{c}_{1}}$ означает скорость распространения продольной волны в упругом грунте, а t $ - $ время. Лучи ($Oz'$ и параллельные ей), вдоль которых распространяется плоская волна, образует угол ${{\alpha }}$ с осью трубопровода $Oz$ (рис. 1). Этот угол меняется в пределах от 0 до ${{\pi }}$ (поскольку естественно предположить, что фокус землетрясения находится на большей глубине, чем трубопровод) и можно считать, что $0 < {{\alpha }} < {{\pi /}}2$ ; случай ${{\pi /}}2 < {{\alpha }} < {{\pi }}$ сводится к предыдущему изменением положительных направлений осей $z$ и $x$.

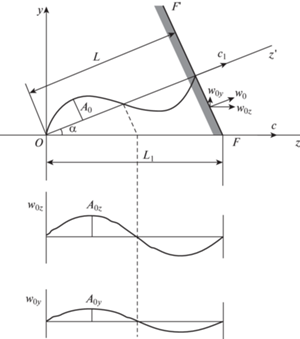
Представляя перемещение в волне (2.1) в виде суммы перемещений в направлениях $z$ и y, т.е. в виде суммы ${{{\mathbf{w}}}_{0}} = {{{\mathbf{w}}}_{{0z}}} + {{{\mathbf{w}}}_{{0y}}}$, можно ее воздействие на протяженное в направлении $Oz$ сооружение, в частности трубопровод, заменить воздействием следующих двух волн

изображенных на рис. 1 и распространяющихся вдоль трубопровода со скоростью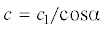 . Первая из этих волн (${{w}_{{0z}}}$ с амплитудой 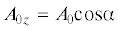) является продольной, а вторая (${{w}_{{0y}}}$ с амплитудой 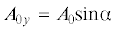) – поперечной SV-волной. В выражениях (2.2) величины c, ${{L}_{1}}$, ${{A}_{{0z}}}$ и ${{A}_{{0y}}}$ положительны в силу предположения, что ${{\alpha }} \in \left( {0,{{\pi /2}}} \right)$.

Идею подобного рассмотрения эффекта действия наклонной волны на протяженные подземные сооружения высказал впервые Т. Кюезель [11]. Такое рассмотрение может быть принято, когда поперечный размер сооружения является значительно меньшим длины волны $L$ и протяженности самого сооружения вдоль оси z. Применительно к трубопроводу это означает, что представление (2.2), верно, когда он рассматривается как стержень, совершающий продольные и изгибные колебания (т.е. движется без искажений поперечных сечений) и не приемлемо, когда трубопровод рассматривается как цилиндрическая оболочка (представления для волны (2.1) в этом случае даны, например, в работах [12, 13]).

Если падающая плоская наклонная волна является продольной и распространяется в горизонтальной плоскости $Ozx$ (проходящей через ось трубопровода и параллельной поверхности Земли), т.е. если вектор перемещения u₀ в волне лежит в плоскости $Ozx$ (или в плоскостях параллельной ей), образуя угол ${{\beta }}$ с осью трубопровода, то, повторяя приведенные выше рассуждения, волна u₀, также как и w₀, может быть представлена в виде суммы двух волн (продольной и поперечной), распространяющихся вдоль трубопровода со скоростью .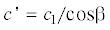

В более общем случае, когда падающая продольная волна произвольно ориентирована в пространства и вектор перемещений ${\mathbf{\xi }}{{{\text{\;}}}_{0}}$ в ней не принадлежит ни одной из названных выше плоскостей, то он может быть двумя способами выражен в виде суммы двух векторов (рис. 2):

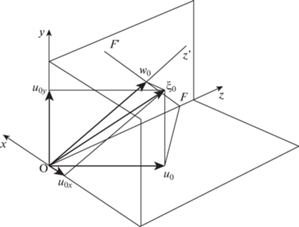
Здесь w₀ и u₀ соответственно проекции вектора ${\mathbf{\xi }}{{{\text{\;}}}_{0}}$ на вертикальную и горизонтальную плоскости, а ${{{\mathbf{u}}}_{{0x}}}$ и ${{{\mathbf{w}}}_{{0y}}}$ представляют собой поперечные волны, распространяющиеся в направлениях осей x и $y$.

Представляя теперь каждую из волн w₀ и u₀ указанным выше способом через сумму продольной и поперечной волн, распространяющихся вдоль трубопровода, приходим к следующему результату. Действие произвольно ориентированной продольной волны на трубопровод эквивалентно действию трех волн: двух поперечных и одной продольной волн, распространяющихся вдоль трубопровода со скоростью c = 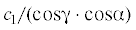, где ${{\gamma }}$ угол между вектором ${\mathbf{\xi }}{{{\text{\;}}}_{0}}$ и вертикальной плоскостью $Ozy$, а ${{\alpha }}$ угол, образуемый проекцией вектора ${\mathbf{\xi }}{{{\text{\;}}}_{0}}$ на эту плоскость с осью $Oz$ (осью трубопровода). Аналогичное представление, очевидно, имеет место и при падении на трубопровод (или протяженное сооружение) сдвиговой наклонной волны.

3. Постановка связанных задач о колебаниях грунта и трубопровода. Метод квазиодномерной деформации. Результаты наблюдений показывают, что наибольшие внутренние усилия (напряжения) и, соответственно, разрушения трубопроводов в местах стыков возникают, как правило, при их продольных колебаниях под воздействием сейсмических волн. Сказанное справедливо по крайней мере тогда, когда общая длина трубопровода или в случае трубопровода, рассматриваемого как бесконечно длинный, длины его представительных участков (содержащие, скажем, несколько стыков) значительно малы в сравнении с длинами сейсмических волн. Такие участки трубы практически не деформируются под воздействием поперечных волн и движутся в поперечном направлении как абсолютно твердые тела. Если такое рассмотрение не приемлемо и могут возникать заметные деформации и усилия в результате изгиба, то оценки этих величин можно получить, считая, что поперечные движения трубы совпадают с поперечными перемещениями в сейсмической волне [14].

Принимая, для определенности, наклонную нестационарную падающую волну в виде (2.1), дадим постановку задачи о совместных продольных колебаниях трубопровода и упругого грунта под воздействием продольной составляющей падающей волны, выделенной в п. 2, а именно, под воздействием распространяющейся вдоль трубопровода волны ${{w}_{{0z}}}$ из (2.2). Такие связанные постановки впервые даны в наших работах [7–10]. В этих постановках на границах грунтовой массы принимаются следующие краевые условия.

На расстоянии r = R, достаточно удаленном от трубопровода, перемещения грунта равны перемещениям в продольной волне (2.2), т.е.

Здесь ${{u}_{r}}$, ${{u}_{{{\theta }}}}$, ${{u}_{z}} \equiv w$ – компоненты вектора перемещений грунта вдоль осей цилиндрической системы координат $\left( {r,{{\theta }},z} \right)$, с осью $z$, совпадающей с осью трубопровода.

Сформулированные условия означают, что на внешней границе грунта краевые условия сносятся на коаксиальную поверхности трубы цилиндрическую поверхность, радиус $R$ которой может быть принят равным глубине залегания трубопровода.

Если трубопровод находится в неограниченной среде (что можно считать, когда глубина заложения $R$ многократно превосходит внешний радиус трубопровода a), то условия (3.1) должны выполняться на бесконечности (при $r \to \infty $).

На внутренней границе грунта, т.е. на границе контакта грунта с трубопроводом, ставятся обычные условия непрерывности перемещений

где $\mathcal{U}\left( {z,t} \right)$ означает осевое (продольное) перемещение трубопровода, определяемое из уравнения продольных колебаний стержня. Физически условия (3.2) означают, что радиальные перемещения в трубопроводе пренебрежимо малы в сравнении с продольными и принято условие прилипания на поверхности контакта трубы с грунтом. Оценки величин радиальных перемещений ${{u}_{r}}$ на поверхности металлических (стальных, чугунных) и бетонных труб получены в [15].

При сформулированных краевых условиях (3.1), (3.2) имеет место осевая симметрия, когда ${{u}_{{{\theta }}}} \equiv 0$, а перемещения ${{u}_{r}}$ и ${{u}_{z}} \equiv w$ не зависят от угловой координаты ${{\theta }}$. Тогда уравнения движения упругого грунта сводятся к системе двух уравнений Ламе для названных ненулевых компонент вектора перемещений (системе (1.3) из [9]).

Гипотеза квазиодномерности деформации грунта. С целью упрощения задачи для грунта предположим, что радиальная ${{{{\varepsilon }}}_{{rr}}} = \partial {{u}_{r}}{\text{/}}\partial r$ и окружная ${{{{\varepsilon }}}_{{{{\theta \theta }}}}} = {{u}_{r}}{\text{/}}r$ деформации являются малыми (по абсолютной величине) в сравнении с деформацией ${{{{\varepsilon }}}_{{zz}}} = \partial w{\text{/}}\partial z$ в направлении распространения падающей продольной волны w_0z. Тогда тензор деформации имеет лишь две ненулевые компоненты: ${{{{\varepsilon }}}_{{zz}}}$ и ${{{{\varepsilon }}}_{{rz}}} = {{{{\varepsilon }}}_{{zr}}}$.

Метод квазиодномерной деформации предложен и использовался нами в работах [8–10, 15]. В задаче о сейсмических колебаниях трубопровода в бесконечной упругой среде [10], допускающей точное решение, установлено, что приближенное ее решение, полученное по данному методу, весьма близко к точному решению.

В условиях принятой гипотезы, в одном из двух уравнений Ламе, указанных выше, а именно, в уравнении движения в направлении оси$~z$, членами, содержащими перемещение ${{u}_{r}}$ можно пренебречь в сравнении с другими членами и оно сводится к отдельному (“анизотропному”) волновому уравнению относительно продольного перемещения $w$:

где ${{с}_{2}} = \sqrt {{{\mu /\rho }}} $ есть скорость распространения сдвиговых волн в грунте (${{\mu }}$ – модуль сдвига, ${{\rho }}$ – плотность грунта).

Другое уравнение Ламе содержит оба перемещения ${{u}_{r}}$ и $w$ и может быть решено после нахождения функции $w$. Однако в этом нет необходимости для полной постановки и решения задачи о совместных продольных колебаниях трубопровода и грунта. Действительно, в силу граничного условия для ${{u}_{r}}$ из (3.2), касательное напряжение, действующее на поверхности контакта среды и трубопровода, вычисляется по формуле

и не зависит от u_r (предполагается, что операции дифференцирования по $z$ и предельного перехода по $r$ перестановочны).

Тогда равнодействующая касательных напряжений (3.4), действующих на боковой поверхности элемента трубопровода длины $dz$ и вовлекающего его в движение, есть

Поверхностная сила (3.5), отнесенная к объему $dV = {{\pi }}({{a}^{2}} - {{b}^{2}})dz$ элемента dz (b –внутренний диаметр трубы), принимается за объемную силу, действующую на трубопровод: $\mathcal{F} = P{\text{/}}[{{\pi }}({{a}^{2}} - {{b}^{2}})]$. Следовательно, уравнение вынужденных продольных колебаний трубопровода имеет вид

где $E'$ – модуль Юнга, а ${{\rho '}}$ – плотность материала трубопровода.

Для определения силы взаимодействия $\mathcal{F}$ между трубопроводом и средой не требуется знание радиального перемещения среды ${{u}_{r}}$. Это следует из равенства (3.4), справедливого при выполнении граничного условия (3.2) для ${{u}_{r}}$, означающим, что пренебрегается радиальным расширением трубопровода или влиянием этого расширения на деформации и напряжения в грунте. В работе [15] нами показано, что задача для $w$ выделяется в отдельную задачу и при учете поперечного расширения трубы.

Данная выше постановка является связанной, поскольку в задачу для грунта входит перемещение трубы (через краевое условие в (3.2)) и уравнение движения трубопровода (3.6) содержит продольное перемещение грунта.

Уравнение (3.6) отличается от уравнений движения трубопровода, приведенных в работах [1, 5], тем, что в нем присутствует теоретическое выражение для силы взаимодействия с грунтом (которое в явном виде получено ниже путем решения внешней задачи для грунта), в то время как в указанных работах подразумевается, что сила взаимодействия определена опытным путем. Этот факт является существенным преимуществом рассматриваемой здесь постановки еще и в силу того обстоятельства, что установки и опыты для измерения силы и коэффициента взаимодействия, описанные в работах [6, 16], не отражают адекватно физические условия сейсмической задачи и вопрос их корректного определения из опытов остается открытым [17].

Ввиду важности задачи и для внесения ясности в ее постановку, отметим неточности, допущенные в работе [5] при выписывании уравнения движения трубопровода.

1) Применительно к продольному движению трубопровода утверждается, что “… эффективная масса единицы ее длины ${{{{\rho }}}_{a}}F$ несколько больше действительной за счет присоединенной массы грунта” (здесь $~F$ есть площадь поперечного сечения трубы, а ${{{{\rho }}}_{a}}$ понимается как приведенная погонная плотность трубы с учетом присоединенной массы). Далее эта величина, т.е. ${{{{\rho }}}_{a}}F$, входит в уравнение движения трубопровода через выражение для скорости звука в трубе. Однако для продольных движений трубопровода в грунте не может быть введено понятие присоединенной массы в его классическом (Стоксовом [18]) понимании, чего и нет в работе. Более того, предположение о существовании присоединенной массы противоречит принятому в ней же положению о том, что при распространении вдоль трубопровода сейсмической волны все влияние грунта на трубопровод сводится к силе взаимодействия. Раз эта сила учтена в уравнении движения трубопровода, то никаких других сил со стороны грунта на трубопровод не действует и потому рассуждения о присоединенной массе не состоятельны.

2) Представленные в работе (на инженерном уровне) соображения по поводу вывода формулы приведенной жесткости на растяжение для трубопровода с демпфирующими стыками не разъясняют этот вопрос и содержат путаницу в обозначениях. То же относится и к изложению этого вопроса в монографии Т. Рашидова [6]. Инженерные и строгие методы вывода средних (или усредненных) модулей упругости и скоростей распространения продольных волн в трубопроводе с демпфирующими стыками приведены в работе [19].

Нетрудно показать, что сформулированная выше задача в случае бесконечного трубопровода является автомодельной, т.е. когда заданная сейсмическая волна ${{w}_{{0z}}}$, входящая в граничное условие (3.1), является функцией аргумента $Z \equiv ct - z$, она допускает решение, в котором обе неизвестные функции w и $\mathcal{U}$ также зависят от Z вместо зависимости от двух переменных $z$ и $t$ в отдельности: $w\left( {r,z,t} \right) = w\left( {r,Z} \right)$, $\mathcal{U}(z,t)\, = \,\mathcal{U}(Z)$. Следовательно, уравнения колебаний грунта (3.3) и трубопровода (3.6) сводятся к следующим уравнениям:

При этом может реализоваться один из следующих двух, физически различных, режимов протекания волновых процессов в системе грунт–трубопровод: a) сверхзвуковой режим $(M > 1)$, когда скорость сейсмической волны c в грунте больше стержневой скорости распространения возмущений в трубопроводе 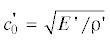и b) дозвуковой режим $(M < 1)$, когда $c < c_{0}^{'}$.

Скорость движения волны вдоль трубы 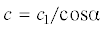при наклонном падении волны на трубопровод может быть сколь угодно большой (при $0 < {{\alpha }} < {{\pi /}}2)$. По этой причине сверхзвуковой случай, впервые введенный в рассмотрение в работе [5], может возникать и когда трубопровод не содержит демпфирующих стыков.

В условиях, когда падающая волна (2.1) и ее составляющая ${{w}_{{0z}}}$ из (3.1), распространяющаяся вдоль трубопровода, являются стационарными волнами, в грунте и трубопроводе реализуется установившийся колебательный режим, т.е. перемещения w и $\mathcal{U}$ могут разыскиваться в виде

Тогда уравнения (3.7), (3.8) для W(r) и $U$ принимают вид

К этой системе уравнений необходимо присоединить краевые условия для W, получаемые при подстановке представлений (3.9) в (3.1), (3.2), т.е. условия

4. Вывод теоретического значения для силы взаимодействия. Решение задачи для трубопровода. Интегрируя уравнение колебаний грунта (3.10) (являющееся уравнением Бесселя) и удовлетворяя краевым условиям (3.12), получаем решение внешней задачи для грунта в виде

Здесь ${{J}_{0}}$ ,$~{{Y}_{0}}$ означают функции Бесселя первого и второго рода нулевого порядка.

Из (4.1) следует, что

если воспользоваться правилами дифференцирования бесселевых функций [20].

Равенство (4.2) показывает, что при произвольных значениях параметров, входящих в аргументы бесселевых функций, касательное напряжение (3.4) на поверхности трубы, а значит, и сила взаимодействия с грунтом не пропорциональны относительному перемещению ${{W}_{0}} - U$, как это предполагается в работах [1, 5, 6]. Однако, если предположить, что безразмерный параметр $pR \ll 1$ (тогда и $pa \ll 1$) или, что эквивалентно, ${{\varepsilon }} \equiv R{\text{/}}L \ll 1$, т.е. малость глубины залегания трубопровода и его диаметра в сравнении с длиной сейсмической волны, то пользуясь в (4.2) разложениями бесселевых функций при малых значениях аргументов [20], приходим к асимптотическому представлению для касательного напряжения на поверхности трубы в виде (σ_rz = = ${{\sigma }}_{{rz}}^{0}{\text{exp}}\left( { - ihZ} \right))$:

Легко показать, что следующий член в асимптотическом разложении касательного напряжения при малом ε имеет порядок 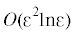и он не пропорционален относительному смещению ${{W}_{0}} - U$ (содержит разные коэффициенты при ${{W}_{0}}$ и $ - U$). Таким образом, в случае линейно упругого грунта установлена справедливость принятой в инженерных теориях гипотезы о пропорциональности касательных напряжений на поверхности трубопровода (а значит, и силы взаимодействия с грунтом) относительному смещению в первом приближении, когда глубина заложения трубопровода и его диаметр малы в сравнении с длиной сейсмической волны. При этом, из (4.3) следует теоретическое выражение для коэффициента взаимодействия, а именно ${{k}_{z}}\, = \,\mu {\text{/}}[a{\text{ln}}(R{\text{/}}a)]$. Этот коэффициент в инженерных теориях должен определяться в опытах.

Отметим, что в частном, но важном случае $c = {{c}_{1}}$ (не наклонного падения волны на трубопровод, когда ${{\alpha }} = 0$ и падающая волна движется вдоль трубы) закон (4.3) выполняется точно. Действительно, тогда в уравнении (3.10) ${{m}^{{ - 1}}} = 0$ и решение краевой задачи (3.10), (3.12) есть

Подстановка найденного из решения внешней задачи выражения (4.3) для касательного напряжения в уравнение (3.11) приводит последнее к виду

Следовательно, амплитуда связанных стационарных колебаний трубопровода дается выражением

В формулах (4.4), (4.5) верхние знаки берутся в дозвуковом случае $(M < 1)$, а нижние – в сверхзвуковом $(M > 1)$.

Решение уравнения (3.7) для дозвукового случая (формула (4.5) с верхними знаками плюс) формально совпадает с решением А. Сакураи и Т. Такахаши [1], однако, есть и существенные различия. Во-первых, амплитуда падающей волны ${{W}_{0}} = {{A}_{{0z}}}$ и параметры h и $k$, входящие в решение (4.5), зависят от угла падения наклонной падающей волны (формулы (2.2), (3.8), (3.9), (4.4)); в [1] же возможность наклонного падения волны на трубопровод не предполагалась. Во-вторых, что более важно, параметр $k$ в (4.5) имеет теоретическое значение (4.4), вытекающее из решения внешней задачи для грунта, в то время как в работе [1] (а также в работе [5]) этот параметр остается неопределенным.

Сверхзвуковой режим (когда число Маха $M > 1$ и волна в грунте распространяется вдоль трубопровода со скоростью большей, чем скорость звука в трубе) также не изучался А. Сакураи и Т. Такахаши. Этот режим естественным образом возникает при увеличении угла наклона плоской волны к трубопроводу (напомним, что под углом падения понимается угол, образуемый нормалью к фронту волны с осью трубопровода (рис. 1)), поскольку в этом случае 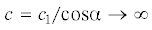при $~{{\alpha }} \to {{\pi /}}2$. Другой случай, когда может возникать сверхзвуковой режим, – это сегментный трубопровод с демпфирующими стыками (гасящими скорость распространения звука в нем) или трубопроводы из композитных или полимерных материалов. В особенности, если такие трубопроводы уложены в плотных или скалистых грунтах с большими скоростями распространения объемных волн.

5. Анализ решения и выводы. Соотношения (4.5) отражают существенное отличие в поведении решений для сверхзвукового и дозвукового режимов, связанное, прежде всего, с возможностью существования резонанса в первом случае: когда параметр k, определенный формулой (4.4), становится по своим значениям близким к $h$, амплитуда стационарных колебаний при $M > 1$ неограниченно возрастает. Однако и при $k \ne h$ динамические напряжения в сверхзвуковом случае превышают соответствующие напряжения, вычисленные по теории “жесткого защемления” (принятой в нормативных документах при расчете подземных трубопроводов на сейсмостойкость [4]), согласно которой продольные перемещения и деформации трубы совпадают с продольными перемещениями и деформациями грунта в волне ${{w}_{{0z}}}$ из (2.2). Согласно этой простейшей теории, максимальные напряжения в трубопроводе .

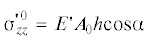Следовательно, существующее убеждение [2], что рассчитанные по теории полного защемления напряжения являются верхней границей напряжений в трубопроводе неверно, если реализуется сверхзвуковой режим, а он имеет место при наклонном падении сейсмической волны на трубопровод для углов ${{\alpha }}$, для которых $\cos {{\alpha }} < {{c}_{1}}{\text{/}}c_{0}^{'}$ (подразумевается обычная ситуация, когда скорость объемных волн в грунте ${{c}_{1}}$ меньше стержневой скорости трубопровода $c_{0}^{'}$).

При землетрясениях интенсивности 3 и выше (по шкале Рихтера) основную часть энергии несут волны с длинами от многих десятков до нескольких сотен метров. Тогда для металлических и бетонных (асбестоцементных) трубопроводов в реальных условиях их пролегания численное значение h может на порядок или даже на два порядка быть меньше значения параметра k. В этом случае $\left( {h{\text{/}}k \ll 1} \right)$ также справедлив приведенный выше анализ.

В качестве примера исследуем важный вопрос о поведении амплитуды колебаний трубопровода (и амплитуды напряжений в нем) при изменении глубины пролегания. С этой целью подставим значения $h$ из (3.9) и $k$ из (4.4) в решения (4.5) и представим их в виде

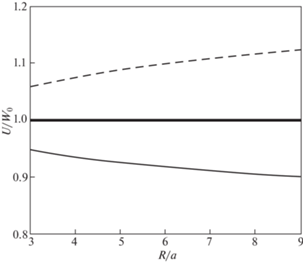
На рис. 3 изображены графики безразмерной амплитуды колебаний $U{\text{/}}{{W}_{0}}$ железного трубопровода, заложенного в мягкий грунт, в зависимости от глубины заложения при следующих значениях входящих в (5.1) констант и параметров: $E' = 21.3 \times {{10}^{{10}}}~$ Н/м², ${{\mu }} = 3.38 \times {{10}^{8}}$ Н/м², $b{\text{/}}a = 0.9$, $a = 0.15~$ м, ${{L}_{1}} = 110~$ м, $M = 1.1$ и $M = 0.9$ соответственно в сверхзвуковом и дозвуковом случаях (значение модуля Юнга $E'$ для железа взято из справочника [21], а модуля сдвига ${{\mu }}$ для мягкого грунта – из [22]).

Теми же выражениями (5.1) определяются и безразмерные амплитуды продольных напряжений в трубопроводе .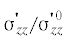

Из графиков рис. 3 видно, что амплитуды перемещений (и напряжений) в дозвуковом режиме убывают с возрастанием глубины заложения (сплошная линия), а в сверхзвуковом режиме они, наоборот, возрастают с увеличением $R$ (штриховая линия). Полужирная прямая на рис. 3 обозначает не зависящий от глубины залегания результат элементарной теории полного защемления трубопровода в грунте.

Таким образом, если в дозвуковом случае для обеспечения большей сейсмостойкости трубопровод необходимо заглублять на бόльшую глубину (известный факт), то в сверхзвуковом случае, как следует из результатов настоящего исследования, нужно поступать ровно противоположным образом (разумеется в предположении, что глубина заложения остается все еще достаточной для того, чтобы можно было пренебречь влиянием поверхностных волн, затухающих экспоненциально с глубиной).

Если же трубопровод или протяженное сооружение цилиндрической формы (скажем тоннель метрополитена) в силу разных причин располагается на небольшой глубине, в зоне интенсивного воздействия поверхностных волн (волн Рэлея), то для уменьшения эффекта этого воздействия и обеспечения большей сейсмозащиты могут быть использованы расположенные вдоль сооружения вертикальные сейсмические барьеры. В работе [23] предложены различные варианты таких барьеров и расчетами подтверждена их эффективность для гашения наиболее опасных для протяженного сооружения вертикальных колебаний в волнах Рэлея.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 20-08-00024.