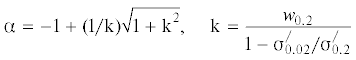Известия РАН. Механика твердого тела, 2022, № 4, стр. 85-89

Введение. В процессе деформирования гетерогенных материалов образуются повреждения в виде микротрещин отрыва и сдвига либо в виде площадок текучести. Микроповреждения в материале существенно влияют на значения основных деформационных характеристик типа предел пропорциональности, предел пластичности, временное сопротивление и коэффициент поперечного сужения. Это обстоятельство сказывается на результатах расчетов на прочность, устойчивость и др. для реальных конструкций. Как правило, такие расчеты идут в запас прочности. Очевидно, в связи с этим указанный вопрос обсуждался недостаточно. В настоящее время существуют различные подходы к моделированию микроповреждаемости материалов [1–6, 14–17]. Есть подходы, где учитывается взаимодействие соседних структурных элементов в процессе деформирования, что приводит к изменению масштаба и типа структурных элементов. При взаимодействии микротрещин в материале возникает развитие регулярной структуры разрушения. Например, взаимодействие микротрещин в пористом теле при сжатии с образованием такой структуры разрушения, рассматривается в работе [7]. Следует отметить подходы с использованием метода минимизации целевой функции осуществляемого с помощью алгоритма Левенберга–Марквардта [8–10].

Структурно-вероятностная модель повреждаемости материала описана в работах [1, 3, 4]. Результаты исследований особенностей деформирования, разрушения конструкций, устойчивости тонкостенных конструкций, а также работы по электроупругим материалам, с учетом микроразрушений отражены в работах [1–6, 11].

В указанных работах для оценки степени поврежденности материала используется параметр $p = {{{\text{F}}}_{r}}{\text{/}}{{{\text{F}}}_{0}}$, где ${{{\text{F}}}_{0}}$ – исходная эффективная площадь сечений, ${{{\text{F}}}_{r}}$ – разрушенная часть исходной площади. Для определения параметра $p$ используются функции распределения случайных значений пределов прочности структурных элементов материала.

Концентрация микроразрушений $p$ является одной из основных характеристик материала, поэтому поиск способов определения этой характеристики представляет теоретический и практический интерес. Наряду с аналитическим способом определения концентрации микроразрушений в образцах на основе функции распределения пределов прочности (текучести) в структурных элементах материала, приводится новый экспериментальный способ на основе замеров текущих значений удлинения образцов в макроэксперименте.

1. Экспериментальный способ. При растяжении экспериментальных образцов силой ${\text{P}}$ образуется остаточная деформация

где ${{\varepsilon }} = \bar {\sigma }{\text{/}}\overline {{{{\text{E}}}_{c}}} $ – полная деформация; ${{{{\varepsilon }}}_{y}} = \bar {\sigma }{\text{/}}\overline {{{{\text{E}}}_{0}}} $ – упругая деформация; $\overline {{{{\text{E}}}_{{\text{c}}}}} $ – секущий модуль; $\overline {{{{\text{E}}}_{{\text{0}}}}} $ – модуль упругости растягиваемого образца. Истинные напряжения $\bar {\sigma }$ определяются выражением

В (1.2) обозначено: ${{{\text{F}}}_{{{\nu }}}},\,{{{\text{F}}}_{r}}$ – соответственно уменьшение эффективной площади сечения за счет эффекта Пуассона и микроразрушений в материале. ${{p}_{{{\nu }}}},p$ – относительные доли ${{{\text{F}}}_{{{\nu }}}},\,{{{\text{F}}}_{r}}$; ${{{{\sigma }}}^{/}} = {\text{P/}}{{{\text{F}}}_{0}}$ – условные напряжения, в которых приводятся справочные данные об основных механических характеристиках материала; (${{\sigma }}_{{0.02}}^{/}$ – условный предел пропорциональности; ${{\sigma }}_{{0.2}}^{/}$ – условный предел текучести).

В процессе деформирования образца эффективная площадь сечений с учетом эффекта Пуассона и микроразрушений в материале определяется выражением

где ${{\nu }}$– коэффициент поперечного сужения, изменяющийся в процессе деформирования. С учетом (1.2), (1.3) выражение (1.1) преобразуется к виду

С учетом, что первое слагаемое в (1.4) обозначает общую деформацию ${{\varepsilon }}$ следует соотношение

С учетом малости ${{\nu \varepsilon }} \ll 1$ для конструкционных материалов типа сталей соотношение (1.5) принимает вид

В (1.6) выражение ${{\varepsilon }}_{y}^{/} = \frac{{{{{{\sigma }}}^{/}}}}{{{{{\overline {\text{E}} }}_{0}}}}$ – обозначает условную упругую деформацию, ${{\bar {\varepsilon }}_{y}} = {{\varepsilon }} - {{{{\varepsilon }}}_{0}}$ обозначает истинную упругую деформацию, ${{\varepsilon }}_{y}^{/} = (1 - p) \cdot {{\bar {\varepsilon }}_{y}}.$

В абсолютно упругом теле ${{{{\varepsilon }}}_{0}} = 0$, в частично упругом ${{{{\varepsilon }}}_{0}} \ne 0$ [18]. При деформировании частично упругого материала в упругой области $0 < {{{{\sigma }}}^{/}} \leqslant {{\sigma }}_{{0.02}}^{/}$ имеет место выражение

где ${{{\text{E}}}_{0}}$ – модуль упругости сплошного материала, ${{\overline {\text{E}} }_{0}}$ – модуль упругости частично упругого материала. $p$ – концентрация микродефектов отрыва. В случае малых остаточных деформаций ${{{\text{E}}}_{0}} \approx {{\overline {\text{E}} }_{0}} \approx {{{\text{E}}}_{ - }}$, где E_– – модуль упругости при сжатии образца. Остаточная деформация при растяжении образца в упругой области в случае микроразрушений отрывом будет определяться разностью значений деформаций при растяжении ${{{{\varepsilon }}}_{ + }}$ и сжатии |ε_–|.

Из (1.7) следует выражение для концентрации микротрещин отрыва

Абсолютно упруго материал ведет себя в диапазоне напряжений $0 < {{{{\sigma }}}^{/}} \leqslant {{\sigma }}_{{{\text{ce}}}}^{/},$ где ${{\sigma }}_{{c\,e}}^{/}$ – минимальный предел прочности структурных элементов материала. Параметр ${{\sigma }}_{{c\,e}}^{/}$ представляет собой максимальное условное напряжение в образце, при котором ${{{{\varepsilon }}}_{0}}$ = 0.

Методика аналитического определения величин ${{{\text{E}}}_{ + }},{{\overline {\text{E}} }_{0}},{{{\text{E}}}_{ - }}$ изложена в [3]. В частично упругом материале предел пропорциональности является условной величиной, которая зависит от принимаемого в качестве приближенного значения ${{{{\varepsilon }}}_{0}},$ при котором материал в некотором приближении считается упругим.

2. Аналитический способ. Физическая суть параметра p состоит в том, что он представляет относительную долю площади пересекаемых структурных элементов, в которых локальные напряжения достигают уровня пределов прочности либо текучести. В [13] на основе анализа тонких срезов осадков в петрографии показано, что $p = \frac{{{{N}_{0}}}}{N}\,,$ где N и N₀ соответственно общее число и число разрушенных структурных элементов. Существует несколько подходов к определению распределения пределов прочности (текучести). Для аппроксимации распределения прочностных свойств кристаллитов и зерен различной ориентации в микронеоднородных материалах предложены различные законы: степенной закон [4], нормальный закон распределения микропрочности [4], функция распределения Вейбулла [4], функция распределения Пирсона третьего рода [16] и др.

В качестве примера рассматривается степенной закон. Согласно этому закону плотность и интегральная функция распределения пределов прочности (текучести) структурных элементов имеют вид

В (2.1), (2.2) обозначено: $\bar {\sigma }$ – случайные значения пределов прочности (текучести) структурных элементов при растяжении; ${{\bar {\sigma }}_{0}},{{\bar {\sigma }}_{1}}$ – соответственно минимальное и максимальное значения пределов прочности (текучести); α – коэффициент рассеивания пределов прочности.

В случае микродефектов сдвига в формулах (2.1), (2.2) следовало бы перейти к касательным напряжениям. Однако в этом нет необходимости, поскольку характерные сдвиговые параметры определяются через соответствующие параметры в нормальных напряжениях. Поэтому независимо от критериев текучести конечный результат (значение $p$) будет одинаковым. В случае касательных напряжений отсутствует эффект Пуассона, которым пренебрегается в конечных выражениях при нормальных напряжениях.

Способы определения параметров интегральной функции распределения $p(\bar {\sigma })$ изложены в [1, 6].

Очевидно, интенсивное разрушение либо текучесть в структурных элементах начинаются при напряжениях больших предела пропорциональности. Поэтому принимается ${{\bar {\sigma }}_{0}} = {{\sigma }_{{0.02}}}$.

В дальнейшем в качестве примера микроразрушение в материале рассматривается в интервале напряжений ${{\bar {\sigma }}_{{0.02}}} < {{\bar {\sigma }}^{/}} \leqslant {{\bar {\sigma }}_{{0.2}}}$, где цифрами внизу обозначены значения остаточной деформации в долях процента. В указанном интервале параметры α и ${{\bar {\sigma }}_{1}}$ определяются выражениями [6]:

Основанием для определения параметра $\alpha $ для истинного ${{\bar {\sigma }}_{{0.2}}}$ по формулам (2.3) является равенство дисперсии для случайных значений условного и истинного пределов текучести. Вследствие этого коэффициент вариации ${{w}_{{0.2}}}$ для условного $({{\sigma }}_{{0.2}}^{/})$ и истинного $({{\bar {\sigma }}_{{0.2}}})$ пределов текучести будет одинаковым. Выражение (2.2) с учетом (2.4) преобразуется к виду

По экспериментальным данным концентрация микродефектов определяется формулой (1.6). Соотношение (1.6) позволяет проверить достоверность выражения (2.5) в частном случае условного ${{\sigma }}_{{0.2}}^{/}$. В случае других условных пределов текучести ${{\sigma }}_{х}^{/}$ такая проверка возможна при известных значениях коэффициента вариации ${{w}_{х}}$ для заданного ${{\sigma }}_{х}^{/}$.

3. Числовой пример. Проверка достоверности выражений (1.6), (2.5) проводится путем сравнения результатов расчета по этим формулам для стали 15 × 2МФА, стандартные характеристики для которой составляют [14]:

Из формулы (2.3) для заданного ${{\sigma }}_{{0.2}}^{/}$ следует ${{\alpha }} = 1.5813$. По формуле (2.5) p = 0.4608, а согласно (1.6) $p = 0.4901$. Значения концентраций микродефектов, рассчитанные по соотношениям (1.6), (2.5) согласуются в рамках допустимой точности.

Заключение. Изложены экспериментальный и структурно-вероятностный подходы к определению концентрации микроразрушений при растяжении повреждающихся образцов. Случай сжатия образцов требует отдельного рассмотрения. Показано, что остаточная деформация является следствием микроразрушений в материале. При отрывном микроразрушении образцов остаточная деформация определяется разностью значений деформации при растяжении и сжатии, поскольку при растяжении в материале образца происходят микроразрушения, а при сжатии материал ведет себя как сплошной. С учетом изложенного выше было бы полезно расширить список основных стандартных механических параметров типа предел пропорциональности, условный предел текучести, предел прочности, дополнив его соответствующими указанным параметрам значениями коэффициентов вариации, полной и остаточной деформациями.