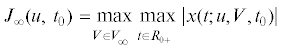Известия РАН. Механика твердого тела, 2022, № 4, стр. 51-69

Введение. В работе рассматривается построение способов управления противоударным изолятором при ограниченных наихудших возмущениях. Используемая математическая модель системы состоит из основания и защищаемого объекта, находящегося на нем, и обладает одной степенью свободы. Предполагается, что имеет место внешнее воздействие кинематического типа, задаваемое ускорением основания, определенным как функция времени. Основание и защищаемый объект могут двигаться поступательно вдоль одной заданной прямой. Управляющая сила между основанием и объектом создается изолирующим устройством и ограничена по величине. Впервые задача о минимизации максимума модуля смещения объекта относительно основания при заданном заранее возмущении была сформулирована в [1–3]. В дальнейшем теория оптимальной противоударной изоляции получила развитие в [4–7]. В [8] изучалась задача защиты объекта, расположенного на подвижном основании, от ударных воздействий малой длительности с помощью изолятора с управлением без упреждения. Численное решение задачи из [8] при заданном возмущении и построение ее аналитических решений для некоторых классов возмущений с упреждающим управлением рассмотрены в [9]. Аналитическое гарантирующее упреждающее управление с одним переключением и оптимальным временем упреждения и отвечающее им минимальное значение наибольшей величины смещения объекта относительно основания для класса возмущений заданной длительности с неограниченной амплитудой получены в [10, 11]. Для этого же класса возмущений в [12, 13] показано, что, используя упреждение и запаздывание для двух простых управлений, предназначенных для конкретных возмущений, и оптимизируя функционал только по моменту начала управления, можно получить значение критерия качества близкое к оптимальному. В [14] рассмотрена задача защиты объекта на подвижном основании для класса возмущений заданной длительности и ограниченной амплитуды. Доказано, что при заданном управлении наихудшими возмущениями являются непрерывные прямоугольные возмущения наибольшей амплитуды, начинающиеся в момент начала возмущения или заканчивающиеся в момент окончания допустимого интервала возмущения. Кроме того, в [14] для рассматриваемого класса возмущений изучалась возможность применения двух управлений, полученных в [9, 11] для прямоугольного возмущения и для возмущений заданной длительности с неограниченной амплитудой соответственно. Оптимизация критерия качества проводилась по моменту начала действия этих управлений. Предложено использовать комбинированное управление, сочетающее достоинства обоих управлений.

Обзор современного состояния проблемы противоударной изоляции, включающий в себя публикации по оптимальному управлению противоударными изоляторами, представлен в [15].

В данной работе, так же как и в [14], рассматривается задача защиты объекта на подвижном основании для класса возмущений заданной длительности и ограниченной амплитуды. В классе постоянных управлений ограниченной длительности проводится минимизация возможной величины смещения защищаемого объекта по начальному моменту действия управления. Варьирование момента начала действия управления из рассматриваемого класса предполагает, что возможно упреждение и запаздывание. Приведены сравнительные оценки по значению критерия качества предлагаемого управления со способами управления, рассмотренными в [14]. Выбор для изучения простых законов управления, зависящих от амплитуды возмущения и не зависящих от его длительности, обусловлен тем, что такие способы управления легче реализовать на практике, когда закон управления задан и выбирается только момент начала его действия в зависимости от длительности и амплитуды возмущения.

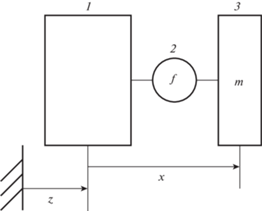
1. Механическая система. Рассматриваемая механическая система (рис. 1) содержит основание и объект, соединенный с основанием с помощью противоударного изолятора – устройства, которое генерирует управляющую силу f между основанием и объектом и предназначено для защиты объекта при ударном воздействии на основание. Основание и защищаемый объект движутся поступательно вдоль заданной прямой. Пусть $z$ – смещение основания относительно инерциальной (неподвижной) системы отсчета, $x$ – смещение объекта относительно основания, $m$ – масса объекта. Ударное воздействие на основание определяется его ускорением $\ddot {z}$, функцией времени, некоторые свойства которой известны до начала воздействия.

Движение объекта относительно основания выражается уравнением

в котором сила f  удовлетворяет ограничению $|{\kern 1pt} {\kern 1pt} f{\kern 1pt} {\kern 1pt} |\, \leqslant {{F}_{0}}$, где F₀ – заданная величина. Величина u удовлетворяет неравенству

Далее полагаем, что в начальный момент времени t = 0 основание и объект имеют нулевые значения координат и скоростей:

Допустимыми управлениями будем считать кусочно-непрерывные функции $u(t),$ удовлетворяющие ограничению

2. Внешние возмущения. Будем рассматривать возмущения ${v}(t)$ вида

где $V(\xi )$ – кусочно-непрерывная функция, заданная для всех вещественных $\xi $, причем $V(\xi ) \equiv 0$ для $\xi < 0$, а ${{t}_{0}} \geqslant 0$ – некоторый момент времени, который может быть известен заранее или подлежать определению. Возмущение V начинает действовать на основание только в момент ${{t}_{0}}$ после включения системы противоударной изоляции (управление с упреждением).

Будем предполагать, что 1) возмущение $V(\xi )$ действует только в одном заданном направлении и не меняет знака ($V(\xi ) \geqslant 0$), 2) $V(\xi )$ имеет заданную длительность T ($V(\xi ) \equiv 0$, если $\xi > T$), 3) $V(\xi )$ ограничена максимальной величиной воздействия, обозначаемой параметром b,

и 4) только на одном интервале, ${{t}_{1}} < \xi < {{t}_{2}}$, величина абсолютного ускорения $V(\xi )$ основания превышает верхнюю величину u₀ абсолютного ускорения защищаемого объекта:

Если $V(0) > {{u}_{0}}$ или $V(T) > {{u}_{0}}$, то один или оба из интервалов $0 \leqslant \xi < {{t}_{1}}$, ${{t}_{2}} < \xi \leqslant T$ могут быть пустыми. Если функция $V(\xi ),\;0 \leqslant \xi \leqslant T,$ предполагается известной и удовлетворяет в каждый момент $\xi $ ограничению $V(\xi ) \leqslant {{u}_{0}}$, оптимальное управление задается тождеством $u(t) \equiv V(t - {{t}_{0}})$ и обеспечивает нулевое смещение объекта по отношению к основанию. Далее предполагаем выполнение неравенства

Полагаем также, что заранее известны и заданы слдующие характеристики ударного воздействия: его длительность T, максимально возможная величина воздействия b и параметр ${{{v}}_{0}}$

характеризующий значение скорости, приобретенной (или потерянной) основанием в результате удара. Класс возмущений без ограничений на максимальную величину воздействия $V(\xi )$ с известными и заданными параметрами T, ${{{v}}_{0}}$ обозначим ${{V}_{T}}.$ Обозначим ${{V}_{\infty }}$ класс возмущений с заданной величиной ${{{v}}_{0}}$ из (2.4) без ограничений на максимальную величину воздействия $V(\xi )$ и на максимальную длительность T. Классам воздействий ${{V}_{T}}$, ${{V}_{\infty }}$ соответствует значение $b = + \infty .$ Классы возмущений ${{V}_{b}}$ и ${{V}_{{bT}}}$ определим параметрами b, ${{{v}}_{0}}$ и T, b, ${{{v}}_{0}}$ соответственно. Из неравенств $0 \leqslant V(\xi ) \leqslant b$ и условия (2.4) следует выполнение соотношений т.е. неравенство $bT \geqslant {{{v}}_{0}}$ есть необходимое условие существования возмущений из класса ${{V}_{{bT}}}$. Случай $bT = {{{v}}_{0}}$ соответствует прямоугольным возмущениям и исследован в [9], поэтому далее предполагаем выполнение неравенства

Введенные классы возмущений удовлетворяют включениям ${{V}_{{bT}}} \subset {{V}_{T}} \subset {{V}_{\infty }}$, ${{V}_{{bT}}} \subset {{V}_{b}} \subset {{V}_{\infty }}.$

3. Критерий качества. Далее полагаем, что известно множество $\Omega \subset {{V}_{\infty }}$, которому принадлежат возможные возмущения $V(\xi )$, но само возмущение может быть неизвестно. При заданных управлении $u(t)$ и времени упреждения ${{t}_{0}}$ качество изоляции будем оценивать функционалом J, характеризующим наибольшую величину смещения объекта относительно основания при наихудшем возмущении:

где $x(t;u,V,{{t}_{0}})$ – решение уравнения (1.1) с начальными условиями (1.2) для заданных $u(t)$, $V(\xi )$ и ${{t}_{0}}$. Далее величину J будем минимизировать выбором закона управления и времени упреждения. Для случаев, когда $\Omega = {{V}_{b}}$, $\Omega = {{V}_{{bT}}}$, $\Omega = {{V}_{T}}$, $\Omega = {{V}_{\infty }}$, для значения функционала из (3.1) введем соответствующие обозначения ${{J}_{b}}(u,{\kern 1pt} \;{{t}_{0}})$, ${{J}_{{bT}}}(u,\;{\kern 1pt} {{t}_{0}})$, ${{J}_{T}}(u,{\kern 1pt} \;{{t}_{0}})$, ${{J}_{\infty }}(u,{\kern 1pt} \;{{t}_{0}})$, т.е.

4. Задачи оптимизации. Учитывая различную возможную информированность управляющей стороны о внешнем возмущении и различие допустимых законов управления U, поставим следующие задачи.

Задача 1. Для системы (1.1) с начальными условиями (1.2) построить кусочно-непрерывное управление $u_{{}}^{*}$, удовлетворяющее ограничению (1.3), и время упреждения $t_{0}^{*}$, доставляющие минимум величине (3.1):

где U – заданное множество законов управления $u(t)$.

Это задача о гарантирующем управления u* с моментом упреждения ${\kern 1pt} t_{0}^{*}$, которые позволяют защищать объект от ударов из множества $\Omega $. Задача 1 обобщает задачу из [1–3] с заданным возмущением и отсутствием упреждения.

Задача 2. Для системы (1.1) при начальных условиях (1.2) и заданном возмущении (2.1) построить кусочно-непрерывное управление u*, удовлетворяющее ограничению (1.3), и время упреждения $t_{0}^{*}$, минимизирующие наибольшую величину смещения объекта относительно основания:

Задачу 2 можно рассматривать как задачу 1, в которой множество допустимых возмущений $\Omega $ содержит лишь один элемент.

В качестве множества допустимых законов управления может быть рассмотрено параметрическое семейство управлений ${{u}_{s}}(t) \in {{U}_{S}}$, зависящих от параметра $s,s \in S.$

Задача 3. Для заданного класса допустимых управлений ${{u}_{s}}(t) \in {{U}_{S}}$ найти время упреждения $t_{0}^{*}$ и значение параметра s*, минимизирующие величину (3.1):

Решение задачи 3 позволяет улучшать качество противоударной защиты с помощью изменения времени упреждения ${{t}_{0}}$ и параметра s при заданном семействе законов управления ${{u}_{s}}(t)$, которое, например, может быть построено на основе оптимального управления для некоторого заданного возмущения $V \in \Omega $ и представлено аналитическими выражениями. При заданном управлении $u(t)$ с условием $u(t) \equiv 0,\;t < 0$ параметрическое семейство управлений может состоять из функций ${{u}_{c}}(t) = u(t - c),\;c \geqslant 0$, и тогда параметр $c$ играет роль запаздывания для управления ${{u}_{c}}(t)$. Заметим, что, если множество $S$ состоит из одного элемента, задача 3 решается для фиксированного управления.

5. Определение наихудшего возмущения. Вычисление функционала (3.1) предполагает процедуру построения наихудшего возмущения $V \in \Omega \subset {{V}_{T}}$, максимизирующего максимум модуля отклонения защищаемого объекта относительно основания (${\text{ma}}{{{\text{x}}}_{t}}{\text{|}}{\kern 1pt} x(t;u,V,{{t}_{0}}){\kern 1pt} |$) при заданных $u(t)$ и ${{t}_{0}}$.

Лемма 1 (см. [9]). При заданных управлении $u(t)$ и времени упреждения ${{t}_{0}}$ среди возмущений $V \in {{V}_{T}}$ наихудшее возмущение представляет собой мгновенный удар интенсивности ${{{v}}_{0}}$, подаваемый в начальный момент ${{t}_{0}}$ или в конечный момент ${{t}_{0}} + T$ допустимого интервала возмущения. Таким образом, наихудшее возмущение есть либо ${{V}_{\delta }}(\xi ) = {{{v}}_{0}}{\kern 1pt} \delta {\kern 1pt} {\kern 1pt} (\xi )$ либо ${{V}_{{\delta T}}}(\xi ) = {{{v}}_{0}}\delta {\kern 1pt} {\kern 1pt} (\xi - T)$.

Следуя лемме 1, для нахождения наихудшего возмущения в классе ${{V}_{T}}$ при заданных $u(t)$ и ${{t}_{0}}$ необходимо решить дифференциальное уравнение (1.1) с начальными условиями (1.2) при ${v}(t) = {{{v}}_{0}}{\kern 1pt} \delta {\kern 1pt} {\kern 1pt} (t - {{t}_{0}})$ и ${v}(t) = {{{v}}_{0}}\delta {\kern 1pt} {\kern 1pt} (t - {{t}_{0}} - T)$, затем для каждого из решений вычислить $ma{{x}_{t}}{\kern 1pt} |{\kern 1pt} x(t;u,{{V}_{\delta }},{{t}_{0}}){\kern 1pt} |$, $ma{{x}_{t}}{\kern 1pt} |{\kern 1pt} x(t;u,{{V}_{{\delta {\kern 1pt} T}}},{{t}_{0}}){\kern 1pt} |$ и выбрать возмущение, отвечающее большему значению абсолютного отклонения.

Лемма 2 (см. [14]). При заданных управлении $u(t)$ и времени упреждения ${{t}_{0}}$ среди возмущений $V \in {{V}_{{bT}}}$ наихудшее возмущение есть либо

либо

Это означает, что при любом заданном управлении наихудшими возмущениями являются прямоугольные возмущения наибольшей амплитуды, либо начинающиеся в момент начала возмущения ${{t}_{0}}$, либо заканчивающиеся в момент окончания допустимого интервала возмущения ${{t}_{0}} + T$.

Примечание. Справедливо равенство ${{V}_{1}}(\xi ) = {{V}_{0}}(\xi - T + {{{v}}_{0}}{\text{/}}b).$

Следуя лемме 2, для нахождения наихудшего возмущения в классе ${{V}_{{bT}}}$ при заданных $u(t)$ и ${{t}_{0}}$ необходимо решить дифференциальное уравнение (1.1) с начальными условиями (1.2) при ${v}(t) = {{V}_{0}}(t - {{t}_{0}})$ и ${v}(t) = {{V}_{1}}(t - {{t}_{0}})$, затем для каждого из решений вычислить $ma{{x}_{t}}{\kern 1pt} {\kern 1pt} |{\kern 1pt} x(t;u,{{V}_{0}},{{t}_{0}}){\text{|}}$, $ma{{x}_{t}}{\kern 1pt} {\kern 1pt} |{\kern 1pt} x(t;u,{{V}_{1}},{{t}_{0}}){\text{|}}$, сравнить эти величины и выбрать возмущение, отвечающее большему значению. Таким образом, критерий качества J при заданном управлении $u$ для наихудших возмущений определяется выражением

Определим безразмерные переменные

Далее при использовании безразмерных переменных опускаем штрихи. В безразмерных единицах имеем ${{u}_{0}} = 1$ и ${{{v}}_{0}} = 1$, а неравенства (2.3), (2.5) приобретают следующий вид

6. Решение задачи 3 для класса ограниченных возмущений при использовании управления для прямоугольного возмущения с дополнительным запаздыванием. Возмущение в виде прямоугольного импульса в размерных переменных задается кусочно-постоянной функцией $V(t)$

а в безразмерных переменных – функцией

Для возмущения (6.2) задача 2 решена в [9] с использованием графо-аналитического метода [1, 2]. Оптимальные значения управления $u(t)$, времени упреждения ${{t}_{0}}$ и критерия качества J задаются соотношениями

Управление из (6.3) назовем r-управлением. Зададим класс управлений ${{U}_{{rC}}} = \{ {{u}_{{rc}}}\} $ параметрическим семейством допустимых управлений ${{u}_{{rc}}}(t)$, где

Равенство ${{u}_{{rc}}}(t) = {{u}_{r}}(t - c)$ означает, что управление ${{u}_{{rc}}}(t)$ представляет собой r-управление с запаздыванием c.

В [14] на основе леммы 2 в классах возмущений ${{V}_{{bT}}}$ и управлений ${{U}_{{rC}}}$ получено решение задачи 3:

Здесь ${{J}_{R}}(b,T) \equiv {{J}_{{bT}}}({{u}_{{rc}}},{{t}_{c}})$, т.е. искомое значение функционала ${{J}_{{bT}}}({{u}_{{rc}}},{{t}_{c}})$ задается функцией ${{J}_{R}}(b,T)$, у которой аргументы $b,T$ указывают на зависимость значения функционала ${{J}_{{bT}}}({{u}_{{rc}}},{{t}_{c}})$ от этих параметров. Оптимальное управление в классах управлений ${{U}_{{rC}}} = \{ {{u}_{{rc}}}\} $ и возмущений ${{V}_{{bT}}}$ для задачи 3 определяется формулой (6.6) со значением параметра c, удовлетворяющему неравенству из (6.7). Значения ${{t}_{c}},c$ из (6.7), доставляющие значение функционалу ${{J}_{R}}(b,T)$ из (6.8), не единственны. Оптимальные минимально возможные момент упреждения $t_{c}^{*}$ и величина запаздывания c* определяются как

При значениях $t_{c}^{{}} = t_{c}^{*}$, c = c* из (6.9) оптимальное управление определяется формулой $u_{{rc}}^{*}(t) = {{u}_{r}}(t - c{\text{*}})$ и справедливо равенство $\min \{ t_{c}^{*},c{\text{*}}\} = 0$, т.е. имеет место либо упреждение, либо запаздывание. При не минимально выбранных моменте упреждения $t_{c}^{{}}$ и величине запаздывания c имеем неравенство $\min \{ t_{c}^{{}},c\} > 0$. В этом случае на интервале времени $0 \leqslant t < \min \{ t_{c}^{{}},c\} $ рассматриваемая система бездействует и значения управления и возмущения имеют нулевые значения.

7. Решение задачи 3 для класса ограниченных возмущений при использовании управления, предназначенного для возмущений ограниченной длительности. В [10, 11] на основе леммы 1 получено решение $\{ {{u}_{\tau }},{{t}_{\tau }}\} $ задачи 3 в классе неограниченных возмущений ${{V}_{T}}$ для управлений из класса ${{U}_{\Sigma }} = \{ {{u}_{\tau }}\} $ – параметрического семейства допустимых релейных управлений ${{u}_{\tau }}(t)$ с переключением cо значения $ - {{u}_{0}}$ на значение ${{u}_{0}}$ в момент времени $\tau $ и cо значения ${{u}_{0}}$ на значение 0 в момент времени ${{{v}}_{0}}{\kern 1pt} /{\kern 1pt} {{u}_{0}} + 2\tau $, где

Временные отрезки со значениями $ \pm {{u}_{0}}$ выбраны таким образом, чтобы обеспечить выполнение равенства

для того чтобы движение объекта относительно основания прекратилось за конечное время ${{T}_{f}} = max\left( {{{t}_{0}} + T,{\kern 1pt} \,{{T}_{\tau }}} \right)$ и в дальнейшем не возобновилось.

В безразмерных переменных управление ${{u}_{\tau }}(t)$ из (7.1) имеет вид

Оптимальное управление в классах управлений ${{U}_{\Sigma }} = \{ {{u}_{\tau }}\} $ и возмущений V_T для задачи 3 определяется формулой (7.2) со значением параметра $\tau $ ([10, 11]):

а значение функционала и момент упреждения находят как

Решение (7.2)–(7.4) задачи 3 при $T > 1/2$ не единственно. Значение функционала ${{J}_{T}} = T{\kern 1pt} /{\kern 1pt} 2$ при $T > 1/2$ обеспечивается значениями $\tau $ и ${{t}_{\tau }}$, удовлетворяющими соотношениям

Обозначим через $u_{\tau }^{*}(t)$ функцию из (7.2) со значением $\tau = \tau _{{}}^{*}$ из (7.3) и используем функцию $u_{\tau }^{*}(t)$ и значение $t_{\tau }^{*}$ из (7.4) для вычисления значения функционала ${{J}_{{bT}}}(u_{\tau }^{*},t_{\tau }^{*})$ из (3.3) в классе ограниченных возмущений ${{V}_{{bT}}}$. Определим функцию ${{J}_{{b\tau }}}\left( {t{\text{*}}} \right)$ соотношениями

${{J}_{{b\tau }}}\left( {t{\text{*}}} \right)$ отвечает наибольшему относительному смещению защищаемого объекта при использовании управления $u_{\tau }^{*}(t)$ и применении возмущения ${v}(t) = {{V}_{0}}\left( {t - t{\text{*}}} \right)$ – прямоугольного возмущения с амплитудой b с началом действия в момент времени t*. Согласно лемме 2 величина ${{J}_{{bT}}}(u_{\tau }^{*},t_{\tau }^{*})$ определяется значением выражения

Отсюда получаем решение задачи 3 в классе ограниченных возмущений ${{V}_{{bT}}}$ для случая, когда класс допустимых управлений состоит из одного элемента $u_{\tau }^{*}$ и множество выбора моментов упреждения ${{t}_{0}}$ также состоит из одного элемента $t_{\tau }^{*}$.

Введем функцию ${{J}_{\Sigma }}(b,T) \equiv {{J}_{{bT}}}(u_{\tau }^{*},t_{\tau }^{*})$, у которой аргументы $b,T$ указывают на зависимость значения функционала ${{J}_{{bT}}}(u_{\tau }^{*},t_{\tau }^{*})$ от этих параметров.

Значение ${{J}_{\Sigma }}(b,T)$ для всех $1 < b \leqslant 2$ определяется выражением

Значение ${{J}_{\Sigma }}(b,T)$ для всех $b > 2$ определяется более сложным выражением

8. Решение задачи 3 для возмущений ограниченной длительности из класса V_T и ограниченных возмущений из класса ${{V}_{{bT}}}$ при использовании постоянных управлений. Зададим класс управлений ${{U}_{D}} = \{ {{u}_{d}}\} $ – параметрическим семейством допустимых управлений ${{u}_{d}}(t)$, где ${{u}_{d}}(t)$ в размерных и безразмерных переменных задается соответственно соотношениями (8.1) и (8.2)

Управление ${{u}_{d}}(t)$ при d = 0 обозначим ${{u}_{{0d}}}(t)$. Управление ${{u}_{{0d}}}(t)$ с моментом упреждения ${{t}_{0}} = 0$ представляет собой оптимальное управление для задачи 2 без упреждения при возмущении 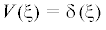(см. [6]). Управление ${{u}_{d}}(t)$ есть ${{u}_{{0d}}}$-управление с запаздыванием d, так как ${{u}_{d}}(t) = {{u}_{{0d}}}(t - d)$.

Решение задачи 3 в классе неограниченных возмущений ${{V}_{T}}$ для постоянных управлений класса U_D. В [13] на основе леммы 1 получено решение $\{ {{u}_{d}},{{t}_{d}}\} $ задачи 3 в классе неограниченных возмущений ${{V}_{T}}$ для управлений класса U_D. Это решение в указанных классах для задачи 3 определяется формулой для управления (8.2) и выражениями для момента упреждения ${{t}_{d}}$ и значения функционала ${{J}_{d}}$:

Значение функционала ${{J}_{d}}(T)$ из (8.4) обеспечивается переменными ${{t}_{d}}$, d из (8.3) не единственным образом. При этом профиль управления ${{u}_{d}}(t)$ из (8.2) остается одинаковым, меняется лишь начало его действия. Оптимальные минимально возможные момент упреждения $t_{d}^{*}$ и величина запаздывания d* определяются соотношениями

При значениях $t_{d}^{{}} = t_{d}^{*}$, $d = d_{{}}^{*}$ из (8.5) оптимальное управление определяется формулой $u_{d}^{*}(t) = {{u}_{{0d}}}\left( {t - d{\text{*}}} \right)$ и справедливо равенство $\min \{ t_{d}^{*},d{\text{*}}\} = 0$, т.е. имеет место либо упреждение, либо запаздывание. При не минимально выбранных моменте упреждения $t_{d}^{{}}$ и величине запаздывания d имеем неравенство $\min \{ {{t}_{d}},d\} > 0$. В этом случае на интервале времени $0 \leqslant t < \min \{ {{t}_{d}},\,d\} $ рассматриваемая система бездействует и значения управления и возмущения имеют нулевые значения.

Решение задачи 3 в классе ограниченных возмущений ${{V}_{{bT}}}$ для постоянных управлений класса U_D. При описании этого решения будем использовать обозначения: ${{u}_{{bd}}}$ для элементов U_D, ${{t}_{{bd}}}$ для момента упреждения, ${{d}_{b}}$ для величины запаздывания, поскольку при описании решения задачи 3 эти величины и их области изменения могут зависеть от параметра b. Допустимые управления ${{u}_{{b0}}}$, ${{u}_{{bd}}}$ в безразмерных переменных задаются соотношениями (8.6)

Управление ${{u}_{{bd}}}(t)$ есть ${{u}_{{b0}}}$-управление с запаздыванием d_b, так как u_bd(t) = ${{u}_{{b0}}}(t - {{d}_{b}})$.

Определим функции ${{J}_{{b0}}}\left( {t{\text{*}}} \right),{{J}_{{bd}}}\left( {t{\text{*}}} \right)$ выражениями

Эти функции определяются следующими соотношениями

Функции ${{J}_{{b0}}}\left( {t{\text{*}}} \right),{{J}_{{bd}}}\left( {t{\text{*}}} \right)$ отвечают наибольшему относительному смещению защищаемого объекта при использовании соответственно управлений ${{u}_{{b0}}}(t),\;{{u}_{{bd}}}(t)$ и применении возмущения ${v}(t) = {{V}_{0}}\left( {t - t{\text{*}}} \right)$ – прямоугольного возмущения с амплитудой b и началом действия в момент времени $t_{{}}^{*}$. Очевидное равенство ${{J}_{{bd}}}\left( {t{\text{*}}} \right) = {{J}_{{b0}}}\left( {t{\text{*}} - {{d}_{b}}} \right)$ при $t_{{}}^{*} \geqslant {{d}_{b}}$ означает, что график функции ${{J}_{{bd}}}\left( {t{\text{*}}} \right)$ получается смещением графика ${{J}_{{b0}}}\left( {t{\text{*}}} \right)$ на величину ${{d}_{b}}$ вдоль оси абсцисс с доопределением на интервале $[0,{{d}_{b}})$ согласно формуле для ${{J}_{{bd}}}\left( {t{\text{*}}} \right).$ При $b \to + \infty $ функция ${{J}_{{b0}}}\left( {t{\text{*}}} \right) \to {{J}_{{d0}}}\left( {t{\text{*}}} \right)$, где функция ${{J}_{{d0}}}\left( {t{\text{*}}} \right)$ предназначена для дельта возмущения и имеет тот же смысл, что и функция ${{J}_{{b0}}}\left( {t{\text{*}}} \right)$ для ограниченного возмущения. Функция ${{J}_{{d0}}}\left( {t{\text{*}}} \right)$ задается формулой

и приведена на рис. 2. Функция ${{J}_{{b0}}}\left( {t{\text{*}}} \right)$ имеет аналогичный вид.

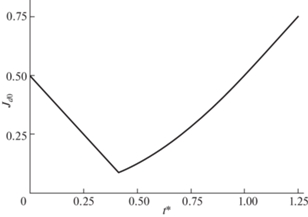
Функция ${{J}_{{bd}}}\left( {t{\text{*}}} \right)$ линейно убывает при $t{\text{*}} \in [0,(\sqrt 2 - 1)(1 - {{b}^{{ - 1}}}) + {{d}_{b}}]$ от значения $(1 - {{b}^{{ - 1}}}){\text{/}}2$ до значения

затем при $t{\text{*}} \in [\sqrt 2 - 1)(1 - {{b}^{{ - 1}}}) + {{d}_{b}}, + \infty )$ монотонно возрастает от значения (8.8) до бесконечности. При этом функция ${{J}_{{bd}}}\left( {t{\text{*}}} \right)$ на отрезке $[\sqrt 2 - 1)(1 - {{b}^{{ - 1}}}) + {{d}_{b}},(1 - {{b}^{{ - 1}}}) + {{d}_{b}}]$ растет квадратично до значения а затем линейно до бесконечности. Функция ${{J}_{{bd}}}\left( {t{\text{*}}} \right)$ из (8.7) дает возможность оценить влияние возможной ошибки в определении момента удара при вычислении упреждающего оптимального управления на величину критерия качества.

Согласно лемме 2 величина ${{J}_{{bT}}}({{u}_{{bd}}},\,{{t}_{{bd}}})$ определяется значением выражения

Минимизируя выражение J_bT(u_bd, t_bd) по переменной t_bd получаем решение задачи 3 в классе ограниченных возмущений ${{V}_{{bT}}}$

Здесь ${{J}_{D}}(b,T) \equiv {{J}_{{bT}}}({{u}_{{bd}}},{{t}_{{bd}}})$, т.е. искомое значение функционала ${{J}_{{bT}}}({{u}_{{bd}}},{{t}_{{bd}}})$ задается функцией ${{J}_{D}}(b,T)$, у которой аргументы b, T указывают на зависимость значения функционала ${{J}_{{bT}}}({{u}_{{bd}}},{{t}_{{bd}}})$ от этих параметров.

Значение функционала ${{J}_{D}}(b,T)$ из (8.11) обеспечивается переменными ${{t}_{{bd}}}$, ${{d}_{b}}$ из (8.10) не единственным образом. При этом профиль управления ${{u}_{{bd}}}(t)$ из (8.6) остается одинаковым, меняется лишь начало его действия. Оптимальные минимально возможные момент упреждения $t_{{bd}}^{*}$ и величина запаздывания $d_{b}^{*}$ определяются соотношениями

При значениях ${{t}_{{bd}}} = t_{{bd}}^{*}$, ${{d}_{b}} = d_{b}^{*}$ из (8.12) оптимальное управление определяется формулой $u_{{bd}}^{*}(t) = {{u}_{{b0}}}(t - d_{b}^{*})$ и справедливо равенство $min\{ t_{{bd}}^{*},d_{b}^{*}\} = 0$, т.е. имеет место либо упреждение, либо запаздывание. При не минимально выбранных моменте упреждения ${{t}_{{bd}}}$ и величине запаздывания d_b имеем неравенство $min\{ {{t}_{{bd}}},{{d}_{b}}\} > 0.$ В этом случае на интервале времени $0 \leqslant t < min\{ {{t}_{{bd}}},{{d}_{b}}\} $ рассматриваемая система бездействует и значения управления и возмущения имеют нулевые значения.

Решение задачи 3 в классе ограниченных возмущений ${{V}_{{bT}}}$ при использовании постоянного управления без упреждения и запаздывания. В частном случае решения задачи 3 при заданных значениях параметров ${{t}_{{bd}}} = 0$, ${{d}_{b}} = 0$ и при использовании управления ${{u}_{{b0}}}$ из (8.6) получаем значение функционала

При этом начало действия наихудшего возмущения определяется соотношениями

9. Сравнение по критерию качества различных способов управления. Значения функционалов ${{J}_{R}}(b,T),{{J}_{\Sigma }}(b,T),{{J}_{D}}(b,T),{{J}_{0}}(b,T)$ из (6.8), (7.5), (7.6), (8.11), (8.13) представляют собой функции от параметров $b,T$, заданные в области

При этом выполнены следующие тождества

Соответственно сравнение функций ${{J}_{R}}(b,T)$, ${{J}_{\Sigma }}(b,T)$, ${{J}_{D}}(b,T)$ можно проводить лишь при

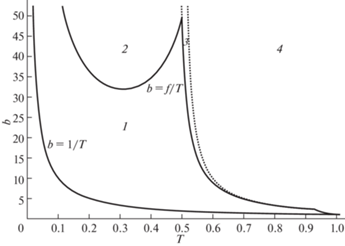
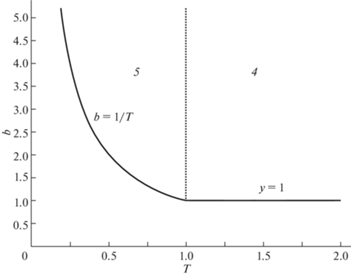
Сравнение функций ${{J}_{R}}(b,T),\;{{J}_{\Sigma }}(b,T)$. Сравнение функций ${{J}_{R}}(b,T)$, ${{J}_{\Sigma }}(b,T)$ проведено в работе [14]. Вычисления показывают, что равенство ${{J}_{R}}(b,T) = {{J}_{\Sigma }}(b,T)$ достигается при $1{\kern 1pt} /{\kern 1pt} {\kern 1pt} b < T < 1$ на кривой $l$, описываемой функцией $b = f(T),\;0 < T \leqslant 1$, где

При этом кривая l стремится к плюс бесконечности при $T \to + 0$, лежит выше кривой $b = 1{\kern 1pt} /{\kern 1pt} T$ при $0 < T < 1$ и пересекается с ней в точке $T = 1,\;b = 1.$ Кривые l и $b = 1{\kern 1pt} /{\kern 1pt} T$ изображены сплошными линиями на рис. 3. Кривая l  делит область ${{G}_{{bT}}}$ на две подобласти ${{G}_{R}},{{G}_{\Sigma }},$ располагающиеся ниже и выше кривой l соответственно. При этом в нижней области ${{G}_{R}}$ выполнено неравенство ${{J}_{R}}(b,T) < {{J}_{\Sigma }}(b,T)$, а в верхней области ${{G}_{\Sigma }}$ выполнено неравенство ${{J}_{R}}(b,T) > {{J}_{\Sigma }}(b,T).$ Зададим функцию ${{J}_{{comb}}}(b,T)$ соотношением

и поясним, как эта функция вычисляется. Дополнительно область ${{G}_{\Sigma }}$ на рис. 3 разделена двумя пунктирными линиями ${{l}_{1}},{{l}_{2}}$, задаваемыми формулами

Линия l₁ имеет общую точку с кривой $l$:

а кривая l₂ имеет общую точку с кривой $l$:

В каждой из четырех областей, помеченных на рис. 3 значение ${{J}_{{comb}}}(b,T)$ из (9.2) вычисляется по своей формуле с соответствующим индексом. То есть области со значением индекса $i\;{\kern 1pt} (i = 1,2,3,4)$ соответствует своя функция ${{J}_{i}}(b,T)$. Функции ${{J}_{i}}(b,T)$ имеют следующий вид

Функция ${{J}_{{comb}}}(b,T)$ представляет собой значение функционала (3.3) при использовании в качестве управления и момента упреждения величин $u_{{rc}}^{*},\;t_{c}^{*}$ в области ${{G}_{R}}$ и при использовании в качестве управления и момента упреждения величин $u_{\tau }^{*},t_{\tau }^{*}$ в области ${{G}_{\Sigma }}$. Такой способ управления с моментом упреждения назовем комбинированным управлением.

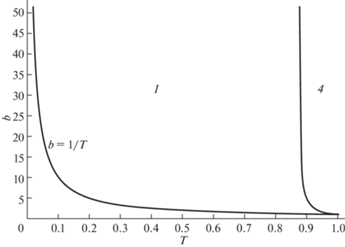
На рис. 4 изображено разбиение области ${{G}_{{bT}}}$ на две подобласти, которые описывает формула (6.8). Цифры 1 и 4, которыми помечены эти области, означают что функционал ${{J}_{R}}(b,T)$ имеет значения ${{J}_{1}}$ и ${{J}_{4}}$ из (9.3) в соответствующих подобластях.

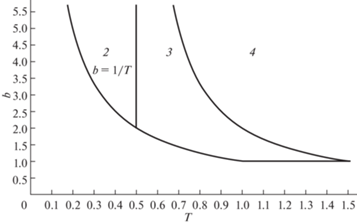
На рис. 5 изображено разбиение области ${{G}_{{bT}}}$ на три подобласти, которые фигурируют в формулах (7.5), (7.6). Цифры 2–4, которыми помечены эти подобласти, означают что функционал ${{J}_{\Sigma }}(b,T)$ имеет значения ${{J}_{2}}$, ${{J}_{3}}$, ${{J}_{4}}$ из (9.3) в соответствующих подобластях.

В [14] показано, что применение комбинированного управления приводит к улучшению значения функционала, доходящему до 10% по сравнению со значением функционала J_R, полученным для управления $u_{{rc}}^{*}$ и момента упреждения $t_{c}^{*}$. Применение комбинированного управления приводит к улучшению значения функционала, доходящему до 700% по сравнению со значением функционала ${{J}_{\Sigma }}(b,T)$, полученным для управления $u_{\tau }^{*}$ и момента упреждения $t_{\tau }^{*}$.

Сравнение функций ${{J}_{R}}(b,T),\;{{J}_{D}}(b,T)$, ${{J}_{{comb}}}(b,T)$. Заметим, что все три функции ${{J}_{R}}(b,T)$, ${{J}_{D}}(b,T)$, ${{J}_{\Sigma }}(b,T)$ при фиксированном $b$ суть возрастающие функции T, а неотрицательная функция ${{J}_{D}}(b,T) - {{J}_{R}}(b,T)$ при $b > 36{\kern 1pt} /{\kern 1pt} 19$ убывает до нуля по T на полуинтервале $(1{\text{/}}b,1]$. Поэтому относительная разность $\gamma (b,T)$ значений ${{J}_{R}}(b,T),\;{{J}_{D}}(b,T)$ при $b > 36{\kern 1pt} /{\kern 1pt} 19$ удовлетворяет соотношениям

Численные расчеты максимальной величины $\gamma (b,T)$ в области $1{\kern 1pt} /{\kern 1pt} T < b \leqslant 36{\kern 1pt} /{\kern 1pt} 19$ также приводят к значению 0.372583, которое тоже достигается при $T = 1{\text{/}}b$ и составляет 37%.

Относительная разность $\mu (b,T)$ значений ${{J}_{{comb}}}(b,T)$, ${{J}_{D}}(b,T)$, задаваемая равенством

удовлетворяет предельным соотношениям

Численный анализ показал, что при фиксированном b, удовлетворяющем неравенствам $1 < b \leqslant 7/3$, функция $\mu (b,T)$ на полуинтервале $\left( {1{\text{/}}b,1} \right]$ удовлетворяет соотношениям

Было показано, что при b, удовлетворяющем неравенствам $7{\kern 1pt} /{\kern 1pt} 3 < b$, функция $\mu (b,T)$ убывает по T на полуинтервале $(1{\kern 1pt} {\kern 1pt} /{\kern 1pt} {\kern 1pt} b,\;1{\kern 1pt} /{\kern 1pt} 2]$, затем возрастает по T на $(1{\text{/}}2,1{\text{/}}2 + 1{\text{/}}b]$, и затем на на полуинтервале $\left( {1{\text{/}}2 + 1{\text{/}}b,1} \right]$ убывает до нуля. При этом локальный максимум функции $\mu (b,T)$ при $T = 1{\kern 1pt} /{\kern 1pt} 2 + 1{\kern 1pt} /{\kern 1pt} b$ равен

и не превышает величины $7 - 4{\mkern 1mu} \sqrt 3 \approx 0.0718$. Тем самым было доказано, что относительная разность $\mu (b,T)$ значений ${{J}_{{comb}}}(b,T)$, ${{J}_{D}}(b,T)$ удовлетворяет соотношениям (9.4) во всей области ${{G}_{{bT}}}$ из (9.1). и не превышает 37%.

Сравнение функций ${{J}_{0}}(b,T)$, ${{J}_{D}}(b,T)$. Относительная разность $\nu (b,T)$ функций ${{J}_{0}}(b,T)$, ${{J}_{D}}(b,T)$ удовлетворяет соотношениям

и при фиксированном b убывает по T на полуинтервале $(1{\kern 1pt} /{\kern 1pt} b,1]$ от значения $\nu (b,1{\text{/}}b) = 2 + 2\sqrt 2 \approx 4.8284$ до значения $\nu (b,1) = 0$, а затем возрастает на интервале $(1, + \infty )$ и при $T \to + \infty $ стремится к 1. Это означает, что использование упреждения и запаздывания приводит к уменьшению значения функционала в 5.8 раза, а для больших T приводит к уменьшению значения функционала почти в 2 раза.

Заключение. Рассмотрена задача изоляции объекта на подвижном основании, которое подвержено однонаправленным возмущениям ограниченной длительности и амплитуды с заданным интегралом от возмущения. Для этой модели изучалась возможность применения наиболее простого, постоянного управления заданной длительности, полученного ранее для мгновенного удара для задачи без упреждения. Предложена оптимизация критерия качества по моменту начала действия предложенного управления. Проведено сравнение по значению критерия качества предлагаемой оптимизации с наиболее эффективными управлениями, предложенными автором в предыдущих работах.

Работа выполнена по теме государственного задания АААА-А20-120011690138-6.