1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2022

Известия РАН. Механика твердого тела, 2022, № 4, стр. 38-50

ФОРМУЛИРОВКА ЗАДАЧИ N ТЕЛ В ПАРАМЕТРАХ РАСШИРЕННОЙ ГРУППЫ НЬЮТОНА

В. Ф. Чуб a, *

a Ракетно-космическая корпорация “Энергия” им. С.П. Королева
Королев, Россия

* E-mail: post2@rsce.ru

Поступила в редакцию 27.07.2020
После доработки 10.07.2021
Принята к публикации 17.07.2021

Полный текст (PDF)

Аннотация

Рассмотрен нерелятивистский аналог конформной группы – 15-параметрическая расширенная группа Галилея–Ньютона, включающая пространственно-временные переносы и гравитационные преобразования, пространственные повороты, бусты и масштабные преобразования. На основе ее 12-параметрической подгруппы (без поворотов) сформулирована нерелятивистская задача n тел с учетом известного эффекта замедления времени в гравитационном поле.

Ключевые слова: конформная группа, группа Галилея–Ньютона, масштабное преобразование, расширение группы, инерциальная навигация, масса фотона, гравитационное замедление времени, задача n тел

1. Введение. “Итак, если классическая механика представляет собой теорию движений тел, основанную на группе Галилея, то специальная теория относительности – это такая физическая теория, группой симметрии которой является группа Пуанкаре” [1, с. 142]. Упомянутые в приведенной цитате из школьного учебника 10-параметрические группы преобразований включают пространственно-временные переносы (3 + 1 = 4 параметра), пространственные повороты (3 параметра) и бусты (3 параметра). Различаются эти группы только бустами: нерелятивистскими для группы Галилея (преобразования Галилея в узком смысле) и релятивистскими для группы Пуанкаре (чистые преобразования Лоренца) [2].

Как широко известно [3, с. 12–13; 4, с. 338–339; 5, с. 139–140], Анри Пуанкаре считал Вселенную инвариантной еще и относительно масштабного преобразования, а группы Галилея и Пуанкаре легко расширить до соответствующих 11-параметрических групп за счет добавления масштабных преобразований (1 параметр).

В [6] группы Галилея и Пуанкаре были расширены (в рамках развития программы теоретико-группового подхода к постановке задачи инерциальной навигации) путем включения гравитационных g-преобразований (3 параметра). Расширенная (за счет добавления нерелятивистских g-преобразований) группа Галилея позднее [7, с. 150] была названа группой Галилея–Ньютона (этим термином иногда называют и саму группу Галилея). Группу же Пуанкаре пришлось сразу расширить до широко известной в физике конформной группы. Помимо преобразований из группы Пуанкаре в конформную группу входят релятивистские g-преобразования, w-преобразования (1 параметр) и масштабные преобразования.

Цель настоящей работы – найти и использовать для уточнения классической постановки задачи n тел нерелятивистский аналог 15-параметрической конформной группы, более близкий к ней, чем 13-параметрическая группа Галилея–Ньютона.

2. Расширение группы Галилея–Ньютона. Исходя из сказанного во введении, представляется естественным расширить 11-параметрическую группу Галилея (включающую масштабные преобразования) за счет добавления нерелятивистских g-преобразований или расширить 13-параметрическую группу Галилея–Ньютона за счет добавления масштабных преобразований. В обоих случаях получается одна и та же 14-параметрическая группа (с четырьмя векторными параметрами и двумя скалярными). В этом легко убедиться, вычисляя коммутаторы соответствующих инфинитезимальных операторов (генераторов преобразований); при записи генераторов используются сокращенные обозначения (${{\partial }_{{{\tau }}}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial {{\tau }}}}} \right. \kern-0em} {\partial {{\tau }}}}$, ${{\partial }_{x}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0em} {\partial x}}$ и т.д.):

(1) временной перенос:

$T = {{\partial }_{{{\tau }}}}$

(2) пространственные переносы (по осям x, y, z):

${{R}_{x}} = {{\partial }_{x}},\quad {{R}_{y}} = {{\partial }_{y}},\quad {{R}_{z}} = {{\partial }_{z}}$

(3) пространственные повороты:

${{\Theta }_{x}} = z{{\partial }_{y}} - y{{\partial }_{z}},\quad {{\Theta }_{y}} = x{{\partial }_{z}} - z{{\partial }_{x}},\quad {{\Theta }_{z}} = y{{\partial }_{x}} - x{{\partial }_{y}}$

(4) нерелятивистские бусты:

${{V}_{x}} = {{\tau }}{{\partial }_{x}},\quad {{V}_{y}} = {{\tau }}{{\partial }_{y}},\quad {{V}_{z}} = {{\tau }}{{\partial }_{z}}$

(5) нерелятивистские g-преобразования:

${{G}_{x}} = \frac{1}{2}{{{{\tau }}}^{2}}{{\partial }_{x}},\quad {{G}_{y}} = \frac{1}{2}{{{{\tau }}}^{2}}{{\partial }_{y}},\quad {{G}_{z}} = \frac{1}{2}{{{{\tau }}}^{2}}{{\partial }_{z}}$

(6) масштабное преобразование:

$\Gamma = {{\tau }}{{\partial }_{{{\tau }}}} + x{{\partial }_{x}} + y{{\partial }_{y}} + z{{\partial }_{z}}$

Нетривиальным оказывается следующий этап – расширение упомянутой 14-параметрической группы до 15-параметрической за счет включения w-преобразований. Приведенный в [6] генератор w-преобразования конформной группы

$W = - \frac{1}{2}({{{{\tau }}}^{2}} - {{x}^{2}} - {{y}^{2}} - {{z}^{2}}){{\partial }_{{{\tau }}}} + {{\tau }}\left( {{{\tau }}{{\partial }_{{{\tau }}}} + x{{\partial }_{x}} + y{{\partial }_{y}} + z{{\partial }_{z}}} \right)$
не может быть использован: например, коммутатор
$\left[ {{{G}_{x}},W} \right] = {{G}_{x}}W - W{{G}_{x}} = \frac{1}{2}{{{{\tau }}}^{2}}x{{\partial }_{\tau }} - \tfrac{1}{2}{{\tau }}({{x}^{2}} + {{y}^{2}} + {{z}^{2}}){{\partial }_{x}}$
не является линейной комбинацией генераторов (1)÷(6) и W, поскольку имеет уже третий порядок по компонентам вспомогательного 4-вектора ${\text{X}} = ({{\tau }},x,y,z)$. Естественно, поэтому назвать выписанный генератор w-преобразования конформной группы “релятивистским” и попытаться найти “нерелятивистский” генератор w-преобразования, исключив “релятивистские добавки”.

Согласно данной в [6] физической интерпретации, рассматриваемое скалярное w‑преобразование представляет собой временнýю составляющую гравитационного преобразования (пространственно-временного), при этом векторное g-преобразование – пространственная его часть. Аналогия с переходом от релятивистских g-преобразований к нерелятивистским подсказывает: оставить в генераторе нерелятивистского w-преобразования только один (первый) член:

$W = - \frac{1}{2}{{{{\tau }}}^{2}}{{\partial }_{{{\tau }}}}$

Но вычисление, например, коммутатора такого генератора с ${{G}_{x}}$

$\left[ {{{G}_{x}},W} \right] = {{G}_{x}}W - W{{G}_{x}} = \frac{1}{2}{{{{\tau }}}^{3}}{{\partial }_{x}}$
показывает ошибочность описанного подхода. К успеху же приводит использование следующего генератора (найденного методом проб и ошибок после осознания необходимости построения нерелятивистского аналога конформной группы той же размерности):

(7) нерелятивистское w-преобразование:

$W = - \frac{1}{2}{{{{\tau }}}^{2}}{{\partial }_{{{\tau }}}} + {{\tau }}\left( {{{\tau }}{{\partial }_{{{\tau }}}} + x{{\partial }_{x}} + y{{\partial }_{y}} + z{{\partial }_{z}}} \right) = \frac{1}{2}{{{{\tau }}}^{2}}{{\partial }_{{{\tau }}}} + {{\tau }}x{{\partial }_{x}} + {{\tau }}y{{\partial }_{y}} + {{\tau }}z{{\partial }_{z}}$

В табл. 1 выписаны коммутаторы $[U,V] = UV - VU$ инфинитезимальных операторов (1)÷(7) из левого столбца (U) и верхней строки (V). Поскольку в таблице не появилось никаких новых генераторов, рассматриваемые 15 генераторов порождают, согласно второй обратной теореме Ли, 15-параметрическую группу [8, с. 204] – расширенную группу Галилея–Ньютона. Генераторы пространственных поворотов в табл. 1 выписаны последними, чтобы легко выделялась ее 12-параметрическая подгруппа – расширенная группа Ньютона, использующаяся в шестом разделе статьи. В табл. 1 также легко выделяется сама группа Ньютона (10-параметрическая) и 11-параметрическая группа, получающаяся из группы Ньютона добавлением масштабного преобразования. Из таблицы также видно отсутствие 11-параметрической группы, включающей пространственно-временные переносы, нерелятивистские бусты и нерелятивистские пространственно-временные гравитационные преобразования, поскольку временны́е переносы и нерелятивистские w-преобразования незамкнуты и порождают масштабное преобразование: $[T,W] = \Gamma $.

Таблица 1.

Алгебра Ли нерелятивистского аналога конформной группы

$U{{\backslash }}V$ $T$ ${{R}_{x}}$ ${{R}_{y}}$ ${{R}_{z}}$ ${{V}_{x}}$ ${{V}_{y}}$ ${{V}_{z}}$ ${{G}_{x}}$ ${{G}_{y}}$ ${{G}_{z}}$ $\Gamma $ $W$ ${{\Theta }_{x}}$ ${{\Theta }_{y}}$ ${{\Theta }_{z}}$
$T$ 0 0 0 0 ${{R}_{x}}$ ${{R}_{y}}$ ${{R}_{z}}$ ${{V}_{x}}$ ${{V}_{y}}$ ${{V}_{z}}$ $T$ $\Gamma $ 0 0 0
${{R}_{x}}$ 0 0 0 0 0 0 0 0 0 0 ${{R}_{x}}$ ${{V}_{x}}$ 0 ${{R}_{z}}$ –${{R}_{y}}$
${{R}_{y}}$ 0 0 0 0 0 0 0 0 0 0 ${{R}_{y}}$ ${{V}_{y}}$ –${{R}_{z}}$ 0 ${{R}_{x}}$
${{R}_{z}}$ 0 0 0 0 0 0 0 0 0 0 ${{R}_{z}}$ ${{V}_{z}}$ ${{R}_{y}}$ –${{R}_{x}}$ 0
${{V}_{x}}$ –${{R}_{x}}$ 0 0 0 0 0 0 0 0 0 0 ${{G}_{x}}$ 0 ${{V}_{z}}$ –${{V}_{y}}$
${{V}_{y}}$ –${{R}_{y}}$ 0 0 0 0 0 0 0 0 0 0 ${{G}_{y}}$ –${{V}_{z}}$ 0 ${{V}_{x}}$
${{V}_{z}}$ –${{R}_{z}}$ 0 0 0 0 0 0 0 0 0 0 ${{G}_{z}}$ ${{V}_{y}}$ –${{V}_{x}}$ 0
${{G}_{x}}$ –${{V}_{x}}$ 0 0 0 0 0 0 0 0 0 –${{G}_{x}}$ 0 0 ${{G}_{z}}$ –${{G}_{y}}$
${{G}_{y}}$ –${{V}_{y}}$ 0 0 0 0 0 0 0 0 0 –${{G}_{y}}$ 0 –${{G}_{z}}$ 0 ${{G}_{x}}$
${{G}_{z}}$ –${{V}_{z}}$ 0 0 0 0 0 0 0 0 0 –${{G}_{z}}$ 0 ${{G}_{y}}$ –${{G}_{x}}$ 0
$\Gamma $ –$T$ –${{R}_{x}}$ –${{R}_{y}}$ –${{R}_{z}}$ 0 0 0 ${{G}_{x}}$ ${{G}_{y}}$ ${{G}_{z}}$ 0 $W$ 0 0 0
$W$ –$\Gamma $ –${{V}_{x}}$ –${{V}_{y}}$ –${{V}_{z}}$ –${{G}_{x}}$ –${{G}_{y}}$ –${{G}_{z}}$ 0 0 0 –$W$ 0 0 0 0
${{\Theta }_{x}}$ 0 0 ${{R}_{z}}$ –${{R}_{y}}$ 0 ${{V}_{z}}$ –${{V}_{y}}$ 0 ${{G}_{z}}$ –${{G}_{y}}$ 0 0 0 ${{\Theta }_{z}}$ –${{\Theta }_{y}}$
${{\Theta }_{y}}$ 0 –${{R}_{z}}$ 0 ${{R}_{x}}$ –${{V}_{z}}$ 0 ${{V}_{x}}$ –${{G}_{z}}$ 0 ${{G}_{x}}$ 0 0 –${{\Theta }_{z}}$ 0 ${{\Theta }_{x}}$
${{\Theta }_{z}}$ 0 ${{R}_{y}}$ –${{R}_{x}}$ 0 ${{V}_{y}}$ –${{V}_{x}}$ 0 ${{G}_{y}}$ –${{G}_{x}}$ 0 0 0 ${{\Theta }_{y}}$ –${{\Theta }_{x}}$ 0

Приведем теперь выражения для конечных элементарных преобразований расширенной группы Галилея–Ньютона (активная трактовка, ${\text{X}} = {{\tau }} + {\mathbf{\rho }}$ → $X{\kern 1pt} _{{}}^{'} = {{\tau }}_{{}}^{'} + {\mathbf{\rho }}_{{}}^{'}$):

(1) временной перенос ${{T}_{t}}$:

${{\tau '}} = {{\tau }} + t,\quad {\mathbf{\rho }}{\text{'}} = {\mathbf{\rho }}$

(2) пространственный перенос ${{R}_{{\mathbf{r}}}}$:

${{\tau }}{\kern 1pt} ' = {{\tau ,}}\quad {\mathbf{\rho }}{\kern 1pt} ' = {\mathbf{\rho }} + {\mathbf{r}}$

(3) пространственный поворот ${{\Theta }_{{\text{Q}}}}$ (или ${{\Theta }_{\vartheta }}$):

${{\tau }}{\kern 1pt} ' = {{\tau ,}}\quad {\mathbf{\rho }}{\kern 1pt} ' = {\text{Q}} \circ {\mathbf{\rho }} \circ {{{\text{Q}}}^{{ - 1}}},\quad {\text{Q}} = {{e}^{{{{i\vartheta } \mathord{\left/ {\vphantom {{i\vartheta } 2}} \right. \kern-0em} 2}}}}$

(4) нерелятивистский буст ${{V}_{{\mathbf{v}}}}$:

${{\tau }}{\kern 1pt} ' = {{\tau ,}}\quad {\mathbf{\rho }}{\kern 1pt} ' = {\mathbf{\rho }} + {\mathbf{v}}{{\tau }}$

(5) нерелятивистское g-преобразование ${{G}_{{\mathbf{g}}}}$:

${{\tau }}{\kern 1pt} ' = {{\tau ,}}\quad {\mathbf{\rho }}{\kern 1pt} ' = {\mathbf{\rho }} + {{{\mathbf{g}}{{{{\tau }}}^{2}}} \mathord{\left/ {\vphantom {{{\mathbf{g}}{{{{\tau }}}^{2}}} 2}} \right. \kern-0em} 2}$

(6) масштабное преобразование ${{\Gamma }_{{{\gamma }}}}$ (или ${{\Gamma }_{{{\alpha }}}}$):

${{\tau }}{\kern 1pt} ' = {{\gamma \tau ,}}\quad {\mathbf{\rho }}{\kern 1pt} ' = {{\gamma }}{\mathbf{\rho }},\quad {{\gamma }} = {{e}^{{{\alpha }}}}$

(7) нерелятивистское w-преобразование ${{W}_{{\text{w}}}}$:

${{\tau }}_{{}}^{'} = \frac{{{\tau }}}{{{\text{1}} + {{w{{\tau }}} \mathord{\left/ {\vphantom {{w{{\tau }}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}},\quad {\mathbf{\rho }}_{{}}^{'} = \frac{{\mathbf{\rho }}}{{{{{\left( {{\text{1}} + {{w{{\tau }}} \mathord{\left/ {\vphantom {{w{{\tau }}} {\text{2}}}} \right. \kern-0em} {\text{2}}}} \right)}}^{2}}}}$

При описании поворотов в дальнейшем будет использоваться нормированный кватернион поворота Q вместо вектора ориентации $\vartheta $, а при описании масштабного преобразования – масштабный множитель ${{\gamma }}$ вместо канонического параметра ${{\alpha }}$. При восстановлении [8, с. 205–207] конечного нерелятивистского w-преобразования по соответствующему генератору изменен знак параметра (так же, как это было сделано в [6]). Поэтому физическая интерпретация всех параметров – та же, что для соответствующих параметров конформной группы в [6, 7]. Отметим только, что в конформной группе, включающей релятивистские бусты, более естественным (каноническим) параметром оказывается не скорость v, а быстрота ${\mathbf{\psi }}$ (параметр скорости, связанный с ней соотношением ${\mathbf{v}} = th{\mathbf{\psi }}$), и появляется ограничение на величину скорости (${\text{v}} = \left| {\mathbf{v}} \right|$ < 1).

Перейдем к определяющим соотношениям 15-параметрической расширенной группы Галилея–Ньютона, то есть к формулам для композиции однотипных элементарных преобразований и перестановочным формулам для элементарных преобразований разных типов. Приведем табличку, позволяющую их систематизировать (см. табл. 2), и выпишем подряд в соответствии с принятой системой нумерации:

(2.1)
${{T}_{{{{t}_{2}}}}}{{T}_{{{{t}_{1}}}}} = {{T}_{t}},\quad t = {{t}_{1}} + {{t}_{2}}$
(2.2)
${{R}_{{\mathbf{r}}}}{{T}_{t}} = {{T}_{t}}{{R}_{{\mathbf{r}}}}$
(2.3)
${{T}_{t}}{{R}_{{\mathbf{r}}}} = {{R}_{{\mathbf{r}}}}{{T}_{t}}$
(2.4)
${{R}_{{{{{\mathbf{r}}}_{2}}}}}{{R}_{{{{{\mathbf{r}}}_{1}}}}} = {{R}_{{\mathbf{r}}}},\quad {\mathbf{r}} = {{{\mathbf{r}}}_{1}} + {{{\mathbf{r}}}_{2}}$
(2.5)
${{V}_{{\mathbf{v}}}} \circ {{T}_{t}} = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}},\quad {\mathbf{r}} = {\mathbf{v}}t$
(2.6)
${{T}_{t}} \circ {{V}_{{\mathbf{v}}}} = {{V}_{{\mathbf{v}}}}{{R}_{{\mathbf{r}}}}{{T}_{t}},\quad {\mathbf{r}} = - {\mathbf{v}}t$
(2.7)
${{V}_{{\mathbf{v}}}}{{R}_{{\mathbf{r}}}} = {{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}$
(2.8)
${{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}} = {{V}_{{\mathbf{v}}}}{{R}_{{\mathbf{r}}}}$
(2.9)
${{V}_{{{{{\mathbf{v}}}_{2}}}}}{{V}_{{{{{\mathbf{v}}}_{1}}}}} = {{V}_{{\mathbf{v}}}},\quad {\mathbf{v}} = {{{\mathbf{v}}}_{1}} + {{{\mathbf{v}}}_{2}}$
(2.10)
${{G}_{{\mathbf{g}}}} \circ {{T}_{t}} = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}},\quad {\mathbf{r}} = {{{\mathbf{g}}{{t}^{2}}} \mathord{\left/ {\vphantom {{{\mathbf{g}}{{t}^{2}}} 2}} \right. \kern-0em} 2},\quad {\mathbf{v}} = {\mathbf{g}}t$
(2.11)
${{T}_{t}} \circ {{G}_{{\mathbf{g}}}} = {{G}_{{\mathbf{g}}}}{{V}_{{\mathbf{v}}}}{{R}_{{\mathbf{r}}}}{{T}_{t}},\quad {\mathbf{r}} = {{{\mathbf{g}}{{t}^{2}}} \mathord{\left/ {\vphantom {{{\mathbf{g}}{{t}^{2}}} 2}} \right. \kern-0em} 2},\quad {\mathbf{v}} = - {\mathbf{g}}t$
(2.12)
${{G}_{{\mathbf{g}}}}{{R}_{{\mathbf{r}}}} = {{R}_{{\mathbf{r}}}}{{G}_{{\mathbf{g}}}}$
(2.13)
${{R}_{{\mathbf{r}}}}{{G}_{{\mathbf{g}}}} = {{G}_{{\mathbf{g}}}}{{R}_{{\mathbf{r}}}}$
(2.14)
${{G}_{{\mathbf{g}}}}{{V}_{{\mathbf{v}}}} = {{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}}$
(2.15)
${{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}} = {{G}_{{\mathbf{g}}}}{{V}_{{\mathbf{v}}}}$
(2.16)
${{G}_{{{{{\mathbf{g}}}_{2}}}}}{{G}_{{{{{\mathbf{g}}}_{1}}}}} = {{G}_{{\mathbf{g}}}},\quad {\mathbf{g}} = {{{\mathbf{g}}}_{1}} + {{{\mathbf{g}}}_{2}}$,
(2.17)
${{\Gamma }_{{{\gamma }}}} \circ {{T}_{t}} = {{T}_{{t{\kern 1pt} '}}} \circ {{\Gamma }_{{{\gamma }}}},\quad t{\kern 1pt} ' = {{\gamma }}t$
(2.18)
${{T}_{t}} \circ {{\Gamma }_{{{\gamma }}}} = {{\Gamma }_{{{\gamma }}}} \circ {{T}_{{t'}}},\quad t' = {{{{\gamma }}}^{{ - 1}}}t$
(2.19)
${{\Gamma }_{{{\gamma }}}} \circ {{R}_{{\mathbf{r}}}} = {{R}_{{{\mathbf{r}}'}}} \circ {{\Gamma }_{{{\gamma }}}},\quad {\mathbf{r}}{\kern 1pt} ' = {{\gamma }}{\mathbf{r}}$
(2.20)
${{R}_{{\mathbf{r}}}} \circ {{\Gamma }_{{{\gamma }}}} = {{\Gamma }_{{{\gamma }}}} \circ {{R}_{{{\mathbf{r}}'}}},\quad {\mathbf{r}}{\kern 1pt} ' = {{{{\gamma }}}^{{ - 1}}}{\mathbf{r}}$
(2.21)
${{\Gamma }_{{{\gamma }}}}{{V}_{{\mathbf{v}}}} = {{V}_{{\mathbf{v}}}}{{\Gamma }_{{{\gamma }}}}$
(2.22)
${{V}_{{\mathbf{v}}}}{{\Gamma }_{{{\gamma }}}} = {{\Gamma }_{{{\gamma }}}}{{V}_{{\mathbf{v}}}}$
(2.23)
${{\Gamma }_{{{\gamma }}}} \circ {{G}_{{\mathbf{g}}}} = {{G}_{{{\mathbf{g}}{\kern 1pt} '}}} \circ {{\Gamma }_{{{\gamma }}}},\quad {\mathbf{g}}_{{}}^{'} = {{{{\gamma }}}^{{ - 1}}}{\mathbf{g}}$
(2.24)
${{G}_{{\mathbf{g}}}} \circ {{\Gamma }_{{{\gamma }}}} = {{\Gamma }_{{{\gamma }}}} \circ {{G}_{{{\mathbf{g}}'}}},\quad {\mathbf{g}}{\kern 1pt} ' = {{\gamma }}{\mathbf{g}}$
(2.25)
${{\Gamma }_{{{{{{\gamma }}}_{{\text{2}}}}}}}{{\Gamma }_{{{{{{\gamma }}}_{{\text{1}}}}}}} = {{\Gamma }_{{{\gamma }}}},\quad {{\gamma }} = {{{{\gamma }}}_{2}}{{{{\gamma }}}_{1}}$
(2.26)
${{W}_{w}} \circ {{T}_{t}} = {{T}_{{t'}}} \circ {{\Gamma }_{{{\gamma }}}} \circ {{W}_{{w'}}},\quad t_{{}}^{'} = \frac{t}{{{\text{1}} + {{wt} \mathord{\left/ {\vphantom {{wt} {\text{2}}}} \right. \kern-0em} {\text{2}}}}},\quad {{\gamma }} = \frac{1}{{{{{\left( {{\text{1}} + {{wt} \mathord{\left/ {\vphantom {{wt} {\text{2}}}} \right. \kern-0em} {\text{2}}}} \right)}}^{2}}}},\quad w_{{}}^{'} = \frac{w}{{{\text{1}} + {{wt} \mathord{\left/ {\vphantom {{wt} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}$
(2.27)
${{T}_{t}} \circ {{W}_{w}} = {{W}_{{w'}}} \circ {{\Gamma }_{{{\gamma }}}} \circ {{T}_{{t'}}},\quad t{\kern 1pt} ' = \frac{t}{{{\text{1}} + {{wt} \mathord{\left/ {\vphantom {{wt} {\text{2}}}} \right. \kern-0em} {\text{2}}}}},\quad {{\gamma }} = {{\left( {{\text{1}} + {{wt} \mathord{\left/ {\vphantom {{wt} {\text{2}}}} \right. \kern-0em} {\text{2}}}} \right)}^{2}},\quad w{\text{'}} = \frac{w}{{{\text{1}} + {{wt} \mathord{\left/ {\vphantom {{wt} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}$
(2.28)
${{W}_{w}} \circ {{R}_{{\mathbf{r}}}} = {{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}}{{W}_{w}},\quad {\mathbf{v}} = - {\mathbf{r}}w{\text{,}}\quad {\mathbf{g}} = {\mathbf{r}}{{{{w}^{2}}} \mathord{\left/ {\vphantom {{{{w}^{2}}} 2}} \right. \kern-0em} 2}$
(2.29)
${{R}_{{\mathbf{r}}}} \circ {{W}_{w}} = {{W}_{w}}{{G}_{{\mathbf{g}}}}{{V}_{{\mathbf{v}}}}{{R}_{{\mathbf{r}}}},\quad {\mathbf{v}} = {\mathbf{r}}w{\text{,}}\quad {\mathbf{g}} = {\mathbf{r}}{{w}^{2}}{\text{/2}}$
(2.30)
${{W}_{w}} \circ {{V}_{{\mathbf{v}}}} = {{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}}{{W}_{w}},\quad {\mathbf{g}} = - {\mathbf{v}}w$
(2.31)
${{V}_{{\mathbf{v}}}} \circ {{W}_{w}} = {{W}_{w}}{{G}_{{\mathbf{g}}}}{{V}_{{\mathbf{v}}}},\quad {\mathbf{g}} = {\mathbf{v}}w$
(2.32)
${{W}_{{\text{w}}}}{{G}_{{\mathbf{g}}}} = {{G}_{{\mathbf{g}}}}{{W}_{{\text{w}}}}$
(2.33)
${{G}_{{\mathbf{g}}}}{{W}_{{\text{w}}}} = {{W}_{{\text{w}}}}{{G}_{{\mathbf{g}}}}$
(2.34)
${{W}_{w}} \circ {{\Gamma }_{{{\gamma }}}} = {{\Gamma }_{{{\gamma }}}} \circ {{W}_{{w'}}},\quad w{\kern 1pt} ' = {{\gamma }}w$
(2.35)
${{\Gamma }_{{{\gamma }}}} \circ {{W}_{w}} = {{W}_{{w'}}} \circ {{\Gamma }_{{{\gamma }}}},\quad w{\kern 1pt} ' = {{{{\gamma }}}^{{ - 1}}}w$
(2.36)
${{W}_{{{{w}_{{\text{2}}}}}}}{{W}_{{{{w}_{{\text{1}}}}}}} = {{W}_{w}},\quad w = {{w}_{1}} + {{w}_{2}}$
(2.37)
${{\Theta }_{{\text{Q}}}}{{T}_{t}} = {{T}_{t}}{{\Theta }_{{\text{Q}}}}$
(2.38)
${{T}_{t}}{{\Theta }_{{\text{Q}}}} = {{\Theta }_{{\text{Q}}}}{{T}_{t}}$
(2.39)
${{\Theta }_{Q}} \circ {{R}_{{\mathbf{r}}}} = {{R}_{{{\mathbf{r}}'}}} \circ {{\Theta }_{{\text{Q}}}},\quad {\mathbf{r}}' = Q \circ {\mathbf{r}} \circ {{Q}^{{ - 1}}}$
(2.40)
${{R}_{{\mathbf{r}}}} \circ {{\Theta }_{Q}} = {{\Theta }_{Q}} \circ {{R}_{{{\mathbf{r'}}}}},\quad {\mathbf{r}}{\kern 1pt} ' = {{Q}^{{ - 1}}} \circ {\mathbf{r}} \circ Q$
(2.41)
${{\Theta }_{Q}} \circ {{V}_{{\mathbf{v}}}} = {{V}_{{{\mathbf{v}}'}}} \circ {{\Theta }_{Q}},\quad {\mathbf{v}}' = Q \circ {\mathbf{v}} \circ {{Q}^{{ - 1}}}$
(2.42)
${{V}_{{\mathbf{v}}}} \circ {{\Theta }_{Q}} = {{\Theta }_{Q}} \circ {{V}_{{{\mathbf{v}}'}}},\quad {\mathbf{v}}{\kern 1pt} ' = {{Q}^{{ - 1}}} \circ {\mathbf{v}} \circ Q$
(2.43)
${{\Theta }_{Q}} \circ {{G}_{{\mathbf{g}}}} = {{G}_{{{\mathbf{g}}'}}} \circ {{\Theta }_{Q}},\quad {\mathbf{g}}{\kern 1pt} ' = Q \circ {\mathbf{g}} \circ {{Q}^{{ - 1}}}$
(2.44)
${{G}_{{\mathbf{g}}}} \circ {{\Theta }_{Q}} = {{\Theta }_{Q}} \circ {{G}_{{{\mathbf{g}}'}}},\quad {\mathbf{g}}_{{}}^{'} = {{Q}^{{ - 1}}} \circ {\mathbf{g}} \circ Q$
(2.45)
${{\Theta }_{{\text{Q}}}}{{\Gamma }_{{{\gamma }}}} = {{\Gamma }_{{{\gamma }}}}{{\Theta }_{{\text{Q}}}}$
(2.46)
${{\Gamma }_{{{\gamma }}}}{{\Theta }_{{\text{Q}}}} = {{\Theta }_{{\text{Q}}}}{{\Gamma }_{{{\gamma }}}}$
(2.47)
${{\Theta }_{{\text{Q}}}}{{W}_{{\text{w}}}} = {{W}_{{\text{w}}}}{{\Theta }_{{\text{Q}}}}$
(2.48)
${{W}_{{\text{w}}}}{{\Theta }_{{\text{Q}}}} = {{\Theta }_{{\text{Q}}}}{{W}_{{\text{w}}}}$
(2.49)
${{\Theta }_{{{{Q}_{{\text{2}}}}}}} \circ {{\Theta }_{{{{Q}_{{\text{1}}}}}}} = {{\Theta }_{Q}},\quad Q = {{Q}_{2}} \circ {{Q}_{1}}$
Таблица 2.

Принятая система нумерации определяющих соотношений

  $T$ $R$ $V$ $G$ $\Gamma $ $W$ $\Theta $
$T$ (2.1) (2.2) (2.5) (2.10) (2.17) (2.26) (2.37)
$R$ (2.3) (2.4) (2.7) (2.12) (2.19) (2.28) (2.39)
$V$ (2.6) (2.8) (2.9) (2.14) (2.21) (2.30) (2.41)
$G$ (2.11) (2.13) (2.15) (2.16) (2.23) (2.32) (2.43)
$\Gamma $ (2.18) (2.20) (2.22) (2.24) (2.25) (2.34) (2.45)
$W$ (2.27) (2.29) (2.31) (2.33) (2.35) (2.36) (2.47)
$\Theta $ (2.38) (2.40) (2.42) (2.44) (2.46) (2.48) (2.49)

Для наглядности символ ($ \circ $) между сомножителями (преобразованиями или числами – параметрами преобразований) опускался только в случае, если операция перестановки этих сомножителей коммутативна.

Если хотя бы одно из исходных преобразований бесконечно малое (а только такие случаи встречаются при выводе уравнений инерциальной навигации и задачи n тел), то особенности, имеющиеся в соотношениях (2.26) и (2.27), становятся несущественными.

3. Вывод уравнений инерциальной навигации. Будем использовать следующую последовательность элементарных преобразований в разложении преобразования общего вида из расширенной группы Галилея–Ньютона на элементарные:

$\Lambda = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{\Gamma }_{{{\gamma }}}}{{\Theta }_{{\text{Q}}}} \circ {{G}_{{\mathbf{g}}}}{{W}_{{\text{w}}}}$
(она совпадает со стандартной последовательностью элементарных преобразований, принятой в [6, 7] для преобразования общего вида из конформной группы).

Процедура теоретико-группового вывода уравнений инерциальной навигации сводится к нахождению стандартного разложения на элементарные преобразования композиции конечного и бесконечно малого преобразований (подробности см., например, в [6, 7]). С учетом выписанных в предыдущем разделе определяющих соотношений (для наглядности подчеркиваниями показаны места, в которых они применяются на каждом шаге выкладок) получаем:

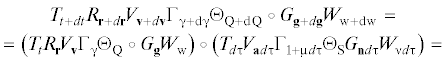$ = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{\Gamma }_{{{\gamma }}}}{{\Theta }_{{\text{Q}}}} \circ {{G}_{{\mathbf{g}}}}\underleftrightarrow {{{W}_{{\text{w}}}} \circ {{T}_{{d{{\tau }}}}}}{{V}_{{{\mathbf{a}}d{{\tau }}}}}{{\Gamma }_{{{\text{1}} + {{\mu }}d{{\tau }}}}}{{\Theta }_{{\text{S}}}}{{G}_{{{\mathbf{n}}d{{\tau }}}}}{{W}_{{{{\nu }}d{{\tau }}}}} = $
$ = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{\Gamma }_{{{\gamma }}}}{{\Theta }_{{\text{Q}}}} \circ \underleftrightarrow {{{G}_{{\mathbf{g}}}} \circ {{T}_{{d{{\tau }}}}}}{{\Gamma }_{{{\text{1}} - {\text{w}}d{{\tau }}}}}\underleftrightarrow {{{W}_{{{\text{w}} - {{{{{\text{w}}}^{{\text{2}}}}d{{\tau }}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}d{{\tau }}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}} \circ {{V}_{{{\mathbf{a}}d{{\tau }}}}}}{{\Gamma }_{{{\text{1}} + {{\mu }}d{{\tau }}}}}{{\Theta }_{{\text{S}}}}{{G}_{{{\mathbf{n}}d{{\tau }}}}}{{W}_{{{{\nu }}d{{\tau }}}}} = $
$ = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{\Gamma }_{{{\gamma }}}}\underleftrightarrow {{{\Theta }_{{\text{Q}}}}{{T}_{{d{{\tau }}}}}}{{V}_{{{\mathbf{g}}d{{\tau }}}}}{{G}_{{\mathbf{g}}}}\underleftrightarrow {{{\Gamma }_{{{\text{1}} - {\text{w}}d{{\tau }}}}}{{V}_{{{\mathbf{a}}d{{\tau }}}}}}{{G}_{{ - {\mathbf{a}}{\text{w}}d{{\tau }}}}}\underleftrightarrow {{{W}_{{{\text{w}} - {{{{{\text{w}}}^{{\text{2}}}}d{{\tau }}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}d{{\tau }}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}} \circ {{\Gamma }_{{{\text{1}} + {{\mu }}d{{\tau }}}}}}{{\Theta }_{{\text{S}}}}{{G}_{{{\mathbf{n}}d{{\tau }}}}}{{W}_{{{{\nu }}d{{\tau }}}}} = $
$ = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}\underleftrightarrow {{{\Gamma }_{{{\gamma }}}} \circ {{T}_{{d{{\tau }}}}}}\underleftrightarrow {{{\Theta }_{{\text{Q}}}} \circ {{V}_{{{\mathbf{g}}d{{\tau }}}}}}\underleftrightarrow {{{G}_{{\mathbf{g}}}}{{V}_{{{\mathbf{a}}d{{\tau }}}}}}{{\Gamma }_{{{\text{1}} - {\text{w}}d{{\tau }}}}}\underleftrightarrow {{{G}_{{ - {\mathbf{a}}{\text{w}}d{{\tau }}}}}{{\Gamma }_{{{\text{1}} + {{\mu }}d{{\tau }}}}}}\underleftrightarrow {{{W}_{{{\text{w}} + ({{\mu w}} - {{{{{\text{w}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}} {\text{2}}}} \right. \kern-0em} {\text{2}}})d{{\tau }}}}}{{\Theta }_{{\text{S}}}}}{{G}_{{{\mathbf{n}}d{{\tau }}}}}{{W}_{{{{\nu }}d{{\tau }}}}} = $
$ = {{T}_{t}}{{R}_{{\mathbf{r}}}}\underleftrightarrow {{{V}_{{\mathbf{v}}}} \circ {{T}_{{{{\gamma }}d{{\tau }}}}}} \circ \underleftrightarrow {{{\Gamma }_{{{\gamma }}}}{{V}_{{{\text{Q}} \circ {\mathbf{g}} \circ {{{\text{Q}}}^{{{\text{ - 1}}}}}d{{\tau }}}}}}\underleftrightarrow {{{\Theta }_{{\text{Q}}}} \circ {{V}_{{{\mathbf{a}}d{{\tau }}}}}}{{G}_{{\mathbf{g}}}} \circ \underleftrightarrow {{{\Gamma }_{{{\text{1}} - {\text{w}}d{{\tau }}}}}{{\Gamma }_{{{\text{1}} + {{\mu }}d{{\tau }}}}}}\underleftrightarrow {{{G}_{{ - {\mathbf{a}}{\text{w}}d{{\tau }}}}}{{\Theta }_{{\text{S}}}}}\underleftrightarrow {{{W}_{{{\text{w}} + ({{\mu w}} - {{{{{\text{w}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}} {\text{2}}}} \right. \kern-0em} {\text{2}}})d{{\tau }}}}}{{G}_{{{\mathbf{n}}d{{\tau }}}}}}{{W}_{{{{\nu }}d{{\tau }}}}} = $
$ = \,{{T}_{t}}\underleftrightarrow {{{R}_{{\mathbf{r}}}}{{T}_{{{{\gamma }}d{{\tau }}}}}}{{R}_{{{{\gamma }}{\mathbf{v}}d{{\tau }}}}}\underleftrightarrow {{{V}_{{\mathbf{v}}}}{{V}_{{{\text{Q}} \circ {\mathbf{g}} \circ {{{\text{Q}}}^{{ - 1}}}d{{\tau }}}}}}\underleftrightarrow {{{\Gamma }_{{{\gamma }}}}{{V}_{{{\text{Q}} \circ {\mathbf{a}} \circ {{{\text{Q}}}^{{ - 1}}}d{{\tau }}}}}}\, \circ {{\Theta }_{{\text{Q}}}}\, \circ \,\underleftrightarrow {{{G}_{{\mathbf{g}}}}\, \circ \,{{\Gamma }_{{{\text{1}} + \left( {{{\mu }} - {\text{w}}} \right)d{{\tau }}}}}}{{\Theta }_{{\text{S}}}}\underleftrightarrow {{{G}_{{ - {\mathbf{a}}{\text{w}}d{{\tau }}}}}{{G}_{{{\mathbf{n}}d{{\tau }}}}}}\underleftrightarrow {{{W}_{{{\text{w}} + ({{\mu w}} - {{{{{\text{w}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}} {\text{2}}}} \right. \kern-0em} {\text{2}}})d{{\tau }}}}}{{W}_{{{{\nu }}d{{\tau }}}}}}\, = $
$ = \underleftrightarrow {{{T}_{t}}{{T}_{{{{\gamma }}d{{\tau }}}}}}\underleftrightarrow {{{R}_{{\mathbf{r}}}}{{R}_{{{{\gamma }}{\mathbf{v}}d{{\tau }}}}}}\underleftrightarrow {{{V}_{{{\mathbf{v}} + {\text{Q}} \circ {\mathbf{g}} \circ {{{\text{Q}}}^{{ - 1}}}d{{\tau }}}}}{{V}_{{{\text{Q}} \circ {\mathbf{a}} \circ {{{\text{Q}}}^{{ - 1}}}d{{\tau }}}}}}{{\Gamma }_{{{\gamma }}}}\underleftrightarrow {{{\Theta }_{{\text{Q}}}}{{\Gamma }_{{{\text{1}} + ({{\mu }} - {\text{w}})d{{\tau }}}}}}\, \circ \,\underleftrightarrow {{{G}_{{{\mathbf{g}} + {\mathbf{g}}({{\mu }} - {\text{w}})d{{\tau }}}}}\, \circ \,{{\Theta }_{{\text{S}}}}}{{G}_{{({\mathbf{n}} - {\mathbf{a}}{\text{w}})d{{\tau }}}}}{{W}_{{{\text{w}} + ({{\nu }} + {{\mu w}} - {{{\text{w}}}^{{\text{2}}}}{\text{/2}})d{{\tau }}}}}\, = $
$ = \,{{T}_{{t + {{\gamma }}d{{\tau }}}}}{{R}_{{{\mathbf{r}} + {{\gamma }}{\mathbf{v}}d{{\tau }}}}}{{V}_{{{\mathbf{v}} + {\text{Q}} \circ \left( {{\mathbf{a}} + {\mathbf{g}}} \right) \circ {{{\text{Q}}}^{{ - 1}}}d{{\tau }}}}}\underleftrightarrow {{{\Gamma }_{{{\gamma }}}}{{\Gamma }_{{{\text{1}} + \left( {{{\mu }} - {\text{w}}} \right)d{{\tau }}}}}}\underleftrightarrow {{{\Theta }_{{\text{Q}}}}\, \circ \,{{\Theta }_{{\text{S}}}}}\, \circ \,\underleftrightarrow {{{G}_{{{{{\text{S}}}^{{ - 1}}} \circ {\mathbf{g}} \circ {\text{S}} + {\mathbf{g}}\left( {{{\mu }} - {\text{w}}} \right)d{{\tau }}}}}{{G}_{{\left( {{\mathbf{n}} - {\mathbf{a}}{\text{w}}} \right)d{{\tau }}}}}}{{W}_{{{\text{w}} + ({{\nu }} + {{\mu w}} - {{{{{\text{w}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}} {\text{2}}}} \right. \kern-0em} {\text{2}}})d{{\tau }}}}} = $
$ = {{T}_{{t + {{\gamma }}d{{\tau }}}}}{{R}_{{{\mathbf{r}} + {{\gamma }}{\mathbf{v}}d{{\tau }}}}}{{V}_{{{\mathbf{v}} + {\text{Q}} \circ \left( {{\mathbf{a}} + {\mathbf{g}}} \right) \circ {{{\text{Q}}}^{{ - 1}}}d{{\tau }}}}}{{\Gamma }_{{{{\gamma }} + {{\gamma }}\left( {{{\mu }} - {\text{w}}} \right)d{{\tau }}}}}{{\Theta }_{{{\text{Q}} \circ {\text{S}}}}} \circ {{G}_{{{{{\text{S}}}^{{ - 1}}} \circ {\mathbf{g}} \circ {\text{S}} + {\mathbf{n}} - {\mathbf{a}}{\text{w}} + {\mathbf{g}}\left( {{{\mu }} - {\text{w}}} \right)d{{\tau }}}}}{{W}_{{{\text{w}} + ({{\nu }} + {{\mu w}} - {{{{{\text{w}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{w}}}^{{\text{2}}}}} {\text{2}}}} \right. \kern-0em} {\text{2}}})d{{\tau }}}}}$

Выше для сокращения записи было принято обозначение ${\text{S}} = {{e}^{{{{i{\mathbf{\omega }}d{{\tau }}} \mathord{\left/ {\vphantom {{i{\mathbf{\omega }}d{{\tau }}} 2}} \right. \kern-0em} 2}}}} = 1 + {{i{\mathbf{\omega }}d{{\tau }}} \mathord{\left/ {\vphantom {{i{\mathbf{\omega }}d{{\tau }}} 2}} \right. \kern-0em} 2}$, поэтому (везде сохраняются члены только первого порядка малости по $d{{\tau }}$):

$Q\; \circ S = Q\; + {{Q\; \circ \left( {i{\mathbf{\omega }}} \right)d{{\tau }}} \mathord{\left/ {\vphantom {{Q\; \circ \left( {i{\mathbf{\omega }}} \right)d{{\tau }}} 2}} \right. \kern-0em} 2},\quad {{{\text{S}}}^{{ - 1}}} \circ {\mathbf{g}} \circ {\text{S}} = {\mathbf{g}} + [{\mathbf{g}} \times {\mathbf{\omega }}]d{{\tau }}$,

В результате получается следующая система нерелятивистских уравнений инерциальной навигации (для расширенной группы Галилея–Ньютона):

$\frac{{dt}}{{d{{\tau }}}} = {{\gamma ,}}\quad \frac{{d{\mathbf{r}}}}{{d{{\tau }}}} = {{\gamma }}{\mathbf{v}},\quad \frac{{d{\mathbf{v}}}}{{d{{\tau }}}} = {\text{Q}} \circ \left( {{\mathbf{a}} + {\mathbf{g}}} \right) \circ {{{\text{Q}}}^{{ - 1}}},\quad \frac{{d{{\gamma }}}}{{d{{\tau }}}} = {{\gamma }}\left( {{{\mu }} - {\text{w}}} \right)$
$\frac{{d{\text{Q}}}}{{d{{\tau }}}} = \frac{1}{2}{\text{Q}} \circ \left( {i{\mathbf{\omega }}} \right),\quad \frac{{d{\mathbf{g}}}}{{d{{\tau }}}} = {\mathbf{n}} + {\mathbf{g}} \times {\mathbf{\omega }} + {{\mu }}{\mathbf{g}} - {\text{w}}\left( {{\mathbf{a}} + {\mathbf{g}}} \right),\quad \frac{{d{\text{w}}}}{{d{{\tau }}}} = {{\nu }} - \frac{{{{{\text{w}}}^{{\text{2}}}}}}{{\text{2}}} + {{\mu w}}$

Ее легко сравнить с соответствующей системой релятивистских уравнений (для конформной группы); с другой стороны, из нее можно получить (просто отбрасывая “лишние” параметры) систему уравнений инерциальной навигации для группы Галилея–Ньютона (13-параметрической) [6, 7].

4. Массы тел. Используемые в работе массы тел это положительные константы (m > 0).

В работе используется естественная система единиц Планка [9]. “Планковские величины (длина, время, масса, энергия, температура и т.д.) не представляют (по крайней мере до сих пор) существенного значения для метрологии, но, как оказалось, имеют исключительную важность для теоретической физики как границы применимости современных физических теорий” [10, с. 239]. Планковская масса составляет ~10–8 кг. В небесной механике (масса Земли ~1025 кг) и в механике космического полета обычно имеют дело с массами существенно больше планковской, а в теории элементарных частиц (масса электрона ~10–30 кг) – с массами на много порядков меньше планковской, которая там считается “экспериментально недостижимой” [11, с. 191].

“Физика не будет делиться на микроскопическую и космическую, она должна стать и станет единой и нераздельной” М.П. Бронштейн [12, с. 27]. В механике космического полета масса космического аппарата пренебрежимо мала по сравнению с массами небесных тел, поэтому его иногда называют “телом бесконечно малой массы” [13, с. 42]. Эта терминология никого не вводит в заблуждение, поскольку всем известно, что массы космических аппаратов заметно больше нуля. Сложнее ситуация с массами в теории элементарных частиц. Еще из школьного курса физики всем “известно”, что по современным представлениям: “Фотон является безмассовой частицей, т.е. его масса равна нулю: m = 0” [14, с. 66]. Аналогичное утверждение (“Как известно, масса фотона равна нулю”) имеется даже в книге специалиста по теории элементарных частиц академика Л.Б. Окуня, для которого “вопрос о массе фотона послужил отправной точкой в продумывании оснований теории относительности” [15, с. 94, 112]. Результаты упомянутого продумывания выражены следующими словами: “В пользу того, что масса фотона строго равна нулю, иногда приводят следующие аргументы:

1. Из существования электромагнитного дальнодействия следует, что масса фотона очень мала по сравнению с массами других частиц, а очень малых параметров в теории не должно быть.

2. Теория (теория относительности, квантовая электродинамика) требует, чтобы масса фотона равнялась нулю.

Легко видеть, однако, что оба эти аргумента неправильны” [16, с. 131]. С другой стороны: “Масса фотона настолько мала, что ни в каких экспериментах ее обнаружить не удалось. Поэтому обычно полагают, что масса фотона равна нулю” [17, с. 657]. В литературе приводятся различные экспериментальные ограничения на массу фотона (m < < 10–62 кг [18]; m < 10–52 кг [19]).

В физике до сих пор распространены различные подходы к построению релятивистской механики или специальной теории относительности (СТО), использующей преобразования Лоренца (релятивистские бусты). Наиболее известные из них связаны с именами Пуанкаре, Эйнштейна и Минковского [20, с. 47–51]. При теоретико-групповом построении СТО на основе группы Пуанкаре скорость строго меньше предельной (в естественной системе единиц ${\text{v}} = th{{\psi }} < {\text{1}}$), поэтому частицы с нулевой массой невозможны. При построении СТО на основе постулатов Эйнштейна помимо нормальных частиц приходится рассматривать безмассовые частицы, двигающиеся с предельной скоростью (v = 1), а также обсуждать возможность существования тахионов (v > 1) [21, с. 117]. При построении релятивистской механики на основе концепции пространства–времени Минковского принимают во внимание “основную аксиому Минковского”, исключающую существование частиц с нулевой массой [22; 23, с. 171].

5. Гравитационное замедление времени. В классической задаче n тел постулируется, что тело (материальная точка) массы $m$ создает на расстоянии $r = \sqrt {{{{\mathbf{r}}}^{2}}} $ гравитационный потенциал

$\varphi = - \frac{m}{r}$
(с которым связан вектор гравитационного ускорения ${\mathbf{g}} = - grad\varphi = - {{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial {\mathbf{r}}}}} \right. \kern-0em} {\partial {\mathbf{r}}}}$) [24, с. 188], но не учитывается известный эффект замедления времени в гравитационном поле: “Всякий раз из двух часов, находящихся на разных расстояниях от тяготеющего тела, быстрее идут те, которые дальше от этого тела” [25, с. 120]. Расширенная группа Галилея–Ньютона, включающая масштабное преобразование, позволяет учесть этот эффект, если связать гравитационный потенциал с масштабным множителем. Гравитационный эффект замедления времени в поле тяготения (или эффект гравитационного смещения частоты) [26] следует отличать от релятивистского эффекта замедления времени в движущихся телах (эффекта СТО, который, как и эффект замедления времени в гравитационном поле, может быть измерен с использованием эффекта Мессбауэра) [27].

Пусть $d{{\tau }}$ – приращение собственного времени тела, находящегося в гравитационном поле, а dt – приращение координатного времени для наблюдателя, находящегося вне гравитационного поля. Тогда эффект замедления времени в поле тяготения означает, что $d{{\tau }} < dt$, то есть масштабный множитель должен быть, согласно первому из уравнений инерциальной навигации, больше единицы ${{\gamma }} = {{dt} \mathord{\left/ {\vphantom {{dt} {d{{\tau }}}}} \right. \kern-0em} {d{{\tau }}}} > 1$. Поскольку, с другой стороны, $\varphi < 0$, то естественно принять ${{\gamma }} = 1 - \varphi $.

Воспользуемся теперь общепринятым положением квантовой (волновой) механики о том, что с каждой частицей связана волна [14, с. 79, 179], точнее, тем, что “частица характеризуется внутренними колебаниями, в силу чего можно рассматривать ее как некие часы бесконечно малых размеров” [28, с. 30]. Частота волны де Бройля частицы пропорциональна ее энергии (с учетом энергии покоя). В естественной системе единиц энергия покоящейся частицы равна ее массе m. С другой стороны, частота волны де Бройля (собственная частота колебаний частицы) обратно пропорциональна собственному периоду колебаний частицы ${\text{T}}$, который, соответственно, обратно пропорционален массе частицы T ~ 1/m.

Рассмотрим две покоящиеся частицы с массами ${{m}_{1}}$ и ${{m}_{2}}$, причем ${{m}_{1}} < {{m}_{2}}$. Тогда для их собственных периодов колебаний ${{{\text{T}}}_{{\text{1}}}}$ и ${{{\text{T}}}_{{\text{2}}}}$ выполняется ${{{\text{T}}}_{{\text{1}}}} > {{{\text{T}}}_{{\text{2}}}}$. Пусть прошел промежуток времени $\Delta t$. За это время первая частица совершит ${{n}_{1}} = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {{{{\text{T}}}_{{\text{1}}}}}}} \right. \kern-0em} {{{{\text{T}}}_{{\text{1}}}}}}$ колебаний, а вторая ${{n}_{2}} = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {{{{\text{T}}}_{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{T}}}_{{\text{2}}}}}}$ колебаний, поэтому ${{n}_{1}} < {{n}_{2}}$. Естественно считать ${{n}_{1}}$ временем $\Delta {{{{\tau }}}_{{\text{1}}}}$, измеренным первой частицей (в ее масштабе), а ${{n}_{2}}$ временем $\Delta {{{{\tau }}}_{{\text{2}}}}$, измеренным второй частицей (в ее масштабе), поэтому $\Delta {{{{\tau }}}_{{\text{1}}}} < \Delta {{{{\tau }}}_{{\text{2}}}}$. Переходя к масштабным множителям ${{{{\gamma }}}_{{\text{1}}}} = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {\Delta {{{{\tau }}}_{{\text{1}}}}}}} \right. \kern-0em} {\Delta {{{{\tau }}}_{{\text{1}}}}}}$ и ${{{{\gamma }}}_{{\text{2}}}} = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {\Delta {{{{\tau }}}_{{\text{2}}}}}}} \right. \kern-0em} {\Delta {{{{\tau }}}_{{\text{2}}}}}}$, получим ${{{{\gamma }}}_{{\text{1}}}} > {{{{\gamma }}}_{{\text{2}}}}$. То есть масштабный множитель больше у легкой частицы и меньше у тяжелой. В общем случае получаем, что масштабный множитель частицы обратно пропорционален ее массе  γ ~ 1/m.

Примем следующее выражение для гравитационного потенциала, создаваемого телом массы $m$ на расстоянии $r$:

$\varphi = - \frac{m}{{\sqrt {{{m}^{4}} + {{r}^{2}}} }}$

В пределе малых масс ($m \to 0$) или больших расстояний ($r \to \infty $) этот гравитационный потенциал стремится к классическому ($\varphi \to - {m \mathord{\left/ {\vphantom {m r}} \right. \kern-0em} r}$). При нулевом расстоянии (r = 0) в принятом выражении11 отсутствует характерная для классического (ньютоновского) потенциала сингулярность и при малых массах обеспечивается обратная пропорциональность масштабного множителя массе частицы (${{\gamma }} = 1 - \varphi \to {1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}$).

Для построения гравитационного потенциала в задаче n тел используется принцип суперпозиции: “потенциалы полей от разных частиц складываются” [24, с. 188]. Гравитационный потенциал макроскопического тела создается гравитационными потенциалами составляющих его элементарных частиц. Условие малости гравитационного потенциала (${\text{|}}\varphi {\text{|}} \ll 1$), ограничивающее область применимости теории тяготения Ньютона, не накладывается.

6. Формулировка задачи n тел. В [29] задача n тел была сформулирована на основе 10-параметрической группы, полученной из группы Галилея–Ньютона исключением пространственных поворотов. Позднее эта 10-параметрическая группа была названа [7, с. 150] группой Ньютона (чтобы подчеркнуть ее отличие от другой подгруппы группы Галилея–Ньютона – 10-параметрической группы Галилея). Преобразование общего вида из группы Ньютона имеет вид [7, 29]:

$\Lambda = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}}$

Если исходить из 15-параметрической расширенной группы Галилея–Ньютона, то после исключения пространственных поворотов получится расширенная 12-параметрическая группа Ньютона с определяющими соотношениями (2.1)÷(2.36). Преобразование общего вида из расширенной группы Ньютона будем записывать в виде:

$\Lambda = {{T}_{t}}{{R}_{{\mathbf{r}}}}{{V}_{{\mathbf{v}}}}{{G}_{{\mathbf{g}}}}{{W}_{{\text{w}}}} \circ {{\Gamma }_{{{\gamma }}}}$

Исключение пространственных поворотов и перемещение масштабного преобразования на последнее место позволяет существенно упростить правые части дифференциальных уравнений инерциальной навигации, которые теперь становятся такими:

$\frac{{dt}}{{d{{\tau }}}} = {{\gamma ,}}\quad \frac{{d{\mathbf{r}}}}{{d{{\tau }}}} = {{\gamma }}{\mathbf{v}},\quad \frac{{d{\mathbf{v}}}}{{d{{\tau }}}} = {\mathbf{a}} + {{\gamma }}{\mathbf{g}}$
$\frac{{d{\mathbf{g}}}}{{d{{\tau }}}} = {{{{\gamma }}}^{{ - 1}}}{\mathbf{n}} - {\mathbf{a}}{\text{w,}}\quad \frac{{d{\text{w}}}}{{d{{\tau }}}} = {{{{\gamma }}}^{{ - 1}}}{{\nu }} + \frac{{\text{1}}}{{\text{2}}}{{\gamma }}{{{\text{w}}}^{{\text{2}}}},\quad \frac{{d{{\gamma }}}}{{d{{\tau }}}} = {{\gamma }}\left( {{{\mu }} - {{\gamma w}}} \right)$

Выписанную систему уравнений можно получить обычной процедурой теоретико-группового вывода уравнений инерциальной навигации с принятым порядком расположения элементарных преобразований в преобразовании общего вида для расширенной группы Ньютона. С другой стороны, можно воспользоваться уже выведенными во втором разделе статьи уравнениями, отбросив в них члены, связанные с пространственными поворотами (положив ${\text{Q}} = 1$ и ${\mathbf{\omega }} = 0$), и сделав замену параметров, соответствующую перестановке ${{\Gamma }_{{{\gamma }}}} \circ {{G}_{{\mathbf{g}}}}{{W}_{{\text{w}}}} = {{G}_{{{\mathbf{g}}'}}}{{W}_{{{\text{w}}'}}} \circ {{\Gamma }_{{{\gamma }}}}$.

Переходя к задаче n тел, будем считать, что положение i-го тела в момент его собственного времени ${{{{\tau }}}_{i}}$ определяется преобразованием, связывающим базовую систему отсчета $I$ с мгновенно сопутствующей телу системой отсчета ${{E}_{i}}({{{{\tau }}}_{i}})$:

${{\Lambda }_{{I{{E}_{i}}({{{{\tau }}}_{i}})}}} = {{T}_{{{{t}_{i}}({{{{\tau }}}_{i}})}}}{{R}_{{{{{\mathbf{r}}}_{i}}({{{{\tau }}}_{i}})}}}{{V}_{{{{{\mathbf{v}}}_{i}}({{{{\tau }}}_{i}})}}}{{G}_{{{{{\mathbf{g}}}_{i}}({{{{\tau }}}_{i}})}}}{{W}_{{{{{\text{w}}}_{i}}({{{{\tau }}}_{i}})}}} \circ {{\Gamma }_{{{{{{\gamma }}}_{i}}({{{{\tau }}}_{i}})}}}$

Исключим теперь негравитационные ускорения тел (ai = 0) и негравитационные изменения масштабов (${{{{\mu }}}_{i}} = 0$). Тогда система уравнений движения i-го тела еще заметно упростится:

$\frac{{d{{t}_{i}}}}{{d{{{{\tau }}}_{i}}}} = {{{{\gamma }}}_{i}},\quad \frac{{d{{{\mathbf{r}}}_{i}}}}{{d{{{{\tau }}}_{i}}}} = {{{{\gamma }}}_{i}}{{{\mathbf{v}}}_{i}},\quad \frac{{d{{{\mathbf{v}}}_{i}}}}{{d{{{{\tau }}}_{i}}}} = {{{{\gamma }}}_{i}}{{{\mathbf{g}}}_{i}}$
$\frac{{d{{{\mathbf{g}}}_{i}}}}{{d{{{{\tau }}}_{i}}}} = {{\gamma }}_{i}^{{{\text{ - 1}}}}{{{\mathbf{n}}}_{i}},\quad \frac{{d{{{\text{w}}}_{i}}}}{{d{{{{\tau }}}_{i}}}} = {{\gamma }}_{i}^{{ - 1}}{{{{\nu }}}_{i}} + \frac{{\text{1}}}{{\text{2}}}{{{{\gamma }}}_{i}}{\text{w}}_{i}^{2},\quad \frac{{d{{{{\gamma }}}_{i}}}}{{d{{{{\tau }}}_{i}}}} = - {{\gamma }}_{i}^{{\text{2}}}{{{\text{w}}}_{i}}$

Перейдем от множества собственных времен тел ${{{{\tau }}}_{i}}$ к единому (системному) времени $t$ как независимому параметру. Положение i-го тела в момент $t$ запишем в виде:

${{\Lambda }_{{I{{E}_{i}}(t)}}} = {{T}_{t}}{{R}_{{{{{\mathbf{r}}}_{i}}(t)}}}{{V}_{{{{{\mathbf{v}}}_{i}}(t)}}}{{G}_{{{{{\mathbf{g}}}_{i}}(t)}}}{{W}_{{{{{\text{w}}}_{i}}(t)}}} \circ {{\Gamma }_{{{{{{\gamma }}}_{i}}(t)}}}$
(по определению ${{t}_{i}} = t$, поэтому ${{d{{t}_{i}}} \mathord{\left/ {\vphantom {{d{{t}_{i}}} {d{{{{\tau }}}_{i}}}}} \right. \kern-0em} {d{{{{\tau }}}_{i}}}} = {{{{\gamma }}}_{i}} = {{dt} \mathord{\left/ {\vphantom {{dt} {d{{{{\tau }}}_{i}}}}} \right. \kern-0em} {d{{{{\tau }}}_{i}}}}$; тривиальное уравнение ${{d{{t}_{i}}} \mathord{\left/ {\vphantom {{d{{t}_{i}}} {dt}}} \right. \kern-0em} {dt}} = 1$ в дальнейшем выписывать не будем). Заменим в дифференциальных уравнениях движения i-го тела дифференцирование по ${{{{\tau }}}_{i}}$ на дифференцирование по $t$:

$\frac{{d{{{\mathbf{r}}}_{i}}}}{{dt}} = {{{\mathbf{v}}}_{i}},\quad \frac{{d{{{\mathbf{v}}}_{i}}}}{{dt}} = {{{\mathbf{g}}}_{i}},\quad \frac{{d{{{\mathbf{g}}}_{i}}}}{{dt}} = {{\gamma }}_{i}^{{ - 2}}{{{\mathbf{n}}}_{i}},\quad \frac{{d{{{\text{w}}}_{i}}}}{{dt}} = {{\gamma }}_{i}^{{ - 2}}{{{{\nu }}}_{i}} + \frac{{{\text{w}}_{i}^{2}}}{{\text{2}}},\quad \frac{{d{{{{\gamma }}}_{i}}}}{{dt}} = - {{{{\gamma }}}_{i}}{{{\text{w}}}_{i}}$

Из последних трех уравнений получаем:

${{{\text{w}}}_{i}} = - {{\gamma }}_{i}^{{ - 1}}\frac{{d{{{{\gamma }}}_{i}}}}{{dt}},\quad {{{\mathbf{n}}}_{i}} = {{\gamma }}_{i}^{{\text{2}}}\frac{{d{{{\mathbf{g}}}_{i}}}}{{dt}},\quad {{{{\nu }}}_{i}} = {{\gamma }}_{i}^{{\text{2}}}\left( {\frac{{d{{{\text{w}}}_{i}}}}{{dt}} - \frac{{{\text{w}}_{i}^{2}}}{{\text{2}}}} \right) = \frac{1}{2}{{\left( {\frac{{d{{{{\gamma }}}_{i}}}}{{dt}}} \right)}^{2}} - {{{{\gamma }}}_{i}}\frac{{{{d}^{2}}{{{{\gamma }}}_{i}}}}{{d{{t}^{2}}}}$

В соответствии с изложенными в предыдущем разделе соображениями:

${{{{\gamma }}}_{i}} = 1 - {{\varphi }_{i}},\quad {{\varphi }_{i}} = - \sum\limits_{j = 1}^n {\frac{{{{m}_{j}}}}{{\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} }}} $

Полученная нетривиальная связь параметра wi с гравитационным потенциалом ${{\varphi }_{i}}$:

${{{\text{w}}}_{i}} = - {{\gamma }}_{i}^{{ - 1}}\frac{{d{{{{\gamma }}}_{i}}}}{{dt}} = {{(1 - {{\varphi }_{i}})}^{{ - 1}}}\frac{{d{{\varphi }_{i}}}}{{dt}}$
ставит под сомнение обычную формулу, связывающую гравитационный потенциал ${{\varphi }_{i}}$ с гравитационным ускорением ${{{\mathbf{g}}}_{i}}$. Заменим ее (из соображений пространственно-временной симметрии для пространственной и временнóй составляющих гравитационного преобразования) на “уточненную”:

${{{\mathbf{g}}}_{i}} = {{\gamma }}_{i}^{{ - 1}}\frac{{\partial {{{{\gamma }}}_{i}}}}{{\partial {{{\mathbf{r}}}_{i}}}} = - {{(1 - {{\varphi }_{i}})}^{{ - 1}}}\frac{{\partial {{\varphi }_{i}}}}{{\partial {{{\mathbf{r}}}_{i}}}}$

В результате математическую модель задачи n тел, основанную на расширенной 12‑параметрической группе Ньютона, можно представить в виде системы из n уравнений:

${{\Lambda }_{{I{{E}_{i}}(r + dt)}}} = {{\Lambda }_{{I{{E}_{i}}(t)}}} \circ {{\Lambda }_{{{{E}_{i}}(t){{E}_{i}}(t + dt)}}},\quad i = 1{\kern 1pt} \div {\kern 1pt} n$
${{\Lambda }_{{I{{E}_{i}}(r + dt)}}} = {{T}_{{t + dt}}}{{R}_{{{{{\mathbf{r}}}_{i}} + d{{{\mathbf{r}}}_{i}}}}}{{V}_{{{{{\mathbf{v}}}_{i}} + d{{{\mathbf{v}}}_{i}}}}}{{G}_{{{{{\mathbf{g}}}_{i}} + d{{{\mathbf{g}}}_{i}}}}}{{W}_{{{{w}_{i}} + d{{w}_{i}}}}} \circ {{\Gamma }_{{{{\gamma }_{i}} + d{{\gamma }_{i}}}}}$
${{\Lambda }_{{I{{E}_{i}}(t)}}} = {{T}_{t}}{{R}_{{{{{\mathbf{r}}}_{i}}}}}{{V}_{{{{{\mathbf{v}}}_{i}}}}}{{G}_{{{{{\mathbf{g}}}_{i}}}}}{{W}_{{{{w}_{i}}}}} \circ {{\Gamma }_{{{{\gamma }_{i}}}}},\quad {{\Lambda }_{{{{E}_{i}}(t){{E}_{i}}(t + dt)}}} = {{T}_{{\gamma _{i}^{{ - 1}}dt}}}{{G}_{{{{{\mathbf{n}}}_{i}}\gamma _{i}^{{ - 1}}dt}}}{{W}_{{{{\nu }_{i}}\gamma _{i}^{{ - 1}}dt}}}$
${{{{\gamma }}}_{i}} = 1 + \sum\limits_{j = 1}^n {\frac{{{{m}_{j}}}}{{\sqrt {m_{j}^{4} + {{{\left( {{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}} \right)}}^{2}}} }}} $
${{{\mathbf{g}}}_{i}} = {{\gamma }}_{i}^{{ - 1}}\sum\limits_{j = 1}^n {\frac{{{{m}_{j}}({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{3}}}}} ,\quad {{{\text{w}}}_{i}} = {{\gamma }}_{i}^{{ - 1}}\sum\limits_{j = 1}^n {\frac{{{{m}_{j}}({{{\mathbf{v}}}_{j}} - {{{\mathbf{v}}}_{i}}) \cdot ({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{3}}}}} $
${{{\mathbf{n}}}_{i}} = {{{{\gamma }}}_{i}}\sum\limits_{j = 1}^n {{{m}_{j}}\left\{ {\frac{{{{{\mathbf{v}}}_{j}} - {{{\mathbf{v}}}_{i}}}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{3}}}} - 3({{{\mathbf{v}}}_{j}} - {{{\mathbf{v}}}_{i}}) \cdot ({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})\frac{{{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{5}}}}} \right\}} $
$\begin{gathered} {{{{\nu }}}_{i}} = {{{{\gamma }}}_{i}}\sum\limits_{j = 1}^n {{{m}_{j}}\left\{ {\frac{{({{{\mathbf{g}}}_{j}} - {{{\mathbf{g}}}_{i}}) \cdot ({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}) + {{{({{{\mathbf{v}}}_{j}} - {{{\mathbf{v}}}_{i}})}}^{2}}}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{3}}}} - 3\frac{{{{{(({{{\mathbf{v}}}_{j}} - {{{\mathbf{v}}}_{i}}) \cdot ({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}))}}^{2}}}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{5}}}}} \right\}} + \\ \, + \frac{{\text{1}}}{{\text{2}}}{{\left\{ {\sum\limits_{j = 1}^n {{{m}_{j}}\frac{{({{{\mathbf{v}}}_{j}} - {{{\mathbf{v}}}_{i}}) \cdot ({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}{{{{{(\sqrt {m_{j}^{4} + {{{({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}})}}^{2}}} )}}^{3}}}}} } \right\}}^{2}} \\ \end{gathered} $

Предполагается, что наблюдатель (базовая система отсчета I) находится вне гравитационного поля (“на бесконечности”).

Отметим, что расширение группы Ньютона только за счет масштабного преобразования (то есть до 11-параметрической группы с определяющими соотношениями (2.1)÷(2.25)) не позволяет адекватно учесть эффект гравитационного замедления времени, поскольку при нулевых параметрах wi масштабные множители γi не будут изменяться (так как dγi/dt = –γiwi).

7. Заключение. В работе исследован ранее неизвестный (насколько известно автору) нерелятивистский аналог конформной группы, совпадающий с ней по числу параметров: 15-параметрическая расширенная группа Галилея–Ньютона. Приведены определяющие соотношения этой группы и выведены соответствующие ей уравнения инерциальной навигации.

В части формулировки задачи n тел работа носит, по сути, методический характер. Приведенные результаты и соображения могут быть полезны при построении релятивистской теории гравитационного взаимодействия тел, основанной на конформной группе [7, с. 142, 153], и теории квантовой гравитации [30].

Благодарности. Автор признателен своему научному руководителю Г.И. Макарову [31, с. 375]22 за стимулирующие обсуждения и поддержку в конце XX века.

Список литературы

  1. Громов С.В. Физика: Механика. Теория относительности. Электродинамика. М.: Просвещение, 2003. 383 с.

  2. Чуб В.Ф. Незамкнутость элементарных преобразований пространства–времени // Гиперкомплексные числа в геометрии и физике. 2005. № 2 (4). С. 153–160.

  3. Гарднер М. Теория относительности для миллионов. М.: Атомиздат, 1967. 191 с.

  4. Пуанкаре А. О науке. М.: Наука, 1983. 560 с.

  5. Пуанкаре А. Пространство и время // Метафизика. Век XXI. Альманах. Вып. 4: метафизика и математика. М.: БИНОМ. Лаборатория знаний, 2011. С. 133–147.

  6. Чуб В.Ф. Применение конформной группы в теории инерциальной навигации // Изв. РАН. МТТ. 2006. № 5. С. 3–17.

  7. Чуб В.Ф. Основы инерциальной навигации. М.: URSS, 2014. 200 с.

  8. Журавлев В.Ф. Основы теоретической механики. М.: Физматлит, 2008. 304 с.

  9. Смородинский Я.А. Естественные системы единиц // Физическая энциклопедия. Т. 2. М.: Сов. энциклопедия, 1990. С. 29–30.

  10. Томилин К.А. Фундаментальные физические постоянные в историческом и методологическом аспектах. М.: Физматлит, 2006. 368 с.

  11. Окунь Л.Б. Фундаментальные константы физики // Успехи физических наук. 1991. Т. 161. № 9. С. 177–194.

  12. Горелик Г. c$ \times $G$ \times $h$ = $? // Знание-сила. 1988. № 2. С. 21–27.

  13. Балк М.Б. Элементы динамики космического полета. М.: Наука, 1965. 339 с.

  14. Громов С.В. Физика: Оптика. Тепловые явления. Строение и свойства вещества. М.: Просвещение, 2001. 287 с.

  15. Окунь Л.Б. О движении материи. М.: Физматлит, 2012. 228 с.

  16. Кобзарев И.Ю., Окунь Л.Б. О массе фотона // Успехи физических наук. 1968. Т. 95. Вып. 1. С. 131–137.

  17. Окунь Л.Б. Теория относительности и теорема Пифагора // Успехи физических наук. 2008. Т. 178. № 6. С. 653–663.

  18. Тагиров Э.А. Фотон // Физическая энциклопедия. Т. 5. М.: Большая Рос. энциклопедия, 1998. С. 354.

  19. Как взвесить фотон // Природа. 2009. № 8. С. 81–82.

  20. Журавлев В.Ф. Основания механики: О проблемах аксиоматики. М.: URSS, 2019. 100 с.

  21. Биланюк О., Сударшан Е. Частицы за световым барьером // Эйнштейновский сборник, 1973. М.: Наука, 1974. С. 112–133.

  22. Герштейн С.С., Логунов А.А., Мествиришвили М.А. Полевая теория гравитации и масса покоя частиц // Докл. РАН. 2005. Т. 405. № 6. С. 753–754.

  23. Минковский Г. Пространство и время // Принцип относительности. Сб. работ по специальной теории относительности. М.: Атомиздат, 1973. С. 167–180.

  24. Новиков И.Д. Тяготение // Физическая энциклопедия. Т. 5. М.: Большая Рос. энциклопедия, 1998. С. 188–193.

  25. Чернин А.Д. Физика времени. М.: URSS, 2020. 230 с.

  26. Баранов А.Г. Гравитационное смещение // Эйнштейновский сборник, 1967. М.: Наука, 1967. С. 215–232.

  27. Хенль Г., Бенневитц Ф. Проверка замедления времени с помощью эффекта Мессбауэра // Эйнштейновский сборник, 1969–1970. М.: Наука, 1970. С. 170–176.

  28. Бройль де Л. Об истинных идейных основаниях волновой механики // Бройль де Л. Соотношения неопределенности Гейзенберга и вероятностная интерпретация волновой механики. М.: Мир, 1986. С. 30–33.

  29. Чуб В.Ф. Формулировка задачи двух тел в параметрах расширенной группы Галилея // Изв. РАН. МТТ. 2012. № 4. С. 16–20.

  30. Горелик Г.Е. Матвей Бронштейн и квантовая гравитация. К 70-летию нерешенной проблемы // Успехи физических наук. 2005. Т. 175. № 10. С. 1093–1108.

  31. Бранец В.Н. Записки инженера. М.: Изд-во “РТСофт” – “Космоскоп”, 2018. 592 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал