Известия РАН. Механика твердого тела, 2022, № 2, стр. 25-34

1. Введение. Для ответственных инженерных объектов машиностроения, эксплуатирующихся в условиях нестационарных термосиловых воздействий с длительными периодическими выдержками при высоких температурах и уровнях действующих напряжений становится существенной деградация конструкционного материала в результате ползучести. Наиболее сложной задачей определения ресурса таких конструкций становится при воздействии медленно изменяющегося знакопеременного нагружения с учетом наличия конструктивных концентраторов напряжений точное описание кинетики напряженно-деформированного состояния, которая используется как основа для применения подходов оценки накопленной поврежденности в процессе эксплуатации [1–5]. Для достоверного описания реономных процессов деформирования необходимо использование математических моделей, которые способны описывать процессы ползучести и накопления повреждений в конструкционном материале при воздействии нестационарного поля температур и сложных непропорциональных силовых нагружениях.

В настоящее время большинство работ посвященных математическому моделированию процессов ползучести основываются на применении одномерных моделей, описывающих процесс ползучести материалов с использованием в своей основе эквивалентных величин напряжений и деформаций [5, 6]. В условиях знакопеременного нагружения применяются модели, основанные на деформационном упрочнении [3, 5, 6]. Однако, при выполнении расчетных оценок поведения конструкций в условиях нестационарного нагружения необходимо учитывать векторные свойства параметров процесса ползучести, влияние поврежденности материала на кинетику процесса ползучести и необходим учет эффекта обратной ползучести при разгрузке материала, влияющий на кинетику тензора деформаций ползучести при знакопеременном нагружении с длительными разгрузками. Вследствие чего необходимо построение более сложных математических моделей, описывающих кинетику процесса ползучести. Многих исследователей объединяет мнение о том, что применении концепции введения в математическую модель внутренних параметров состояния позволяет удовлетворительно описывать кинетику процесса ползучести при нестационарном нагружении. Данные модели отличает, то, что они позволяют описывать как склерономную (не зависимую от времени нагружения), так и реономную (зависимую от времени нагружения) части неупругой деформации конструкционных материалов и удобны для анализа действующих напряжений с учетом влияния поврежденности материала.

В настоящей статье на основании работ отечественных и зарубежных авторов [1–12] развита математическая модель нестационарной ползучести и представлены численные исследования процесса высокотемпературной ползучести стали Х18Н10Т при одноосном нагружении и для стали 304 при многоосном нагружении. По результатам сравнения численных и экспериментальных результатов проведена оценка достоверности применяемой математической модели нестационарной ползучести.

2. Математическая модель. Математическая модель поврежденной среды включает в себя: уравнения, описывающие вязкоупругое поведение материала и кинетику процесса накопления повреждений, а также критерий разрушения деградирующего материала.

Модель основывается на следующих положениях [5]:

− конструкционный материал обладает начальной изотропией свойств;

− процессы деформирования конструкционных материалов, характеризующиеся малыми деформациями;

− поверхности текучести и скоростей деформаций ползучести определяются формой Мизеса;

− изменение эквипотенциальных поверхностей скоростей деформаций ползучести определяется смещением координат центра ${{\rho }}_{{ij}}^{с}$ и величиной радиуса ${{С}_{с}}$;

− изменение поверхности текучести определяется смещением координат центра ${{{{\rho }}}_{{ij}}}$ и величиной радиуса ${{C}_{p}}$;

− скорости деформаций пластичности и ползучести определяются из ассоциированного закона течения;

− изменение объема материала упругое (принимается пластическая несжимаемость $e_{{ii}}^{p} = 0$);

− степень поврежденности материала учитывается параметром ${{\omega }}$ – поврежденности, которая изменяется в диапазоне ${{{{\omega }}}_{0}} \leqslant {{\omega }} \leqslant {{{{\omega }}}_{f}}$ (${{\omega }_{0}}$ – начальный уровень поврежденности материала, а ${{\omega }_{f}}$ – критическая величина поврежденности, характеризующаяся образованием макротрещины);

− влияние степени деградации на процессы упругого и неупругого деформирования конструкционного материала осуществляется введением деградирующего континуума эффективных напряжений ${{\tilde {\sigma }}_{{ij}}}$.

Постулируется, что компоненты тензора деформаций ${{e}_{{ij}}}$ и тензора скорости деформаций ${{\dot {e}}_{{ij}}}$ подчиняются правилу аддитивности и являются суммой упругих деформаций $e_{{ij}}^{e}$, $\dot {e'}_{{ij}}^{e}$ и деформаций ползучести $e_{{ij}}^{c}$, $\dot {e'}_{{ij}}^{c}$:

Тензор напряжений связан с тензором упругих деформаций уравнениями термоупругости:

где $\sigma $, $e$ – гидростатические, а $\sigma _{{ij}}^{'}$, $e_{{ij}}^{'}$ – девиаторные части тензоров напряжений ${{\sigma }_{{ij}}}$ и деформаций ${{e}_{{ij}}}$ соответственно; $G(T)$ – модуль Юнга 2-го рода (сдвига), $K(T)$ – объемный модуль упругости, $\alpha (T)$ – коэффициент линейного расширения при изменении температуры.

Для описания процессов ползучести вводим в пространстве напряжений эквипотенциальные поверхности ползучести ${{F}_{c}}$ имеющие общий центр $\rho _{{ij}}^{c}$ и различные радиусы ${{C}_{c}}$, определяемые текущим напряженным состоянием:

где ${{\lambda }_{c}}$ – соответствует текущей поверхности $F_{c}^{{(k)}}$, определяющей текущее напряженное состояние $S_{{ij}}^{c}$.

Поверхность с радиусом ${{\bar {С}}_{c}}$, соответствует нулевой скорости ползучести с определенным заданным допуском на величину деформации ползучести на определенной временной базе:

где $\bar {S}_{{ij}}^{c}$ и $\bar {\sigma }_{{ij}}^{'}$ – совокупность напряженных состояний, отвечающих нулевой скорости ползучести. где ${{\bar {С}}_{с}}$ и ${{\lambda }_{c}}$ – функции температуры Т, определяемые экспериментальным путем.

Эволюционное уравнение для изменения координат центра поверхности ползучести имеет вид [13]:

где $g_{1}^{c}$ и $g_{2}^{c}$ > 0 – параметры кинематического упрочнения, $g_{T}^{c}$ – температурный модуль.

Конкретизируя соотношение (2.3) закон градиентальности можно представить в виде:

Выражение для длины траектории деформирования при ползучести имеет следующий вид:

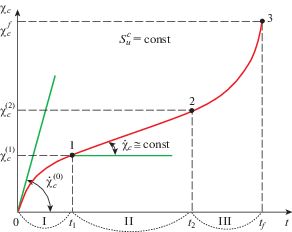
Кривая длины траектории деформирования при ползучести ${{\chi }_{с}}$ в зависимости от времени процесса t при $S_{u}^{c} = {\text{const}}$ имеет вид, представленный на рис. 1.

На кривой ${{\chi }_{с}}(t)$ (рис. 1) можно выделить три характерные зоны ползучести материала:

I. зона неустановившейся ползучести (0–1), где скорость деформации ползучести ${{\dot {\chi }}_{с}}$ убывает;

II. зона установившейся ползучести (1–2), где скорость деформации ползучести ${{\dot {\chi }}_{с}}$ приблизительно постоянна ${{\dot {\chi }}_{с}} \cong {\text{сonst}}$;

III. зона активного накопления повреждений (2–3), где постоянно увеличивается скорость деформации ползучести ${{\dot {\chi }}_{с}}$ и начинается прогрессивное влияние поврежденности на механические свойства материала.

Наличие и протяженность I и II зоны зависит от конструкционного материала и от величины интенсивности активных напряжений $S_{u}^{c}$.

Выражение для $\lambda _{с}^{I}$ на первом участке кривой ползучести можно представить в виде:

где $\lambda _{с}^{{(0)}}$, $\lambda _{с}^{{(1)}}$ – значения параметра $\lambda _{с}^{{}}$ в точках “0” и “1” первого участка кривой ползучести материала (см. рис. 1).

На третьем участке предшествующему разрушению:

где $\omega $ – величина поврежденности.

Зависимости (2.1)–(2.10) позволяют моделировать процессы ползучести при неизотермическом нестационарном нагружении и описывают стадии неустановившиеся и установившиеся скорости ползучести.

Определяющие соотношения (2.1)–(2.10), описывающие процесс нестационарной неизотермической ползучести, разработаны как система “вложенных” математических моделей. При исключении из уравнений параметров (приравнивая к нулю), ответственных за определенные эффекты деформирования при ползучести, можно получить частные математические модели, используемые при решении простых задач.

Поврежденность влияет на физико-механические свойства на стадии ее развития и активного слияния рассеянных несплошностей в объеме конструкционного материала. Для учета влияния поврежденности используются эффективные напряжения, которые определяются как:

где $\tilde {G}$, $\tilde {К}$ – эффективные модули упругости, определяемые по формулам Мак-Кензи [13, 15]:

Аналогичным образом определяются эффективные внутренние переменные $\tilde {\rho }_{{ij}}^{р}$, $\tilde {\rho }_{{ij}}^{c}$:

При разработке определяющих соотношений кинетики накопления повреждений принято, что процесс накопления повреждений условно состоит из двух стадий: первая стадия сопровождается зарождением несплошностей (микропор, микротрещин), вторая стадия представляет собой развитие и активное слияние рассеянных несплошностей. Кинетическое уравнение накопления повреждений в конструкционных материалах принимается в наиболее простом виде произведений функций от внутренних параметров, влияющих на скорость накопления повреждений:

В зависимости (2.14) функции  f_i позволяют учитывать зависимость скорости накопления повреждений $\dot {\omega }$ от следующих параметров процесса деформирования:

− вида напряженного состояния – функция ${{f}_{1}}\left( \beta \right)$;

− текущего уровня накопленной поврежденности – функция ${{f}_{2}}\left( \omega \right)$;

− текущего значения поглощенной энергии, идущей на образование несплошностей (микропор и микротрещин) – функция ${{f}_{3}}\left( {{{W}_{c}}} \right)$;

− текущей скорости изменения поглощенной энергии ${{W}_{c}}$ – функция ${{f}_{4}}\left( {{{{\dot {W}}}_{c}}} \right)$.

В уравнениях (2.15) и (2.16) введены следующие обозначения:

− $\beta $ – параметр “жесткости” напряженного состояния ($\beta = {\sigma \mathord{\left/ {\vphantom {\sigma {{{\sigma }_{u}}}}} \right. \kern-0em} {{{\sigma }_{u}}}}$);

− $W_{c}^{a}$ – значение поглощенной энергии $W_{c}^{{}}$ в конце стадии зарождения рассеянных несплошностей в условиях ползучести;

− $W_{c}^{f}$ – значение поглощенной энергии, соответствующее образованию макротрещины в условиях ползучести;

− $с$ – константа интегрирования уравнения (2.15).

Стадия развития и слияния несплошностей в конструкционном материале завершается достижением уровня накопленной поврежденности $\omega $ критического значения ${{\omega }_{f}}$.

По заданной истории изменения во времени температурного и механического нагружения при совместном интегрирований уравнении, описывающих вязкоупругое поведение (2.1)–(2.10) и кинетики накопления повреждений (2.14)–(2.16), определяется ресурс конструктивных элементов инженерных объектов в условиях протекания процесса ползучести в конструкционных материалах.

3. Численные результаты. В рамках оценки достоверности математической модели путем численного моделирования процессов ползучести в одноосной постановке задачи для стали Х18Н10Т были численно моделированы кривые ползучести при уровнях интенсивности напряжений ${{\sigma }_{{11}}}$ = 40, 50, 60 и 80 МПа и температуре $T = 850$°C. Экспериментальной базой для сравнения численных исследований являлась работа [14], где приведены кривые ползучести указанной стали при идентичных условиях нагружения. В таблице 1 приведены физико-механические характеристики и параметры модели термоползучести для стали Х18Н10Т.

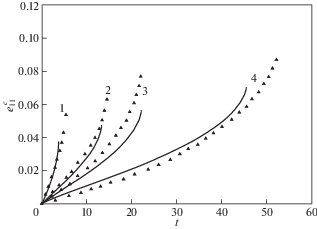
На рис. 2 представлены кривые ползучести при температуре $T = 850$°C и уровнях напряжений ${{\sigma }_{{11}}}$ = 40, 50, 60 и 80 МПа. Сплошными линиями отмечены результаты численного моделирования, а пунктирной – соответствующие экспериментальные результаты. Видно качественное и количественное совпадение опытных и расчетных данных.

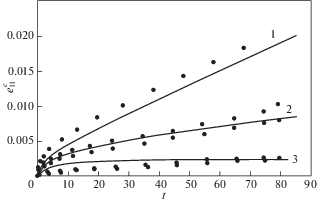
В рамках оценки достоверности математической модели термоползучести при многоосном нагружении были проведены численные исследования процесса ползучести стали 304 при температуре 650°C при двухосном нагружении. Экспериментальные исследования при двухосных законах нагружения данной стали приведены в работе [7] и были выполнены на трубчатых лабораторных образцах. Испытания проводили при постоянной температуре и периодическом изменении главных осей тензора напряжений (рис. 4). В испытаниях использовали тонкостенные трубчатые образцы с наружным диаметром $d = 21 \pm 0.05$ мм, толщиной стенки $h = 1 \pm 0.05$ мм и рабочей длиной $l = 98$ мм. На рис. 3 приведено сравнение численных результатов и экспериментальных данных при одноосном нагружении указанной стали для трех уровней действующих напряжений (${{\sigma }_{{11}}}$ = 117.7; 137.3 и 156.9 МПа).

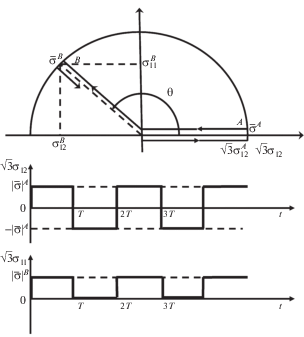
Для испытаний в условиях совместного действия нормальных и сдвиговых компонент тензоров напряжений и деформаций ползучести на образец в соответствии с установленным законом нагружения прикладывались осевое усилие и крутящий момент. Каждый цикл повторяющегося многоосного нагружения состоял из чистого кручения ${{\bar {\sigma }}_{A}}$ в течение $t_{{\text{ч}}}^{*}$ с последующей полной разгрузкой и совместного растяжения с кручением ${{\bar {\sigma }}_{B}}$ в течение $t_{{\text{ч}}}^{*}$ с последующей разгрузкой. Векторы ${{\bar {\sigma }}_{A}}$ и ${{\bar {\sigma }}_{B}}$ имеют равную величину, по различным направлениям ($\theta $ – угол между векторами, см. рис. 4). Такой цикл нагружения повторялся 5 раз при значении $t_{{}}^{*} = 8\,{\text{ч}}$ и $\left| {{{{\bar {\sigma }}}_{A}}} \right| = \left| {{{{\bar {\sigma }}}_{B}}} \right| = 137.3$ МПа, что близко к пределу текучести стали 304 при $T = 650$°C.

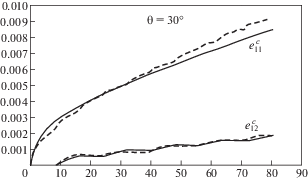
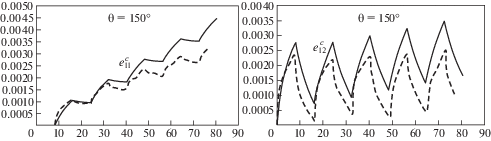
Результаты испытаний показали, что в случае $\theta = 30^\circ $ сразу же после поворота тензора напряжений скорость деформации несколько повышается. При повороте на 90° наблюдается временное увеличение скорости осевой и сдвиговой деформаций после смены растяжения кручением и кручения растяжением. Это переходное увеличение скорости деформаций снижается по мере увеличения продолжительности циклического нагружения.

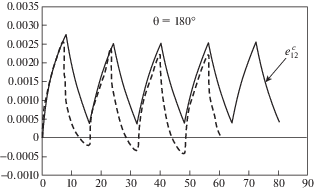
При больших углах вращения вектора напряжений $\theta = 150^\circ $ и 180° происходит заметное временное увеличение скорости деформации после каждого поворота вектора напряжения, аналогичное наблюдаемому при начальном приложении нагрузки (рис. 5–8). Таким образом, можно сделать вывод, что разупрочнение материала после вращения вектора напряжений с увеличением угла вращения становится наиболее ярко выраженным.

Другой существенной особенностью деформаций ползучести при сложном нагружении является неколлинеарность вектора напряжений и скоростей деформаций ползучести на переходной стадии сразу же после вращения вектора напряжений.

4. Заключение. Разработана математическая модель, описывающая процессы нестационарной ползучести конструкционных материалов при нестационарном сложном нагружении.

Проведено сравнение результатов численного моделирования и экспериментальных данных процессов ползучести для сталей Х18Н10Т и 304. Показано, что развитый вариант определяющих соотношений нестационарной ползучести позволяет с достаточной для инженерных расчетов точностью описывать процессы ползучести металлов при одноосных и многоосных напряженных состояниях.

Благодарности. Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект 0729-2020-0054).