Известия РАН. Механика твердого тела, 2022, № 2, стр. 3-13

1. Введение. Современные математические модели континуума основываются на понятии о дифференцируемом многообразии (или дифференцируемом пространстве) [1, 2]. Подобные модели вполне пригодны для описания механического поведения твердых деформируемых тел, включая твердые тела с микроструктурой [3]. Континуум при этом мыслится как дифференцируемое многообразие некоторой данной размерности M в прикладных вопросах обычно достаточно полагать, что M = 3.

На дифференцируемом многообразии часто приходится вводить дополнительные структуры. Например, риманова структура на многообразии позволяет говорить о целом классе дифференцируемых пространств [1, 2], которые имеют важное прикладное значение. Для континуума с римановой структурой особенно просто может быть разработана теория конечных деформаций.

Исторически теория многообразий восходит к геометрии искривленных поверхностей в трехмерном евклидовом пространстве. Со временем концепция многообразия освободилась от необходимости существования “внешнего пространства”, в котором располагалось бы многообразие; сформировалась специальная часть теории – внутренняя геометрия многообразий. Однако в механике континуума внешнее пространство, в которое “погружены” материальные объекты, до сих пор выступает как неизменный атрибут теории.

Относительные тензоры естественным образом возникают в математических моделях микрополярного материала [4–6]. Литературный поиск показывает, что применение относительных тензоров в теориях механики сплошных сред не имеет широкого распространения, несмотря на глубокие математические исследования (алгебра, теория инвариантов и дифференцирование относительных тензоров) [7–13].

В ходе изложения вопросов связанных с многомерной геометрией будем следовать терминологии и идеям [13, 14]. Минимальные сведения о тензорных элементах объема и площади можно найти в [10], см. приложение Дж.Л. Эриксена. Вопросы применения алгебры псевдотензоров к задачам механики растущих тел и микрополярной теории упругости обсуждаются в работах [4, 5].

В представленной работе рассмотрим вопросы вычисления элементарного тензорного объема (площади) M-ячейки для многообразия, погруженного в “плоское” конечномерное пространство. Соответствующие рассмотрения подразумевают выбор ориентации репера, определяющего элемент объема (площади). Последнее обстоятельство имеет исключительное значение в микрополярных теориях упругости [15–17]. Указанные теории корректно развивать только в рамках псевдотензорного формализма. В особенности это касается теории гемитропных упругих сред [4, 5]. Рассматриваются альтернативные определения тензоров силовых и моментных напряжений с использованием естественных элементов объема и площади поверхности. Веса псевдотензоров в N-мерном плоском пространстве и псевдотензоров, ассоциированные с M-мерным многообразием приведены в таблицах 1 и 2 соответственно.

2. Псевдотензоры в N-мерном пространстве. В данной работе мы не будем воспроизводить определение и свойства псевдотензоров. Подробное изложение алгебры псевдотензоров можно найти в руководствах по тензорному анализу [9–13] и в статьях [4, 5]. В дальнейшем изложении сверху корневого символа относительного тензора в квадратных скобках будем отмечать его вес. Нулевой вес, присущий абсолютным тензорам, не отражается нами в обозначениях.

Одним из фундаментальных объектов многомерной геометрии является абсолютный тензор $\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}}$, называемый обобщенной дельтой Кронекера. $\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}}$ можно определить в N-мерном пространстве для $M \leqslant N$ согласно правилу

С помощью тензора $\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}}$ можно легко вычислить символы перестановок:¹¹

1. относительный ковариантный M-вектор ${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}}$ веса –1

2. относительный контравариантный M-вектор ${{\varepsilon }^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}}$ веса $ + 1$

Определение косого произведения N абсолютных векторов $\mathop {\mathbf{a}}\limits_1 $, $\mathop {\mathbf{a}}\limits_2 $, …, $\mathop {\mathbf{a}}\limits_N $ в N-мерном пространстве

где ${{e}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}} = e{{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}}$, $e = {{e}_{{12 \ldots N}}}$ – псевдоскаляр веса +1. $e = {{e}_{{12 \ldots N}}}$ позволяет ввести понятие фундаментального ориентирующего псевдоскаляра и разделить правые и левые локальные базисные системы. В самом деле, если в качестве системы векторов $\mathop {\mathbf{a}}\limits_1 $, $\mathop {\mathbf{a}}\limits_2 $, …, $\mathop {\mathbf{a}}\limits_N $ принять векторы ковариантного базиса $\mathop {\mathbf{\iota }}\limits_1 $, $\mathop {\mathbf{\iota }}\limits_2 $, …, $\mathop {\mathbf{\iota }}\limits_N $ в N-мерном пространстве, то на основании (2.4) находим

В трехмерном пространстве e определяется смешанным произведением базисных векторов

а фундаментальный ориентирующей псевдоскаляр отрицательного веса –1 есть

Здесь $\mathop {\mathbf{\iota }}\limits^1 ,\mathop {\mathbf{\iota }}\limits^2 ,\mathop {\mathbf{\iota }}\limits^3 $ векторы базиса взаимного (reciprocal) с базисом $\mathop {\mathbf{\iota }}\limits_1 ,\mathop {\mathbf{\iota }}\limits_2 ,\mathop {\mathbf{\iota }}\limits_3 $.

Отметим, что фундаментальный ориентирующий псевдоскаляр позволяет легко преобразовывать псевдотензоры произвольного веса W в абсолютные тензоры.²² Введем тензор T согласно

Сравнивая веса, приходим к заключению о том, что T является абсолютным тензором. Веса основных псевдотензоров в N-мерном плоском пространстве приведем в таблице 1. В дальнейшем изложении у фундаментальных символов, таких как $\varepsilon $, $e$ и $g$, указание на их вес будем опускать.

3. Тензорные элементы площади M-многообразия. Поскольку континуум моделируется некоторым дифференцируемым многообразием, то немедленно встает вопрос о возможности его погружения во внешнее пространство.³³ Хорошо известно, что такое погружение в трехмерное плоское пространство не всегда возможно. Так, например, риманово многообразие размерности М в общем случае погружается в плоское пространство размерности $N = M(M + 1){\text{/}}2$. В любом случае можно считать выполненным следующее неравенство:

Уточним понятие плоского пространства. Плоское пространство лучше всего определить как специальный класс римановых пространств (см. [1, 2]): риманово пространство называется плоским, если в нем существует координатная система, в которой компоненты метрического тензора пространства постоянны. В плоском пространстве всегда имеется такая предпочтительная система координат ${{y}^{j}}(j = 1,2, \ldots ,N)$, что его метрика определяется квадратичной дифференциальной формой

где постоянные ${{c}_{j}} = \pm 1$ в зависимости от типа пространства. Для координатной системы ${{y}^{j}}$ используется термин декартова система координат. Ясно, что для внешнего пространства декартова система координат является предпочтительной.

В N-мерном “плоском” пространстве выберем криволинейную систему координат ${{x}^{k}}(k = 1,2, \ldots ,N)$. Рассмотрим погруженное в него многообразие (поверхность) $\Sigma $ размерности $M$ ($M \leqslant N$). Пусть многообразие $\Sigma $ задано его Гауссовой параметризацией ${{u}^{\alpha }}(\alpha = 1,2, \ldots ,M)$

В формуле (3.3) ${{x}^{k}}$ являются внешними координатами для $\Sigma $, а ${{u}^{\alpha }}$ – внутренними.

Разобьем многообразие $\Sigma $ на систему M-ячеек (M-cell). Каждая M-ячейка задается угловым репером, который характеризуется угловой вершиной (c внешними координатами x^k и внутренними координатами ${{u}^{\alpha }}$) и концевыми точками репера, имеющими внутренние координаты

и внешние координаты где индекс $\mathfrak{c}$ нумерует реперные направления ($\mathfrak{c} = 1,2, \ldots ,M$). С внешней (пространственной) точки зрения направления рассматриваемого репера задаются абсолютными контравариантными векторами

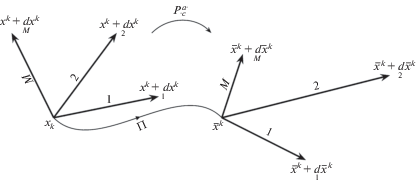
Рассмотрим два репера с различными угловыми точками x^k и ${{\bar {x}}^{k}}$ и концевыми точками ${{x}^{k}} + \mathop d\limits_\mathfrak{c} {{x}^{k}}$ и ${{\bar {x}}^{k}} + \mathop d\limits_\mathfrak{c} {{\bar {x}}^{k}}$, изображенными на рис. 1. Тогда координаты векторов первого и второго реперов будут $\mathop d\limits_\mathfrak{c} {{x}^{k}}$ и $\mathop d\limits_\mathfrak{c} {{\bar {x}}^{k}}$ соответственно. Всегда существует линейное преобразование одного репера к другому, действующее по формуле

где $P_{{ \cdot \mathfrak{c}}}^{{\mathfrak{a} \cdot }}$ – матрица перехода от старого базиса (репера) к новому [18–20]⁴⁴. В этом случае легко сформулировать критерий сравнения ориентаций реперов $\mathop d\limits_\mathfrak{b} {{x}^{k}}$ и $\mathop d\limits_\mathfrak{a} {{\bar {x}}^{k}}$. Для этого должен существовать непрерывный путь $\Pi $ переноса одного M-репера в другой. Далее, если $\det (P_{{ \cdot \mathfrak{c}}}^{{\mathfrak{a} \cdot }}) > 0$, то тогда считаем, что реперы имеют одинаковые ориентации или коориентированы, а если $\det (P_{{ \cdot \mathfrak{c}}}^{{\mathfrak{a} \cdot }}) < 0$, то тогда реперы имеют противоположные ориентации.

В микрополярных теориях механики континуума [15–17] исключительное значение имеют ориентации реперов. Ясно, что ориентация репера задается нумерацией реперных направлений. При перестановке двух номеров реперных направлений ориентация всего репера изменяется на противоположную, т.е. правоориентированный репер становится левоориентированным. В механике континуума ориентацию базисного репера удобно задавать фундаментальным ориентирующим скаляром e [4, 5].

Составим из абсолютных контравариантных пространственных векторов $\mathop d\limits_\mathfrak{b} {{x}^{k}}$ детерминанты

Нетрудно заметить, что ${{d}^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}}$ – абсолютный антисимметричный тензор, т.е. имеет нулевой вес. Детерминант (3.8) может изменять знак при изменении порядка нумерации реперных направлений M-ячейки, что приведет к перестановке строк в детерминанте (3.8).

С помощью (3.8) определим тензорный элемент объема M-ячейки (the tensor element of area [10, см. приложение Дж.Л. Эриксена])⁵⁵ согласно

или, раскрывая детерминант (3.8), c помощью $\varepsilon $-символа находим

Здесь ${{\varepsilon }^{{{{\mathfrak{b}}_{1}}{{\mathfrak{b}}_{2}} \ldots {{\mathfrak{b}}_{M}}}}}$ никак не изменяется при замене “внешней” координатной системы, т.е. выступает как абсолютный инвариант.

На основании (3.8) имеем также [21, 22]

Здесь в квадратные скобки заключены индексы по которым выполняется альтернирование.

Учитывая следующую формулу для дифференциалов внешних координат вдоль реперных направлений M-ячейки

соотношение (3.8) можно записать в виде

Несложно заметить, что формулу (3.13) можно представить в следующем виде [13, см. c. 256—257]

или, переходя к символам перестановок,

Если элементарные M-ячейки нарезаны с помощью координатных поверхностей ${{u}^{\alpha }} = {{c}^{\alpha }}$, то тогда для $\mathfrak{c} \ne \gamma $ имеем

а для случая $\mathfrak{c} = \gamma $

В результате находим

Для случая $M = N$ получим

где ${{\mathop {d\tau }\limits^{[ - 1]} }^{{12 \ldots M}}}$ – естественный элемент объема, представляющий собой псевдоскаляр веса $ - 1$, который определяется, следующим образом

Если

то тогда ${\text{det}}({{\partial }_{\alpha }}{{x}^{k}}) = 1$ и

С помощью псевдоскаляра ${{\mathop {d\tau }\limits^{[ - 1]} }^{{12 \ldots M}}}$ и фундаментального ориентирующего скаляра e можно образовать абсолютный скаляр $d\tau $, являющийся инвариантным элементом объема

4. Тензорные элементы объема и площади поверхности в трехмерном пространстве. Рассмотрим случай трехмерного пространства. В качестве многообразия выберем поверхность, заданную естественной (Гауссовой) параметризацией ${{u}^{1}},{{u}^{2}}$ и 2 ячейками, нарезанными координатными линиями ${{u}^{1}} = {{c}^{1}},{{u}^{2}} = {{c}^{2}}$. Для этого случая в данных выше формулах принимается $N = 3$, M = 2. Тогда тензорный элемент площади поверхности (3.15) преобразуется к виду

или

Соотношение (4.2) определяет тензорный элемент площади поверхности, играющий исключительно важную роль при определении тензоров силовых и моментных напряжений в механике континуума.

Антисимметричному абсолютному тензору $d{{\tau }^{{ij}}}$ сопутствует ковариантный псевдовектор веса $ - 1$:

определяющий псевдовекторный элемент площади, а абсолютный вектор задает векторный элемент площади поверхности.

Векторный и псевдовекторный элементы площади поверхности связаны соотношением

Естественный элемент площади поверхности задается следующей формулой

Инвариантный элемент площади поверхности задается следующей формулой

Ясно, что

Сравнивая формулы (4.4) и (2.4), заметим, что определение векторного элемента площади поверхности (4.4) строится на векторном (косом) произведении касательных векторов ${{\partial }_{1}}{{x}^{i}}$ и ${{\partial }_{2}}{{x}^{j}}$ к поверхности. Веса основных псевдотензоров, ассоциированных с M-мерным мноогобразием приведем в таблице 2.

В качестве примера, рассмотрим определения тензоров силовых и моментных напряжений. Выберем внутри тела элементарную двумерную площадку с инвариантным элементом площади dS и единичным вектором нормали ${{n}_{k}}$.

Единичный вектор нормали, в случае неявного задания поверхности

вычисляется согласно формуле где $f({{x}^{i}})$ является абсолютным скаляром (можно считать, что $f({{x}^{i}})$ имеет вес, не равный 0, но тогда его можно привести к абсолютному скаляру, домножив на соответствующую степень псевдоскаляра e). Откуда заключаем, что единичный вектор нормали ${{n}_{i}}$ является абсолютным вектором.

Равнодействующие поверхностных сил и моментов, действующих на элементарную двумерной площадку сведется к абсолютному вектору поверхностных сил ${{t}^{k}}$ и псевдовектору поверхностных моментов ${{\mathop m\limits^{[ - 1]} }_{k}}$, отнесенных к инвариантному элементу площади $dS$. Следуя стандартному подходу, для произвольно ориентированной элементарной площадки определим тензоры силовых ${{t}^{{ik}}}$ и моментных напряжений 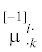соотношениями

Откуда заключаем, что тензор силовых напряжений ${{t}^{{ik}}}$ имеет нулевой вес и является абсолютным тензором, а псевдотензор моментных напряжений 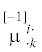имеет вес –1.

Далее рассмотрим ту же самую элементарную площадку, приписывая ей естественный элемент площади⁶⁶ $\mathop {dA}\limits^{[ - 1]} $. Тогда вместо векторов ${{t}^{k}}$ и ${{m}_{k}}$, появляются псевдовектор поверхностных сил ${{\mathop t\limits^{[ + 1]} }^{k}}$ и абсолютный вектор поверхностных моментов ${{m}_{k}}$. Определения тензоров силовых и моментных напряжений, для этого случая, примут вид

Откуда замечаем, что псевдотензор силовых напряжений ${{\mathop t\limits^{[ + 1]} }^{{ik}}}$ имеет вес +1, а тензор моментных напряжений $\mu _{{ \cdot k}}^{{i \cdot }}$ оказывается абсолютным тензором.

Заключение. В статье обсуждаются вопросы вычисления тензорных элементов площади для M-мерного многообразия, погруженного в “плоское” конечномерное пространство.

1. Приводятся необходимые сведения из алгебры псевдотензоров, включая символы перестановок, дельта–символы и фундаментальный ориентирующий псевдоскаляр.

2. Рассматриваются многообразия, заданные внутренней Гауссовой параметризацией. Вводится понятие M-ячейки на многообразии и определяется ее репер.

3. Обсуждаются представление об ориентациях тензорного элемента объема и критерий коориентированности M-реперов в разных точках M-многообразия.

4. Вводится понятие тензорного элемента объема M-ячейки и тензорного элемента площади M-многообразия.

5. Определяются: естественный элемент объема, инвариантный элемент объема в $3$-мерном пространстве, псевдовекторный, векторный, естественный и инвариантный элементы площади поверхности.

6. В качестве примера рассматриваются два варианта определения тензоров силовых и моментных напряжений, пригодные для использования в микрополярных теориях.

Благодарности. Работа выполнена в рамках государственного задания (№ госрегистрации АААА-А20-120011690132-4) и при поддержке Российского фонда фундаментальных исследований проекты (№№ 19-51-60001, 20-01-00666).