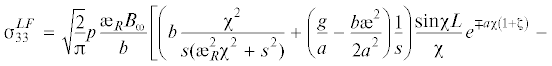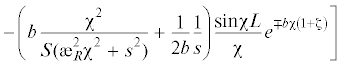Известия РАН. Механика твердого тела, 2022, № 2, стр. 35-49

АСИМПТОТИЧЕСКАЯ ТЕОРИЯ ВОЛНОВЫХ ПРОЦЕССОВ В ОБОЛОЧКАХ ВРАЩЕНИЯ ПРИ УДАРНЫХ ПОВЕРХНОСТНЫХ И ТОРЦЕВЫХ НОРМАЛЬНЫХ ВОЗДЕЙСТВИЯХ

И. В. Кириллова^a, *, Л. Ю. Коссович^a, **

^a ФГБОУ ВО “СГУ имени Н.Г. Чернышевского”
Саратов, Россия

^* E-mail: nano-bio@info.sgu.ru
^** E-mail: president@info.sgu.ru

Поступила в редакцию 14.10.2021
После доработки 20.10.2021
Принята к публикации 21.10.2021

EDN: HHWAXC
DOI: 10.31857/S057232992202012X

Аннотация

В данной статье обобщаются работы авторов по математическому моделированию нестационарного напряженно-деформированного состояния (НДС) оболочек при ударных воздействиях на их лицевые поверхности и на торцы. Математическое моделирование основывается на использовании асимптотического метода построения приближенных теорий для составляющих в разных областях фазовой плоскости решения, где имеют место принципиально разные его свойства и наблюдаются разные значения показателей изменяемости и динамичности. Выделены области, в которых работают двумерная изгибная составляющая теории Кирхгофа–Лява, квазиплоская задача теории упругости, гиперболический погранслой в окрестности волны сдвига и эллиптический погранслой в окрестности условного фронта поверхностных волн Рэлея.

Приведен вывод асимптотически оптимальных уравнений эллиптического погранслоя, имеющего место как в случае касательных ударных поверхностных воздействий, так и в случае ударных торцевых воздействий нормального типа. При этом в случае торцевого воздействия задача для полубесконечной оболочки сводится с помощью выделения частного решения к эквивалентной задаче для оболочки бесконечной.

В качестве примера построены решения для эллиптического погранслоя в цилиндрических оболочках для обоих случаев нагрузки. Использованы интегральные преобразования Лапласа по времени и Фурье по продольной координате. Обращение интегральных преобразований дало возможность представить решения с помощью элементарной функции arctg от сложных аргументов. Анализ этих решений в малой окрестности квазифронта (условного фронта поверхностных волн Рэлея) позволил определить их свойства при удалении от квазифронта по продольной координате.

Ключевые слова: асимптотический метод, фазовая плоскость, оболочка вращения, цилиндрическая оболочка, условный фронт поверхностных волн Рэлея, преобразование Лапласа, преобразование Фурье

1. Введение. Классификация ударных воздействий на торец оболочек вращения, вызывающих в них нестационарные волны, приведена в работе [1]. Выделены три типа граничных условий, определяющих различные виды нестационарного НДС: продольное, тангенциального типа (LT), продольное, изгибающего типа (LM) и нормальный тип воздействия (NW).

Для описания нестационарных волн в тонких оболочках традиционно применялись как трехмерная теория упругости, так и приближенные двумерные теории: теория Кирхгофа–Лява и теория типа Тимошенко. Численные методы, метод перевала и метод прифронтовой асимптотики использовались в работах [2–5] с целью анализа применения двумерных теорий в различных областях фазовой плоскости.

В [6–10] представлены основы асимптотической теории волновых процессов в оболочках вращения при ударных воздействиях. Эта теория использует схему расчленения нестационарного НДС на составляющие с различными значениями показателей изменяемости и динамичности в различных участках фазовой плоскости решения.

Асимптотические методы, разработанные для решения задач статики и стационарной динамики [11, 12] использовали методы наложения решений с различными показателями изменяемости, таких как безмоментная и моментная составляющие по двумерной теории Кирхгофа–Лява, и погранслоя типа Сен-Венана. Представленная асимптотическая теория явилась принципиально новой и представляет собой вариант метода сращиваемых разложений. При этом доказано существование областей согласования составляющих с различными показателями изменяемости. Используются безмоментная составляющая и динамический простой краевой эффект по теории Кирхгофа–Лява, квазистатический погранслой типа Сен-Венана, квазиплоские и квазиантиплоские трехмерные составляющие и различные виды погранслоев.

Самым принципиально новым в работах [6–10] явилось также построение асимптотических уравнений погранслоев. В случае воздействия вида LT (продольное, тангенциального типа) в окрестности фронта трехмерной волны расширения имеет место погранслой, описываемый уравнениями гиперболического типа, а в окрестности фронта двумерной волны растяжения–сжатия имеет место погранслой с уравнениями параболического типа. В случае воздействия вида LM (продольное, изгибающего типа) существует только один погранслой – гиперболического типа в окрестности фронта волны расширения.

В случае воздействия вида NW имеют место два погранслоя: один – гиперболический в окрестности фронта волны сдвига, и другой – очень специфический, действующий в окрестности условного фронта поверхностной волны Рэлея и названный погранслоем эллиптического типа [13–16]. Этот погранслой уточняет картину НДС по двумерной теории типа Тимошенко, где появляется дополнительный, так называемый, фронт волны сдвига в окрестности фронта волны Рэлея. Назван этот погранслой так потому, что асимптотически он описывается внутри тела оболочки уравнениями эллиптического типа, а граничные условия на поверхностях задаются уравнениями гиперболического типа. Отметим, что построение таких уравнений основано на результатах асимптотического анализа решения и уравнений для классической задачи о волнах Рэлея для упругой полуплоскости [17].

В данной работе систематизировано описание асимптотическим методом нестационарных волн в оболочках вращения при ударных воздействиях на поверхность оболочки и торцевых воздействиях вида NW. Сначала приводятся схемы расчленения нестационарных НДС при этих двух типах воздействий. Затем для каждого вида воздействия выводятся асимптотически оптимальные уравнения эллиптического погранслоя и описываются решения краевых задач для этих погранслоев в случае цилиндрической оболочки. Решения получены с помощью интегральных преобразований Лапласа по времени и Фурье по продольной координате.

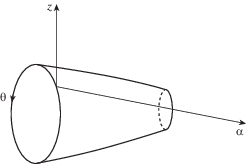
2. Постановка задачи. Рассмотрим оболочку вращения (рис. 1) с криволинейной системой координат (α, θ, z), где α – длина дуги вдоль образующей срединной поверхности, θ – угол в окружном направлении, z – внешняя нормаль к срединной поверхности. Напряжения и перемещения оболочки обозначим, как ${{{{\sigma }}}_{{ij}}}$ и ${{{v}}_{i}}~(i = 1,~2,~3)$ соответственно.

Рис. 1.

Полубесконечная оболочка вращения.

Рассмотрим два вида граничных условий. Первое определяет ударное воздействие на лицевые поверхности бесконечной оболочки $z = \pm h$ (h – полутолщина оболочки), задаваемое граничными условиями

(2.1)

$\begin{gathered} {{{{\sigma }}}_{{33}}} = - {\text{P}}\left( {{{\alpha }},t} \right),\quad {{{{\sigma }}}_{{13}}} = 0\quad {\text{при}}\quad ~z = \pm h,\quad \left| {{\alpha }} \right| \leqslant L \\ {{{{\sigma }}}_{{33}}} = 0,~\quad {{{{\sigma }}}_{{13}}} = 0\quad {\text{при}}\quad z = \pm h,\quad \left| {{\alpha }} \right| > L \\ \end{gathered} $

где $t~$ – время. При этом рассматриваются однородные начальные условия

(2.2)

${{{v}}_{i}} = \frac{{\partial {{{v}}_{i}}}}{{\partial t}} = 0~~(i = 1,~\,\,2,~\,\,3)\quad {\text{при}}\quad t = 0~$

Второй вид граничных условий определяет ударное воздействие на торец и имеет вид

(2.3)

${{{{\sigma }}}_{{13}}} = IH\left( t \right),\quad {{{v}}_{1}} = 0\quad {\text{при}}\quad {{\alpha }} = 0$

где I – амплитуда нагрузки, $H\left( t \right)$ – единичная функция Хевисайда. Начальные условия рассматриваются однородными в виде (2.2), а лицевые поверхности считаются свободными от напряжений:

${{{{\sigma }}}_{{33}}} = {{{{\sigma }}}_{{13}}} = 0\quad {\text{при}}\quad z = \pm h$

Исходные уравнения теории упругости приведены в [7].

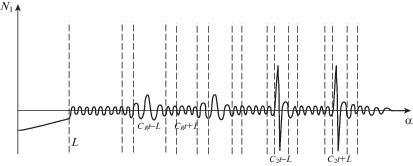
3. Асимптотическая модель нестационарных волн в оболочках вращения при ударных торцевых и поверхностных воздействиях. Схема расчленения нестационарного НДС на составляющие с различными показателями изменяемости при торцевом ударном воздействии с учетом областей согласования впервые приведена в [9] и имеет вид, представленный на рис. 2 для примера перерезывающей силы N₁.

Рис. 2.

Схема расчленения НДС при торцевом воздействии вида NW на примере перерезывающей силы ${{N}_{1}}$.

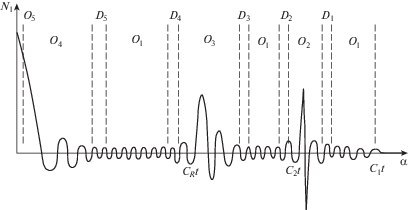
На представленной схеме обозначениями ${{O}_{i}}~(i = \overline {1,~5} )$ и ${{D}_{i}}~(i = \overline {1,~5} )$ изображены схематично области применения приближенных теорий и области согласования этих теорий, где решения совпадают с некоторой асимптотической погрешностью. Здесь в указанных областях действуют: ${{O}_{1}}$ – квазиплоская квазисимметричная задача теории упругости (коротковолновое приближение); ${{O}_{2}}$ – погранслой в окрестности фронта волны сдвига, распространяющегося со скоростью c₂; ${{O}_{3}}$ – погранслой в окрестности квазифронта поверхностной волны Рэлея, распространяющегося со скоростью ${{с}_{R}}$; ${{O}_{4}}$ – изгибное длинноволновое приближение (изгибная составляющая по теории Кирхгофа–Лява); ${{O}_{5}}$ – наложение двумерной изгибной компоненты и квазистатического погранслоя Сен-Венана. Анализ схемы решения показывает, что непрерывный скачок на фронте поверхностной волны Рэлея рассматривается двумерной теорией типа Тимошенко как разрыв решения на фронте сдвиговой волны по этой теории. Таким образом, ошибочность теории типа Тимошенко заключается в неправильной трактовке квазифронта поверхностной волны Рэлея как дополнительного фронта волны сдвига. Схема применения рассмотренных приближенных теорий на фазовой плоскости $\left( {{{\alpha }},t} \right)$ приведена на рис. 3.

Рис. 3.

Схема применения приближенных теории при торцевом воздействии вида NW на фазовой плоскости $\left( {{{\alpha }},t} \right)$.

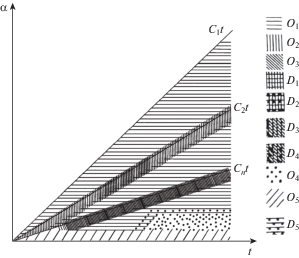
Рассмотрим теперь случай ударного воздействия на поверхность бесконечной оболочки вращения, определяемого граничными условиями (2.1). Отличительной чертой такого нагружения является тот факт, что границы ${{\alpha }} = \pm L$ определяют волны, распространяющиеся в обе стороны от каждой границы. Поэтому, при использовании тех же приближенных теорий, что и в случае торцевого воздействия, картина решения для перерезывающей силы имеет вид, представленный на рис. 4.

Рис. 4.

Схема расчленения НДС при ударном поверхностном воздействии на примере перерезывающей силы.

4. Асимптотические уравнения эллиптического погранслоя при ударном воздействии на лицевые поверхности. Выпишем разрешающие уравнения НДС рассматриваемой оболочки. Для этого введем безразмерные переменные

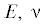${{\xi }} = \alpha {\text{/}}h,\quad {{\zeta }} = z{\text{/}}h,\quad {{\tau }} = t{{с}_{2}}{\text{/}}h,\quad {{с}_{2}} = \sqrt {E{\text{/}}2\left( {1 + {{\nu }}} \right){{\rho }}} $

где

, ${{\rho }}$ – модуль Юнга, коэффициент Пуассона и плотность материала оболочки. Тогда разрешающие уравнения в перемещениях принимают вид

${{\unicode{230} }^{{ - 2}}}\frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{{{\zeta }}}^{2}}}} + \frac{1}{{1 - 2{{\nu }}}}\frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{\xi }}\partial {{\zeta }}}} - \frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{{{\tau }}}^{2}}}} + {{\eta }}\frac{{{\zeta }}}{{{{R}_{1}}}}\left( { - {{\unicode{230} }^{{ - 2}}}\frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}{v}{{v}_{1}}}}{{\partial {{{{\zeta }}}^{2}}}} - \frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{{{\tau }}}^{2}}}}} \right) + $

(4.1)

$ + \,{{\eta }}{{{{\unicode{230} }}}^{{ - 2}}}\frac{{B'}}{B}\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }}}} + {{\eta }}\left( {\frac{1}{{{{R}_{1}}}} + \frac{1}{{{{R}_{2}}}}} \right)\frac{{\partial {{{v}}_{1}}}}{{\partial {{\zeta }}}} + {{\eta }}\left( {\frac{{3 - 4{{\nu }}}}{{1 - 2{{\nu }}}}\frac{1}{{{{R}_{1}}}} + \frac{1}{{1 - 2{{\nu }}}}\frac{1}{{{{R}_{2}}}}} \right)\frac{{\partial {{{v}}_{3}}}}{{\partial {{\xi }}}} = 0,$

$\frac{1}{{1 - 2{{\nu }}}}\frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{\xi }}\partial {{\zeta }}}} + \frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\xi }}}^{2}}}} + {{\unicode{230} }^{{ - 2}}}\frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\zeta }}}^{2}}}} - \frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\tau }}}^{2}}}} + {{\eta }}\frac{{{\zeta }}}{{{{R}_{1}}}}\left( { - \frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\xi }}}^{2}}}} + {{\unicode{230} }^{{ - 2}}}\frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\zeta }}}^{2}}}} - \frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\tau }}}^{2}}}}} \right) - $

$ - \,{{\eta }}\frac{{3 - 4{{\nu }}}}{{1 - 2{{\nu }}}}\frac{1}{{{{R}_{1}}}}\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }}}} + {{\eta }}~\frac{1}{{1 - 2{{\nu }}}}\frac{{B'}}{B}\frac{{\partial {{v}_{1}}}}{{\partial {{\zeta }}}} + {{\eta }}\frac{{B'}}{B}\frac{{\partial {{{v}}_{3}}}}{{\partial {{\xi }}}} + {{\eta }}{{\unicode{230} }^{{ - 2}}}\left( {\frac{1}{{{{R}_{1}}}} + \frac{1}{{{{R}_{2}}}}} \right)\frac{{\partial {{{v}}_{3}}}}{{\partial {{\zeta }}}} = 0$

где B – расстояние до оси вращения; ${{R}_{1}},~{{R}_{2}}$ – главные радиусы кривизн срединной поверхности оболочки; ${{{{\unicode{230} }}}^{2}} = \left( {1 - 2{{\nu }}} \right){\text{/}}\left( {2 - 2{{\nu }}} \right)$. Уравнения связи между напряжениями и перемещениями имеют форму

${{{{\sigma }}}_{{11}}} = \frac{E}{{2\left( {1 + {{\nu }}} \right){{\unicode{230} }^{2}}h}}\left( {\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }}}} + \frac{{{\nu }}}{{1 - {{\nu }}}}\frac{{\partial {{{v}}_{3}}}}{{\partial {{\zeta }}}} + {{\eta }}\left( { - \frac{{{\zeta }}}{{{{R}_{1}}}}\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }}}} + \frac{{{\nu }}}{{1 - {{\nu }}}}\frac{{B'}}{B}{{{v}}_{1}} + \left( {\frac{1}{{{{R}_{1}}}} + \frac{{{\nu }}}{{1 - {{\nu }}}}\frac{1}{{{{R}_{2}}}}} \right){{{v}}_{3}}} \right)} \right)$

${{{{\sigma }}}_{{33}}} = \frac{E}{{2\left( {1 + {{\nu }}} \right){{{{\unicode{230} }}}^{2}}h}}\left( {\frac{{{\nu }}}{{1 - {{\nu }}}}\frac{{\partial {{{v}}_{1}}}}{{\partial {{\xi }}}} + \frac{{\partial {{{v}}_{3}}}}{{\partial {{\zeta }}}} + {{\eta }}\left( { - \frac{{{\nu }}}{{1 - {{\nu }}}}\frac{{{\zeta }}}{{{{R}_{1}}}}\frac{{\partial {{{v}}_{1}}}}{{\partial {{\zeta }}}} + } \right.\frac{{{\nu }}}{{1 - {{\nu }}}}\frac{{B'}}{B}{{{v}}_{1}} + \left. {\frac{{{\nu }}}{{1 - {{\nu }}}}\left( {\frac{1}{{{{R}_{1}}}} + \frac{1}{{{{R}_{2}}}}} \right){{{v}}_{3}}} \right)} \right)$

${{{{\sigma }}}_{{13}}} = \frac{E}{{2\left( {1 + {{\nu }}} \right)h}}\left( {\frac{{\partial {{{v}}_{1}}}}{{\partial {{\zeta }}}} + \frac{{\partial {{{v}}_{3}}}}{{\partial {{\xi }}}} - {{\eta }}\left( {\frac{{{{{v}}_{1}}}}{{{{R}_{1}}}} + \frac{{{\zeta }}}{{{{R}_{2}}}}\frac{{\partial {{{v}}_{3}}}}{{\partial {{\xi }}}}} \right)} \right)$

В уравнениях (4.1) введен малый параметр тонкостенности оболочки ${{\eta }} = h{\text{/}}R$, где $R$ – характерное значение радиусов кривизн.

Предполагается, что рассматриваемая составляющая НДС может быть классифицирована как коротковолновая антисимметричная при единичных значениях показателей изменяемости и динамичности. При этом асимптотически главная составляющая решения является симметричной [14] и асимптотические разрешающие уравнения могут быть записаны в виде

(4.2)

$\frac{1}{{1 - 2{{\nu }}}}\frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{\xi }}\partial {{\zeta }}}} + \frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\xi }}}^{2}}}} + {{{{\unicode{230} }}}^{{ - 2}}}\frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\zeta }}}^{2}}}} - \frac{{{{\partial }^{2}}{{{v}}_{3}}}}{{\partial {{{{\tau }}}^{2}}}} + {{\eta }}~\left( {\frac{1}{{1 - 2{{\nu }}}}\frac{{B'}}{B}\frac{{\partial {{{v}}_{1}}}}{{\partial {{\zeta }}}} + \frac{{B'}}{B}\frac{{\partial {{{v}}_{3}}}}{{\partial {{\zeta }}}}} \right) = 0$

${{{{\sigma }}}_{{13}}} = \frac{E}{{2\left( {1 + {{\nu }}} \right)h}}\left( {\frac{{\partial {{{v}}_{1}}}}{{\partial {{\zeta }}}} + \frac{{\partial {{{v}}_{3}}}}{{\partial {{\xi }}}}} \right)$

Построение уравнения погранслоя было выполнено с помощью символического метода Лурье [18]. Вводя операторы

${{\partial }_{{{\xi }}}} = \frac{\partial }{{\partial {{\xi }}}},\quad {{\partial }_{{{\tau }}}} = \frac{\partial }{{\partial {{\tau }}}}$

можно решить систему (4.2), рассматривая ее как систему обыкновенных дифференциальных уравнений:

(4.3)

${{{v}}_{1}} = {{\partial }_{{{\xi }}}}{{e}^{{ - i\left( {1 - {{\zeta }}} \right){{{{\alpha }}}_{1}}}}}{{D}_{1}} + {{\partial }_{{{\xi }}}}{{e}^{{ - i\left( {1 + {{\zeta }}} \right){{{{\alpha }}}_{1}}}}}{{D}_{2}} + {{{{\beta }}}_{1}}{{e}^{{ - i\left( {1 - {{\zeta }}} \right){{{{\beta }}}_{1}}}}}{{D}_{3}} + {{{{\beta }}}_{1}}{{e}^{{ - i\left( {1 + {{\zeta }}} \right){{{{\beta }}}_{1}}}}}{{D}_{4}}$

${{{v}}_{3}} = i{{{{\alpha }}}_{1}}{{e}^{{ - i\left( {1 - {{\zeta }}} \right){{{{\alpha }}}_{1}}}}}{{D}_{1}} - i{{{{\alpha }}}_{1}}{{e}^{{ - i\left( {1 + {{\zeta }}} \right){{{{\alpha }}}_{1}}}}}{{D}_{2}} + i\left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{e}^{{ - i\left( {1 - {{\zeta }}} \right){{{{\beta }}}_{1}}}}}{{D}_{3}} - $

$ - ~\,i\left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{e}^{{ - i\left( {1 + {{\zeta }}} \right){{{{\beta }}}_{1}}}}}{{D}_{4}}$

где ${{D}_{i}}~(i = \overline {1,~4} )$ – произвольные операторы, ${{{{\alpha }}}_{1}}$ и ${{{{\beta }}}_{1}}$ определяются выражениями

(4.4)

${{\alpha }}_{1}^{2} = \partial _{{{\xi }}}^{2} - {{\unicode{230} }^{2}}\partial _{{{\tau }}}^{2} + {{\eta }}\frac{{B'}}{B}{{\partial }_{{{\xi }}}},\quad {{\beta }}_{1}^{2} = \partial _{{{\xi }}}^{2} - \partial _{{{\tau }}}^{2} + {{\eta }}\frac{{B'}}{B}$

Анализ символического решения (4.4) может быть выполнен на основе прямой аналогии с методами интегральных преобразований Лапласа по времени ${{\tau }}$ и Фурье по пространственной переменной ${{\xi }}$. В рассматриваемом решении слагаемые с множителями ${{e}^{{ - i\left( {1 - {{\zeta }}} \right){{{{\alpha }}}_{1}}}}}$ и ${{e}^{{ - i\left( {1 - {{\zeta }}} \right){{{{\beta }}}_{1}}}}}$ соответствуют волновым составляющим, инициируемым лицевой поверхностью ${{\zeta }} = 1$ и распространяющимся в отрицательном направлении оси ζ, а слагаемые с множителями ${{e}^{{ - i\left( {1 + {{\zeta }}} \right){{{{\alpha }}}_{1}}}}}$ и ${{e}^{{ - i\left( {1 + {{\zeta }}} \right){{{{\beta }}}_{1}}}}}$ – составляющим, инициируемым поверхностью ${{\zeta }} = - 1$ и распространяющимся в положительном направлении оси ${{\zeta }}$.

Подставляя операторное решение (4.3) в граничные условия на лицевых поверхностях, получим систему алгебраических уравнений для операторов ${{D}_{i}}$

${{\gamma }}_{1}^{2}{{D}_{1}} + {{\gamma }}_{1}^{2}{{e}^{{i2{{{{\alpha }}}_{1}}}}}{{D}_{2}} + \left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{{{\beta }}}_{1}}{{D}_{3}} + \left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{{{\beta }}}_{1}}{{e}^{{i2{{{{\beta }}}_{1}}}}}{{D}_{4}} = - P$

(4.5)

${{\gamma }}_{1}^{2}{{e}^{{i2{{{{\alpha }}}_{1}}}}}{{D}_{1}} + {{\gamma }}_{1}^{2}{{D}_{2}} + \left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{{{\beta }}}_{1}}{{e}^{{i2{{{{\beta }}}_{1}}}}}{{D}_{3}} + \left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{{{\beta }}}_{1}}{{D}_{4}} = - P$

${{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{D}_{1}} - {{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{e}^{{i2{{{{\alpha }}}_{1}}}}}{{D}_{2}} + {{\gamma }}_{1}^{2}{{D}_{3}} - {{\gamma }}_{1}^{2}{{e}^{{i2{{{{\beta }}}_{1}}}}}{{D}_{4}} = 0$

${{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{e}^{{i2{{{{\alpha }}}_{1}}}}}{{D}_{1}} - {{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{D}_{2}} + {{\gamma }}_{1}^{2}{{e}^{{i2{{{{\beta }}}_{1}}}}}{{D}_{3}} - {{\gamma }}_{1}^{2}{{D}_{4}} = 0$

где ${{\gamma }}_{1}^{2} = \partial _{{{\xi }}}^{2} - \partial _{{{\tau }}}^{2}{\text{/}}2 + {{\eta }}B'{\text{/}}B$. Анализ уравнений (4.5) показывает [14], что в них можно пренебречь членами с множителями ${{e}^{{ - i2{{{{\alpha }}}_{1}}}}}$ и ${{e}^{{ - i2{{{{\beta }}}_{1}}}}}$, после чего они приобретут следующий вид

${{\gamma }}_{1}^{2}{{D}_{1}} + \left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{{{\beta }}}_{1}}{{D}_{3}} = - P$

(4.6)

${{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{D}_{1}} + {{\gamma }}_{1}^{2}{{D}_{3}} = 0~$

${{\gamma }}_{1}^{2}{{D}_{2}} + \left( {{{\partial }_{{{\xi }}}} + {{\eta }}\frac{{B'}}{B}} \right){{{{\beta }}}_{1}}{{D}_{4}} = - P$

${{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{D}_{2}} + {{\gamma }}_{1}^{2}{{D}_{4}} = 0$

Воспользовавшись методикой модельной работы [17], рассмотрим большие значения времени, когда τ ≫ 1. В этом случае фронты волн проходят расстояние, много больше толщины оболочки. Введем малый параметр ${{\varepsilon }} = 1{\text{/}}T~$ ($T \gg 1,~{{\tau }} = O\left( T \right)$) и переменные, позволяющие построить асимптотику в дальнем поле волны Рэлея:

$y = \frac{{{{\xi }} - {{\unicode{230} }_{R}}{{\tau }}}}{{{\varepsilon }}},\quad {{{{\tau }}}_{0}} = {{\varepsilon \tau }}$

где ${{{{\unicode{230} }}}_{R}} = {{c}_{R}}{\text{/}}{{c}_{2}}$. Введем также новые операторы ${{\partial }_{y}} = \partial {\text{/}}\partial y$, ${{\partial }_{{{{{{\tau }}}_{0}}}}} = \partial {\text{/}}\partial {{{{\tau }}}_{0}}$.

Раскладываем уравнения (4.6) и выражения для перемещений и напряжений в ряд по малому параметру ε. Оставляя в них асимптотически главные части, вернемся к дифференциальной форме искомых уравнений. Введем также объемные и сдвиговые потенциалы Ламе в соответствии с направлением по ${{\zeta }}$ распространения возмущений: ${{{{\varphi }}}_{1}}$ и ${{{{\psi }}}_{1}}$ – отрицательное направление, ${{{{\varphi }}}_{2}}$ и ${{{{\psi }}}_{2}}$ – положительное. Тогда в исходных размерных координатах потенциалы ${{{{\varphi }}}_{{\text{i}}}}$, ${\text{\;}}{{{{\psi }}}_{{\text{i}}}}$ (i = 1, 2) описываются эллиптическими уравнениями

${{a}^{2}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{i}}}}{{\partial {{{{\alpha }}}^{2}}}} + \frac{{{{\partial }^{2}}{{{{\varphi }}}_{i}}}}{{\partial {{z}^{2}}}} = 0$

${{b}^{2}}\frac{{{{\partial }^{2}}{{{{\psi }}}_{i}}}}{{\partial {{{{\alpha }}}^{2}}}} + \frac{{{{\partial }^{2}}{{{{\psi }}}_{i}}}}{{\partial {{z}^{2}}}} = 0$

при следующих граничных условиях на лицевых поверхностях

$\frac{{{{\partial }^{2}}{{{{\Psi }}}_{i}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{1}{{c_{R}^{2}}}\frac{{{{\partial }^{2}}{{{{\Psi }}}_{i}}}}{{\partial {{t}^{2}}}} + {{\eta }}\frac{1}{{\unicode{230} _{R}^{2}}}\frac{{B'}}{B}\frac{{\partial {{{{\Psi }}}_{i}}}}{{\partial {{\alpha }}}} = \frac{{\left( {1 + \nu } \right){{B}_{{{\omega }}}}}}{{Eh{{\unicode{230} }_{R}}b}}P,\quad z = \pm h$

$\left( {a + \frac{{{{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{i}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{{{{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2ac_{R}^{2}}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{i}}}}{{\partial {{t}^{2}}}} + {{\eta }}\frac{1}{{2a}}\frac{{B'}}{B}\frac{{\partial {{{{\varphi }}}_{i}}}}{{\partial {{\alpha }}}} + $

$ + \left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}{{{{\psi }}}_{i}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{{\unicode{230} _{R}^{2}}}{{2c_{R}^{2}}}\frac{{{{\partial }^{2}}{{{{\psi }}}_{i}}}}{{\partial {{t}^{2}}}} + {{\eta }}\frac{{B'}}{B}\frac{{\partial {{{{\psi }}}_{i}}}}{{\partial {{\alpha }}}} = 0,\quad z = \pm h$

Перемещения и напряжения выражаются через потенциальные функции следующим образом:

${{{v}}_{1}} = h\left( {\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial {{\alpha }}}} + \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial {{\alpha }}}} + b\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial {{\alpha }}}} + b\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial {{\alpha }}}}} \right)$

${{{v}}_{3}} = h\left( {\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} + \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} + \frac{1}{b}\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} + \frac{1}{b}\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}}} \right)$

${{{{\sigma }}}_{{33}}} = - \frac{{Eh}}{{1 + {{\nu }}}}\left( {{{L}_{3}}\left( {{{{{\varphi }}}_{1}}} \right) + {{L}_{3}}\left( {{{{{\varphi }}}_{2}}} \right) + {{L}_{4}}\left( {{{{{\psi }}}_{1}}} \right) + {{L}_{4}}\left( {{{{{\psi }}}_{2}}} \right)} \right)$

${{{{\sigma }}}_{{13}}} = \frac{{Eh}}{{1 + {{\nu }}}}\left( {\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial {{\alpha }}\partial z}} + \frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial {{\alpha }}\partial z}} + \frac{g}{b}\frac{{{{\partial }^{2}}{{{{\psi }}}_{1}}}}{{\partial {{\alpha }}\partial z}} + \frac{g}{b}\frac{{{{\partial }^{2}}{{{{\psi }}}_{2}}}}{{\partial {{\alpha }}\partial z}}} \right)$

где операторы ${{L}_{3}}$, ${{L}_{4}}$ задаются выражениями

${{L}_{3}} = \left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{{\unicode{230} _{R}^{2}}}{{2c_{R}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + {{\eta }}\frac{{B'}}{B}\frac{\partial }{{\partial {{\alpha }}}}$

${{L}_{4}} = \left( {b + \frac{{\unicode{230} _{R}^{2}}}{{2b}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{{\unicode{230} _{R}^{2}}}{{2bc_{R}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + {{\eta }}\left( {b + \frac{1}{{2b}}} \right)\frac{{B'}}{B}\frac{\partial }{{\partial {{\alpha }}}}$

5. Асимптотические уравнения эллиптического погранслоя при ударном торцевом воздействии вида NW. Задачу о нестационарных волнах в полубесконечных оболочках вращения при ударных торцевых воздействиях удобно свести к задаче о таких волнах в бесконечных оболочках при ударных воздействиях на их лицевые поверхности путем выделения частного решения волнового типа, удовлетворяющего только торцевым граничным условиям [16]. Найти такое медленно изменяющееся по продольной координате и времени частное решение для исходных уравнений с переменными коэффициентами можно с помощью простейшего метода прифронтовой асимптотики путем его разложения по степеням отклонения от фронта сдвиговой волны:

(5.1)

${v}_{1}^{{\left( 0 \right)}} = 0,\quad {v}_{3}^{{\left( 0 \right)}} = - I\mathop \sum \limits_{n = 1}^\infty {{F}_{n}}\left( {{{{{\xi }}}_{0}}} \right){{\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)}^{n}}H\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)~$

где ${{F}_{n}}\left( {{{{{\xi }}}_{0}}} \right)$ – искомые функции, а безразмерные переменные определяются следующим образом: ${{{{\xi }}}_{0}} = {{\alpha /}}R$, ${{{{\tau }}}_{0}} = t{{c}_{2}}{\text{/}}R$. Подставляя (5.1) в разрешающие уравнения (4.1), получаем следующие уравнения для искомых функций:

$2\frac{{d{{F}_{n}}}}{{d{{{{\xi }}}_{0}}}} + \frac{{B'}}{B}{{F}_{n}} = \frac{1}{n}\left( {\frac{{{{d}^{2}}{{F}_{{n - 1}}}}}{{d{{\xi }}_{0}^{2}}} + \frac{{B'}}{B}\frac{{d{{F}_{{n - 1}}}}}{{d{{{{\xi }}}_{0}}}}} \right)$

Для функций ${{F}_{n}}\left( {{{{{\xi }}}_{0}}} \right)$ найдена форма, которая при учете граничных условий (2.3) определяет рассматриваемое частное решение в виде

${v}_{1}^{{\left( 0 \right)}} = 0,~\quad {v}_{3}^{{\left( 0 \right)}} = - \frac{{2\left( {1 + {{\nu }}} \right)hI}}{E}\left[ {\sqrt {\frac{{B\left( 0 \right)}}{B}} \left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right) + \mathop \sum \limits_{n = 2}^\infty {{F}_{n}}\left( {{{{{\xi }}}_{0}}} \right){{{\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)}}^{n}}} \right]H\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)$

${{\sigma }}_{{11}}^{{\left( 0 \right)}} = {{\sigma }}_{{33}}^{{\left( 0 \right)}} = 0,\quad {{\sigma }}_{{13}}^{{\left( 0 \right)}} = I\left[ {\sqrt {\frac{{B\left( 0 \right)}}{B}} + \mathop \sum \limits_{n = 2}^\infty (n{{F}_{n}}\left( {{{{{\xi }}}_{0}}} \right) - F_{{n - 1}}^{'}\left( {{{{{\xi }}}_{0}}} \right)){{{\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)}}^{{n - 1}}}} \right]H\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)$

${{F}_{1}} = \frac{1}{{\sqrt B }}$

${{F}_{n}} = \frac{1}{{2n\sqrt B }}\mathop \smallint \limits_0^{{{{{\xi }}}_{0}}} \frac{1}{{\sqrt B }}\frac{d}{{d{{{{\xi }}}_{0}}}}\left( {\frac{1}{B}\frac{{d{{F}_{{n - 1}}}}}{{d{{{{\xi }}}_{0}}}}} \right)d{{{{\xi }}}_{0}},\quad n \geqslant 2$

где индексом ⁽⁰⁾ обозначено решение частной задачи.

Представим решение исходной задачи в виде

$SSS = SS{{S}^{{\left( 0 \right)}}} + SS{{S}^{{\left( 1 \right)}}}$

с граничными условиями для $SS{{S}^{{\left( 1 \right)}}}$ в виде

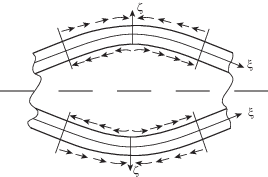
$\frac{{\partial {v}_{3}^{{\left( 1 \right)}}}}{{\partial {{\xi }}}} = 0,\quad {v}_{1}^{{\left( 1 \right)}} = 0,\quad {{\xi }} = 0$

(5.2)

${{\sigma }}_{{33}}^{{\left( 1 \right)}} = 0,\quad {{\sigma }}_{{13}}^{{\left( 1 \right)}} = - S,\quad z = \pm h$

$S = \pm I\left[ {\sqrt {\frac{{B\left( 0 \right)}}{B}} + \mathop \sum \limits_{n = 2}^\infty (n{{F}_{n}} - F_{{n - 1}}^{'}{{{\left( {{{{{\tau }}}_{0}} \mp {{{{\xi }}}_{0}}} \right)}}^{{n - 1}}})} \right]H\left( {{{{{\tau }}}_{0}} \mp {{{{\xi }}}_{0}}} \right)$

где знаки “$ \pm $” и “$ \mp $” соответствуют в представлении для S области ${{\alpha }} > 0$ (верхний знак) и ${{\alpha }} < 0$ (нижний знак).

Граничные условия (5.2) определяют форму торцевого сечения деформируемой оболочки: торец остается прямолинейным и перпендикулярным оси ξ. Следовательно, деформация такой оболочки эквивалентна деформации каждой симметричной относительно оси ζ части бесконечной оболочки, изображенной на рис. 5. Следовательно, для удобства решения возможно перейти к исследованию задачи для $SS{{S}^{{\left( 1 \right)}}}$, которую назовем эквивалентной.

Рис. 5.

Эквивалентная задача для полубесконечной оболочки.

Для рассматриваемой эквивалентной задачи отличие в построении разрешающих уравнений искомого погранслоя от случая, рассмотренного в разделе 4 поверхностного нормального воздействия на лицевые поверхности, заключается в отличии граничных условий: здесь воздействие на лицевые поверхности является касательным. Следовательно, при выводе искомых разрешающих уравнений символическим методом Лурье вместо уравнений (4.5) следует записать граничные условия в следующей форме:

$i{{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{D}_{1}} - i{{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{e}^{{i2{{{{\alpha }}}_{1}}}}}{{D}_{2}} + i{{\gamma }}_{1}^{2}{{D}_{3}} - i{{\gamma }}_{1}^{2}{{e}^{{i2{{{{\beta }}}_{1}}}}}{{D}_{4}} = - S$

$i{{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{e}^{{i2{{{{\alpha }}}_{1}}}}}{{D}_{1}} - i{{\partial }_{{{\xi }}}}{{{{\alpha }}}_{1}}{{D}_{2}} + i{{\gamma }}_{1}^{2}{{e}^{{i2{{{{\beta }}}_{1}}}}}{{D}_{3}} - i{{\gamma }}_{1}^{2}{{D}_{4}} = - S$

Тогда использование методики, изложенной для предыдущего типа эллиптического погранслоя, дает следующий вид граничных условий на лицевых поверхностях и выражений для перемещений и напряжений:

$\frac{{{{\partial }^{2}}{{{{\chi }}}_{m}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{1}{{c_{R}^{2}}}\frac{{{{\partial }^{2}}{{{{\chi }}}_{m}}}}{{\partial {{t}^{2}}}} + \frac{{{{k}_{c}}}}{{{{\unicode{230} }}_{R}^{2}}}\frac{{B'}}{B}\frac{{\partial {{{{\chi }}}_{m}}}}{{\partial {{\alpha }}}} = \frac{{{{B}_{{{\omega }}}}}}{{g{{{{\unicode{230} }}}_{R}}}}\frac{{\partial S}}{{\partial {{\alpha }}}},\quad z = \mp h$

$\left( {g + \frac{{{{\unicode{230} }}_{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{m}}}}{{\partial {{{{\alpha }}}^{2}}}} - \frac{{{{\unicode{230} }}_{R}^{2}}}{{2c_{R}^{2}}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{m}}}}{{\partial {{t}^{2}}}} + \frac{{B'}}{B}\frac{{\partial {{{{\varphi }}}_{m}}}}{{\partial {{\alpha }}}} + \left( {b + \frac{{{{\unicode{230} }}_{R}^{2}}}{{2b}}} \right)\frac{{{{\partial }^{2}}{{{{\psi }}}_{m}}}}{{\partial {{{{\alpha }}}^{2}}}} - $

$ - \frac{{{{\unicode{230} }}_{R}^{2}}}{{2bc_{R}^{2}}}\frac{{{{\partial }^{2}}{{{{\psi }}}_{m}}}}{{\partial {{t}^{2}}}} + \left( {b + \frac{1}{{2b}}} \right)\frac{{B'}}{B}\frac{{\partial {{{{\psi }}}_{m}}}}{{\partial {{\alpha }}}} = 0,\quad z = \mp h$

(5.3)

${{{v}}_{1}} = h\left( {\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial {{\alpha }}}} + \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial {{\alpha }}}} + b\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial {{\alpha }}}} + b\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial {{\alpha }}}}} \right)$

${{{v}}_{3}} = h\left( {\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} + \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} + \frac{1}{b}\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial z}} + \frac{1}{b}\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial z}}} \right)$

${{{{\sigma }}}_{{33}}} = - \frac{{Eh}}{{1 + {{\nu }}}}\left( {g\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial {{{{\alpha }}}^{2}}}} + g\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial {{{{\alpha }}}^{2}}}} + b\frac{{{{\partial }^{2}}{{{{\psi }}}_{1}}}}{{\partial {{{{\alpha }}}^{2}}}} + b\frac{{{{\partial }^{2}}{{{{\psi }}}_{2}}}}{{\partial {{{{\alpha }}}^{2}}}}} \right)$

${{{{\sigma }}}_{{13}}} = \frac{{Eh}}{{1 + {{\nu }}}}\left( {\frac{1}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial {{\alpha }}\partial z}} + \frac{{{{{{\unicode{230} }}}^{2}}{{\unicode{230} }}_{R}^{2}}}{{{{a}^{2}}{{c}_{R}}}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial z\partial t}} + \frac{1}{{2{{a}^{2}}}}\frac{{B'}}{B}\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} + \frac{1}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial {{\alpha }}\partial z}} + \frac{{{{{{\unicode{230} }}}^{2}}{{\unicode{230} }}_{R}^{2}}}{{{{a}^{2}}{{c}_{R}}}}\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial z\partial t}} + \frac{1}{{2{{a}^{2}}}}\frac{{B'}}{B}\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} + } \right.$

$\left. { + \frac{{g + {{\unicode{230} }}_{R}^{2}}}{b}\frac{{{{\partial }^{2}}{{{{\psi }}}_{1}}}}{{\partial {{\alpha }}\partial z}} + \frac{{{{\unicode{230} }}_{R}^{2}}}{{b{{c}_{R}}}}\frac{{{{\partial }^{2}}{{{{\psi }}}_{1}}}}{{\partial z\partial t}} + \frac{1}{b}\frac{{B'}}{B}\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial z}} + \frac{{g + {{\unicode{230} }}_{R}^{2}}}{b}\frac{{{{\partial }^{2}}{{{{\psi }}}_{2}}}}{{\partial {{\alpha }}\partial z}} + \frac{{{{\unicode{230} }}_{R}^{2}}}{{b{{c}_{R}}}}\frac{{{{\partial }^{2}}{{{{\psi }}}_{2}}}}{{\partial z\partial t}} + \frac{1}{b}\frac{{B'}}{B}\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial z}}} \right)$

где

${{{{\chi }}}_{1}} = \frac{h}{b}\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial z}},\quad {{{{\chi }}}_{2}} = - \frac{h}{b}\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial z}}$

${{B}_{{{\omega }}}} = 2{{\left[ {\frac{{{{{{\unicode{230} }}}_{R}}}}{{1 - {{\unicode{230} }}_{R}^{2}}} + \frac{{{{\unicode{230} }}{{{{\unicode{230} }}}_{R}}}}{{1 - {{{{\unicode{230} }}}^{2}}{{\unicode{230} }}_{R}^{2}}} - \frac{{4{{{{\unicode{230} }}}_{R}}}}{{2 - {{\unicode{230} }}_{R}^{2}}}} \right]}^{{ - 1}}}$

6. Анализ решений для эллиптического погранслоя при нормальных поверхностных и торцевых ударных воздействиях. Рассмотрим эллиптический погранслой в цилиндрической оболочке в случае ударного воздействия на лицевые поверхности вида (2.1), где нагрузка $P$ определяется следующим образом

$P = pH\left( {L - {{\xi }}} \right)H\left( {{\tau }} \right)\quad {\text{при}}\quad {{\xi }} \geqslant 0$

$P = pH\left( {L + {{\xi }}} \right)H\left( {{\tau }} \right)\quad {\text{при}}\quad {{\xi }} \leqslant 0$

где p, L – постоянные.

Будем рассматривать только волну, инициируемую лицевой поверхностью $z = - h$, (${{\zeta }} = - 1$) и определяемую потенциалами ${{{{\varphi }}}_{1}}$, ${{{{\psi }}}_{1}}$. Тогда разрешающие уравнения для этой составляющей НДС запишутся в виде (индекс “1” у потенциальных функций будем опускать)

(6.1)

${{a}^{2}}\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\zeta }}}^{2}}}} = 0~$

${{b}^{2}}\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\zeta }}}^{2}}}} = 0$

(6.2)

${{\unicode{230} }}_{R}^{2}\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\tau }}}^{2}}}} = \frac{{\left( {1 + {{\nu }}} \right)h}}{E}\frac{{{{\unicode{230} }_{R}}{{B}_{{{\omega }}}}}}{b}P,\quad {{\zeta }} = - 1$

$\left( {a + \frac{{{{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}} \right)\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{{{{\unicode{230} }^{2}}}}{{2a}}\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\tau }}}^{2}}}} + \left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{1}{2}\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\tau }}}^{2}}}} = 0,~\quad {{\zeta }} = - 1$

(6.3)

${{{v}}_{1}} = \frac{{\partial {{\varphi }}}}{{\partial {{\xi }}}} + b\frac{{\partial {{\psi }}}}{{\partial {{\xi }}}},\quad {{{v}}_{3}} = \frac{{\partial {{\varphi }}}}{{\partial {{\zeta }}}} + \frac{1}{b}\frac{{\partial {{\psi }}}}{{\partial {{\zeta }}}}$

${{\sigma }_{{33}}} = - \frac{E}{{\left( {1 + {{\nu }}} \right)h}}\left( {\left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{1}{2}\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\tau }}}^{2}}}} + \left( {b + \frac{{\unicode{230} _{R}^{2}}}{{2b}}} \right)\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{1}{{2b}}\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\tau }}}^{2}}}}} \right)$

${{{{\sigma }}}_{{13}}} = \frac{E}{{\left( {1 + {{\nu }}} \right)h}}\left( {\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{\xi }}\partial {{\zeta }}}} + \frac{g}{b}\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{\xi }}\partial {{\zeta }}}}} \right)$

где $a = \sqrt {1 - {{\unicode{230} }^{2}}\unicode{230} _{R}^{2}} ,b = \sqrt {1 - \unicode{230} _{R}^{2}} $, ${{\unicode{230} }_{R}} = {{c}_{R}}{\text{/}}{{c}_{2}}$, $g = 1 - \unicode{230} _{R}^{2}{\text{/}}2$.

Для решения рассматриваемой граничной задачи применим интегральное преобразование Лапласа по времени и преобразование Фурье по продольной координате. Тогда уравнения (6.1)–(6.3) преобразуются к виду

(6.4)

$ - {{a}^{2}}{{{{\chi }}}^{2}}{{{{\varphi }}}^{{LF}}} + \frac{{{{\partial }^{2}}{{{{\varphi }}}^{{LF}}}}}{{\partial {{{{\zeta }}}^{2}}}} = 0~$

$ - {{b}^{2}}{{{{\chi }}}^{2}}{{{{\psi }}}^{{LF}}} + \frac{{{{\partial }^{2}}{{{{\psi }}}^{{LF}}}}}{{\partial {{{{\zeta }}}^{2}}}} = 0$

(6.5)

$(\unicode{230} _{R}^{2}{{{{\chi }}}^{2}} + {{s}^{2}}){{{{\Psi }}}^{{LF}}} = - \frac{{\left( {1 + {{\nu }}} \right)h}}{E}\frac{{{{\unicode{230} }_{R}}{{B}_{{{\omega }}}}}}{b}P,\quad {{\zeta }} = - 1$

$\left[ {\left( {a + \frac{{{{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}} \right){{{{\chi }}}^{2}} + \frac{{{{\unicode{230} }^{2}}}}{{2a}}{{s}^{2}}} \right]{{{{\varphi }}}^{{LF}}} + \left[ {\left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right){{{{\chi }}}^{2}} + \frac{1}{2}{{s}^{2}}} \right]{{{{\psi }}}^{{LF}}} = 0,\quad {{\zeta }} = - 1$

${{\sigma }}_{{33}}^{{LF}} = \frac{E}{{\left( {1 + {{\nu }}} \right)h}}\left[ {\left( {\left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right){{{{\chi }}}^{2}} + \frac{1}{2}{{s}^{2}}} \right){{\varphi }}_{1}^{{LF}} + \left( {\left( {b + \frac{{\unicode{230} _{R}^{2}}}{{2b}}} \right){{{{\chi }}}^{2}} + \frac{1}{2}{{s}^{2}}} \right){{{{\Psi }}}^{{LF}}}} \right]$

где индексы L и F обозначают интегральные преобразования Лапласа и Фурье соответственно:

${{{{\varphi }}}^{F}} = \frac{1}{{\sqrt {2{{\pi }}} }}\mathop \smallint \limits_{ - \infty }^\infty {{\varphi }}{{e}^{{ - i{{\chi \xi }}}}}d{{\xi }},\quad {{{{\varphi }}}^{L}} = \mathop \smallint \limits_0^\infty {{\varphi }}{{e}^{{ - s{{\tau }}}}}d{{\tau }}$

Решая уравнения (6.4) с учетом граничных условий (6.5), получаем выражение для изображения искомого напряжения ${{\sigma }_{{33}}}$:

(6.6)

Асимптотический анализ оригиналов для изображения (6.6) показывает [14, 15], что искомое решение для напряжения ${{\sigma }_{{33}}}$ может быть записано в виде

(6.7)

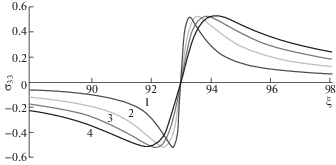
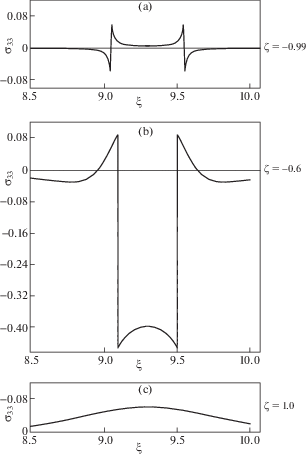
${{{{\sigma }}}_{{33}}} = p\frac{{{{B}_{{{\omega }}}}}}{{\sqrt {2{{\pi }}} {{\unicode{230} }_{R}}}}\left[ { - {\text{arctg}}\left( {\frac{{2La\left( {1 + {{\zeta }}} \right)}}{{{{a}^{2}}{{{\left( {1 + {{\zeta }}} \right)}}^{2}} - {{L}^{2}} + {{{\left( {{{\xi }} - {{\unicode{230} }_{R}}{{\tau }}} \right)}}^{2}}}}} \right)} \right. + ~$

$\left. { + \,{\text{arctg}}\left( {\frac{{2Lb\left( {1 + {{\zeta }}} \right)}}{{{{b}^{2}}{{{\left( {1 + {{\zeta }}} \right)}}^{2}} - {{L}^{2}} + {{{\left( {{{\xi }} - {{\unicode{230} }_{R}}{{\tau }}} \right)}}^{2}}}}} \right)} \right]$

На рис. 6 представлены графики зависимости напряжения ${{{{\sigma }}}_{{33}}}$ (6.7) от продольной координаты ${{\xi }}$ для окрестностей условных фронтов волн Рэлея ${{\xi }} = {{\unicode{230} }_{R}}{{\tau }} + L$, ${{\xi }} = {{\unicode{230} }_{R}}{{\tau }}$ – L.

Рис. 6.

Графики зависимости напряжения ${{{{\sigma }}}_{{33}}}$ от продольной координаты ${{\xi }}$ в момент времени ${{\tau }} = 10$ при $L = 0.25$ и при различных значениях нормальной координаты ${{\zeta }} = - 0.99$ (а), ${{\zeta }} = - 0.6$ (b), ${{\zeta }} = 1.0$ (c).

Здесь видно свойство убывания решения при удалении от этих фронтов. Также видно, как эволюционирует решение в зависимости от нормальной координаты. Рассмотрим теперь эллиптический погранслой в цилиндрической оболочке в случае ударного воздействия на торец.

Тогда частное решение для $SS{{S}^{{\left( 0 \right)}}}$ принимает вид

(6.8)

${v}_{1}^{{\left( 0 \right)}} = 0,\quad {v}_{3}^{{\left( 0 \right)}} = - \frac{{\left( {1 + {{\nu }}} \right)h}}{E}I\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)H\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)~$

${{\sigma }}_{{11}}^{{\left( 0 \right)}} = {{\sigma }}_{{33}}^{{\left( 0 \right)}} = 0,\quad {{\sigma }}_{{13}}^{{\left( 0 \right)}} = IH\left( {{{{{\tau }}}_{0}} - {{{{\xi }}}_{0}}} \right)$

Рассмотрим далее эквивалентную задачу и, как ранее, только волну, инициируемую лицевой поверхностью $z = - h$, (${{\zeta }} = - 1$). Тогда разрешающие уравнения при ${{\xi }} \geqslant 0$ сохраняют форму (6.1), а граничные условия при ${{\zeta }} = - 1$ и выражение для напряжения σ₁₃ при ${{\xi }} > 0$ записываются следующим образом:

(6.9)

$\unicode{230} _{R}^{2}\frac{{{{\partial }^{2}}{{\chi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{{{{\partial }^{2}}{{\chi }}}}{{\partial {{{{\tau }}}^{2}}}} = \frac{{{{\unicode{230} }_{R}}{{B}_{{{\omega }}}}}}{g}IH\left( {{{\tau }} - {{\xi }}} \right),\quad {{\zeta }} = - 1$

$\left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{1}{2}\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\tau }}}^{2}}}} + \left( {b + \frac{{{{\unicode{230} }_{R}}}}{2}} \right)\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{1}{{2b}}\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{{{\tau }}}^{2}}}} = 0,\quad {{\zeta }} = - 1$

Выражение для σ₁₃ в (5.3) не позволяет использовать интегральное преобразование Фурье по продольной координате. В этом случае мы будем использовать альтернативную форму [16]

$\frac{{\partial {{{{\sigma }}}_{{13}}}}}{{\partial {{\zeta }}}} = \frac{E}{{\left( {1 + {{\nu }}} \right)h}}\left( {\frac{{2 - {{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}\frac{{{{\partial }^{2}}{{\chi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{{{{\unicode{230} }^{2}}{{\unicode{230} }_{R}}}}{{2a}}\frac{{{{\partial }^{2}}{{\chi }}}}{{\partial {{{{\tau }}}^{2}}}} + \frac{{{{\partial }^{2}}{{\Psi }}}}{{\partial {{{{\xi }}}^{2}}}} - \frac{1}{2}\frac{{{{\partial }^{2}}{{\Psi }}}}{{\partial {{{{\tau }}}^{2}}}}} \right),\quad {{\Psi }} = \frac{1}{b}\frac{{\partial {{\psi }}}}{{\partial {{\zeta }}}}$

Тогда аналогично предыдущему случаю получаем решение для погранслоя

${{{{\sigma }}}_{{13}}} = - I + \frac{{{{B}_{{{\omega }}}}}}{{{{\pi }}{{\unicode{230} }_{R}}{{b}^{2}}}}\left[ { - {\text{arctg}}\left( {\frac{{2a{{\xi }}\left( {1 + {{\zeta }}} \right)}}{{{{a}^{2}}{{{\left( {1 + {{\zeta }}} \right)}}^{2}} - {{{{\xi }}}^{2}} + \unicode{230} _{R}^{2}{{{{\tau }}}^{2}}}}} \right)} \right. + ~$

$\left. { + \,{\text{arctg}}\left( {\frac{{2b{{\xi }}\left( {1 + {{\zeta }}} \right)}}{{{{b}^{2}}{{{\left( {1 + {{\zeta }}} \right)}}^{2}} - {{{{\xi }}}^{2}} + \unicode{230} _{R}^{2}{{{{\tau }}}^{2}}}}} \right)} \right]$

Зависимость напряжения от продольной координаты ξ в малой окрестности фронта волны Рэлея показана на рис. 7 для момента времени τ = 100. Здесь видно стремление суммарного решения к нулю при удалении от этого фронта.

Рис. 7.

Напряжение ${{{{\sigma }}}_{{13}}}$ в момент времени ${{\tau }} = 100$ для ${{\zeta }} = - 0.5~$; 0; 0.5; 1 (номера 1–4, соответственно).

Список литературы

Nigul U. Regions of effective application of the methods of three-dimensional and two-dimensional analysis of transient stress waves in shells and plates // Int. J. Solid Struct. 1969. V. 5. № 6. P. 607–627. https://doi.org/10.1016/0020-7683(69)90031-6
Нигул У.К. О методах и результатах анализа переходных волновых процессов изгиба упругой плиты // Изв. АН ЭССР. Сер. физ.-мат. техн. наук. 1965. № 3. С. 345–384.
Нигул У.К. О применимости приближенных теорий при переходных процессах деформаций круговых цилиндрических оболочек // Тр. 6-й Всесоюз. конф. по теории оболочек и пластин. М., 1966. С. 593–599.
Нигул У.К. Сопоставление результатов анализа переходных волновых процессов в оболочках и пластинах по теории упругости и приближенным теориям // ПММ. 1969. Т. 33. Вып. 2. С. 308–322.
Айнола Л.Я., Нигул У.К. Волновые процессы деформации упругих плит и оболочек // Изв. АН Эст. ССР. Сер. физ.-мат. техн. наук. 1965. Т. 14. № 1. С. 3–63.
Коссович Л.Ю. Нестационарные задачи теории упругих тонких оболочек. Саратов: Изд-во Сарат. ун-та, 1986. 176 с.
Kaplunov J.D., Kossovich L.Yu., Nolde E.V. Dynamics of thin walled elastic bodies. San Diego: Academic Press, 1998. 226 p.
Коссович Л.Ю., Каплунов Ю.Д. Асимптотический анализ нестационарных упругих волн в тонких оболочках вращения при ударных торцевых воздействиях // Изв. Сарат. ун-та, 2001. Т. 1. № 2. С. 111–131.
Kossovich L.Yu., Kirillova I.V. Dynamics of shells under shock loading: an asymptotic approach // Proceedings of the Ninth International Conference on Computational Structures Technology. Stirlingshire, UK: Civil-Comp Press, 2008. Paper 207. P. 1–20.
Kossovich L.Yu., Kirillova I.V. Transient waves in shells of revolution under normal shock loading // Topical Problems in Theoretical and Applied Mechanics. New Delhi: Elite Publishion House, LTD, India, 2013. P. 186–200.
Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука, 1976. 512 с.
Гольденвейзер А.Л., Лидский В.Б., Товстик П.Е. Свободные колебания тонких упругих оболочек. М.: Наука, 1979. 384 с.
Кириллова И.В., Коссович Л.Ю. Асимптотическая теория волн в тонких упругих оболочках при ударных нагрузках тангенциального, изгибающего и нормального видов // Доклады XI Всероссийской конференции по фундаментальным проблемам теоретической и прикладной механике. Казань: Изд-во Казанского ун-та, 2015. С. 2008–2015.
Кириллова И.В., Коссович Л.Ю. Уточненные уравнения эллиптического погранслоя в оболочках вращения при ударных поверхностных воздействиях нормального типа // Вестн. СПбГУ. Мат. Мех. 2017. Т. 4 (62). С. 113–120. https://doi.org/10.21638/11701/spbu01/2017/113
Кириллова И.В., Коссович Л.Ю. Асимптотические методы исследования эллиптического погранслоя в оболочках вращения при ударных торцевых нагрузках эллиптического типа // Изв. РАН. МТТ. 2020. № 5. С. 131–137. https://doi.org/10.31857/S0572329920050104
Kirillova I.V., Kossovich L.Yu. Elliptic boundary layer in shells of revolution under normal edge shock loading // (eds) Multiscale Solid Mechanics – Strength, Durability and Dynamics. Advanced Structured Materials / Ed. by H. Altenbach, V.A. Eremeyev, L.A. Igumnov. Cham: Springer, 2021. V. 141. P. 249–360.
Каплунов Ю.Д., Коссович Л.Ю. Асимптотическая модель для вычисления дальнего поля волны Рэлея в случае упругой полуплоскости // Докл. АН. 2004. Т. 395. № 4. С. 482–484.
Лурье А.И. Пространственные задачи теории упругости. М.: Гостехиздат, 1955. 491 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал