Известия РАН. Механика твердого тела, 2022, № 2, стр. 90-98

Введение. Нахождение критических состояний адгезионных слоев в композиционных материалах основано на классическом представлении трещиноподобного дефекта в виде математического разреза [1–3]. В этом случае продолжение математического разреза в массив слоистого композита ассоциируется с адгезионным слоем нулевой толщины. Отсутствие материального объема в адгезиве не дает возможности рассматривать его реальные механические свойства при построении соответствующих моделей деформирования. Как и для механики квазихрупкого разрушения основными моделями здесь являются либо сингулярная трещина Гриффитса либо когезионная трещина Баренблатта [4].

Введение в модель адгезионного слоя толщины [5–7] дает возможность отразить его реальные механические свойства. Однако в этом случае возникает вопрос о влиянии данных свойств на критическое вешнее воздействие. Определение предельных состояний тонких, но конечных адгезионных слоев в данной работе связываем с нахождением J_C-интеграла [5]. В работе обсуждаются результаты исследования линейно-упругой модели поведения адгезионного слоя и модели с линейным распределением поля напряжений в зоне ослабленных связей слоя на значение J_C-интеграла.

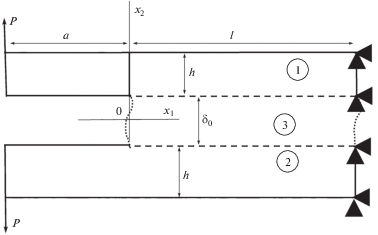
1. Постановка задачи. На рис. 1 показано нагружение нормальным отрывом двухконсольной балки (ДКБ-образца) длиной $l + a$ с тонким адгезионным слоем конечной толщины ${{{{\delta }}}_{0}}$. Тела 1 и 2 с одинаковыми толщинами $h$ связаны по длине $l$ адгезивом. Материал пластин принимаем линейно упругим, с нулевым коэффициентом Пуассона. Правый торец образца жестко закреплен от горизонтальных и вертикальных перемещений, на левых торцах консолей действует вертикальная симметричная нагрузка интенсивностью ${\mathbf{P}}$. Вся остальная поверхность образца свободна от внешней нагрузки. Рассматривается состояние плоской деформации.

Для описания взаимодействия адгезива 3 с телами 1 и 2 применим концепцию “слоя взаимодействия”, развитую в [5, 6]. В этом случае условия равновесия тел 1 и 2 запишем в вариационной форме для тела 1:

и тела 2: где $ \cdot \cdot $ – двойное скалярное умножение; $ \cdot $ – скалярное умножение; ${{S}_{1}}$, ${{S}_{2}}$ – площади тел 1 и 2; ${\mathbf{\sigma }}$, ${\mathbf{\varepsilon }}$ – тензоры напряжений и деформаций; ${\mathbf{\bar {\sigma }}}$ – тензор средних напряжений слоя; ${\mathbf{\bar {\varepsilon }}}$ – тензор средних деформаций слоя с компонентами: где $u_{k}^{ \pm }$ – компоненты векторов перемещений верхней и нижней границ слоя соответственно; $i = 1,2$; ${{L}_{1}},{{L}_{2}}$ – граница приложения внешней нагрузки для тела 1 и 2. Постулируется жесткое сцепление между границами области 3 и областями 1, 2.

Для материала пластин 1 и 2 примем определяющие соотношения в форме закона Гука с нулевым коэффициентом Пуассона:

где $E$ – модуль упругости; $j = 1,2$.

Предполагаем, что напряженное состояние слоя для данного вида нагружения однородно по его толщине и определятся одной компонентой тензора средних напряжений ${{{{\bar {\sigma }}}}_{{22}}}{\text{,}}{{{{\bar {\sigma }}}}_{{11}}} = {{{{\bar {\sigma }}}}_{{12}}} = {\text{0}}$, что соответствует представлению связей Прандтля [8–10].

В силу симметрии задачи проекции поля перемещений удовлетворяют условиям $u_{1}^{1}\left( {{{x}_{1}},{{x}_{2}}} \right) = u_{1}^{2}\left( {{{x}_{1}},{{x}_{2}}} \right) = {{u}_{1}}\left( {{{x}_{1}},{{x}_{2}}} \right)$, $u_{2}^{1}\left( {{{x}_{1}},{{x}_{2}}} \right) = - u_{2}^{2}\left( {{{x}_{1}},{{x}_{2}}} \right) = {{u}_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right)$, а вектор распределенной внешней нагрузки – ${{{\mathbf{P}}}^{{\mathbf{1}}}}{\mathbf{ = }} - {{{\mathbf{P}}}^{{\mathbf{2}}}}{\mathbf{ = P}}$. Таким образом, достаточно ограничиться рассмотрением тела 1. С учетом ограничения на напряженное состояние в слое система уравнений (1)–(2) преобразуется в вариационное уравнение:

Решение уравнения (1.6) с учетом (1.5) и заданных определяющих соотношений в слое сводится к нахождению поля перемещений ${\mathbf{u}}\left( {{{x}_{{\text{1}}}}{\text{,}}\,{{x}_{{\text{2}}}}} \right)$ в теле 1 (см. рисунок) c учетом граничных условий на его торцах:

Для упрощения задачи принимаем, что поле перемещений в теле 1 определено следующим образом:

Входящий в представление (1.9) параметр ${{\varphi }}$ имеет геометрический смысл малого угла поворота материальной нормали к плоскости ${{x}_{2}} = {{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}$ в теле 1. Согласно распределению (1.9) деформации в консоли будут определяться в виде:

Выражения (1.10) подобно теории Тимошенко [11] и работам [12, 13], учитывают сдвиговые деформации и повороты нормалей в теле.

Подставив (1.10) в (1.6) и приравняв слагаемые при равных вариациях, приходим к двум системам дифференциальных уравнений равновесия для участка ${{x}_{1}} \in \left[ { - a;{\text{0}}} \right)$:

для участков ${{x}_{1}} \in \left( {0;l} \right]$: с условиями сопряжения:

${{\left. {u_{1}^{ + }} \right|}_{{{{x}_{1}} = - {\text{0}}}}} = {{\left. {u_{1}^{ + }} \right|}_{{{{x}_{1}} = + {\text{0}}}}}$, ${{\left. {{\varphi }} \right|}_{{{{x}_{1}} = - {\text{0}}}}} = {{\left. {{\varphi }} \right|}_{{{{x}_{1}} = + {\text{0}}}}}$, ${{\left. {u_{2}^{ + }} \right|}_{{{{x}_{1}} = - {\text{0}}}}} = {{\left. {u_{2}^{ + }} \right|}_{{{{x}_{1}} = + 0}}}$, ${{\left. {{{M}_{{11}}}} \right|}_{{{{x}_{1}} = - {\text{0}}}}} = {{\left. {{{M}_{{11}}}} \right|}_{{{{x}_{1}} = + {\text{0}}}}}$, ${{\left. {{{Q}_{{12}}}} \right|}_{{{{x}_{1}} = - {\text{0}}}}}$ = = ${{\left. {{{Q}_{{12}}}} \right|}_{{{{x}_{1}} = + {\text{0}}}}}$, ${{\left. {{{Q}_{{11}}}} \right|}_{{{{x}_{1}} = - {\text{0}}}}} = {{\left. {{{Q}_{{11}}}} \right|}_{{{{x}_{1}} = + {\text{0}}}}}$ и естественным граничным условиям на левом торце:

На правом торце из (1.7), (1.8) с учетом (1.11), (1.12) рассматриваем граничные условия:

где ${{Q}_{{11}}}({{x}_{{\text{1}}}}) = \int\limits_{{{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}}^{h + {{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}} {{{{{\sigma }}}_{{11}}}d{{x}_{2}}} ,$ ${{Q}_{{12}}}({{x}_{1}}) = \int\limits_{{{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}}^{h + {{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}} {{{{{\sigma }}}_{{12}}}d{{x}_{2}}} $ – обобщенные силы; M₁₁(x₁) = = $\int\limits_{{{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}}^{h + {{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2}} {{{{{\sigma }}}_{{11}}}({{x}_{2}} - {{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} 2}} \right. \kern-0em} 2})d{{x}_{2}}} $ – обобщенный момент.

С учетом (1.10) и условия плоской деформации (${{{{\varepsilon }}}_{{33}}} = {\text{0}}$), определяющие соотношения (1.5) для тела 1 представим в виде:

Запишем выражения обобщенных сил и момента с учетом (1.15):

В результате задача (1.11)–(1.16), (1.6) с учетом определяющих соотношений для адгезива становится замкнутой относительно трех неизвестных функций: $u_{1}^{ + }\left( {{{x}_{1}}} \right)$, $u_{2}^{ + }\left( {{{x}_{{\text{1}}}}} \right)$, ${{\varphi }}\left( {{{x}_{{\text{1}}}}} \right)$.

2. Упругое деформирование слоя. Полагаем определяющие соотношения для адгезива в виде:

где E₃ – модуль упругости материала слоя.

Рассмотрим решение задачи на участке сопряжения слоя и консоли. Из системы уравнений (1.11) осуществим перенос граничных условий (1.13) в точку ${{x}_{1}} = {\text{0}}$:

Полагая ${{{{E}_{3}}} \mathord{\left/ {\vphantom {{{{E}_{3}}} E}} \right. \kern-0em} E} \geqslant {{6{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{6{{{{\delta }}}_{0}}} h}} \right. \kern-0em} h}$, запишем решение (1.12) для участка ${{x}_{1}} \in \left( {{\text{0}};l \to \infty } \right)$ в виде [14]:

Из (2.3) найдем вертикальное перемещение в вершине слоя:

Рассмотрим представление (2.4) при условии ${{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} h}} \right. \kern-0em} h} \ll 1$

Из (1.3), (2.1) и последнего выражения находим значение напряжения в вершине слоя:

Из работы [5] следует выражение J_C-интеграла через критические значения термомеханических характеристик и толщину слоя в торцевом сечении адгезива:

где ${{{{\rho }}}_{{\text{0}}}}{{{{\psi }}}_{k}}$ – критическое изменение удельной свободной энергии торцевого сечения; ${{{{\rho }}}_{{\text{0}}}}{{w}_{k}}$ – критическое изменение удельной диссипации торцевого сечения.

В случае упругого деформирования выражение (2.6) приводит к связи J-интеграла с энергетическим произведением (ЭП) [6] $J = 2{{\gamma }} = {{{{\delta }}}_{{\text{0}}}}{{{{\rho }}}_{{\text{0}}}}{{\psi }}$. Для одноосного напряженного состояния в слое из (2.6) находим: $J = 2{{\gamma }} = \frac{{{{\bar {\sigma }}}_{{{\text{22}}}}^{{\text{2}}}}}{{2{{E}_{{\text{3}}}}}}{{{{\delta }}}_{{\text{0}}}}$.

С учетом (2.5) получаем:

В [15] для слоя нулевой толщины найдено выражение потока упругой энергии в рамках теории пластин с учетом сдвиговых деформаций. При ${{\nu }} = {\text{0}}$ выражение потока упругой энергии принимает вид:

Таким образом закон распределения поля перемещений в виде (1.9) дает близкий результат к решению на основе теории пластин.

Согласно данным работы [16] для образца со следующими геометрическими и механическими характеристиками: $a = {\text{0}}{\text{.055}}$ м, $h = {\text{0}}{\text{.0127}}$ м, $b = {\text{0}}{\text{.025}}$ м, $E = {\text{2}} \times {\text{1}}{{{\text{0}}}^{{11}}}$ Па, где b – толщина образца, оценим значение ${{G}_{1}} = $ ${{G}_{{IC}}}$ в момент инициализации трещины при критической внешней нагрузке. В работе [6] приведены экспериментальные значения внешней нагрузки при инициализации трещины в адгезиве, которые составили ${{P}_{{cr}}} = {\text{1}}{\text{.1}}$ кН для смолы Araldite AV138, ${{P}_{{cr}}} = {\text{1}}{\text{.5}}$ кН для смолы Araldite 2015, ${{P}_{{cr}}} = {\text{3}}{\text{.1}}$ кН для смолы Sikaforce 7752.

Следуя данным работы [16], приведем в табл. 1 механические характеристики ряда адгезивов согласно данным производителя.

В табл. 1 приняты следующие обозначения: ${{G}_{{IC}}}$ – критический поток энергии; ${{{{\sigma }}}_{0}}$– предел текучести; ${{{{\sigma }}}_{f}}$ – предел прочности.

В этом случае ${{Q}_{2}} = {{Q}_{{cr}}} = {{{{P}_{{cr}}}} \mathord{\left/ {\vphantom {{{{P}_{{cr}}}} b}} \right. \kern-0em} b}$ где ${{Q}_{{cr}}}$ – критическое значение внешней нагрузки. Поместим в табл. 2 результаты расчета по формулам (2.7) и (2.8).

Из данных табл. 1, табл. 2 видно, что чем более выраженные пластические свойства имеет адгезив, тем большее занижение критического потока энергии дает результат расчета по упругой модели. При этом для адгезива Sikaforce 7752 результат может отличаться значительно.

Отметим, что полученный результат предполагает, согласно (2.5), сингулярное распределение поля напряжений при ${{{{\delta }}}_{0}} \to {\text{0}}$. Рассмотрим построение J-интеграла при аппроксимации поля перемещений в консоли (1.9), с учетом конечности напряженного состояния и учета реальных механических свойств адгезива.

3. Решение задачи с учетом конечности напряженного состояния адгезива. Для материала слоя 3 определяющие соотношения при обратимом деформировании, когда ${{{{\bar {\sigma }}}}_{{22}}} \leqslant {{{{\sigma }}}_{0}}$, принимаем в виде (2.5). Стадия упругого деформирования продолжается до момента достижения в точке x₁ = 0 слоя взаимодействия предела текучести ${{{{\bar {\sigma }}}}_{{22}}} = {{{{\sigma }}}_{0}}$. Из формулы (2.5) находим значение внешней нагрузки в этот момент

Из данной формулы следует, что стадия чисто обратимого деформирования при отсутствии диссипации возможна при конечном значении толщины адгезива. В случае вырождения в математический разрез стадия упругого деформирования, как и в модели Дагдейла [17], отсутствует.

Увеличение внешней нагрузки ${{Q}_{2}} > {{Q}_{{2p}}}$ приводит к образованию зоны ослабленных связей длиной $\Delta $. Данный участок ассоциируем с проявлением пластических свойств адгезива. При достижении внешней нагрузкой критического значения $\left( {{{Q}_{2}} = {{Q}_{{cr}}}} \right)$ длина зоны ослабленных связей достигает величины $\Delta = {{\Delta }_{{cr}}}$.

Распределение напряжений для участка ослабленных связей принимаем в виде:

Условия равновесия (1.15) для участка консоли ${{x}_{1}} \in \left( {0;\Delta } \right)$ запишем с учетом (3.1) в виде:

Осуществим перенос граничных условий (2.2) в точку ${{x}_{1}} = \Delta $ с учетом (3.2):

Запишем решение (1.12) на участке ${{x}_{1}} \in \left( {\Delta ;l \to \infty } \right)$ для случая ${{{{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{0}}} h}} \right. \kern-0em} h} \ll 1$ в виде:

Из (3.4) запишем выражение вертикального перемещения в точке ${{x}_{1}} = \Delta $:

и с учетом (1.3), (2.1) напряжения в слое:

Основной неизвестной предлагаемой модели поведения адгезива является значение ${{\Delta }_{{cr}}}$.

Из (3.6) получим выражение критической длины зоны ослабленных связей при условиях: ${{Q}_{2}} = {{Q}_{{cr}}}$, $\Delta = {{\Delta }_{{cr}}}$, ${{{{\bar {\sigma }}}}_{{22}}}\left( \Delta \right) = {{{{\sigma }}}_{0}}$ и известном значении k:

где $С = \frac{h}{{\sqrt 6 \left( {1 + \frac{{2k}}{{3{{{{\sigma }}}_{0}}}}} \right)}}$.

При ${{{{\delta }}}_{0}} = {\text{0}}$ выражение (3.7) может рассматриваться в качестве длины когезионной трещины [4] с конечностью напряженного состояния в точке сопряжения сил сцепления и поврежденной среды.

Запишем решение (3.2) в области ослабленных связей $0 \leqslant {{x}_{1}} < \Delta $. С учетом (1.16) и граничных условий (3.3) получим

где ${{c}_{1}},{{c}_{2}},{{c}_{3}}$ – постоянные интегрирования.

Постоянные интегрирования найдем из условий непрерывности функций $u_{1}^{ + },u_{2}^{ + },{{\varphi }}$ в точке ${{x}_{1}} = \Delta $ с учетом решения (3.4):

В критическом состоянии выражение (2.6) принимает вид:

где $u_{2}^{f}$ – предельное значение перемещения в точке ${{x}_{1}} = {\text{0}}$; $u_{2}^{f} = {{c}_{3}}\left( {{{\Delta }_{{cr}}}} \right)$.

Нахождение (3.9) показывает, что имеет место вычислительная сходимость результата при ${{{{\bar {\delta }}} = {{{{\delta }}}_{0}}} \mathord{\left/ {\vphantom {{{{\bar {\delta }}} = {{{{\delta }}}_{0}}} h}} \right. \kern-0em} h} \to {\text{0}}$. Так для ${{\bar {\delta }}} \leqslant {\text{1}}{{{\text{0}}}^{{ - 5}}}$ значение (3.9) практически не меняется. Приведем в табл. 3 расчетные данные J_C – интеграла для ${{\bar {\delta }}} = {\text{1}}{{{\text{0}}}^{{ - 10}}}$ и характеристик адгезивов из табл. 1.

Сравнивая результаты расчетов J_C – интеграла по упругой модели (см. табл. 2) и модели, учитывающей конечность напряженного состояния (см. табл. 3), с критическим потоком упругой энергии из табл. 3 видим, что модель с зоной ослабленных связей лучше согласуется с экспериментальными данными для адгезивов с выраженными пластическими свойствами.

Заключение. При заданном законе распределения поля перемещений в консолях ДКБ-образца для упругого поведения материала слоя получено аналитическое выражение J-интеграла. Данное решение не зависит от модуля упругости адгезива и практически совпадает с известным решением в рамках теории пластин для адезионного слоя нулевой толщины.

Для материала адгезива, учитывающего конечность напряженного состояния, найдена аналитическая зависимость J_C-интеграла от предела текучести и предела прочности материала адгезива. Показано, что при малой, но конечной относительной толщине слоя, имеет место сходимость J_C-интеграла. Для заданной длины трещины и критической внешней нагрузке адгезива Sikaforce 7752 с выраженными пластическими свойствами значение J_C-интеграла существенно (в 1.7 раза) отличается от значения, найденного при упругом поведении материала слоя.

Исследование выполнено при финансовой поддержке РФФИ и правительства Тульской области в рамках научного проекта № 19-41-710001 р_а.