Известия РАН. Механика твердого тела, 2022, № 2, стр. 154-162
ОПТИМАЛЬНАЯ СИСТЕМА ПОДВЕСКИ ДЛЯ МОДАЛЬНЫХ ИСПЫТАНИЙ БАЛКИ С УЛЬТРАНИЗКИМИ ЧАСТОТАМИ УПРУГИХ КОЛЕБАНИЙ
В. А. Бужинский a, *, С. Ю. Гаев a, **
a Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Россия
* E-mail: buzhinsky.valery@yandex.ru
** E-mail: gaev.syu@phystech.edu
Поступила в редакцию 28.07.2021
После доработки 04.09.2021
Принята к публикации 05.09.2021
- EDN: IVZIKO
- DOI: 10.31857/S0572329922020088
Аннотация
Представлены результаты теоретического исследования влияния систем струнной и пружинно-струнной подвески при модальных испытаниях балки с ультранизкими частотами упругих колебаний. Целью испытаний является определение собственных частот и форм упругих колебаний балки в условиях невесомости. Рассматривается традиционный способ вывешивания с точками подвеса в центре масс или за концы выделенных однородных участков балки. Предлагается струнная подвеска, матрица жесткости которой пропорциональна матрице масс балки для линейной аппроксимации форм колебаний на выделенных участках подвески. При этом определение собственных частот и форм упругих колебаний балки в условиях невесомости основывается на свойстве сохранения собственных векторов и сдвиге собственных значений линейных систем на постоянную величину. Проведением численных экспериментов установлено, что такая система подвески обеспечивает высокую точность воспроизведения собственных форм колебаний в условиях невесомости при небольшом числе точек подвеса. Собственная частота определяется из результатов модальных испытаний по простой формуле с погрешностью на порядок меньше, чем при традиционном способе подвески.
Балки являются типовыми элементами многих космических конструкций: выносных штанг, на конце которых располагаются измерительные приборы; каркасов панелей солнечных батарей; рефлекторов радиотелескопов. Проведение наземных модальных испытаний таких крупногабаритных космических конструкций, имеющих низкие до 0.05 Гц частоты упругих колебаний, сопряжено со значительными техническими трудностями. В наземных условиях эти конструкции не держат свой собственный вес и под действием силы тяжести сильно деформируются, что может привести к их разрушению.
Общие проблемы механики и оптимизации динамических свойств больших космических конструкций рассмотрены в [1]. Динамические модели этих конструкций создаются методом конечных элементов с использованием современных программных комплексов типа NASTRAN. Для синтеза динамической модели космического аппарата в целом конечно-элементные модели входящих в него конструкций упрощают применением статической конденсации Гайана–Айронса и динамической редукции Крейга–Бемптона [2]. Отсутствие вполне надежных сведений о конструкционных свойствах новых используемых материалов, сложное моделирование узлов соединений раскрываемых элементов конструкции вызывает необходимость экспериментального уточнения конечно-элементных моделей путем проведения модальных испытаний [3, 4]. В этих испытаниях определяются также модальные коэффициенты демпфирования, которые характеризуют важные диссипативные свойства конструкций.
При проведении модальных испытаний сохранение формы конструкций, которую они имеют в условиях невесомости, обеспечивается системами подвески. Самыми простыми и наиболее часто применяемыми являются системы струнной или пружинно-струнной подвески. Для исключения влияния системы подвески на определяемые при модальных испытаниях собственные формы и частоты упругих колебаний обычным является требование снижения частоты конструкции на подвеске в несколько раз ниже ее низшей собственной частоты упругих колебаний в условиях невесомости [5]. Выполнить это требование для многих перспективных космических конструкций невозможно из-за их весьма низкой жесткости.
При вертикальном вывешивании конструкции по консольной схеме, что не всегда возможно, сохраняется ее форма для условий невесомости, но не исключается влияние сил тяжести на ее колебания, нагружаются элементы конструкции и узлы соединения, что нежелательно, так как приводит к изменению демпфирующих сил. Разработка систем подвески с активной компенсацией сил тяжести специальными управляемыми устройствами – сложная техническая проблема [6, 7]. Включение системы подвески в расчетную схему конечно-элементной модели, если не сохраняются формы упругих колебаний для условий невесомости, может привести к недостоверному определению модальных коэффициентов демпфирования.
В настоящей работе исследуется влияние струнной и пружинно-струнной подвески на собственные частоты и формы упругих колебаний балки с ультранизкими собственными частотами. Рассматриваются стандартная система такой подвески, когда балка подразделяется на отдельные участки, с точками подвески в центре или на концах каждого из них, и предлагаемая легко реализуемая оптимальная система подвески. Метод компенсации влияния подвески основывается на свойствах линейных систем. Применение оптимальной подвески с высокой точностью сохраняет формы упругих колебаний для условий невесомости и освобождает от необходимости удовлетворять часто невыполнимому требованию по снижению жесткости подвески.
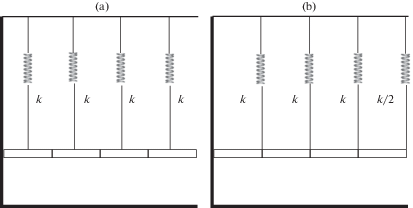
1. Упругая подвеска балки на струнах. Балка подразделяется на однородные участки с постоянной жесткостью и погонной массой. Точки подвески струн располагаются в центре каждого из этих участков. Натяжение каждой струны ${{T}_{n}}$ участка $n$ равно весу этого участка балки ${{m}_{n}}g$, где ${{m}_{n}}$ – масса, $g$ – ускорение свободного падения. Если при модальных испытаниях колебания возбуждаются в вертикальной плоскости, то в систему струн необходимо внести пружины. Жесткости пружин ${{k}_{n}}$ выбираются пропорционально массам участков балки, т.е. ${{k}_{n}} = \omega _{*}^{2}{{m}_{n}}$. Если струны принять нерастяжимыми, то частота ${{\omega }_{ * }}$ характеризует жесткость упругой подвески. Статическое удлинение пружин в состоянии равновесия $\Delta w = {{m}_{n}}g{\text{/}}{{k}_{n}} = g{\text{/}}\omega _{*}^{2}$. Даже для снижения частоты $\nu _{*}^{{}} = \omega _{*}^{{}}{\text{/}}(2\pi )$ до 0.3 Гц это удлинение составляет 2.8 м. Схема подвески консольной балки показана на рис. 1, a.
Рис. 1.
Схема подвески балки: a – в центре обезвешиваемых участков, b – на концах обезвешиваемых участков.
Если при модальных испытаниях колебания возбуждаются в горизонтальном направлении, то пружины в подвеске не требуются. Действующая в точке подвеса восстанавливающая сила ${{F}_{n}} = {{w}_{n}}{{T}_{n}}{\text{/}}{{\ell }_{n}} = {{w}_{n}}{{m}_{n}}g{\text{/}}{{\ell }_{n}}$, где ${{w}_{n}}$ – перемещение точки подвеса, ${{\ell }_{n}}$ – длина струны подвеса. Если длины всех струн одинаковы и равны $\ell $, то в этом случае $\omega _{*}^{2} = g{\text{/}}\ell $. При длине струн 10 м частота ${{\nu }_{ * }} \approx 0.16$ Гц. Обеспечить требуемое снижение частоты $\nu _{*}^{{}}$ при струнной подвеске для колебаний в горизонтальном направлении существенно проще.
Если в линейной системе матрицы жесткости и масс изменяются пропорционально матрице масс исходной системы, то задача на собственные значения записывается в виде
Из эквивалентного представления этой задачи
следует, что собственные формы не изменяются, а собственные значения $\omega _{n}^{2}$ и $\Omega _{n}^{2}$ исходной задачи $Kw = {{\omega }^{2}}Mw$ и новой задачи (1.1) связаны соотношениемЗаметим, что для выбранного способа подвески вносимая дополнительная матрица жесткости пропорциональна матрице масс для кусочно-постоянной аппроксимации формы упругих колебаний балки между точками подвеса с коэффициентом пропорциональности $\beta = \omega _{*}^{2}$. Массы системы струнной подвески весьма малы. Но при необходимости обеспечить требуемую пропорциональность этих масс матрице масс балки достаточно просто. Равенство (1.2) выполняется тем точнее, чем больше число точек подвеса, т.е. чем точнее кусочно-постоянная аппроксимация низшей формы упругих колебаний. С увеличением точек подвеса низшая форма упругих колебаний балки приближается к форме в условиях невесомости. Для получения удовлетворительных результатов может потребоваться достаточно большое число точек подвески.
2. Оптимальная система подвески. Очевидный интерес представляет система подвески, в которой точки подвеса выбраны на концах однородных участков балки. Как и выше принимаем, что в струнной подвеске одинаковы длины все струн, а в пружинно-струнной подвеске все пружины имеют одинаковое статические удлинение.
Сила веса каждого участка балки ${{T}_{n}} = {{m}_{n}}g$ распределяется поровну на струны на его концах. Натяжение струны на стыке участков будет $({{m}_{{n - 1}}} + {{m}_{n}})g{\text{/}}2$. На свободном конце балки натяжение струны равно половине веса участка. Для консольной балки реакция в заделке $R = {{m}_{1}}g{\text{/}}2$, где m1 – масса примыкающего к ней участка. Если T натяжение какой-либо струны в пружинно-струнной подвеске, то соответствующая жесткость пружины $k = T{\text{/}}\Delta w$, где $\Delta w$ – ее статическое удлинение. Такая схема подвески консольной балки показана на рис. 1, b.
Условие пропорциональности матрицы жесткости, вносимой такой подвеской, матрице масс балки не выполняются даже для кусочно-постоянной аппроксимации формы упругих колебаний между точками подвеса. Поэтому погрешность определения частоты по формуле (1.2) будет выше. Низшая форма упругих колебаний сильнее отклоняется от формы в условиях невесомости, чем с подвеской в центре участков балки.
Будем называть оптимальной такую подвеску, для которой ее матрица жесткости пропорциональна матрице масс балки на каждом ее участке при линейной аппроксимации формы упругих колебаний на этом участке. Внесем в подвеску дополнительные струны в центре каждого из участков балки. Струну на стыке участков можно мысленно разделить на две струны, каждая из которых служит для компенсации веса своего участка. Натяжения этих струн на концах участка обозначим ${{T}_{{n,1}}}$, ${{T}_{{n,2}}}$, натяжение струны в центре участка – ${{T}_{{n,0}}}$. Для выбранного участка энергия деформации пружин подвески записывается в виде
где(2.2)
${{k}_{1}} = {{T}_{{n,1}}}{\text{/}}\Delta w,\;{{k}_{2}} = {{T}_{{n,2}}}{\text{/}}\Delta w,\;{{k}_{0}} = {{T}_{{n,0}}}{\text{/}}\Delta w$Форму колебаний балки на участке представим линейной аппроксимацией
(2.3)
$E = (\dot {w}_{1}^{2} + {{\dot {w}}_{1}}{{\dot {w}}_{2}} + \dot {w}_{2}^{2}){{m}_{n}}{\text{/}}6$Подставляя в (2.1) ${{w}_{0}} = ({{w}_{1}} + {{w}_{2}}){\text{/}}2$, получим
(2.4)
$U = [({{k}_{1}} + {{k}_{0}}{\text{/}}4)w_{1}^{2} + {{k}_{0}}\,{{w}_{1}}{{w}_{2}}{\text{/}}2 + \left( {{{k}_{2}} + {{k}_{0}}{\text{/}}4} \right)]{\text{/}}2$Сравнивая (2.3) и (2.4), находим, что для пропорциональности матриц масс и жесткости должны выполняться условия
Эти условия выполняются, если ${{k}_{1}} = {{k}_{2}} = {{k}_{0}}{\text{/}}4$.
Из (2.2) следует ${{T}_{{n,1}}} = {{T}_{{n,2}}} = {{T}_{{n,0}}}{\text{/}}4$. Сумма сил натяжения равна весу участка балки, поэтому
И для струнной и для пружинно-струнной подвески коэффициенты жесткости пружин удобно представить в виде
(2.5)
${{k}_{1}} = {{k}_{2}} = {{m}_{n}}\omega _{*}^{2}{\text{/}}6,\quad {{k}_{0}} = 2{{m}_{n}}\omega _{*}^{2}{\text{/}}3$3. Результаты численных экспериментов. Модальные испытания балки на системе подвески заменялись численным экспериментом. Собственные частоты и формы упругих колебаний определялись численно с использованием программных пакетов MATLAB и NX.NASTRAN. Полученные при этом значения принимались за экспериментально определенные собственные частоты ${{\Omega }_{n}}$ и формы упругих колебаний балки на системе подвески. Собственные частоты балки в невесомости ${{\omega }_{n}}$ определялись по формуле (1.2), в которой $\beta = \omega _{*}^{2}$. Частота ${{\omega }_{ * }}$ согласно (2.5) характеризует жесткость подвески. Вносимые системой подвески изменения масс не учитывались, т.е. в (1.2) принималось $\alpha = 0$. Возможные погрешности экспериментального определения собственных частот ${{\Omega }_{n}}$ также не учитывались.
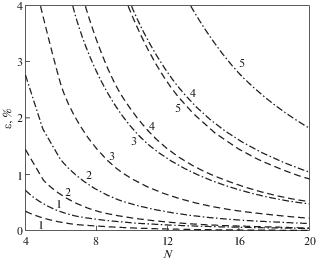
Погрешности определения по формуле (1.2) собственной частоты ${{\omega }_{1}}$ упругих колебаний однородной консольной балки в численном эксперименте, имитирующем модальные испытания балки, приведены на рис. 2. Балка подразделялась на участки одинаковой длины. Исследовались схемы подвески с присоединением ее струн в центре масс участков и к концам участков. Как видно, погрешность определения частоты ${{\omega }_{1}}$ в схеме с подвеской в центре участков вдвое ниже. Приведены абсолютные величины погрешности, но для подвески в центре участков получаются заниженные значения частоты ${{\omega }_{1}}$, а при подвеске за концы участков – завышенные значения частоты ${{\omega }_{1}}$.
Рис. 2.
Погрешность $\varepsilon $ определения собственной частоты низшей формы упругих колебаний балки в невесомости в зависимости от числа точек подвески N при различной жесткости систем подвески: 1 – ${{\omega }_{*}}{\text{/}}{{\omega }_{1}}$ = = 0.5, 2 – $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}} = 1$, 3 – $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}} = 2$, 4 – $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}} = 3$, 5 – $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}} = 4$. Штриховые линии – точки подвески в центре участков, штрихпунктирные линии – точки подвески на концах участков.
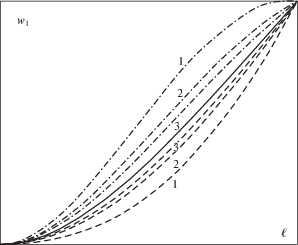
На рис. 3 показано влияние систем подвески на низшую форму упругих колебаний балки. Для большей наглядности результаты приведены для отношения ${{\omega }_{ * }}{\text{/}}{{\omega }_{1}} = 6$. Как видно, подвеска в центре выделенных участков, на которые подразделяется балка, и за концы этих участков по-разному влияет на форму упругих колебаний. При подвеске в центре участков погрешность определения формы упругих колебаний вдвое меньше. С увеличением числа точек подвески форма колебаний приближается к форме упругих колебаний балки в невесомости.
Рис. 3.
Влияние числа точек подвески N на низшую форму упругих колебаний балки в невесомости: 1 – $N = 4$, 2 – $N = 6$, 3 – $N = 8$. Формы колебаний: сплошная линия – в невесомости, штриховые линии – точки подвески в центре участков, штрихпунктирные линии – точки подвески на концах участков.
Приводимые погрешности определялись сравнением с аналитическим решением [8]. В частности, собственные частоты однородной консольной балки в невесомости
Применение оптимальной системы подвески позволяет определить собственные частоты и формы упругих колебаний балки с весьма высокой точностью при малом числе точек подвеса и высоком отношении частот $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}}$. Погрешности определения по формуле (1.2) собственной частоты ${{\omega }_{1}}$ упругих колебаний однородной консольной балки в численном эксперименте, имитирующем модальные испытания балки, приведены на рис. 4. Балка подразделялась на участки одинаковой длины. Точки подвеса располагались на концах и в центре участков, а жесткости задавались по формуле (2.5). В оптимальной схеме число точек подвеса четное. Для наглядности дискретные точки погрешности соединены отрезками прямых линий. Цифрами обозначено отношение частот $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}}$.
Рис. 4.
Погрешность $\varepsilon $ определения собственной частоты низшей формы упругих колебаний балки в невесомости в зависимости от числа точек подвески N при различной жесткости оптимальной системы подвески: $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}}$ = 1, 2, 3, 4, 5.
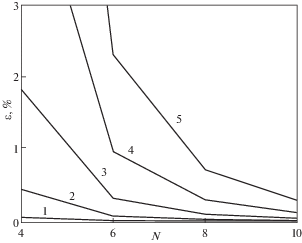
Из сравнения результатов, представленных на рис. 2 и рис. 4, следует, что при оптимальной схеме подвески погрешность определения частоты снижается на порядок. Например, если жесткость системы подвески такова, что $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}} = 4$, то в оптимальной схеме при количестве точек подвески $N = 10$ низшая частота по формуле (1.2) определяется с погрешностью $\varepsilon \approx 0.2$%, а в обычной схеме с подвеской в центре участков и с тем же количеством точек подвески с погрешностью $\varepsilon \approx 4$%, т.е. погрешность уменьшается в 20 раз.
Выше приведены результаты анализа влияния систем подвески на определение низшей частоты и формы упругих колебаний балки. С увеличением номера моды колебаний $n$ отношение частот $\omega _{*}^{{}}{\text{/}}{{\omega }_{n}}$ уменьшается, поэтому точность определения частоты ${{\omega }_{n}}$ и соответствующей формы упругих колебаний балки существенно повышается.
Приведем некоторые результаты анализа применения оптимальной системы подвески для модальных испытаний неоднородной консольной тонкостенной штанги кругового поперечного сечения с грузом на ее свободном конце. Схема штанги и ее подвески показана на рис. 5. Штанга состоит из однородного участка длиной $\ell {\text{/}}4$, примыкающего к заделке, и однородного участка длиной $3\ell {\text{/}}4$. Ограничимся рассмотрением системы вывешивания с шестью точками подвеса. Второй однородный участок штанги при этом подразделяется на два участка одинаковой длины. Определяемые по формулам (2.5) жесткости подвески слева направо от заделки:
Рис. 5.
Схема оптимальной подвески неоднородной балки с грузом на конце. Точки подвески на концах и в центре трех участков.
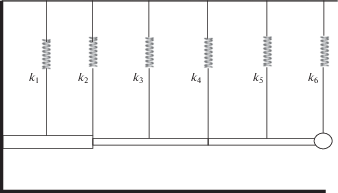
Ниже в табл. 1 представлены результаты численного эксперимента, имитирующего модальные испытания штанги длиной $\ell = 20$ метров. Геометрические и физические параметры примыкающего к заделке первого участка штанги: внешний радиус поперечного сечения 30 мм, толщина стенки 1 мм, модуль Юнга $E = 2.1$ × 1011 Н/м2, плотность $\rho = 7800$ кг/м3. Геометрические и физические параметры второго участка штанги: внешний радиус поперечного сечения 20 мм, толщина стенки 1 мм, модуль Юнга $E = 2.1$ × 1011 Н/м2, плотность $\rho = 7800$ кг/м3. Масса груза на конце штанги ${{m}_{0}} = 10$ кг, что приблизительно в три разе меньше массы штанги. Расчеты выполнены в программном пакете Femap с решателем NX.NASTRAN для отношения частот $\omega _{*}^{{}}{\text{/}}{{\omega }_{1}} \approx 5$. Приняты следующие обозначения: ${{\omega }_{n}}$ – частота моды колебаний штанги в невесомости; ${{\Omega }_{n}}$ – частота моды колебаний, полученная в модальных испытаниях с оптимальной системой подвески; ${{\sigma }_{n}}$ – оценка частоты моды колебаний по формуле (1.2); n – номер моды колебаний; $\varepsilon $ – погрешность оценки в процентах.
Таблица 1.
Результаты численного эксперимента, имитирующего модальные испытания штанги с оптимальной системой подвески. Значения частот в герцах, погрешности в процентах
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| ${{\Omega }_{n}}{\text{/}}(2\pi )$ | 0.3841 | 0.7076 | 1.708 | 3.321 | 5.695 |
| ${{\omega }_{n}}{\text{/}}(2\pi )$ | 0.07533 | 0.5974 | 1.656 | 3.296 | 5.677 |
| ${{\sigma }_{n}}{\text{/}}(2\pi )$ | 0.07414 | 0.5989 | 1.666 | 3.300 | 5.682 |
| $\varepsilon $ | –1.6 | 0.26 | 0.60 | 0.11 | 0.089 |
Как видно из представленных в таблице данных, применение при модальных испытаниях оптимальной подвески штанги весьма эффективно даже в том случае, когда в этих испытаниях частота низшей моды колебаний штанги в пять раз выше частоты низшей моды колебаний штанги в невесомости.
Заключение. Исследовано влияние пружинно-струнной подвески при модальных испытаниях балки с ультранизкими частотами упругих колебаний. Предложена оптимальная система подвески, применение которой на порядок снижает погрешности экспериментального определения собственных частот и форм упругих колебаний балки в условиях невесомости по сравнению с традиционной подвеской. При этом частота упругих колебаний балки на системе подвески может быть в несколько раз выше частоты низшей формы упругих колебаний балки в условиях невесомости.
Список литературы
Баничук Н.В., Карпов И.И., Климов Д.М., Маркеев А.П., Соколов Б.Н., Шаранюк А.В. Механика больших космических конструкций. М.: Изд-во “Факториал”, 1997. 302 с.
Geradin M., Rixen D.J. Mechanical vibrations: theory and application to structural dynamics. Third edition. John Willey & Sons Ltd, 2015. 598 p.
Ewins D.J. Modal Testing: Theory, Practice and Applications. Second Edition. Baldock, Hertfordshire, England: Research Studies Press LTD, 2000. 562 p.
Межин В.С., Обухов В.В. Практика применения модальных испытаний для целей верификации конечно-элементных моделей конструкции изделий ракетно-космической техники // Косм. техн. технол. 2014. № 1 (4). С. 86–91.
Микишев Г.Н. Экспериментальные методы в динамике космических аппаратов. М.: Машиностроение, 1978. 247 с.
Дрыжак В.Б., Верхогляд А.Г., Емельянов Э.Л., Макаров С.Н., Маринин Д.А., Матюха Н.В. Способ обезвешивания и возбуждения колебаний при модальных испытаниях и устройство для его осуществления. Патент RU 2 677 942 C2. Опубликовано: 22.01.2019. Бюл. № 3.
Агашкин С.В., Баданина Ю.О., Башкарев В.С., Дроздов А.А., Ушаков А.Р. Автоматизированная система компенсации весовой составляющей для испытаний крупногабаритных трансформируемых антенн космических аппаратов // Косм. техн. технол. 2019. № 1 (24). С. 84–94.
Вибрации в технике. Справочник в 6-ти томах. Том 1. Колебания линейных систем / Под ред. В.В. Болотина. М.: Машиностроение, 1978. 352 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела


