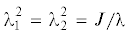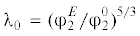Известия РАН. Механика твердого тела, 2022, № 2, стр. 106-123

1. Введение. Полимерные гели – это сетчатые полимеры, содержащие жидкость (растворитель) и находящиеся в высокоэластичном состоянии [1]. В рамках механики сплошных сред их естественной моделью является смесь, представляющая собой упругий материал и растворенную в нем жидкость. К смесям такого рода также относятся многие пластифицированные полимеры и, в частности, набухшие в растворителе эластомеры.

Растворенная в материале жидкость оказывает существенное влияние на его упругие свойства и деформационное поведение. В частности, механические нагрузки могут вызывать миграцию и перераспределение жидкости внутри материала. При этом, достаточно большие сжимающие нагрузки могут выдавливать часть жидкости из материала во внешнюю среду. В свою очередь, если гель находится в среде растворителя, то растягивающие нагрузки приводят к дополнительному поглощению жидкости из внешней среды, что вызывает частичную релаксацию внутренних напряжений. Однако если растяжение геля осуществляется в атмосфере, то поглощение жидкости из внешней среды исключено.

Таким образом, условия массообмена с внешней средой могут существенно влиять на деформационное поведение полимерных гелей, и это влияние должно учитываться при теоретическом описании таких явлений.

Данная работа посвящена формулировке краевых задач, описывающих напряженно-деформированное состояние полимерных гелей, находящихся в состоянии термодинамического равновесия. Такие состояния возникают при статическом нагружении гелей после завершения диффузионных процессов, связанных с перераспределением растворителя внутри материала и массообменом с внешней средой. Основное внимание сосредоточено на задачах, описывающих деформирование геля в атмосфере. Показано, что условия массообмена с внешней средой в этом случае естественным образом формулируются как односторонние ограничения (связи) в форме неравенств. Эти неравенства, с одной стороны, отражают тот факт, что поглощение жидкости из внешней среды отсутствует, а с другой – дают критерий, при выполнении которого происходит выделение жидкости из полимера во внешнюю среду.

Благодаря свойству поглощать и удерживать в себе большие объемы жидкости полимерные гели находят применение в медицине и фармакологии, в биотехнологии, в технологиях разделения жидких смесей и во многих других современных технологиях [2–12]. При этом, деформационные свойства полимерных гелей и описанные выше явления в них могут играть важную роль.

Для успешной разработки и совершенствования технологических режимов и процессов, связанных с применением полимерных гелей и пластифицированных полимеров, необходимо понимать основные закономерности их деформационного поведения в различных средах и при различных условиях массообмена с внешней средой. Очевидно, что для этого необходимо иметь достаточно адекватную теоретическую модель указанных явлений.

Одна из первых успешных теорий, позволяющих описать равновесное набухание сетчатых полимеров в растворителях, была построена П. Флори и Дж. Ренером [13]. В частности, она позволила установить наличие деформационной зависимости равновесной степени набухания полимера при его одноосном растяжении в среде растворителе.

Описание произвольного сложно-напряженного состояния материала, содержащего жидкость, оказалось весьма нетривиальной задачей. В настоящее время наиболее общий подход к ее решению развивается в рамках теории смесей [14], основы которой заложены Трусделлом [15]. Теория Трусделла хорошо приспособлена для описания свойств гетерогенных сред, например, насыщенных жидкостью пористых материалов. Однако ее применение к растворам приводит к значительным трудностям, основная причина которых заключается в использовании нетрадиционных параметров состояния системы – парциальных тензоров напряжений, характеризующих механические напряжения, действующие в каждом из компонентов смеси, и внутренних сил, учитывающих взаимодействие между компонентами. По существу, для применения теории смесей Трусделла к растворам (в частности, к полимерным растворам), требуется разработать особый вариант механики и термодинамики, в котором текущее состояние смеси должно описываться в терминах этих парциальных величин. Это приводит к значительным трудностям, связанным с постановкой граничных условий, характеризующих механическое нагружение материала и его взаимодействие с внешней средой [14].

В [16] показано, что используя подход Трусделла в качестве отправной точки, теорию смесей можно сформулировать в терминах глобального тензора напряжений и химического потенциала растворителя. Это делает ее более прозрачной как с точки зрения механики деформируемого твердого тела, так и термодинамики растворов и позволяет избежать многих трудностей, присущих теории смесей.

Применение предложенной в [16] теории к полимерам, позволило описать неравновесные процессы их набухания в растворителях, в частности, объяснить так называемые аномалии кинетических кривых набухания и предложить новые экспериментальные методы исследования термодинамических и диффузионных свойств сетчатых полимеров [16–19]. Показано, что в качестве частных случаев из нее вытекают уравнения, описывающие состояние смеси в условиях термодинамического и механического равновесия. Эти же уравнения, как показано в [20], можно вывести из условия минимума свободной энергии смеси, который является следствием законов классической термодинамики равновесных процессов. В этих же работах сформулированы основные типы краевых задач, описывающих напряженно-деформированное состояние набухшего в растворителе упругого материала в условиях механического и термодинамического равновесия при конечных деформациях [20] и в приближении малых деформаций [21]. С физической точки зрения предложенный вариационный подход еще более сближает данную теорию как с термодинамикой растворов, так и с механикой деформируемого твердого тела.

2. Постановка задачи. Рассмотрим набухший в растворителе образец полимерного геля в ненагруженном состоянии и находящийся в атмосфере. Будем полагать, что это состояние является равновесным и растворитель в полимере распределен равномерно. Исходная концентрация растворителя в геле, вообще говоря, может не совпадать с предельным значением, которое достигается при набухании геля в жидкости до полного равновесия. Гель будем считать химически инертным, однородным и изотропным материалом, а растворитель – нелетучей жидкостью. Последнее обстоятельство позволяет пренебречь эффектами, связанными с испарением растворителя, и делает общее количество растворителя ${{\mathcal{N}}_{1}}$ в системе (измеряемое в молях) сохраняющейся величиной.

Исходное (однородное и ненагруженное) состояние геля будем использовать как отсчетное. Пусть ${{\Omega }^{0}}$ – ограниченная область пространства, которую занимает гель в отсчетной конфигурации. Материальную систему координат свяжем с полимерной матрицей геля. Положение материальных частиц полимерной матрицы в отсчетной конфигурации ${{\Omega }^{0}}$ будем задавать радиус-вектором r, а их положение в деформированной конфигурации $\Omega $ – радиус-вектором ${\mathbf{R}}({\mathbf{r}})$.

Под действием приложенных статических нагрузок гель деформируется. При этом, в зависимости от характера действующих нагрузок и исходной концентрации растворителя в геле, часть растворителя может быть выдавлена из полимера во внешнюю среду, а оставшаяся часть неоднородным образом перераспределиться в объеме полимера. Такое перераспределение растворителя происходит в результате диффузионного процесса [16, 17]. Однако в случае статических нагрузок с течением времени диффузионный процесс завершается, и вся система переходит в состояние термодинамического равновесия.

Рассмотрим условия механического нагружения геля. Будем полагать, что положение части границы геля $\Gamma _{0}^{0}$ в деформированном состоянии задано и имеет конфигурацию ${{\Gamma }_{0}}$. Эта конфигурация задается функцией ${\mathbf{R}} = {{{\mathbf{R}}}_{0}}({\mathbf{r}})$, которая отображает $\Gamma _{0}^{0}$ на ${{\Gamma }_{0}}$. На остальной части границы $\Gamma _{1}^{0} = \partial {{\Omega }^{0}}{{\backslash }}\Gamma _{0}^{0}$ действуют поверхностные силы с плотностью ${{{\mathbf{g}}}^{0}}({\mathbf{r}})$. Поверхностные силы будем считать замороженными нагрузками [22, 23]. В деформированной конфигурации плотность поверхностных сил описывает функция ${\mathbf{g}}({\mathbf{R}})$. Она определена на ${{\Gamma }_{1}}$ – деформированной конфигурации границы $\Gamma _{1}^{0}$. Плотности ${\mathbf{g}}$ и ${{{\mathbf{g}}}^{0}}$ связаны соотношением ${{{\mathbf{g}}}^{0}}({\mathbf{r}})d{{S}^{0}} = {\mathbf{g}}({\mathbf{R}}({\mathbf{r}}))dS$, где $d{{S}^{0}}$ и $dS$ – элементы площади в отсчетной и деформированной конфигурациях соответственно.

Также будем считать, что давление внешней среды имеет фиксированное значение и не меняется в процессе деформирования геля. Постоянной является и температура всей системы, то есть деформирование геля осуществляется в изотермических условиях.

Для описания деформированного состояния геля будем использовать градиент места ${\mathbf{F}} = \mathop \nabla \limits^ \circ {\mathbf{R}}({\mathbf{r}})$, где $\mathop \nabla \limits^ \circ $ – набла-оператор, действующий в отсчетной конфигурации. (Здесь и далее используется система представления тензорных соотношений, принятая в [22]). Третий инвариант градиента места $J = \det {\mathbf{F}}$ описывает объемные деформации геля. В частности, с его помощью устанавливается связь между элементами объемов в деформированной dV и отсчетной $d{{V}^{0}}$ конфигурациях геля: $dV = Jd{{V}^{0}}$.

Компонентный состав геля характеризуют ${{N}_{1}}$ и ${{N}_{2}}$ – мольные плотности (концентрации) растворителя и вещества полимерной матрицы соответственно, отнесенные к единичному объему отсчетной конфигурации. В деформированном состоянии распределение растворителя в геле может быть неоднородным, и его концентрация является функцией ${{N}_{1}} = {{N}_{1}}({\mathbf{r}})$. Что касается концентрации вещества полимерной матрицы ${{N}_{2}}$, то эта величина от материальных координат не зависит и имеет одно и то же значение как в отсчетной, так и в деформированной конфигурациях, то есть является константой:

Это следует из однородности исходного состояния геля и из закона сохранения вещества полимерной матрицы.

Наша цель состоит в том, чтобы описать напряженно-деформированное состояние геля в состоянии термодинамического равновесия. В частности, требуется выяснить, при каких условиях произойдет выделение растворителя из геля во внешнюю среду, какое количество растворителя выделится из образца и каким образом оставшийся в геле растворитель распределится в его объеме. Ответы на эти вопросы можно получить из решения соответствующих уравнений, которые далее выводятся из основных принципов термодинамики.

3. Уравнения равновесия геля. При макроскопическом подходе гель, растворитель и приложенные нагрузки представляет собой термодинамическую систему. В состоянии термодинамического равновесия ее свободная энергия достигает минимального значения:

Здесь $f({\mathbf{F}},{{N}_{1}},{{N}_{2}})$ – плотность свободной энергии геля, отнесенная к единичному объему отсчетной конфигурации; ${{\mathcal{N}}_{1}}$ – исходное количество молей растворителя в геле; ${{{{\mu }}}_{L}}$ – химический потенциал жидкой фазы чистого растворителя, который является константой, поскольку давление внешней среды постоянно, а деформирование геля осуществляется в изотермических условиях.

Первое слагаемое в выражении (3.1) – это свободная энергия геля, второе – свободная энергия выделившейся из геля жидкости, и последнее слагаемое – потенциальная энергия поверхностных сил. Действующее в геле давление здесь отсчитывается от давления внешней среды, и это учтено в выражении свободной энергии (3.1).

Величина, стоящая в скобках второго слагаемого левой части выражения (3.1), равна количеству выдавленного из геля растворителя. Поскольку количество растворителя ${{\mathcal{N}}_{1}}$ в системе фиксировано, и в исходном состоянии он весь содержался в геле, то количество выделившегося из геля растворителя должно удовлетворять очевидному неравенству

Таким образом, задача о термодинамическом равновесии геля сводится к задаче минимизации функционала свободной энергии (3.1) с односторонним ограничением (3.2) в форме неравенства. Она заключается в поиске таких функций ${\mathbf{R}}({\mathbf{r}})$ и ${{N}_{1}}({\mathbf{r}})$, которые удовлетворяют условиям ${\mathbf{R}}({\mathbf{r}}) = {{{\mathbf{R}}}_{0}}({\mathbf{r}})$ на $\Gamma _{0}^{0}$, (3.2) и доставляют минимум функционала (3.1). Допустим, что она имеет решение. Также предположим, что это решение и все исходные данные обладают достаточной гладкостью. Опираясь на эти допущения и используя метод множителей Лагранжа, выведем соответствующие уравнения Эйлера–Лагранжа, описывающие состояние термодинамического равновесия геля. Для этого левую часть неравенства (3.2) умножим на ${{{{\mu }}}_{*}} - {{{{\mu }}}_{L}}$ (лагранжев множитель) и полученное выражение прибавим к левой части (3.1). В результате получим функционал Лагранжа

Лагранжев множитель здесь удобно представлять в виде ${{\mu }}_{*}^{{}} - {{{{\mu }}}_{L}}$, поскольку новая неизвестная ${{\mu }}_{*}^{{}}$, как показано ниже, имеет простой физический смысл. Она равна химическому потенциалу растворителя в геле, находящемся в состоянии термодинамического равновесия.

Предположим, что найдется такое значение ${{\mu }}_{*}^{{}}$, что решение исходной задачи (3.1), (3.2) доставляет минимум функционала (3.3). При этом, согласно методу Лагранжа, величина ${{{{\mu }}}_{*}}$ должна удовлетворять дополнительным условиям

Таким образом, исходная задача минимизации с ограничениями сведена к задаче безусловной минимизации. Необходимое условие минимума функционала (3.3) заключается в обращении в нуль его первой вариации:

Здесь $\delta {{N}_{1}}({\mathbf{r}})$, $\delta {\mathbf{R}}({\mathbf{r}})$, $\delta {\mathbf{F}} = \mathop \nabla \limits^{^{ \circ }} \delta {\mathbf{R}}({\mathbf{r}})$ – вариации концентрации растворителя, векторного поля ${\mathbf{R}}({\mathbf{r}})$ и градиента места соответственно. Вариация $\delta {\mathbf{R}}$ должна удовлетворять условию $\delta {\mathbf{R}}({\mathbf{r}}) = 0$ на $\Gamma _{0}^{0}$. Соотношения (3.7) являются естественным обобщением известных в механике [22, 23] и в термодинамике [24] выражений для тензора напряжений Пиолы ${\mathbf{P}}$ и химического потенциала ${{\mu }}$.

Уравнение (3.6) – это уравнение Эйлера–Лагранжа, представленное в вариационной форме и описывающее состояние термодинамического равновесия геля. Применив интегрирование по частям и теорему Остроградского–Гаусса, из него получим (с учетом (3.4) и (3.5)) следующую краевую задачу:

где n⁰ – вектор внешней нормали в отсчетной конфигурации. Ее решение заключается в поиске функций ${\mathbf{R}}({\mathbf{r}})$, ${{N}_{1}}({\mathbf{r}})$ и неизвестной константы ${{\mu }}_{*}^{{}}$, которые обращают систему уравнений и граничных условий (3.8)–(3.13) в тождества. К исходным данным относятся функции ${{{\mathbf{R}}}_{0}}({\mathbf{r}})$, ${{{\mathbf{g}}}^{0}}({\mathbf{r}})$, константы ${{{{\mu }}}_{L}}$, ${{\mathcal{N}}_{1}}$, ${{N}_{2}}$, а также определяющие соотношения для тензора напряжений ${\mathbf{P}}$ и химического потенциала ${{\mu }}$, которые можно получить, воспользовавшись формулами (3.7).

Задача (3.8)–(3.13) имеет простую физическую интерпретацию. Первое из уравнений (3.8) – это условие механического равновесия геля, второе уравнение – условие термодинамического равновесия, которое означает, что в каждой точке геля химический потенциал растворителя должен иметь одно и то же значение ${{{{\mu }}}_{*}}$, которое неизвестно и должно определяться в процессе решения задачи. Физический смысл (3.9) и (3.10) очевиден – они задают условия механического нагружения геля. Неравенство (3.11) уже обсуждалось выше. Соотношения (3.12) и (3.13) описывают условия, при которых происходит выделение части растворителя из геля во внешнюю среду. В частности, неравенство (3.13) выражает известный в термодинамике факт, что химический потенциал растворенного в смеси вещества в состоянии равновесия не может превосходить величину химического потенциала этого же вещества, находящегося в чистом состоянии. Нарушение этого неравенства означает отсутствие термодинамического равновесия, что приводит к самопроизвольному разделению смеси. Из уравнения (3.12) следует, что если имеет место строгое неравенство ${{\mu }}_{*}^{{}} < {{{{\mu }}}_{L}}$, то весь растворитель остается в геле. Но как только достигается равенство ${{\mu }}_{*}^{{}} = {{{{\mu }}}_{L}}$, что возможно при достаточно больших сжимающих нагрузках, растворитель начинает выделяться во внешнюю среду. При дальнейшем сжатии геля равенство ${{\mu }}_{*}^{{}} = {{{{\mu }}}_{L}}$ остается в силе, а неравенство (3.11) становится строгим, что означает выделение растворителя из геля во внешнюю среду.

Задача (3.8)–(3.13) описывает состояние равновесия геля в отсчетной конфигурации. В деформированной конфигурации она имеет следующий вид:

где n – вектор внешней нормали в деформированной конфигурации; T – тензор напряжений Коши; ${{n}_{a}} = {{J}^{{ - 1}}}{{N}_{a}}$ (a = 1, 2) – концентрации компонентов геля, отнесенные к единичному объему деформированной конфигурации; $\nabla $ – набла-оператор, действующий в деформированной конфигурации. Переход от уравнения механического равновесия (3.8) к уравнению в форме (3.14) осуществляется путем применения тождества Пиолы $\mathop \nabla \limits^{^{ \circ }} \, \cdot (J{{{\mathbf{F}}}^{{ - T}}}) = 0$ и соотношения $\nabla = {{{\mathbf{F}}}^{{ - 1}}} \cdot \mathop \nabla \limits^{^{ \circ }} $ [22]. Тензор напряжений Коши связан с тензором напряжений Пиолы известным соотношением [22]

Рассмотренную выше задачу интересно сравнить с задачей о равновесии геля, деформирование которого осуществляется в среде растворителя. Соответствующие уравнения равновесия в этом случае можно получить в рамках изложенного выше подхода, путем его незначительной модификации. Будем считать, что условия механического нагружения геля остаются прежними. В качестве отсчетного выберем произвольное равновесное состояние геля с однородным распределением растворителя. Общее количество растворителя в системе ${{\mathcal{N}}_{1}}$ будем считать достаточно большой константой, так что всегда выполняется строгое неравенство

Это означает, что во внешней среде всегда присутствует растворитель. Ограничение, что растворитель нелетучий, здесь снимается, и полагается, что образец может находиться как в жидкости, так и в парах растворителя. Пусть ${{{{\mu }}}_{0}}$ – заданная константа, равная химическому потенциалу растворителя во внешней среде. Отметим, что в общем случае ${{{{\mu }}}_{0}} \leqslant {{{{\mu }}}_{L}}$, а равенство ${{{{\mu }}}_{0}} = {{{{\mu }}}_{L}}$ достигается, если гель находится в жидком растворителе или в его насыщенных парах.

Далее, используя те же рассуждения, приходим к задаче минимизации вида (3.1), но уже без ограничений. Соответствующий функционал в ней отличается от (3.1) тем, что вместо ${{{{\mu }}}_{L}}$ в нем фигурирует ${{{{\mu }}}_{0}}$. Поскольку ${{{{\mu }}}_{0}}$ и ${{\mathcal{N}}_{1}}$ являются константами, слагаемое ${{{{\mu }}}_{0}}{{\mathcal{N}}_{1}}$ не влияет на положение минимума функционала (3.1) и его можно опустить. В результате задача минимизации, описывающая состояние термодинамического равновесия геля в среде растворителя приобретает вид

Отсюда получаем уравнения Эйлера–Лагранжа, описывающие состояние равновесия геля в отсчетной конфигурации

и в деформированной конфигурации

Тензор напряжений Пиолы P, химический потенциал растворителя в геле ${{\mu }}$ и тензор напряжений Коши T определяются соотношениями (3.7) и (3.20) соответственно.

4. Приближение несжимаемой смеси. Смесь назовем несжимаемой, если ее объем не зависит от внешних механических нагрузок, в частности, от давления, однако он зависит от компонентного состава и от температуры. В приближении несжимаемой смеси объем полимерного геля является функцией вида

где ${{\mathcal{N}}_{1}}$, ${{\mathcal{N}}_{2}}$ – количество молей растворителя и полимера соответственно. (Поскольку рассматриваются изотермические режимы деформирования, то температурная зависимость здесь опущена). Объем – экстенсивная величина, поэтому $\bar {V}({{\mathcal{N}}_{1}},{{\mathcal{N}}_{2}})$ – однородная функция первого порядка и может быть представлена в виде [24] где ${{\bar {V}}_{a}} = \partial{ \bar {V}}{\text{/}}\partial {{\mathcal{N}}_{a}}$ (a = 1, 2) – парциальные мольные объемы компонентов смеси, которые являются однородными функциями нулевого порядка относительно переменных ${{\mathcal{N}}_{1}}$ и ${{\mathcal{N}}_{2}}$.

Условие несжимаемости (4.1) представим в локальном виде. Для этого поделим обе части равенства (4.1) на V  ⁰ – объем геля в отсчетном состоянии. Левая часть полученного равенства $V{\text{/}}{{V}^{0}} = J = \det {\mathbf{F}}$, а отношение ${v} = \bar {V}({{\mathcal{N}}_{1}},{{\mathcal{N}}_{2}}){\text{/}}{{V}^{0}}$ в его правой части, используя свойство однородности $\bar {V}({{\mathcal{N}}_{1}},{{\mathcal{N}}_{2}})$, можно представить как функцию концентраций компонентов: ${v} = \bar {V}({{\mathcal{N}}_{1}},{{\mathcal{N}}_{2}}){\text{/}}{{V}^{0}} = \bar {V}({{\mathcal{N}}_{1}}{\text{/}}{{V}^{0}},{{\mathcal{N}}_{2}}{\text{/}}{{V}^{0}}) = \bar {V}({{N}_{1}},{{N}_{2}})$. Отсюда и из равенства (4.2) следует, что

Окончательно условие несжимаемости геля запишем в виде

Из него следует, что вариации деформации геля и концентрации растворителя связаны соотношением

Здесь использованы соотношения (2.1), (4.4) и известная формула производной [22] $\partial J{\text{/}}\partial {\mathbf{F}} = J{{{\mathbf{F}}}^{{ - T}}}$.

Таким образом, если гель рассматривается как несжимаемая смесь, то задача минимизации функционала (3.1) с ограничением (3.2) должна включать дополнительное ограничение (4.5), и функционал Лагранжа (3.3) заменяется на

где лагранжев множитель p имеет смысл гидростатического давления. Используя (4.6), вариационное уравнение Эйлера–Лагранжа представим в виде, аналогичном (3.6): где тензор напряжений Пиолы P и химический потенциал растворителя в геле ${{\mu }}$ определяются соотношениями

Из вариационного уравнения получаем следующую краевую задачу:

В отличие от задачи (3.8)–(3.13), здесь появляется дополнительное уравнение связи (4.13), два новых уравнения состояния геля ${v}({{N}_{1}},{{N}_{2}})$, ${{\bar {V}}_{1}} = \partial {v}{\text{/}}\partial {{N}_{1}}$ и новая неизвестная функция $p({\mathbf{r}})$. Еще одно отличие состоит в том, что тензор напряжений Пиолы и химический потенциал растворителя (4.9) уже не являются функциями состояния геля, поскольку содержат гидростатическое давление, являющееся лагранжевым множителем.

В деформированной конфигурации задача (4.10)–(4.16) приобретает следующий вид:

где ${\mathbf{T}}$ – тензор напряжений Коши; ${\mathbf{E}}$ – единичный тензор.

Если деформирование геля осуществляется в среде растворителя, то его термодинамически равновесное состояние определяется из решения задачи минимизации (3.22) с ограничением (4.5). Соответствующий функционал Лагранжа

С его помощью получаем уравнения Эйлера–Лагранжа, описывающие состояние равновесия геля в отсчетной конфигурации

и в деформированной конфигурации

Тензор напряжений Пиолы ${\mathbf{P}}$, химический потенциал растворителя в геле ${{\mu }}$ и тензор напряжений Коши ${\mathbf{T}}$ определяются соотношениями (4.9) и (4.24) соответственно.

5. Несжимаемая, аддитивная смесь. Полимерные гели обычно рассматривают в приближении несжимаемой, аддитивной смеси. Несжимаемая смесь называется аддитивной, если ее объем равен сумме объемов ее компонентов. Парциальные мольные объемы компонентов аддитивной смеси ${{\bar {V}}_{1}}$ и ${{\bar {V}}_{2}}$ являются константами, которые равны мольным объемам чистых компонентов. Тогда, согласно равенству (4.3), величина ${v}$ является линейной функцией мольных концентраций, и условие несжимаемости приобретает вид

Компонентный состав геля в приближении несжимаемой аддитивной смеси удобно характеризовать с помощью объемных долей компонентов:

${{{{\varphi }}}_{1}}$, ${{{{\varphi }}}_{2}}$ – объемные доли растворителя и полимера соответственно. Из соотношений (5.1)–(5.3) следует, что где ${{\varphi }}_{2}^{0} = {{\bar {V}}_{2}}{{N}_{2}}$ – константа, равная объемной доли полимера в отсчетном состоянии.

Равенства (5.4) означают, что распределение растворителя в геле (в приближении несжимаемой аддитивной смеси) можно описывать в терминах объемных деформаций $J$. В частности, с помощью второго равенства (5.4) количество выделившейся из геля жидкости можно выразить через изменение объема геля:

где V⁰ – объем геля в отсчетном (исходном) состоянии; ${{\bar {V}}_{1}}{{\mathcal{N}}_{1}} = (1 - {{\varphi }}_{2}^{0}){{V}^{0}}$ – исходный объем растворителя в геле; $V = \int\limits_{{{\Omega }^{0}}} {Jd{{V}^{0}}} $ – объем геля в деформированном состоянии.

Далее, используя выражение химического потенциала (4.9), уравнение термодинамического равновесия ${{\mu }} = {{\mu }}_{*}^{{}}$ запишем в виде $\partial f{\text{/}}\partial {{N}_{1}} + {{\bar {V}}_{1}}p = {{\mu }}_{*}^{{}}$. Отсюда выразим гидростатическое давление и запишем его так:

Выражение (5.6) подставим в соотношение (4.24). В результате тензор напряжений Коши примет вид

В термодинамике растворов $\pi $ называется осмотическим давлением [24]. По аналогии тензор (5.10) назовем осмотическим тензором напряжений Коши. В отличие от тензора напряжений (4.24), согласно выражениям (5.7) и (5.10), он является функцией состояния геля. Более того, его зависимость от концентрации растворителя с помощью (5.4) можно выразить в терминах $J = \det {\mathbf{F}}$, и осмотический тензор напряжений будет иметь такую же структуру, как и тензор напряжений сжимаемого материала в нелинейной теории упругости.

Используя соотношения (5.5)–(5.10), задачу о термодинамическом равновесии геля (4.17)–(4.24) в деформированной конфигурации представим следующим образом:

В ней требуется найти функцию ${\mathbf{R}}({\mathbf{r}})$, определяющую равновесную деформированную конфигурацию геля и равновесное значение ${{\pi }}_{*}^{{}}$ осмотического давления. Текущее распределение растворителя в геле, а также количество растворителя, выделившегося во внешнюю среду можно рассчитать с помощью соотношений (5.4). Внутренние механические напряжения в геле определяются равенством (5.9).

Можно заметить, что уравнение равновесия (5.11), граничные условия (5.12), (5.13), а также структура тензора ${\mathbf{\Pi }}$, аналогичны соответствующим уравнениям и граничным условиям, используемым в статических задачах нелинейной теории упругости сжимаемого материала. Отличие от стандартных задач теории упругости заключается в том, что “внешнее давление” ${{\pi }}_{*}^{{}}$ неизвестно и заданы дополнительные ограничения (5.14)–(5.16). С точки зрения обычной механики их можно интерпретировать следующим образом. При растягивающих нагрузках и при достаточно малых сжимающих нагрузках объем геля остается постоянным. Неизменность объема обеспечивает давление ${{\pi }}_{*}^{{}}$, компенсирующее ту часть нагрузок, которые способны вызвать изменение объема геля. То есть глобально гель ведет себя как несжимаемый материал, однако локально он проявляет свойства сжимаемого материала, поскольку растворитель внутри него может существенным образом перераспределяться, порождая локальные объемные деформации. Объем геля сохраняется, пока давление ${{\pi }}_{*}^{{}}$ строго больше предельного значения ${{{{\pi }}}_{L}}$ – осмотического давления жидкой фазы растворителя. Если достигается равенство ${{\pi }}_{*}^{{}} = {{{{\pi }}}_{L}}$ (это возможно при достаточно больших сжимающих нагрузках), объем геля начинает уменьшаться за счет выделения растворителя во внешнюю среду. При дальнейшем росте сжимающих нагрузок равенство ${{\pi }}_{*}^{{}} = {{{{\pi }}}_{L}}$ сохраняется, а неравенство (5.14) становится строгим, что означает дальнейшее сжатие геля.

В отсчетной конфигурации задача (5.11)–(5.16) имеет следующий вид:

Осмотический тензор напряжений Пиолы ${{{\mathbf{\Pi }}}^{0}}$ определяется равенством

Если деформирование геля осуществляется в среде растворителя с заданным (фиксированным) значением химического потенциала ${{{{\mu }}}_{0}}$, то состояние термодинамического равновесия геля определяется из решения следующей задачи:

где ${{{{\pi }}}_{0}} = - \bar {V}_{1}^{{ - 1}}{{{{\mu }}}_{0}}$ – осмотическое давление растворителя внешней среды. Осмотический тензор напряжений по-прежнему задается соотношением (5.10), а тензор напряжений Коши

Из сравнения задач (5.11)–(5.16) и (5.24)–(5.27) нетрудно видеть, что вторая задача получается из первой, если снять ограничения (5.14)–(5.16) и в соответствующих соотношениях заменить неизвестную величину ${{\pi }}_{*}^{{}}$ на заданную константу ${{{{\pi }}}_{0}}$. С физической точки зрения такая замена объясняется тем, что в состоянии термодинамического равновесия химический потенциал растворителя в геле должен быть постоянным и равным химическому потенциалу растворителя внешней среды. Снятие ограничений (5.14)–(5.16) означает, что возможно не только выделение растворителя из геля, но и его поглощение гелем из внешней среды. При этом здесь достигается полная аналогия со статическими задачами теории упругости сжимаемого материала.

6. Определяющие соотношения полимерных гелей. Одной из наиболее популярных моделей сетчатых полимеров и полимерных гелей, описывающих их свойства, является теория Флори–Ренера [13]. Согласно этой теории плотность свободной энергии геля, отнесенная к единице объема отсчетной конфигурации, дается выражением [20]

где $T$ – абсолютная температура; $R$ – универсальная газовая постоянная; ${{\chi }}$ – параметр Флори–Хаггинса; ${{N}_{1}}$ – мольная концентрация растворителя в геле; ${{N}_{2}}$ – мольная концентрация субцепей полимерной сетки. В теории Флори–Ренера гель рассматривается как несжимаемая, аддитивная смесь, поэтому все соотношения (5.1)–(5.4) здесь остаются в силе. Как и прежде ${{{{\varphi }}}_{1}}$, ${{{{\varphi }}}_{2}}$ – это объемные доли растворителя и полимера соответственно; ${{\bar {V}}_{1}}$ – мольный объем растворителя; ${{\bar {V}}_{2}}$ – средний мольный объем субцепей полимерной сетки.

Свободная энергия (6.1) зависит от деформаций. Эту зависимость характеризует величина ${{\hat {I}}_{1}}$, которая является первым инвариантом меры деформации искажения формы ${\mathbf{\hat {B}}}$:

где ${\mathbf{B}}$ – мера деформации Фингера (левая мера деформации Коши–Грина).

Применив формулы (4.9), (4.24) и (5.10) к выражению (6.1), учитывая при этом равенства (5.2) и (5.3), получим следующую систему определяющих соотношений:

Здесь ${{G}_{0}} = RT\bar {V}_{2}^{{ - 1}}{{({{\varphi }}_{2}^{0})}^{{1{\text{/}}3}}}$ – модуль сдвига полимерного геля в отсчетном состоянии; $Z = {{\bar {V}}_{2}}{\text{/}}{{\bar {V}}_{1}}$ – безразмерный параметр, величина которого для полимеров обычно удовлетворяет условию $Z \gg 1$. Поскольку в теории Флори–Ренера гель рассматривается как несжимаемая, аддитивная смесь, в систему (6.4)–(6.8) должны быть также включены соотношения (5.1)–(5.4).

Приведенные выше соотношения, в частности, позволяют описать важное для многих приложений явление свободного набухания сетчатых полимеров, то есть набухание механически ненагруженного полимера, помещенного в растворитель. В теории Флори–Ренера химический потенциал жидкой фазы чистого растворителя полагается равным нулю:

В этом случае ${\mathbf{T}} = {\mathbf{\Pi }} = 0$. Отсюда следует, что ${\mathbf{\hat {B}}} = {\mathbf{E}}$, ${{\hat {I}}_{1}} = 3$, p = 0 и соотношение (6.8) дает уравнение

которое позволяет определить ${{\varphi }}_{2}^{E}$ – предельное значение объемной доли полимера в геле, набухшем до равновесия в чистом растворителе.

7. Деформационное поведение полимерных гелей. Для иллюстрации общей теории рассмотрим деформационное поведение призматического образца полимерного геля в условиях термодинамического равновесия при одноосном растяжении и сжатии. Будем полагать, что деформирование геля производится в атмосфере. Растворитель – нелетучий, его исходная концентрация в геле не превосходит предельного (равновесного) значения, то есть выполняется неравенство

где ${{\varphi }}_{2}^{E}$ – объемная доля полимера в равновесно набухшем состоянии геля.

Образец подвергается растяжению (сжатию) в продольном направлении и испытывает деформации в поперечных направлениях. Боковая поверхность геля механическому нагружению не подвергается. Материальную систему координат в отсчетной конфигурации выберем следующим образом: оси $x$ и $y$ направим поперек образца, а ось $z$ – вдоль. При таком выборе координат меры деформации (6.2), осмотический тензор напряжений (6.8) и тензор напряжений Коши приобретают диагональный вид. В частности,

где ${{{{\lambda }}}_{k}}$ – относительные удлинения образца. В этом случае

Будем считать, что текущее (равновесное) состояние образца является однородным и, следовательно, уравнение равновесия $\nabla \cdot {\mathbf{\Pi }} = 0$ выполняется тождественно. На боковую поверхность образца внешние силы не действуют, поэтому

Отсюда следует, что ${{\lambda }_{1}} = {{\lambda }_{2}}$, а из равенства (5.4) находим

где ${{\lambda }_{3}} = \lambda $ – относительное удлинение образца в продольном направлении. Используя равенства (7.2) и (7.6), поперечные компоненты осмотического тензора напряжений запишем в виде

${{\Pi }_{{11}}} = {{\Pi }_{{22}}} = RT\bar {V}_{1}^{{ - 1}}({{Z}^{{ - 1}}}{{({{\varphi }}_{2}^{0})}^{{1{\text{/}}3}}}{{{{\lambda }}}^{{ - 1}}} + \ln (1 - {{{{\varphi }}}_{2}}) + {{{{\varphi }}}_{2}} + {{\chi \varphi }}_{2}^{2})$

С помощью равенств (7.2)–(7.6) находим упругую реакцию образца

где $P = {{P}_{{33}}} = {{{{\lambda }}}^{{ - 1}}}J{{T}_{{33}}}$ – продольная компонента тензора напряжений Пиолы; G₀ = = $RT\bar {V}_{2}^{{ - 1}}{{({{\varphi }}_{2}^{0})}^{{1{\text{/}}3}}}$ – модуль сдвига полимерного геля в отсчетном состоянии.

Соотношение (7.7) представляет собой условие термодинамического равновесия геля в деформированном состоянии. Из него следует, что поперечные компоненты осмотического тензора напряжений не могут превышать нулевого значения. Это вытекает из ранее полученного ограничения ${{\pi }}_{*}^{{}} \geqslant 0$. При этом, если ${{\pi }}_{*}^{{}} > 0$, то есть левая часть выражения (7.7) строго меньше нуля, то исходное количество растворителя в образце сохраняется. В этом случае J = 1 и ${{{{\varphi }}}_{2}} = {{\varphi }}_{2}^{0}$, и упругая реакция образца, согласно (7.8), описывается классической формулой высокоэластичности

Такой режим деформирования геля справедлив при достаточно больших значениях ${{\lambda }}$, в частности, при растяжении образца. Это непосредственно вытекает из соотношений (6.10), (7.1) и (7.7).

Уменьшение величины ${{\lambda }}$ (при фиксированном значении ${{{{\varphi }}}_{2}} = {{\varphi }}_{2}^{0}$) вызывает рост левой части (7.7) и обращение ее в нуль при достижении ${{\lambda }}$ критического значения

При ${{\lambda }} < {{{{\lambda }}}_{0}}$, то есть при дальнейшем сжатии геля, осмотическое давление растворителя в геле ${{{{\pi }}}_{*}}$ должно оставаться равным нулю, то есть осмотическому давлению жидкой фазы растворителя. В этом случае происходит выдавливание растворителя из образца. Приравняв левую часть (7.7) нулю, получим уравнение

которое описывает деформационную зависимость равновесной концентрации растворителя в образце при ${{\lambda }} < {{{{\lambda }}}_{0}}$. Определив из него ${{{{\varphi }}}_{2}}$ и $J = {{\varphi }}_{2}^{0}{\text{/}}{{{{\varphi }}}_{2}}$, упругую реакцию образца можно рассчитать по формуле (7.8).

В общем случае уравнение (7.11) можно решить только численно. Однако легко построить его приближенное решение при ${{{{\varphi }}}_{2}} \ll 1$. Такое условие обычно реализуется при набухании гелей в хороших растворителях, для которых параметр Флори–Хаггинса ${{\chi }} < 1{\text{/}}2$. Если ${{{{\varphi }}}_{2}} \ll 1$, то можно воспользоваться разложением

С его помощью из уравнений (7.10) и (7.11) с точность до членов второго порядка получим

и ${{{{\lambda }}}_{0}} = {{\left[ {Z\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {{\chi }}} \right)} \right]}^{{ - 1}}}{{({{\varphi }}_{2}^{0})}^{{ - 5{\text{/}}3}}}$. С той же точностью из уравнения (6.10) находим, что ${{\left[ {Z\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {{\chi }}} \right)} \right]}^{{ - 1}}} = {{({{\varphi }}_{2}^{E})}^{{5{\text{/}}3}}}$. Из последних двух равенств имеем приближенную формулу которая позволяет оценить критическое значение λ₀ по непосредственно измеримым характеристикам образца. Она справедлива при условии ${{\varphi }}_{2}^{E} \leqslant {{\varphi }}_{2}^{0} \ll 1$.

Задача об одноосном деформировании геля, помещенного в растворитель, формулируется аналогичным образом. Отличие заключается в следующем. В качестве отсчетного удобно использовать состояние ненагруженного образца, набухшего до равновесия в растворителе. В этом случае ${{\varphi }}_{2}^{0} = {{\varphi }}_{2}^{E}$ и ${{{{\varphi }}}_{2}} = {{\varphi }}_{2}^{E}{\text{/}}J$. В условиях термодинамического равновесия химический потенциал растворителя в геле равен химическому потенциалу чистого растворителя, то есть ${{\pi }}_{*}^{{}} = 0$, и это следует учесть в формулах (7.3) и (7.7). Уравнение (7.11) приобретает вид

где ${{{{\varphi }}}_{2}} = {{\varphi }}_{2}^{E}{\text{/}}J$. Оно описывает деформационную зависимость $J(\lambda )$ как при растяжении, так и при сжатии геля. Упругую реакцию образца при всех ${{\lambda }}$ описывает формула (7.8). При ${{{{\varphi }}}_{2}} \ll 1$ можно воспользоваться разложением (7.12) и получить приближенное решение уравнения (7.15): $J = {{{{\lambda }}}^{{1{\text{/}}2}}}$.

При экспериментальном изучении рассмотренных выше равновесных режимов деформирования геля важно иметь в виду следующие обстоятельства. Если растяжение образца осуществляется в атмосфере и ${{\lambda }} > {{{{\lambda }}}_{0}}$, то количество растворителя в образце сохраняется, и при достаточно медленном (квазистатическом) растяжении гель остается в состоянии термодинамического равновесия. Этот участок диаграммы растяжения–сжатия можно установить в ходе непрерывного процесса деформирования образца при стандартных скоростях, используемых при механических испытаниях эластомеров и полимерных гелей.

Сжатие геля в атмосфере (при ${{\lambda }} < {{{{\lambda }}}_{0}}$) инициирует процесс выделения растворителя из образца. Этот процесс диффузионный, то есть неравновесный и весьма длительный. В ходе диффузионного процесса в образце возникают неоднородные поля концентрации растворителя, которые порождают неоднородные деформации и внутренние напряжения [16, 17]. Термодинамическое равновесие в геле (при фиксированном ${{\lambda }} < {{{{\lambda }}}_{0}}$) устанавливается после завершения диффузионного процесса. На это может понадобиться, в зависимости от размеров образца и диффузионных свойств системы полимер–растворитель, десятки и сотни часов. Если деформирование геля производится в растворителе, то большая продолжительность установления термодинамического равновесия имеет место как при сжатии, так и при растяжении образца, то есть при всех ${{\lambda }}$. Таким образом, экспериментальное изучение термодинамически равновесных режимов деформирования полимерных гелей может представлять собой весьма трудоемкую и продолжительную во времени процедуру.

7. Заключение. В работе рассмотрены термодинамически равновесные режимы деформирования полимерных гелей при различных условиях массообмена с внешней средой. Гель рассматривается как смесь, представляющая собой упругий материал и растворенную в нем жидкость (растворитель). Состояние термодинамического равновесия геля определяется из решения задачи минимизации функционала свободной энергии системы “полимер–растворитель” и потенциальной энергии приложенных сил. Рассмотрены два случая: 1) деформирование геля осуществляется в атмосфере, при этом растворитель полагается нелетучей жидкостью; 2) гель деформируется в среде растворителя с фиксированным значением химического потенциала.

Условия массообмена геля с внешней средой в каждом из этих случаев существенно различаются. При деформировании геля в атмосфере, под действием приложенных нагрузок растворитель может выделяться из геля во внешнюю среду. Количество растворителя в системе фиксировано и равно исходному количеству растворителя в ненагруженном геле. Поглощение растворителя из внешней среды исключено. Показано, что такое условие массообмена геля с внешней средой формулируется в виде одностороннего ограничения в форме неравенства. Уравнения Эйлера–Лагранжа выведены с помощью метода лагранжевых множителей. Соответствующая краевая задача сформулирована в терминах механического тензора напряжений и химического потенциала растворителя. Показано, что напряженно-деформированное состояние геля в состоянии равновесия описывается системой уравнений и граничных условий, которые имеют такой же вид, как и соответствующие уравнения равновесия теории упругости и классической термодинамики. Отличие заключается в том, что данная система содержит дополнительные соотношения, налагающие ограничения на концентрацию растворителя в геле и величину его химического потенциала. Также они описывают условия, при которых происходит выделение растворителя из геля во внешнюю среду.

Если деформирование геля происходит в среде растворителя, то режим массообмена геля с внешней средой коренным образом меняется: растворитель может как выделяться из геля, так и поглощаться гелем из внешней среды. Показано, что состояние равновесия геля, как и прежде, определяется из решения задачи минимизации функционала аналогичного вида, но без ограничений. Из нее получены уравнения Эйлера–Лагранжа и соответствующая краевая задача, из решения которой определяется равновесное состояние геля.

Рассмотрено описание геля как несжимаемой смеси. В рамках приближения несжимаемой смеси объем геля при фиксированном распределении растворителя не зависит от приложенных механических нагрузок, а объемные деформации могут возникать только за счет поглощения или выделения растворителя. В этом случае появляется дополнительное уравнение связи – условие несжимаемости смеси. Это приводит к появлению в определяющих соотношениях для тензора напряжений и химического потенциала лагранжева множителя, имеющего смысл гидростатического давления.

Рассмотрено приближение аддитивной несжимаемой смеси. Показано, что равновесное напряженно-деформированное состояние геля в этом случае может быть описано в терминах осмотического давления и осмотического тензора напряжений. Последний имеет такую же структуру, как тензор напряжений сжимаемого материала в нелинейной теории упругости. Задача о равновесном деформировании геля в среде растворителя оказывается полностью аналогичной статической задаче теории упругости для сжимаемого материала. Описание равновесных режимов деформирования геля в атмосфере приводит к задачам с односторонними ограничениями, налагаемыми на его объем.

Общая теория проиллюстрирована на примере описания деформационного поведения полимерных гелей в условиях одноосного растяжения и сжатия в среде растворителя и в атмосфере.

Рассмотренные задачи являются нетривиальными обобщениями известных статических задач нелинейной теории упругости. Они могут быть полезны при проектировании технических устройств и конструкций, основанных на применении полимерных гелей и пластифицированных полимеров. Также они могут служить теоретической основой новых экспериментальных методов исследования свойств полимерных материалов.